
Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
1
Ćwiczenie 5.
Sterowanie wahadła z nap
ędem śmigłowym
(PID)
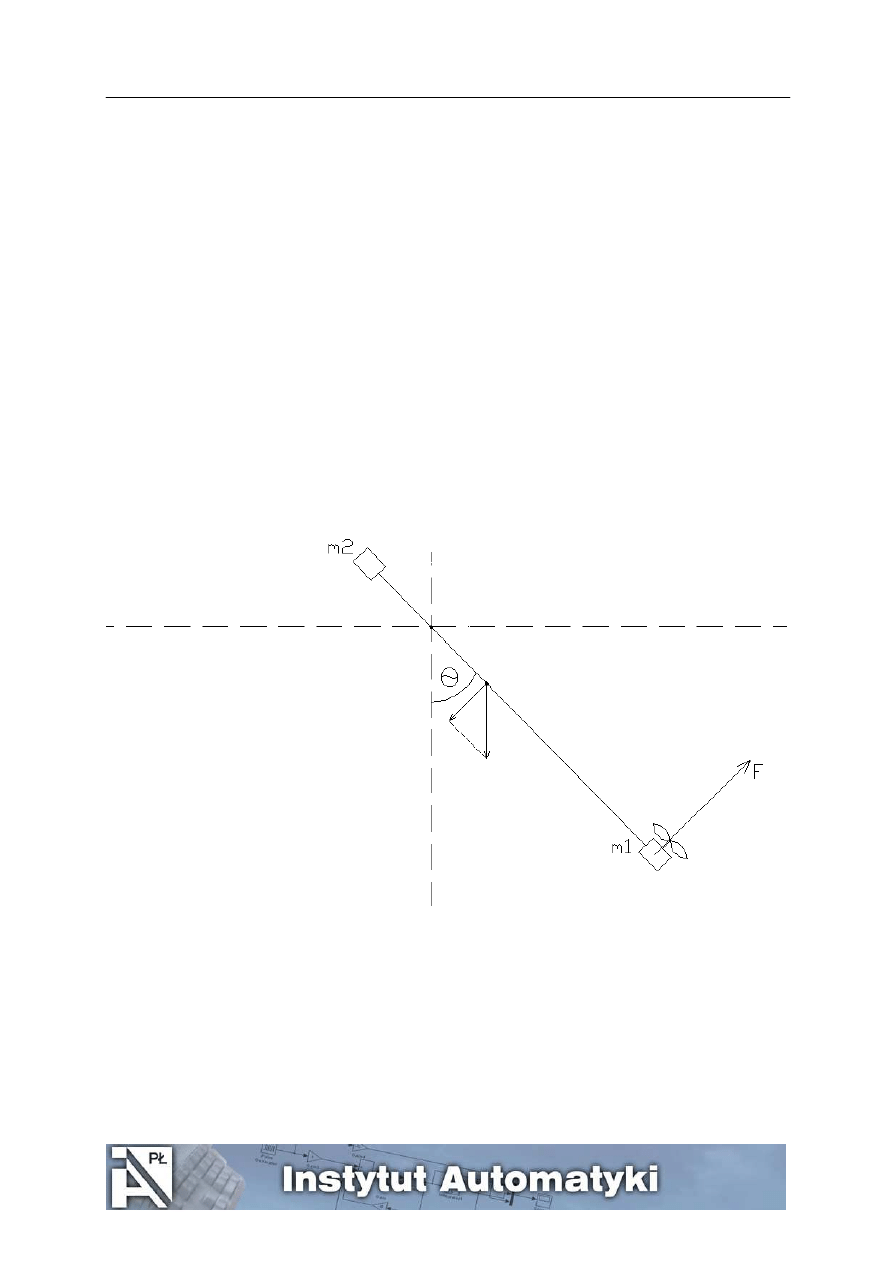
Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
2
1. Program
ćwiczenia
W trakcie ćwiczenia należy:
•
Przeprowadzić identyfikację parametrów wahadła z napędem śmigłowym
•
Korzystając z pakietu Matlab-Simulink zbudować model obiektu i sprawdzić jego zgodność z obiektem
rzeczywistym
•
Wyznaczyć parametry sterowania PID
•
Sprawdzić skuteczność regulacji kąta wahadła w układzie rzeczywistym
2. Obiekt sterowania
Obiektem regulacji jest wahadło fizyczne złożone z belki o przekroju kwadratowym łączącej silnik o masie m
1
z
przeciwwagą o masie m
2
. Wymuszeniem (wejściem obiektu) działającym na obiekt jest napięcie podawane na
silnik, podczas gdy położenie wahadła jest wielkością wyjściową. Budowę układu silnik-wahadło przedstawia
rysunek 1.
Rys. 1. Schemat układu silnik-wahadło
Napęd zrealizowany jest za pomocą silnika prądu stałego połączonego bezpośrednio ze śmigłem o średnicy
24cm. Regulację napięcia zasilającego silnik realizuje się sterując współczynnikiem wypełnienia (Pulse Width
Modulatoin, w skrócie PWM) sygnału prostokątnego. Oś obrotu wahadła zamocowana jest za pomocą łożyska
do podstawy. Z drugiej strony mocowania zamontowane jest sprzęgło i enkoder służący do pomiaru położenia
(kąta odchylenia od pionu).

Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
3
3. Model matematyczny obiektu
3.1. Układ silnik-
śmigło-wahadło
Sygnałem wejściowym dla sterowanego układu jest współczynnik wypełnienia fali PWM napięcia podawanego
na zaciski silnika prądu stałego. Wartość średnia napięcia U za okres jest wprost proporcjonalna do
współczynnika wypełnienia PWM.
Dynamik
ę prądu silnika określa równanie
)
(
)
(
)
(
)
(
t
E
dt
t
dI
L
t
I
R
t
U
t
t
t
t
+
+
=
, (1)
gdzie R
t
, L
t
i I
t
są kolejno rezystancją, indukcyjnością i prądem twornika, a E jest siłą elektromotoryczną zależną
od stałej silnika c i prędkości obrotowej silnika.
s
E( t )
c
( t )
= Ω
(2)
Przy małej indukcyjności (L
t
≅
0)otrzymamy:
t t
s
U ( t )
R I ( t ) c
( t )
=
+ Ω
, (3)
które wiąże ze sobą wielkości elektryczne w silniku.
Dynamik
ę ruchu obrotowego układu silnik-śmigło opisuje wyrażenie
(
)
s
s
t
o
s
d
J
kI
M
( t )
dt
Ω = −
Ω
, (4)
w którym J
s
jest momentem bezwładności układu silnik-śmigło, k jest stałą określającą związek między prądem
silnika a momentem napędowym, M
o
jest momentem oporowym zależnym od prędkości silnika
Ω
s
, który po
zlinearyzowaniu M
o
(t)=c
Ω
s
(t) i związaniu z napięciem U doprowadzi nas do równań
(
)
s
s
s
s
t
d
k
J
U ( t ) c
( t )
b
( t )
dt
R
Ω =
− Ω
− Ω
, (5)
)
(
)
(
)
(
t
U
R
k
t
b
c
R
k
dt
t
d
J
t
s
t
s
s
+
Ω
⋅
+
−
=
Ω
⋅
(6)
Zależność między napięciem, a prędkością śmigła ma więc charakter inercyjny i odpowiada transmitancji
)
(
)
(
)
(
s
U
R
k
s
b
c
R
k
s
s
J
t
s
t
s
s
+
Ω
⋅
+
−
=
Ω
⋅
⋅
(7)
)
(
)
(
)
(
s
U
R
k
s
b
c
R
k
s
s
J
t
s
t
s
s
=
Ω
⋅
+
+
Ω
⋅
⋅
(8)
Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
4
)
(
)
(
)
(
s
U
b
c
R
k
R
k
s
s
b
c
R
k
s
J
t
t
s
s
t
s
+
=
Ω
⋅
+
Ω
+
⋅
(9)
)
(
)
(
1
s
U
b
R
c
k
k
s
s
b
R
c
k
R
J
t
s
t
t
s
⋅
+
⋅
=
Ω
+
⋅
+
⋅
⋅
(10)
1
1
)
(
)
(
+
=
+
⋅
+
⋅
⋅
⋅
+
⋅
=
Ω
s
s
t
t
s
t
s
sT
k
s
b
R
c
k
R
J
b
R
c
k
k
s
U
s
, (11)
w której k
s
i T
s
jest wzmocnieniem i stałą czasową liniowego modelu silnika.
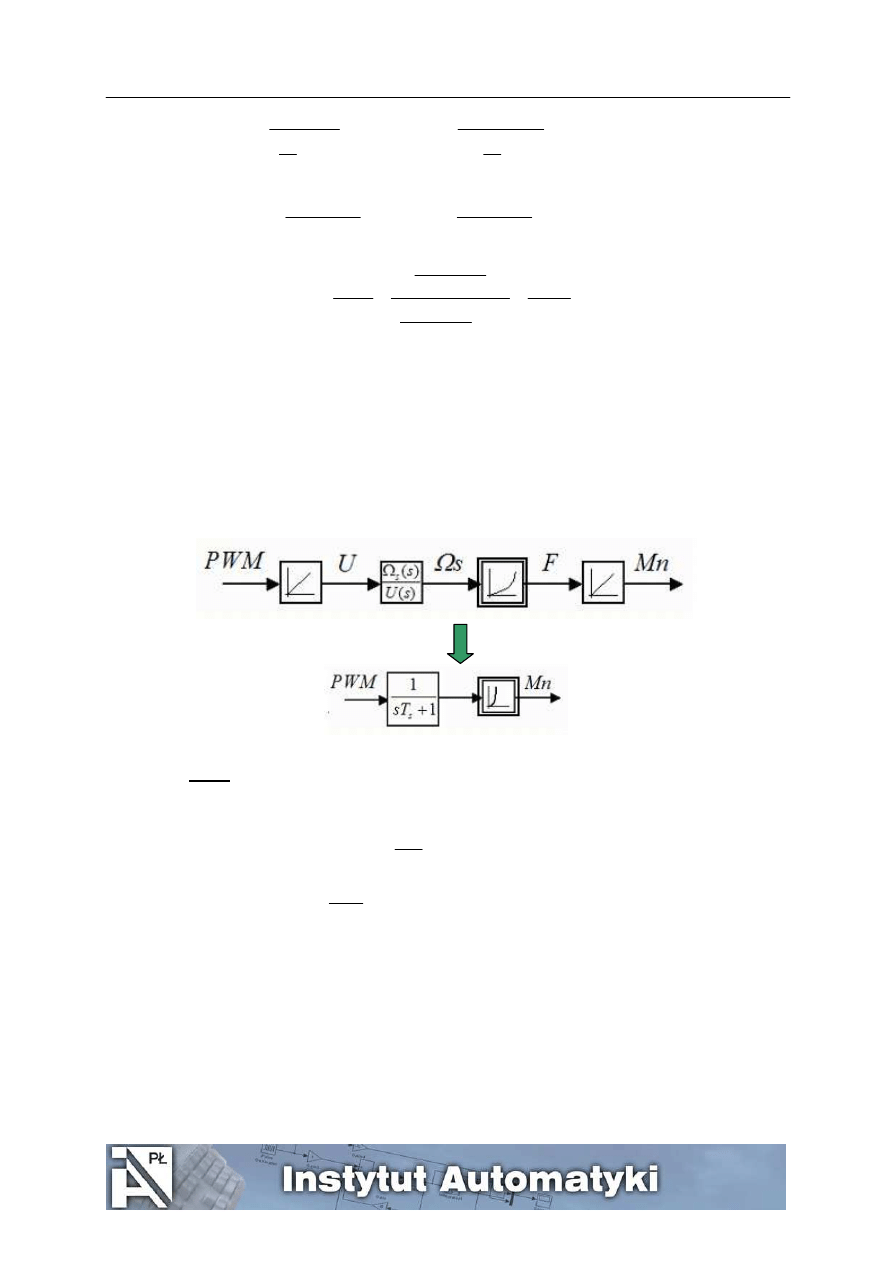
Siła ciągu F, która powoduje ruch wahadła jest nieliniową funkcją prędkości śmigła. Podsumowując te
rozważania możemy zaproponować model zależności między sygnałem wejściowym (współczynnikiem
wypełnienia fali PWM) a momentem napędowym M
n
wahadła w postaci szeregowego połączenia elementu
inercyjnego o współczynniku wzmocnienia równym 1 i statycznego elementu nieliniowego, którego
charakterystykę wyznaczymy eksperymentalnie.
Rys.2. Włączenie do nieliniowości części liniowych układu
3.2. Układ silnik-
śmigło-wahadło
Dynamika ruchu obrotowego wahadła jest opisana równaniami
)
(t
dt
d
w
Ω
=
θ
(12)
(
)
)
(
)
(
)
(
t
M
t
M
t
M
dt
d
J
w
op
g
n
w
w
Ω
−
−
=
Ω
(13)
gdzie J
w
to moment bezwładności układu, M
g
jest momentem pochodzącym od siły grawitacji
)
sin(
)
sin(
)
sin(
)
(
0
0
0
θ
α
θ
θ
⋅
=
⋅
⋅
⋅
=
⋅
⋅
=
⋅
=
d
g
m
d
Q
d
Q
t
M
y
g
(14)
a moment oporowy (tarcie) M
op
jest proporcjonalny do prędkości
)
(
)
(
t
t
M
w
op
Ω
⋅
=
β
(15)
Istotnym elementem układu jest ograniczenie sygnału wejściowego. W układzie stosuje się tylko dodatnie
wartości współczynnika wypełnienia, co odpowiada obrotom śmigła powodującym powstanie siły ciągu
skierowanej „ do góry”.
Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
5
3.3. Model liniowy układu silnik-
śmigło-wahadło
Sposobem na stworzenie liniowego modelu jest zlinearyzowanie nieliniowości występujących w równaniach
różniczkowych. Jeżeli przyjmiemy, że kąt wychylenia wahadła jest niewielki, to sin(
θ
)=
θ
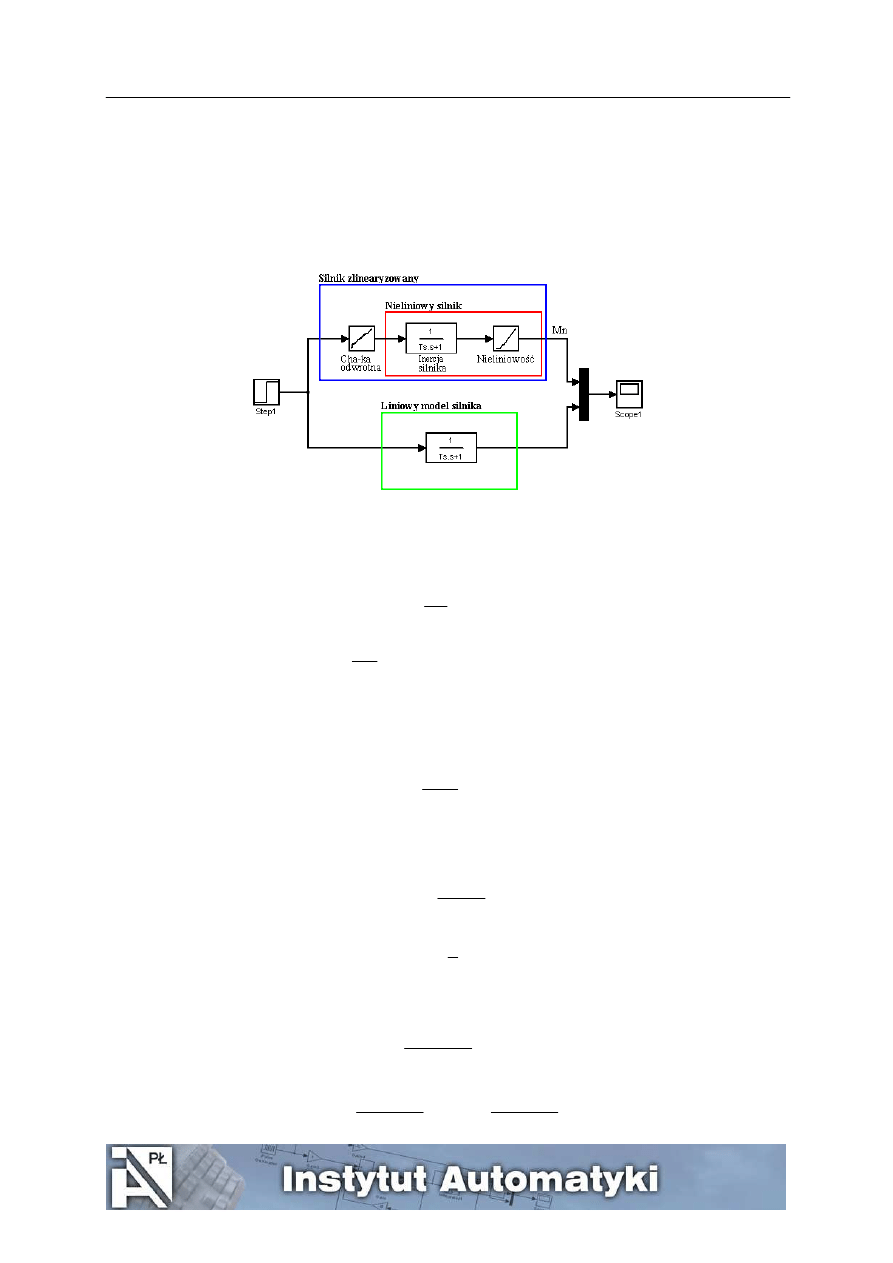
. Innym sposobem
linearyzacji układu, a raczej kompensacji nieliniowości jest zastosowanie na wejściu układu charakterystyki
odwrotnej do rozważanej nieliniowości (rys.3.)
Rys. 3. Linearyzacja napędu wahadła poprzez dołączenie charakterystyki odwrotnej
Stosuj
ąc linearyzację otrzymamy równania:
)
(t
dt
d
Ω
=
θ
(16)
))
(
(
)
(
)
(
0
t
M
t
M
t
M
dt
d
J
w
g
n
w
Ω
−
−
=
Ω
(17)
θ
α
θ
⋅
=
⋅
⋅
⋅
=
g
m
d
t
M
g
0
0
)
(
(18)
w
t
M
Ω
⋅
=
β
)
(
0
(19)
)
(
)
(
t
u
t
M
dt
dM
T
n
n
s
+
−
=
⋅
(20)
Z równa
ń tych otrzymujemy transmitancję
θ
(s) / u (s) :
)
(
1
1
)
(
s
u
sT
s
M
s
n
⋅
+
=
(21)
)
(
1
)
(
s
s
s
w
Ω
⋅
=
θ
(22)
)
(
)
(
)
(
)
(
s
s
s
M
s
s
J
w
n
w
w
Ω
⋅
−
⋅
−
=
Ω
⋅
⋅
β
θ
α
(23)
(
)
)
(
)
(
1
)
(
s
s
M
s
J
s
n
w
w
θ
α
β
⋅
−
⋅
+
⋅
=
Ω
(24)
)
(
1
)
(
s
M
s
J
s
s
J
s
n
w
w
⋅
+
⋅
=
⋅
+
⋅
+
β
θ
β
α
(25)

Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
6
)
(
1
)
(
2
s
M
s
J
s
s
J
s
s
J
n
w
w
w
⋅
+
⋅
=
⋅
+
⋅
+
⋅
+
⋅
β
θ
β
α
β
(26)
)
(
1
1
1
)
(
2
s
u
T
s
s
s
J
s
s
w
⋅
+
⋅
⋅
+
⋅
+
⋅
=
α
β
θ
(27)
Zagadnienia do opracowania przed laboratorium:
•
Zastanowić się w jaki sposób można wyznaczyć parametry obiektu, w tym charakterystykę statyczną
nieliniowości M
n
=f(PWM) z rys.2.
4. Identyfikacja parametrów modelu
Identyfikacja jest zadaniem, którego celem jest poznanie struktury i parametrów badanego obiektu. Zazwyczaj
uzyskana wiedza wykorzystywana jest do budowy modelu obiektu. W rozważanym przykładzie znana jest już
struktura obiektu i niektóre jego parametry fizyczne. W części praktycznej ćwiczenia należy wyznaczyć
brakujące parametry.
(1) Wykorzystując podane przez prowadzącego parametry obiektu (np. d
1
=0,89m, d
2
=0,2m, m
1
=0,161kg,
m
2
=0,63kg, m
pręta
=0,134kg), należy wyznaczyć moment bezwładności wahadła J
w
oraz współczynnik
α
wiążący kąt wychylenia wahadła z działającym na nie momentem grawitacyjnym. Do wyznaczenia
współczynnika
α
potrzebne będzie położenie środka masy układu d
0.
J
w
= .....
d
0
= .....
α
= .....
T
s
= 0,66s
(2) Poprosić prowadzącego o uruchomienie układu. Na podstawie obserwacji odpowiedzi impulsowej
wahadła, wyznaczyć okres T i amplitudy dwóch sąsiednich drgań A
1
, A
2
.
W sposób analityczny wyznaczyć odpowiedź impulsową transmitancji
α
β
θ
+
⋅
+
⋅
=
s
s
J
s
M
s
w
n
2
1
)
(
)
(
,
skorzystać ze wzoru
{
}
(
)
2
2
)
sin(
ω
ω
ω
+
+
=
−
a
s
e
t
L
at
. Z porównania ilorazu sąsiednich amplitud A
1
/A
2
wyznaczonych eksperymentalnie i analitycznie θ(t)/ θ(t+T) wyznaczyć współczynnik β.
β = ....
(3) Dokonać identyfikacji statycznej charakterystyki momentu napędowego wahadła w funkcji
współczynnika wypełnienia. W tym celu należy ponownie poprosić prowadzącego zajęcia o
uruchomienie układu rzeczywistego i zebrać potrzebne dane.
Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
7
PWM
θ
obliczenia
M
n
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
odrzucić jeżeli
θ
>90
o
(4) Zarejestrować odpowiedź skokową obiektu, dla wymuszenia np. PWM=0,30. Będzie ona potrzebna do
oceny jakości otrzymanego modelu
5. Dostrajanie parametrów modelu
W tej części ćwiczenia należy ocenić dokładność otrzymanego modelu i w razie konieczności dostroić parametry
wahadła J
w
,
α
,
β
. W tym celu należy skorzystać z modelu zapisanego na dysku (plik modelnielinoiwy.mdl) a
następnie:
(5)
Wypełnić strukturę zbudowanego modelu nieliniowego otrzymanymi parametrami i nieliniowością.
Parametry alfa, beta, Jw i Ts należy wpisać w oknie Matlaba (do przestrzeni roboczej Matlaba),
parametry nieliniowej charakterystyki śmigła w bloku Lookup Table. Uruchomić symulację i porównać
odpowiedź modelu z zarejestrowaną odpowiedzią obiektu rzeczywistego
Blok NCD dotępny w programie Simulink służy do dobierania nieznanych parametrów wykorzystanych w
układzie (np. modelu czy regulatora) tak, aby interesujący nas sygnał (np. odpowiedź obiektu czy błąd modelu)
nie wychodził poza zdefiniowane przez użytkownika ograniczenia. Wynik strojenia (skorygowane parametry)
dostępny jest w przestrzeni roboczej Matlaba.
(6) Korzystając z bloku NCD dostroić parametry modelu wahadła
α
,
β
, i J
w
. Założyć, że stała silnika T
s
została wyznaczona dokładnie.
α
= .....
β
= .....
J
w
= .....
T
s
= 0,66s
(7) Zapisać transmitancję obiektu w różnych postaciach
( )
(
)
0
1
2
0
1
2
2
3
3
2
1
1
1
1
)
(
c
s
c
s
t
s
b
s
a
s
a
s
a
k
T
s
s
s
J
s
G
s
w
ob
+
+
+
=
+
+
+
=
+
⋅
⋅
+
⋅
+
⋅
=
α
β
(27)
a
3
= .....
a
2
= .....
a
1
= .....
k = .....
b
0
= .....
t = .....
c
1
= .....
c
0
= .....
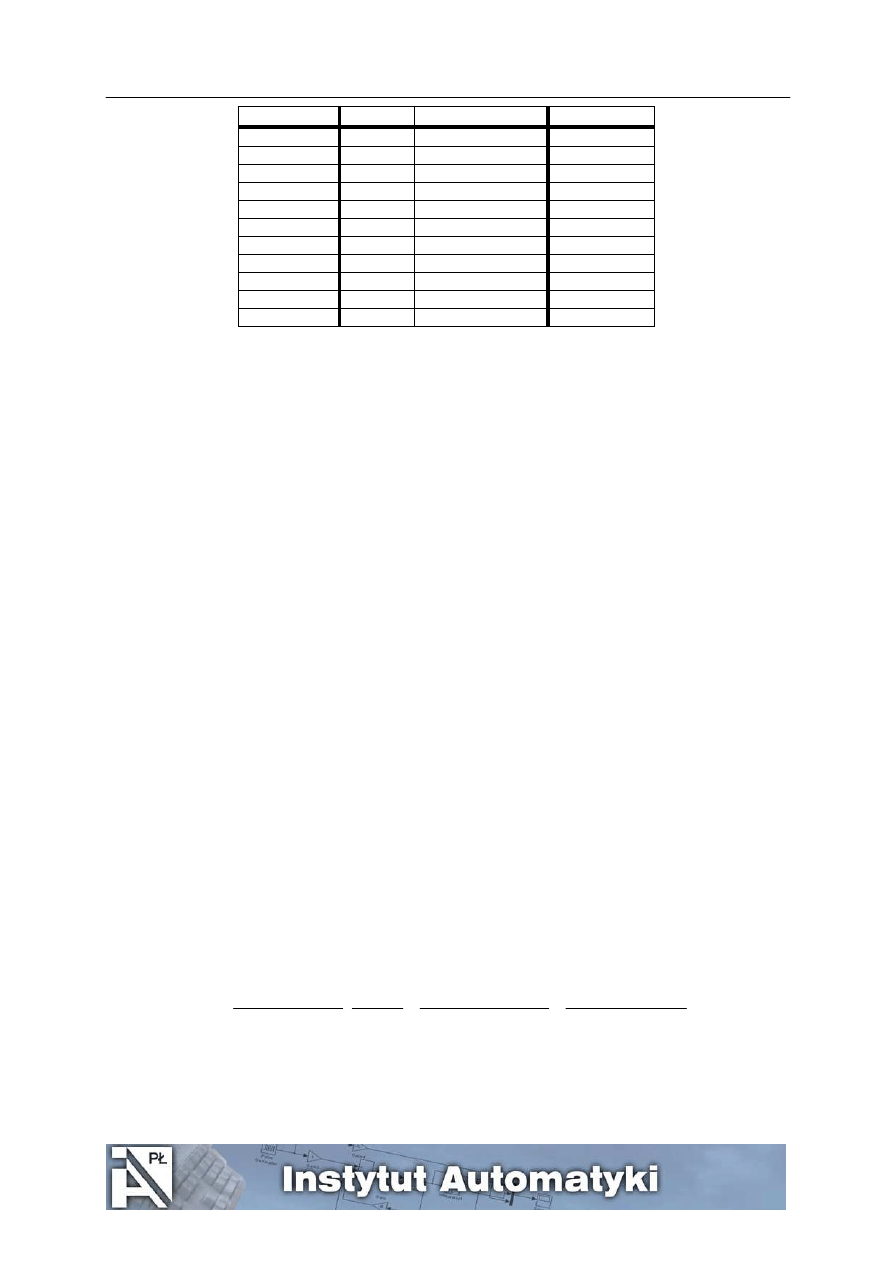
i korzystając z pliku modelliniowy.mdl porównać model liniowy obiektu z modelem zlinearyzowanym.
Laboratorium Automatyki.
Instrukcja do ćwiczenia nr 5.
8
6. Regulator PID
Zadaniem będzie dobranie transmitancji regulatora PID zapisanej w postaci:
d
d
i
d
p
reg
T
s
T
T
T
s
s
k
s
G
⋅
+
+
⋅
=
1
)
(
2
(28)
tak, aby nastąpiło skrócenie mianownika transmitancji obiektu z licznikiem transmitancji regulatora a następnie
dobranie współczynnika wzmocnienia k
p
. W tym celu należy:
(8) Porównując licznik regulatora i mianownik obiektu wyznaczyć nastawy T
i
i T
d
.
T
i
= .....
T
d
= .....
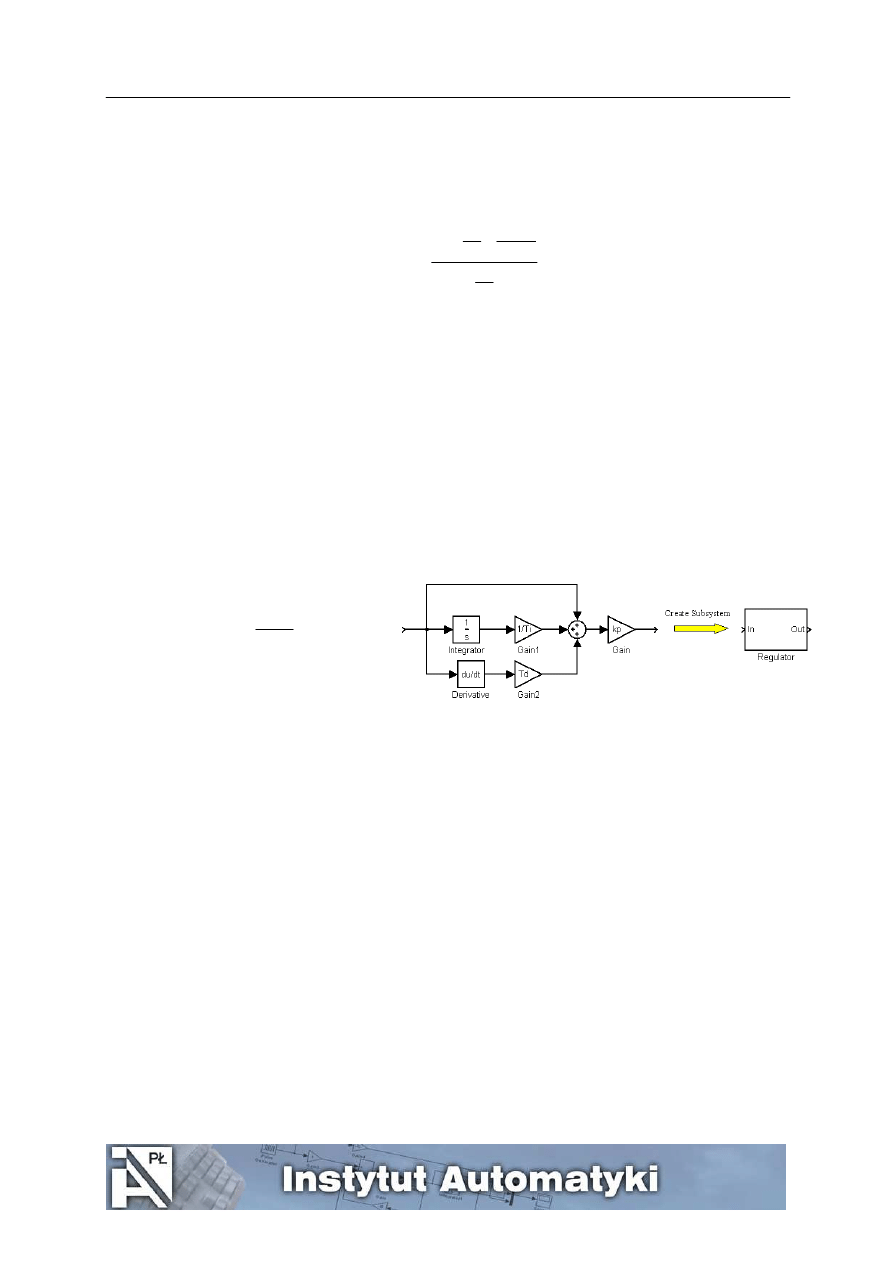
(9) Według poniższego schematu zbudować regulator w Simulinku
(10) Zbudować układ regulacji. Dla wartości zadanej kąta równej θ
zad
=1rad dobrać w sposób doświadczalny
k
p
tak, aby układ pracował bez przeregulowań.
k
p
= ............
Uwaga 1. : W układzie regulacji należy uwzględnić ograniczenie sygnału sterującego (blok Saturation)
Uwaga 2. : W układzie regulacji należy także uwzględnić dyskretyzację pomiaru wartości kąta (blok Quantizer)
Uwaga 3. : Do doboru nastaw można też wykorzystać blok NCD
(11) Działanie zaprojektowanego układu regulacji zweryfikować w układzie rzeczywistym.
KONIEC
=
+
⋅
+
=
d
i
p
reg
sT
T
s
k
G
1
1
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron