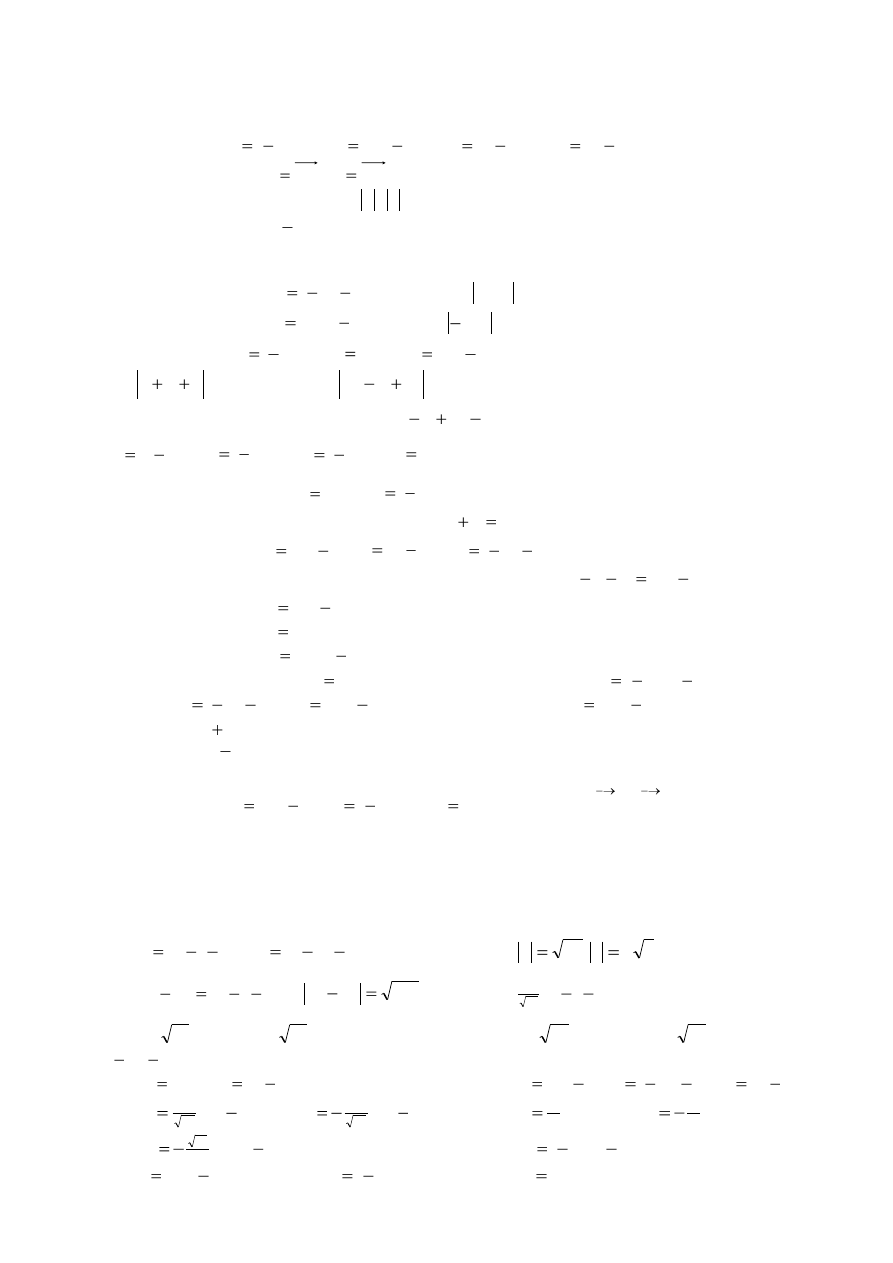
DZIAŁANIA NA WEKTORACH.

1. Dane są punkty

)

4

,

1

,

1

,

2

(

B

),

3

,

1

,

2

,

2

(

A

,

)

2

,

3

,

2

,

6

(

D

),

5

,

2

,

1

,

3

(

C

.

(a) Znaleźć wektory

AB

a



,

CD

c



.

(b) Obliczyć długości wektorów a



, c



.

(c) Znaleźć wektor

c

a





2

3

oraz jego długość.

(d) Znaleźć wektor jednostkowy (wersor) równoległy do a



.

(e) Sprawdzić nierówność trójkąta w trójkącie o wierzchołkach B,C,D.

2. (a) Dany jest wektor

]

2

,

3

,

1

,

1

,

2

[

a



. Obliczyć

a



327 .

(b) Dany jest wektor

]

8

,

12

,

4

[

a



. Obliczyć

a



52 .

3. Dane są wektory

]

3

,

1

,

2

[

a



,

]

1

,

2

,

0

[

b



]

1

,

2

,

1

[

c



. Obliczyć

(a)

c

b

a







(b)

c

b

a







3

2

.

4. Znaleźć kombinację liniową wektorów

d

c

b

a









2

3

, jeśli

]

0

,

1

,

1

[

a



,

]

4

,

1

,

2

[

b



,

]

11

,

1

[

c



,

]

2

,

0

,

3

[

d



.

5. (a) Dane są dwa wektory

]

3

,

2

[

a



,

]

4

,

1

[

b



. Znaleźć wektory u



, v



, o kierunkach

zgodnych, odpowiednio, z a



,

b



takie, że

]

1

,

8

[

v

u





.

(b) Dane są wektory

]

2

,

3

,

1

[

a



,

]

1

,

2

,

4

[

b



,

]

1

,

1

,

2

[

c



. Znaleźć wektory u



, v



, w



o kierunkach zgodnych, odpowiednio, z a



,

b



, c



takie, że

]

3

,

3

,

1

[

w

v

u







.

6. (a) Dany jest wektor

]

4

,

2

,

3

,

1

[

a



. Znaleźć wektor

b



równoległy do a



o długości 1.

(b) Dany jest wektor

]

4

,

3

,

0

[

u



. Znaleźć wektor v



równoległy do u



o długości 12.

(c) Dany jest wektor

]

5

,

1

,

3

,

1

,

2

[

p



. Znaleźć wektor

q



przeciwny do

p



o długości 5.

7. Znaleźć koniec

Q

wektora

]

5

,

4

,

1

,

2

,

3

[

a



zaczepionego w punkcie

)

9

,

7

,

2

,

4

,

5

(

P

.

8. Wektory

]

4

,

1

,

1

,

2

[

u



,

]

3

,

3

,

2

,

4

[

v



zaczepiono w punkcie

)

5

,

2

,

4

,

3

(

A

. Znaleźć koniec B

(a) wektora

v

u





,

(b) wektora

v

u





2

3

,

jeśli jego początkiem jest punkt A .

9. Dane są punkty

)

2

,

1

,

4

(

A

,

)

4

,

5

,

1

(

B

,

)

2

,

2

,

6

(

D

. Wektory AB i AD wyznaczają dwa

sąsiednie boki pewnego równoległoboku. Znaleźć czwarty wierzchołek C tego równoległoboku.

Odpowiedzi.

1. (a)

]

1

,

2

,

1

,

4

[

a



,

]

3

,

1

,

1

,

3

[

c



(b)

5

2

,

22 c

a





(c)

]

9

,

8

,

1

,

6

[

2

3

c

a





,

182

2

3

c

a





(d)

]

1

,

2

,

1

,

4

[

22

1

2. (a)

19

327

(b)

14

208

3. (a)

35

(b)

41

4.

]

5

,

1

,

6

[

5. (a)

]

9

,

6

[

u



,

]

8

,

2

[

v



(b)

]

2

,

3

,

1

[

u



,

]

1

,

2

,

4

[

v



,

]

2

,

2

,

4

[

w



6. (a)

]

4

,

2

,

3

,

1

[

30

1

b



lub

]

4

,

2

,

3

,

1

[

30

1

b



(b)

]

4

,

3

,

0

[

5

12

u



lub

]

4

,

3

,

0

[

5

12

u



(c)

]

5

,

1

,

3

,

1

,

2

[

4

10

q



7.

)

14

,

3

,

3

,

6

,

2

(

Q

8. (a)

)

12

,

6

,

7

,

5

(

B

(b)

)

11

,

1

,

3

,

11

(

B

9.

)

8

,

4

,

7

(

C