Z. Kąkol-Notatki do Wykładu z Fizyki

32-1

Wykład 32

32. Światło a fizyka kwantowa

32.1

Źródła światła

Najbardziej znanymi źródłami światła są rozgrzane ciała stałe i gazy, w których za-

chodzi wyładowanie elektryczne; np.

•

wolframowe włókna żarówek

•

jarzeniówki

Promieniowanie wysyłane przez ogrzane (do pewnej temperatury) ciała nazywamy

pro-

mieniowaniem termicznym

.

Wszystkie ciała

emitują

takie promieniowanie do otoczenia, a także z tego otoczenia je

absorbują

.

Jeżeli ciało ma wyższą temperaturę od otoczenia to będzie się oziębiać ponieważ szyb-
kość promieniowania przewyższa szybkość absorpcji (ale oba procesy występują !!).
Gdy osiągnięta zostanie równowaga termodynamiczna wtedy te prędkości będą równe.
Za pomocą spektrometru możemy zanalizować światło emitowane przez te źródła tzn.
dowiedzieć się jak silnie i jakie długości fal wypromieniowuje.
Dla przykładu, na rysunku poniżej pokazane jest widmo promieniowania dla taśmy wol-
framowej ogrzanej do T = 2000 K. Zanotujmy, że:

•

Widmo emitowane przez ciała stałe ma charakter ciągły,

•

Szczegóły tego widma są prawie niezależne od rodzaju substancji,

•

Widmo silnie zależy od temperatury.

Zwróćmy uwagę, że w zwykłych temperaturach większość ciał jest dla nas widoczna
dlatego, że odbijają one (lub rozpraszają) światło, które na nie pada a nie dlatego, że cia-

0

1

2

3

4

5

zakres
widzialny

wolfram
T = 2000 K

cia

ło doskonale czarne

T = 2000 K

R

λ

λ

(

µ

m)

Z. Kąkol-Notatki do Wykładu z Fizyki

32-2

ła te wysyłają promieniowanie widzialne (świecą). Jeżeli nie pada na nie światło (np. w
nocy) to są one niewidoczne.
Dopiero gdy ciała mają wysoką temperaturę wtedy świecą własnym światłem. Ale jak
widać z rysunku i tak większość emitowanego promieniowania jest niewidzialna bo
przypada na zakres promieniowania cieplnego (podczerwień). Dlatego ciała, świecące
własnym światłem są bardzo gorące.
Jeżeli będziemy rozgrzewać kawałek metalu to początkowo chociaż jest on gorący to
z jego wyglądu nie można tego stwierdzić (bo nie świeci); można to tylko zrobić doty-
kiem. Emituje więc promieniowanie podczerwone (ciepło). Ze wzrostem temperatury
kawałek metalu staje się początkowo ciemno-czerwony, następnie jasno-czerwony, aż
wreszcie świeci światłem niebiesko-białym.
Wielkość R

λ

przedstawiona na wykresie na osi pionowej nazywana jest

widmową zdol-

nością emisyjną promieniowania

i jest tak zdefiniowana, ze wielkość R

λ

d

λ oznacza

szybkość, z jaką jednostkowy obszar powierzchni wypromieniowuje energię odpowia-
dającą długościom fal zawartym w przedziale

λ, λ+dλ.

Czasami chcemy rozpatrywać całkowitą energię wysyłanego promieniowania w całym
zakresie długości fal. Wielkość ta nazywana jest

całkowitą emisja energetyczna promie-

niowania R

. Emisję całkowitą R możemy obliczyć sumując emisję dla wszystkich dłu-

gości fal tzn. całkując R

λ

po wszystkich długościach fal.

∫

∞

=

0

λ

λ

d

R

R

Oznacza to, że możemy interpretować emisję energetyczną promieniowania R jako po-
wierzchnię pod wykresem R

λ

od

λ.

Ilościowe interpretacje widm promieniowania przedstawiają poważne trudności.
Dlatego posługujemy się wyidealizowanym obiektem (modelem), ogrzanym ciałem sta-
łym, zwanym

ciałem doskonale czarnym

. (Takie postępowaliśmy już w przypadku ga-

zów; rozważaliśmy modelowy obiekt tzw. gaz doskonały.)
Przykładem takiego ciała może być obiekt pokryty sadza (obiekt nie odbija światła, jego
powierzchnia absorbuje światło).
My jednak omówimy inny przykład.

32.2

Ciało doskonale czarne

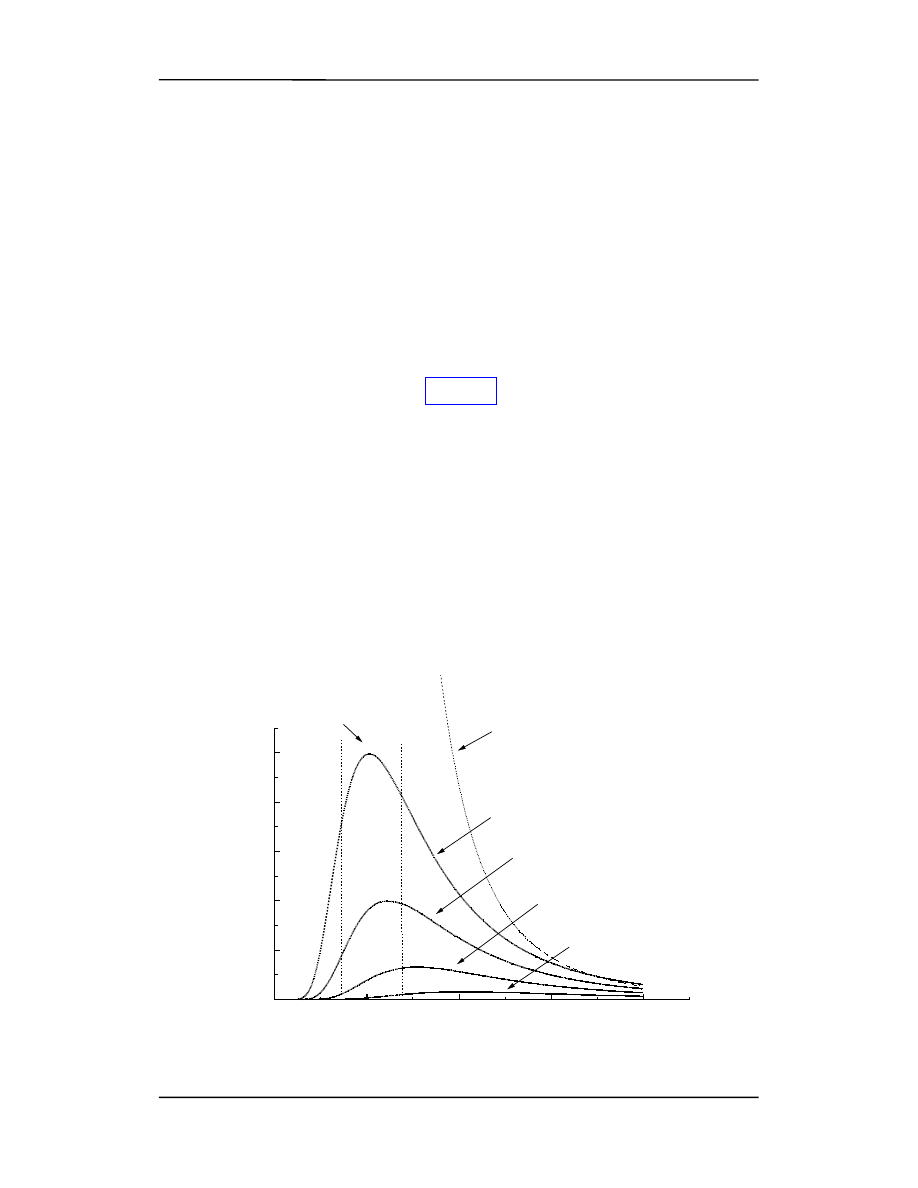
Rozważmy trzy bloki metalowe posiadające

puste wnęki wewnątrz (takie jak na rysunku
obok). W ściankach tych bloków wywiercono
otworki (do tych wnęk).
Promieniowanie pada na otwór z zewnątrz i po
wielokrotnych odbiciach od wewnętrznych ścian
zostaje całkowicie pochłonięte. Oczywiście
ścianki wewnętrzne też emitują promieniowa-
nie, które może wyjść na zewnątrz przez otwór
(przykład - otwór okienny).

Z. Kąkol-Notatki do Wykładu z Fizyki

32-3

Każdy z tych bloków (np. wolfram, tantal, molibden) ogrzewamy równomiernie do jed-
nakowej temperatury np. 2000 K.
Bloki znajdują się w nieoświetlonym pomieszczeniu, tak że obserwujemy tylko światło
wysyłane przez nie.
Pomiary wykonane pokazują, że:

•

Promieniowanie wychodzące z wnętrza bloków ma zawsze większe natężenie niż
promieniowanie ze ścian bocznych (rysunek powyżej),

•

Dla danej temperatury emisja promieniowania wychodzącego z otworów jest

iden-

tyczna dla wszystkich źródeł promieniowania

, pomimo że dla zewnętrznych po-

wierzchni te wartości są różne,

•

Emisja energetyczna promieniowania ciała doskonale czarnego (nie jego powierzch-
ni) zmienia się wraz z temperaturą według

prawa Stefana

4

T

R

C

σ

=

(32.1)

gdzie

σ jest uniwersalną stałą (stała Stefana-Boltzmana) równą 5.67·10

-8

W/(m

2

K). Dla

zewnętrznych powierzchni to empiryczne prawo ma postać:

4

T

e

R

C

σ

=

gdzie zdolność emisyjna e jest wielkością zależną od substancji i, co jeszcze bardziej
skomplikowane, od temperatury.
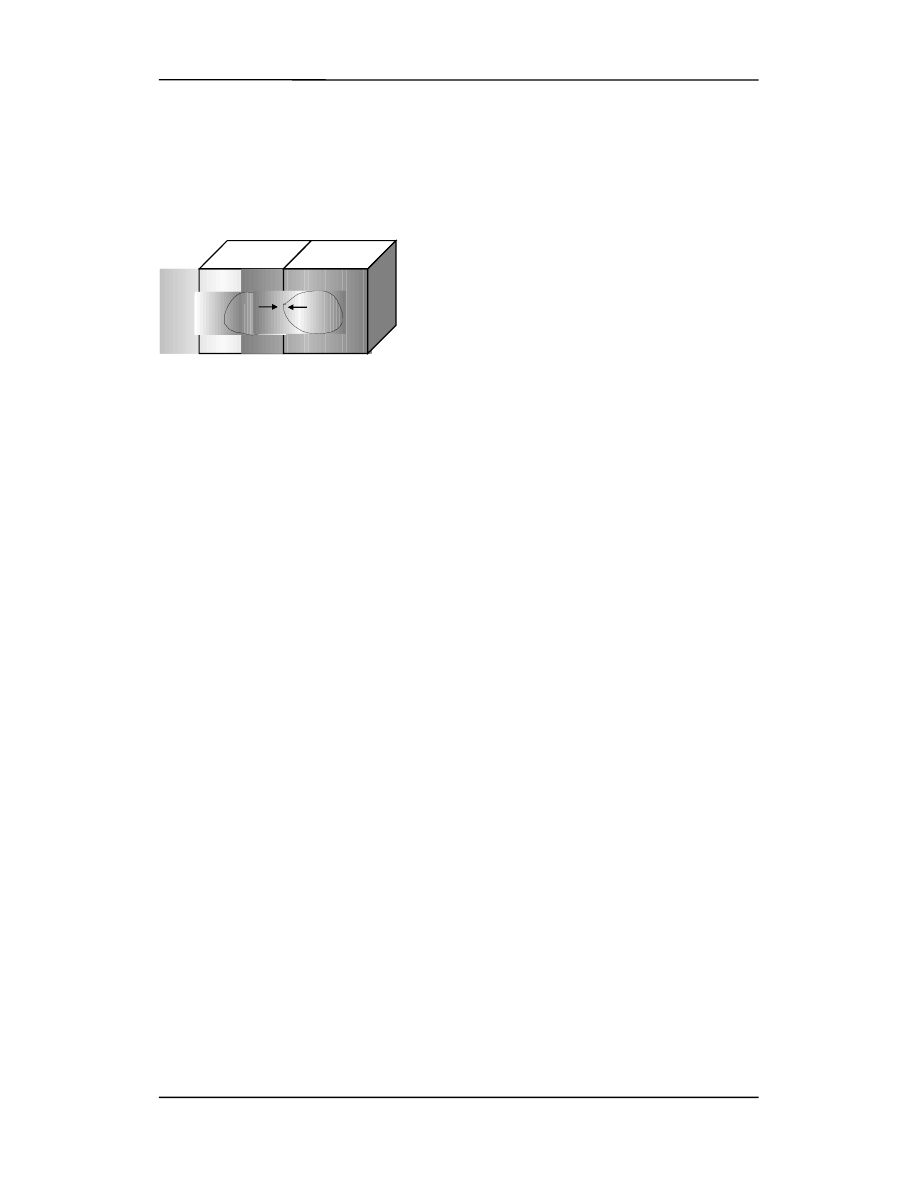
R

λ

dla ciała doskonale czarnego zmienia się z temperaturą tak jak na rysunku poniżej.

Długość fali dla której przypada maksimum emisji jest odwrotnie proporcjonalna do
temperatury ciała.

0.0

0.5

1.0

1.5

2.0

T = 3000 K

T = 4000 K

T = 5000 K

T = 6000 K

obszar widzialny

klasyczna teoria

R

λ

λ

(

µ

m)

Z. Kąkol-Notatki do Wykładu z Fizyki

32-4

Uwaga: Krzywe te zależą tylko od temperatury i są całkiem niezależne od materiału
oraz kształtu i wielkości ciała czarnego.

Rozpatrzmy teraz, pokazane na rysunku poniżej, dwa ciała doskonale czarne

(dwie wnęki).

•

Kształty wnęk są dowolne,

•

Temperatura ścianek obu wnęk jest jedna-
kowa.

Promieniowanie oznaczone R

A

przechodzi z

wnęki A do wnęki B, a promieniowanie R

B

w

odwrotnym kierunku. Jeżeli te szybkości nie
byłyby równe wówczas jeden z bloków
ogrzewałby się a drugi stygł. Oznaczałoby to
pogwałcenie drugiej zasady termodynamiki.
Mamy więc

R

A

= R

B

= R

C

gdzie R

C

opisuje całkowite promieniowanie dowolnej wnęki.

Nie tylko energia całkowita ale również jej rozkład musi być taki sam dla obu wnęk.
Stosując to samo rozumowanie co poprzednio można pokazać, że

R

λA

= R

λB

= R

λC

gdzie R

λC

oznacza widmową zdolność emisyjną dowolnej wnęki.

32.3

Teoria promieniowania we wnęce, prawo Plancka

32.3.1 Rozważania klasyczne

Na przełomie ubiegłego stulecia Rayleigh i Jeans wykonali obliczenia energii pro-

mieniowania we wnęce (czyli promieniowania ciała doskonale czarnego.
Najpierw zastosowali oni klasyczną teorię pola elektromagnetycznego do pokazania, że
promieniowanie wewnątrz wnęki ma charakter fal stojących (węzły na ściankach wnę-
ki).

Zgodnie z fizyką klasyczną,

energia każdej fali może przyjmować dowolną wartość od

zera do nieskończoności

, przy czym energia jest proporcjonalna do kwadratu amplitudy.

Następnie Rayleigh i Jeans obliczyli wartości średniej energii w oparciu o znane nam
prawo ekwipartycji energii i w oparciu o nią znaleźli widmową zdolność emisyjną.
Uzyskany wynik jest pokazany na wykresie na stronie 4. Jak widać rozbieżność między
wynikami doświadczalnymi i teorią jest duża. Dla fal długich (małych częstotliwości)
wyniki teoretyczne są bliskie krzywej doświadczalnej, ale dla wyższych częstotliwości
wyniki teoretyczne dążą do nieskończoności podczas gdy gęstość energii zawsze pozo-
staje skończona. Ten sprzeczny z rzeczywistością wynik rozważań klasycznych nazy-
wany jest „katastrofą w nadfiolecie”.

R

A

R

B

T

T

Z. Kąkol-Notatki do Wykładu z Fizyki

32-5

32.3.2 Teoria Plancka promieniowania ciała doskonale czarnego

W 1900 roku Max Planck przedstawił Berlińskiemu Towarzystwu Fizycznemu em-

piryczny wzór opisujący widmową zdolność emisyjną dający wyniki zgodne z doświad-
czeniem.

1

1

2

5

1

−

=

T

c

e

c

R

λ

λ

λ

(32.2)

Wzór ten stanowił modyfikację znanego już prawa Wiena i chociaż ważny nie stanowił
sam nowej teorii (był to wzór empiryczny).
Próbując znaleźć taką teorię Planck założył, że atomy ścian zachowują się jak oscylatory
elektromagnetyczne, które emitują (i absorbują) energię do wnęki, z których każdy ma
charakterystyczną częstotliwość drgań.
Rozumowanie Plancka doprowadziło do przyjęcia dwóch radykalnych założeń dotyczą-
cych tych oscylatorów atomowych:
1. Oscylator nie może mieć dowolnej energii, lecz tylko energie dane wzorem

E = nhv

(32.3)

gdzie v oznacza częstość oscylatora, h -stałą (zwaną obecnie stałą Plancka),
n - pewną liczbę całkowitą (zwaną obecnie liczbą kwantową).
Z powyższego wzoru wynika, że

energia jest skwantowana

i może przyjmować tyl-

ko ściśle określone wartości. Tu jest zasadnicza różnica bo teoria klasyczna zakłada-
ła dowolną wartość energii od zera do nieskończoności.

2. Oscylatory nie wypromieniowują energii w sposób ciągły, lecz porcjami czyli

kwan-

tami

. Kwanty są emitowane gdy oscylator przechodzi z jednego stanu o danej ener-

gii do drugiego o innej energii

∆

E =

∆

nhv = hv

gdy n zmienia się o jedność.
Dopóki oscylator pozostaje w jednym ze swoich stanów kwantowych (stany stacjonar-
ne) dopóty ani nie emituje ani nie absorbuje energii.

Sprawdźmy czy ta hipoteza stosuje się do znanych nam oscylatorów takich jak np. sprę-
żyna o masie m = 1 kg i stałej sprężystości k = 20 N/m wykonująca drgania o amplitu-
dzie 1 cm.
Dla takiej sprężyny częstotliwość drgań własnych wynosi

Hz

m

k

v

71

.

0

2

1

=

=

π

Wartość energii całkowitej (mechanicznej) tej sprężyny wynosi

J

kA

E

3

2

10

1

2

1

−

⋅

=

=

Z. Kąkol-Notatki do Wykładu z Fizyki

32-6

Jeżeli energia jest skwantowana to jej zmiany dokonują się skokowo przy czym

∆

E =

hv. Względna zmiana energii wynosi więc

∆

E/E = 4.7·10

-31

W celu zaobserwowania (zarejestrowania) tych nieciągłych zmian energii trzeba by wy-
konać pomiar energii z dokładnością przewyższającą wielokrotnie czułość przyrządów
pomiarowych.
Tak więc dla „dużych” oscylatorów natura kwantowa drgań nie jest widoczna podobnie
jak w układach makroskopowych nie widzimy dyskretnej natury materii (cząsteczek,
atomów, elektronów itp.).
Wnioskujemy, że doświadczenia ze zwykłym wahadłem nie mogą rozstrzygnąć o słusz-
ności postulatu Plancka.
Zanim przejdziemy do przedstawienia innych doświadczeń (zjawisko fotoelektryczne i
efekt Comptona) omówmy zastosowanie prawa promieniowania w termometrii.

32.3.3 Zastosowanie prawa promieniowania w termometrii

Promieniowanie emitowane przez gorące ciało można wykorzystać do wyznaczenia

jego temperatury. Jeżeli mierzy się całkowite promieniowanie, to można zastosować
prawo Stefana-Boltzmana.

Przykład 1

Średnia ilość energii (na jednostkę czasu) promieniowania słonecznego padającego na
jednostkę powierzchni Ziemi wynosi 355 W/m

2

. Jaką temperaturę będzie miała po-

wierzchnia Ziemi, jeżeli przyjąć, że Ziemia jest ciałem doskonale czarnym, wypromie-
niowującym w przestrzeń właśnie tyle energii na jednostkę powierzchni i czasu?

4

T

R

C

σ

=

C

8

K

281

4

o

=

=

=

σ

C

R

T

(Wynik bardzo dobrze zgodny z doświadczeniem.)

Ponieważ dla większości źródeł trudno dokonać pomiaru całkowitego promieniowania
więc mierzy się ich zdolność emisyjną dla wybranego zakresu długości fal. Z prawa
Plancka wynika, że dla dwu ciał o temperaturach T

1

i T

2

stosunek natężeń promieniowa-

nia o długości fali

λ wynosi

1

1

2

1

2

1

−

−

=

kT

hc

kT

hc

e

e

I

I

λ

λ

Jeżeli T

1

przyjmiemy jako standardową temperaturę odniesienia to możemy wyznaczyć

T

2

wyznaczając doświadczalnie I

1

/I

2

.

Z. Kąkol-Notatki do Wykładu z Fizyki

32-7

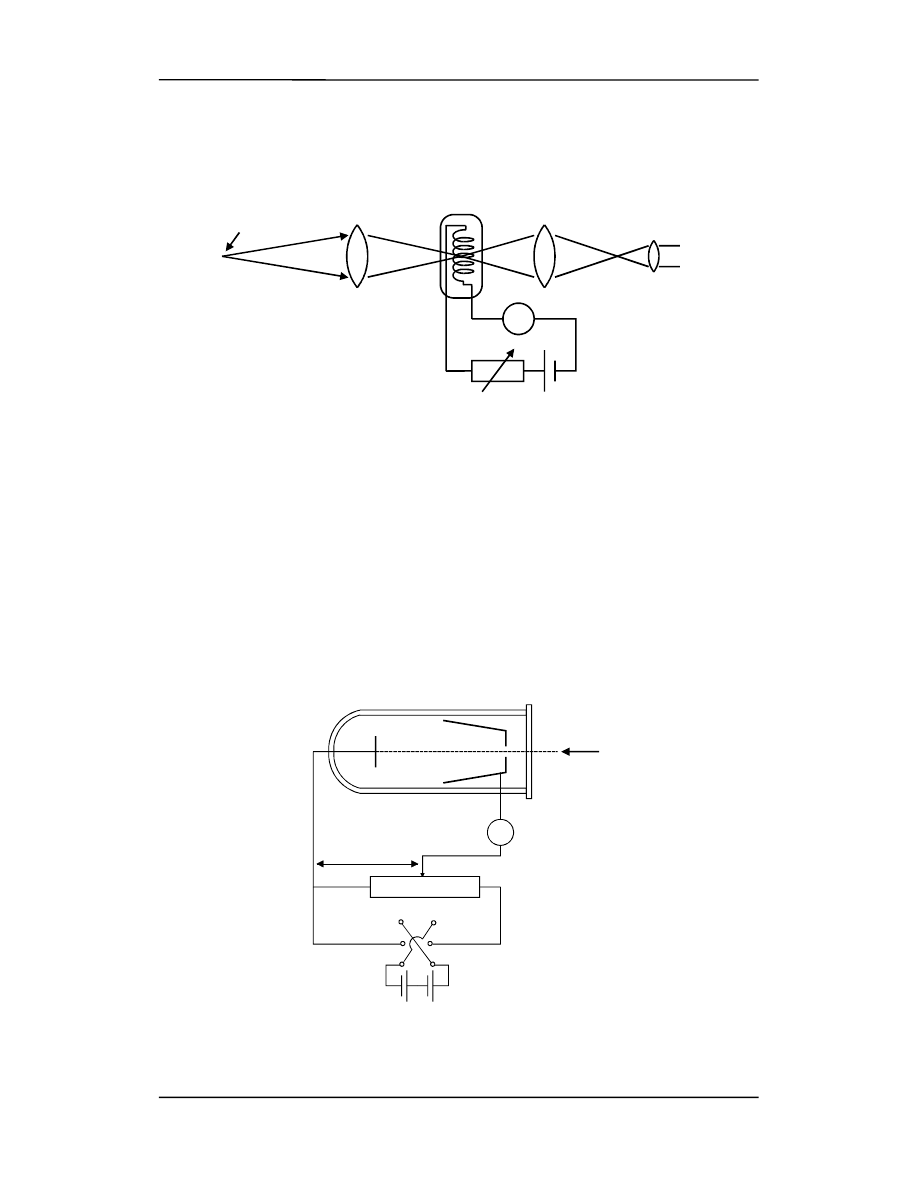
Do tego celu posługujemy się

pirometrem

(rysunek poniżej).

Obraz źródła (o nieznanej temperaturze) powstaje w miejscu gdzie znajduje się włókno
żarowe pirometru. Dobieramy prąd żarzenia tak aby włókno stało się niewidoczne na tle
źródła (świeci tak samo jasno). Ponieważ urządzenie jest wyskalowane możemy teraz
odczytać temperaturę źródła.

32.4

Zjawisko fotoelektryczne

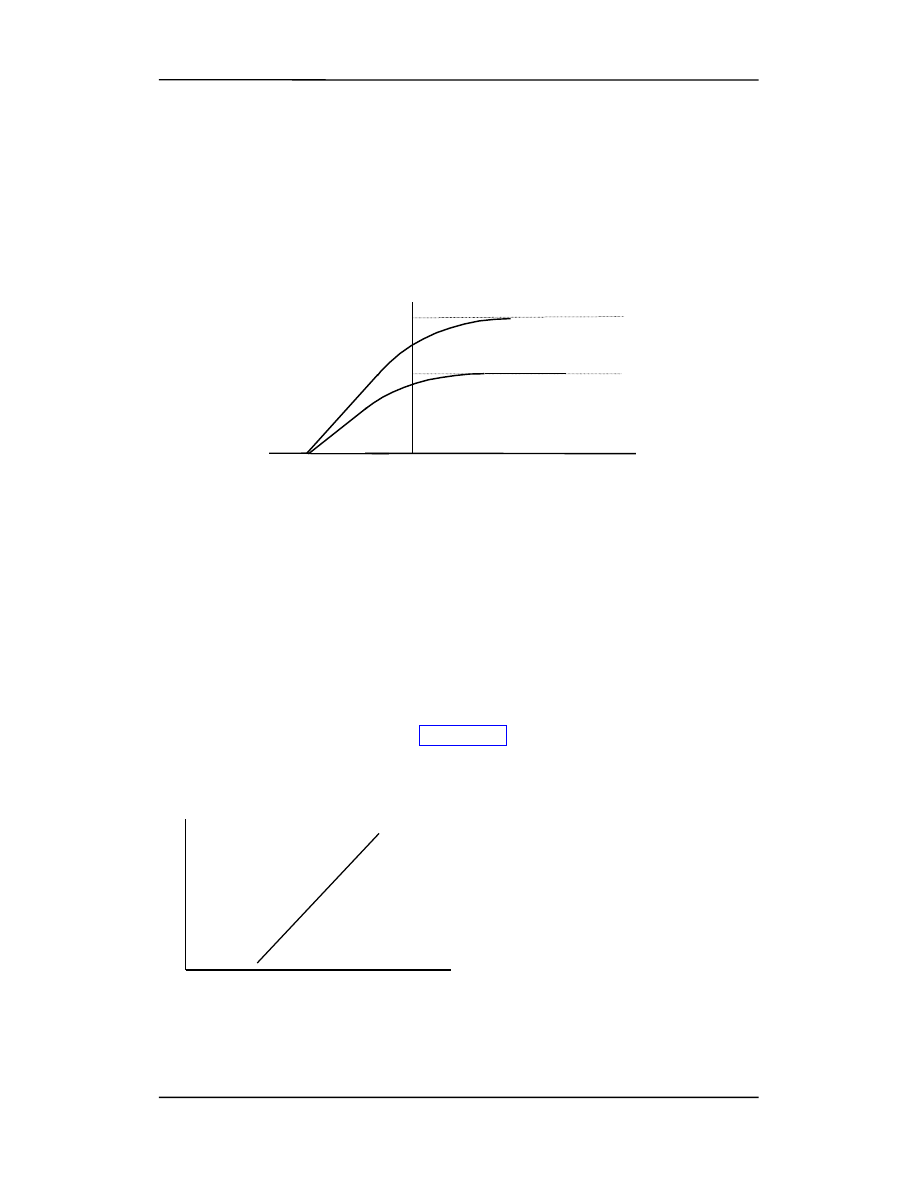
Na rysunku przedstawiono aparaturę do badania zjawiska fotoelektrycznego. W

szklanej bańce, w której panuje wysoka próżnia, znajdują się dwie metalowe elektrody
A i B.

A

źródło
promieniowania

w

łókno pirometru

mikroskop

A

B

G

V

światło
padaj

ące

prze

łącznik

Z. Kąkol-Notatki do Wykładu z Fizyki

32-8

•

Światło pada na metalową płytkę A i uwalnia z niej elektrony, które nazywamy

fotoelektronami

.

•

Fotoelektrony można zarejestrować jako prąd elektryczny płynący między płytką A
oraz elektrodą zbierającą B przy wytworzeniu między nimi odpowiedniej różnicy
potencjałów V (tak aby elektrony były przyciągane do B). Do pomiaru prądu stosu-
jemy czułe galwanometry.

Poniżej pokazana jest zależność prądu fotoelektrycznego od przyłożonego napięcia (róż-
nicy potencjałów V).

Gdy V jest dostatecznie duże, wtedy prąd fotoelektryczny osiąga maksymalną wartość
(prąd nasycenia). Wszystkie elektrony wybijane z płytki A docierają do elektrody B. Je-
żeli zmienimy znak napięcia V, to prąd nie spada do zera natychmiast (przy V = 0 mamy
niezerowy prąd).

Oznacza to, że fotoelektrony emitowane z płytki A mają pewną energię kinetyczną

.

Nie wszystkie elektrony mają jednakowo duża energię kinetyczną bo tylko część z nich
dolatuje do elektrody B (prąd mniejszy od maksymalnego). Przy dostatecznie dużym
napięciu (V

0

) zwanym

napięciem hamowania

prąd zanika. Różnica potencjałów V

0

po-

mnożona przez ładunek elektronu e jest miarą energii najszybszych elektronów (przy V

0

nawet najszybsze elektrony są zahamowane, nie dochodzą do B)

E

kmax

= eV

0

(32.4)

Krzywe a i b na rysunku różnią się natęże-
niem padającego światła (I

b

> I

a

). Widać

więc, że E

kmax

nie zależy od natężenia

światła. Zmienia się tylko prąd nasycenia,
a to oznacza, że wiązka o światła więk-
szym natężeniu wybija więcej elektronów
(ale nie szybszych).
Wynik innego doświadczenia pokazuje ry-
sunek obok. Pokazano tu zależność napię-
cia hamowania od częstotliwości światła
padającego dla sodu. (Millikan, Nobel w
1923).
Zauważmy, że istnieje pewna wartość pro-
gowa częstotliwości, poniżej której zjawi-
sko fotoelektryczne nie występuje.

I

a

I

b

+

-

V

0

V

12

8

4

0

cz

ęstotliwość (10

14

Hz)

V

h

(V)

3

2

1

Z. Kąkol-Notatki do Wykładu z Fizyki

32-9

Opisane zjawisko fotoelektryczne ma trzy cechy, których nie można wyjaśnić na gruncie
klasycznej falowej teorii światła:
1. Z teorii klasycznej wynika, że większe natężenia światła oznacza większe pole elek-

tryczne E (I ~ E

2

). Ponieważ siła działająca na elektron wynosi eE więc gdy rośnie

natężenie światła to powinna rosnąć ta siła, a w konsekwencji energia kinetyczna
elektronów. Tymczasem stwierdziliśmy, że E

kmax

nie zależy od natężenia światła.

2. Zgodnie z teorią falową zjawisko fotoelektryczne powinno występować dla każdej

częstotliwości światła pod warunkiem dostatecznego natężenia. Jednak dla każdego
materiału istnieje progowa częstotliwość v

0

, poniżej której nie obserwujemy zjawi-

ska fotoelektrycznego bez względu na jak silne jest oświetlenie.

3. Ponieważ energia w fali jest „rozłożona” w całej przestrzeni to elektron absorbuje

tylko niewielką część energii z wiązki (bo jest bardzo mały). Można więc spodzie-
wać się opóźnienia pomiędzy początkiem oświetlania, a chwilą uwolnienia elektro-
nu (elektron musi mieć czas na zgromadzenie dostatecznej energii). Jednak nigdy
nie stwierdzono żadnego mierzalnego opóźnienia czasowego.

Einsteinowi udało się wyjaśnić efekt fotoelektryczny dzięki nowemu założeniu, że ener-
gia wiązki świetlnej rozchodzi się w przestrzeni w postaci skończonych porcji (kwan-
tów) energii zwanych

fotonami

. Energia pojedynczego fotonu jest dana wzorem

E = hv

(32.5)

Przypomnijmy sobie, że Planck utrzymywał, że źródło emituje światło w sposób niecią-
gły ale w przestrzeni rozchodzi się ono jako fala elektromagnetyczna.
Hipoteza Einsteina sugeruje, że światło rozchodzi się w przestrzeni nie jak fala ale jak
cząstka.
Stosując tę hipotezę do efektu fotoelektrycznego otrzymamy

hv = W + E

kmax

(32.6)

gdzie hv oznacza energię fotonu. Równanie to głosi, że jeden foton dostarcza energii hv,
która w części (W) zostaje zużyta na wyrwanie elektronu z materiału (jego przejście
przez powierzchnię). Ewentualny nadmiar energii (hv – W) elektron otrzymuje w postaci
energii kinetycznej, przy czym część z niej może być stracona w zderzeniach wewnętrz-
nych (przed opuszczeniem materiału).
Rozpatrzmy teraz ponownie (z nowego punktu widzenia) trzy cechy fotoefektu nie dają-
ce się wyjaśnić za pomocą klasycznej teorii falowej.
1. Podwajając natężenie światła podwajamy liczbę fotonów a nie zmieniamy ich ener-

gii. Ulega więc podwojeniu fotoprąd a nie E

kmax

, która nie zależy tym samym od na-

tężenia.

2. Jeżeli mamy taką częstotliwość, że hv

0

= W to wtedy E

kmax

= 0. Nie ma nadmiaru

energii. Wielkość W nazywamy

pracą wyjścia

dla danej substancji. Jeżeli v < v

0

to

fotony niezależnie od ich liczby (natężenia światła) nie mają dosyć energii do wywo-
łania fotoemisji.

3. Dostarczana jest energia w postaci skupionej (kwant, porcja) a nie rozłożonej (fala).

Możemy przepisać równanie dla fotoefektu w postaci

Z. Kąkol-Notatki do Wykładu z Fizyki

32-10

e

W

v

e

h

V

−

=

0

(32.7)

Widać, że teoria przewiduje liniową zależność pomiędzy napięciem hamowania, a czę-
stotliwością, co jest całkowicie zgodne z doświadczeniem.
Teoria fotonowa całkowicie potwierdza więc fakty związane ze zjawiskiem fotoelek-
trycznym, wydaje się jednak być sprzeczna z teorią falową, która też potwierdzona zo-
stała doświadczalnie (np. dyfrakcja).
Nasz obecny punkt widzenia na naturę światła jest taki, że ma ono dwoisty charakter,
tzn. w pewnych warunkach zachowuje się jak fala, a w innych jak cząstka, czyli foton.
Ta dwoista natura będzie jeszcze omawiana na dalszych wykładach.

32.5

Efekt Comptona

Doświadczalne potwierdzenie istnienia fotonu jako skończonej porcji energii

zostało dostarczone prze Comptona w 1923 r (Nobel w 1927).
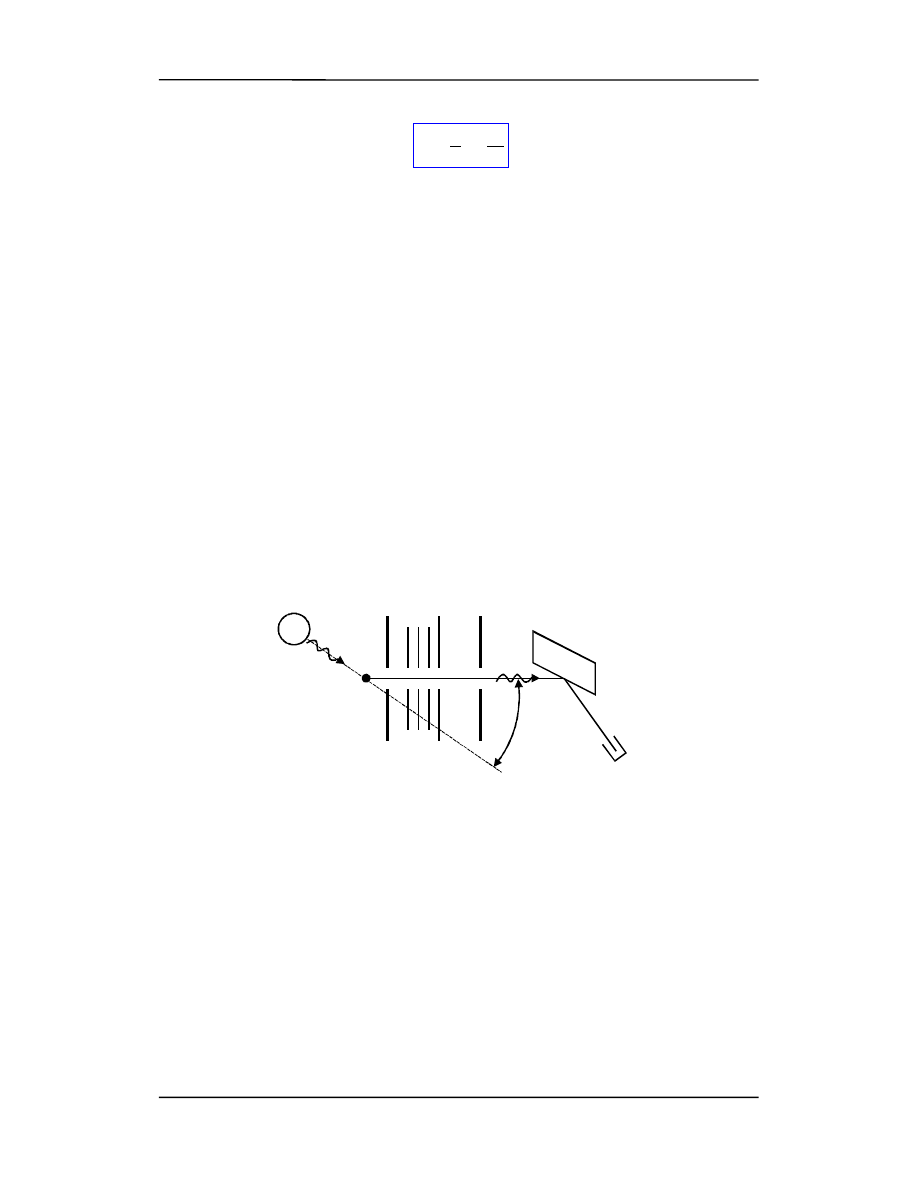
Wiązka promieni X o dokładnie określonej długości fali pada na blok grafitowy (rysu-
nek poniżej).
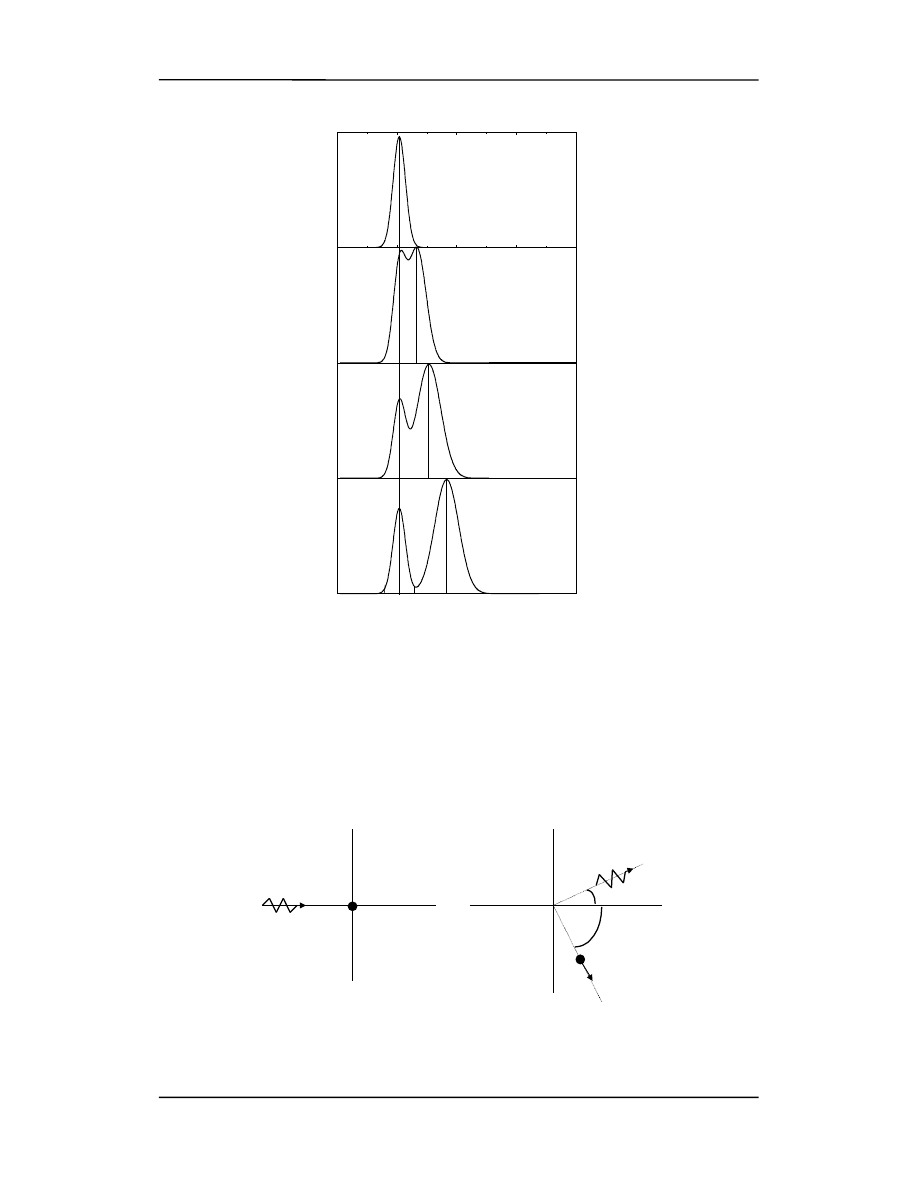
Compton mierzył natężenie wiązki rozproszonej pod różnymi kątami jako funkcję

λ.

Wyniki pokazane są na następnej stronie. Widać, że chociaż wiązka padająca na grafit
ma jedną długość fali to rozproszone promienie X mają maksimum dla dwóch długości
fali. Jedna z nich jest identyczna jak

λ

fali padającej, druga

λ' jest większa (dłuższa) o

∆

λ. To tzw.

przesunięcie Comptona

zmienia się z kątem obserwacji rozproszonego

promieniowania X (czyli

λ' zmienia się z kątem).

Jeżeli padające promieniowanie potraktujemy jako falę to pojawienie się fali rozproszo-
nej o długości

λ' nie da się wyjaśnić.

źródło promieni X

grafitowy blok
rozpraszający

szczeliny
kolimujące

detektor

kryształ grafitu

ϕ

Z. Kąkol-Notatki do Wykładu z Fizyki

32-11

Compton potrafił wyjaśnić swoje wyniki przyjmując, że wiązka promieni X nie jest falą,
a strumieniem fotonów o energii hv. Założył on, że fotony (jak cząstki) ulegają zderze-
niu z elektronami swobodnymi w bloku grafitu. Podobnie jak w typowych zderzeniach
(np. kule bilardowe) zmienia się kierunek poruszania się fotonu oraz jego energia (część
energii przekazana elektronowi). To ostatnie oznacza zmianę częstotliwości i zarazem
długości fali. Sytuacja ta jest schematycznie pokazana na rysunku poniżej.

Stosując zasadę zachowania pędu oraz zasadę zachowania energii (stosujemy wyrażenia
relatywistyczne) otrzymamy ostatecznie wynik

foton

foton

λ

'

λ

elektron

elektron

v=0

v

ϕ

θ

ϕ

= 45°

ϕ

= 90°

ϕ

= 135°

°

A

0.750

0.700

ϕ

= 0°

λ

,

Z. Kąkol-Notatki do Wykładu z Fizyki

32-12

)

cos

1

(

0

ϕ

λ

λ

λ

−

=

−

′

=

∆

c

m

h

(32.8)

gdzie m

0

jest masą elektronu (spoczynkową).

Tak więc przesunięcie Comptona zależy tylko od kąta rozproszenia.
Pozostaje tylko wyjaśnić występowanie maksimum dla nie zmienionej

λ. Za ten efekt

odpowiedzialne są zderzenia z elektronami rdzenia jonowego. W zderzeniu odrzutowi
ulega cały jon o masie M. Dla węgla (grafitu) M = 22000 m

0

więc otrzymujemy niemie-

rzalnie małe przesunięcie Comptona.