Kolokwium 1

 - odpowiedzi 

grupa III

 

Zadanie 1: Zdecydować, czy podane liczby są zapisane w postaci trygonometrycznej (a-c) lub 
kanonicznej (d-f). Jeśli nie są, doprowadzić do tej postaci. 

a) 

 
 

    

  

 

       

  

 

  - poprawnie, 

b)        

 

 

 

 

 

   

 

 

    

        

 

 

       

 

 

             

  

 

 

 

 

           

  

 

 

 

 

           

   

 

       

   

 

 , 

c)   

  

 

 

  

 

  - poprawnie, 

d) 

     

  

        , 

Zadanie 2: Na płaszczyźnie zespolonej narysować następujące obszary: 

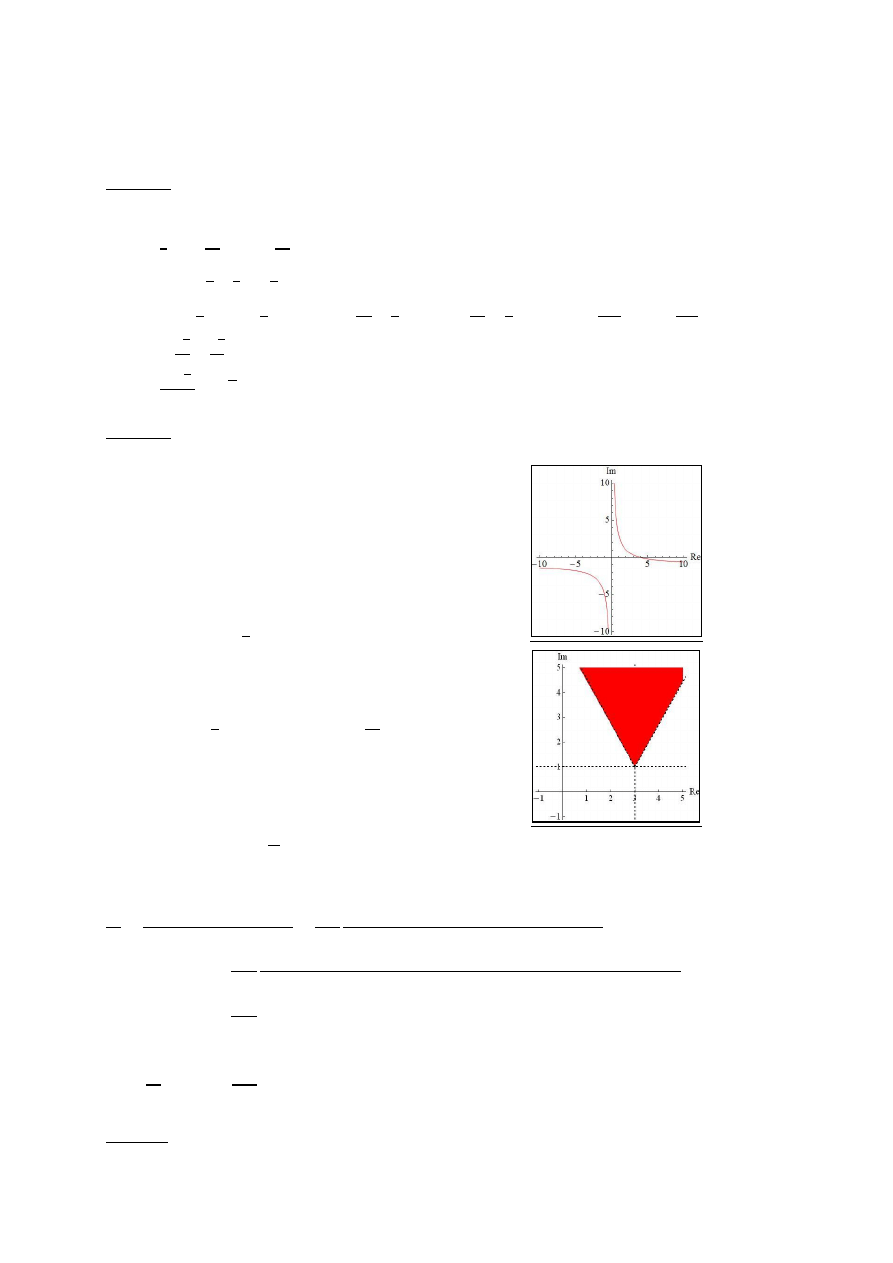
a)              

 

      , 

Niech            . 

               

    

 

        

 

   

 

               

            

 

                        

               

           

             

   

 
 

    - hiperbola 

 

b) 

 

 

                  

  

 

. 

Funkcja        przesunięta o wektor      . 

 

oraz dowieść:      

 

 

 

 

         

 

         

 

 . 

Niech  

 

    

 

      

 

        

 

  oraz  

 

    

 

      

 

        

 

 . 

 

 

 

 

 

  

 

      

 

        

 

 

  

 

      

 

        

 

 

 

  

 

 

  

 

 

     

 

        

 

         

 

        

 

 

    

 

 

 

     

 

 

 

 

 

  

 

 

  

 

 

     

 

    

 

      

 

    

 

         

 

    

 

      

 

    

 

  

 

 

  

 

 

  

 

 

      

 

   

 

           

 

   

 

   

Wtedy  

     

 

 

 

 

         

  

 

 

  

 

 

      

 

   

 

           

 

   

 

       

 

   

 

       

 

         

 

  

Zadanie3: Niech           

 

         . Dla   

 

   

 

 ,   

 

   

 

      kładziemy:  

  

 

   

 

      

 

   

 

       

 

   

 

   

 

 

 

  

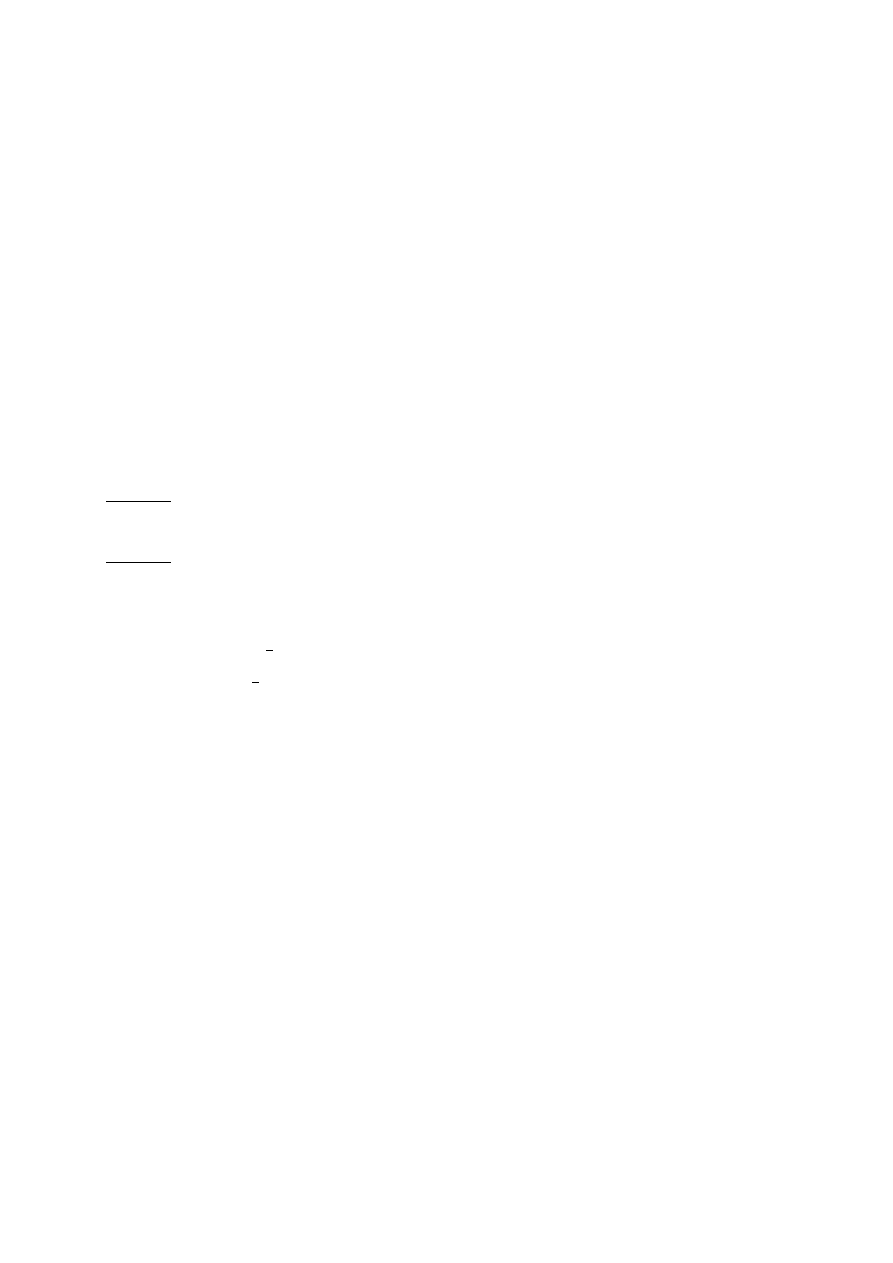
 Wykazać, że   jest działaniem wewnętrznym w zbiorze   i sprawdzić, czy       jest grupą. 

Odpowiedź: 

 Działanie wewnętrzne: 

  

 

   

 

      

 

   

 

      

 

   

 

   

 

 

 

      

 

   

 

   

 

 

 

 

 

      

 

   

 

   

 

 

  

 

  

 

Łączność: dowolne      

 

 ,      

 

 ,      

 

  

          

 

         

 

          

 

             

   

         

 

                   

       

   

         

 

          

 

         

 

          

 

             

   

                   

       

   

      na mocy łączności dodawania liczb rzeczywistych 

 

Element neutralny:      

 

          

     

 

                 

 

         

 

             

 

 

 

         

 

  

 

Element odwrotny: dla      

 

  ->       

  

  

     

 

          

  

             

   

         

 

          

Zadanie 4: Uzasadnić, że zbiór W jest podprzestrzenią liniową przestrzeni liniowej V:  

          

 

                                    ,      

 

    

Zadanie 5: Zbadać z definicji liniową niezależność układu wektorów:      ,      ,        w 
przestrzeni  

 

   . 

 

 

           

 

           

 

             

 

 

         

 

   

 

    

 

      

 

    

 

    

 

      

Rozwiązanie:   

 

   

 
 

 

 

 

 

 

 

 

 
 

 

 

 

Tylko wtedy gdy