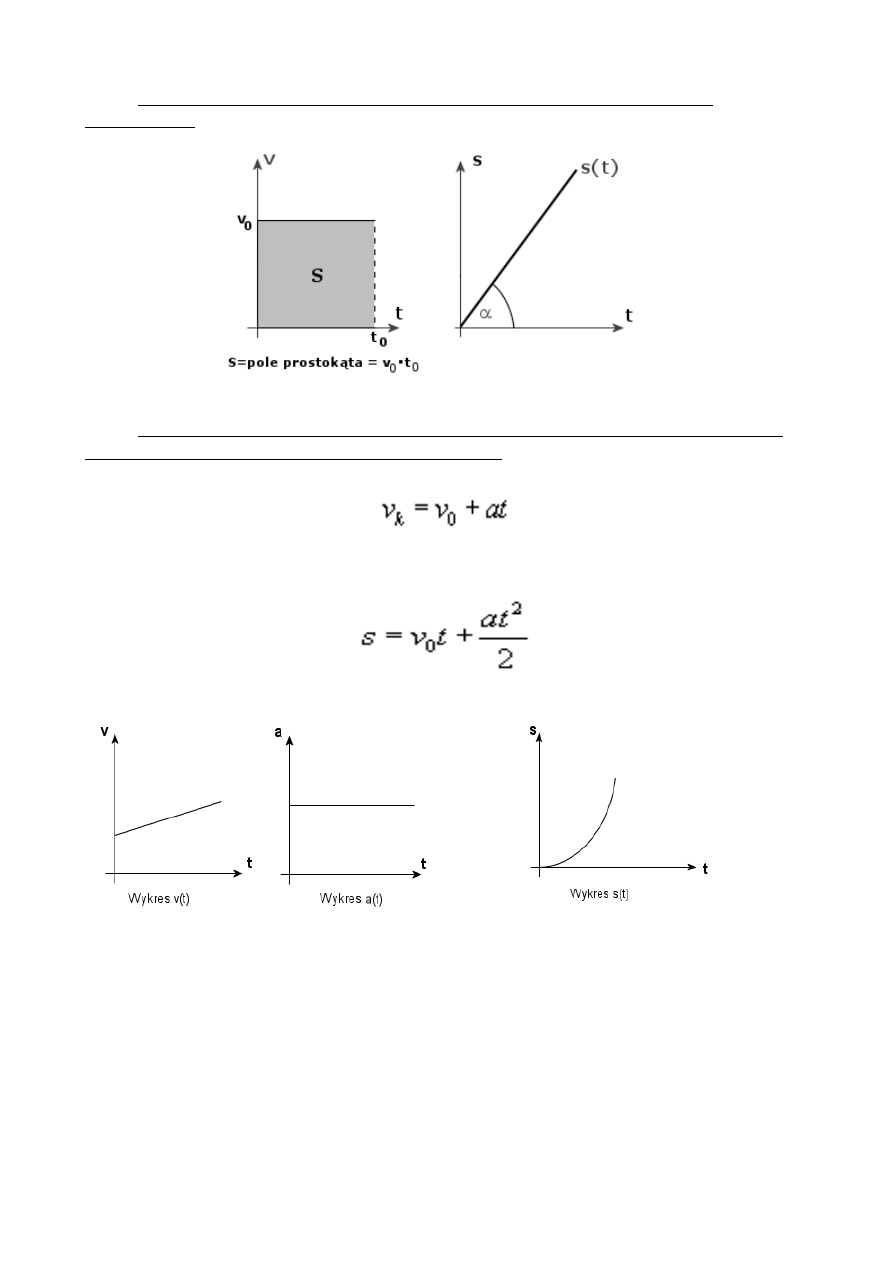
1. Narysuj zależności pomiędzy drogą a czasem oraz prędkością w ruchu 

jednostajnym.

2. Podaj równanie na prędkość w ruchu jednostajnie przyspieszonym oraz narysuj 

zależności między czasem a prędkością w tym ruchu.

Równanie prędkości w ruchu jednostajnie przyśpieszonym.

Równanie drogi w ruchu jednostajnie przyśpieszonym.

Wykresy prędkości od czasu V(t) i przyśpieszenia od czasu a(t), oraz drogi od czasu S(t)

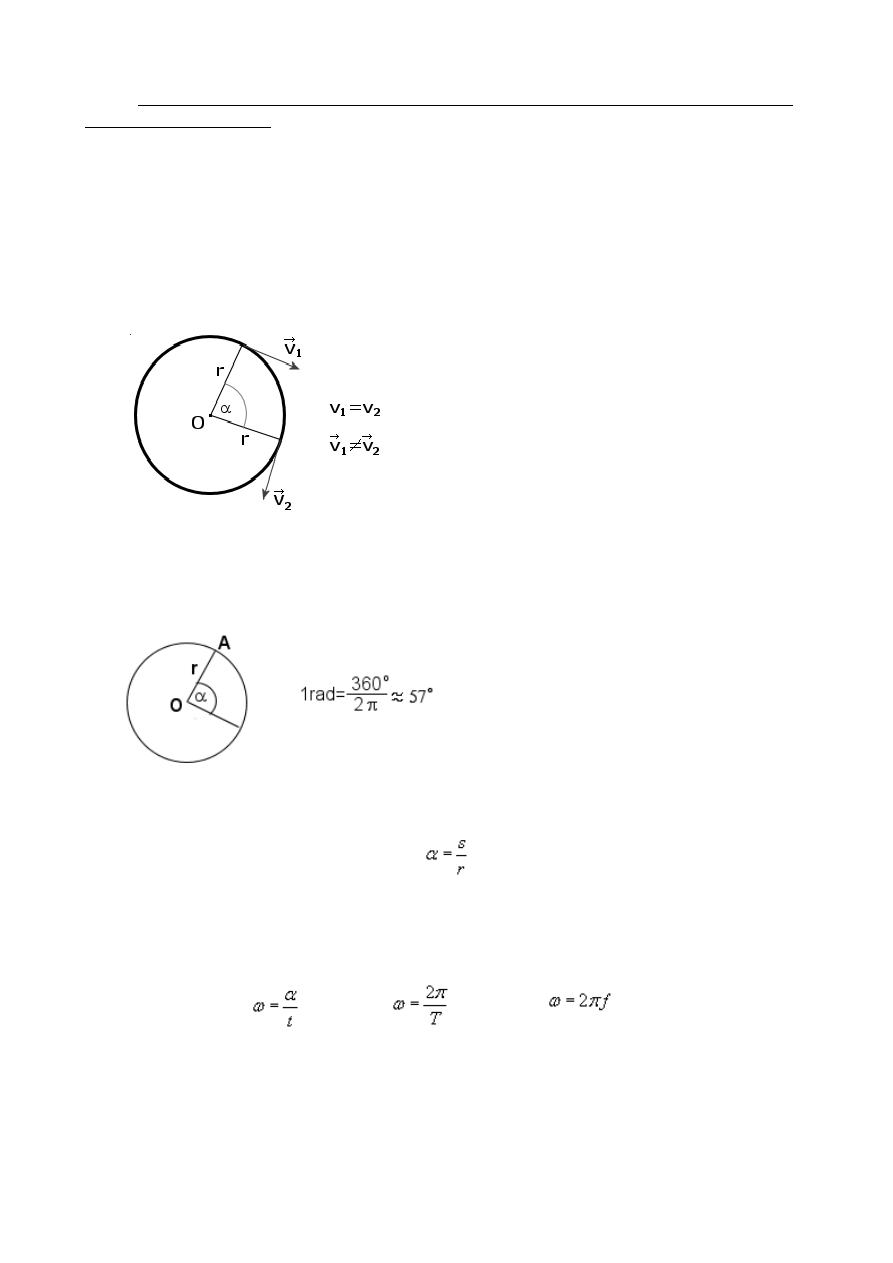
3. Zdefiniuj relację pomiędzy prędkością liniową, czasem i prędkością kątową oraz 

przedstaw je graficznie.

Jeżeli ciało w ruchu po okręgu przebywa jednakowe odcinki łuków w jednakowych 
odstępach czasu, to mówimy, że mamy do czynienia z ruchem jednostajnym po okręgu.

Prędkość liniowa jest wektorem stycznym do okręgu w każdym punkcie chwilowego 
położenia ciała (ponieważ prędkość jest styczna do toru w każdym ruchu krzywoliniowym) 

Jak widać prędkości w każdym punkcie łuku są 
sobie liczbowo równe, jednakże jako wektory 
są już różne (bo mają różne kierunki i zwroty). 

Punkt poruszający się po okręgu zakreśla pewien łuk, zwany też drogą liniową, zaś 
promień wodzący tego punktu (OA) zakreśla kąt α, zwany drogą kątową. Kąt ten 
wyrażamy w radianach. 

Kąt wyrażony w radianach obliczamy ze wzoru: 

gdzie
s - długość łuku,
r - długość promienia 

Prędkością kątową ω ("mała" omega) oznaczamy wielkość fizyczną, której miarą jest iloraz kąta α 
zakreślonego przez promień wodzący punktu poruszającego się po okręgu do czasu t, w którym ten 
kąt został zakreślony. 

związek między prędkością liniową a prędkością kątową: 

po „połączeniu” obydwu wzorów otrzymamy: 

Okresem T nazywamy czas trwania jednego obiegu (czyli czas zakreślenia przez punkt 
materialny całego okręgu). Jednostką okresu jest 1 sekunda.
Częstotliwością nazywamy liczbę obiegów w jednostce czasu (np. 1 s) i oznaczamy ją f. 
Jednostką okresu jest 1 herc (Hz).
1 Hz to częstotliwość ruchu, w którym jeden obieg wykonywany jest przez jedną sekundę.

4. 

   Wyprowadź wzór na trajektorię w ruchu (równanie toru ruchu) w rzucie

 

  

poziomym.

Rzut poziomy to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje się 
ciału prędkość początkową skierowaną poziomo. 

Rzut poziomy jest więc złożeniem dwóch ruchów:
- w kierunku poziomym ruch ciała jest jednostajny prostoliniowy z prędkością v

0

,

- w kierunku pionowym ruch jest jednostajnie przyspieszony bez prędkości początkowej – czyli 
swobodny spadek (w tym ruch działa na ciało siła ciężkości mg).

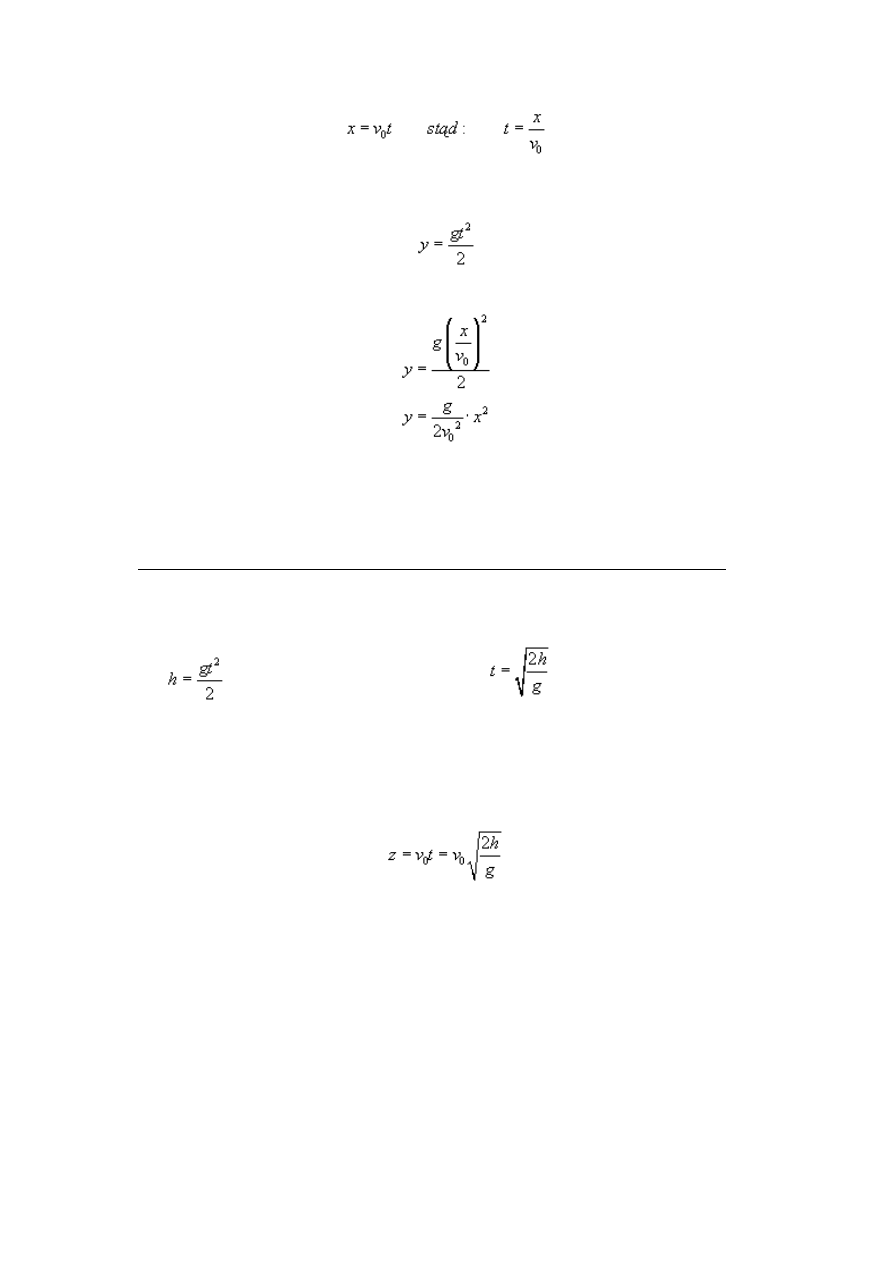
Współrzędna x jest równa drodze przebytej ruchem jednostajnym poziomym 

Współrzędna y jest równa drodze przebytej ruchem jednostajnie przyspieszonym pionowym 
(swobodny spadek), zatem: 

Łączymy oba wzory: 

(jest to równanie praboli)

5.

   Napisz relację pomiędzy współrzędną 

 

 x 

   i   y 

   a czasem w rzucie poziomym.

 

 

Czas rzutu poziomego jest równy czasowi każdego ruchu składowego. Obliczymy go jako 
czas swobodnego spadku z wysokości h: 

stąd po przekształceniu

Zasięg rzutu poziomego z jest równy drodze przebytej w kierunku poziomym ruchem 
jednostajnym w czasie t. 

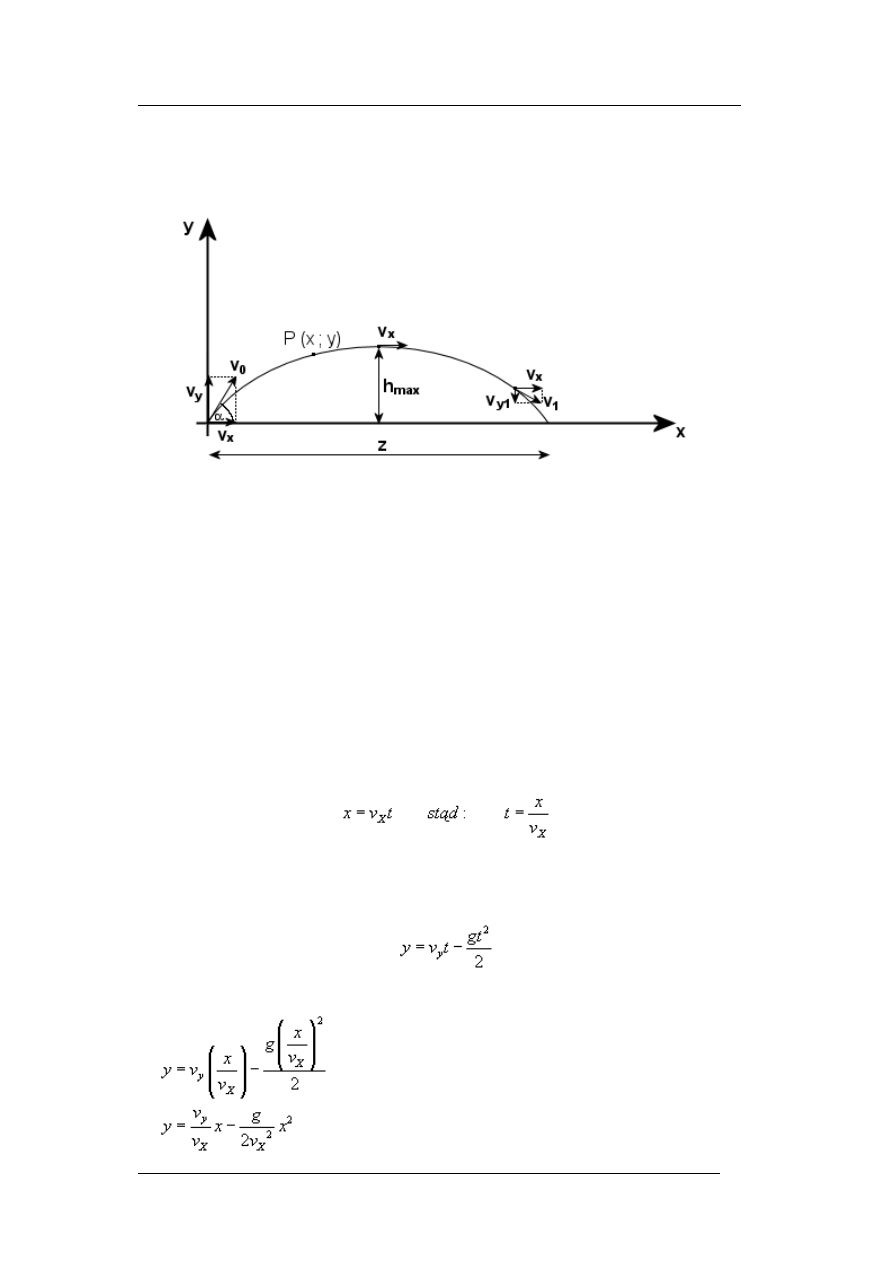
6.Wyprowadź wzór na trajektorię ruchu (równanie ruchu) w rzucie ukośnym.

Rzut ukośny to ruch w polu grawitacyjnym Ziemi blisko jej powierzchni, w którym nadaje 
się ciału prędkość początkową skierowaną do poziomu pod kątem α. 

Podobnie jak w rzucie poziomym, tak i w rzucie ukośnym, ciało wykonuje jednocześnie 
ruch w poziomie i w pionie. Rzut ukośny jest złożeniem dwóch ruchów:
- w kierunku poziomym ruch jednostajny z prędkością vx,
- w kierunku pionowym ruch jest jednostajnie zmienny
+ do hMAX jednostajnie opóźniony (rzut pionowy do góry z prędkością vy),
+ od hMAX jednostajnie przyspieszony (swobodny spadek) – działa tutaj siła
ciężkości mg. 

RÓWNANIE TORU RZUTU UKOŚNEGO 

Współrzędna x równa jest drodze przebytej przez ciało w kierunku poziomym ruchem 
jednostajnym z prędkością vx: 

Współrzędna y równa jest drodze przebytej w ruchu pionowym – jednostajnie opóźnionym 
(rzut pionowy do góry z prędkością vy): 

łącząc dane wzory otrzymamy:

torem rzutu ukośnego jest parabola.

7. Napisz relację pomiędzy współrzędną 

 

 x 

   i   y 

   a czasem u rzucie ukośnym. 

 

 

Czas rzutu ukośnego jest równy czasowi każdego ruchu składowego. Jak wykazaliśmy 
(podczas omawiania rzutu pionowego do góry) czas wznoszenia ciała równy jest czasowi 
spadku z osiągniętej wysokości. Tak więc czas rzutu pionowego w górę t równa się 
podwojonemu czasowi wznoszenia się ciała tW lub spadania tS. 

Korzystając z równań kinematycznych rzutu pionowego: 

Zasięg rzutu ukośnego równy jest drodze przebytej przez ciało w kierunku poziomym – 
ruchem jednostajnym z prędkością vx w czasie t. 

8. Trzy zasady dynamiki Newtona na przykładzie konia ciągnącego sanie:

*  ruchem jednostajnym, prostolinijnym.

 

 

*ruchem jednostajnie przyspieszonym.

I zasada dynamiki Newtona

Jeżeli na ciało nie działają żadne siły lub działające siły równoważą się, to ciało to 
pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

Rozważmy, co będzie się działo z ruchem ciała, gdy usuniemy oddziaływania z wszystkimi innymi 

ciałami? Weźmy tego konia ciągnącego sanie po śniegu. Koń przestaje ciągnąć, sanie zatrzymują 
się wkrótce. Zakładając że postawimy sanie podłożu, np. lodzie, to ich ruch ruch będzie trwał 
zdecydowanie dłużej (po tym jak koń przestanie je ciągnąć). Jeżeli jeszcze zmniejszymy tarcie, to 
sanie będą się poruszał znacznie dłużej. Itd...  do przypadku, gdy usuniemy wszystkie opory ruchu. 
Wtedy oczywiście sanie będą się poruszały dowolnie długo ruchem bezwładnym i 
najprawdopodobniej uderzą konia w dupe, o ile koń ciągnie sanie na sznurku... w ogole zakładamy 
że sznurek był dość długi, bo inaczej będzie trudno to sobie wyobrazić.  

Jasne jest,  dlaczego skacząc do góry i odrywając się od Ziemi spadamy na to samo miejsce. 

Mamy przecież tę samą prędkość co Ziemia. Ponieważ w kierunku poziomym nie działa żadna siła, 
więc nie ma przyczyny, aby wywołać zmianę prędkości w tym kierunku. Podobnie, gdy w jadącym 
ruchem jednostajnym wagonie skoczymy w górę. Również spadniemy w to samo miejsce na 
podłodze wagonu, gdyż mamy tę samą prędkość co wagon i podczas skoku pokonujemy w 
poziomie tę samą drogę co wagon. 

Tym samym, w saniach poruszających się ruchem jednostajnym, jeżeli położymy kulkę na 

„podłodze” to pozostanie ona w spoczynku (oczywiście zakładamy że sanie poruszają się po 
idealnie gładkim terenie, nie wieje wiatr i nie pada śnieg... nie ma żadnych „przeszkadzaczy” , bo 
inaczej nie wyjdzie ku*wa!)  

II zasada dynamiki Newtona

Jeżeli na ciało działa układ sił wzajemnie nie równoważących się 

(niezrównoważonych),  znaczy istnieje wypadkowa tych sił, to ciało porusza się ruchem 
jednostajnie przyspieszonym (lub opóźnionym) z przyspieszeniem (lub opóźnieniem) 
wprost proporcjonalnym do działającej siły zgodnie z nią skierowanym oraz odwrotnie 
proporcjonalnym do masy ciała. 

F

w

 - wypadkowa sił.

Korzystając z II zasady dynamiki, definiujemy jednostkę siły w układzie SI. Jednostką siły jest 1 
niuton (1 N) - jest to siła, która masie jednego kilograma nadaje przyspieszenie 1 m/s

2

. 

Galileusz wykazał, że siła nie jest potrzebna do podtrzymania ruchu jednostajnego ciała. Newton 
ujął to w postaci prawa bezwładności jako pierwszą zasadę dynamiki. Newton poszedł jednakże 
dalej od swojego poprzednika, stwierdzając, że siła nie jest potrzebna do podtrzymania ruchu 
jednostajnego, ale konieczna jest do zmiany wektora prędkości ciała. Żadna zmiana prędkości nie 
zajdzie, jeśli nie zadziała na ciało siła. Innymi słowy, siła działająca na ciało wywołuje zmianę 
prędkości, czyli nadaje mu przyspieszenie. To właśnie jest treścią drugiej zasady dynamiki.

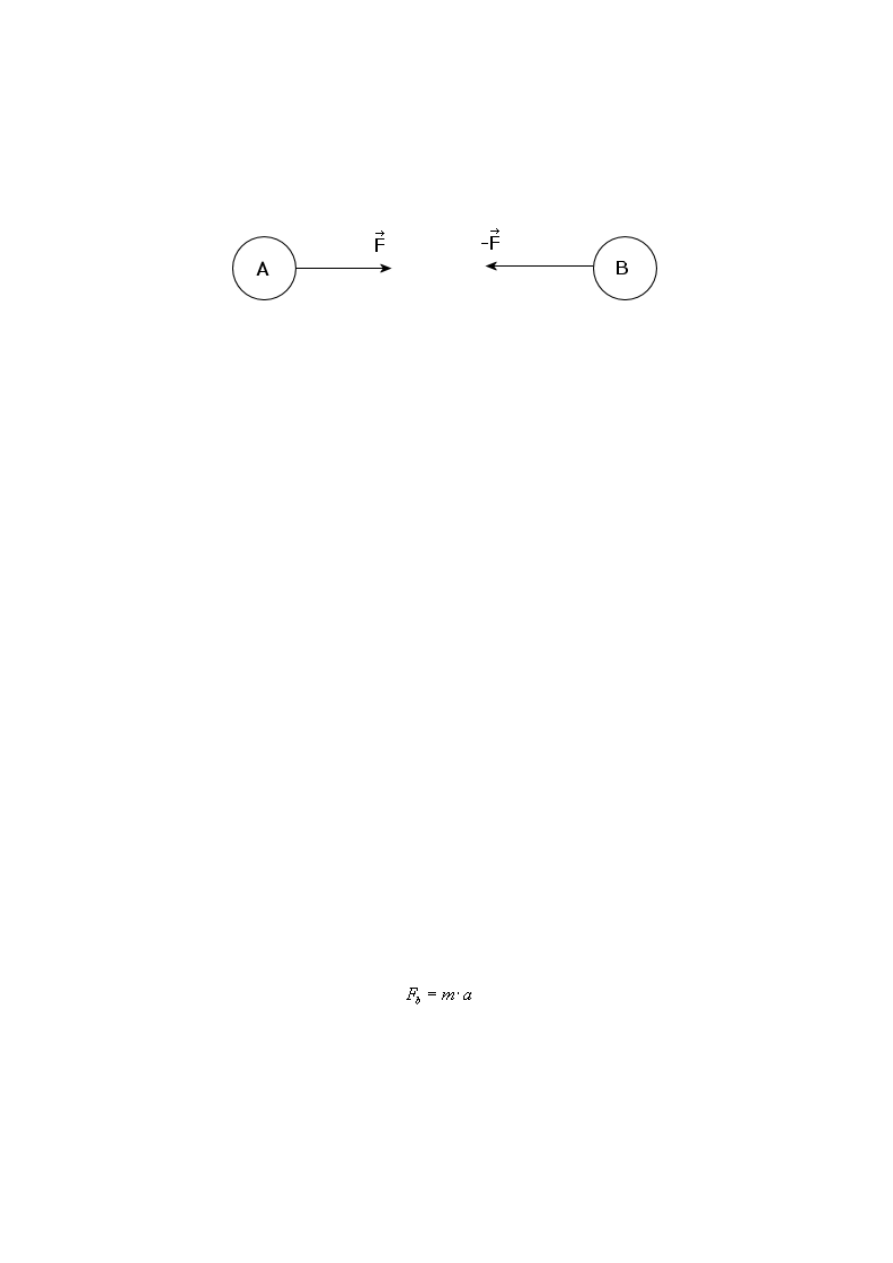
III zasada dynamiki Newtona
Jeżeli ciało A działa na ciało B siłą F, to ciało B działa na ciało A taką samą co do wartości 
siłą -F, lecz zwróconą przeciwnie. 

Zauważmy, że te dwie siły nie równoważą się wzajemnie, mimo że są skierowane przeciwnie. 
Bowiem siły te są przyłożone do różnych ciał.
Zasada ta stwierdza ponadto, że siły zawsze występują parami. Koń działa siłą na sanie, natomiast 
sanie działają na konia taką samą siłą, ale w stronę przeciwną, dzięki temu koń z saniami uzyskuje 
przyspieszenie i pokonuje opory.

Ziemia przyciąga spadający kamień siłą F = mg, a kamień przyciąga Ziemię z siłą o takiej 

samej wartości. Nie zauważamy tego ponieważ masa Ziemi M jest znacznie większa od masy 
kamienia m. 

Pierwsza i druga zasada dynamiki Newtona mówi nam o ruchu ciała, gdy działa, lub nie 

działa na nie siła. Zasady te nie określają skąd pochodzą siły działające na ciało. Newton 
zrozumiał, że aby na ciało (sanie) zadziałała siła, potrzebne jest jakieś inne ciało (koń). To inne 
ciało musi być w bezpośrednim kontakcie z danym ciałem (sznurek łączący sanie z koniem), na 
które oddziałuje siłą.

BEZWŁADNOŚĆ, UKŁADY INERCJALNE I NIEINERCJALN E

Sanie (zaprzęgnięte w konia) poruszają się z przyspieszeniem a. Na „podłodze” sań położono 
kulkę. Ponieważ sanie się poruszają (z przyśpieszeniem), zaobserwujemy że kulka zaczyna 
poruszać się po „podłodze” w kierunku przeciwnym do kierunku ruchu sań. 

Rozpatrzmy to zjawisko z punktu widzenia dwóch różnych obserwatorów, czyli z punktu 

widzenia dwóch układów odniesienia. Jeden z układów, zwany inercjalnym, jest związany z 
otoczeniem. Układ ten nie posiada przyspieszenia, w nim jest obserwator A. Drugi układ 
odniesienia, zwany nieinercjalnym, jest związany z saniami. Układ ten posiada przyspieszenie i w 
nim jest obserwator B. Obserwator B, który siedzi w saniach, powie, że kulka, on i inne przedmioty 
oraz osoby znajdujące się w saniach, poddane są działaniu jakiejś dodatkowej siły, zwróconej 
przeciwnie do kierunku jazdy. Tę siłę nazywamy siłą bezwładności. Natomiast obserwator A 
patrzy na sanie, widzi  kulkę która się przemieściłą, ale żadnej dodatkowej siły nie czuje.

Siły bezwładności działają jedynie w układzie nieinercjalnym. Są to siły pozorne, ponieważ 

nie pochodzą one od żadnego ciała, więc nie posiadają źródła. Siła bezwładności ma wartość: 

m - masa ciała, na które działa siła bezwładności,
a - przyspieszenie układu
Po poznaniu układu inercjalnego można podać ogólniejszą postać I zasady dynamiki:

Istnieje taki układ odniesienia, w którym jeżeli na ciało nie działa żadna siła lub siły 

działające na to ciało równoważą się, to ciało zachowuje stan spoczynku lub porusza się 
ruchem jednostajnym po linii prostej. Taki układ nazywamy układem inercjalnym.  

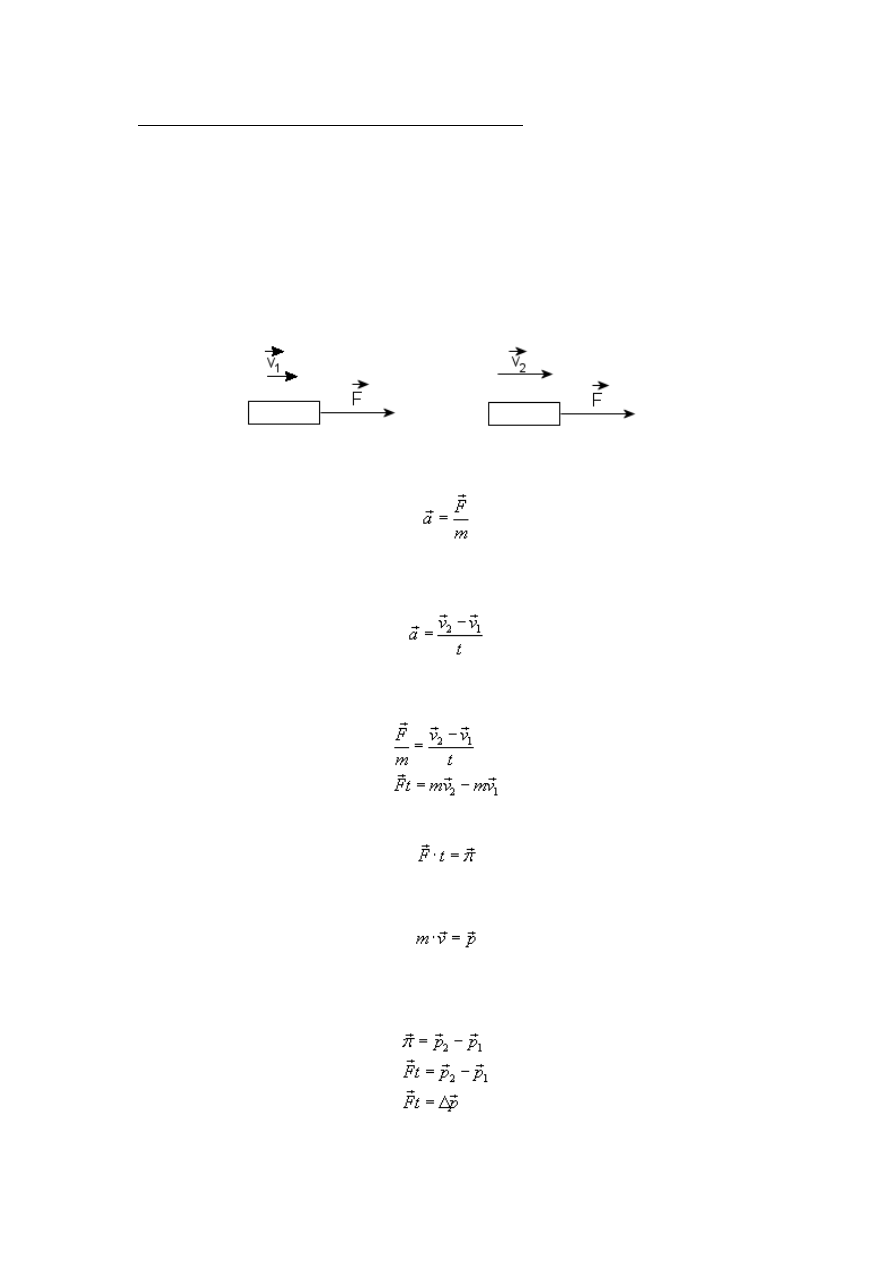
9.

   Wyprowadź wzór na prędkość końcową rakiety

 

 

Pęd i popęd

Na ciało o masie m posiadające prędkość początkową v

1

 działa siła F, której zwrot jest zgodny ze 

zwrotem wektora prędkości ciała. Pod działaniem tej siły prędkość ciała wzrasta do wartości v

2 

(ruch jednostajnie przyspieszony). 

Z II zasady dynamiki 

Z definicji przyspieszenia dla ruchu jednostajnie przyspieszonego 

stąd: 
 

Popęd:

Pęd

łącząc to wszystko w całość

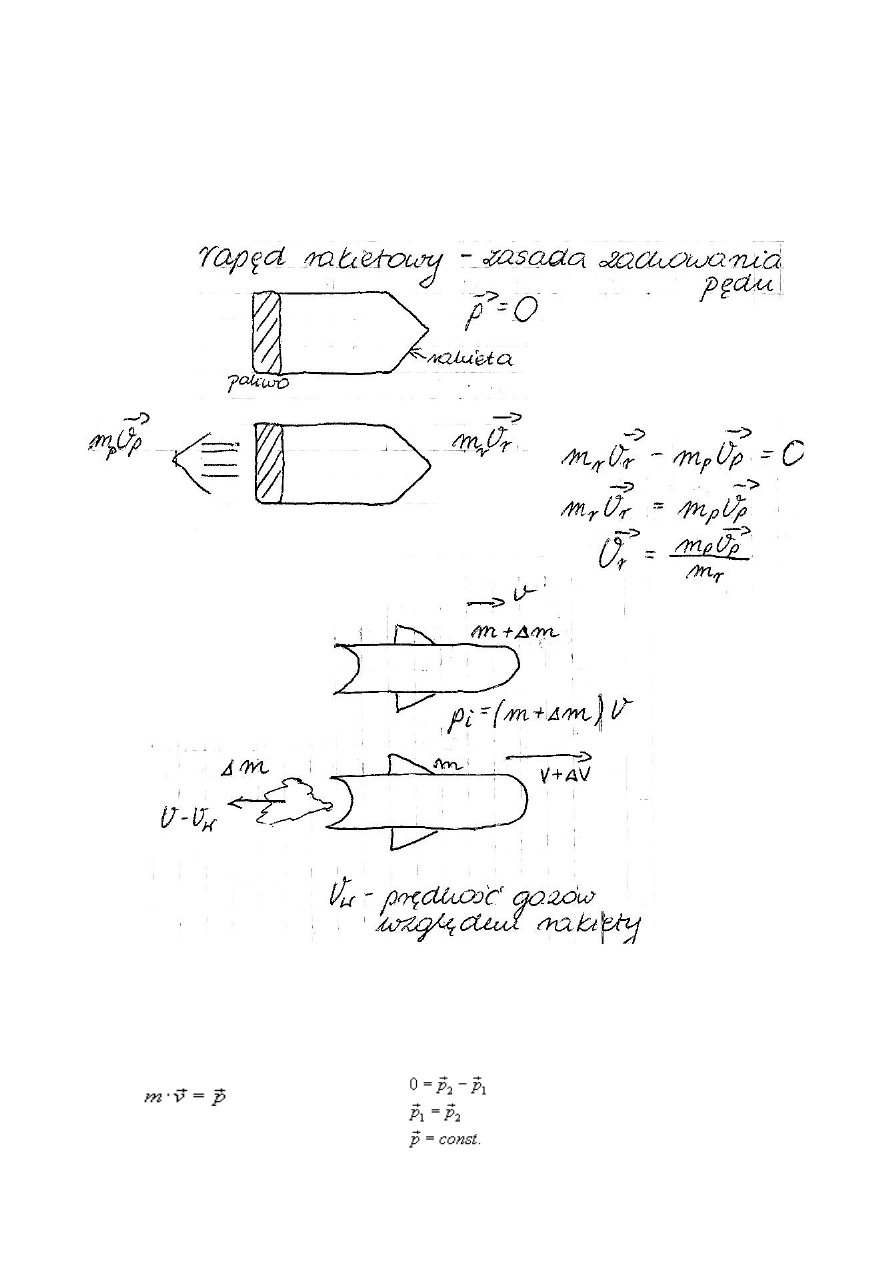
Zasada zachowania pędu

Całkowity pęd układu odosobnionego jest stały i nie ulega zmianie podczas dowolnych procesów 
zachodzących w układzie. 
Oczywiście pędy poszczególnych ciał, wchodzących w skład danego układu mogą się zmieniać, ale 
całkowity pęd układu, to znaczy wektorowa suma wszystkich pędów składowych, nie ulega 
zmianie. 

Różnica polega na tym że w drugim przypadku mamy prędkość początkową,  nie występującą w 
pierwszym. 

Korzystamy głównie ze wzoru 

p – pęd, m – masa , v – pędkość. [ p1 – „pęd rakiety” , p2- „pęd paliwa” ].

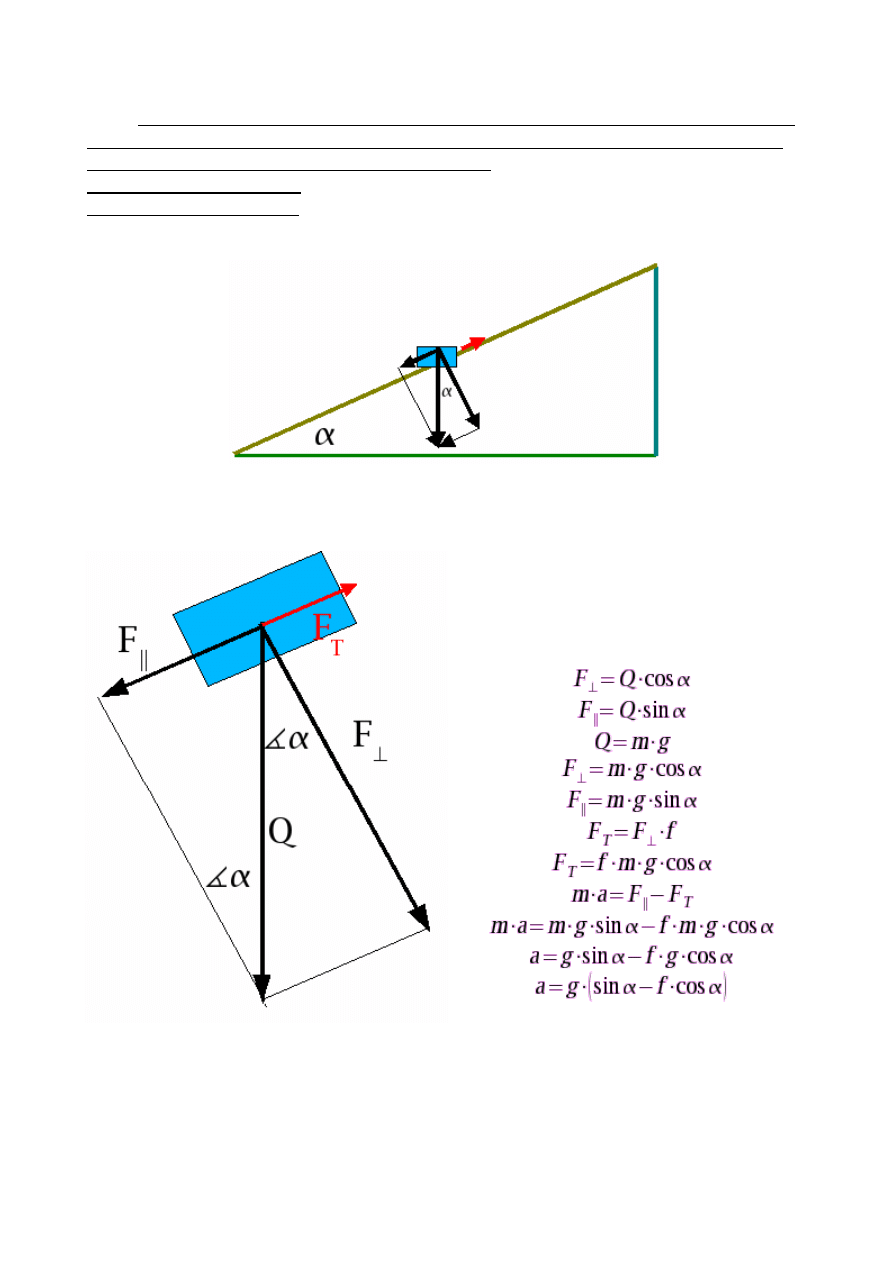
10. 

   Ciało zaczyna zsuwać się po równi pochyłej o długości 

 

 l   i wysokości 

 

 h  . Narysuj

 

  

rozkład sił na równi. Współczynnik tarcia wynosi 

 

 f   a przyśpieszenie ziemskie 

 

 g. 

   Znaleźć

 

  

prędkość ciała przy podstawie równi, korzystając z:
zasady zachowania energii.
zasady dynamiki Newtona.

Rozkład sił na „klocku”. Rozwiązanie z 
„zasad dynamiki Newtona”. 

„l” - długość równi. 

Z prawa zachowania energii:

Należy jednak pamiętać że taka relacja zachodzi jeżeli mamy do czynienia z układem który 

jest „niezależny”.  W tym wypadku tak nie jest gdyż występuje siła tarcia.

Składając te 4 zwory do kupy mamy: 

Teraz uwzględniamy w ogólnym wzorze dodatkową pracę „W”, wynikającą z tarcia.

mgh=

mV

2

2



F

T

⋅

l

Teraz za podstawiamy 

i otrzymujemy:

mgh=

mV

2

2



mgf ⋅cos a

 

Po przekształceniu tego wzoru otrzymamy wynik.

mgh−mgf ⋅cos a=

m⋅V

2

2

V

2

=

2⋅ gh−gf⋅cosa

V =



2g⋅h− f ⋅cos a 

h=l⋅sin a 

V =



2glsin a− f⋅cosa

Jak widzimy prędkość końcowa jest w obydwu przypadkach taka sama, bez względu na 

sposób obliczania.