a
Parametry zadane dla projektowanego filtru cyfrowego:
fpass
400
Apass
3
fstop
500
Astop
40
fpr
1700
Obliczenie pulsacji unormowanych
Ωpass
2 π
fpass
fpr
Ωstop
2 π
fstop
fpr
Ωpass 1.4784
Ωstop 1.848
ωpass
2 fpr
tan
Ωpass
2
ωstop
2 fpr
tan
Ωstop
2
ωpass
3.1
10
3
ωstop
Obliczenie pulsacji filtru prototypowego
ωstop_unor
ωstop
ωpass
ωpass_unor
1
ωstop_unor
1.453
Wyznaczenie wspólczynnika εoraz γ
d
10
0.1 Astop
1
10
0.1 Apass
1
100.233
ε
10
0.1 Apass
1
0.998
k
ωstop
ωpass
1.45
γ
1
ε
1.002
γ
1.002
Wyznaczenie rzedu filtru
N
ceil
acosh d
( )
acosh k
( )
N
6
Obliczenie biegunów transmitancji:
R
cosh
asinh γ
( )
N
1.011
r
sinh
asinh γ
( )
N
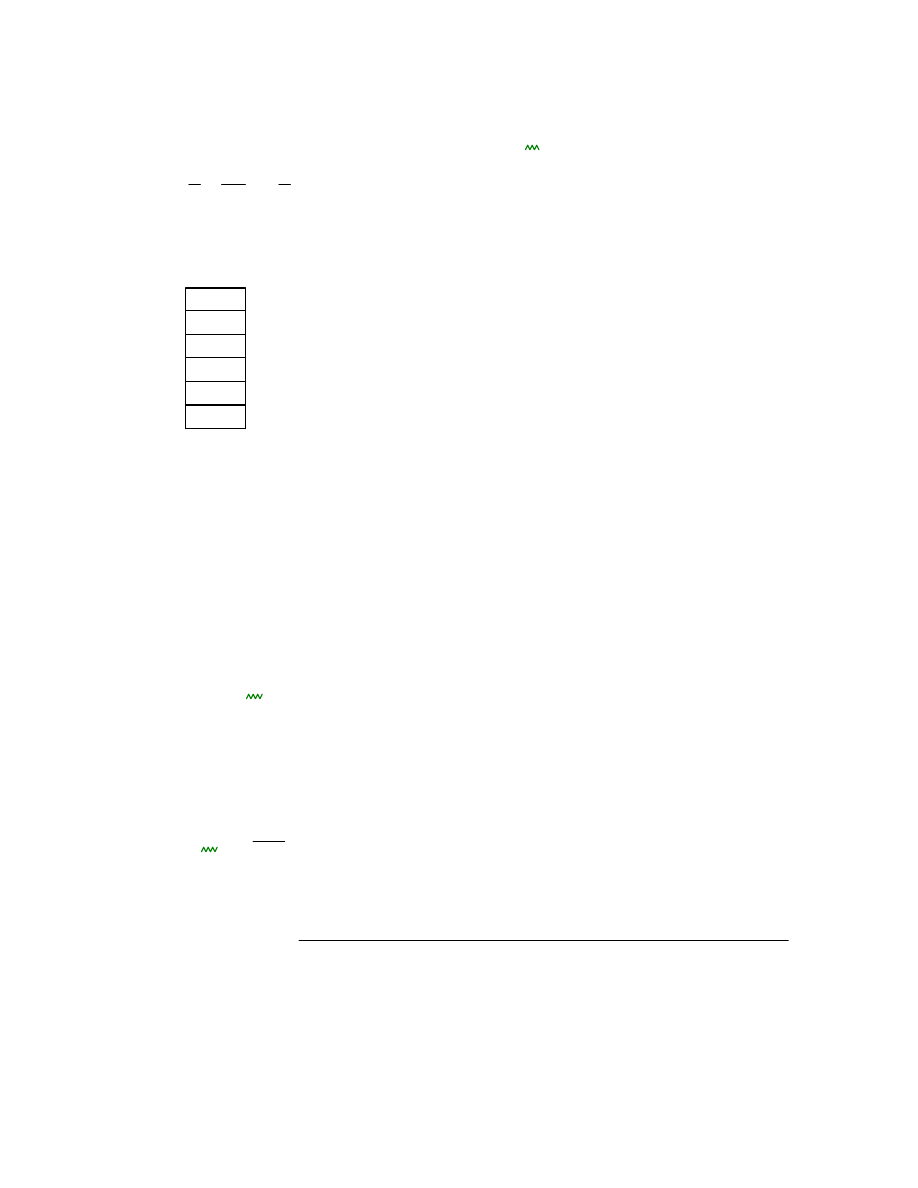
R
1.011
r
0.148
k
0 N
1
ϕ
k
π
2
π
2 N
k
π
N
p
k
Re r e
i ϕ
k
i Im R e
i ϕ
k
ϕ
k
1.833
2.356
2.88
3.403
3.927
4.451
p
k
0.038
0.976i
0.104
0.715i
0.143
0.262i
0.143
0.262i
0.104
0.715i
0.038
0.976i
Odczytanie z tablicy wielomianów Czebyszewa postaci mianownika dla rzędu filtru 6 i
zafalowania równego 2dB
M s
( )
s
2
0.07646s
0.95483
s
2
0.20889s
0.52182
s
2
0.28535s
0.08880
Obliczenie iloczynu sprzężonych
biegunów
L
Re
0
N 1
k
p
k
0.044
Obliczenie wartości licznika
transmitancji
H s
( )
L
M s
( )
Za pomocą funkcji explicit podstawiamy wartość licznika i mianowanika
H s
( ) explicit ALL
0.04424673625782994
0.28535 s
s
2
0.0888
0.20889 s
s
2
0.52182
0.07646 s
s
2
0.95483
Otrzymujemy następującą transmitancję filtru prototypowego
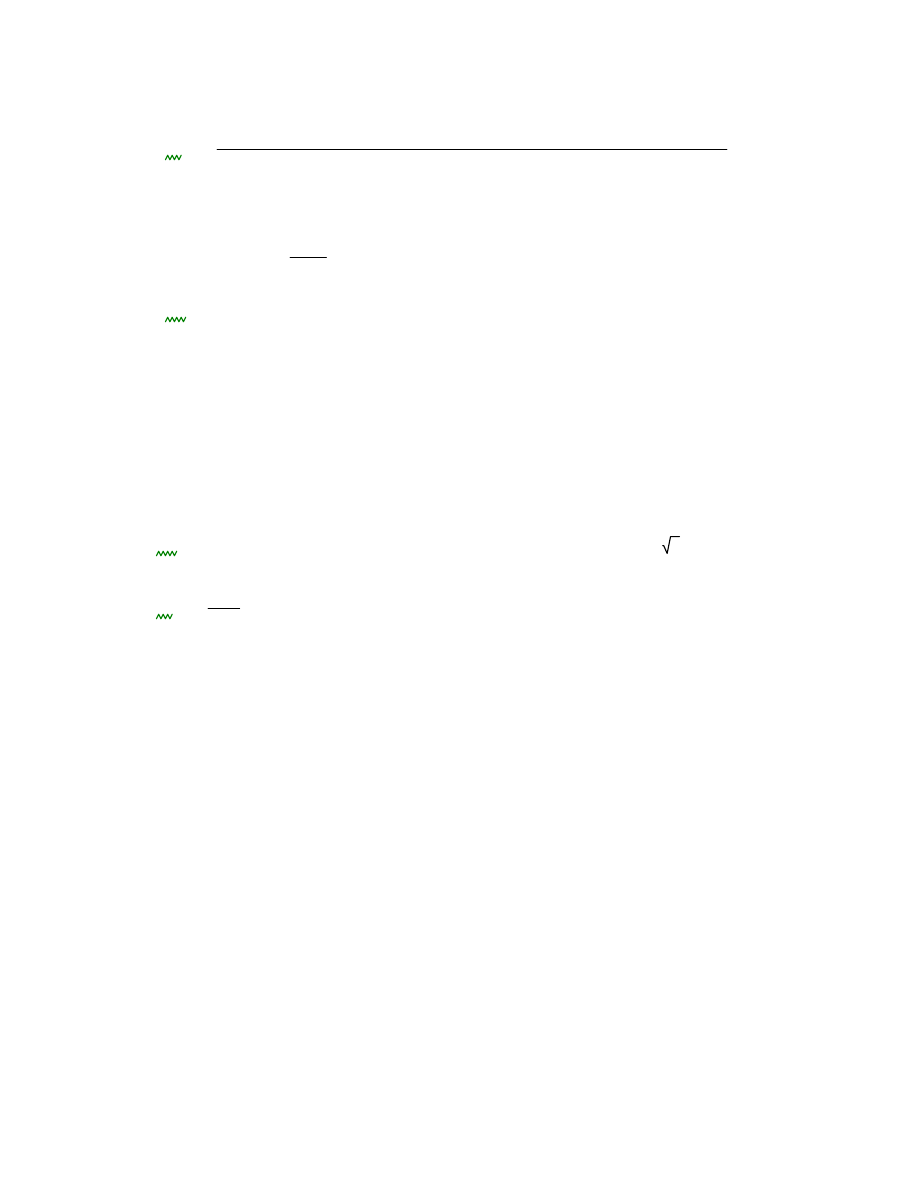
H s
( )
0.051441276666980777
0.35061 s
s
2
0.09993
0.09395 s
s
2
0.96595
0.25667 s
s
2
0.53294
M s
( ) substitute s
s
ωpass
=
1.1278260884886069746e-21 s
6
1.9950003956358954363e-18 s
5
1
M s
( )
9.326232271330151356e-21 s
6
1.4254402266602157165e-17 s
5
7.7353769682405426001e
Przemnożenie wartości liczniki i mianownika przez ω
pass
6
L1
L ωpass
6
3.923
10
19
M s
( ) ωpass
6
expand
8.553712759830705789582943e16 s
1.439831793540817944629861e14 s
2
M s
( )
2.988912882661539554892915e19 s
2.24923599379606564257174e16
5
s
2
1.15974464
H s
( )
L1
M s
( )
Za pomocą funkcji explicit podstawiamy liczniki i mianownik
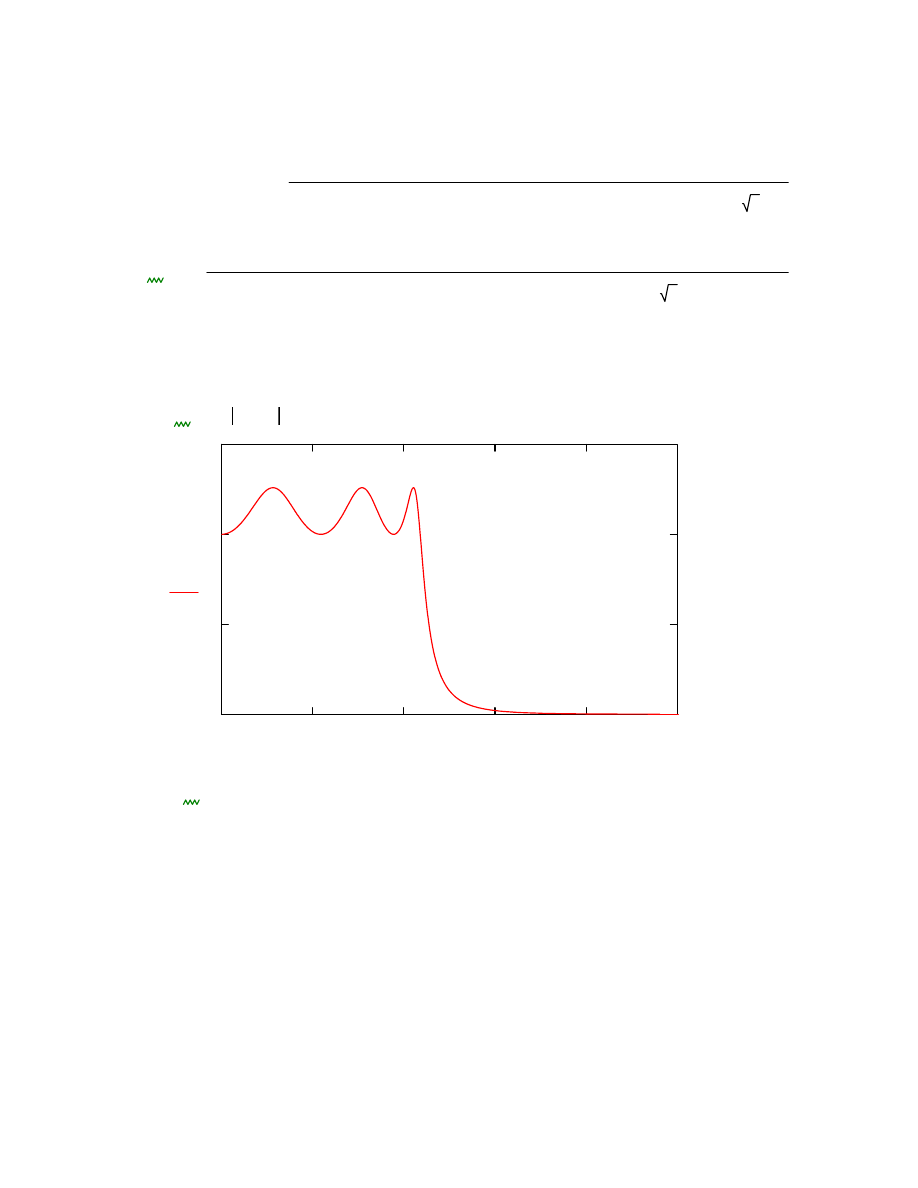
H s
( ) explicit ALL
2.988912882661539554892915e19
s
2.24923599379606564257174e16
5
s
2
H s
( )
2.988912882661539554892915e19
s
2.24923599379606564257174e16
5
s
2
1.159744647
Wyznaczenie charakterystyk czestotliwosciowych
ω
1 5
10000
A ω
( )
H i ω
(
)
0
1 10
3
2 10
3
3 10
3
4 10
3
0
0.5
1
A ω
( )
ω
charakterystyka amplitudowa
L ω
( )
20 log A ω
( )
(
)
charakterystyka amplitudowa logarytmiczna
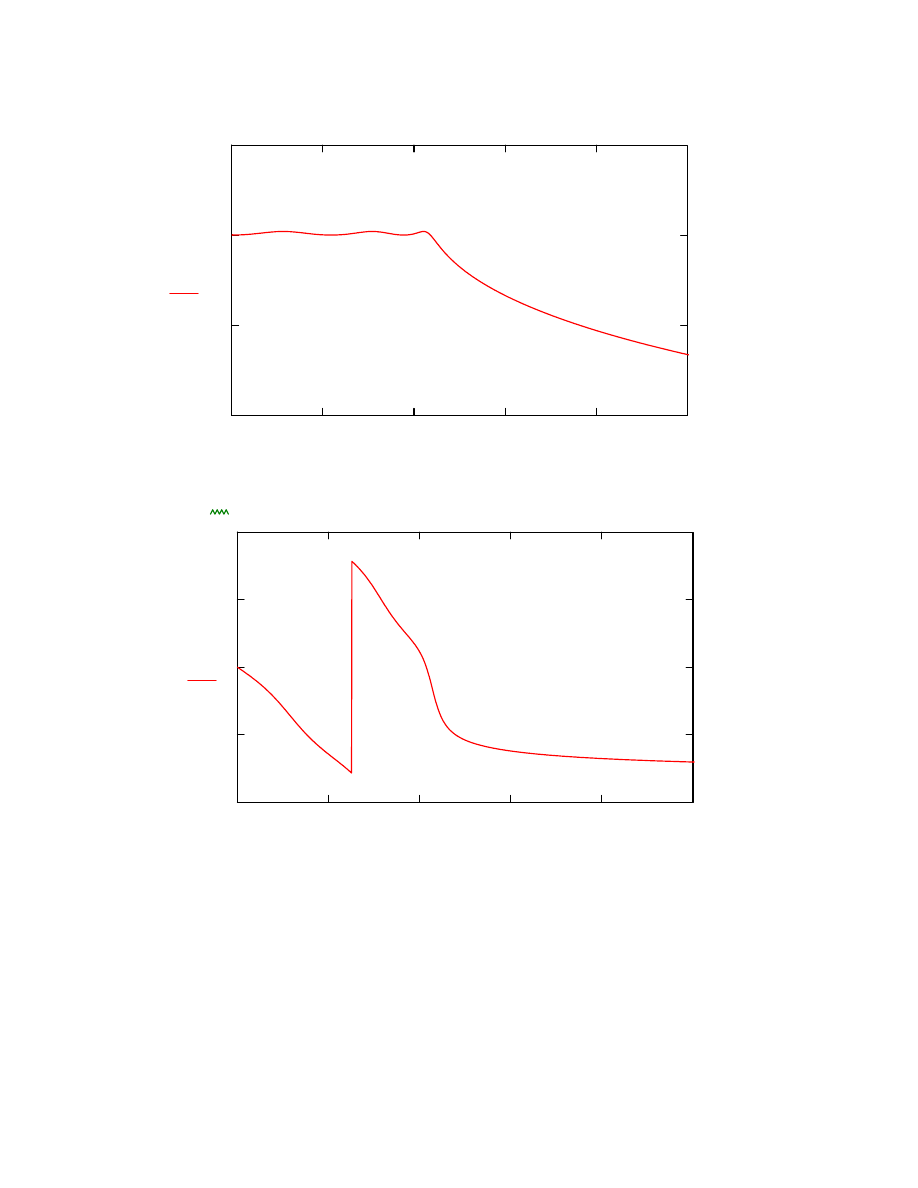
0
1 10
3
2 10
3
3 10
3
4 10
3
100
50
0
L ω
( )
ω
Φ ω
( )
arg H i ω
(
)
(
)
charakterystyka fazowa
0
1 10
3
2 10
3
3 10
3
4 10
3
4
2
0
2
4
Φ ω
( )
ω
P ω
( )
Re H i ω
(
)
(
)
wykres Nyquista
Q ω
( )
Im H i ω
(
)
(
)
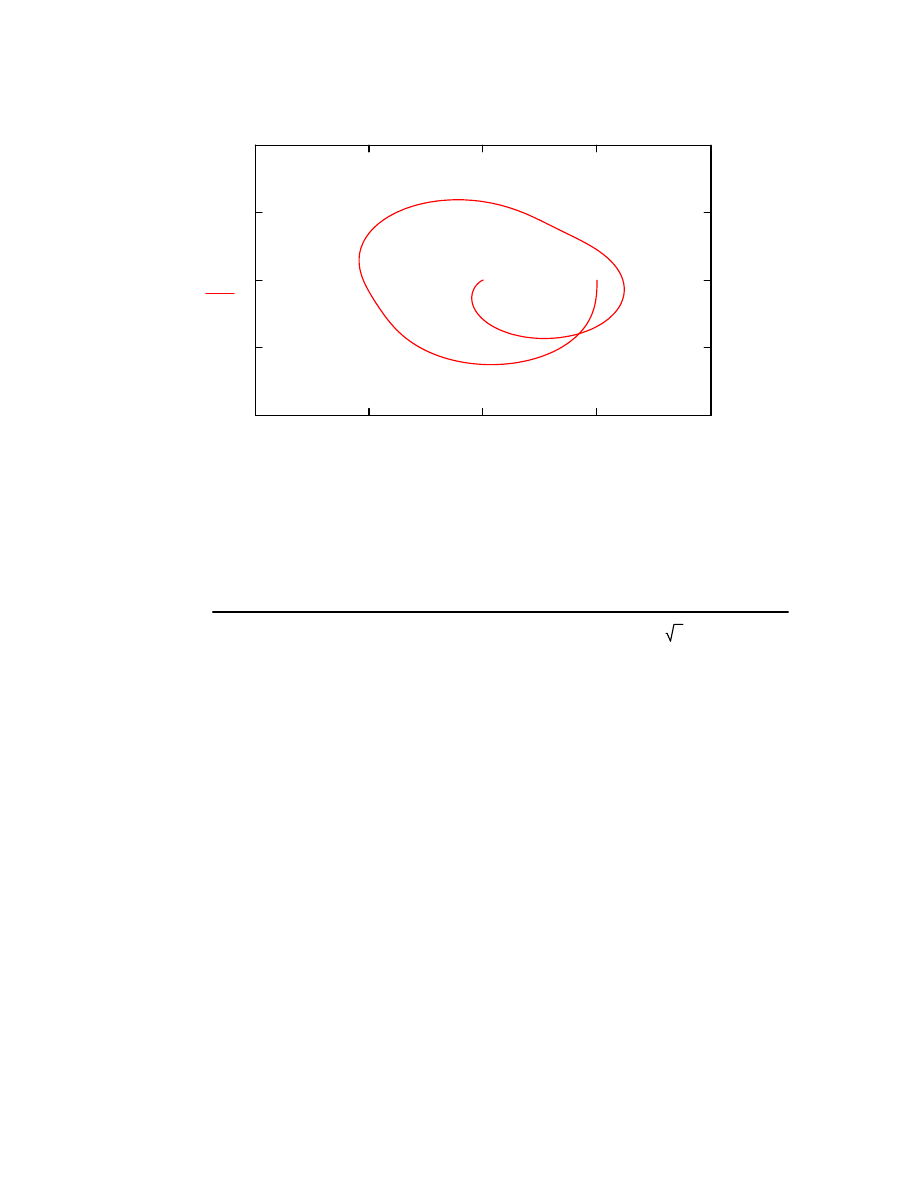
2
1
0
1
2
2
1
0
1
2
Q ω
( )
P ω
( )
Wyznaczenie charakterystyk czasowych
Odpowiedz impulsowa
2.988912882661539554892915e19
s
2.24923599379606564257174e16
5
s
2
1.15974464
Imp t
( )
156.5 e
102.4
t
cos 2140.0 t
(
)
215.9 e
102.4
t
sin 2140.0 t
(
)
133.2 e
382.1
t
cos 573.4
(
t
0 0.0001
0.2
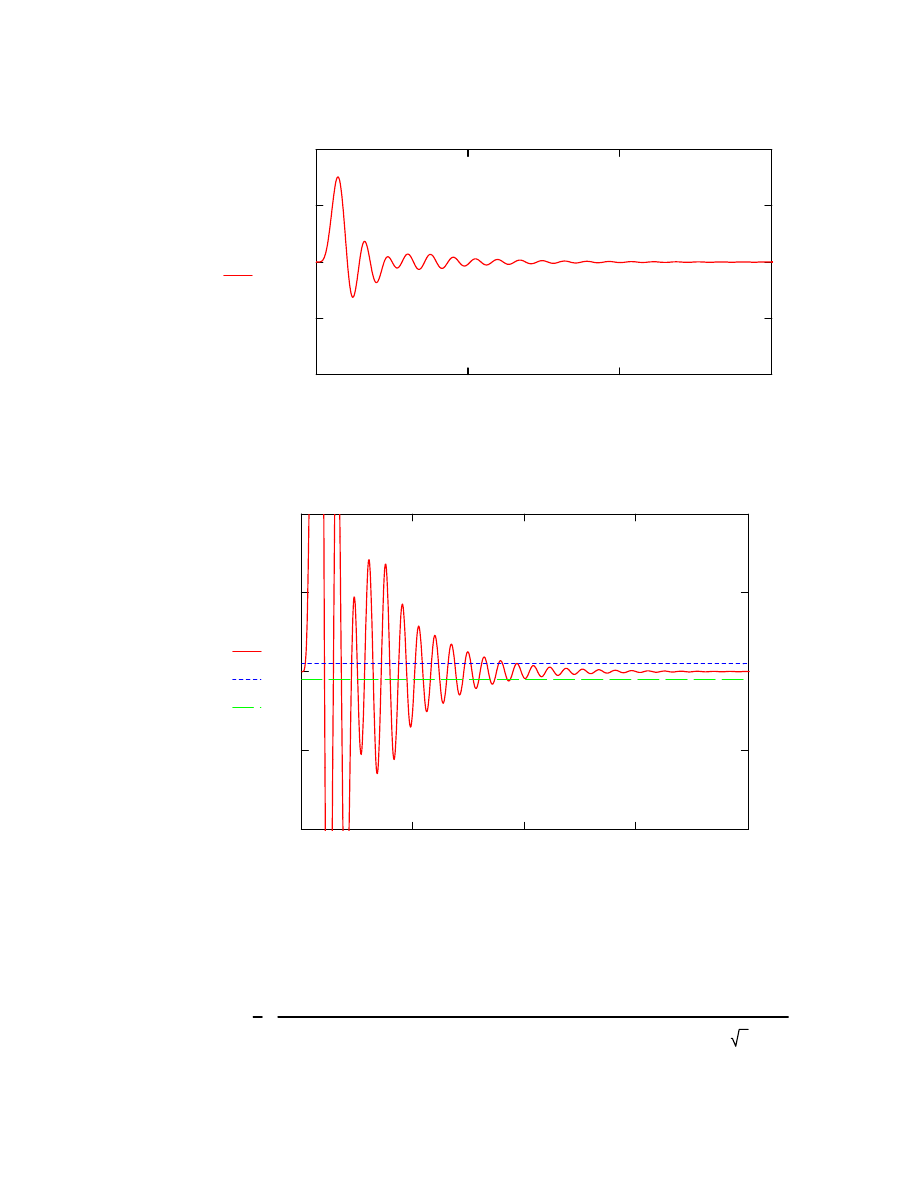
0
0.02
0.04
1
10
3
500
0
500
1 10
3
Imp t
( )
t
Wyznaczenie czasu ustalania
0
0.02
0.04
0.06
0.08
100
50
0
50
100
Imp t
( )
5
5
t
Imp 0.03745
(
)
4.565
Szacunkowy czas ustalania: ok.0.03745 s
Odpowiedz skokowa
Skok t
( )
1
s
2.988912882661539554892915e19
s
2.24923599379606564257174e16
5
s
2
1
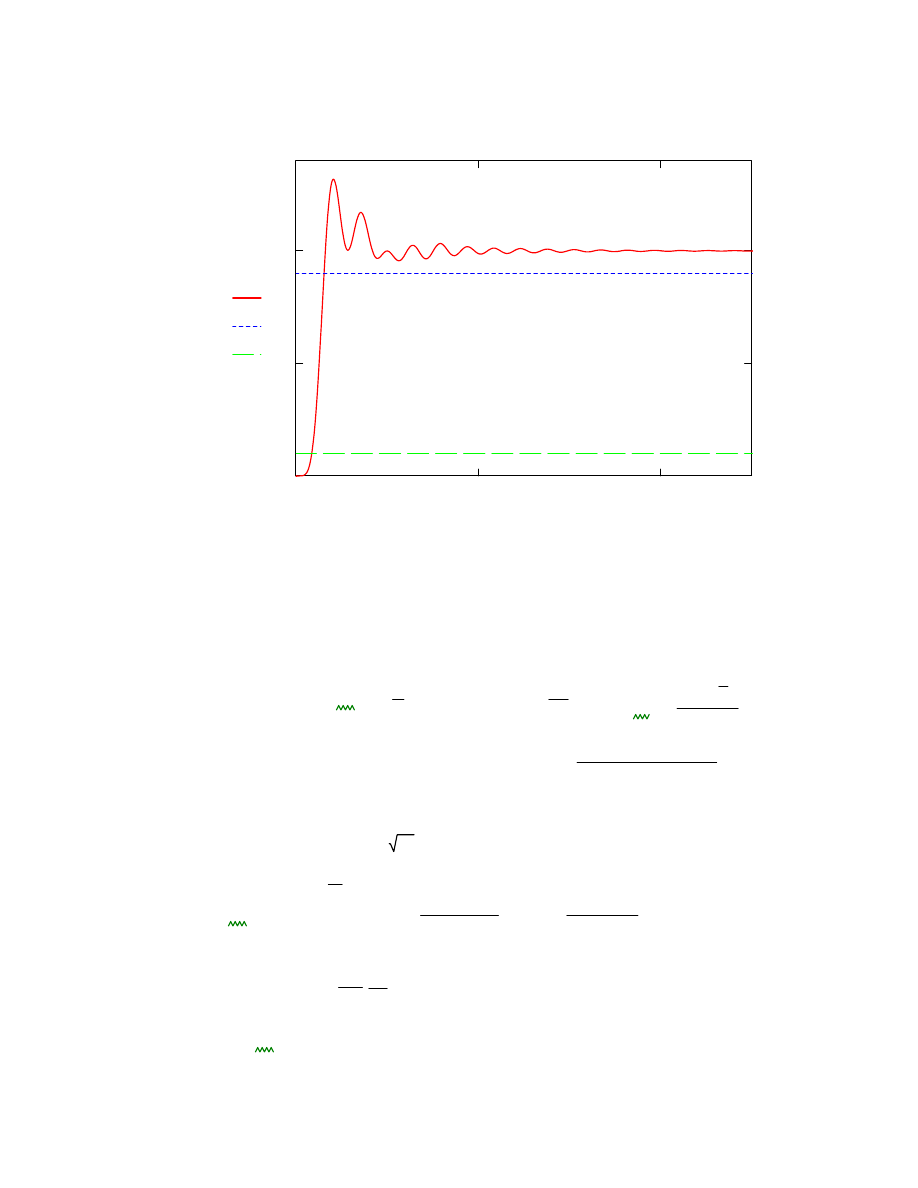
0
0.02
0.04
0
0.5
1
Skok t
( )
0.9
0.1
t
Skok 0.00176
(
)
0.102
0.0031
0.00176
1.34
10
3
Skok 0.0031
(
)
0.901
Szacunkowy czas narastania: 0.00134 s
Opoznienie grupowe
Wspolczynniki
m
2
N
2
α
m
2m
1
(
)
π
2N
γ
m
asinh
1
ε
N
b
m
1
cosh γ
m
2
cos α
m
2
a
m
2 b
m
sinh γ
m
cos α
m
j
1
Φ Ω
( )
arg
2
N
2
m
1
b
m
Ω
2
ωpass_unor
2
j
a
m
Ω
ωpass_unor
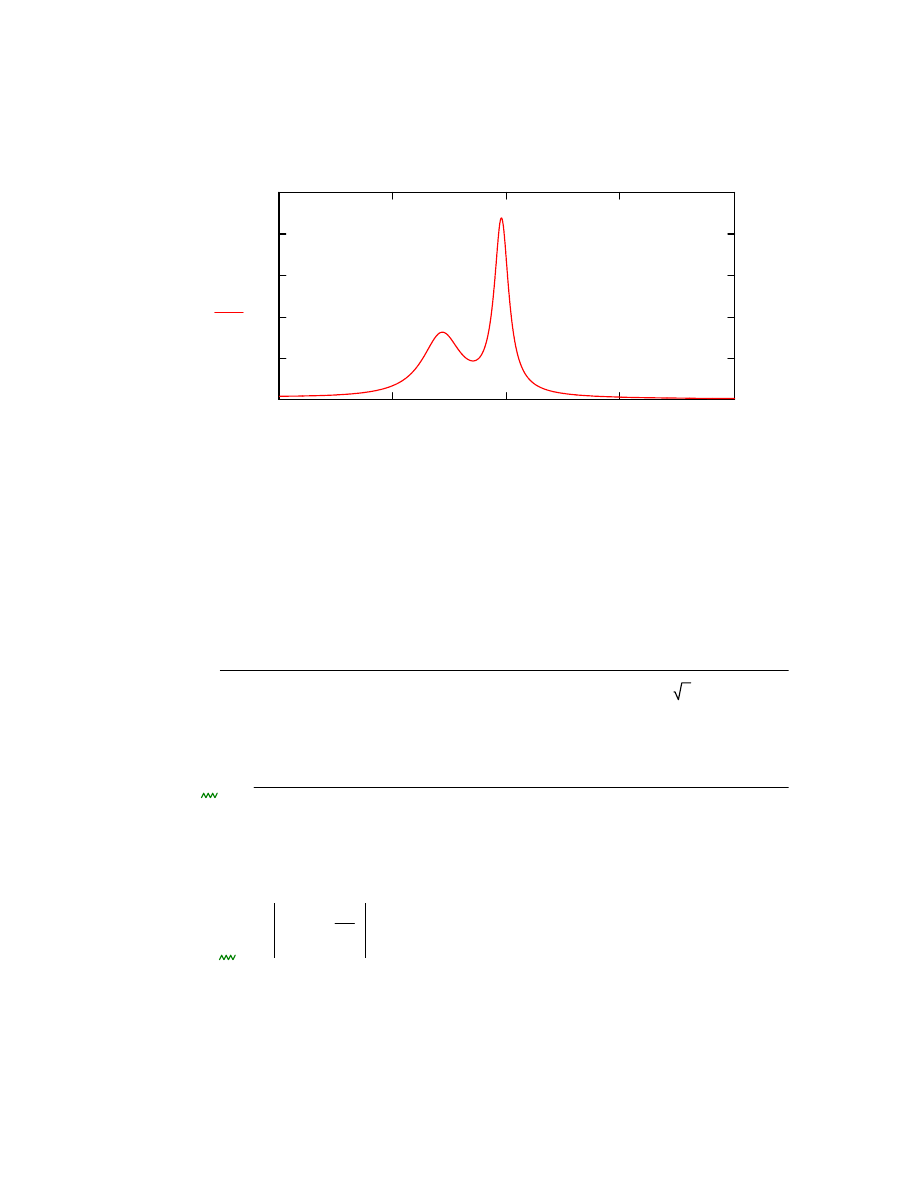
Tgrup Ω
( )
1
2 π
Ω
Φ Ω
( )
d
d
Ω
0.0005 0.001
2
0
0.5
1
1.5
2
0
1
2
3
4
5
Opoznienie grupowe
Pulsacja unormowana
Tgrup Ω
( )
Ω
Wyznaczenie transmitancji filtru cyfrowego
Hcyf z
( )
2.988912882661539554892915e19
s
2.24923599379606564257174e16
5
s
2
1.1597446
H z
( )
6.619e21 z
1.655e22 z
2
2.206e22 z
3
1.655e22 z
4
6.619e21 z
5
1.103e21 z
6
8.019e23
z
1.781e24 z
2
2.482e24
z
3
2.295e24 z
4
1.347e24
z
5
4.416e23 z
6
R
R
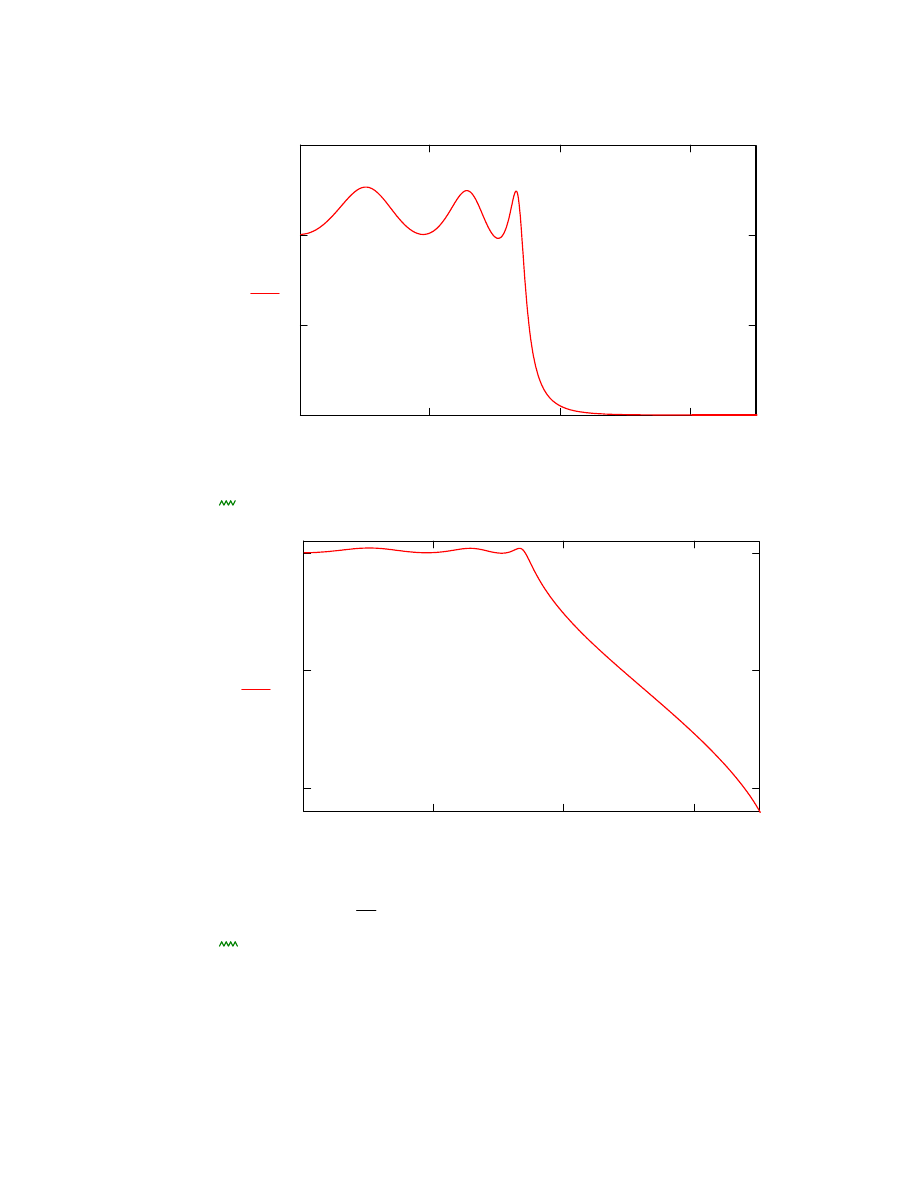
Wyznaczenie charakterystyk czestotliwosciowych
f
0 1000
A f
( )
H e
i 2
π
f
fpr
charakterystyka amplitudowa
0
200
400
600
0
0.5
1
A f
( )
f
L f
( )
20 log A f
( )
(
)
Charakterystyka amplitudowa logarytmiczna
0
200
400
600
100
50
0
L f
( )
f
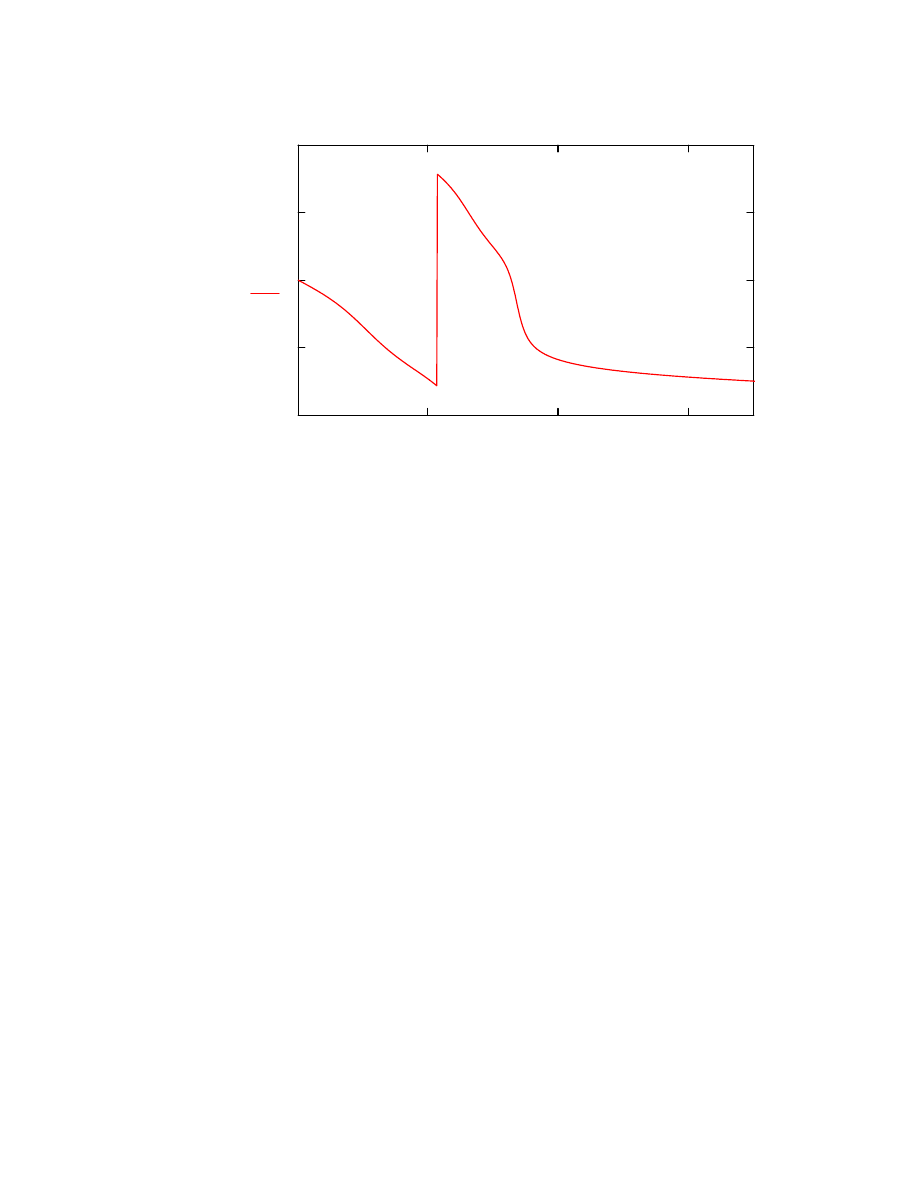
Charakterystyka fazowa
Φ f
( )
arg H e
i 2
π
f
fpr
0
200
400
600
4
2
0
2
4
Φ f
( )
f

4.502
10
3
53

z
k
i sin ϕ
k
z
k
0.966i
0.707i
0.259i
0.259i
0.707i
0.966i
3

.8016906006611633609e-14 s
4
2.3192889855535340335e-11 s
3
7.2769488515195126385e-8 s
2
0.0000
e-14 s
4
8.3730030147621144564e-11 s
3
1.6238798597906762274e-7 s
2
0.000096471004039749521662
7.424019625208994711504148e10 s
3
6.858661142168359674932842e7 s
4
12638.8300573046654406724
47574700473355964e13
5
s
3
1.071427063870997555539851e10
5
s
4
1.97437725794706478892415

1.159744647574700473355964e13
5
s
3
1.071427063870997555539851e10
5
s
4
1.974377257947064
7574700473355964e13
5
s
3
1.071427063870997555539851e10
5
s
4
1.97437725794706478892415e6
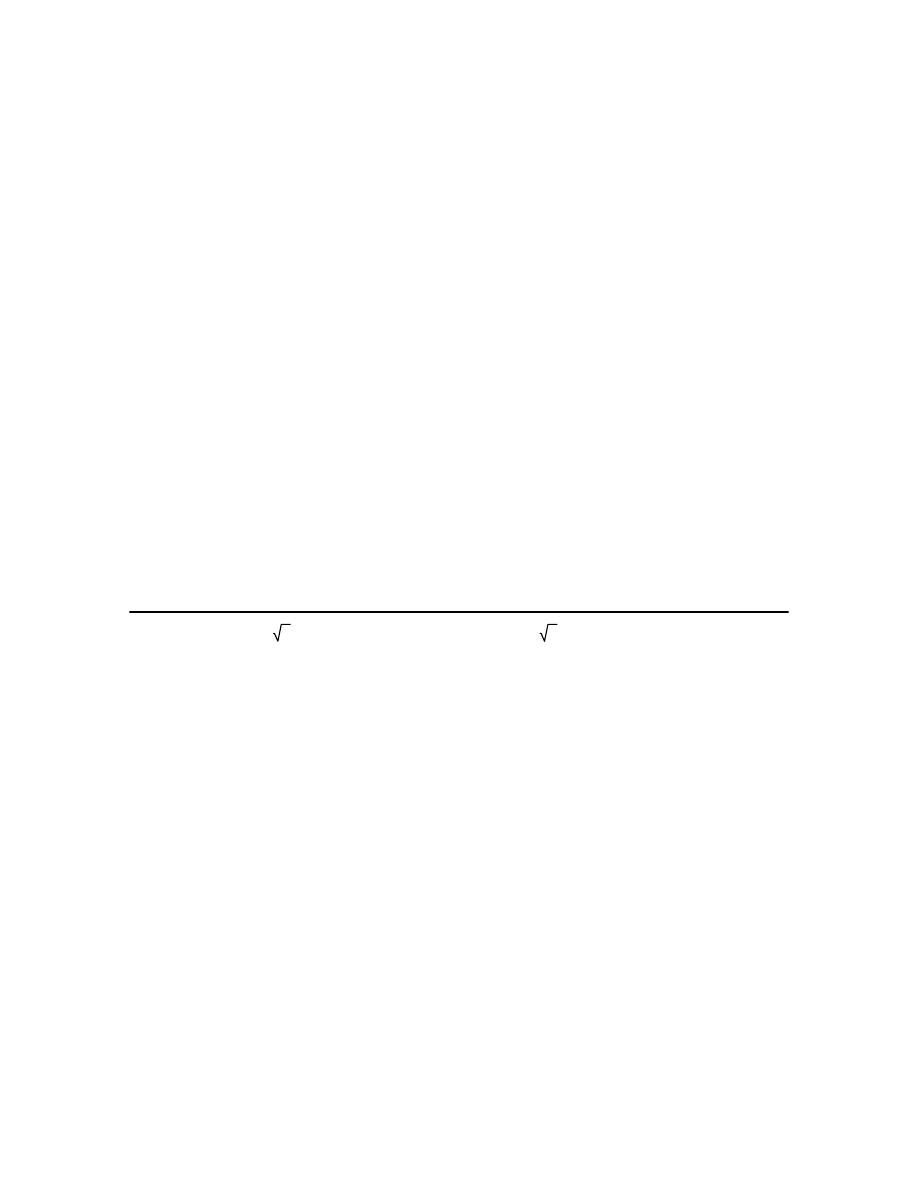
7574700473355964e13
5
s
3
1.071427063870997555539851e10
5
s
4
1.97437725794706478892415e6
t)
1028.0 e
382.1
t
sin 573.4 t
(
)
289.8
cos 1566.0 t
(
)
e
279.7
t
680.2
sin 1566.0 t
(
)
e
279.7
t
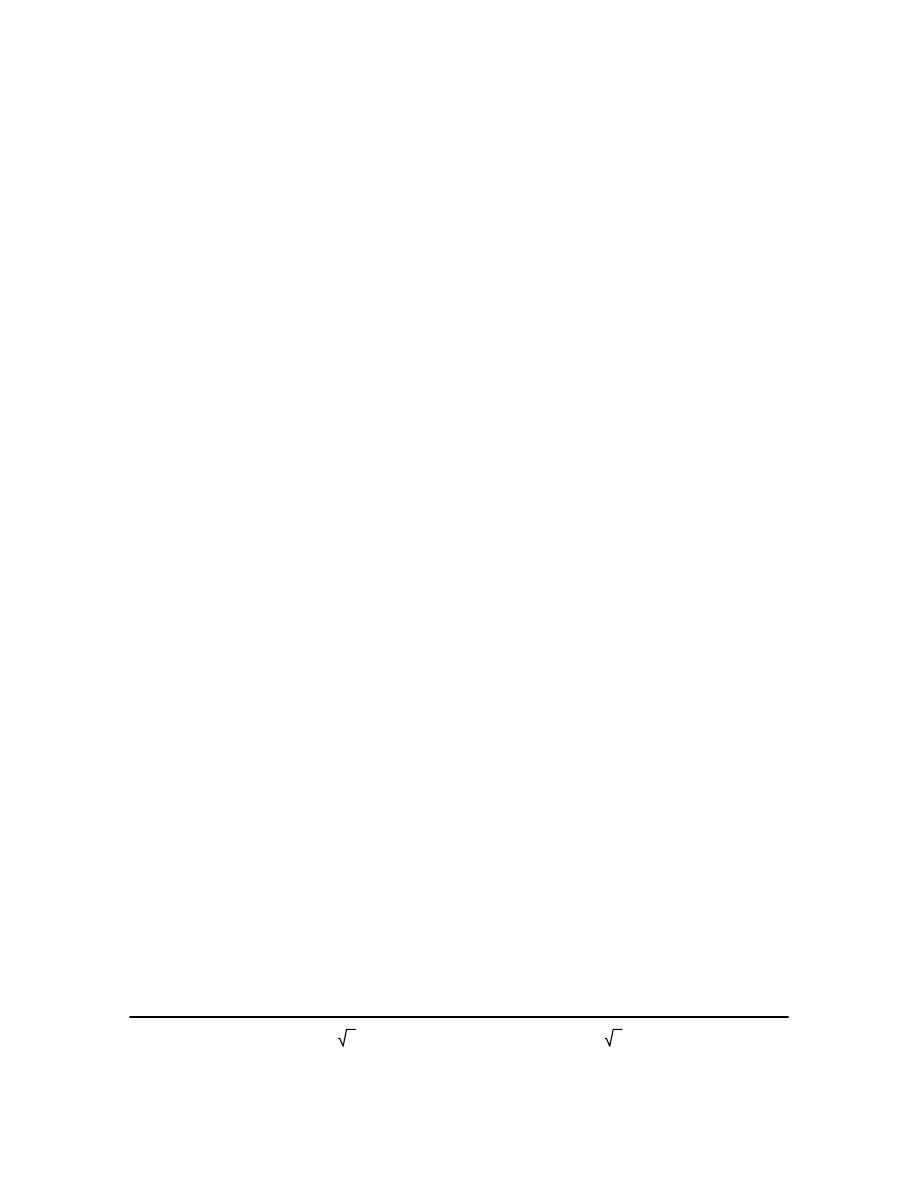
1.159744647574700473355964e13
5
s
3
1.071427063870997555539851e10
5
s
4
1.97437725794706478
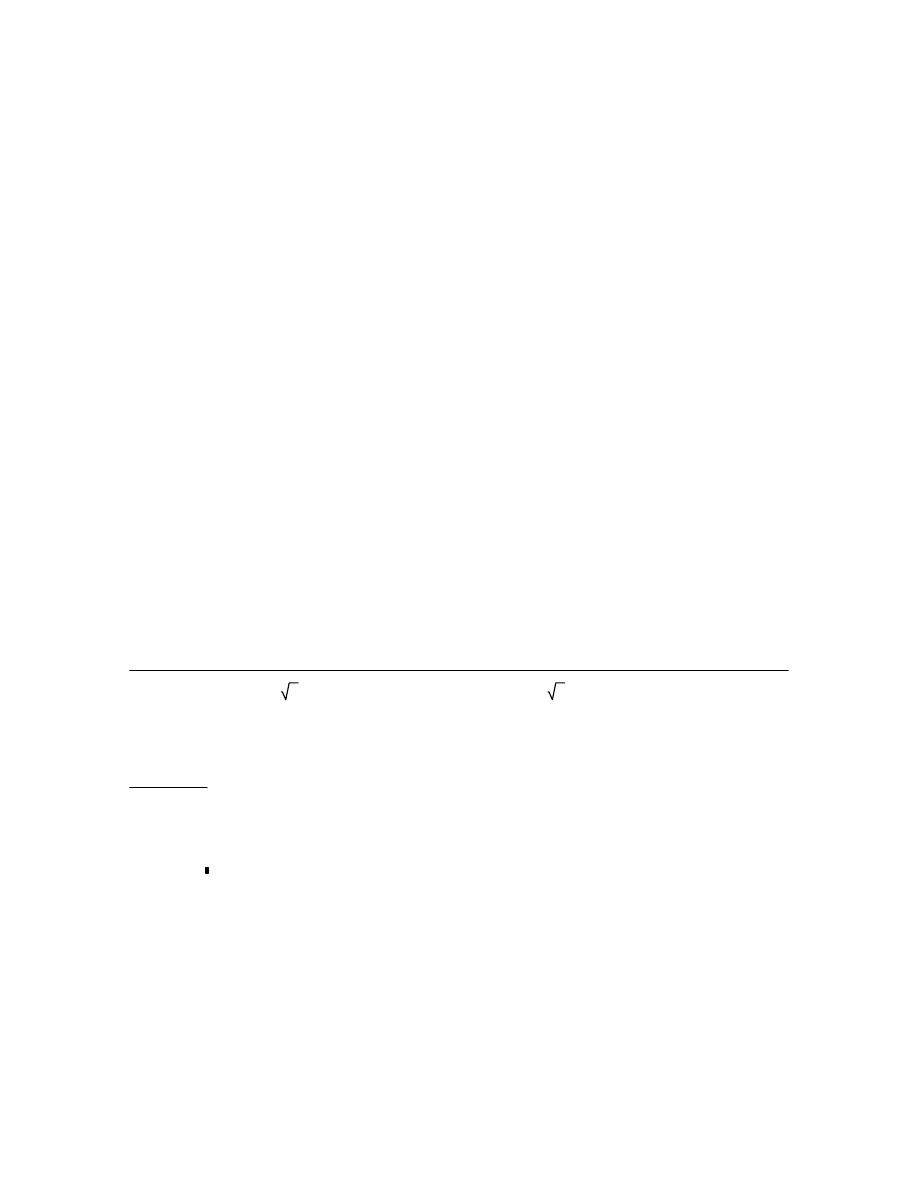
47574700473355964e13
5
s
3
1.071427063870997555539851e10
5
s
4
1.97437725794706478892415e6
1.103e21
6
1.836e23
Real H z
( )
(
)
Real
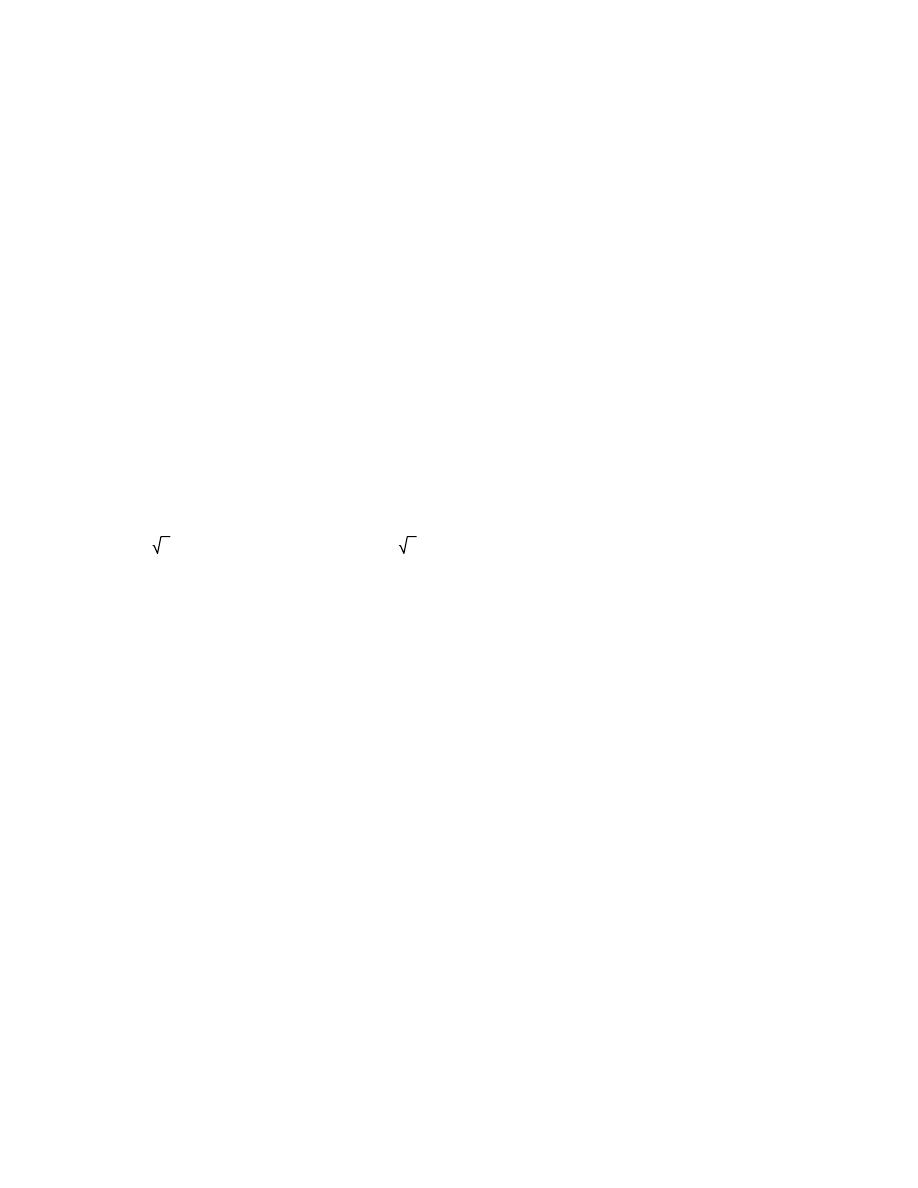
052727694437614653085 s
0.04424454588528
2 s
0.05144330376249
47 s
5
8.269211331889103300049558 s
6
4.561279818542667783649056e19
5e6
5
s
5
1291.77643190193926431956
5
s
6
5.03118577559646262154205e16 s
2
2.594165659048

3.923187866413405e19
478892415e6
5
s
5
1291.77643190193926431956
5
s
6
5.03118577559646262154205e16
s
2
2.5941
5.5157619036700232e18
5 s
5
1291.77643190193926431956
5
s
6
5.03118577559646262154205e16
s
2
2.594165659048672

5.5157619036700232e18
5
s
5
1291.77643190193926431956
5
s
6
5.03118577559646262154205e16
s
2
2.59416565904867
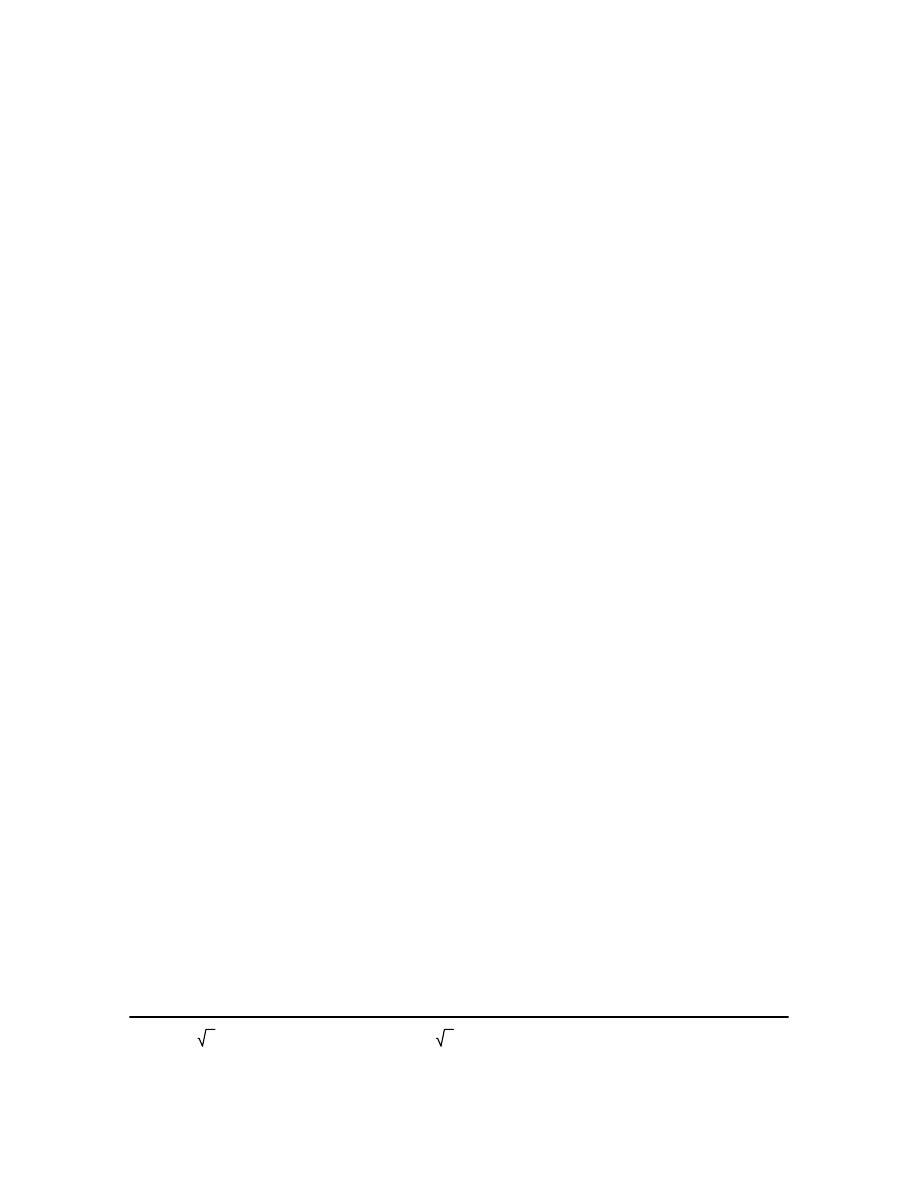
5.5157619036700232e18
8892415e6
5
s
5
1291.77643190193926431956
5
s
6
5.03118577559646262154205e16
s
2
2.59416

5.5157619036700232e18
6
5
s
5
1291.77643190193926431956
5
s
6
5.03118577559646262154205e16
s
2
2.5941656590486

67211145413e13 s
3
2.396613169185126111075982e10 s
4
4.416370182250013343646125e6 s
5
2889.4

16565904867211145413e13 s
3
2.396613169185126111075982e10
s
4
4.416370182250013343646125e6
211145413e13 s
3
2.396613169185126111075982e10
s
4
4.416370182250013343646125e6
s
5
2889.4

7211145413e13 s
3
2.396613169185126111075982e10
s
4
4.416370182250013343646125e6
s
5
2889

6565904867211145413e13 s
3
2.396613169185126111075982e10
s
4
4.416370182250013343646125e6
s

67211145413e13 s
3
2.396613169185126111075982e10
s
4
4.416370182250013343646125e6
s
5
288
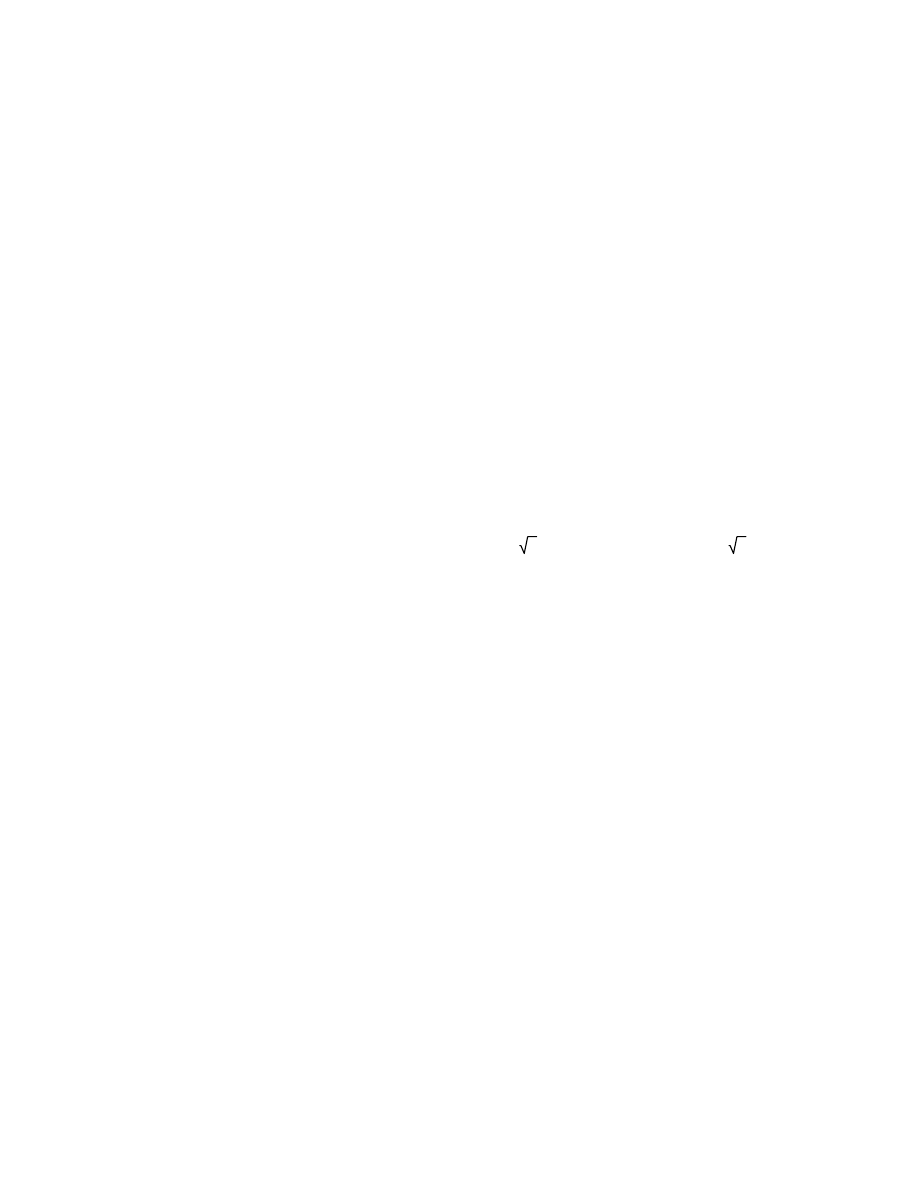
4999134648641438727 s
6
1.336219876954570624540362e19
5
s
7.1254120041424899e21
5
1.59

6 s
5
2889.4999134648641438727
s
6
1.336219876954570624540362e19
5
s
7.1254120041424899e2
4999134648641438727 s
6
1.336219876954570624540362e19
5
s
7.1254120041424899e21
5
1.593
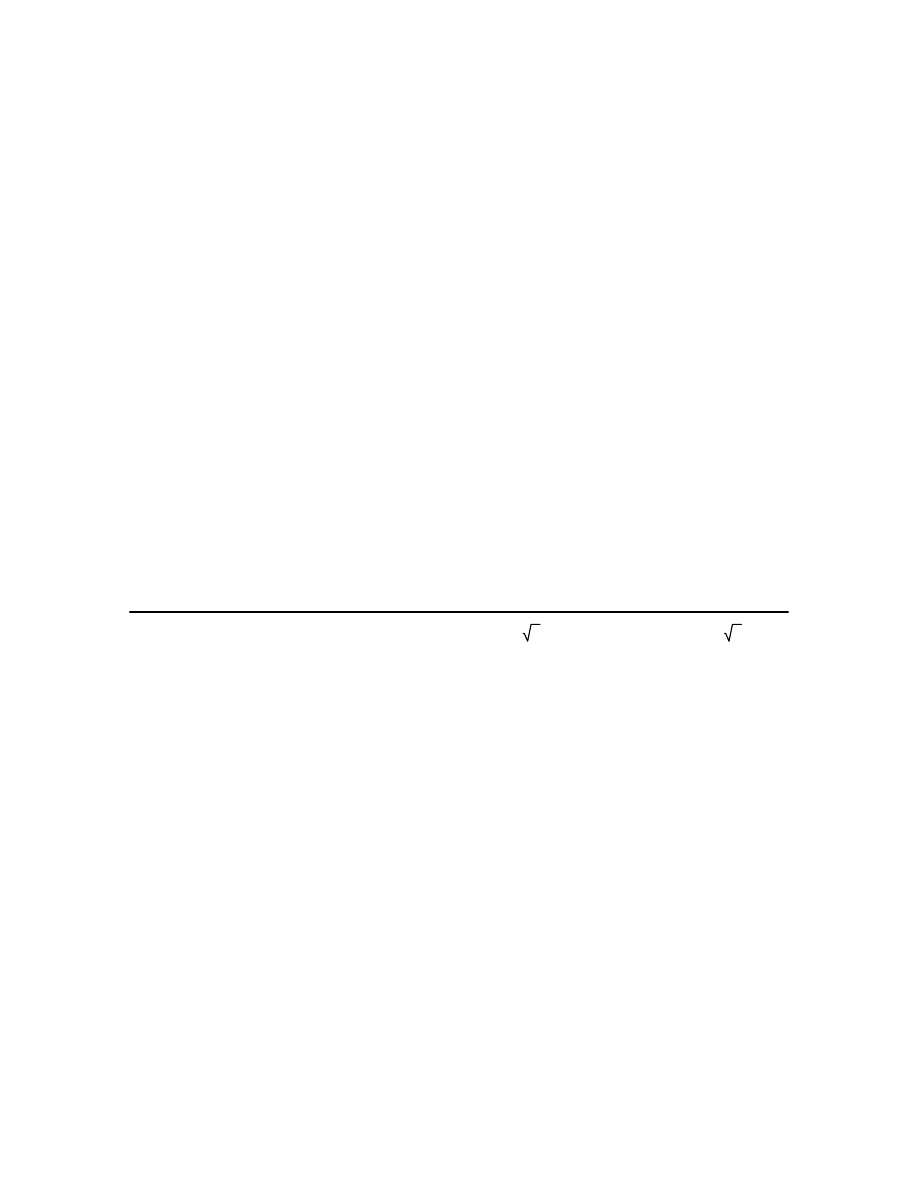
9.4999134648641438727 s
6
1.336219876954570624540362e19
5
s
7.1254120041424899e21
5
1.593
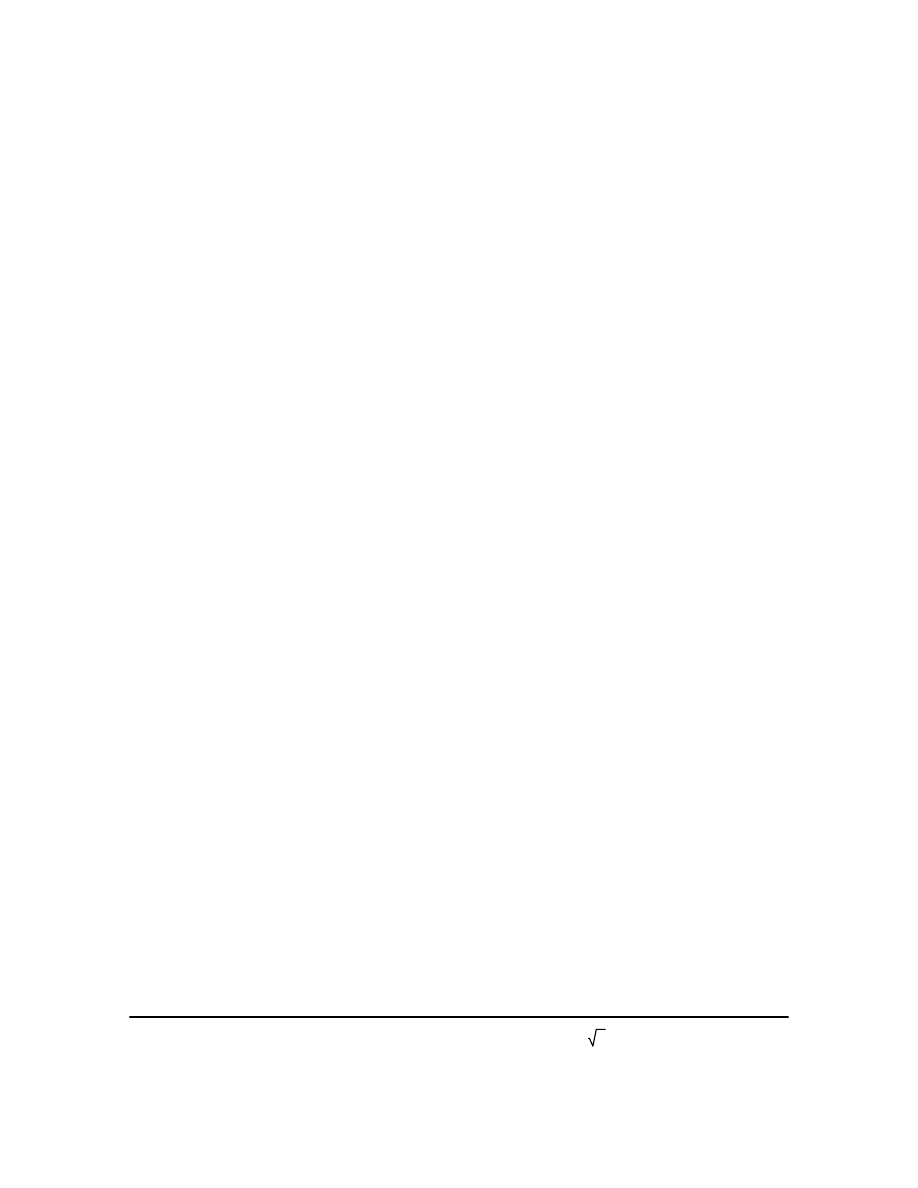
s
5
2889.4999134648641438727
s
6
1.336219876954570624540362e19
5
s
7.1254120041424899e21
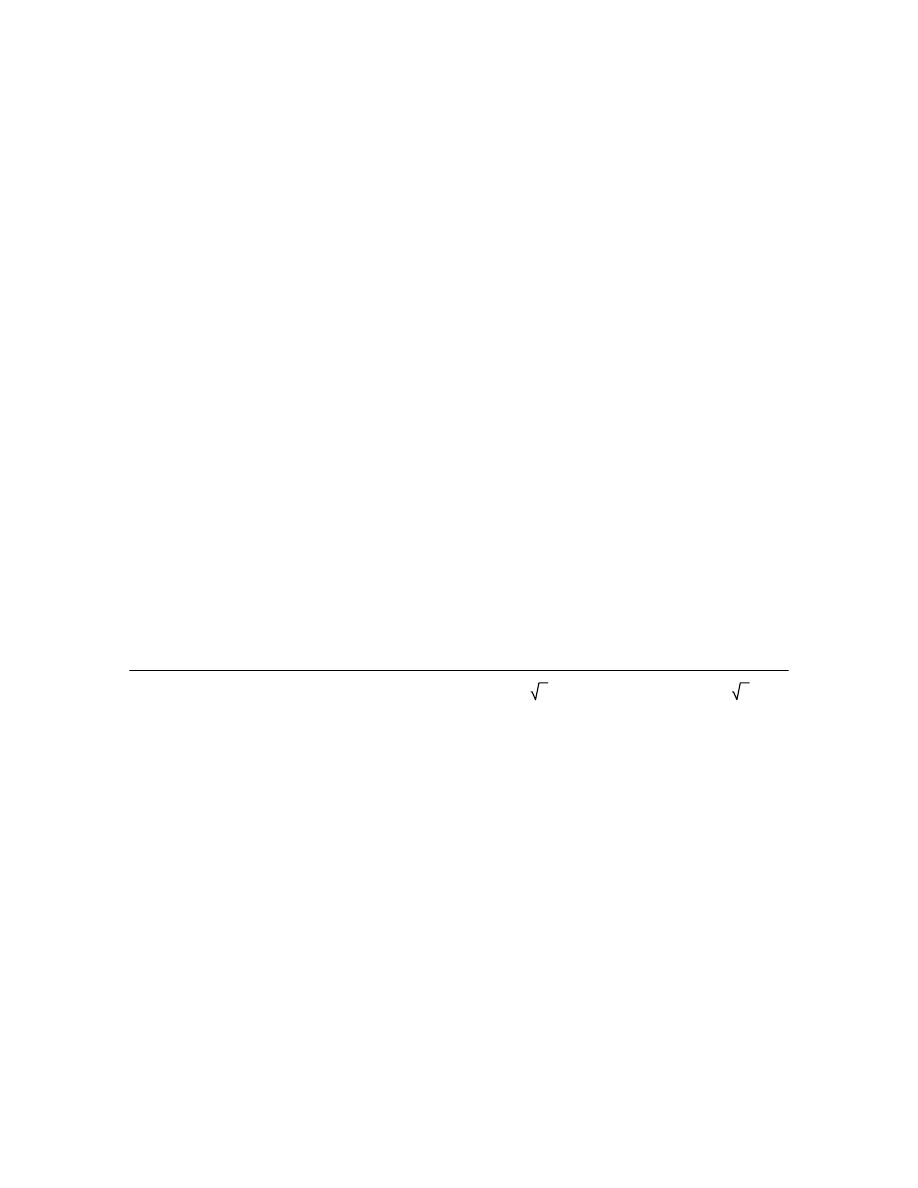
89.4999134648641438727 s
6
1.336219876954570624540362e19
5
s
7.1254120041424899e21
5
1.59

93842158821346425e22

1
5
1.593842158821346425e22
842158821346425e22

3842158821346425e22
invlaplace s
float 4
156.5 e
102.4
t
cos 2140.0 t
(
)
215.9 e
102.4
t
sin 2140.0 t
(
)
133
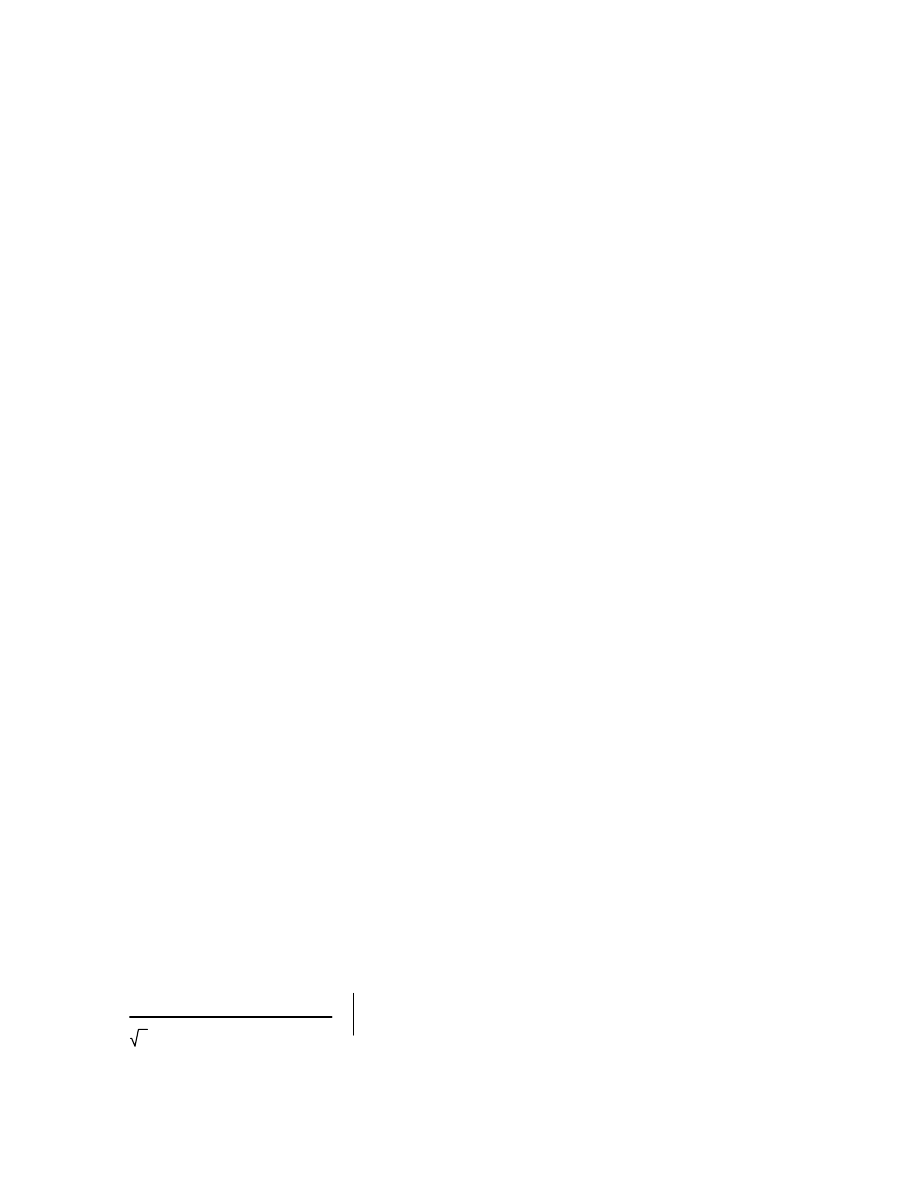
5
1.593842158821346425e22
invlaplace s
float 4
0.1042
e
102.4
t
cos 2140.0 t
(
)
0.06817 e
102.4
t
sin
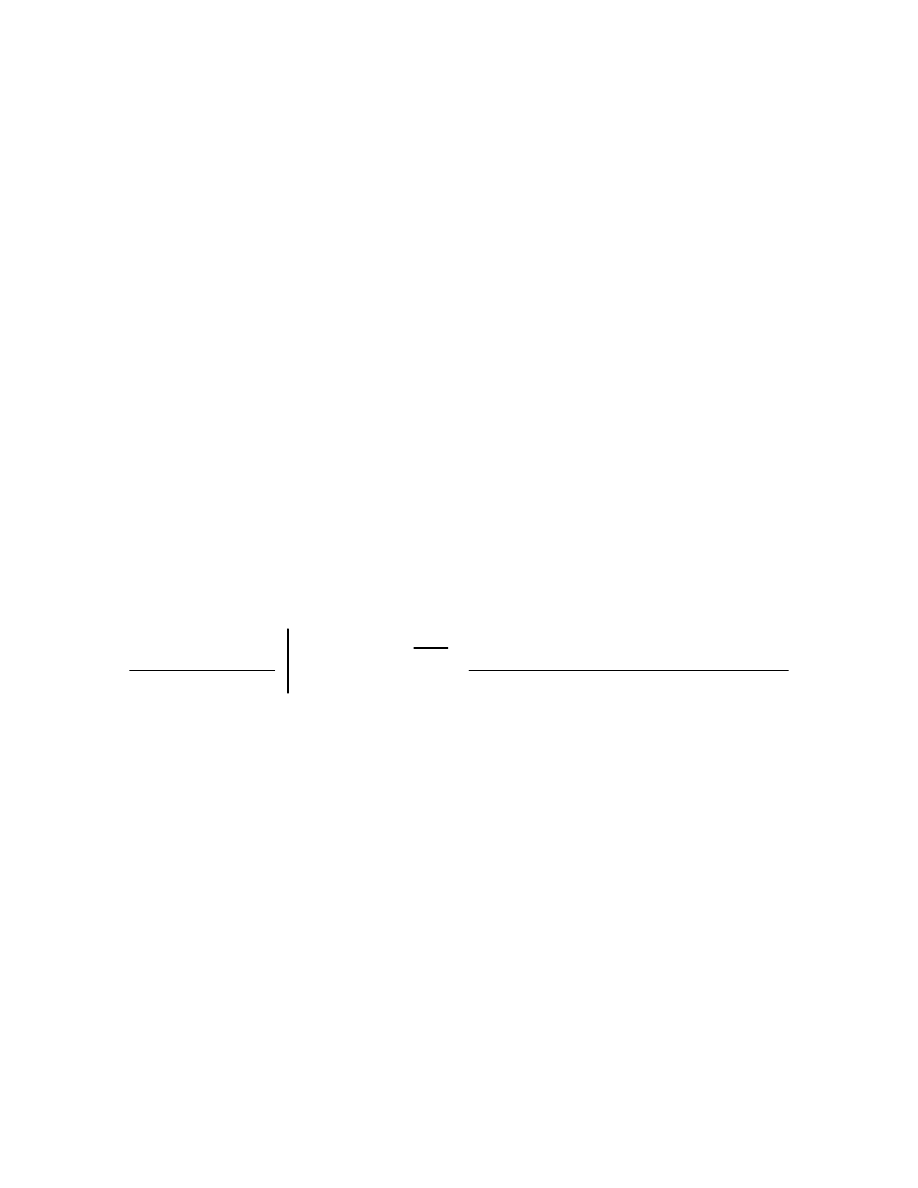
93842158821346425e22
substitute s
2 fpr
z
1
z
1
=
float 4
103420.0 z
258550.0 z
2
344740.0 z
3
258550.0
2.629e7
z
6.049e7 z
2
8.487e7
z
3
7.667e7

.2 e
382.1
t
cos 573.4 t
(
)
1028.0 e
382.1
t
sin 573.4 t
(
)
289.8
cos 1566.0 t
(
)
e
279.7
t
680.2
sin 156
(

n 2140.0 t
(
)
1.349
e
382.1
t
cos 573.4 t
(
)
0.6664
e
382.1
t
sin 573.4 t
(
)
0.4528 cos 1566.0 t
(
)
e
279.7

0 z
4
103420.0 z
5
17237.0 z
6
17237.0
z
4
4.277e7
z
5
1.232e7 z
6
5.555e6

t
0.1041
sin 1566.0 t
(
)
e
279.7
t
0.9999
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron