Politechnika Lubelska
Katedra Automatyki i Metrologii
ĆWICZENIE NR 7
CZUJNIKI PRZYSPIESZEŃ STATYCZNYCH I DYNAMICZNYCH
(opracował Leszek Szczepaniak)
Cel i zakres ćwiczenia
Celem ćwiczenia jest poznanie metod pomiaru przyspieszenia, badanie czujnika
przyspieszenia w stanach statycznych i dynamicznych
1. WSTĘP
Podstawową jednostką drogi w układzie SI jest 1m, a podstawową jednostką czasu jest 1s.
Załóżmy że dane ciało pokonało pewna drogę s w ciągu pewnego czasu t. Jeżeli drogę s
zróżniczkujemy po czasie t, to otrzymamy prędkość v z jaką ciało poruszało się w danej
chwili:
dt
ds
v
=
(1.1.)
Tak więc pochodną drogi po czasie jest prędkość. Jeśli pójdziemy dalej i zróżniczkujemy
prędkość v po czasie t, to otrzymamy przyspieszenie a, jakie posiadało ciało w danej chwili:
2
2
dt
s
d
dt
dv
a
=
=
(1.2.)
Przyspieszenie jest zatem pochodną drugiego rzędu drogi po czasie. Analogicznie całkując
przyspieszenie względem czasu otrzymamy prędkość ciała, a po scałkowaniu prędkości po
czasie otrzymamy drogę jaką przebyło dane ciało.
Zgodnie z Międzynarodowym Układem Jednostek Miar SI, przyspieszenie zaliczane jest
do wielkości mechanicznych, a jego jednostka jest jednostką pochodną. Ze względu na rodzaj
ruchu układ SI rozróżnia dwa typy przyspieszeń:
-
przyspieszenie liniowe – a – jest to granica ilorazu różnicowego przyrostu
∆
v
prędkości i przyrostu
∆
t czasu:
r
dt
r
d
v
t
v
a
t
˙˙
˙
=
=
=
∆
∆
=
→
∆
2
2
0
lim
(1.3.)
gdzie: r – promień wodzący
Jeżeli
∆
v i
∆
t są przyrostami skończonymi, to przyspieszenie liniowe a, jest nazywane
przyspieszeniem liniowym średnim (w czasie). Jednostką przyspieszenia liniowego jest
2
1
s
m
.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
1 / 18
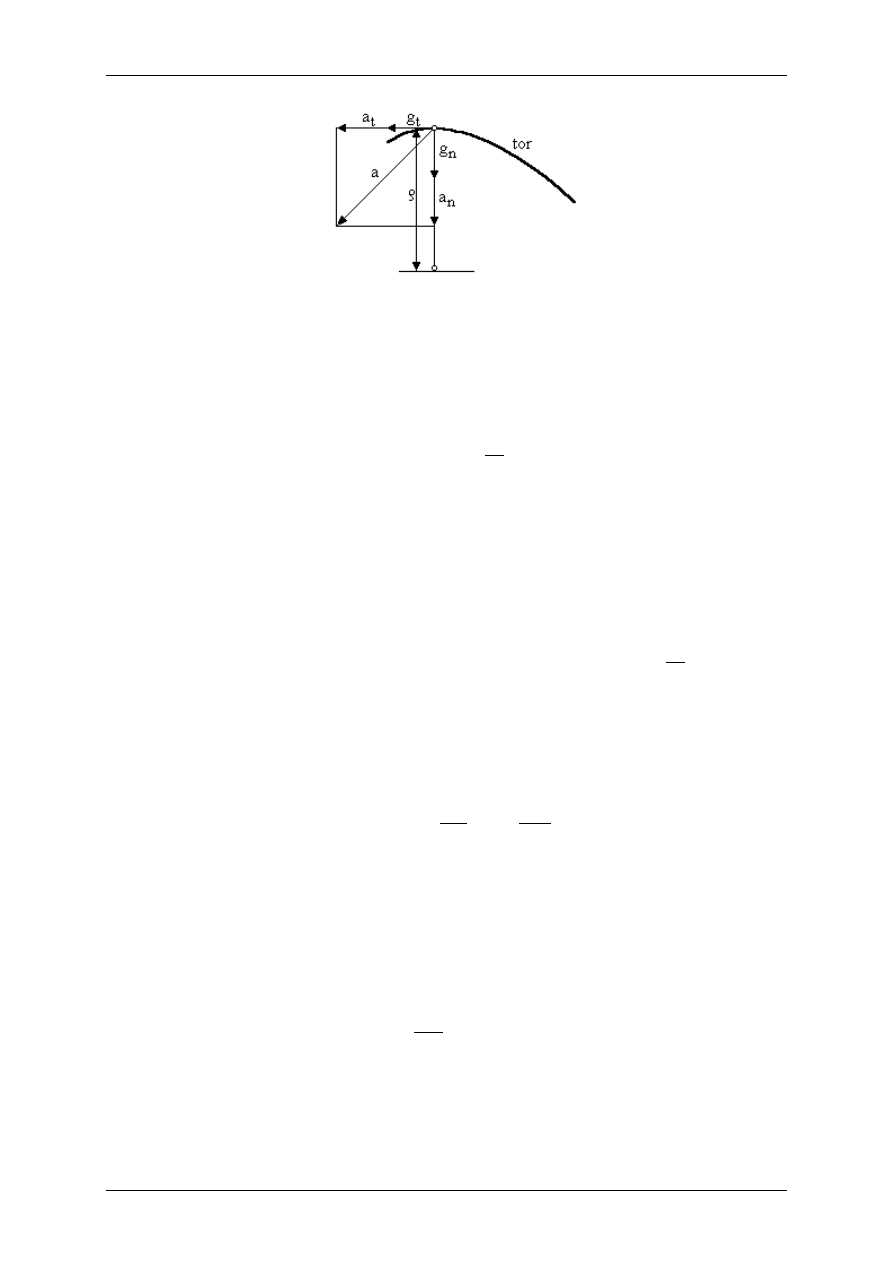
Politechnika Lubelska
Katedra Automatyki i Metrologii
Rysunek 1.1. Składowa styczna a
t
i składowa normalna a
n
, wektora
przyspieszenia liniowego a w układzie współrzędnych
prostokątnych.
W układzie współrzędnych prostokątnych wektor przyspieszenia liniowego a, ma dwie
składowe: styczną a
t
i normalną a
n
, rysunek 1.1.
n
t
g
v
g
v
a
ρ
2
+
=
˙
(1.4.)
gdzie: v – moduł prędkości,
ρ
-promień krzywizny toru, g
t
, g
n
– wektor jednostkowy
styczny i normalny do toru
W ruchu prostoliniowym jednostajnie zmiennym przyspieszenie liniowe jest stałe, w ruchu
prostoliniowym jednostajnym przyspieszenie liniowe jest równe zeru, w ruchu jednostajnym
po okręgu wektor przyspieszenia liniowego co do wartości jest stały, równy
r
v
2
i skierowany
ku środkowi okręgu;
-
przyspieszenie kątowe -
ε
– jest to granica ilorazu różnicowego przyrostu
∆ω
prędkości kątowej i przyrostu
∆
t czasu:
ϕ
ϕ
ω
ω
ε
˙˙
˙
=
=
=
∆
∆
=
→
∆
2
2
0
lim
dt
d
t
t
(1.5.)
gdzie:
ϕ
– kąt obrotu
Jeżeli
∆ω
i
∆
t są przyrostami skończonymi, to
ε
jest przyspieszeniem kątowym średnim.
W przypadku szczególnym obrotu wokół stałej osi wektory
ω
i
ε
są skierowane wzdłuż osi,
zwroty obu wektorów są zgodne dla przyspieszenia dodatniego i przeciwne dla opóźnienia.
Jednostką przyspieszenia kątowego jest
2
1
s
rad
;
Przyspieszenie jest wielkością wektorową, oznacza to że posiada kierunek, zwrot i wartość.
Kierunek jest to prosta wzdłuż której w danym momencie działa na ciało wypadkowa siła
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
2 / 18

Politechnika Lubelska
Katedra Automatyki i Metrologii
powodująca jego przyspieszenie, natomiast zwrot określa w którą stronę wzdłuż kierunku
skierowane jest przyspieszenie. Jeżeli na ciało w danym momencie działa kilka sił o różnych
kierunkach, to każda z nich stanowi źródło przyspieszenia skierowanego w kierunku siły od
której pochodzi, a ponieważ przyśpieszenie jest wektorem to dzięki sumie wektorowej
otrzymamy wypadkowy wektor przyspieszenia działający na ciało.
Ze względu na źródło wymuszające przyspieszenie działające na ciało, istnieje podział na
przyspieszenia statyczne i przyspieszenia dynamiczne.
Pojęcie statyki określa badania praw równowagi ciał materialnych znajdujących się pod
działaniem sił zrównoważonych i jest z nim związana pierwsza zasada dynamiki Newtona :
-
jeżeli siły działające na punkty materialny równoważą się, to ciało porusza się ruchem
jednostajnym prostoliniowym lub spoczywa.
Zgodnie z Prawem Powszechnego Ciążenia, każde dwie masy (m
1
, m
2
) przyciągają się siłą
F wprost proporcjonalną do iloczynu ich mas a odwrotnie proporcjonalną do kwadratu
odległości między ich środkami:
2
2
1
r
m
m
G
F
⋅
=
(1.6.)
stała proporcjonalności w tym związku jest uniwersalną stałą przyrody
2
2
11
10
6720
,
6
kg
m
N
G
⋅
⋅
=
−
zwaną stałą grawitacji (Cavendisha). Zjawisko to powoduje iż na
ciała działa pewna siła statyczna, która jest tym większa im większe są masy danych ciał i im
mniejsza jest odległość między ich środkami. Przyspieszenia ziemskie ma charakter
przyspieszenia statycznego (podobnie jak przyśpieszenia grawitacyjne pochodzące od innych
ciał niebieskich) i wymuszone jest przez siłę oddziaływania między danym ciałem, a Ziemią.
Dokładne wartości przyspieszenia ziemskiego zależą od szerokości geograficznej, co
wynika z kształtu globu (odległość środka ziemi od powierzchni jest inna na innych
szerokościach geograficznych).
Pojęcie dynamiki określa badania praw ruchu ciał materialnych znajdujących się pod
działaniem sił i jest z nim związana druga zasada dynamiki Newtona :
-
jeżeli na ciało działają siły niezrównoważone, to ciało porusza się ruchem zmiennym z
przyspieszeniem wprost proporcjonalnym do działającej siły i odwrotnie
proporcjonalnym do masy ciała.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
3 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
m
F
a
=
(1.7.)
Zgodnie z tą zasadą wszelkie zmiany wartości, kierunku i zwrotu sił działających na ciało
powodują w konsekwencji zmiany wartości, kierunku i zwrotu wypadkowego wektora
przyśpieszenia jakiego doznaje ciało. Przyśpieszenie dynamiczne jest zatem wynikiem
działania pewnej (stałej lub zmiennej) siły, która jest przyłożona do danego obiektu.
Jednym z odrębnych działów fizyki jest zagadnienie ruchu po okręgu. Występują w nim dwie
podstawowe siły które są związane tym rodzajem ruchu :
-
Siła odśrodkowa bezwładności - siła bezwładności występująca w układzie
obracającym się (nieinercjalnym). Siła ta skierowana jest wzdłuż promienia na
zewnątrz. Wyrażona jest wzorem:
r
mv
F
od
2
=
(1.8.)
-
Siła dośrodkowa - siła zmuszająca ciało do ruchu po torze krzywoliniowym i
skierowana do ku środkowi krzywizny toru. W ruchu jednostajnym po okręgu ma
zwrot do środka okręgu, a kierunek wzdłuż promienia krzywizny, tak jak wektora
przyspieszenia dośrodkowego. Jej wartość określona jest wzorem:
r
m
r
mv
F
do
2
2
ϖ
=
=
(1.9.)
Od obydwu tych sił pochodzą przyspieszenia dośrodkowe i odśrodkowe, które jak łatwo się
domyślić będą wyrażone wzorami :
r
r
v
a
a
do
od
2
2
ϖ
=
=
=
(1.10.)
Przyspieszenie odśrodkowe różni się od dośrodkowego jedynie zwrotem, a więc ich wartości
liczbowe będą równe. Wynika stąd, że przyspieszenia określa w jakim tempie zmienia się
prędkość ciała w danym kierunku, bądź w jakim tempie zmieniałaby się prędkość ciała w
danym kierunku tuż po uwolnieniu z więzów.
2. METODY POMIARU PRZYSPIESZENIA
Jedną z prostszych, aczkolwiek pośrednich metod pomiaru przyspieszenia jest
wykorzystanie wahadła matematycznego, którego szkic przedstawiony jest na rysunku 2.1.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
4 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
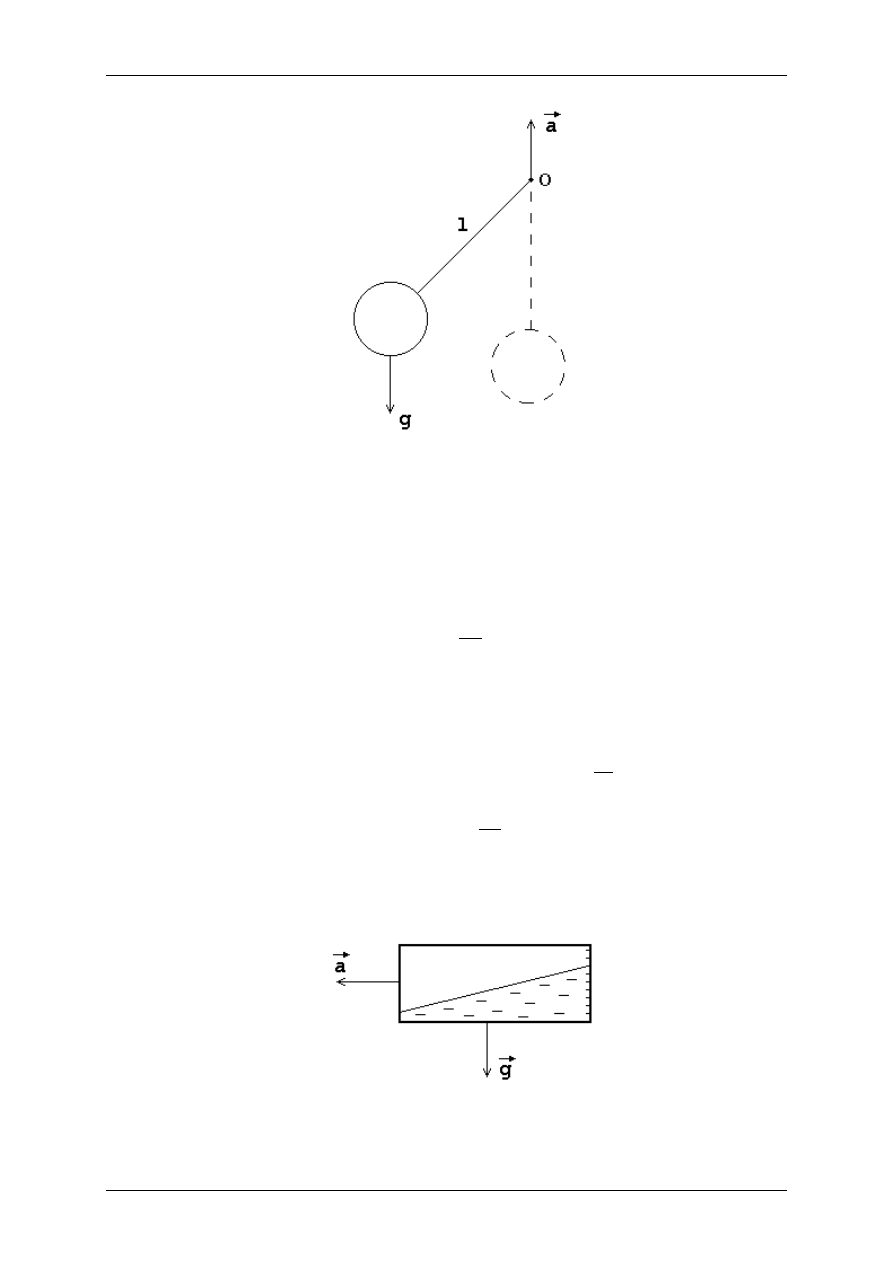
Rysunek 2.1. Schemat wahadła matematycznego
Ogólna zasada pomiaru przyspieszenia polega na wprawieniu wahadła w ruch i
zmierzeniu okresu jego drgań T, następnie znając jego długość l można obliczyć
przyspieszenie a jakie działa na układ ze wzoru (2.1):
g
T
l
a
−
=
2
2
4
π
(2.1)
W ten sposób można również wyznaczyć wartość przyspieszenia ziemskiego, jeżeli na
wahadło nie będzie działało dodatkowe przyspieszenie. Jeżeli a = 0
2
s
m
to:
2
2
4
T
l
g
π
=
(2.2.)
Inną metodą pomiaru przyspieszenia jest zastosowanie naczynia wypełnionego cieczą,
rysunek 2.2.
Rysunek 2.2. Przeźroczyste naczynie wypełnione cieczą
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
5 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
Wartość przyspieszenia działającego na naczynie będzie proporcjonalna do poziomu
cieczy w jednym z końców naczynia. Poziom cieczy odczytujemy z podziałki znajdującej się
na naczyniu i wyskalowanej w jednostce przyspieszenia.
Do pomiaru przyspieszenia wykorzystuje się najczęściej zjawisko bezwładności masy.
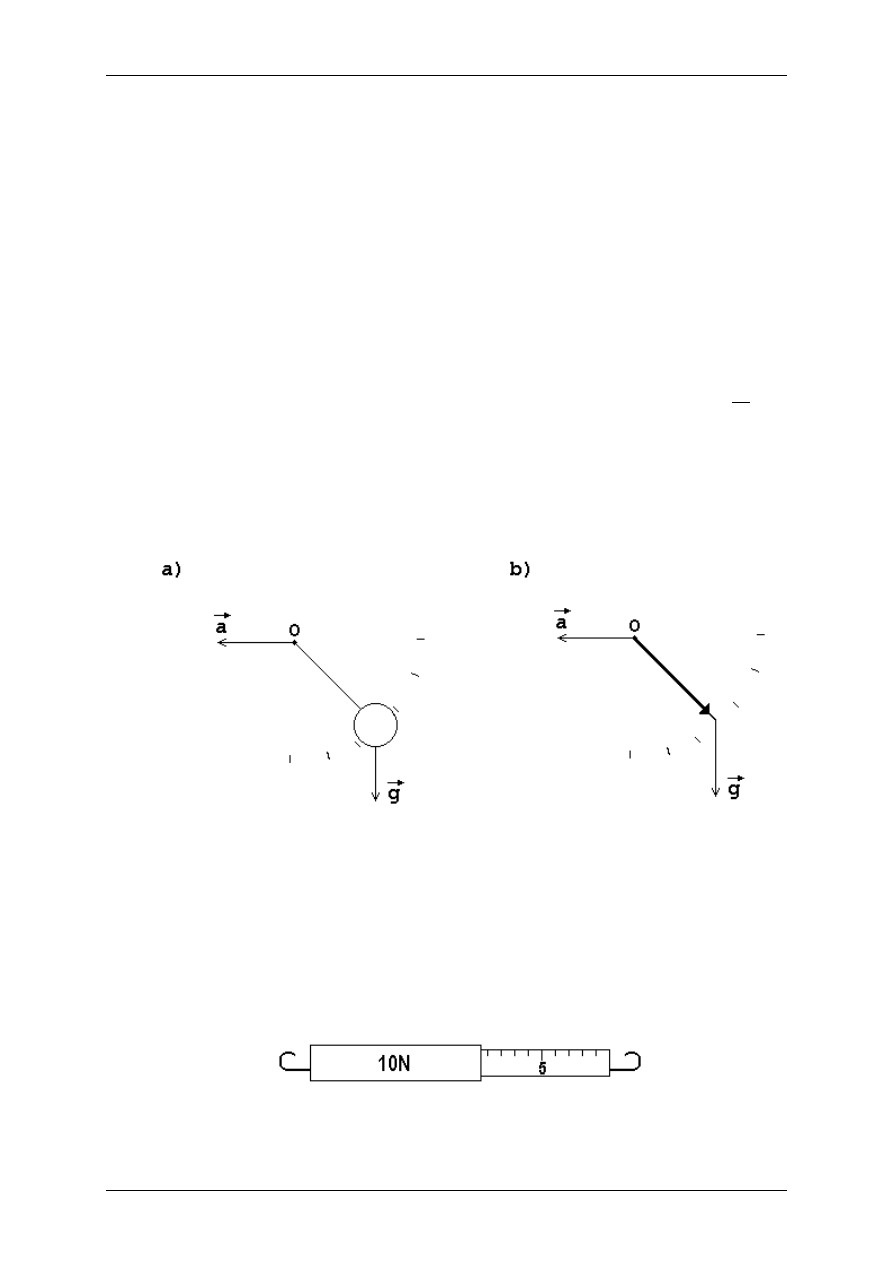
Można to zrealizować np. poprzez użycie obciążnika zawieszonego na nici, co obrazuje
rysunek 2.3.a). W momencie, gdy punkt zaczepienia nici zostanie poddany ruchowi
przyspieszonemu równoległemu do powierzchni ziemi, zaobserwujemy odchylenie się
obciążnika od pozycji pionowej. Odchylenie to będzie proporcjonalne do przyspieszenia
układu. Jeżeli do opisanego przyrządu dołączymy podziałkę wyskalowaną w
2
s
m
to
będziemy w stanie bezpośrednio dokonać pomiaru chwilowego przyspieszenia jakiemu
poddany został układ, Zamiast obciążnika na nici, stosuje się najczęściej wskazówkę, co
ułatwia dokonywanie pomiarów, tak jak na rysunku 2.3.b).
Rysunek 2.3. Wychyłowy przyrząd do pomiaru przyspieszenia a) z obciążnikiem ,
b) ze wskazówką
Przyrząd ten mierzy jedynie przyspieszenia dynamiczne o kierunku równoległym do
powierzchni ziemi.
Kolejnym nieskomplikowanym pod względem budowy przyrządem, który można
wykorzystać do pomiaru przyspieszenia jest dynamometr, przedstawiony na rysunku 2.4.
Rysunek 2.4. Dynamometr
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
6 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
Jeżeli do jednego z zaczepów dynamometru dołączymy znaną masę m, a drugi zaczep
dołączymy do układu poruszającego się ruchem przyspieszonym, to po odpowiednim
wyskalowaniu dynamometru otrzymamy przyrząd do pomiaru przyspieszenia. Przyrządem
tym można mierzyć zarówno przyspieszenia dynamiczne jak i statyczne. Teoretycznie
sposobem tym można dokonać pomiaru przyspieszenia w każdym kierunku, jednak dla
kierunków ukośnych i równoległych do powierzchni ziemi wymogiem stałoby się
zastosowanie specjalnej prowadnicy po której poruszałaby się masa doczepiona do
dynamometru, co z kolei powoduje dodatkowe tarcie narastające nieliniowo względem
przyrostu prędkości, wprowadzając w konsekwencji dodatkowe błędy pomiaru
przyspieszenia.
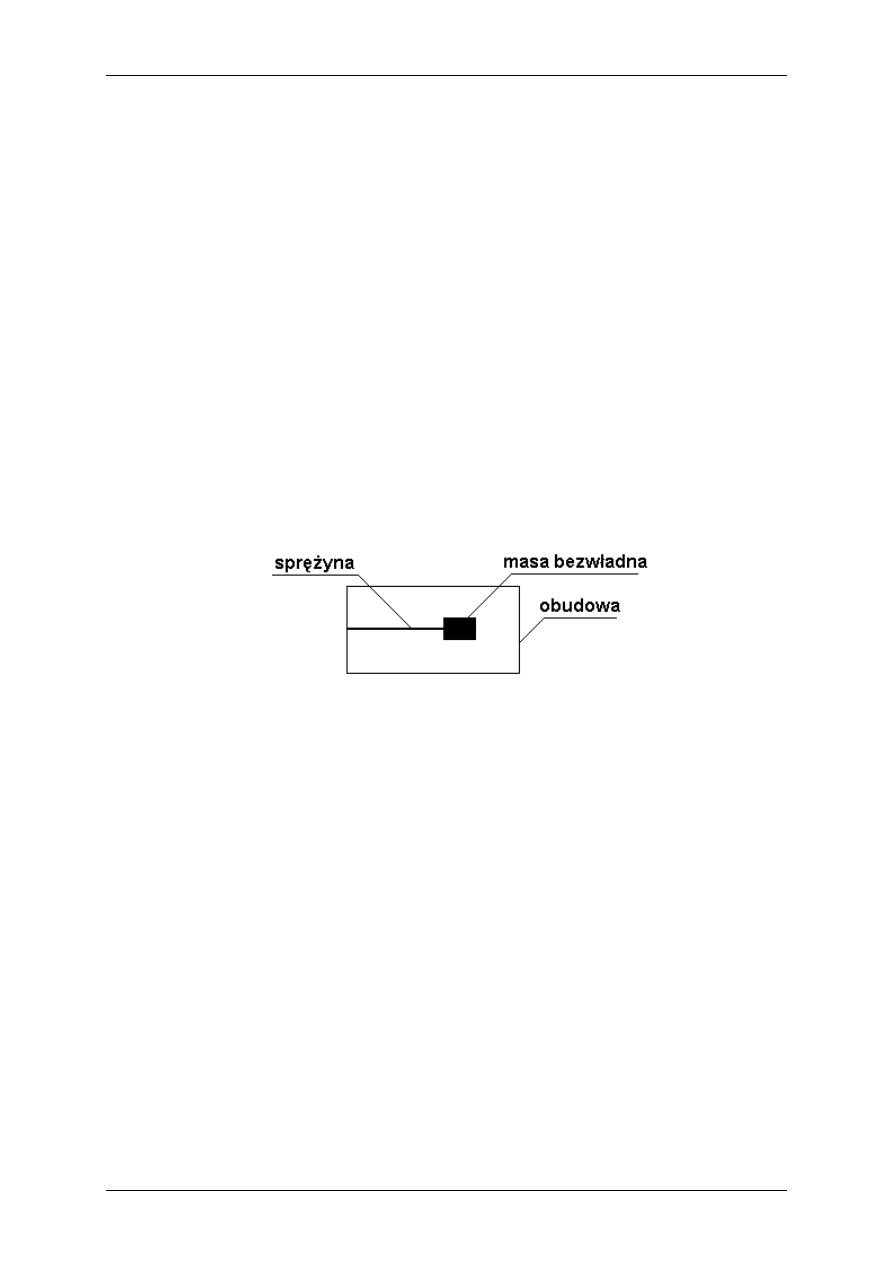
We współczesnych przyrządach służących do pomiaru przyspieszenia, na niewielkiej
sprężynie umieszcza się pewną masę bezwładną, a całość umieszcza się w specjalnej
obudowie, tak jak na rysunku 2.5.
Rysunek 2.5. Uproszczony model czujnika przyspieszenia
Sam odczyt przyspieszenia z powyższego (uproszczonego) modelu czujnika
przyspieszenia, może być realizowany w różny sposób. Najprościej można nanieść na
obudowę skalę i bezpośrednio z niej odczytywać odchylenie masy bezwładnej, nieco bardziej
skomplikowanym sposobem jest np. zastosowanie masy bezwładnej jako jednej z elektrod
zmiennego kondensatora którego drugą elektrodę będzie stanowić obudowa czujnika. W ten
sposób zmiany przyspieszenia będą odzwierciedlone w zmianach pojemności kondensatora,
które można przetworzyć dzięki układom elektronicznym. Rozwiązanie to umożliwia pomiar
przyspieszenia w każdym kierunku, a ponadto dzięki dość dużej częstotliwości rezonansowej
układu sprężyna-masa bezwładna umożliwia pomiar przyspieszeń o częstych zmianach
zwrotu, czyli wibracji, pod warunkiem że ich częstotliwość jest mniejsza od częstotliwości
rezonansowej układu pomiarowego. Obecnie w większości przypadków stosuje się ten
właśnie sposób pomiaru przyspieszenia i wibracji.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
7 / 18

Politechnika Lubelska
Katedra Automatyki i Metrologii
W najbardziej zaawansowanych technicznie metodach pomiaru przyspieszeń
dynamicznych korzysta się z radarów. Metodę pomiaru przedstawia rysunek 2.6.a).
Rysunek 2.6. Pomiar przyspieszenia przy użyciu radaru, a) w linii ruchu obiektu
b) poza linią ruchu obiektu
Fale radiowe, po odbiciu od badanego obiektu wracają po określonym zależnym od
odległości czasie do radaru, w następnych chwili czasu operacja jest powtarzana. W ten
sposób otrzymujemy informacje o prędkości obiektu w danych chwilach czasu, a w
konsekwencji dzięki układom przetwarzającym o jego przyspieszeniu. Nowoczesna technika
umożliwia pomiar przyspieszenia obiektu poruszającego się, niezależnie od położenia i
prędkości radaru, tak jak na rysunku 2.6.b). Specjalnie zaprogramowany procesor dokonuje
analizy geometrycznej współrzędnych położenia oraz kierunku i rodzaju ruchu zarówno
obiektu jak i radaru.
3. OPIS MIKROMECHANICZNEGO CZUJNIKA PRZYSPIESZENIA ADXL202EX
W ćwiczeniu do pomiaru kąta pochylenia wykorzystany został mikromechaniczny czujnik
przyspieszenia ADXL202EX firmy Analog Devices, umożliwiający pomiar zarówno
przyspieszeń statycznych, jak i dynamicznych.
W strukturze ADXL202EX umieszczono półprzewodnikowy sensor oraz obwody
kondycjonujące, powodujące zamianę wartości przyspieszenia na sygnał wyjściowy o
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
8 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
modulowanej szerokości impulsu (PWM). Dzięki temu czujnik może bezpośrednio
współpracować
z
wejściem
licznika
dowolnego
mikroprocesora.
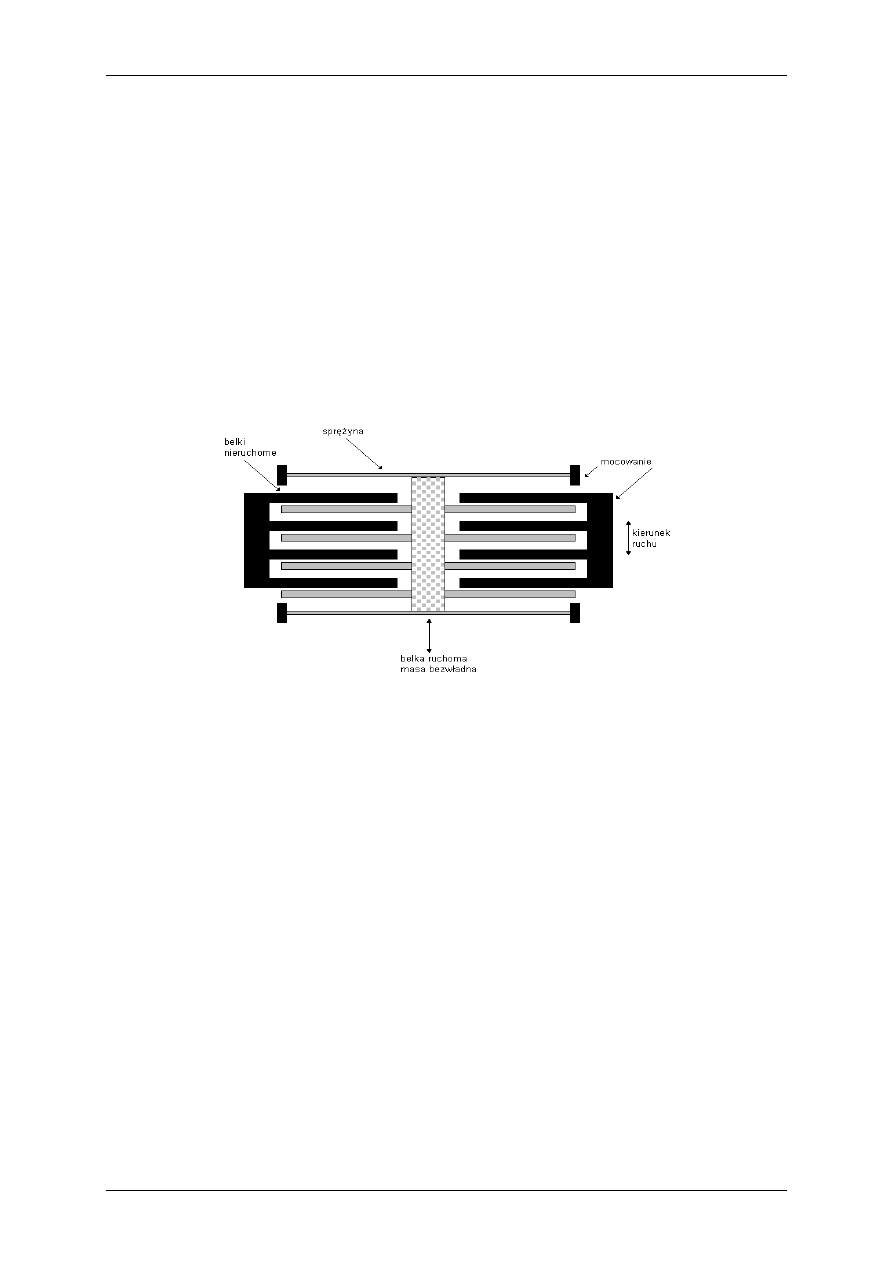
Sensor wykonano w postaci masy zawieszonej na polikrzemowych sprężynach
przeciwdziałających sile przyspieszającej. Ugięcie spowodowane działaniem zewnętrznej siły
określane jest poprzez pomiar pojemności różnicowego kondensatora, którego jedną elektrodę
stanowi poruszająca się masa krzemowa wykonana w postaci szeregu pręcików
umieszczonych na wspólnym rdzeniu, umocowanym na polikrzemowych sprężynach, a drugą
elektrodę stanowi nieruchoma obudowa posiadająca nieruchome pręciki umieszczone
pomiędzy prętami ruchomymi, przedstawia to rysunek 3.1.
Rysunek 3.1. Budowa kondensatora różnicowego układu ADXL202EX
Podczas pracy układu na okładziny zewnętrzne podawany jest przebieg prostokątny o różnicy
faz 180
°
. W przypadku występowania siły przyspieszającej, ugięcie ruchomej masy
stanowiącej elektrodę środkową powoduje zmianę pojemności kondensatora różnicowego i
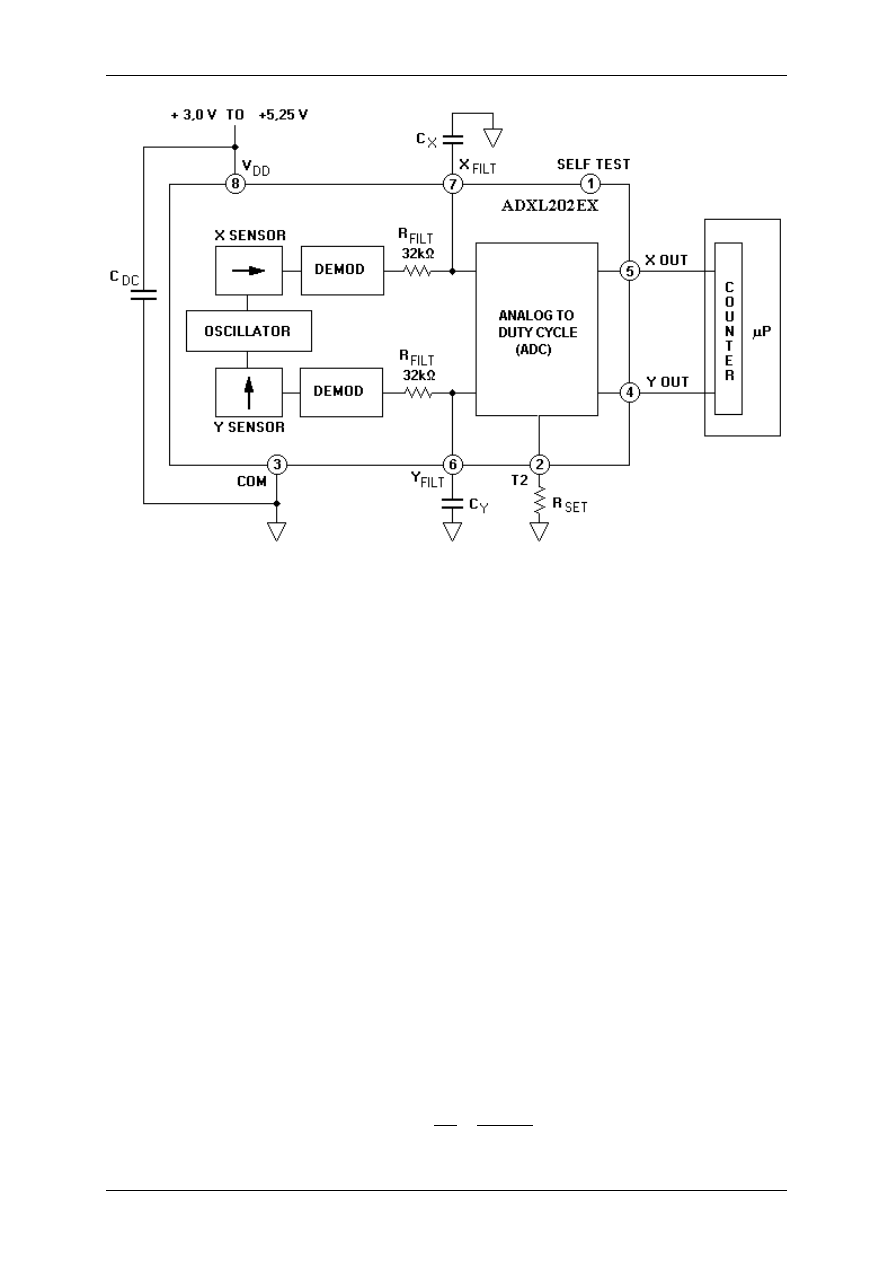
powstanie fali prostokątnej o amplitudzie proporcjonalnej do działającej siły. Schemat
blokowy mikromechanicznego czujnika przyspieszenia ADXL202EX przedstawiony jest na
rysunku 3.2.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
9 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
Rysunek 3.2. Schemat blokowy układu ADXL202EX
Określenie kierunku i stopnia wychylenia masy dokonywane jest przez czuły na zmianę fazy
sygnału demodulator – prostownik ( DEMOD ). Wyjścia obu prostowników połączone są z
właściwym modulatorem PWM ( DUTY CYCLE MODULATOR – DCM ) przez rezystory
32k
Ω
, których końce wyprowadzone są na zewnątrz układu (wyprowadzenia 6 i 7). Dzięki
takiemu rozwiązaniu, możliwe jest ograniczenie pasma pracy modulatora w zakresie 0,01Hz -
6kHz poprzez dołączenie do tych wyprowadzeń kondensatorów C
X
i C
Y
, o odpowiedniej
wartości pojemności. Ograniczenie pasma stosuje się w celu zwiększenia rozdzielczości
pomiarowej i wyeliminowania zjawiska aliasingu. Dodatkowo na wyprowadzeniach tych,
otrzymujemy sygnał analogowy, którego wartość napięcia jest proporcjonalna do mierzonego
przyspieszenia.
Zadaniem końcowego stopnia PWM ( ANALOG TO DUTY CYCLE – ADC ) jest
przetworzenie sygnału analogowego na sygnał cyfrowy o modulowanej szerokości impulsu.
Możliwy jest dobór okresu przebiegu wyjściowego w zakresie od 0,5ms do 10ms poprzez
zmianę wartości rezystora RSET, dołączonego do wyprowadzenia T2 (wyprowadzenie 2).
Częstotliwość przebiegu wyjściowego obliczyć można korzystając ze wzoru (3.1.):
]
[
125
2
1
]
[
Ω
Ω
=
=
set
set
R
M
T
Hz
f
(3.1.)
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
10 / 18

Politechnika Lubelska
Katedra Automatyki i Metrologii
W przypadku gdy na układ nie działa przyspieszenie, współczynnik wypełnienia przebiegu
wyjściowego wynosi typowo 50%. Wartość przyspieszenia mierzona jest poprzez określenie
aktualnego współczynnika wypełnienia. Działające na czujnik przyspieszenie można też
określić poprzez pomiar wartości napięcia sygnału analogowego na wyjściach X
FILT
i Y
FILT
, lub
przetworzenie wyjściowego przebiegu PWM z wyjść X
OUT
i Y
OUT
na sygnał napięciowy, za
pomocą dodatkowego dwójnika RC.
Największą czułość sensora równą ok, 17,5mg na stopień przechyłu uzyskuje się w
przypadku, gdy oś pomiarowa jest prostopadła do kierunku działania siły grawitacyjnej, czyli
równoległa do powierzchni ziemi.
ADXL202EX może być zasilany napięciem o wartości od +3 V do +5,25V, pobierając przy
tym prąd mniejszy niż 0,6mA. Nieliniowość charakterystyki przetwarzania wynosi do 0,5%
wartości zakresowej, a błąd określenia położenia kątowego około
±
1
°
. Czułość sensora na
wyjściach analogowych X
FILT
i Y
FILT
wynosi typowo 312mV/g, a na wyjściach cyfrowych X
OUT
i Y
OUT
określana jest jako procent współczynnika wypełnienia i wynosi 12,5%/g.
Częstotliwość rezonansowa sensora leży poza pasmem pracy układu (ok, 10kHz). W
temperaturze 25
°
C gęstość szumów w paśmie pracy wynosi 500
µ
g/
√
Hz. Podczas pracy
czujnik wytrzymuje bez groźby uszkodzenia, przyspieszenia do 500g (wzdłuż dowolnej osi, o
czasie działania krótszym, niż 0,5ms), a po odłączeniu zasilania maksymalnie do 1000g.
4. WYKONANIE POMIARÓW
4.1.Pomiary statyczne
Przygotowanie stanowiska
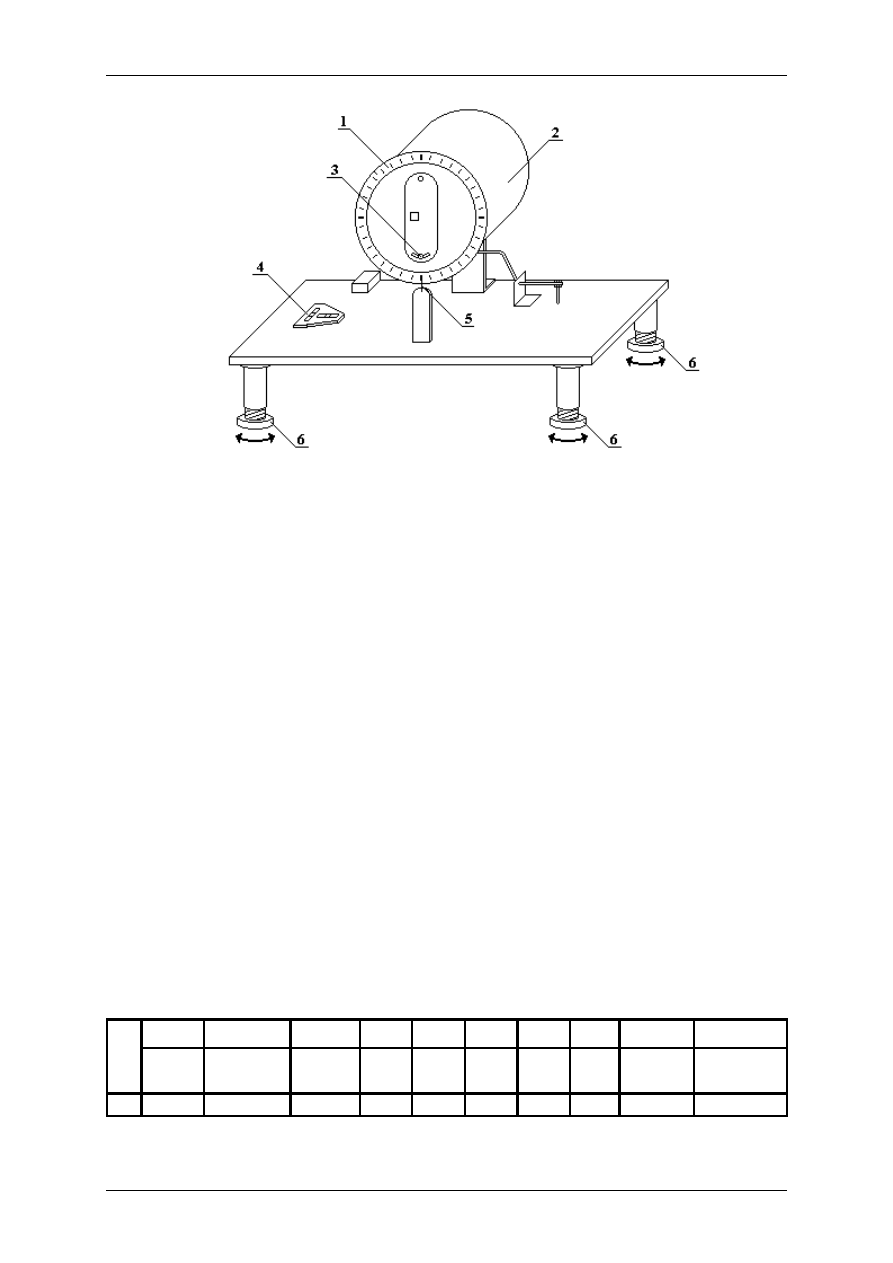
Wypoziomować urządzenie regulując wysokości nóżek podstawy, poprzez ich wkręcanie
i wykręcanie, obserwując przy tym położenie pęcherzyków powietrza w dwukierunkowej
poziomicy rurkowej umieszczonej na blacie urządzenia. Wszystkie elementy niezbędne do
przeprowadzenia regulacji przedstawione są na rysunku 4.1.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
11 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
Rysunek 4.1. Elementy służące do poziomowania urządzenia zadającego
przyspieszenie: 1- skala; 2- obrotowy bęben; 3- nakrętka motylkowa
dociskająca płytkę; 4- poziomica dwukierunkowa; 5- wskazówka;
6- regulowane nóżki podstawy;
Pomiarów dokonujemy odczytując wskazania woltomierzy podłączonych do wyjść
pomiarowych osi X i Y, dla kolejnych położeń bębna z umieszczonym wewnątrz
mikromechanicznym czujnikiem przyspieszenia ADXL202EX. Dodatkowo obserwujemy na
oscyloskopie przebieg sygnału o zmiennym współczynniku wypełnienia w osi X i Y, i
obliczamy współczynnik wypełnienia dzieląc czas trwania wysokiego zbocza przez okres
sygnału.
Należy sporządzić sześć tabel pomiarowych. Cztery tabele wykonujemy według
schematu tabeli 4.1. i notujemy w nich wyniki pomiarów:
1) dla osi X, w zakresie kątów od
α
= 90
°
do
α
= 270
°
2) dla osi X, w zakresie kątów od
α
= -90
°
do
α
= 90
°
3) dla osi Y, w zakresie kątów od
α
= 90
°
do
α
= 270
°
4) dla osi Y, w zakresie kątów od
α
= -90
°
do
α
= 90
°
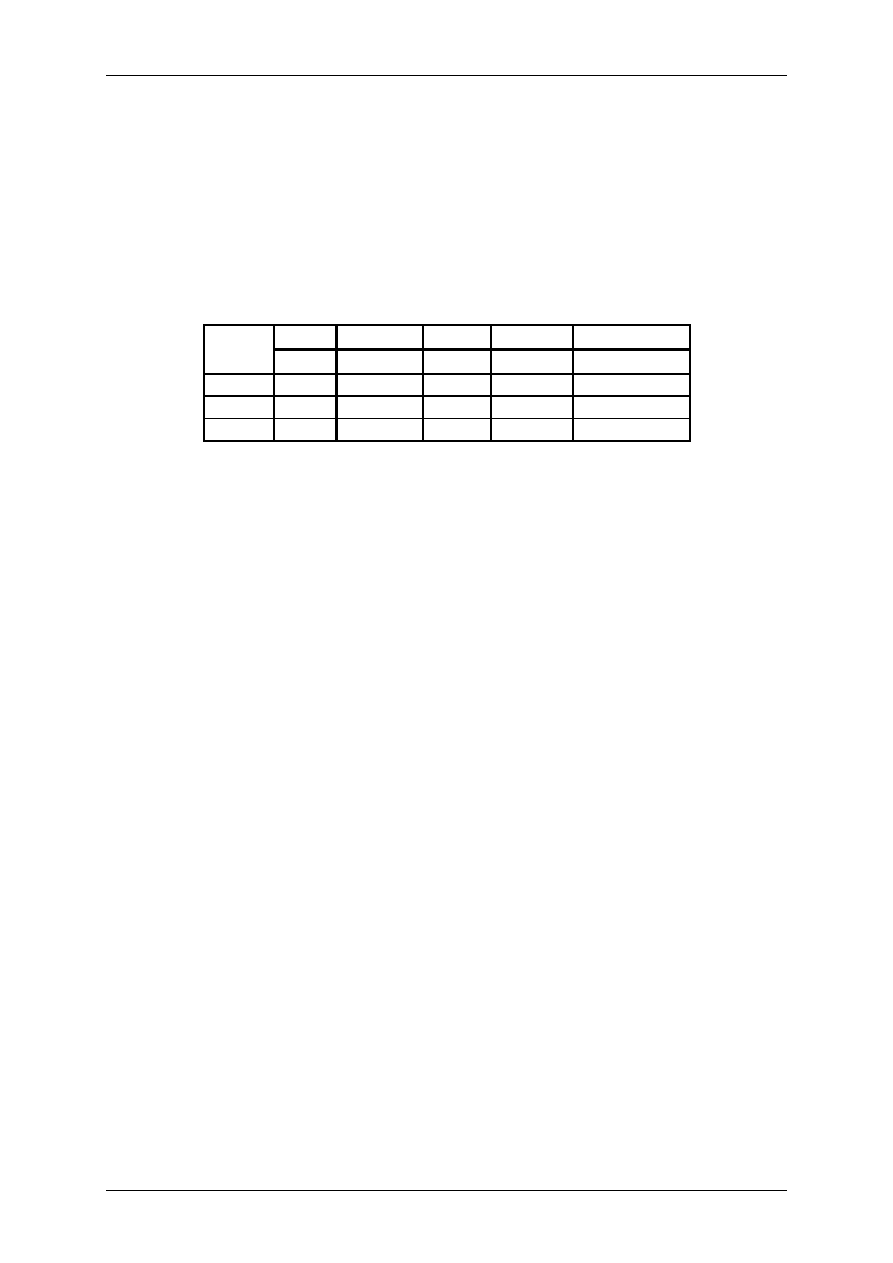
Tabela 4.1. Tabela pomiarowa mikromechanicznego czujnika przyspieszenia
ADXL202EX
L
L.p
α
a
a / g
U
T
H
T
L
T
W
δ
U
δ
W
[
°
]
[m/s
2
]
[-]
[
mV]
[
µ
s]
[
µ
s]
[
µ
s]
%
%
%
1
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
12 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
Dwie tabele wykonujemy według schematu tabeli 4.2. i notujemy w nich wyniki
pomiarów dla woltomierza umieszczonego w obudowie urządzenia:
5) dla osi X, w zakresie kątów od
α
= -90
°
do
α
= 90
°
6) dla osi Y, w zakresie kątów od
α
= -90
°
do
α
= 90
°
Tabela 4.2. Tabela pomiarowa mikromechanicznego czujnika przyspieszenia
ADXL202EX
L,p
α
a
a / g
U
δ
U
[
°
]
[m/s
2
]
[-]
[mV]
%
1
2
(...)
Pomiary należy przeprowadzić dla osi X i osi Y dla pełnego zakresu kątów obrotu bębna.
Przebieg pomiarów:
1) oś X ustawiamy równolegle do powierzchni ziemi, czyli
α
= 0
°
2) notujemy wskazania przyrządów w tabelach sporządzonych według wzoru tabeli 5.1.
obracając bęben co 10
°
, a dla przedziału kątów od
α
= -10
°
do
α
= 10
°
pomiarów
dokonujemy co 1
°
3) notujemy w tabeli według wzoru 5.2. wskazania woltomierza umieszczonego w
obudowie urządzenia, przy przełączniku w pozycji X, w przedziale kątów od
α
=-90
°
do
α
= 90
°
4) oś Y ustawiamy równolegle do powierzchni ziemi, czyli
α
= 0
°
5) notujemy wskazania przyrządów w tabelach sporządzonych według wzoru tabeli 5.1.
obracając bęben co 10
°
, a dla przedziału kątów od
α
= -10
°
do
α
= 10
°
pomiarów
dokonujemy co 1
°
6) notujemy w tabeli według wzoru 5.2. wskazania woltomierza umieszczonego w
obudowie urządzenia, przy przełączniku w pozycji Y, w przedziale kątów od
α
=
-90
°
do
α
= 90
°
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
13 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
4.2.Badanie czujnika w stanach dynamicznych
Układ ADXL202JE został zamocowany na membranie głośnika. Głośnik o mocy 10 W i
impedancji 4
Ω
zasilany jest ze wzmacniacza o zakresie częstotliwości pracy 22 Hz - 22 kHz.
Wychylenie membrany zależy od amplitudy sygnału zasilającego wzmacniacz - optymalna
wartość sygnału z generatora powinna wynosić 700mV. Do kontroli wychylenia membrany
służy transoptor szczelinowy. Na wyjściu transoptora otrzymujemy sygnał napięciowy zależny
od stopnia wychylenia membrany. W układzie pomiarowym wyprowadzone są wyjścia
sygnałów analogowych wystawiające napięcia odpowiadające przyspieszeniu odpowiednio w
osiach X i Y oraz wyjścia PWM, na których wraz ze zmianą przyspieszenia można
obserwować zmianę współczynnika wypełnienia sygnału. Dla przyspieszenia 0g na wyjściu
analogowym napięcie wynosi 2,5V a współczynnik wypełnienia sygnału PWM osiąga wartość
50%. Przy zmianie przyspieszenia o 1 g napięcie ulega zmianie o 322 mV a współczynnik
wypełnienia o 12,5%.
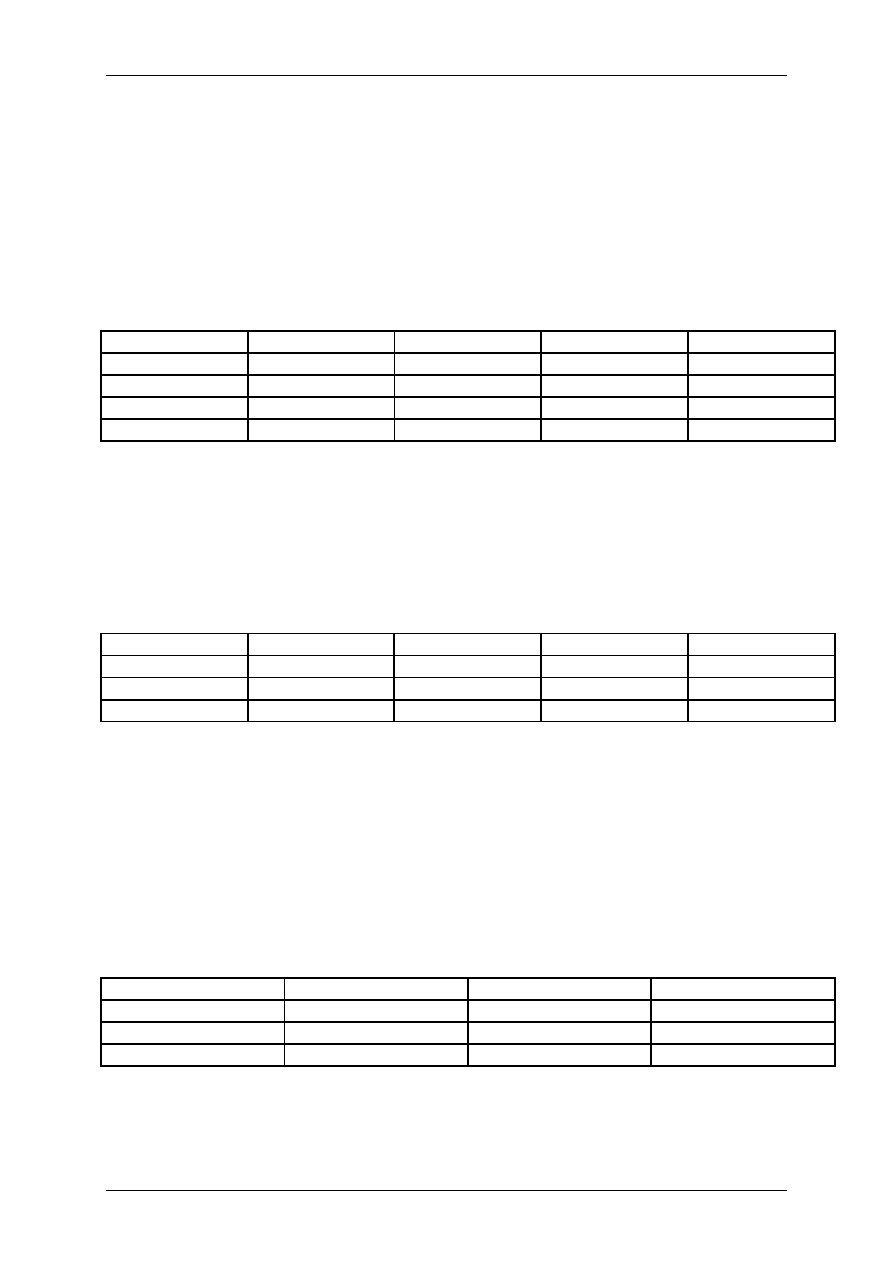
4.2.1. Połączyć układ według schematu 4.1.
Rys. 4.1. Schemat połączeń do badania czujnika w stanach dynamicznych
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
14 / 18
Politechnika Lubelska
Katedra Automatyki i Metrologii
4.2.2. Badanie czujnika przy stałej amplitudzie wychylenia membrany
Utrzymując stałą wartość napięcia z transoptora wykonać pomiary dla różnych wartości
częstotliwości sygnału z generatora. Pomiary wykonujemy dla częstotliwości w zakresie 20-
130Hz. Ze względu na rezonans mechaniczny głośnika nie wykonujemy pomiarów w zakresie
od 30 do 42 Hz. Wartość napięcia z transoptora należy tak dobrać aby nie przekroczyć
wartości sygnału wejściowego wzmacniacza 700mV. Wyniki pomiarów notujemy w tabeli.
Tabela 4.3. Badanie czujnika przy stałej amplitudzie wychylenia membrany
L.p.
f
Ut
Ux
g
[Hz]
[mV]
[mV]
[m/s
2
]
1
20
...
130
4.2.3. Badanie czujnika dla zmieniającej się wartości napięcia wejściowego wzmacniacza
Przy stałej wartości częstotliwości dla której nie następowało przesterowanie i
zniekształcanie sygnału należy wykonać pomiary dla różnych wartości napięcia z generatora
U
g
. Nie przekraczać wartości 700 mV.
Tabela 4.4. Badanie czujnika dla zmiany amplitudy sygnału wejściowego wzmacniacza
L.p.
Ug
Ut
Ux
g
[mV]
[mV]
[mV]
[m/s
2
]
1
...
4.2.3. Badanie czujnika z utrzymaniem stałej wartości przyspieszenia
Utrzymując stałą wartość napięcia na wyjściu czujnika odpowiadającą stałej wartości
przyspieszenia należy wykonać pomiary przy zmieniającej się wartości częstotliwości.
Pomiary wykonać w zakresie od 28 do 150 Hz. Amplitudę sygnału z generatora dobrać tak,
aby możliwe było wykonanie pomiarów w całym zakresie częstotliwości bez zniekształcania
sygnału.
Tabela 4.5. Badanie czujnika przy stałej wartości przyspieszenia
L.p
f
U
g
U
t
[Hz]
[mV]
[mV]
1
...
5. OPRACOWANIE SPRAWOZDANIA
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
15 / 18

Politechnika Lubelska
Katedra Automatyki i Metrologii
5.1. Badanie czujnika w stanach statycznych
Należy wyznaczyć :
1) wartość przyspieszenia działającego na czujnik przyspieszenia ze wzoru (5.1.)
α
sin
⋅
=
g
a
(5.1.)
2) stosunek a/g, dzieląc wartość przyspieszenia a działającego na czujnik przez wartość
przyspieszenia ziemskiego g
3) współczynnik wypełnienia sygnału W, według wzoru (5.2.)
%
100
⋅
=
T
T
W
H
(5.2.)
4) błąd nieliniowości napięcia wyjściowego
δ
U
, według wzoru (5.3.)
%
100
)
(
5
,
0
min
max
⋅
−
∆
=
U
U
U
U
δ
(5.3.)
gdzie:
∆
U – różnica napięcia zmierzonego i odczytanego z aproksymowanej
charakterystyki;
5) błąd nieliniowości współczynnika wypełnienia sygnału
δ
W
, według wzoru (5.4.)
%
100
)
(
5
,
0
min
max
⋅
−
∆
=
W
W
W
W
δ
(5.4.)
gdzie:
∆
W – różnica wspólczynnika wypełnienia zmierzonego i odczytanego z
aproksymowanej charakterystyki;
6) czułość wyjścia napięciowego, ze wzoru (5.5.)
min
max
min
max
a
a
U
U
C
U
−
−
=
(5.5.)
7) czułość wyjścia o zmiennym współczynniku wypełnienia , ze wzoru (5.6.)
min
max
min
max
a
a
W
W
C
W
−
−
=
(5.6.)
8) maksymalny błąd wyjścia napięciowego,
δ
Umax
9) maksymalny błąd wyjścia ze zmiennym współczynnikiem wypełnienia,
δ
Wmax
10) zakres napięć wyjściowych
11) zakres zmian współczynnika wypełnienia na wyjściu
6.1.1. Należy wykonać następujące charakterystyki:
1) dla osi X i zakresu kątów od
α
= 90
°
do
α
= 270
°
:
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
16 / 18

Politechnika Lubelska
Katedra Automatyki i Metrologii
U = f (a /g),
δ
U
= f (a), W = f (a /g),
δ
W
= f (a), U = f (
α
), W = f (
α
);
2) dla osi X i zakresu kątów od
α
= -90
°
do
α
= 90
°
:
U = f (a /g),
δ
U
= f (a), W = f (a /g),
δ
W
= f (a), U = f (
α
), W = f (
α
);
3) dla osi Y i zakresu kątów od
α
= 90
°
do
α
= 270
°
:
U = f (a /g),
δ
U
= f (a), W = f (a /g),
δ
W
= f (a), U = f (
α
), W = f (
α
);
4) dla osi Y i zakresu kątów od
α
= -90
°
do
α
= 90
°
:
U = f (a /g),
δ
U
= f (a), W = f (a /g),
δ
W
= f (a), U = f (
α
), W = f (
α
);
5) dla woltomierza umieszczonego w obudowie urządzenia w osi X i zakresu kątów od
α
= -90
°
do
α
= 90
°
:
U = f (a /g),
δ
U
= f (a), U = f (
α
);
6) dla woltomierza umieszczonego w obudowie urządzenia w osi Y i zakresu kątów od
α
= -90
°
do
α
= 90
°
:
U = f (a /g),
δ
U
= f (a), U = f (
α
);
Należy wyznaczyć czułość wyjścia napięciowego i wyjścia sygnału o zmiennym
współczynniku wypełnienia, dla osi X i Y, oraz dla woltomierza umieszczonego w obudowie
urządzenia. Sprawdzić jaką wartość ma współczynnik wypełnienia dla obu osi przy zerowym
przyspieszeniu i czy mieści się ono w przedziale podanym przez producenta.
W obliczeniach przyjęto wartość przyspieszenia ziemskiego wyliczonego na podstawie
wzoru (5.7.)
2
6
2
)
10
1
,
3
sin
0519
,
0
7803
,
9
(
s
m
H
g
−
⋅
−
+
=
φ
(5.7.)
gdzie:
φ
- szerokość geograficzna;
H - wysokość nad poziomem morza;
5.2. Badanie czujnika w stanach dynamicznych
5.2.1. Należy narysować charakterystyki Ux=e(f), g=e(f), Ut=e(Ug), Ut=e(Ug), g=e(Ug).
5.2.2. Dla utrzymywanej stałej wartości przyspieszenia należy wyznaczyć charakterystyki
Ut=e(f), Ug=(Ug).
6. LITERATURA
1. Miłek M.: Metrologia elektryczne wielkości nieelektrycznych, Wyd. Uniwersytetu
Zielonogórskigo, Zielona Góra 2006.
2. Gajek a., Juda Z.: Czujniki, WkiŁ, Warszawa 2009.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
17 / 18

Politechnika Lubelska
Katedra Automatyki i Metrologii
3. Bosch R.: Czujniki w pojazdach samochodowych, WkiŁ2009.
4. Romer E.: Miernictwo przemysłowe, PWN, Warszawa 1978.
Czujniki przyspieszeń statycznych i dynamicznych
ver.1.0
18 / 18
Document Outline
- CZUJNIKI PRZYSPIESZEŃ STATYCZNYCH I DYNAMICZNYCH
- Tabela 4.1. Tabela pomiarowa mikromechanicznego czujnika przyspieszenia
- TH
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron