
WPROWADZENIE
DO SZTUCZNEJ INTELIGENCJI
POLITECHNIKA WARSZAWSKA
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
MEL
MEL
NS 586
Dr in
ż
. Franciszek Dul
© F.A. Dul 2007

20. UCZENIE STATYSTYCZNE
© F.A. Dul 2007

Uczenie statystyczne
W tym rozdziale zapoznamy si
ę
z uczeniem jako form
ą
wnioskowania
statystycznego prowadzonego
na podstawie obserwacji.
© F.A. Dul 2007
na podstawie obserwacji.

Jak uczy
ć
si
ę
przy niepewno
ś
ci?
Omówione wcze
ś
niej metody uczenia
nie uwzgl
ę
dniały niepewno
ś
ci realnego
ś
wiata.
Uwzgl
ę
dnienie niepewno
ś
ci wymaga opracowania
metod uczenia w postaci wnioskowania
statystycznego.
Uczenie w warunkach niepewno
ś
ci mo
ż
e by
ć
oparte
na wnioskowaniu Bayesa.
©
F.A. Dul 2007
na wnioskowaniu Bayesa.

20.1. Wprowadzenie
• Uczenie jako wnioskowanie statystyczne
• Uczenie bayesowskie
• Sieci Bayesa w metodach uczenia
• Metody uczenia z pami
ę
taniem i przypominaniem
•
Sieci neuronowe
• Maszyny j
ą
drowe
Plan rozdziału
© F.A. Dul 2007
• Maszyny j
ą
drowe

20.1. Sformułowanie statystyczne uczenia
Uczenie statystyczne oparte jest na
hipotezach
i
danych
w postaci
obserwacji
.
Obserwacje s
ą
realizacjami zmiennej losowej
opisuj
ą
cej
wielko
ść
fizyczn
ą
.
Hipotezy s
ą
to
teorie probabilistyczne
opisuj
ą
ce rozwa
ż
an
ą
dziedzin
ę
.
Hipotezy logiczne s
ą
szczególnymi przypadkami hipotez
statystycznych.
© F.A. Dul 2007
statystycznych.

Przykład
20.1. Sformułowanie statystyczne uczenia
Sprzedawca pakuje dwa rodzaje cukierków do identycznych,
wielkich, torebek na pi
ęć
sposobów:
h
1
: 100%
wi
ś
niowych
,
h
2
: 75%
wi
ś
niowych
+ 25%
cytrynowych
,
h
3
: 50%
wi
ś
niowych
+ 50%
cytrynowych
,
h
4
: 25%
wi
ś
niowych
+ 75%
cytrynowych
,
h
5
: 100%
cytrynowych
.
Zmienna losowa H okre
ś
la typ otrzymanej torby: h
1
,..., h
5
.
© F.A. Dul 2007
Zmienna losowa H okre
ś
la typ otrzymanej torby: h
1
,..., h
5
.
Po otwarciu torby jej zawarto
ść
staje si
ę
znana.
Smaki poszczególnych cukierków okre
ś
laj
ą
zmienne losowe
D
1
,..., D
N
, przyjmuj
ą
ce warto
ś
ci
wi
ś
nia
lub
cytryna
.
Zadaniem agenta-łasucha jest przewidzenie smaku
nast
ę
pnego cukierka wyci
ą
gni
ę
tego z torby.
Do rozwi
ą
zania problemu u
ż
yjemy
uczenia bayesowskiego
.
Polega ono na wyznaczeniu prawdopodobie
ń
stwa ka
ż
dej
hipotezy na podstawie obserwacji i przewidzenie na tej
podstawie smaku cukierka.

Uczenie jest sprowadzone do
wnioskowania statystycznego
.
Niech
D
oznacza zbiór wszystkich danych z warto
ś
ciami
obserwowanymi
d
. Ze wzoru Bayesa
)
(
)
|
(
)
|
(
i
i
i
h
P
h
P
h
P
d
d
α
=
Je
ż
eli chcemy przewidzie
ć
warto
ść
nieznanej wielko
ś
ci
X
, to
∑
∑
=
=
h
P
h
X
P
h
P
h
X
P
X
P
)
|
(
)
|
(
)
|
(
)
,
|
(
)
|
(
d
d
d
d
gdzie
P(h
i
) -
prawdopodobie
ń
stwo a priori hipotezy
h
i
za
ś
P(d|h
i
)
-
wiarygodno
ść
danych dla tych hipotez.
20.1. Sformułowanie statystyczne uczenia
© F.A. Dul 2007
∑
∑
=
=
i
i
i
i
i
i
h
P
h
X
P
h
P
h
X
P
X
P
)
|
(
)
|
(
)
|
(
)
,
|
(
)
|
(
d
d
d
d
∏
=
j
i
j
i
h
d
P
h
P
)
|
(
)
|
(d
Je
ż
eli np. torba jest typu
h
5
(same cytrynowe) to pierwszych
10 cukierków jest cytrynowych, zatem
P(d|h
3
) = 0.5
10
gdy
ż
w
torbie
h
3
połowa cukierków jest cytrynowa.
Zakładamy,
ż
e wiarygodno
ść
danych jest wyznaczona przy
zało
ż
eniu ich niezale
ż
no
ś
ci oraz identycznego rozkładu, zatem
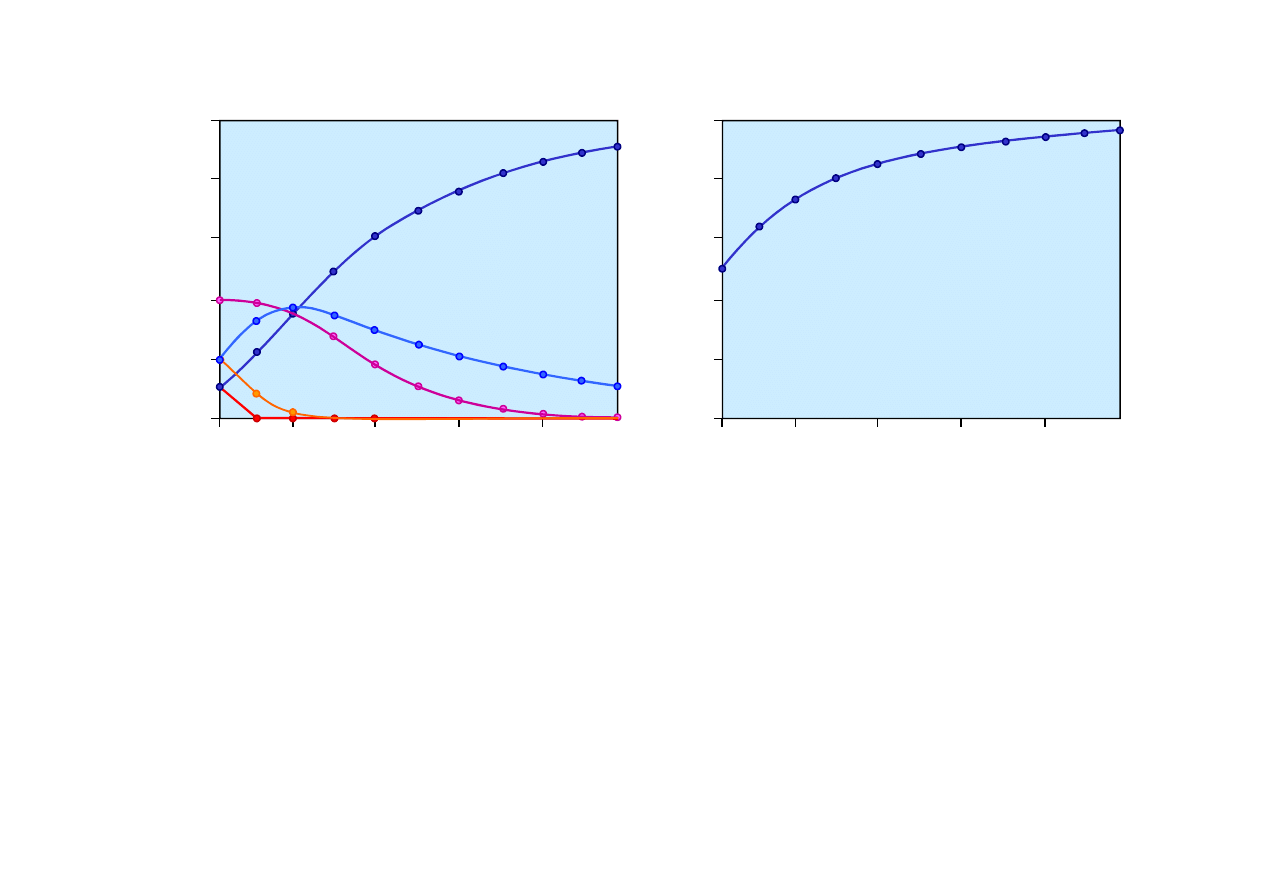
0.2
0.4
0.6
0.8
1.0
0
P(h
5
|d)
P(h
3
|d)
2
4
6
8
10
P(h
4
|d)
P(h
2
|d)
P(h
1
|d)
d
P
ra
w
d
o
p
o
d
o
b
ie
ń
s
tw
o
a
p
o
s
te
rr
io
ri
h
ip
o
te
z
0.2
0.4
0.6
0.8
1.0
0
2
4
6
8
10
d
P
ra
w
d
o
p
o
d
o
b
ie
ń
s
tw
o
k
o
le
jn
e
g
o
c
y
tr
y
n
o
w
e
g
o
c
u
k
ie
rk
a
20.1. Sformułowanie statystyczne uczenia
© F.A. Dul 2007
Liczba próbek w
d
Prawdopodobie
ń
stwa a
posteriori
P(h
i
|d
1
, d
2
,... d
N
)
wybrania cukierka cytrynowego
dla hipotez
h
i
.
Liczba próbek w
d
Oszacowanie Bayesa
prawdopodobie
ń
stwa wybrania
nast
ę
pnego cukierka
cytrynowego,
P(d
N+1
= cytrynowy|d
1
, d
2
,... d
N
)
Ze wzrostem liczby próbek ro
ś
nie prawdopodobie
ń
stwo
hipotezy
h
5
, malej
ą
za
ś
prawdopodobie
ń
stwa hipotez
pozostałych.
Hipoteza prawdziwa w ko
ń
cu zdominuje pozostałe.
20.2. Uczenie z danymi kompletnymi
Najprostsz
ą
metod
ą
uczenia statystycznego jest
uczenie
parametryczne z danymi kompletnymi
.
Uczenie parametryczne polega na wyznaczeniu warto
ś
ci
parametrów modelu statystycznego.
Uczenie parametryczne najwi
ę
kszej wiarygodno
ś
ci ML
dla modeli dyskretnych
Załó
ż
my,
ż
e otrzymali
ś
my torb
ę
cukierków o nieznanej
proporcji
θ
∈
[0,1] cukierków wi
ś
niowych i cytrynowych.
© F.A. Dul 2007
Zmienna losowa Smak przyjmuje
warto
ś
ci: wi
ś
nia i cytryna.
proporcji
θ
∈
[0,1] cukierków wi
ś
niowych i cytrynowych.
Parametrem uczenia jest
θ
,
za
ś
hipotez
ą
ci
ą
gł
ą
h
θ
.
Po rozwini
ę
ciu N cukierków
okazało si
ę
,
ż
e jest c wi
ś
niowych
i N - c cytrynowych.
Smak
P(S=wiśnia)
θ
Sie
ć
Bayesa dla
nieznanej proporcji
θ
cukierków wi
ś
niowych
i cytrynowych.

20.2. Uczenie z danymi kompletnymi
Hipoteza ML,
h
przewiduje,
ż
e najbardziej wiarygodna
Warto
ść
θ
maksymalizuj
ą
ca wiarygodno
ść
wynosi
N
c
c
N
c
c
d
h
dL
=
−
+
=
⇒
=
)
(
0
)
|
(
θ
θ
θ
d
Wiarygodno
ść
zbioru N danych jest równa
)
1
log(
)
(
log
)
|
(
log
)
|
(
log
)
|
(
1
θ
θ
θ
θ
θ
−
−
+
=
=
=
∑
=
c
N
c
h
d
P
h
P
h
L
N
j
j
d
d
© F.A. Dul 2007
Hipoteza ML,
h
ML
przewiduje,
ż
e najbardziej wiarygodna
proporcja cukierków jest równa proporcji obserwowanej.
Zasad
ę
ogólna uczenia parametrycznego ML - wyznaczenie
argumentu maksimum logarytmicznej funkcji wiarygodno
ś
ci.
Kompletno
ść
danych prowadzi do
dekompozycji
zadania
uczenia parametrycznego maksymalnej wiarygodno
ś
ci
z sieci
ą
Bayesa na oddzielne zadania uczenia dla
poszczególnych parametrów.

Uczenie parametryczne Bayesa
Uczenie bayesowskie zakłada aprioryczny rozkład warto
ś
ci
parametru ucz
ą
cego a nast
ę
pnie modyfikuje ten rozkład
wraz z napływem danych.
Niech zmienna losowa
Θ
odpowiadaj
ą
ca parametrowi
θ
∈
[0,1]
ma rozkład pocz
ą
tkowy
P(
Θ
)
który jest ci
ą
gły i niezerowy
w przedziale [0,1].
20.2. Uczenie z danymi kompletnymi
Rozkłady aprioryczne dla zbioru parametrów, np.
P(
Θ
,
Θ
1
,
Θ
2
)
dla parametrów
θ
,
θ
1
,
θ
2
wybiera si
ę
zazwyczaj zakładaj
ą
c,
ż
e
s
ą
one niezale
ż
ne
© F.A. Dul 2007
)
(
)
(
)
(
)
,
,
(
2
1
2
1
Θ
Θ
Θ
=
Θ
Θ
Θ
P
P
P
P
dla parametrów
θ
,
θ
1
,
θ
2
wybiera si
ę
zazwyczaj zakładaj
ą
c,
ż
e
s
ą
one niezale
ż
ne
Przy takim zało
ż
eniu ka
ż
dy parametr ma swój własny rozkład
beta
, który zmienia si
ę
niezale
ż
nie od pozostałych przy
dopływie nowych danych.
Rozkład
P(
Θ
)
mo
ż
e opisany
dystrybucj
ą
beta
zdefiniowan
ą
za pomoc
ą
dwóch
hiperparametrów
a i b,
1
1
)
1
(
)
](
,
[
−
−
−
=
b
a
b
a
beta
θ
θ
α
θ
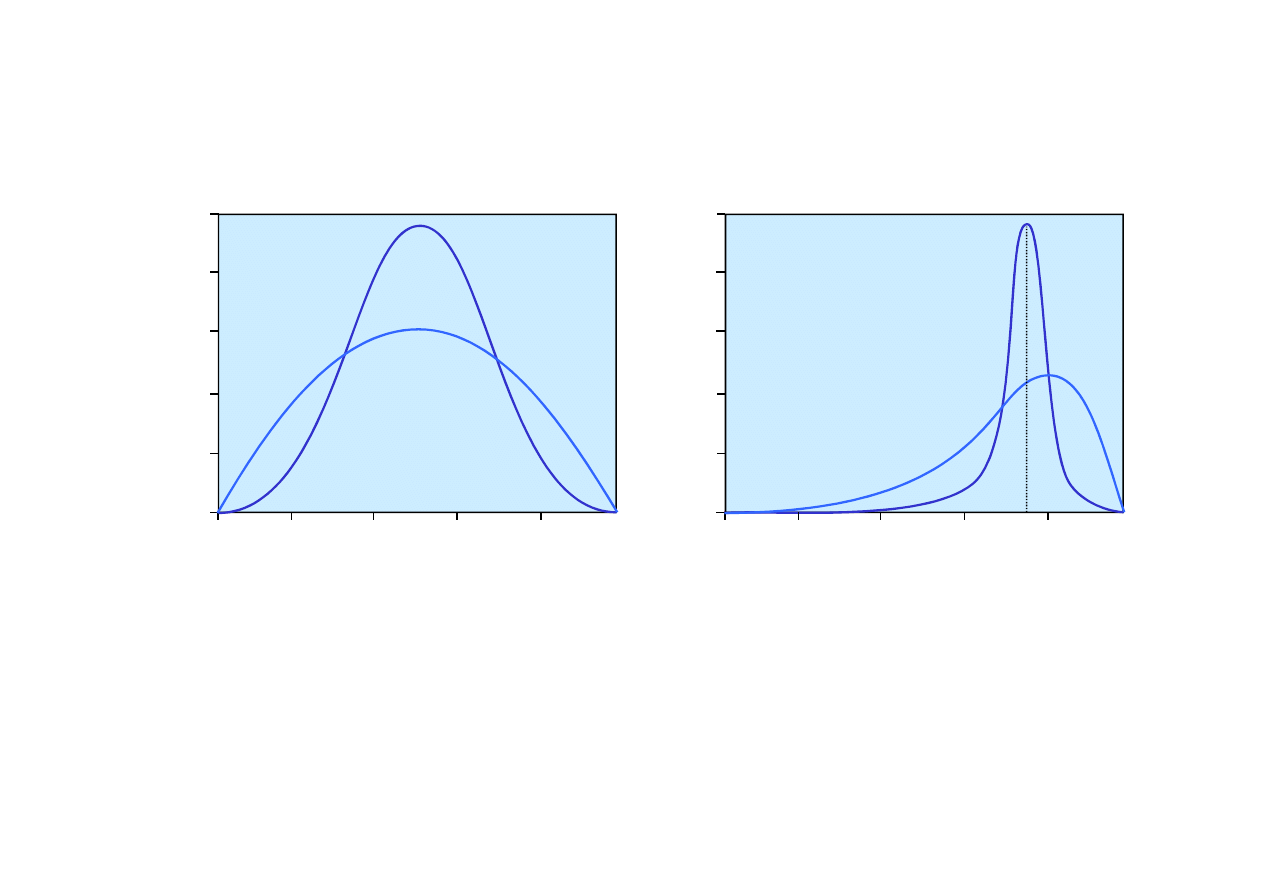
Rozkłady beta parametru
θ
dla ró
ż
nych warto
ś
ci hiperpara-
metrów a i b.
0.5
1.0
1.5
2.0
2.5
[2,2]
[1,1]
[5,5]
P
(
ΘΘΘΘ
=
θθθθ
)
1.0
2.0
3.0
4.0
5.0
[6,2]
[30,10]
P
(
ΘΘΘΘ
=
θθθθ
)
20.2. Uczenie z danymi kompletnymi
© F.A. Dul 2007
0.5
0
0.2
0.4
0.6
0.8
1.0
Parametr
θ
Rozkład beta parametru
θ
przy rosn
ą
cych symetrycznie
warto
ś
ciach hiperparametrów
a i b.
Rozkład beta parametru
θ
przy wyci
ą
ganiu cukierków
z torby zawieraj
ą
cej 75%
cukierków wi
ś
niowych d
ąż
y
do w
ą
skiego piku w pobli
ż
u
prawdziwej warto
ś
ci
θ
=0.75
1.0
0
[3,1]
0.2
0.4
0.6
0.8
1.0
Parametr
θ
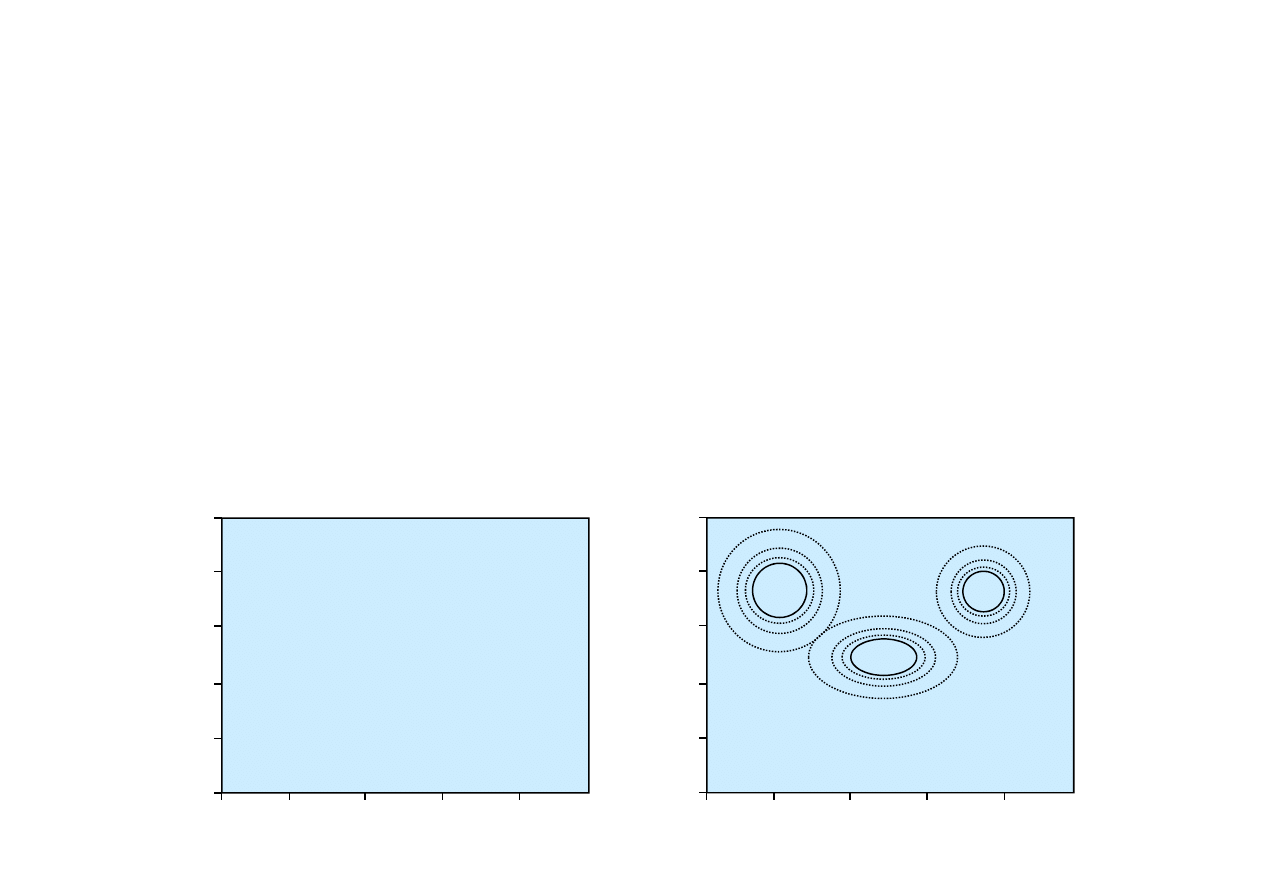
Skupianie nienadzorowane
jest to problem wyodr
ę
bnienia
kategorii w zbiorze obiektów.
20.3. Skupianie nienadzorowane
Przykłady
• Zbiór spektrów gwiazd
.
Istniej
ą
ró
ż
ne typy gwiazd, np. „czerwone olbrzymy” czy
„białe karły”, chocia
ż
gwiazdy nie maj
ą
etykiet z nazwami.
• Klasyfikacja organizmów
ż
ywych
.
Rz
ę
dy, rodzaje, gatunki zwierz
ą
t i ro
ś
lin. Nie maj
ą
one
poj
ę
cia,
ż
e ludzie przypisali im jakie
ś
nazwy.
© F.A. Dul 2007
Istniej
ą
ró
ż
ne typy gwiazd, np. „czerwone olbrzymy” czy
„białe karły”, chocia
ż
gwiazdy nie maj
ą
etykiet z nazwami.
0.2
0.4
0.6
0.8
1.0
0
0.2
0.4
0.6
0.8
1.0
G
ę
sto
ść
spektralna 1
G
ę
s
to
ś
ć
s
p
e
k
tr
a
ln
a
2
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
0.2
0.4
0.6
0.8
1.0
0
0.2
0.4
0.6
0.8
1.0
G
ę
sto
ść
spektralna 1
G
ę
s
to
ś
ć
s
p
e
k
tr
a
ln
a
2
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+

Zakłada si
ę
,
ż
e skupienia maj
ą
rozkład mieszany
zło
ż
ony
z k składników maj
ą
cych niezale
ż
ne rozkłady.
∑
=
=
=
=
k
i
i
C
P
i
C
P
P
1
)
|
(
)
(
)
(
x
x
Rozkłady prawdopodobie
ń
stw składników s
ą
najcz
ęś
ciej
rozkładami mieszanymi Gaussa
w których parametrami s
ą
:
Rozkład mieszany zmiennej losowej
C
maj
ą
cej atrybuty
x
jest
równy
• wagi składników
w
i
= P(C=i),
20.3. Uczenie skupie
ń
nienadzorowanych
© F.A. Dul 2007
• wagi składników
w
i
= P(C=i),
• warto
ś
ci
ś
rednie składników
µ
i
,
• kowariancje składników
Σ
i
.
Zadanie skupiania nienadzorowanego polega na wyznaczeniu
parametrów rozkładu mieszanego na podstawie danych
ucz
ą
cych.
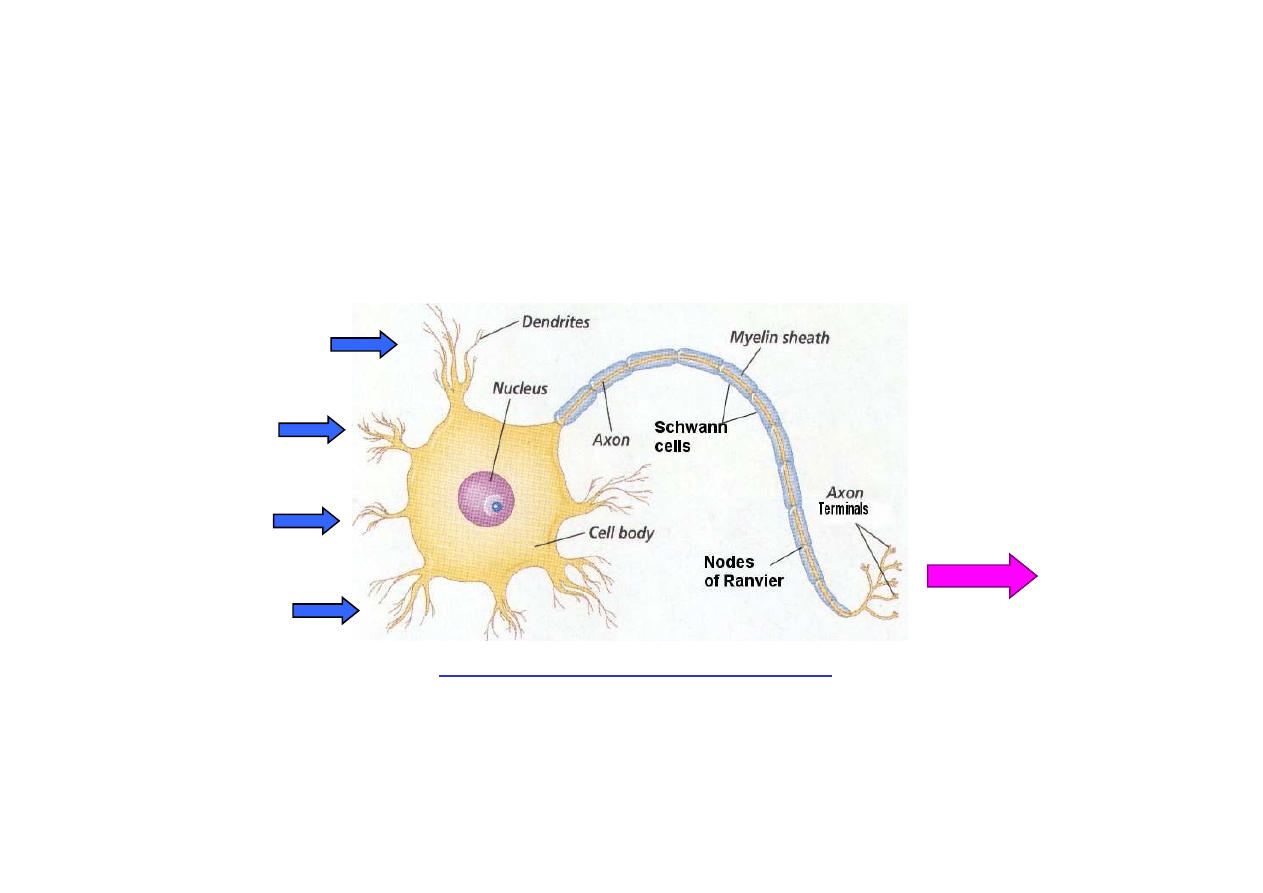
20.5 Sieci neuronowe
Sieci neuronowe stanowi
ą
jedne z najpopularniejszych
oraz najbardziej efektywnych systemów ucz
ą
cych.
Neuron
jest to komórka mózgowa maj
ą
ca za zadanie
zbieranie, przetwarzanie i przesyłanie sygnałów elektrycznych.
© F.A. Dul 2007
www.sirinet.net/~jgjohnso/neuronproject.html
Przekazanie sygnału ma miejsce wówczas, gdy poziom
kombinacji sygnałów wej
ś
ciowych przekroczy pewien próg.
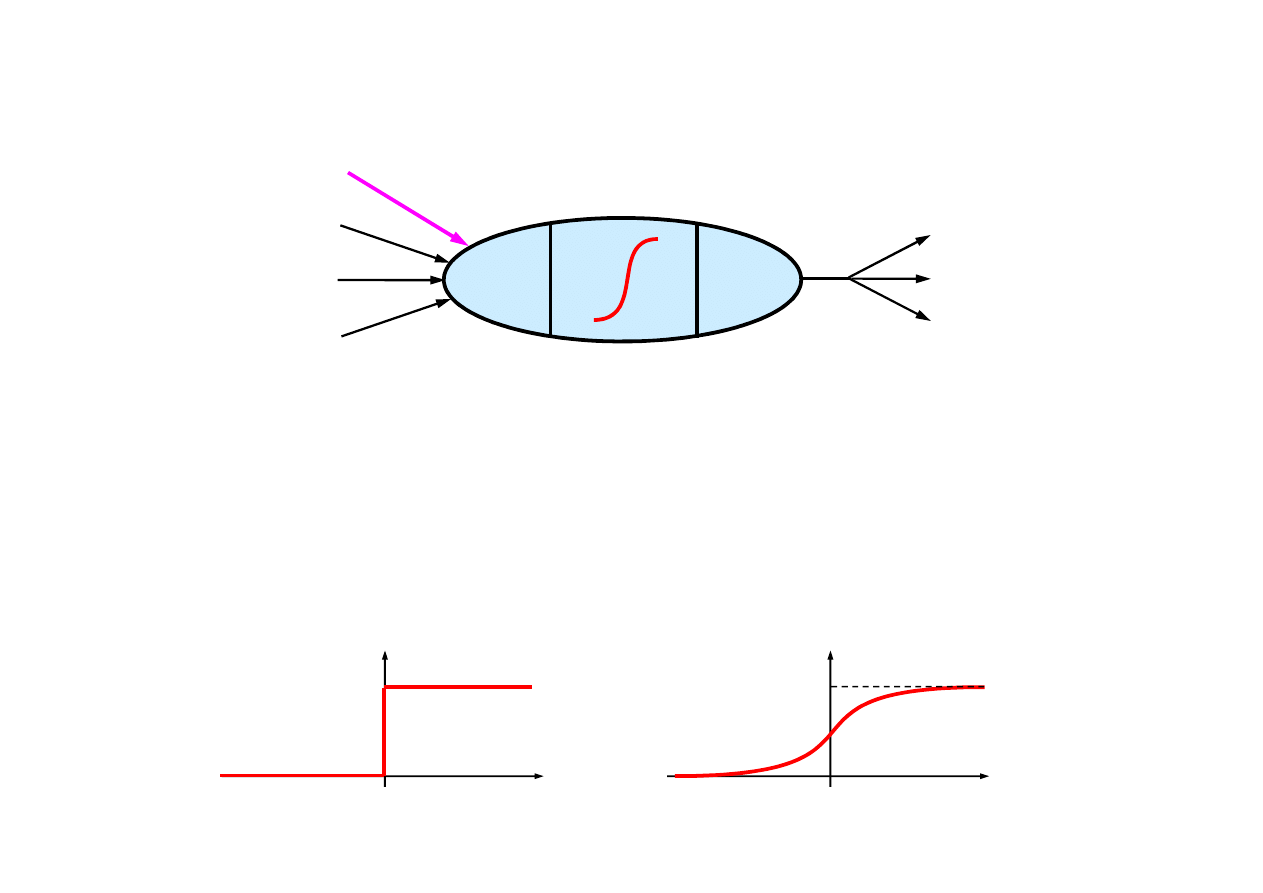
Model matematyczny neuronu
∑
i
in
i
a
g
i
W
,
0
j
a
i
j
W
,
1
0
−
=
a
)
(
i
i
in
g
a
=
Poł
ą
czenia
wej
ś
ciowe
Funkcja
wej
ś
ciowa
Funkcja
aktywacji
Wyj
ś
cie
Poł
ą
czenia
wyj
ś
ciowe
Waga szumu
Wej
ś
cie neuronu
i
jest sum
ą
wa
ż
on
ą
aktywacji
a
j
z
wagami
W
, za
ś
wyj
ś
cie neuronu
i
jest opisane
funkcj
ą
aktywacji
g
20.5. Sieci neuronowe
© F.A. Dul 2007
)
(
)
(
0
,
∑
=
=
=
n
j
j
i
j
i
i
a
W
g
in
g
a
j
W
j,i
, za
ś
wyj
ś
cie neuronu
i
jest opisane
funkcj
ą
aktywacji
g
działaj
ą
c
ą
na wej
ś
cie
in
j
Funkcje aktywacji musz
ą
by
ć
nieliniowe, np.
)
(
i
in
g
i
in
1
+
Funkcja progowa
)
(
i
in
g
i
in
1
+
Funkcja sigmoidalna

20.5. Sieci neuronowe
Istniej
ą
dwie główne kategorie sieci neuronowych:
Struktury sieci neuronowych
• acykliczne (feed-forward networks), bez sprz
ęż
e
ń
zwrotnych,
• cykliczne (recurrent networks), ze sprz
ęż
eniami
zwrotnymi, sieci Hopfielda.
Sieci neuronowe acykliczne s
ą
najcz
ęś
ciej budowane
w postaci
warstwowej
- wyj
ś
cia z jednej warstwy s
ą
wej
ś
ciami
dla warstwy nast
ę
pnej.
© F.A. Dul 2007
Uczenie sieci neuronowych
)
(x
W
h
h
=
Sie
ć
realizuje funkcj
ę
danych wej
ś
ciowych
x,
Najefektywniejszym sposobem uczenia sieci neuronowych
jest
metoda propagacji wstecznej.
Wagi
W
= {
W
j,i
} s
ą
parametrami sieci.
Uczenie sieci neuronowych dokonuje si
ę
poprzez dostrojenie
wag
W
za pomoc
ą
danych ucz
ą
cych.
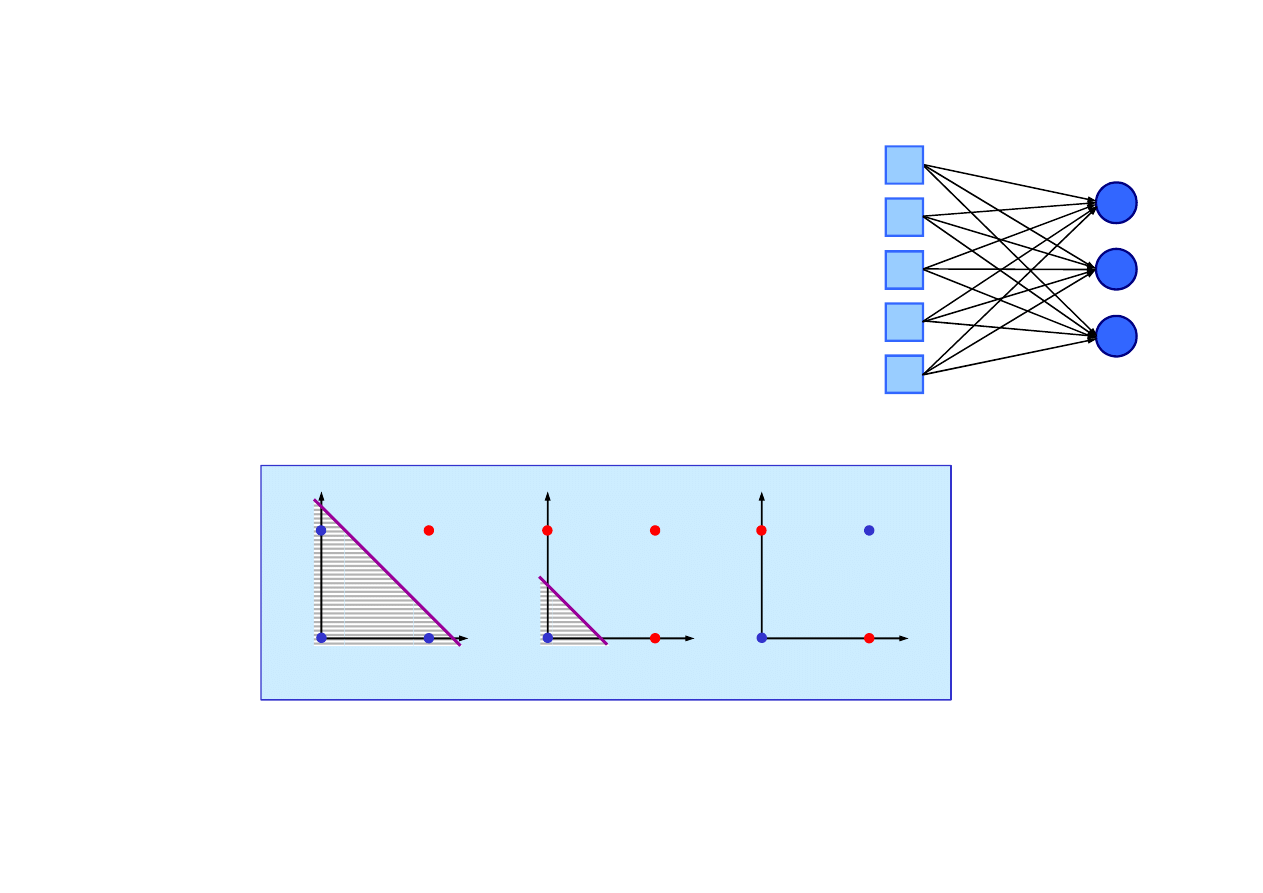
W
perceptronie
(sieci neuronowej
jednowarstwowej) wej
ś
cia s
ą
poł
ą
czone
bezpo
ś
rednio z wyj
ś
ciami.
Perceptron - sie
ć
jednowarstwowa acykliczna
0
0
0
>
⋅
⇒
>
∑
=
x
W
N
j
j
j
x
W
Klasa funkcji które mog
ą
by
ć
reprezentowane
za pomoc
ą
perceptronów jest ograniczona,
20.5. Sieci neuronowe
tj. mog
ą
reprezentowa
ć
tylko funkcje separowalne liniowo.
© F.A. Dul 2007
tj. mog
ą
reprezentowa
ć
tylko funkcje separowalne liniowo.
Perceptron mo
ż
e mie
ć
tak
ż
e charakter probabilistyczny.
Mimo tego ograniczenia perceptrony s
ą
szeroko stosowane
w uczeniu maszynowym.
2
x
1
x
x
1
and x
2
1
1
0
0
2
x
1
x
x
1
or x
2
1
1
0
0
2
x
1
x
x
1
xor x
2
1
1
0
0
?
Algorytm ucz
ą
cy dla perceptronu
2
2
1
2
2
1
))
(
(
x
W
h
y
Err
E
−
=
=
Uczenie sieci neuronowej jest sformułowane jako zadanie
optymalizacji w przestrzeni wagowej ze wska
ź
nikiem jako
ś
ci
j
j
j
x
in
g
Err
W
W
×
×
×
+
←
)
(
'
α
Parametr
α
metody wyznacza
szybko
ść
uczenia
.
Kolejne przybli
ż
enia współczynników wagowych okre
ś
lone s
ą
metod
ą
gradientow
ą
nast
ę
puj
ą
co
20.5. Sieci neuronowe
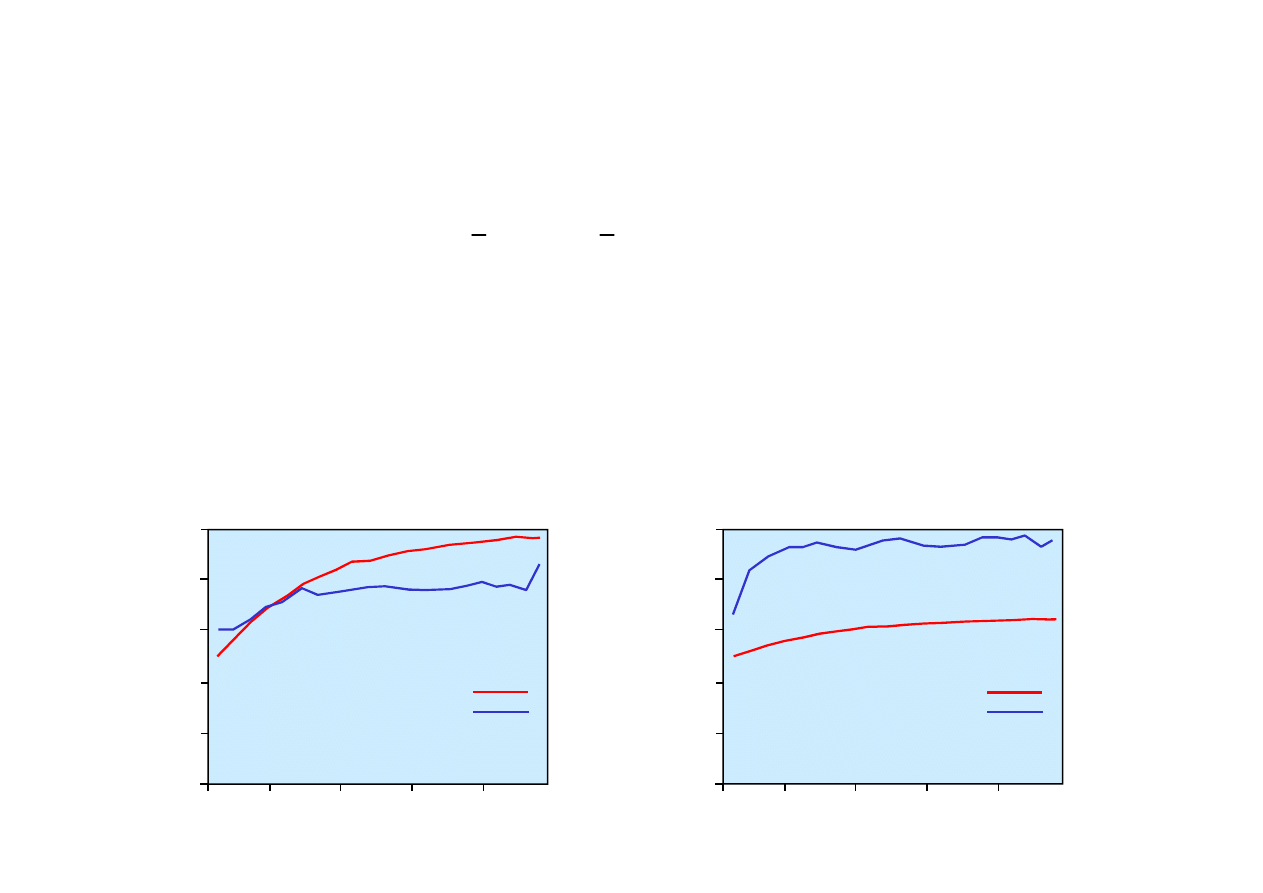
Porównanie uczenia perceptronu i sieci decyzyjnej dla zada
ń
© F.A. Dul 2007
0.2
0.4
0.6
0.8
1.0
0
20
40
60
80
100
Wymiar zbioru ucz
ą
cego
%
p
o
p
ra
w
n
n
a
z
b
io
rz
e
te
st
o
w
ym
Perceptron
Drzewo decyzyjne
0.2
0.4
0.6
0.8
1.0
0
20
40
60
80
100
Wymiar zbioru ucz
ą
cego
P
ro
p
o
rc
je
p
o
p
ra
w
n
e
n
a
z
b
io
rz
e
te
st
o
w
ym
Perceptron
Drzewo decyzyjne
Porównanie uczenia perceptronu i sieci decyzyjnej dla zada
ń
funkcji majoryzuj
ą
cej oraz wyboru restauracji.

Sieci wielowarstwowe acykliczne
U
ż
ycie warstw zło
ż
onych z w
ę
złów ukrytych pozwala
reprezentowa
ć
znacznie szersz
ą
klas
ę
funkcji.
20.5. Sieci neuronowe
)
(x
h
h
W
=
Sie
ć
wielowarstwowa z wieloma wyj
ś
ciami realizuje funkcj
ę
wektorow
ą
h
danych wej
ś
ciowych
x
Wska
ź
nikiem jako
ś
ci jest wektor bł
ę
du
ś
redniokwadratowy
pomi
ę
dzy wektorem wzorców ucz
ą
cych
y
a wektorem wyj
ść
z sieci wielowarstwowej
© F.A. Dul 2007
U
ż
ycie pojedy
ń
czej warstwy ukrytej pozwala reprezentowa
ć
dowoln
ą
funkcj
ę
ci
ą
gł
ą
wej
ść
z dowoln
ą
dokładno
ś
ci
ą
.
U
ż
ycie dwóch warstw ukrytych pozwala reprezentowa
ć
nawet
funkcje nieci
ą
głe.
Dlatego sieci neuronowe zalicza si
ę
do klasy
uniwersalnych
aproksymatorów
.
z sieci wielowarstwowej
))
(
(
))
(
(
2
1
2
1
x
h
y
x
h
y
Err
Err
W
W
−
−
=
=
T
T
E
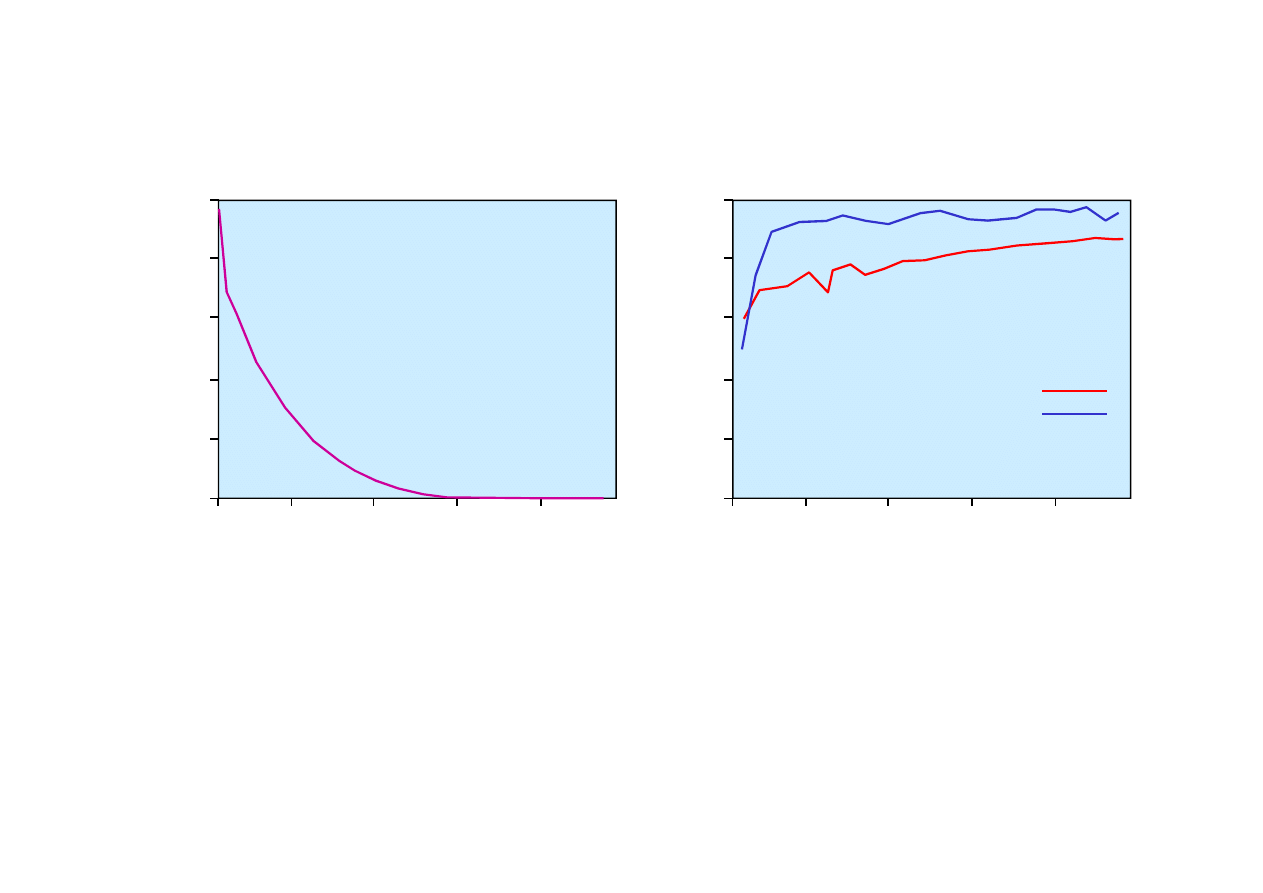
Porównanie uczenia sieci neuronowej z jedn
ą
warstw
ą
ukryt
ą
i sieci decyzyjnej dla zadania wyboru restauracji.
3
6
9
12
15
ą
d
cał
kow
it
y
n
a z
bi
or
ze
t
es
tow
ym
P
ropor
cj
e popr
aw
n
e
n
a z
bi
or
ze
te
st
ow
ym
0.2
0.4
0.6
0.8
1.0
Sie
ć
wielowarstwowa
Drzewo decyzyjne
20.5. Sieci neuronowe
© F.A. Dul 2007
Numer epoki
0
100
200
300
400
500
B
łą
d
cał
kow
it
y
n
a z
bi
or
ze
t
es
tow
ym
P
ropor
cj
e popr
aw
n
e
n
a z
bi
or
ze
0
20
40
60
80
100
Wymiar zbioru ucz
ą
cego
Sieci neuronowe pozwalaj
ą
reprezentowa
ć
nawet bardzo
zło
ż
one zadania, ale problem wyboru wła
ś
ciwej struktury
sieci, odpowiedniej dla danego zadania, nie jest rozwi
ą
zany.
Corocznie ukazuj
ą
si
ę
tysi
ą
ce publikacji dotycz
ą
cych
zastosowa
ń
sieci neuronowych w ró
ż
nych dziedzinach nauki
i techniki.

20.6 Metody j
ą
drowe uczenia
Proste sieci neuronowe ucz
ą
si
ę
szybko, ale maj
ą
ograniczon
ą
ekspresj
ę
.
Zło
ż
one sieci neuronowe maj
ą
wysok
ą
ekspresj
ę
, ale proces
ich uczenia jest zazwyczaj długotrwały i czasami zawodny.
Metody zwane
wspierajacymi maszynami wektorowymi
(support vector machines, SVM) lub
maszynami j
ą
drowymi
(kernel machines) pozwalaj
ą
uczy
ć
wydajnie a jednocze
ś
nie
cechuj
ą
si
ę
wysok
ą
ekspresj
ą
.
© F.A. Dul 2007
Idea SVM - przekształcenie zadania nieseparowalnego
liniowo do postaci separowalnej.
Przekształcenia do postaci separowalnej dokonuje si
ę
za pomoc
ą
odpowiednio dobranej funkcji nieliniowej
F(x)
wektora wej
ść
x
.
Funkcja
F(x)
przekształca przestrze
ń
danych na
przestrze
ń
własno
ś
ci
.
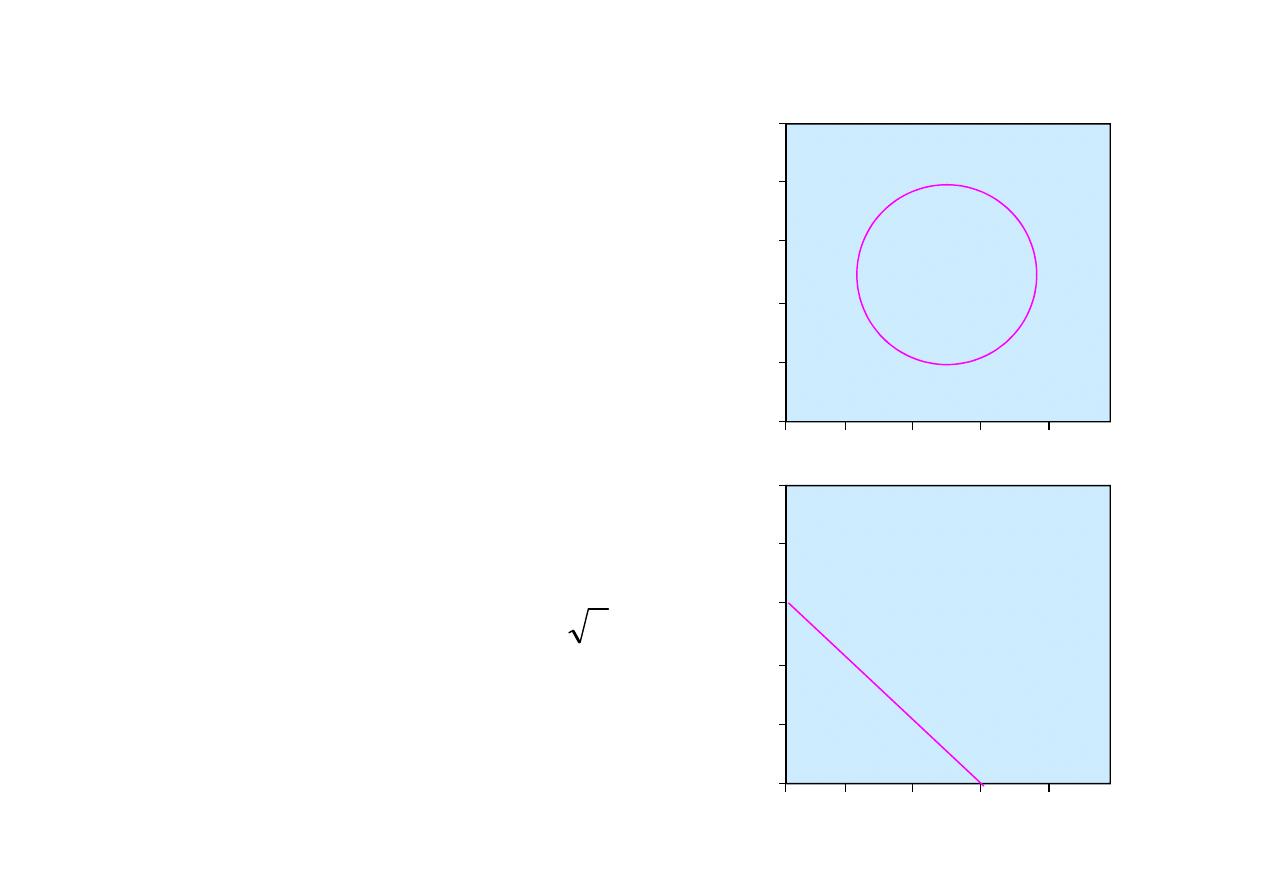
Przykład
-0.6
-0.2
0.2
0.6
1.0
-1.0
-0.6
-0.2
0.2
0.6
1.0
x
2
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
20.6. Metody j
ą
drowe uczenia
Zbiór nie jest separowalny liniowo.
W dwuwymiarowym zbiorze danych
x = (x
1
, x
2
)
wzorce pozytywne
(+1)
znajduj
ą
si
ę
w obszarze kołowym.
© F.A. Dul 2007
0.3
0.7
1.0
1.3
1.7
0
0.3
0.6
1.0
1.3
1.7
f
1
f
2
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
++
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
x
1
2
1
3
2
2
2
2
1
1
2
,
,
x
x
f
x
f
x
f
=
=
=
Funkcja
F: R
2
→
R
3
o składowych
F(x) = ( f
1
(x), f
2
(x) , f
3
(x) )
przekształca zbiór wej
ś
ciowy na
zbiór separowalny liniowo.
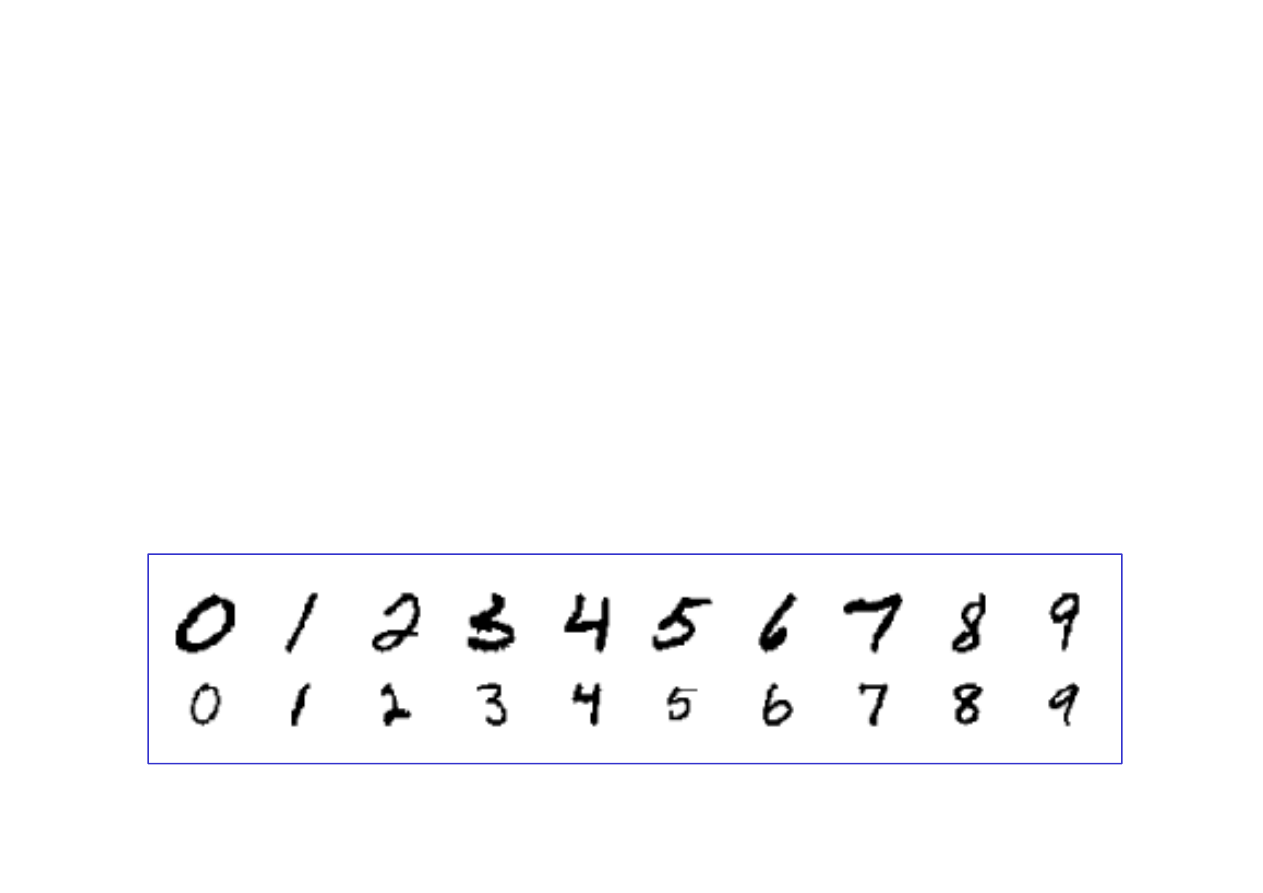
20.7 Zastosowanie - rozpoznawanie pisma
odr
ę
cznego
Rozpoznawanie pisma odr
ę
cznego jest wa
ż
nym zadaniem
praktycznym spotykanym np. przy sortowaniu poczty,
automatycznym odczytywaniu dokumentów, r
ę
cznym
wpisywaniu danych do komputerów, itp.
Obserwuje si
ę
szybki post
ę
p w tej dziedzinie, wyra
ż
aj
ą
cy si
ę
powstawaniem coraz lepszych algorytmów ucz
ą
cych.
Rol
ę
stymuluj
ą
c
ą
pełni baza danych NIST, zawieraj
ą
ca
60,000 odr
ę
cznie zapisanych cyfr w formacie 400 pikseli,
© F.A. Dul 2007
Rol
ę
stymuluj
ą
c
ą
pełni baza danych NIST, zawieraj
ą
ca
60,000 odr
ę
cznie zapisanych cyfr w formacie 400 pikseli,
które stanowi
ą
zbiór wzorców ucz
ą
cych.

20.7. Rozpoznawanie pisma odr
ę
cznego
Algorytmy ucz
ą
ce rozpoznawania cyfr napisanych odr
ę
cznie.
Prosty
klasyfikator trzech najbli
ż
szych s
ą
siadów
nie wymaga wst
ę
pnego uczenia, ale musi przechowywa
ć
wszystkie wzorce ucz
ą
ce a czas klasyfikacji jest długi.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~2.4%.
Sie
ć
neuronowa z jedn
ą
warstw
ą
ukryt
ą
zło
ż
on
ą
z 300
w
ę
złów, z 400 wej
ś
ciami (dla ka
ż
dego piksela) i 10 wyj
ś
ciami
(dla ka
ż
dej cyfry) i 123,000 współczynnikami wagowymi.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~1.6%.
© F.A. Dul 2007
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~1.6%.
Specjalizowane sieci neuronowe LeNet
wykorzystuj
ą
informacj
ę
o postaci wzorca jako tablicy 400 pikseli oraz
zało
ż
enie o nieistotno
ś
ci małych ró
ż
nic w obrazach cyfr.
Warstwy ukryte zawieraj
ą
30-768 w
ę
złów.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~0.9%.
Przy
ś
pieszona sie
ć
neuronowa
zło
ż
ona jest z trzech sieci
LeNet operuj
ą
cych na ró
ż
nych zbiorach wzorców
i wybieraj
ą
cych klasyfikacj
ę
poprzez głosowanie.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~0.7%.

20.7. Rozpoznawanie pisma odr
ę
cznego
Metoda wektorów podtrzymuj
ą
cych
zło
ż
ona z 25,000
wektorów nie wymaga uczenia wst
ę
pnego i nie wykorzystuje
informacji o strukturze zadania, a dorównuje metodzie LeNet.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~1.1%.
Wirtualna metoda wektorów podtrzymuj
ą
cych
działa
w dwóch etapach: najpierw jak zwykła maszyna wektorowa
a nast
ę
pnie wykorzystuje informacj
ę
o postaci wzorca
w formie j
ą
drowej opartej na pikselach przyległych.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~0.56%.
⇐
⇐
⇐
⇐
WINNER!
© F.A. Dul 2007
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~0.56%.
⇐
⇐
⇐
⇐
WINNER!
Metoda dopasowywania kształtów
polega na porównywaniu
kształtu cyfry z kształtami wzorców.
Wyznaczana jest transformacja przekształcaj
ą
ca jeden kształt
na drugi i okre
ś
laj
ą
c
ą
miar
ę
zgodno
ś
ci obu kształtów.
Wska
ź
nik bł
ę
du klasyfikacji wynosi ~0.63%.
Dla porównania -
człowiek osi
ą
ga wska
ź
nik bł
ę
du klasyfikacji
cyfr odr
ę
cznych rz
ę
du ~0.2%
.

Podsumowanie
• Metody uczenia bayesowskiego maj
ą
posta
ć
wnioskowania
probabilistycznego wykorzystuj
ą
cego poj
ę
cie brzytwy
Ockhama.
• Uczenie maksymalnego a posteriori (MAP) wyznacza
najbardziej wiarygodn
ą
hipotez
ę
dla istniej
ą
cych danych.
• Sieci neuronowe s
ą
zło
ż
onymi funkcjami nieliniowymi z
wieloma parametrami. Mog
ą
by
ć
uczone na podstawie
danych zaszumionych i maj
ą
szerokie zastosowanie w
praktyce.
©
F.A. Dul 2007
praktyce.
• Perceptron mo
ż
e reprezentowa
ć
funkcje separowalne liniowo
• Wielowarstwowe sieci acykliczne pozwalaj
ą
reprezentowa
ć
dowolne funkcje.
• Metoda propagacji wstecznej jest najefektywniejszym
sposobem uczenia sieci neuronowych.
• Metody funkcji j
ą
dra umo
ż
liwiaj
ą
wyznaczanie separatorów
nieliniowych dla zada
ń
nieseparowalnych liniowo.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron