Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
1
/
30
POLITECHNIKA POZNAŃSKA
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW
W OKRESIE USZKODZEŃ STARZENIOWYCH
Prognostyczne modele uszkodzeń i wymian nieodnawianych obiektów pojazdów
Materiały pomocnicze do wykładu (v5)
f
n
(t)
A
B C
t

Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
2
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
WPROWADZENIE
MODELE MATEMATYCZNE
Założenia i przyjęte oznaczenia
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych
Prognostyczny model liczby uszkodzeń obiektów w okresie ich starzenia
MODEL KOMPUTEROWY DO ANALIZY USZKODZEŃ OBIEKTÓW W OKRESIE
USZKODZEŃ STARZENIOWYCH
Symulator komputerowy algorytmów modeli matematycznych
Przykładowe problemy badawcze
Konfigurowanie symulatora i wyniki prognozowania
PODSUMOWANIE
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
3
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
MODELE MATEMATYCZNE
Założenia i przyjęte oznaczenia (
1
)
1.
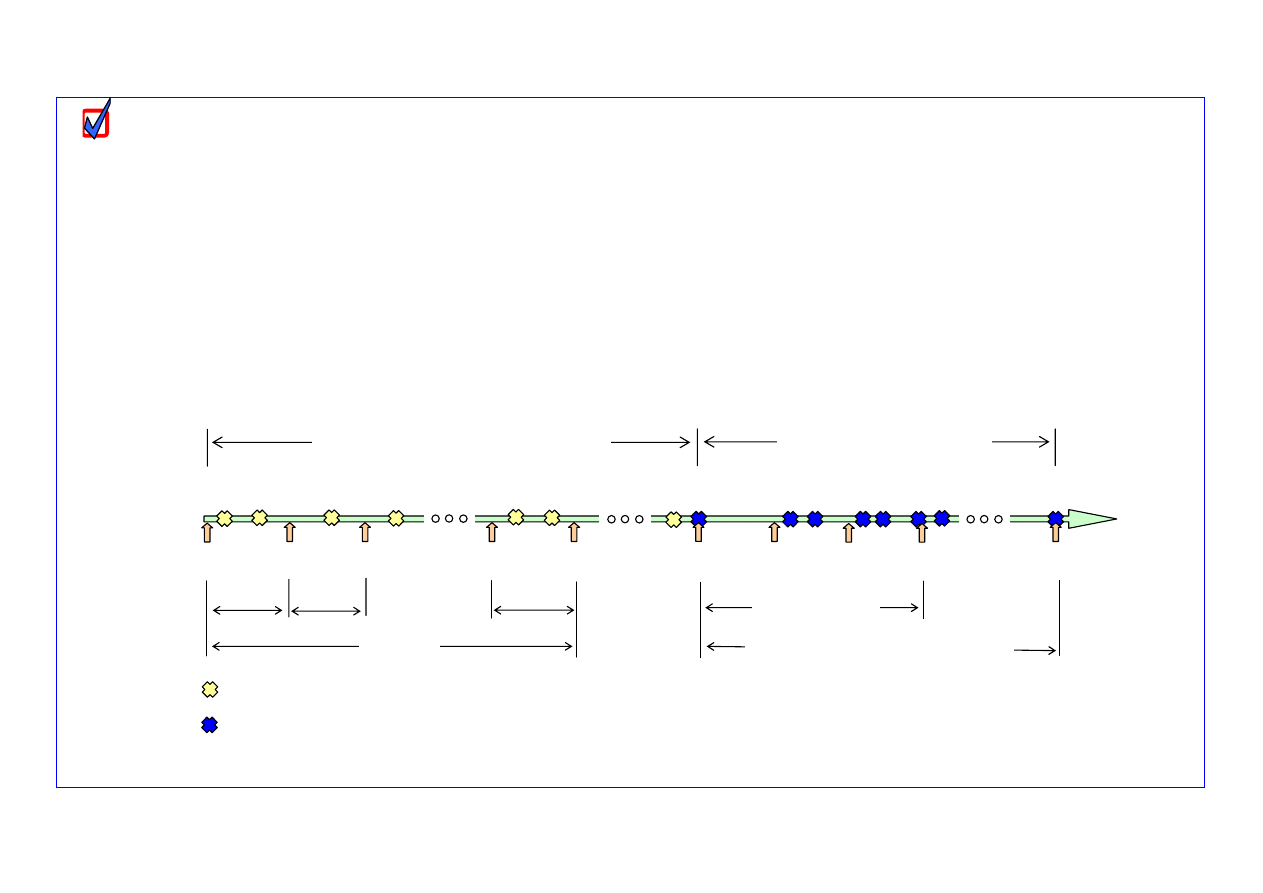
Obserwowana jest grupa N nieodnawianych obiektów typu mechanicznego. Zakłada się podział
tej grupy obiektów na dwie frakcje
(rys. 1)
. Pierwszą z nich
− o liczności
π
− stanowią obiekty,
które ulegają uszkodzeniom wczesnym i przypadkowym. Drugą frakcję obiektów
− o liczności
N
s
− stanowią te, które ulegają uszkodzeniom na skutek starzenia. Chwile czasowe przewidywa-
nych uszkodzeń obiektów tworzą szereg pozycyjny:
.
(1)
( ) ( )
( ) (
)
( )
N
t
...
,
t,
t
...
,
t,
t
,
,
1
2
1
+
π
π
n(
Δ
t
i-1,i
)
n(
Δ
t
1,2
)
n(
Δ
t
0,1
)
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
(1)
t
(2)
t
(3)
t
(4)
t
(N)
t
(
π
)
t
(
π
+1)
t
(
π
+
κ
)
κ
= n(
Δ
t
p,k
)
N
s
= N -
π
= n(
Δ
t
p,k+r
)
n
sk
(t
i
)
−
oznaczenie chwil uszkodzeń obiektów przed okresem uszkodzeń starzeniowych
−
oznaczenie chwil uszkodzeń obiektów w okresie uszkodzeń starzeniowych
t
k+r
Frakcja pierwsza obiektów
Frakcja druga obiektów
Rys. 1. Schemat wybranych oznaczeń w formułach modeli matematycznych
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
4
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Założenia i przyjęte oznaczenia (
2
)
2.
Czas obserwacji uszkodzeń obiektów podzielono na przedziały o równej długości (rys. 1):
...
1,2,
2
1
1
1
=
>
+
=
−
=
−
−
r
p,
k
,
r
k
,
...
,
k
,
...
,
p
,
...
,
,
i
,
t
t
Δt
i
i
i,
i
.
(2)
3.
W kolejnych przedziałach czasu rejestruje się liczby n(
Δ
t
i-1,i
) uszkodzeń obiektów, a w chwilach
pokrywających się z górnymi granicami przedziałów czasowych wyznacza się skumulowane
liczby uszkodzeń (rys. 1):
.
(3)
( )
(
)
...
1,2,
2
1
1
1
=
>
+
=
=
∑
=
−
r
p,
k
,
r
k
,
...
,
k
,
...
,
p
,
...
,
,
i
,
Δt
n
t
n
i
,
i
sk
ν
ν
ν
4.
Zakłada się, że rozkład czasu T do uszkodzeń obiektów nieodnawianych zaliczonych do frakcji
drugiej jest rozkładem normalnym N(
μ
,
σ
).
5.
Przyjmuje się, że początek uszkodzeń starzeniowych przypada na chwilę t
p
(rys. 1), tzn. przyjmu-
je się, że uszkodzenie pierwszego obiektu będące wynikiem jego starzenia pokrywa się z chwilą
t
p
. Zakłada się, że proces starzenia przebiega tak, że wszystkie N
s
obiektów drugiej frakcji
uszkadza się do chwili t
k+r
. Z założeń tych wynika, że:
( )
N
...
,
,
m
,
t,
t
t
r
k
p
m
,
2
1
+
+
=
∈
+
π
π
,
(4)
a dodatkowo zakłada się, że
σ
⋅
=
−
+
6
p
r
k
t
t
.
(5)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
5
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
MODELE MATEMATYCZNE
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
1
)
Prognostyczny model parametrów rozkładu obiektów to formuły matematyczne na estymatory
parametrów rozkładu czasu
T
do uszkodzeń starzeniowych obiektów (rozkład normalny
N(
μ
,
σ
)
). Es-
tymatory te oszacowuje się na podstawie liczby
n(
Δt
p,k
)
uszkodzeń obiektów w okresie od chwili
t
p
do
chwili
t
k
oraz liczności
N
s
obiektów, dla których przewiduje się, że ulegną uszkodzeniom na skutek ich
starzenia. Schemat ideowy tego prognostycznego modelu przedstawiono na
rys. 2
.
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
{n(
Δt
p,k
), N
s
}Ö
N(
μ
,
σ
)
czas
n(
Δt
p,k
)
N
s
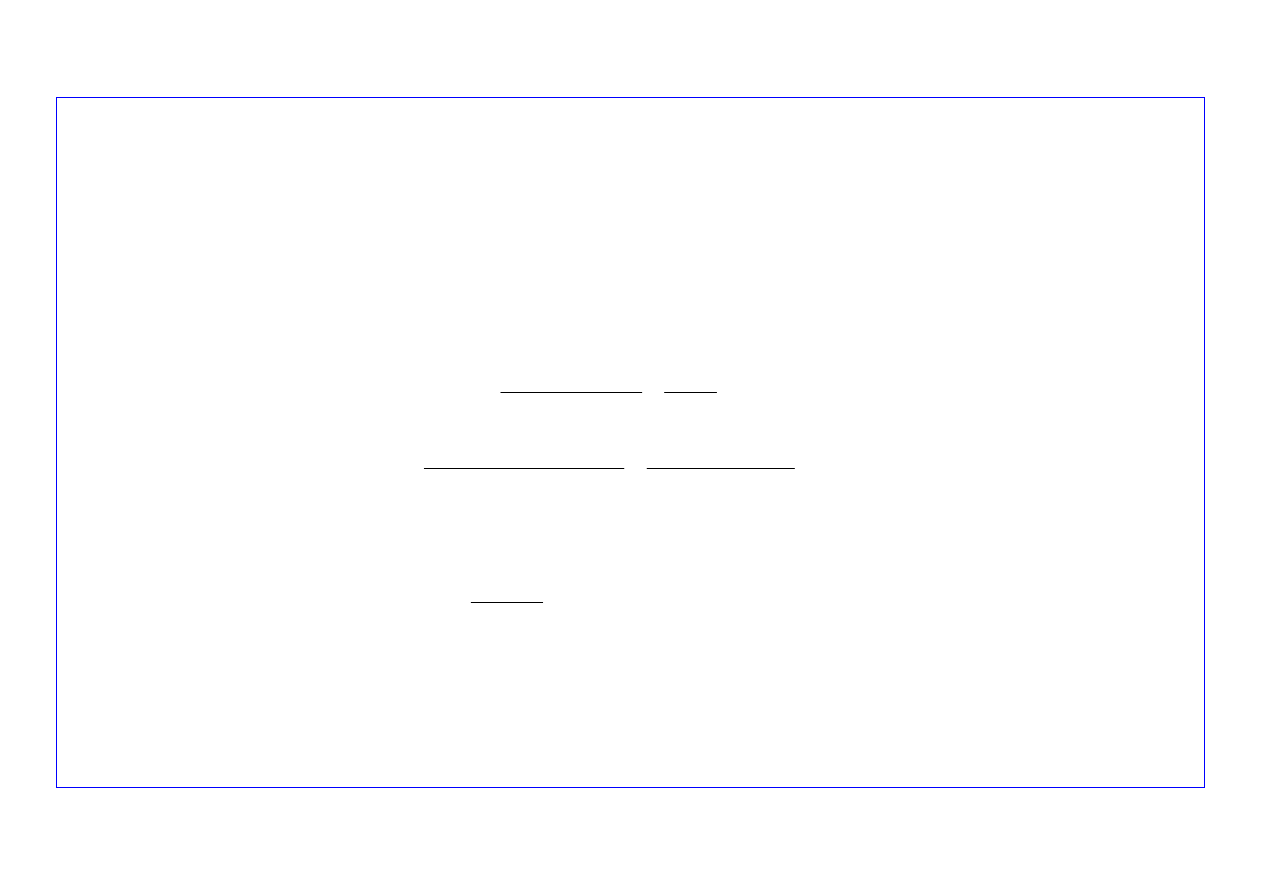
Rys. 2. Schemat ideowy prognostycznego modelu parametrów rozkładu uszkodzeń obiektów
w okresie uszkodzeń starzeniowych
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
6
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
2
)
Obserwując uszkodzenia obiektów w kolejnych przedziałach czasu można wskazać chwilę
t
p
po-
czątku uszkodzeń starzeniowych. Pomocnym w tym względzie może być śledzenie przebiegów empi-
rycznych postaci funkcji
f
n
(t)
gęstości prawdopodobieństwa czasu
T
do uszkodzenia obiektów i funkcji
λ
n
(t)
intensywności uszkodzeń. Wartości tych funkcji na końcach przedziałów czasowych wyznacza
się z zależności:
( )
( )
( )
(
)
( )
...
,
,
i
,
t
N
t
n
t
t
N
t
n
t
n
t
f
i
i
i
i
sk
i
sk
i
n
2
1
1
1
=
⋅
=
−
⋅
−
=
−
−
Δ
Δ
,
(7)
( )
( )
( )
( )
[
]
(
)
( )
( )
[
]
...
,
,
i
,
t
t
n
N
t
n
t
t
t
n
N
t
n
t
n
t
i
sk
i
i
i
i
sk
i
sk
i
sk
i
n
2
1
1
1
1
1
=
⋅
−
=
−
⋅
−
−
=
−
−
−
−
Δ
Δ
λ
.
(8)
Łatwo jest zauważyć, że
(
)
( )
(
)
( )
p
k
s
k
,
p
t
F
t
F
N
t
n
σ
μ
σ
μ
Δ
;
N
;
N
)
(
−
=
,
(9)
gdzie:
(
)
( )
(
)
( ) − są wartościami dystrybuant rozkładu
N(
μ
,
σ
)
uszkodzeń starzeniowych w
chwilach czasowych odpowiednio
t
k
p
t
F
,
t
F
σ
μ
σ
μ
;
N
;
N
p
i
t
k
,
a z przyjętych założeń wynika, że:
(
)
( )
0
;
N
=
p
t
F
σ
μ

Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
7
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
3
)
Jeżeli różnicę realizacji zmiennej losowej
T
odpowiadających chwilom czasowym
t
p
i
t
k
wyrazi się
w jednostkach odchylenia standardowego rozkładu
N(0,1)
, to otrzyma się następującą zależność
(dalej
umieszczono szkice pomocnicze)
:
( )
( )
( )
0
)
(
1
-
1
;
0
1
-
1
;
0
N
N
F
N
t
n
F
t
t
s
k
,
p
p
k
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
μ
Δ
−
−
σ
σ
μ
,
(10)
gdzie:
( )
( )
x
F
,
1
1
0
N
−
− jest zapisem oznaczającym wartości odwrotne dystrybuant rozkładu
N(0,1)
w punkcie
x
.
Ponieważ
( )
( )
0013499
0
3
1
;
0
,
F
=
−
N
,
(11)
to można przyjąć, że
( )
( )
3
0
-1
1
;
0
−
≅
N
F
.
(12)
Zatem uwzględniając zależność
(12)
( )
)
3
(
)
(
1
-
1
;
0
N
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
−
−
s
k
,
p
p
k
N
t
n
F
t
t
Δ
σ
μ
σ
μ
,
(13)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
8
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
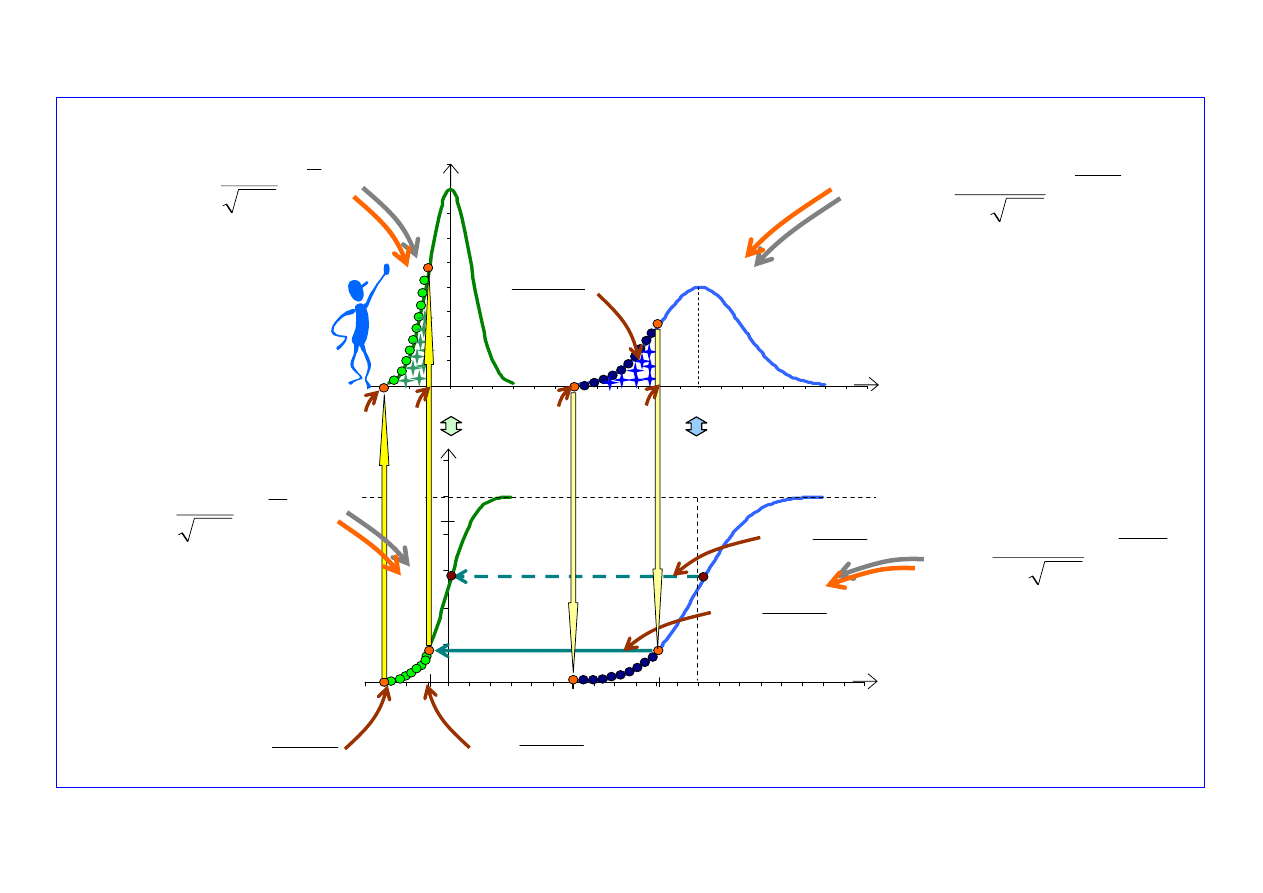
Szkice pomocnicze
Szkice pomocnicze
f(t)
t
μ
0
Ν(
μ,σ
)
Ν(0
,
1)
2
~
2
2
1
)
(
t
t
e
t
f
⋅
Π
=
2
2
2
)
(
2
1
)
(
σ
μ
−
⋅
σ
Π
⋅
=
t
e
t
f
dz
e
t
F
t
z
∫
∞
−
−
Π
⋅
=
2
2
2
)
(
2
1
)
(
σ
μ
σ
dz
e
t
F
t
z
t
∫
∞
−
Π
=
2
~
2
2
1
)
(
t
μ
0
F(t)
Ν(
μ,σ
)
1,0
Ν(0
,
1)
t
p
t
k
σ
μ
−
=
p
p
t
t~
σ
μ
−
=
k
k
t
t~
t
k
k
t~
σ
μ
−
=
t
t~
σ
μ
−
=
k
k
t
t~
t
p
t~
p
s
k
p
N
t
n
)
(
,
Δ
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
9
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
4
)
ostateczną postać modelu (estymator odchylenia standardowego
σ
)
i estymator wartości oczekiwanej
μ
)
) można przedstawić za pomocą formuł:
( )
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
2
1
3
)
(
ent
1
-
1
;
0
N
s
k
,
p
p
k
N
t
n
F
t
t
Δ
σ
)
(14)
oraz
σ
μ
)
)
⋅
+
=
3
p
t
(15)
Dodatkowo
− na podstawie przyjętych założeń − można przyjąć, że uszkodzenie
N
-tego obiektu
nastąpi w chwili
( )
σ
)
⋅
+
=
6
p
N
t
t
.
(16)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
10
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
MODELE MATEMATYCZNE
Prognostyczny model liczby uszkodzeń obiektów w okresie ich starzenia
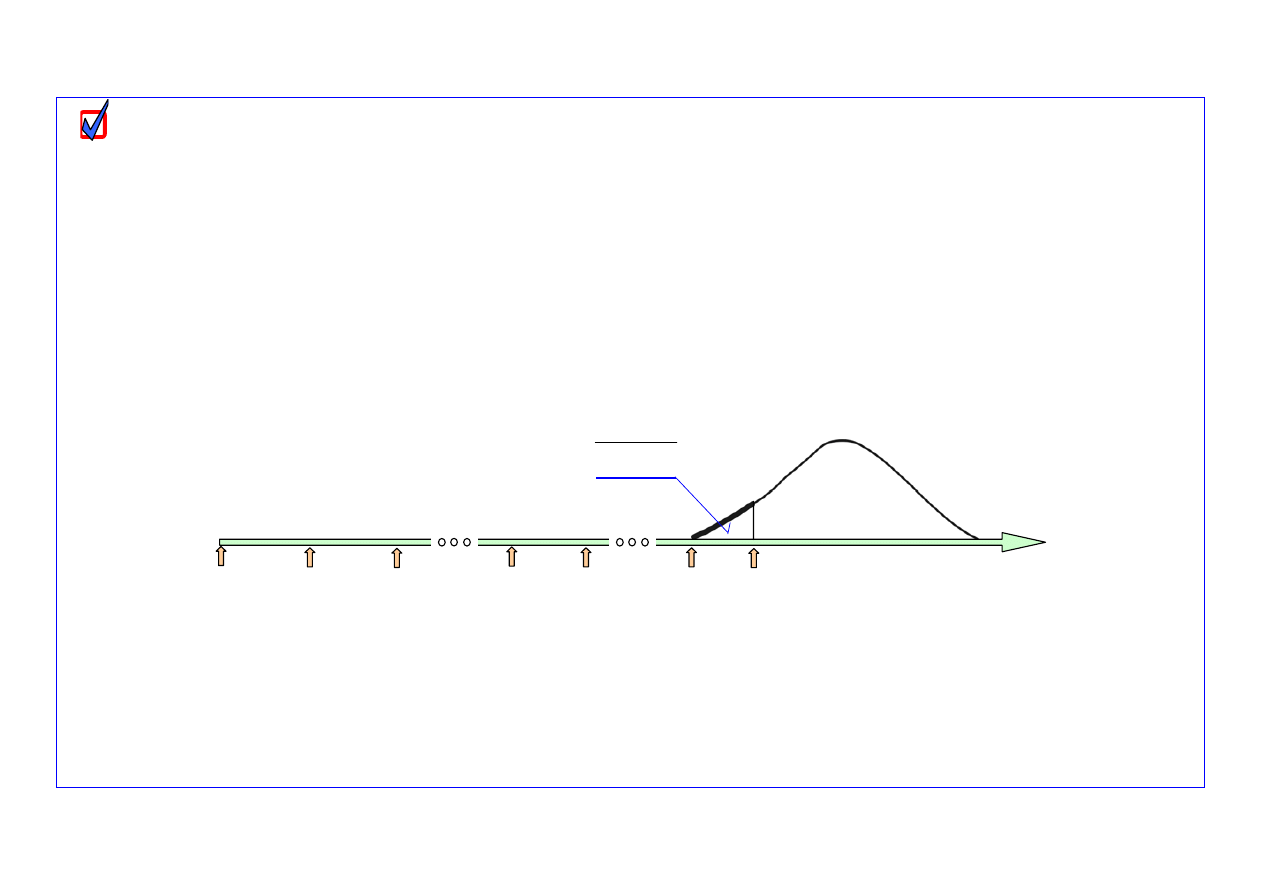
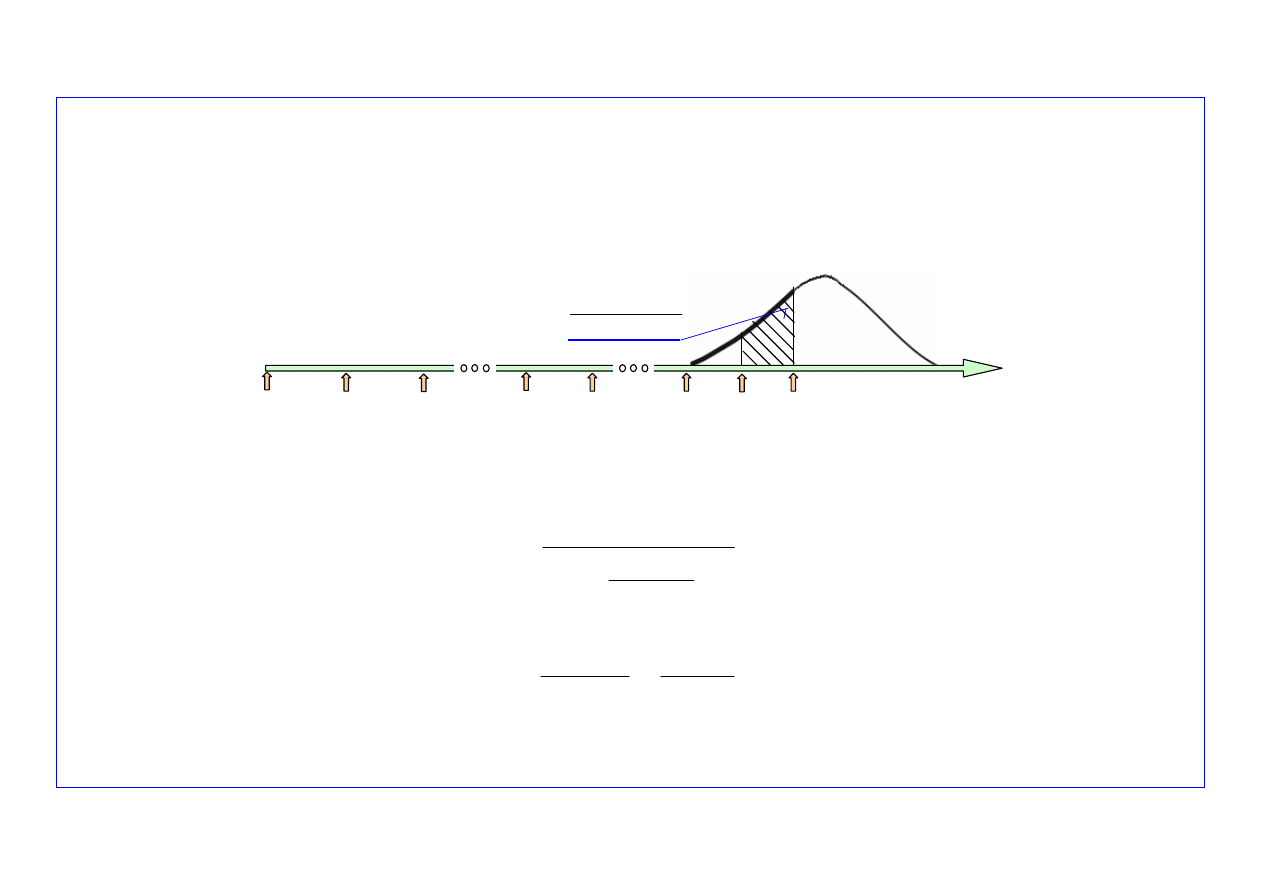
Idea prognostycznego modelu liczb uszkodzeń obiektów w okresie ich starzenia opiera się na
oszacowanych wcześniej wartościach parametrów rozkładu uszkodzeń starzeniowych i znajomości
liczby uszkodzonych obiektów od chwili
t
p
do chwili
t
k+j-1
początku okresu dokonywania prognozy.
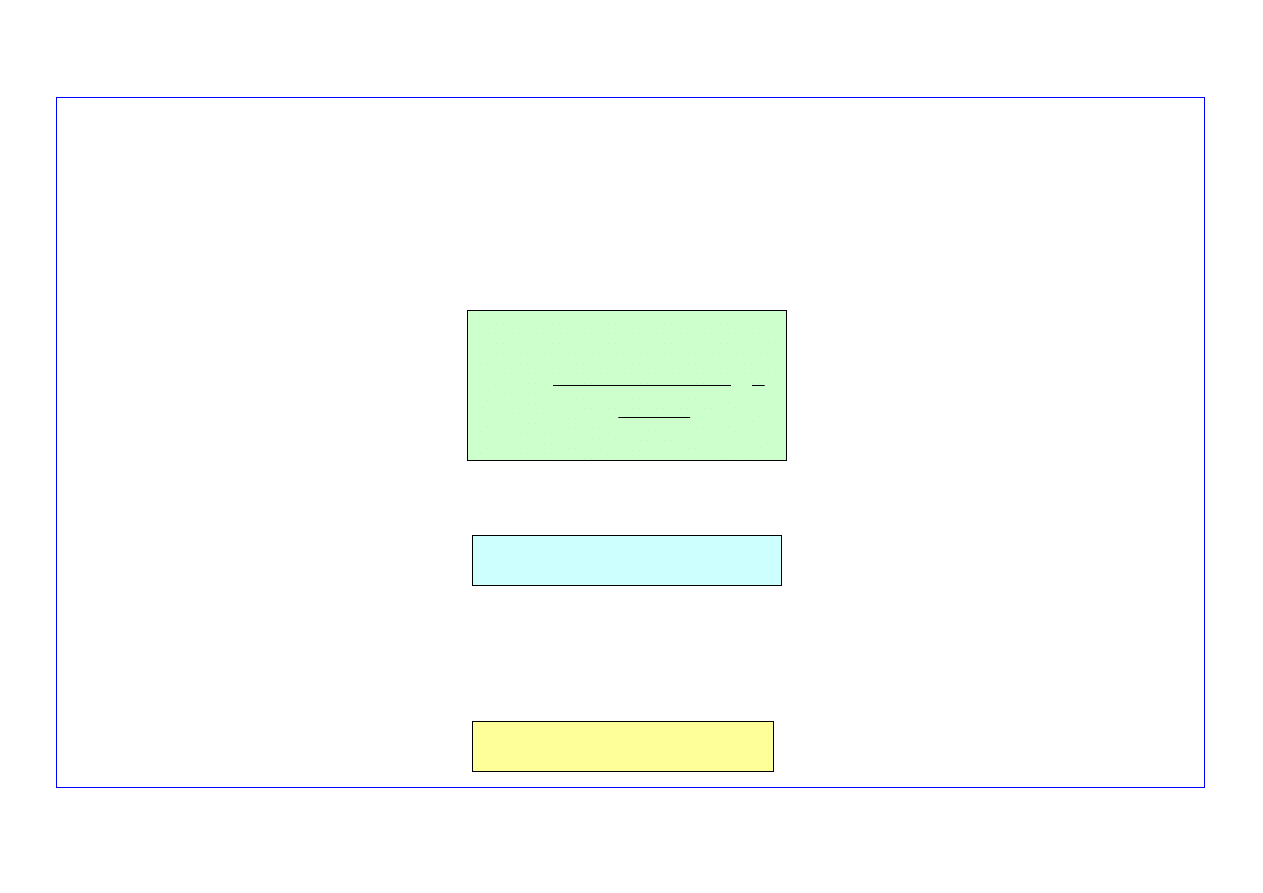
Schemat ideowy algorytmu modelu prognozowania uszkodzeń pokazano na
rys. 3
.
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
k+j-1
t
k+j
{N(
μ
,
σ
), n(
Δt
p,k+j-1
), N
s
}
Ö
n(
Δt
k+j-1, k+j
)
czas
n(
Δ
t
k+j-1,k+j
)
N
s
Rys. 3. Schemat ideowy prognostycznego modelu liczb uszkodzeń obiektów w okresie uszkodzeń starzeniowych
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
11
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
( )
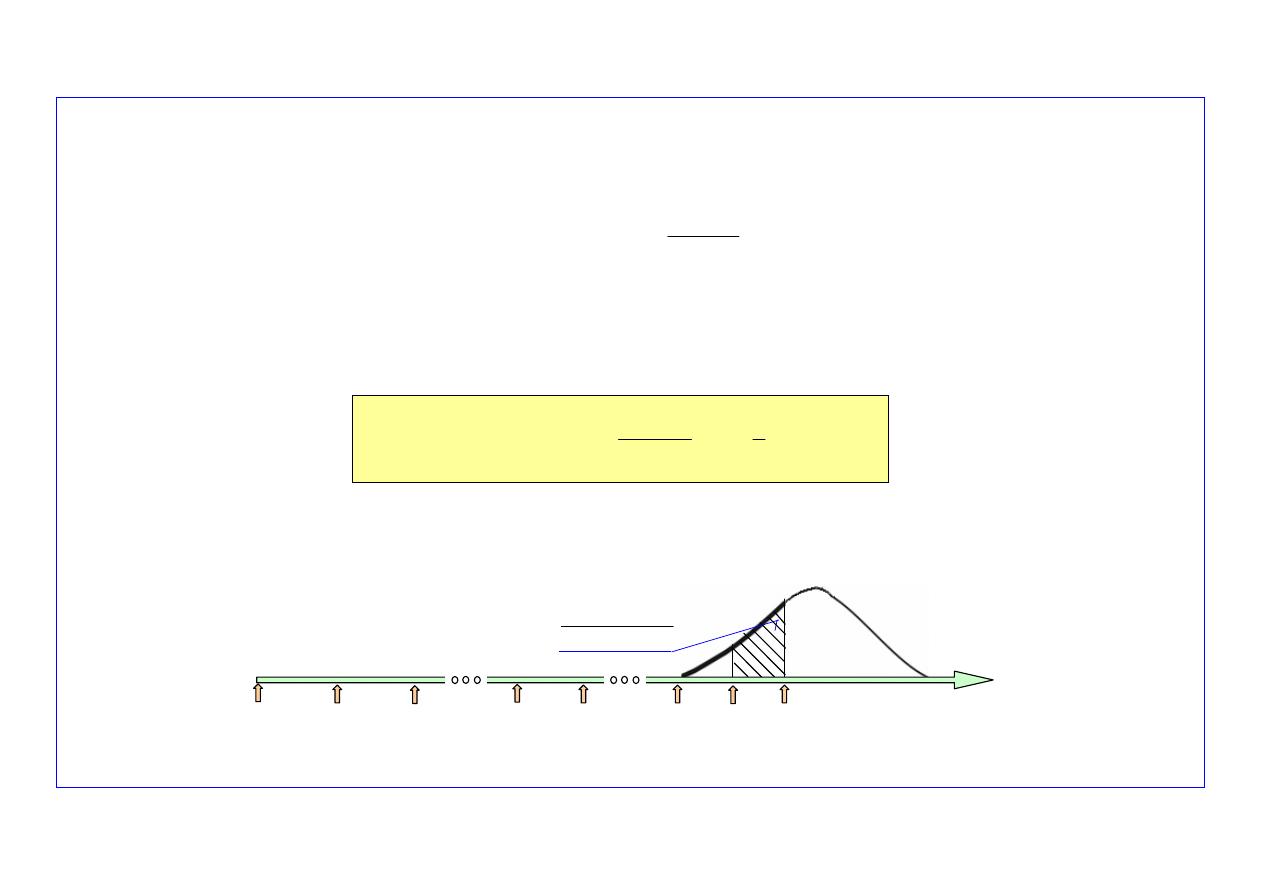
Krok 1-szy. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k
, t
k+1
)
Krok 1-szy. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k
, t
k+1
)
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
k+1
{N(
μ
,
σ
), n(
Δt
p,k
), N
s
}
Ö
n(
Δt
k, k+1
)
czas
n(
Δ
t
k+,k+1
)
N
s
Na podstawie formuły
(14)
i założenia, że parametry rozkładu uszkodzeń starzeniowych nie ulega-
ją zmianie w kolejnych przedziałach czasu, to:
Na podstawie formuły
(14)
i założenia, że parametry rozkładu uszkodzeń starzeniowych nie ulega-
ją zmianie w kolejnych przedziałach czasu, to:
( )
3
)
(
1
1
-
1
;
0
N
1
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
+
+
s
k
,
p
p
k
N
t
n
F
t
t
Δ
σ
)
,
(17)
a stąd
( )
3
)
(
1
1
1
-
1
;
0
N
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
σ
Δ
)
p
k
s
k
,
p
t
t
N
t
n
F
.
(18)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
12
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
(
)
( )
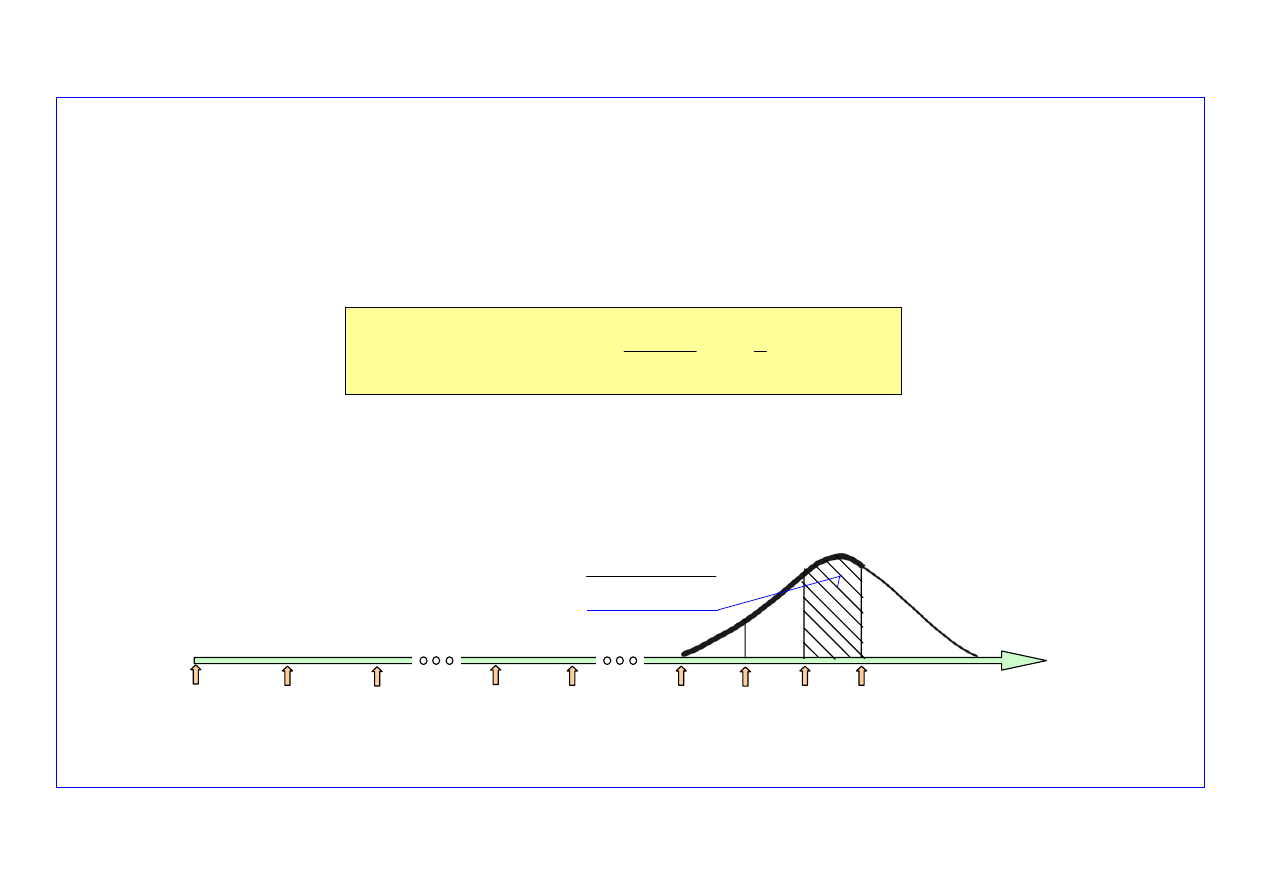
Krok 1-szy. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k
, t
k+1
)
cd.
Krok 1-szy. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k
, t
k+1
)
cd.
Po wykonaniu operacji funkcji odwrotnej otrzymuje się:
Po wykonaniu operacji funkcji odwrotnej otrzymuje się:
(
)
( )
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⋅
=
+
+
3
1
1
;
0
N
1
σ
Δ
)
p
k
s
k
,
p
t
t
F
N
t
n
,
(19)
a gdy zauważy się, że:
(
) (
)
(
)
1
1
+
+
+
=
k
,
k
k
,
p
k
,
p
t
n
t
n
t
n
Δ
Δ
Δ
,
(20)
to liczbę uszkodzeń obiektów w przedziale czasu
(t
k
, t
k+1
)
można wyznaczyć z zależności:
(
)
( )
(
)
k
,
p
p
k
s
k
,
k
t
n
t
t
F
N
t
n
Δ
σ
Δ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⋅
=
+
+
2
1
3
ent
1
1
;
0
N
1
)
.
(21)
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
k+1
{N(
μ
,
σ
), n(
Δt
p,k
), N
s
} Ö n(
Δt
k, k+1
)
czas
n(
Δ
t
k+,k+1
)
N
s
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
13
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
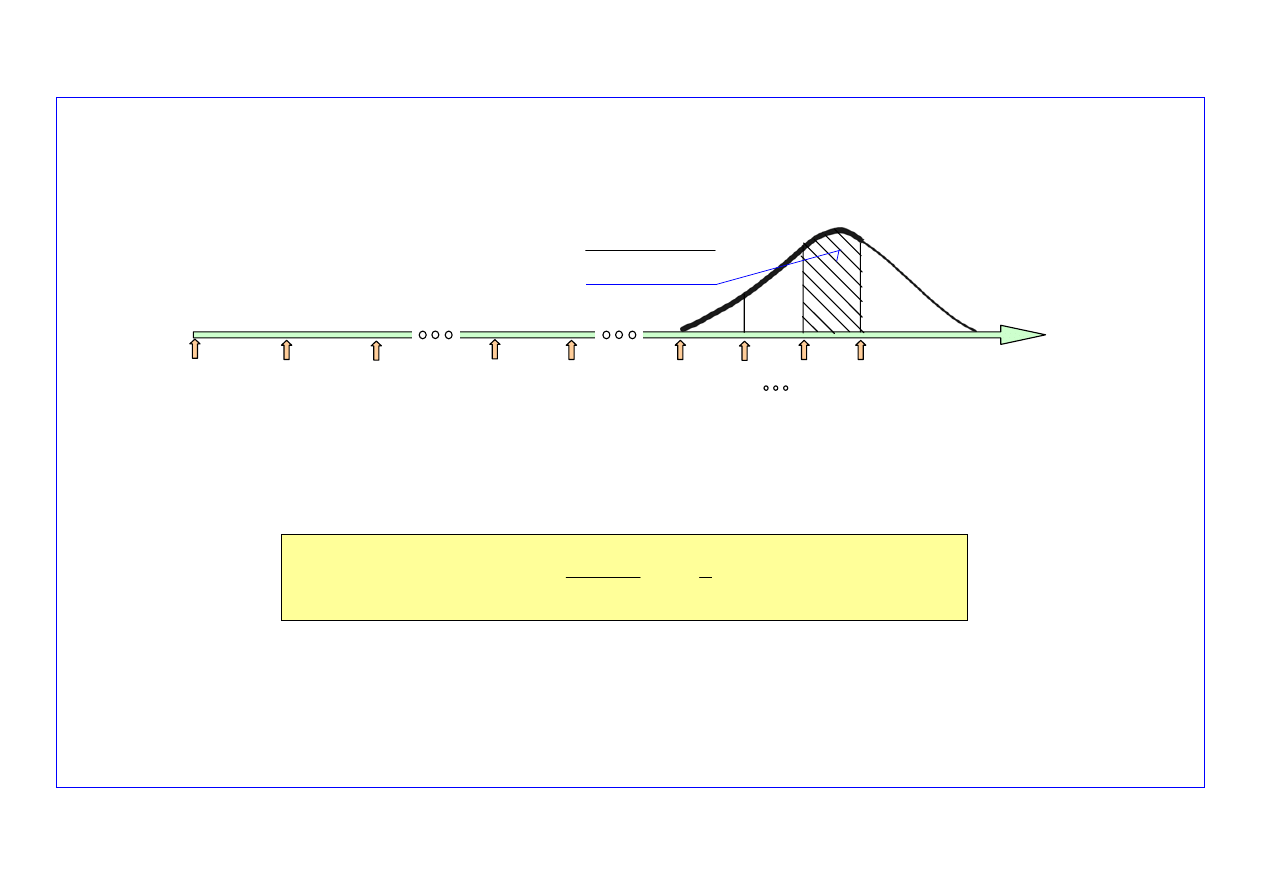
Krok 2-gi.
Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+1
, t
k+2
)
Krok 2-gi.
Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+1
, t
k+2
)
Wykorzystując wyniki obliczeń dokonanych w kroku 1-szym (zależności
(21)
i
(20)
) i powta-
rzając zastosowany w nim algorytm obliczeniowy, liczbę uszkodzeń obiektów w przedziale czasu
(t
k+1
, t
k+2
)
można wyznaczyć z zależności:
Wykorzystując wyniki obliczeń dokonanych w kroku 1-szym (zależności
(21)
i
(20)
) i powta-
rzając zastosowany w nim algorytm obliczeniowy, liczbę uszkodzeń obiektów w przedziale czasu
(t
k+1
, t
k+2
)
można wyznaczyć z zależności:
(
)
( )
(
)
1
2
1
;
0
N
2
1
2
1
3
ent
+
+
+
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⋅
=
k
,
p
p
k
s
k
,
k
t
n
t
t
F
N
t
n
Δ
σ
Δ
)
,
(22)
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
k+1
t
k+2
{N(
μ
,
σ
), n(
Δt
p,k+1
), N
s
} Ö n(
Δt
k+1, k+2
)
czas
n(
Δ
t
k+1,k+2
)
N
s
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
14
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Krok j-ty. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+j-1
, t
k+j
)
Krok j-ty. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+j-1
, t
k+j
)
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
k+j-1
t
k+j
{N(
μ
,
σ
), n(
Δt
p,k+j-1
), N
s
} Ö n(
Δt
k+j-1, k+j
)
czas
n(
Δ
t
k+j-1,k+j
)
N
s
Uogólniając wyniki obliczeń uzyskane w krokach 1-szym i 2-gim, można zauważyć, że liczbę
uszkodzeń obiektów w przedziale czasu
(t
k+j-1
, t
k+j
)
,
j =1,2, ... , r,
(rys. 3) wskazuje zależność:
Uogólniając wyniki obliczeń uzyskane w krokach 1-szym i 2-gim, można zauważyć, że liczbę
uszkodzeń obiektów w przedziale czasu
(t
k+j-1
, t
k+j
)
,
j =1,2, ... , r,
(rys. 3) wskazuje zależność:
(
)
( )
(
)
r
...
,
,
j
,
t
n
t
t
F
N
t
n
j
k
,
p
p
j
k
s
j
k
,
j
k
,
2
1
Δ
2
1
3
ent
Δ
1
1
;
0
N
1
=
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⋅
=
−
+
+
+
−
+
σ
)
,
(23)
gdzie:
(
)
(
)
(
)
(
)
⎪⎩
⎪
⎨
⎧
=
+
=
=
∑
−
=
+
−
+
−
+
r
,
...
,
,
j
,
t
n
t
n
j
,
t
n
t
n
j
k
,
k
k
,
p
k
,
p
j
k
,
p
3
2
Δ
Δ
1
Δ
Δ
1
1
1
1
ν
ν
ν
.
(24)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
15
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
MODEL KOMPUTEROWY DO ANALIZY USZKODZEŃ OBIEKTÓW
W OKRESIE USZKODZEŃ STARZENIOWYCH
Symulator komputerowy
Kaja.xls
algorytmów modeli matematycznych
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
16
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
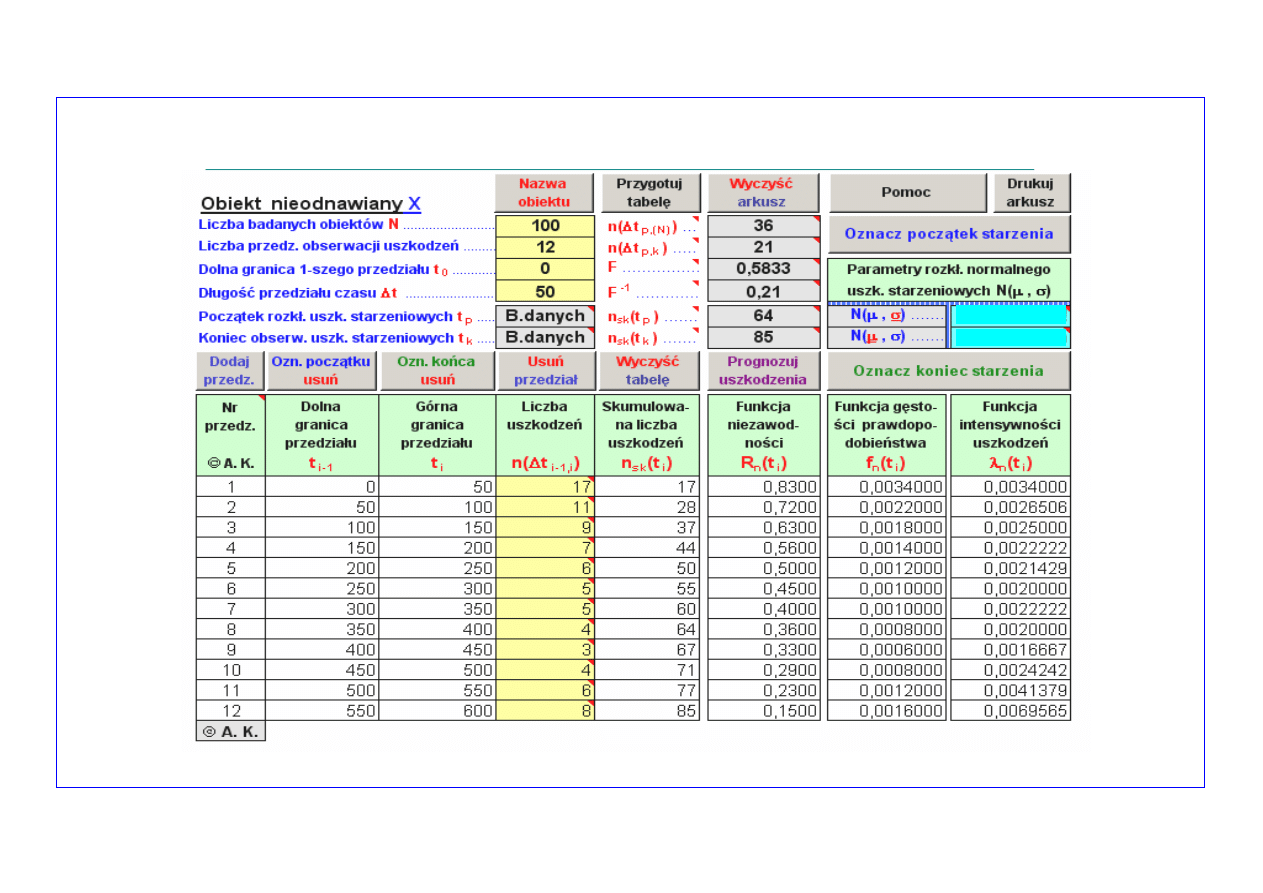
Przykładowy problem badawczy
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
17
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
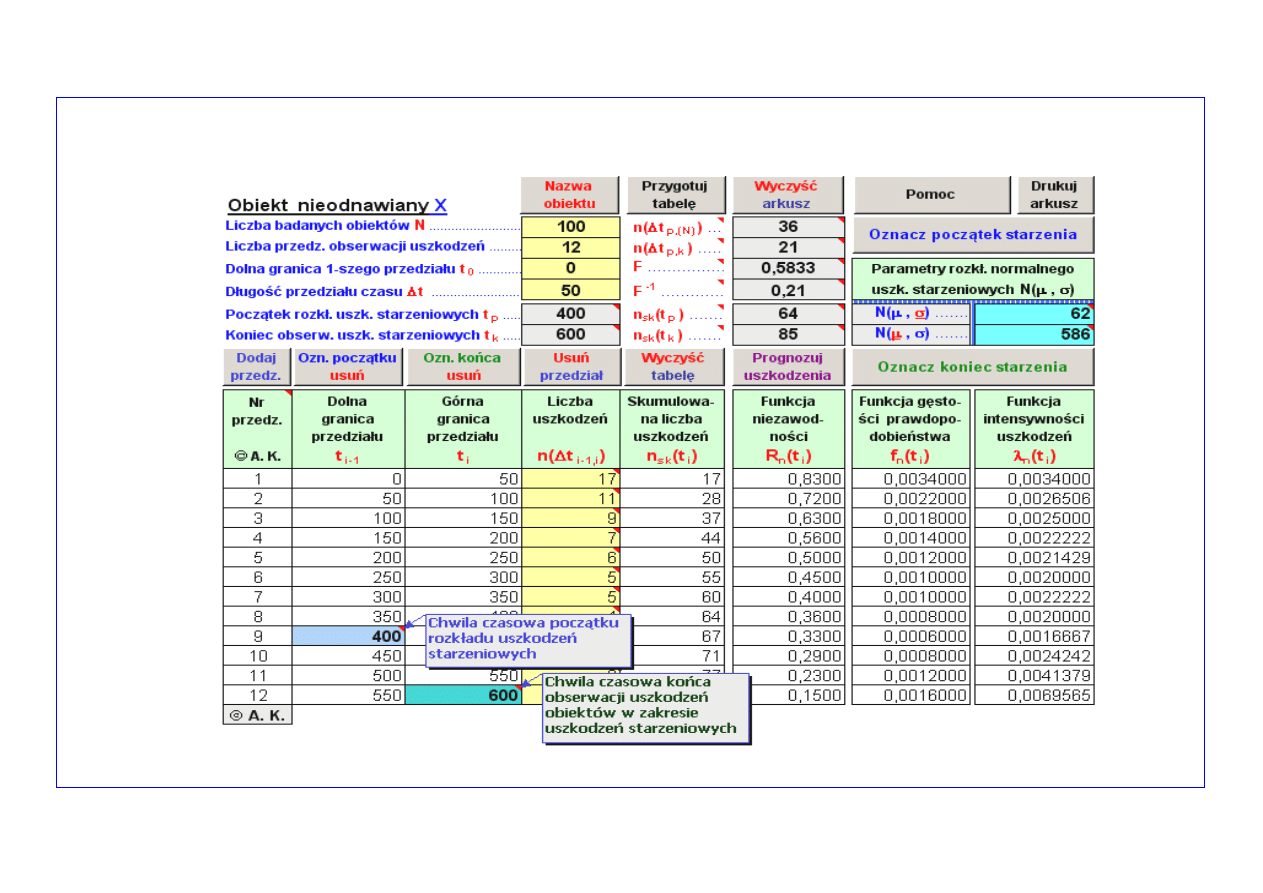
Konfigurowanie symulatora (
1
)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
18
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
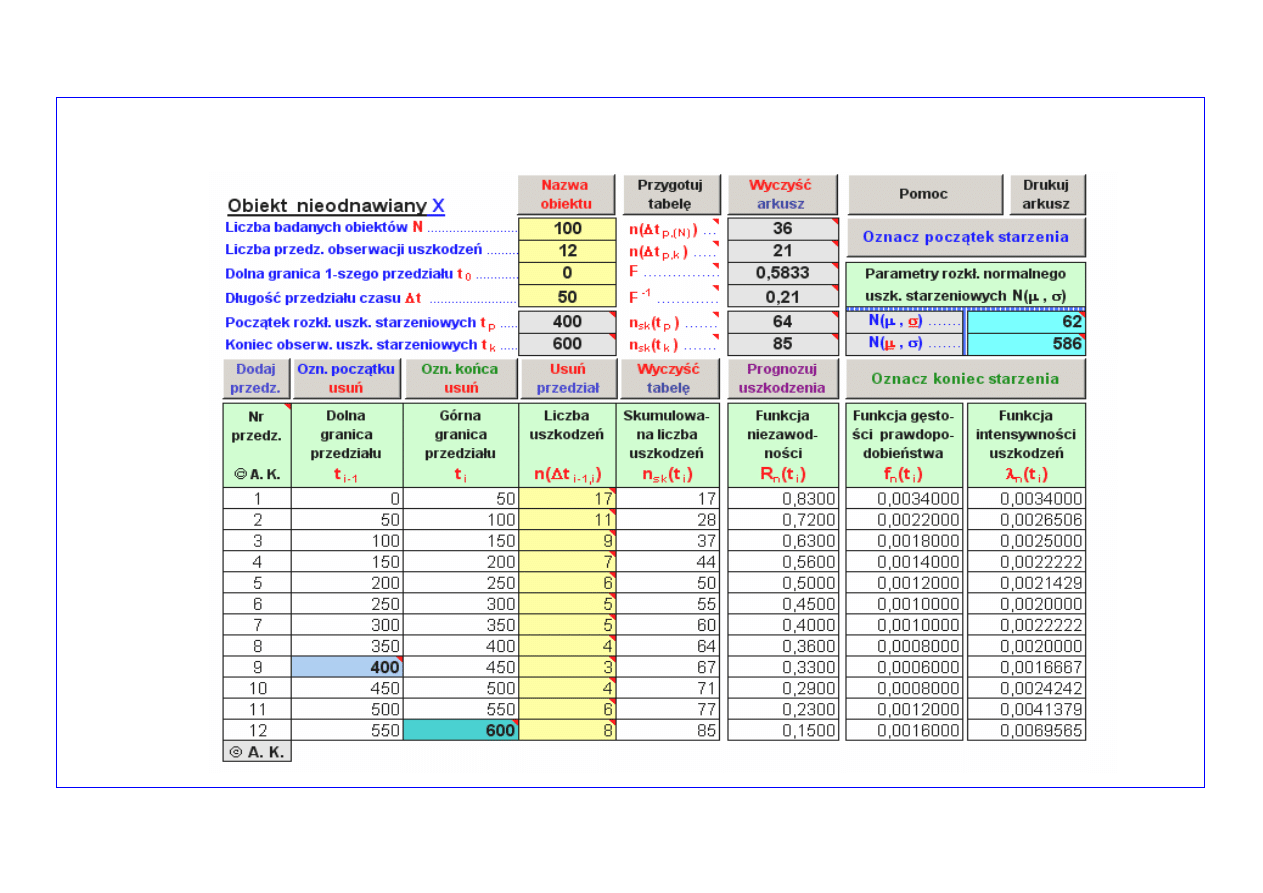
Konfigurowanie symulatora (
2
)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
19
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
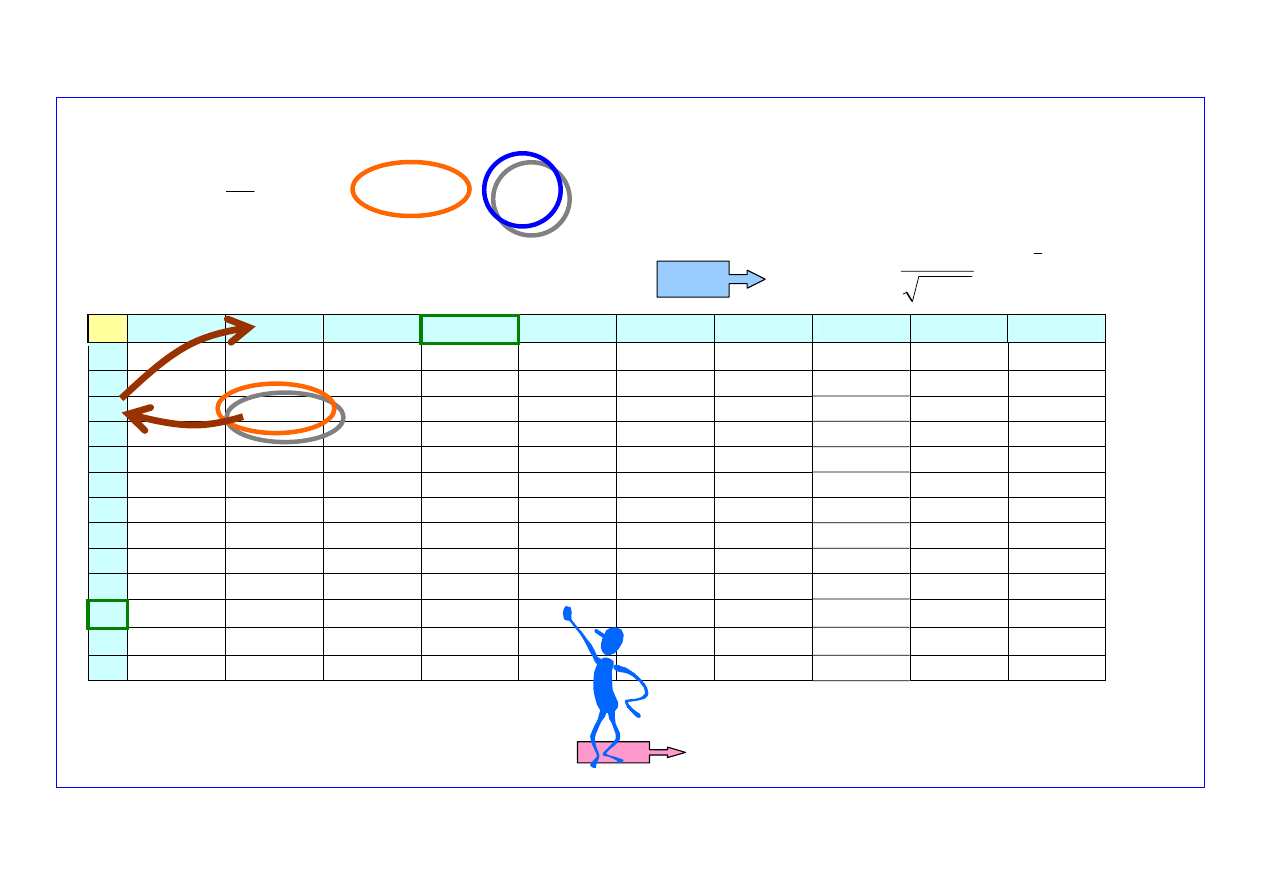
Wyznaczanie parametrów rozkładu uszkodzeń starzeniowych (
1
)
Wyznaczanie parametrów rozkładu uszkodzeń starzeniowych (
1
)
( )
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛ Δ
−
=
2
1
3
)
(
ent
,
1
-
1
;
0
N
s
k
p
p
k
N
t
n
F
t
t
σ
)
( )
( )
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
+
⎟
⎠
⎞
⎜
⎝
⎛
−
=
2
1
3053
,
62
ent
2
1
3
21
,
0
200
ent
2
1
3
36
21
200
ent
2
1
3
36
21
400
600
ent
1
-
1
;
0
N
1
-
1
;
0
N
F
F
σ
)
(
)
62
8053
,
62
ent
=
=
σ
)
σ
μ
)
)
⋅
+
=
3
p
t
586
186
400
62
3
400
=
+
=
⋅
+
=
μ
)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
20
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
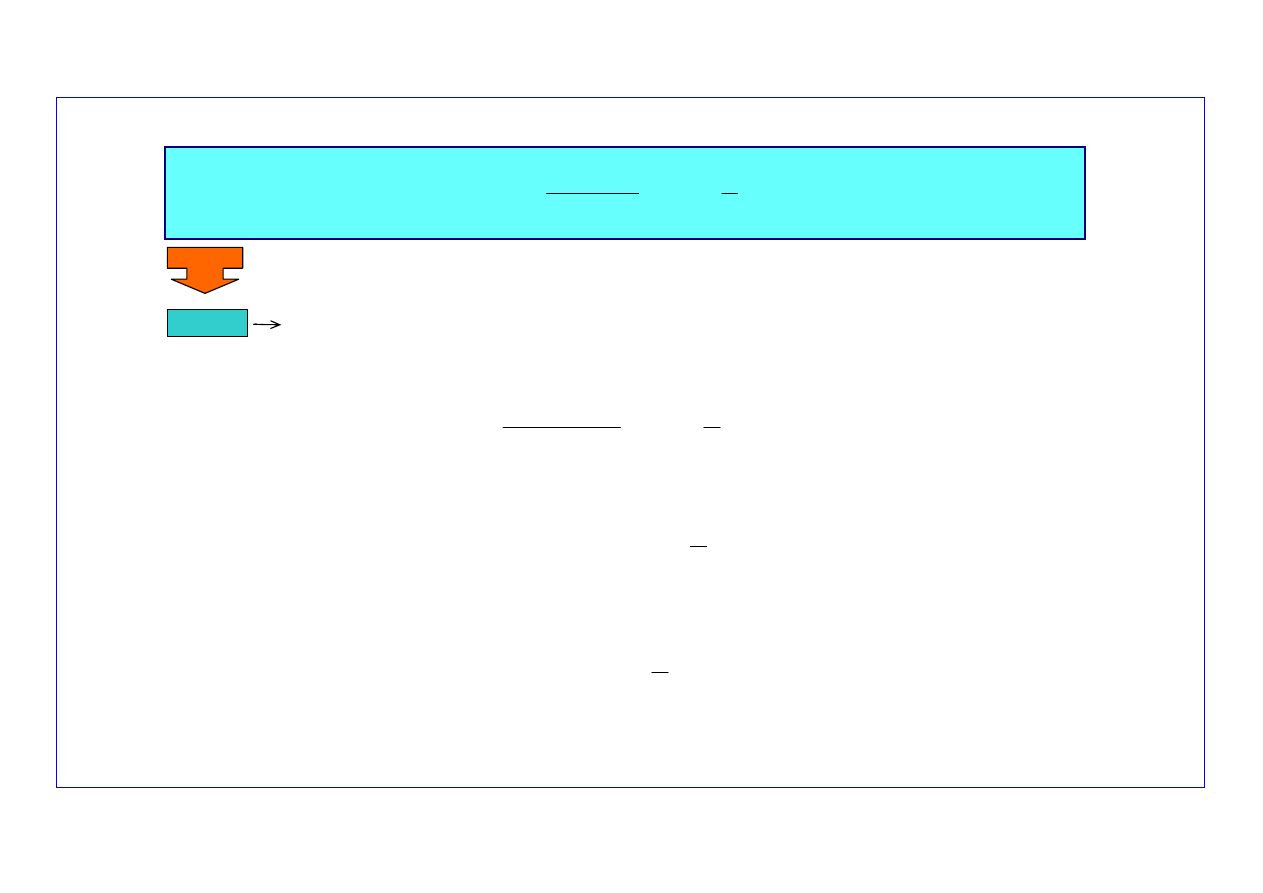
Wyznaczanie parametrów rozkładu uszkodzeń starzeniowych (
2
)
Wyznaczanie parametrów rozkładu uszkodzeń starzeniowych (
2
)
( )
( )
(
)
21
,
0
58333
,
0
36
21
1
-
1
;
0
N
1
-
1
;
0
N
=
=
⎟
⎠
⎞
⎜
⎝
⎛
F
F
dx
e
u
F
u
x
∫
∞
−
⋅
−
⋅
Π
⋅
=
2
2
1
2
1
)
(
Dystrybuanta rozkładu
N(0;1)
Dystrybuanta rozkładu
N(0;1)
u
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
0,50000 0,50399 0,50798 0,51197 0,51595 0,51994 0,52392 0,52790 0,53188 0,53586
0,1
0,53983 0,54380 0,54776 0,55172 0,55567 0,55962 0,56356 0,56749 0,57142 0,57535
0,2
0,57926
0,58317
0,58706 0,59095 0,59483 0,59871 0,60257 0,60642 0,61026 0,61409
0,3
0,61791 0,62172 0,62552 0,62930 0,63307 0,63683 0,64058 0,64431 0,64803 0,65173
0,4
0,65542 0,65910 0,66276 0,66640 0,67003 0,67364 0,67724 0,68082 0,68439 0,68793
0,5
0,69146 0,69497 0,69847 0,70194 0,70540 0,70884 0,71226 0,71566 0,71904 0,72240
0,6
0,72575 0,72907 0,73237 0,73565 0,73891 0,74215 0,74537 0,74857 0,75175 0,75490
0,7
0,75804 0,76115 0,76424 0,76730 0,77035 0,77337 0,77637 0,77935 0,78230 0,78524
0,8
0,78814 0,79103 0,79389 0,79673 0,79955 0,80234 0,80511 0,80785 0,81057 0,81327
0,9
0,81594 0,81859 0,82121 0,82381 0,82639 0,82894 0,83147 0,83398 0,83646 0,83891
1,0
0,84134 0,84375 0,84614 0,84849 0,85083 0,85314 0,85543 0,85769 0,85993 0,86214
1,1
0,86433 0,86650 0,86864 0,87076 0,87286 0,87493 0,87698 0,87900 0,88100 0,88298
1,2
0,88493 0,88686 0,88877 0,89065 0,89251 0,89435 0,89617 0,89796 0,89973 0,90147
lub
=ROZKŁAD.NORMALNY.S.ODW(
0,58333
)
0,21042
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
21
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
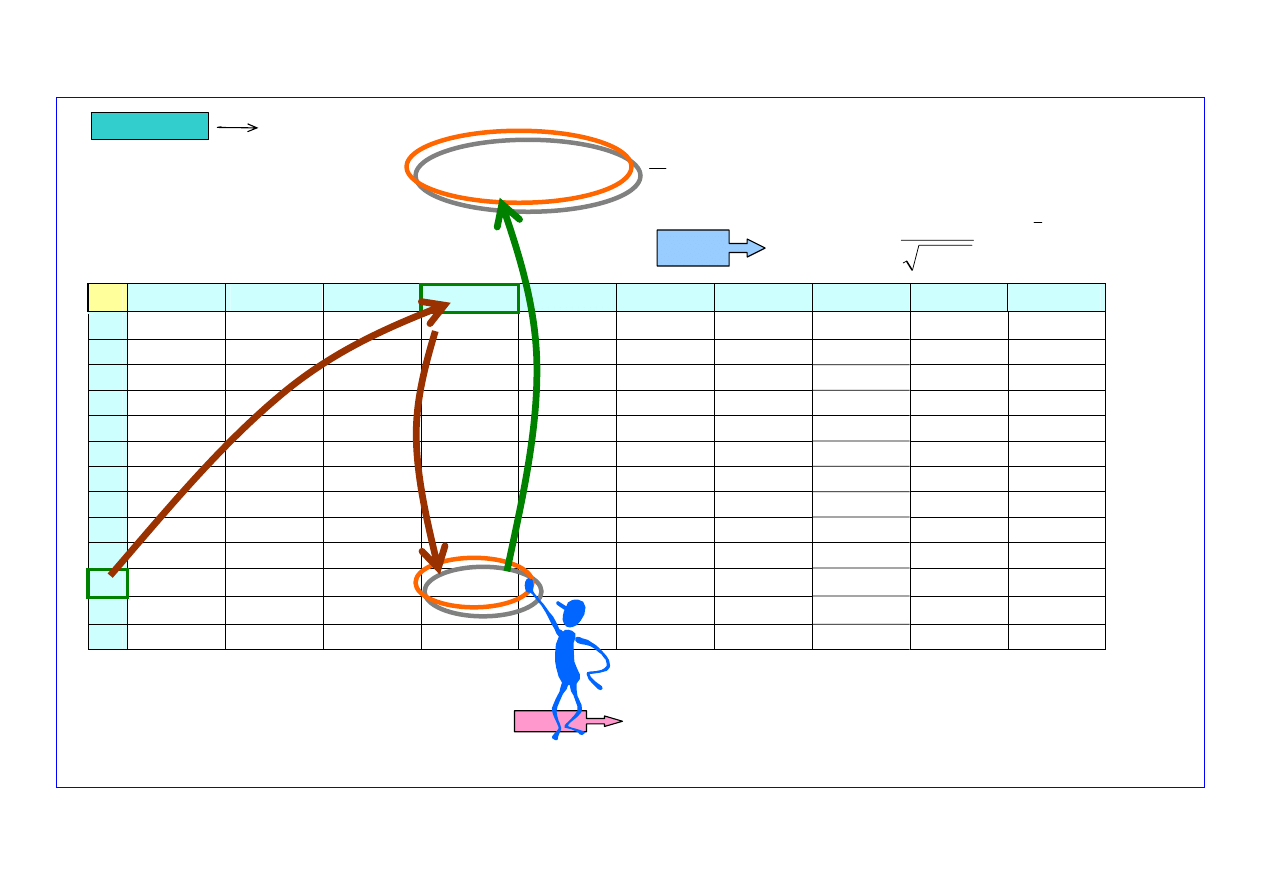
Wyniki prognozowania (
1
)
Wyniki prognozowania (
1
)
(
)
( )
(
)
r
...
,
,
j
t
n
t
t
F
N
t
n
j
k
p
p
j
k
s
j
k
j
k
,
2
1
,
Δ
2
1
3
ent
Δ
1
,
1
;
0
N
,
1
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
−
+
+
+
−
+
σ
)
1
=
j
Krok 1
(
)
( )
21
2
1
3
62
400
650
36
ent
1
;
0
N
650
,
600
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
Δ
F
t
n
(
)
( )
(
)
21
2
1
3
032258
,
4
36
ent
1
;
0
N
650
,
600
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
⋅
=
Δ
F
t
n
(
)
( )
(
)
21
2
1
032258
,
1
36
ent
1
;
0
N
650
,
600
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
F
t
n
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
22
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Dystrybuanta rozkładu
N(0;1)
Dystrybuanta rozkładu
N(0;1)
u
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
0,50000 0,50399 0,50798 0,51197 0,51595 0,51994 0,52392 0,52790 0,53188 0,53586
0,1
0,53983 0,54380 0,54776 0,55172 0,55567 0,55962 0,56356 0,56749 0,57142 0,57535
0,2
0,57926 0,58317 0,58706 0,59095 0,59483 0,59871 0,60257 0,60642 0,61026 0,61409
0,3
0,61791 0,62172 0,62552 0,62930 0,63307 0,63683 0,64058 0,64431 0,64803 0,65173
0,4
0,65542 0,65910 0,66276 0,66640 0,67003 0,67364 0,67724 0,68082 0,68439 0,68793
0,5
0,69146 0,69497 0,69847 0,70194 0,70540 0,70884 0,71226 0,71566 0,71904 0,72240
0,6
0,72575 0,72907 0,73237 0,73565 0,73891 0,74215 0,74537 0,74857 0,75175 0,75490
0,7
0,75804 0,76115 0,76424 0,76730 0,77035 0,77337 0,77637 0,77935 0,78230 0,78524
0,8
0,78814 0,79103 0,79389 0,79673 0,79955 0,80234 0,80511 0,80785 0,81057 0,81327
0,9
0,81594 0,81859 0,82121 0,82381 0,82639 0,82894 0,83147 0,83398 0,83646 0,83891
1,0
0,84134 0,84375 0,84614
0,84849
0,85083 0,85314 0,85543 0,85769 0,85993 0,86214
1,1
0,86433 0,86650 0,86864 0,87076 0,87286 0,87493 0,87698 0,87900 0,88100 0,88298
1,2
0,88493 0,88686 0,88877 0,89065 0,89251 0,89435 0,89617 0,89796 0,89973 0,90147
lub
=ROZKŁAD.NORMALNY.S(
1,032258
)
0,849024
(
)
( )
(
)
21
2
1
032258
,
1
36
ent
1
;
0
N
650
,
600
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
F
t
n
Krok 1
cd.
dx
e
u
F
u
x
∫
∞
−
⋅
−
⋅
Π
⋅
=
2
2
1
2
1
)
(
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
23
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Krok 1
cd.
(
)
21
2
1
84849
,
0
36
ent
650
,
600
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δt
n
(
)
21
2
1
54564
,
30
ent
650
,
600
−
⎟
⎠
⎞
⎜
⎝
⎛
+
=
Δt
n
(
)
(
)
21
04564
,
31
ent
650
,
600
−
=
Δt
n
(
)
10
21
31
650
,
600
=
−
=
Δt
n
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
24
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Wyniki prognozowania (
2
)
Wyniki prognozowania (
2
)
(
)
( )
(
)
r
...
,
,
j
t
n
t
t
F
N
t
n
j
k
p
p
j
k
s
j
k
j
k
,
2
1
,
Δ
2
1
3
ent
Δ
1
,
1
;
0
N
,
1
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
−
+
+
+
−
+
σ
)
2
=
j
Krok 2
(
)
( )
31
2
1
3
62
400
700
36
ent
1
;
0
N
700
,
650
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
Δ
F
t
n
(
)
( )
(
)
31
2
1
3
83871
,
4
36
ent
1
;
0
N
700
,
650
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
⋅
=
Δ
F
t
n
(
)
( )
(
)
31
2
1
83871
,
1
36
ent
1
;
0
N
700
,
650
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
F
t
n
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
25
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Dystrybuanta rozkładu
N(0;1)
Dystrybuanta rozkładu
N(0;1)
u
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,8
0,78814 0,79103 0,79389 0,79673 0,79955 0,80234 0,80511 0,80785 0,81057 0,81327
0,9
0,81594 0,81859 0,82121 0,82381 0,82639 0,82894 0,83147 0,83398 0,83646 0,83891
1,0
0,84134 0,84375 0,84614 0,84849 0,85083 0,85314 0,85543 0,85769 0,85993 0,86214
1,1
0,86433 0,86650 0,86864 0,87076 0,87286 0,87493 0,87698 0,87900 0,88100 0,88298
1,2
0,88493 0,88686 0,88877 0,89065 0,89251 0,89435 0,89617 0,89796 0,89973 0,90147
1,3
0,90320 0,90490 0,90658 0,90824 0,90988 0,91149 0,91309 0,91466 0,91621 0,91774
1,4
0,91924 0,92073 0,92220 0,92364 0,92507 0,92647 0,92785 0,92922 0,93056 0,93189
1,5
0,93319 0,93448 0,93574 0,93699 0,93822 0,93943 0,94062 0,94179 0,94295 0,94408
1,6
0,94520 0,94630 0,94738 0,94845 0,94950 0,95053 0,95154 0,95254 0,95352 0,95449
1,7
0,95543 0,95637 0,95728 0,95818 0,95907 0,95994 0,96080 0,96164 0,96246 0,96327
1,8
0,96407 0,96485 0,96562
0,96638
0,96712 0,96784 0,96856 0,96926 0,96995 0,97062
1,9
0,97128 0,97193 0,97257 0,97320 0,97381 0,97441 0,97500 0,97558 0,97615 0,97670
2,0
0,97725 0,97778 0,97831 0,97882 0,97932 0,97982 0,98030 0,98077 0,98124 0,98169
lub
=ROZKŁAD.NORMALNY.S(
1,83871
)
0,967021
(
)
( )
(
)
31
2
1
83871
,
1
36
ent
1
;
0
N
700
,
650
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
F
t
n
Krok 2
cd.
dx
e
u
F
u
x
∫
∞
−
⋅
−
⋅
Π
⋅
=
2
2
1
2
1
)
(
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
26
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Krok 2
cd.
(
)
31
2
1
96638
,
0
36
ent
700
,
650
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δt
n
(
)
31
2
1
78968
,
34
ent
700
,
650
−
⎟
⎠
⎞
⎜
⎝
⎛
+
=
Δt
n
(
)
(
)
31
28968
,
35
ent
700
,
650
−
=
Δt
n
(
)
4
31
35
700
,
650
=
−
=
Δt
n
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
27
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Wyniki prognozowania (
3
)
Wyniki prognozowania (
3
)
(
)
( )
(
)
r
...
,
,
j
t
n
t
t
F
N
t
n
j
k
p
p
j
k
s
j
k
j
k
,
2
1
,
Δ
2
1
3
ent
Δ
1
,
1
;
0
N
,
1
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
−
+
+
+
−
+
σ
)
3
=
j
Krok 3
(
)
( )
35
2
1
3
62
400
750
36
ent
1
;
0
N
750
,
700
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
Δ
F
t
n
(
)
( )
(
)
35
2
1
3
645161
,
5
36
ent
1
;
0
N
750
,
700
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
⋅
=
Δ
F
t
n
(
)
( )
(
)
35
2
1
645161
,
2
36
ent
1
;
0
N
750
,
700
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
F
t
n
(
)
35
2
1
99598
,
0
36
ent
750
,
700
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δt
n
(
)
1
35
36
750
,
700
=
−
=
Δt
n
( )
(
)
645161
,
2
99598
,
0
1
;
0
N
F
=
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
28
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
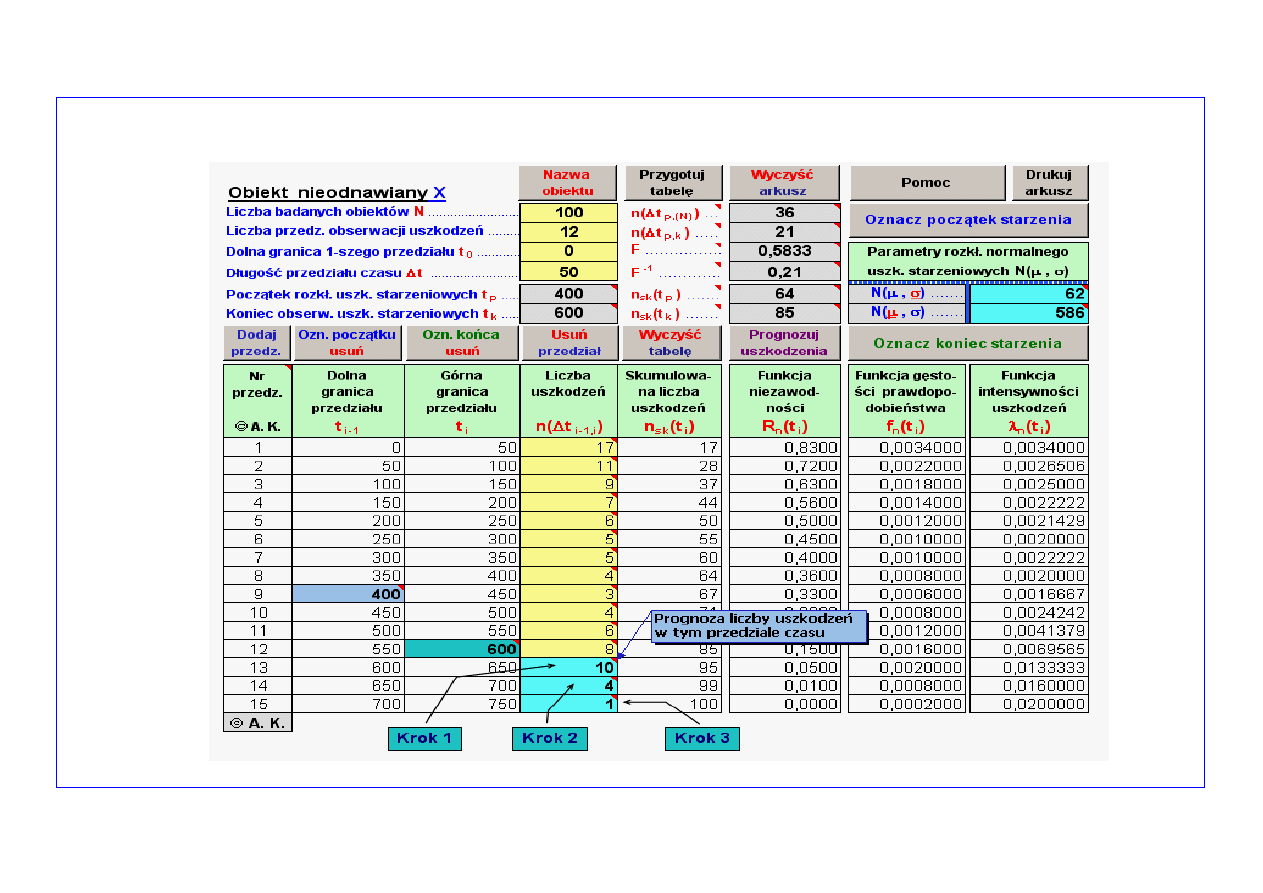
Zebrane wyniki prognozowania (
4
)
Zebrane wyniki prognozowania (
4
)
(
)
( )
(
)
r
...
,
,
j
t
n
t
t
F
N
t
n
j
k
p
p
j
k
s
j
k
j
k
,
2
1
,
Δ
2
1
3
ent
Δ
1
,
1
;
0
N
,
1
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
−
+
+
+
−
+
σ
)
(
)
( )
10
21
2
1
3
62
400
650
36
ent
1
;
0
N
650
,
600
=
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
Δ
F
t
n
Krok 1
(
)
( )
4
31
2
1
3
62
400
700
36
ent
1
;
0
N
700
,
650
=
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
Δ
F
t
n
Krok 2
(
)
( )
1
35
2
1
3
62
400
750
36
ent
1
;
0
N
750
,
700
=
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⋅
=
Δ
F
t
n
Krok 3
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
29
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
Wyniki prognozowania z symulatora
Kaja.xls
(
5
)
Plik:
PP_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v5]
30
/
30
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH
PODSUMOWANIE
1. MODELE MATEMATYCZNE
Założenia
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych
Prognostyczny model liczby uszkodzeń obiektów w okresie ich starzenia
2. MODEL KOMPUTEROWY DO ANALIZY USZKODZEŃ OBIEKTÓW W OKRESIE
USZKODZEŃ STARZENIOWYCH
Symulator komputerowy algorytmów modeli matematycznych
Przykładowe problemy badawcze
Konfigurowanie symulatora i wyniki prognozowania
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron