MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
1
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
3.1. Definicja kratownicy płaskiej
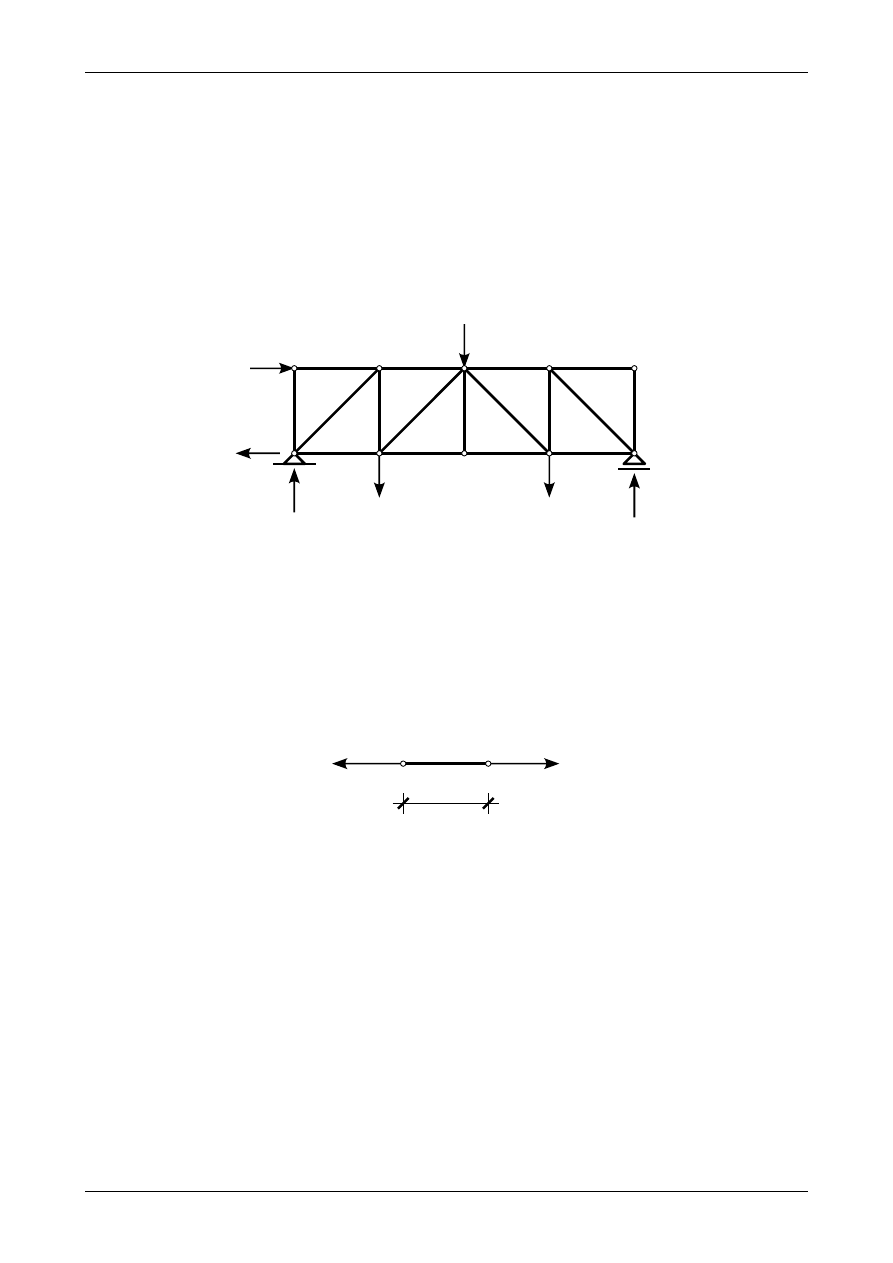
Jak wiadomo kratownicą płaską nazywamy układ prętów prostych leżących na jednej płaszczyźnie,
które są połączone między sobą przegubami. Przeguby nazywa się węzłami kratownicy. Kratownica
następnie jest podparta do podłoża za pomocą podpór przegubowo-przesuwnej i przegubowo-nieprzesuwnej.
W tym miejscu rozszerzymy tą definicję na fakt, że wszystkie siły czynne i bierne (reakcje) są przyłożone
w węzłach (przegubach) kratownicy płaskiej. Kratownicę zgodną z powyższą definicją przedstawia
rysunek 3.1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
3
5
7
9
4
6
8
10
V
1
H
1
V
9
P
1
P
2
P
3
P
4
Rys. 3.1. Obciążona kratownica płaska
3.2. Siła normalna w pręcie kratownicy
Wytnijmy z kratownicy przedstawionej na rysunku 3.1 pręt numer 2. Na pręt ten będą działy dwie
reakcje działające na obu końcach wyciętego pręta. Zgodnie z rysunkiem 2.52 i wzorem (2.23) aby pręt ten
znajdował się w równowadze reakcje te muszą działać na jednej prostej, na której też leży pręt numer 2 oraz
muszą mieć te same wartości ale przeciwne zwroty. Przedstawia to rysunek 3.2.
2
3
5
R
R
L
2
Rys. 3.2. Pręt kratownicy płaskiej w równowadze
Przetnijmy pręt numer 2 w dowolnym miejscu na jego długości. Punkt przecięcia znajduje się w
odległości x od lewego końca pręta. Przedstawia to rysunek 3.3 a). Jak widać na tym rysunku obie części
pręta nie znajdują się w równowadze. Aby były one w równowadze w miejscu przecięcia musi działać
pewna siła N. Siła ta jest równa co do wartości reakcji R działających na cały pręt numer 2 ale musi mieć
przeciwny zwrot, czyli
N
=−R
.
(3.1)
Siłę N nazywamy siłą normalną. Jest to jedna z tak zwanych sił przekrojowych. Siłę normalną
działającą w przekroju pręta przedstawia rysunek 3.4. Jak widać przyłożona ona jest w środku ciężkości
przekroju pręta (punkt sc) a jej kierunek pokrywa się z osią X układu współrzędnych XYZ związanego z
przekrojem pręta.
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
2
2
3
R
2
5
R
x
L
2
-x
a)
2
3
R
2
5
R
x
L
2
-x
b)
N
N
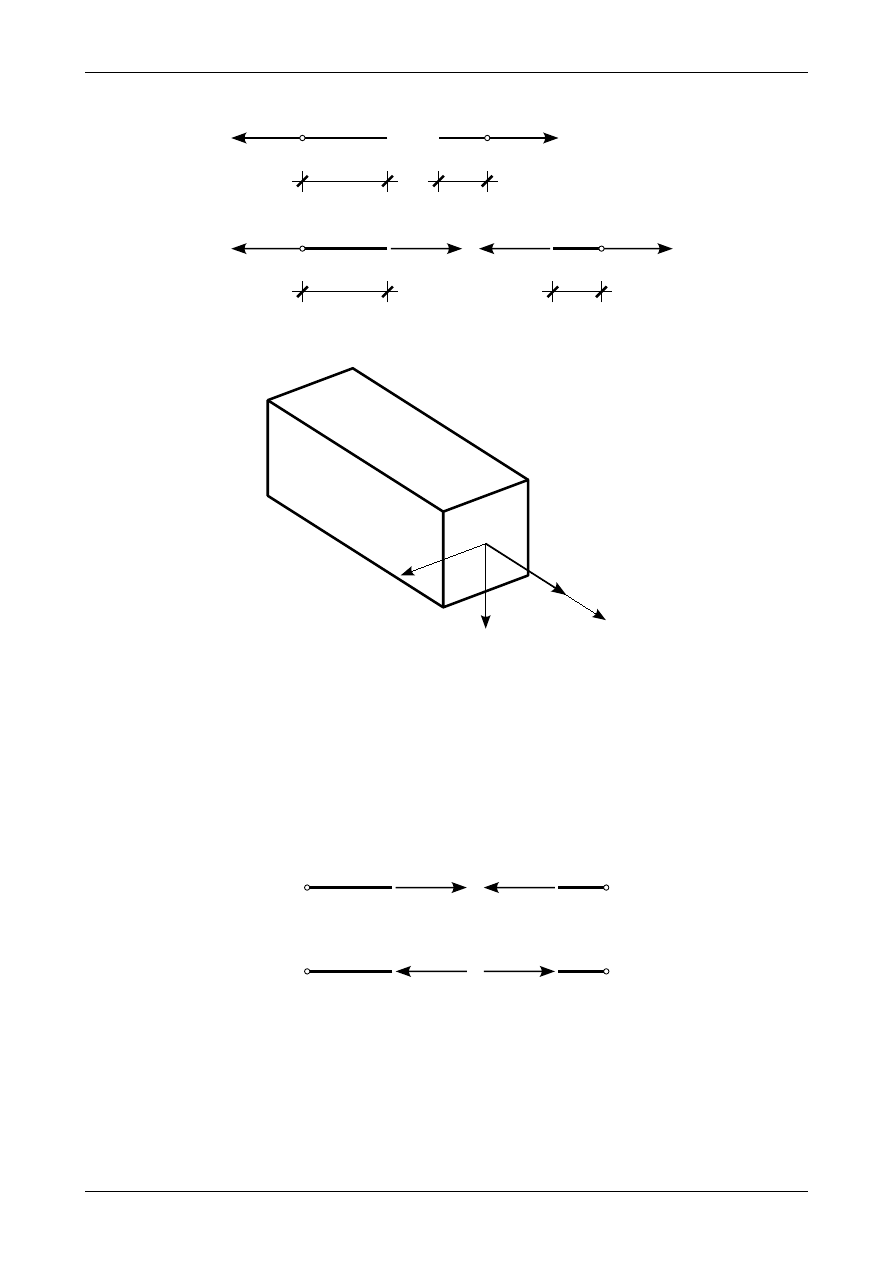
Rys. 3.3. Części pręta kratownicy płaskiej. a) nie będące w równowadze, b) będące w równowadze
N
X
Y=Y
0
Z=Z
0
sc
Rys. 3.4. Siła normalna w przekroju pręta kratownicy płaskiej
Siła normalna w pręcie kratownicy będzie miała swój znak. Będzie ona dodatnia, jeżeli będzie
działała od przekroju pręta. Przedstawia to rysunek 3.5 a). Będzie ona ujemna, jeżeli będzie działa do
przekroju pręta. Przedstawia to rysunek 3.5 b). Innymi słowy dodatnia siła normalna będzie rozciągała
(wydłużała) pręt kratownicy natomiast ujemna siła normalna będzie ściskała (skracała) pręt
kratownicy.
a)
N
N
b)
N
N
Rys. 3.5. Siła normalna. a) dodatnia, b) ujemna
3.3. Metoda zrównoważenia węzłów
Pierwszą z metod wyznaczenia wartości i zwrotów sił normalnych w prętach kratownicy płaskiej jest
metoda zrównoważenia węzłów. W metodzie tej wycinamy każdy węzeł kratownicy płaskiej i
rozpatrujemy równowagę wszystkich sił działających w nim. W każdym węźle mamy do dyspozycji dwa
równania sumy rzutów wszystkich sił działających w węźle na oś poziomą X i pionową Y.
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
3
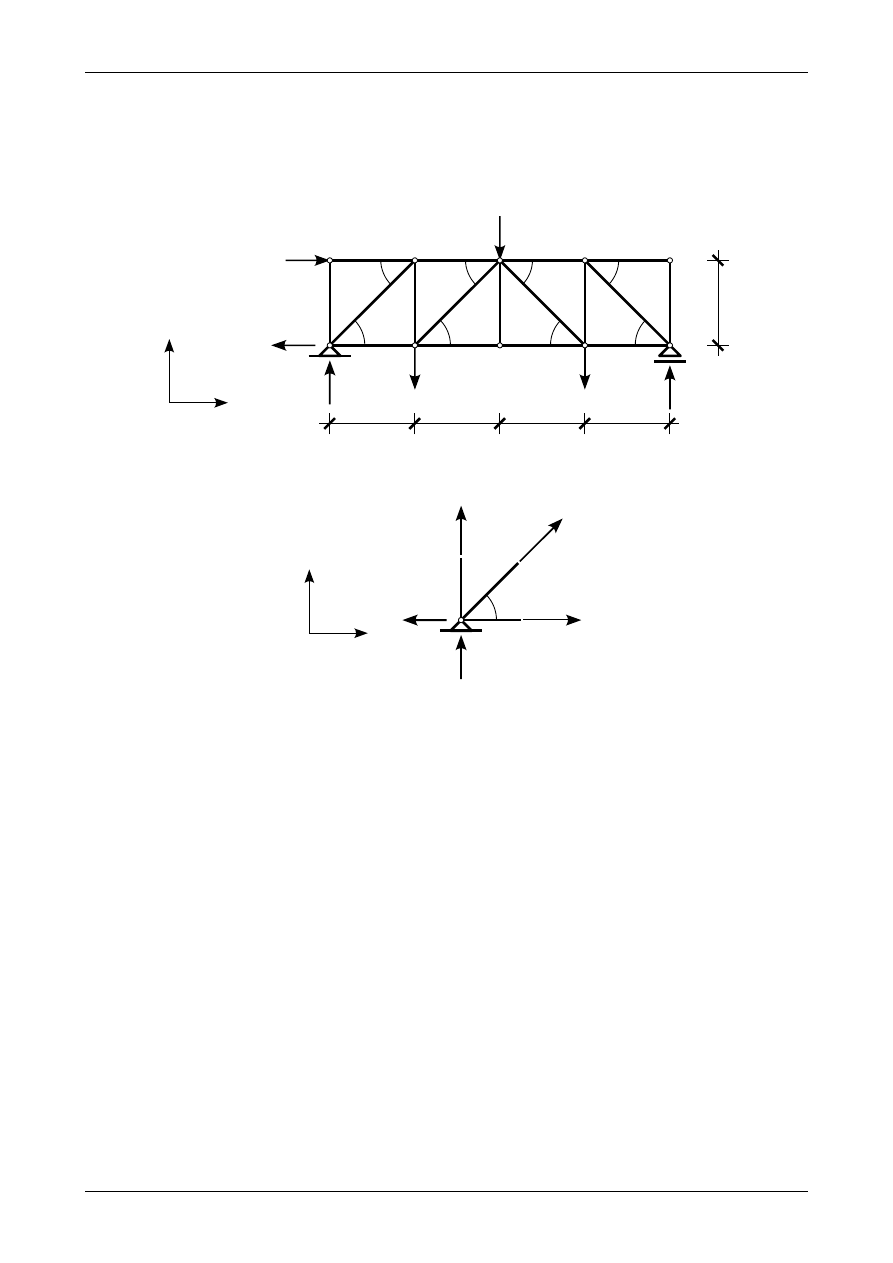
Rysunek 3.6 przedstawia przykładową kratownicę płaską. Jak widać spełnia ona warunki konieczny i
dostateczne geometrycznej niezmienności. Dla kratownicy tej przyjmujemy początkowe zwroty reakcji
podporowych. Musimy także wyznaczyć wartości sinusa i kosinusa kąta
α
pomiędzy prętami pasa dolnego i
górnego a krzyżulcami.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
3
5
7
9
4
6
8
10
V
1
H
1
V
9
P
1
P
2
P
3
P
4
α
α
α
α
α
α
α
α
a
a
a
b
a
X
Y
Rys. 3.6. Kratownica płaska
1
1
V
1
H
1
9
14
N
9
N
14
N
1
α
X
Y
Rys. 3.7. Siły działające w węźle numer 1
Rysunek 3.7 przedstawia wszystkie siły działające w wyciętym węźle numer 1. Siły normalne w
prętach kratownicy płaskiej przyjmujemy jako dodatnie czyli rozciągające. Równania równowagi w
tym węźle mają postać
X
=−
H
1
N
1
N
14
⋅
cos
=
0
,
(3.2)
Y =V
1
N
9
N
14
⋅sin
=0
.
(3.3)
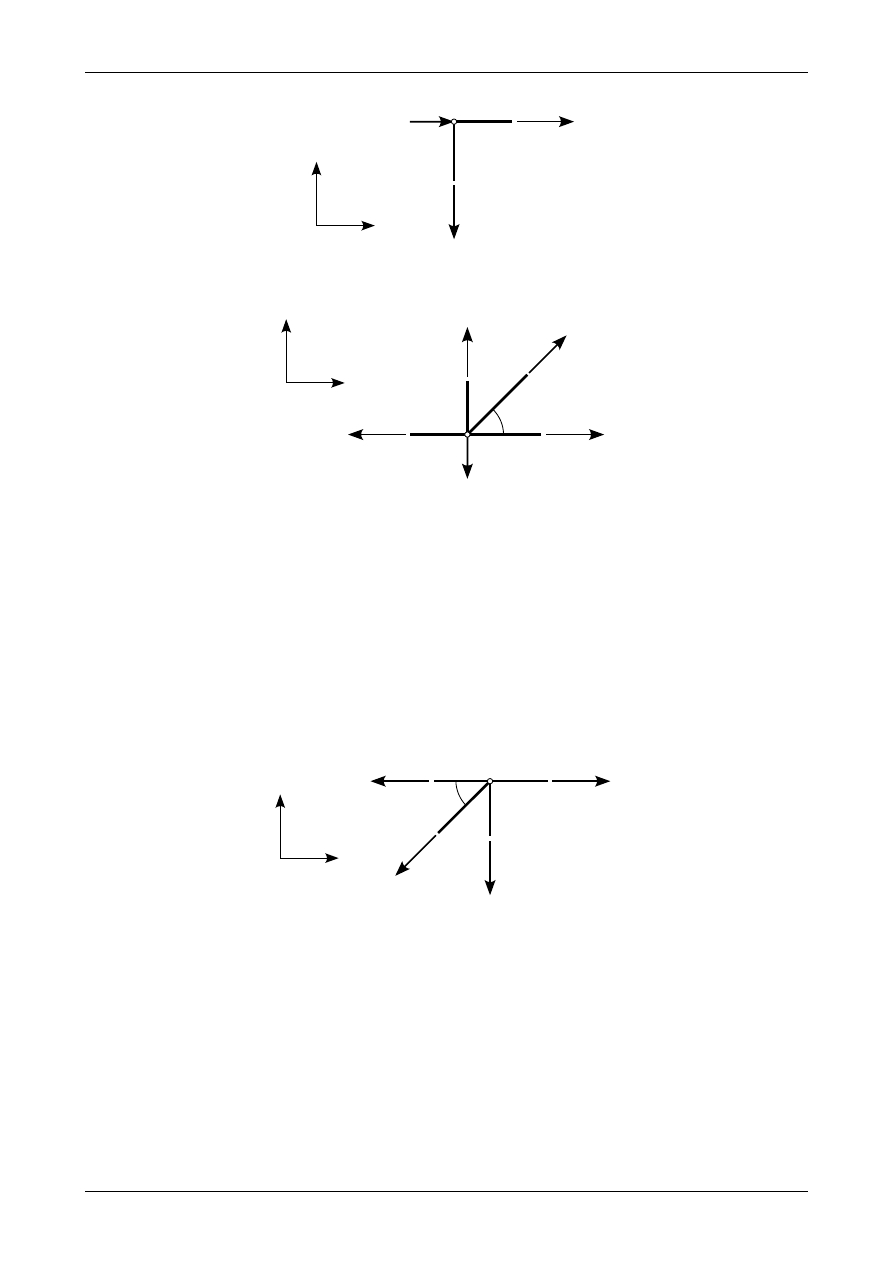
Rysunek 3.8 przedstawia wszystkie siły działające w wyciętym węźle numer 8. Równania równowagi
w tym węźle mają postać
X =P
4
N
5
=0
,
(3.4)
Y =N
9
=0
.
(3.5)
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
4
5
9
2
P
4
N
9
N
5
X
Y
Rys. 3.8. Siły działające w węźle numer 2
3
2
10
15
P
1
α
1
N
1
N
10
N
15
N
2
X
Y
Rys. 3.9. Siły działające w węźle numer 3
Rysunek 3.9 przedstawia wszystkie siły działające w wyciętym węźle numer 3. Równania równowagi
w tym węźle mają postać
X =−N
1
N
2
N
15
⋅cos
=0
,
(3.6)
Y =N
10
−P
1
N
15
⋅sin
=0
.
(3.7)
6
10
14
4
α
N
5
5
N
6
N
10
N
14
X
Y
Rys. 3.10. Siły działające w węźle numer 4
Rysunek 3.10 przedstawia wszystkie siły działające w wyciętym węźle numer 4. Równania
równowagi w tym węźle mają postać
X =−N
5
N
6
−N
14
⋅cos
=0
,
(3.8)
Y =−N
10
−N
14
⋅sin
=0
.
(3.9)
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
5
5
2
3
11
N
2
N
3
N
11
X
Y
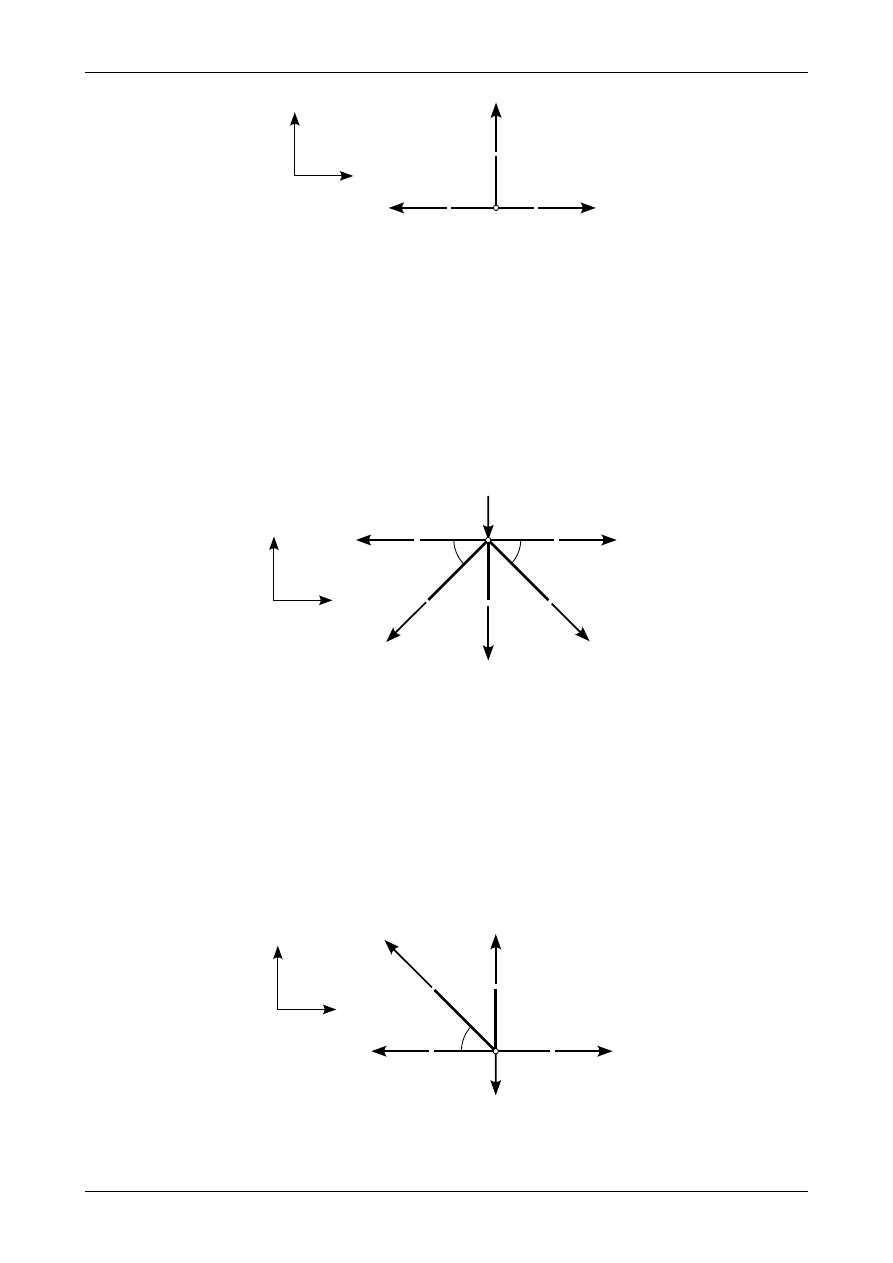
Rys. 3.11. Siły działające w węźle numer 5
Rysunek 3.11 przedstawia wszystkie siły działające w wyciętym węźle numer 5. Równania
równowagi w tym węźle mają postać
X =−N
2
N
3
=0
,
(3.10)
Y =N
11
=0
.
(3.11)
6
7
11
15
16
6
P
2
α
α
N
6
N
7
N
15
N
11
N
16
X
Y
Rys. 3.12. Siły działające w węźle numer 6
Rysunek 3.12 przedstawia wszystkie siły działające w wyciętym węźle numer 6. Równania
równowagi w tym węźle mają postać
X =−N
6
N
7
−N
15
⋅cos
N
16
⋅cos
=0
,
(3.12)
Y =−P
2
− N
11
−N
15
⋅sin
− N
16
⋅sin
=0
.
(3.13)
3
4
12
16
7
α
N
3
N
4
N
12
N
16
X
Y
P
3
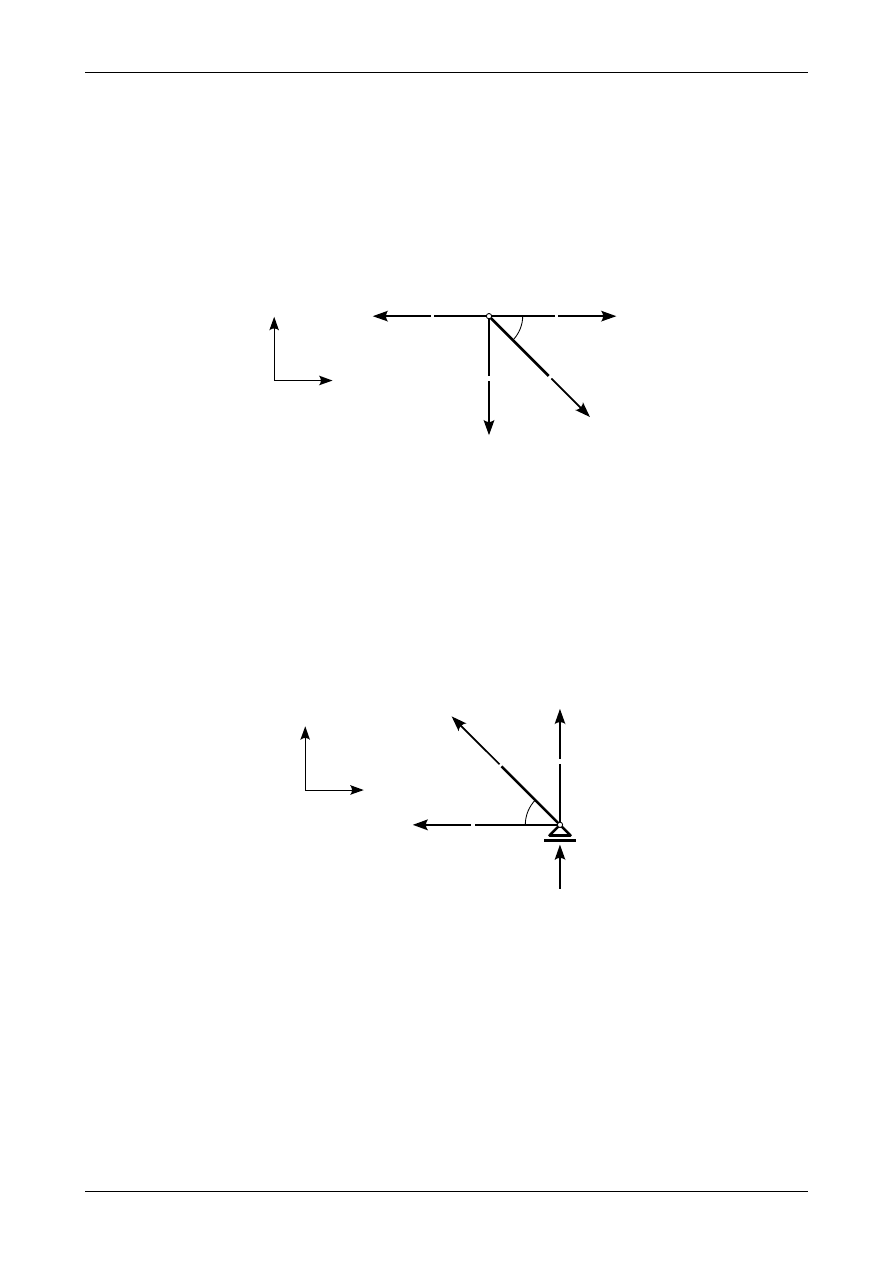
Rys. 3.13. Siły działające w węźle numer 7
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
6
Rysunek 3.13 przedstawia wszystkie siły działające w wyciętym węźle numer 7. Równania
równowagi w tym węźle mają postać
X =−N
3
N
4
−N
16
⋅cos
=0
,
(3.14)
Y =−P
3
N
12
N
16
⋅sin
=0
.
(3.15)
7
8
12
17
8
α
N
7
N
8
N
12
N
17
X
Y
Rys. 3.14. Siły działające w węźle numer 8
Rysunek 3.14 przedstawia wszystkie siły działające w wyciętym węźle numer 8. Równania
równowagi w tym węźle mają postać
X =−N
7
N
8
N
17
⋅cos
=0
,
(3.16)
Y =−N
12
−N
17
⋅sin
=0
.
(3.17)
4
13
17
9
V
9
α
N
4
N
13
N
17
X
Y
Rys. 3.15. Siły działające w węźle numer 9
Rysunek 3.15 przedstawia wszystkie siły działające w wyciętym węźle numer 9. Równania
równowagi w tym węźle mają postać
X =−N
4
−N
17
⋅cos
=0
,
(3.18)
Y =V
9
N
13
N
17
⋅sin
=0
.
(3.19)
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
7
8
13
10
N
8
N
13
X
Y
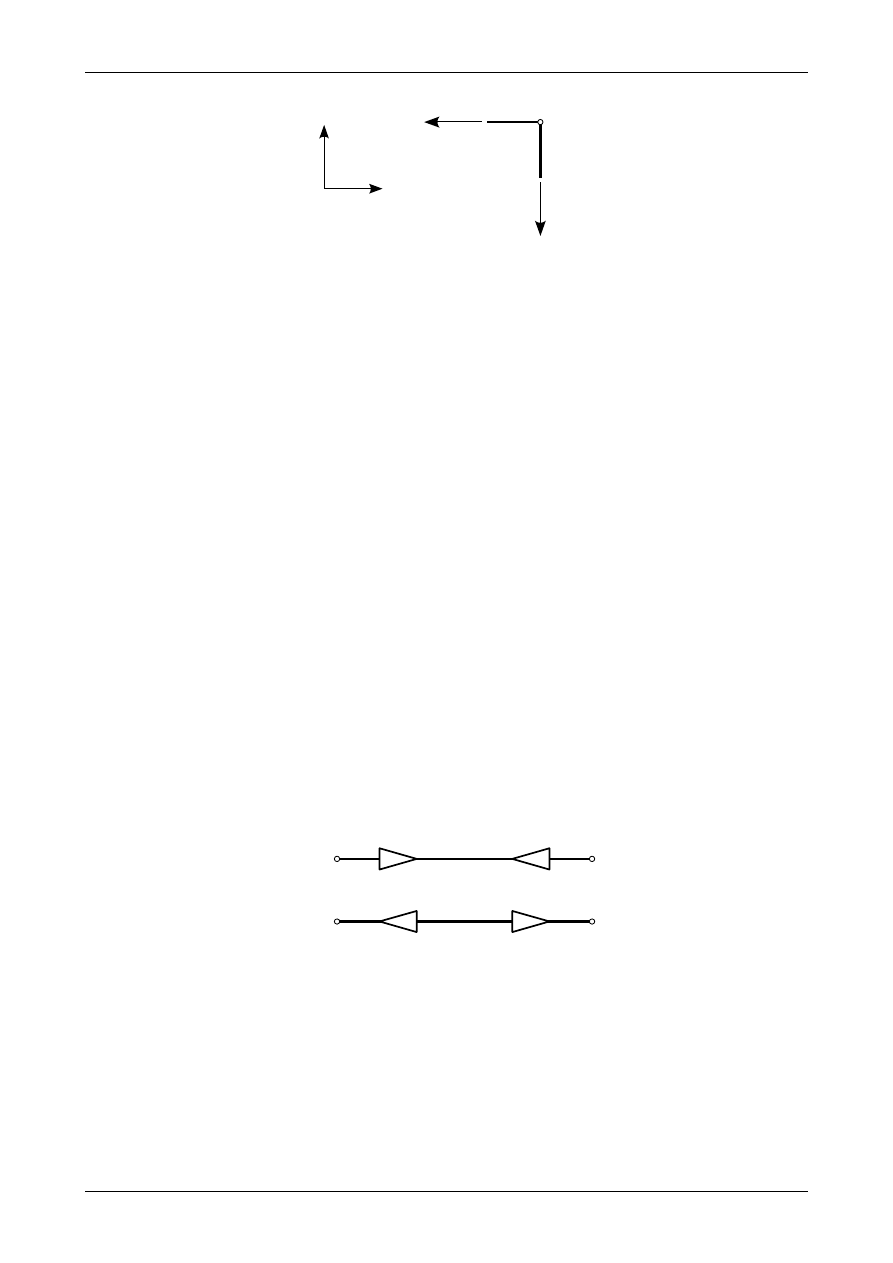
Rys. 3.16. Siły działające w węźle numer 10
Rysunek 3.16 przedstawia wszystkie siły działające w wyciętym węźle numer 10. Równania
równowagi w tym węźle mają postać
X =−N
8
=0
,
(3.20)
Y =−N
13
=0
.
(3.21)
Równania od (3.2) do (3.21) tworzą układ 20 równań z 20 niewiadomymi. Równań jest tyle samo ile
stopni swobody mają wszystkie węzły kratownicy płaskiej. Niewiadomymi w układzie równań są wartości i
zwroty 3 reakcji podporowych oraz 17 sił normalnych w prętach kratownicy płaskiej. Jeżeli wyznacznik
główny tego układu równań jest różny od zera to kratownica jest układem geometrycznie
niezmiennym i statycznie wyznaczalnym. Rozwiązując układ równań wyznaczymy wartości i zwroty
reakcji podporowych oraz sił normalnych w prętach.
Jeżeli z rozwiązania jakaś reakcja jest dodatnia oznacza to, że ma ona zwrot taki sam jak
przyjęty na początku obliczeń. Jeżeli z rozwiązania jakaś reakcja jest ujemna oznacza to, że ma ona
zwrot przeciwny do przyjętego na początku obliczeń.
Jeżeli siła normalna w jakimś pręcie jest dodatnia oznacza to, że pręt jest rozciągany. Jeżeli siła
normalna w jakimś pręcie jest ujemna oznacza to, że pręt jest ściskany.
Na rysunku kratownicy pręty rozciągane będziemy oznaczali tak jak na rysunku 3.17 a) natomiast pręt
ściskany będziemy oznaczali jak na rysunku 3.17 b). Obok pręta będziemy wpisywali wartość bezwzględną
siły normalnej w tym pręcie.
a)
b)
∣
N
∣
∣
N
∣
Rys. 3.17. Oznaczenie pręta. a) rozciąganego, b) ściskanego
Jeżeli jednak kratownica posiada strukturę prostą i tworzy tarczę sztywną reakcje w podporach
możemy wyznaczyć z trzech warunków równowagi dla tej tarczy sztywnej. Dla kratownicy na rysunku 3.6
równania równowagi będą miały postać
X
=−
H
1
P
4
=
0
,
(3.22)
Dr inż. Janusz Dębiński
Zaoczni

MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
8
M
9
=
V
1
⋅
4
⋅
a
−
P
1
⋅
3
⋅
a
−
P
2
⋅
2
⋅
a
−
P
3
⋅
a
P
4
⋅
b
=
0
,
(3.23)
M
1
=−V
9
⋅4⋅aP
1
⋅aP
2
⋅2⋅aP
3
⋅3⋅aP
4
⋅b=0
.
(3.24)
Z równania (3.22) wyznaczymy reakcję H
1
. Z równania (3.23) wyznaczymy reakcję V
1
. Punkt 9 jest
punktem przecięcia kierunków pozostałych reakcji czyli H
1
oraz V
9
. Dzięki temu moment tych reakcji
wynosi zero. Z równania (3.24) wyznaczymy reakcję V
9
. Punkt 1 jest punktem przecięcia kierunków
pozostałych reakcji czyli H
1
oraz V
1
. Dzięki temu moment tych reakcji wynosi zero.
Dla sprawdzenia obliczeń reakcji V
1
oraz V
9
zastosujemy równanie sumy rzutów wszystkich sił na
kierunek pionowy Y czyli
Y =V
1
V
9
−P
1
−P
2
−P
3
=0
.
(3.25)
Jeżeli warunek (3.25) jest spełniony wartości i zwroty reakcji V
1
oraz V
9
są wyznaczone poprawnie i
możemy przystąpić do dalszych obliczeń.
Obliczenia sił normalnych w prętach kratownicy płaskiej zaczynamy od tego węzła, w którym
schodzą się dwa pręty. Węzłem takim jest węzeł numer 2. Z równania (3.4) wyznaczymy siłę normalną N
5
. Z
równania (3.5) wyznaczymy siłę normalną N
9
.
Dalej przechodzimy do węzła numer 1. Z równania (3.3) wyznaczymy siłę normalną N
14
. Z równania
(3.2) wyznaczymy siłę normalną N
1
.
Kolejnym węzłem będzie węzeł numer 4. Z równania (3.9) wyznaczymy siłę normalną N
10
. Z
równania (3.8) wyznaczymy siłę normalną N
6
.
W dalszej kolejności rozpatrujemy węzeł numer 3. Z równania (3.7) wyznaczymy siłę N
15
. Z równania
(3.6) wyznaczymy siłę N
2
.
Dalej przechodzimy do węzła numer 5. Z równania (3.11) wyznaczymy siłę normalną N
11
. Z równania
(3.10) wyznaczymy siłę normalną N
3
.
Kolejnym węzłem będzie węzeł numer 6. Z równania (3.13) wyznaczymy siłę normalną N
16
. Z
równania (3.12) wyznaczymy siłę normalną N
7
.
W dalszej kolejności rozpatrujemy węzeł numer 7. Z równania (3.15) wyznaczymy siłę normalną N
12
.
Z równania (3.14) wyznaczymy siłę normalną N
4
.
Dalej przechodzimy do węzła numer 8. Z równania (3.17) wyznaczymy siłę normalną N
17
. Z równania
(3.16) wyznaczymy siłę normalną N
8
.
Ostatnim węzłem będzie węzeł numer 9. Z równania (3.19) wyznaczymy siłę normalną N
13
. W ten
sposób wyznaczyliśmy siły normalne we wszystkich prętach kratownicy płaskiej. Zostały nam jeszcze trzy
równania równowagi (3.18), (3.21) i (3.22). Wykorzystamy je do sprawdzenia poprawności obliczeń.
3.4. Pręty zerowe
Prętem zerowym nazywamy pręt, w którym siła normalna wynosi zero. Nie oznacza to, że pręt ten
jest niepotrzebny. Usunięcie pręta zerowego spowodowałoby, że kratownica stałaby się geometrycznie
zmienna.
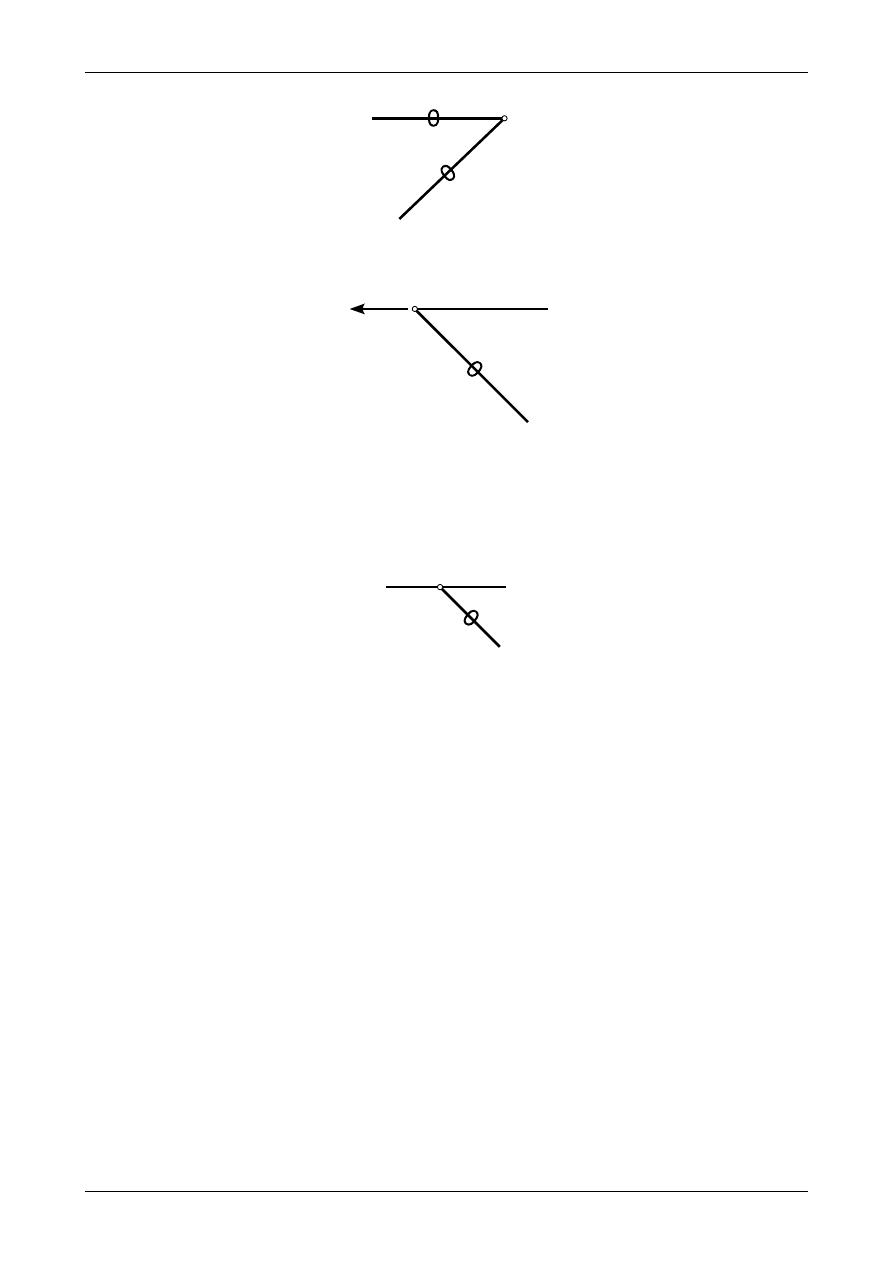
Jeżeli w nieobciążonym węźle schodzą się dwa pręty kratownicy płaskiej to oba są zerowe.
Przedstawia to rysunek 3.18.
Jeżeli w obciążonym węźle schodzą się dwa pręty kratownicy i ponadto siła przyłożona w węźle ma
kierunek jednego z prętów to drugi pręt jest zerowy. Przedstawia to rysunek 3.19.
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
9
1
Rys. 3.18. Pręty zerowe
1
P
Rys. 3.19. Pręt zerowy
Jeżeli w nieobciążonym węźle schodzą się trzy pręty kratownicy płaskiej i ponadto dwa z nich leżą na
jednej prostej to trzeci pręt jest zerowy. Przedstawia to rysunek 3.20.
1
Rys. 3.20. Pręt zerowy
3.5. Metoda Rittera
Metoda Rittera jest metodą przydatną do wyznaczenia siły normalnej w jednym, ściśle określonym
pręcie kratownicy płaskiej. Warunkiem jej zastosowania jest wcześniejsze wyznaczenie wszystkich reakcji
podporowych. Metodę tę możemy więc zastosować głównie do kratownic o strukturze prostej.
Metoda ta polega na przecięciu kratownicy płaskiej i rozpatrywaniu równowagi wyciętej części.
Drugim warunkiem jej zastosowania będzie więc przecięcie kratownicy tylko przez trzy pręty. Istnieją
jednak odstępstwa od tego warunku. Omówimy je w dalszej części niniejszego opracowania.
Istotą tej metody jest wyznaczenie siły normalnej w jednym pręcie z jednego równania
równowagi. Aby to uczynić należy zastosować równanie sumy momentów wszystkich sił działających na
odciętą część kratownicy płaskiej względem punktu przecięcia się kierunków dwóch pozostałych prętów w
przekroju. Punkt ten nazywamy punktem Rittera. Jeżeli dwa pręty w przekroju są do siebie równoległe to
aby wyznaczyć siłę normalną w trzecim pręcie należy zastosować równanie sumy rzutów wszystkich sił
działających na odciętą część kratownicy płaskiej na oś prostopadłą do kierunku prętów równoległych.
Rysunek 3.21 przedstawia kratownicę płaską, w której chcemy wyznaczyć siły normalne w prętach
numer 2, 6 i 15. W tym celu przecinamy kratownicę płaską przekrojem A-A przedstawionym na rysunku
3.21.
Rysunek 3.22 przedstawia siły działające na odciętą lewą część kratownicy płaskiej. Punktem Rittera
dla pręta numer 2 jest punkt przecięcia się kierunków prętów numer 6 i 15 czyli węzeł numer 6.
Odpowiednie równanie, z którego będziemy mogli wyznaczyć siłę normalną w tym pręcie będzie miało
postać
Dr inż. Janusz Dębiński
Zaoczni
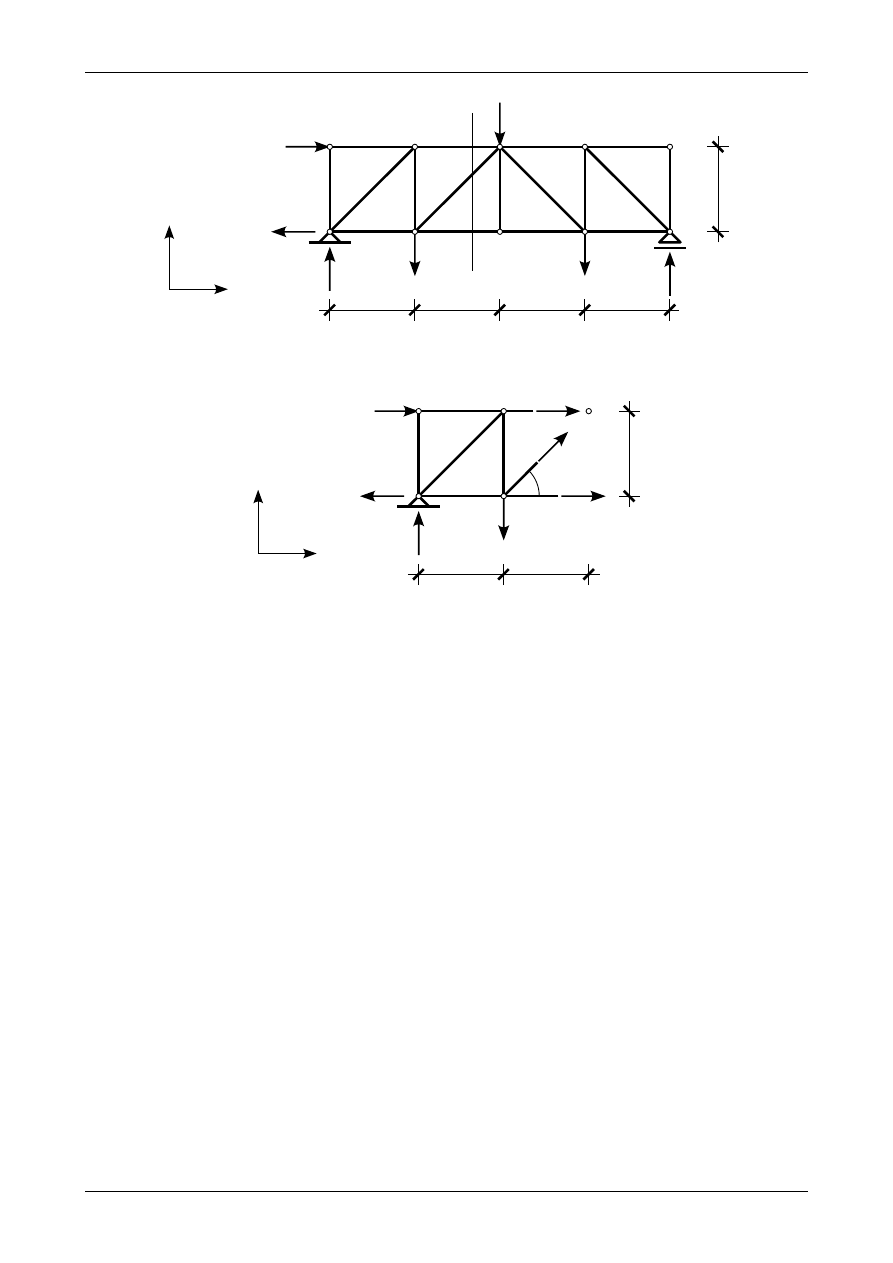
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
3
5
7
9
4
6
8
10
V
1
H
1
V
9
P
1
P
2
P
3
P
4
a
a
a
b
a
X
Y
A
A
Rys. 3.21. Kratownica płaska
1
2
5
6
9
10
14
15
1
2
3
4
6
V
1
H
1
P
1
P
4
α
a
a
X
Y
b
N
6
N
2
N
15
Rys. 3.22. Siły działające na lewą część kratownicy płaskiej
M
6
=−
N
2
⋅
b
V
1
⋅
2
⋅
a
H
1
⋅
b
−
P
1
⋅
a
=
0
.
(3.26)
Punktem Rittera dla pręta numer 6 jest punkt przecięcia się kierunków prętów numer 2 i 15 czyli
węzeł numer 3. Odpowiednie równanie, z którego będziemy mogli wyznaczyć siłę normalną w tym pręcie
będzie miało postać
M
3
= N
6
⋅bV
1
⋅aP
4
⋅b=0
.
(3.27)
Siłę normalną w pręcie numer 5 wyznaczymy z równania sumy rzutów wszystkich sił działających na
odciętą część kratownicy płaskiej na oś pionową Y
Y
=
N
15
⋅
sin
V
1
−
P
1
=
0
.
(3.28)
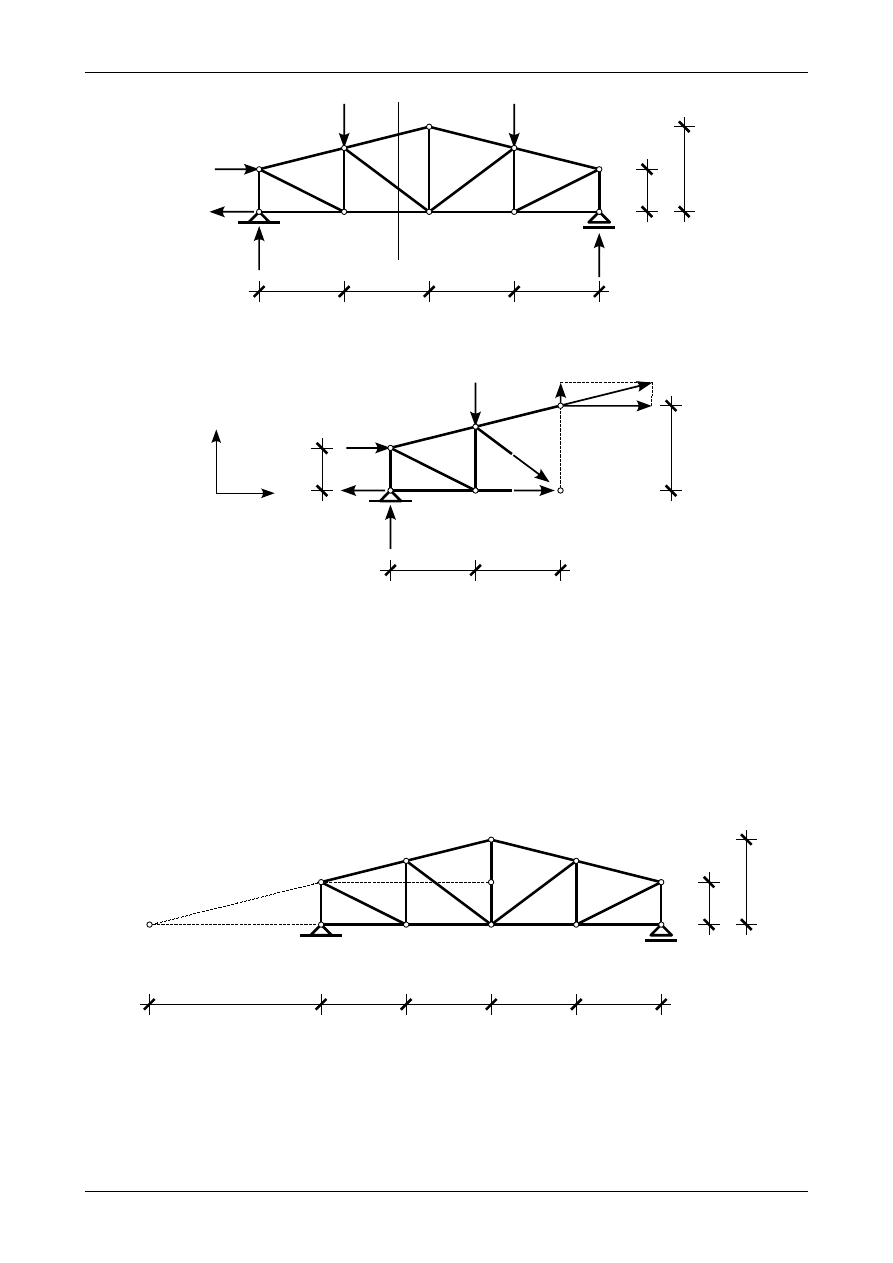
Rysunek 3.23 przedstawia kratownicę płaską, która posiada nierównoległe do siebie pasy górny i
dolny. Chcąc wyznaczyć siły normalne w prętach numer 2, 6 i 15 stosujemy przekrój A-A przedstawiony na
rysunku 3.23.
Punktem Rittera dla pręta numer 2 jest punkt przecięcia się kierunków prętów numer 6 i 15 czyli
węzeł numer 6. Siłę normalną w tym pręcie liczymy podobnie jak w przypadku podanym powyżej.
Punktem Rittera dla pręta numer 6 jest punkt przecięcia się kierunków prętów numer 2 i 15 czyli
węzeł numer 5. Lewą część kratownicy płaskiej przedstawia rysunek 3.24.
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
11
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
3
5
7
4
6
8
9
10
P
1
P
2
P
3
V
1
H
1
V
9
a
b
c
A
A
a
a
a
Rys. 3.23. Kratownica płaska z nierównoległymi pasami
1
1
2
5
6
9
10
14
15
2
3
5
4
P
1
P
2
V
1
H
1
a
a
N
6
b
c
N
15
N
2
6
N
6X
N
6Y
X
Y
Rys. 3.24. Siły działające na lewą część kratownicy płaskiej
Najwygodniej siłę normalną w pręcie numer 6 jest przyłożyć w węźle numer 6, który znajduje się
powyżej punktu Rittera 5. Następnie siłę N
6
rozkładamy na dwie siły składowe po kierunkach osi X i Y.
Kierunki obu sił składowych przecinają się w punkcie 6 znajdującym się na kierunku siły N
6
. Chcąc
wyznaczyć siłę normalną w pręcie numer 6 stosujemy równanie sumy momentów wszystkich sił
działających na lewą część kratownicy płaskiej względem punktu 5. Przyłożenie sił składowych N
6X
oraz
N
6Y
powoduje to, że od siły składowej pionowej N
6Y
moment wynosi zero i w równaniu równowagi
będziemy mieli tylko siłę składową N
6X
.
2
5
6
a
b
c
a
a
a
x
2'
K
2
6
15
Rys. 3.25. Punkt Rittera dla pręta numer 15
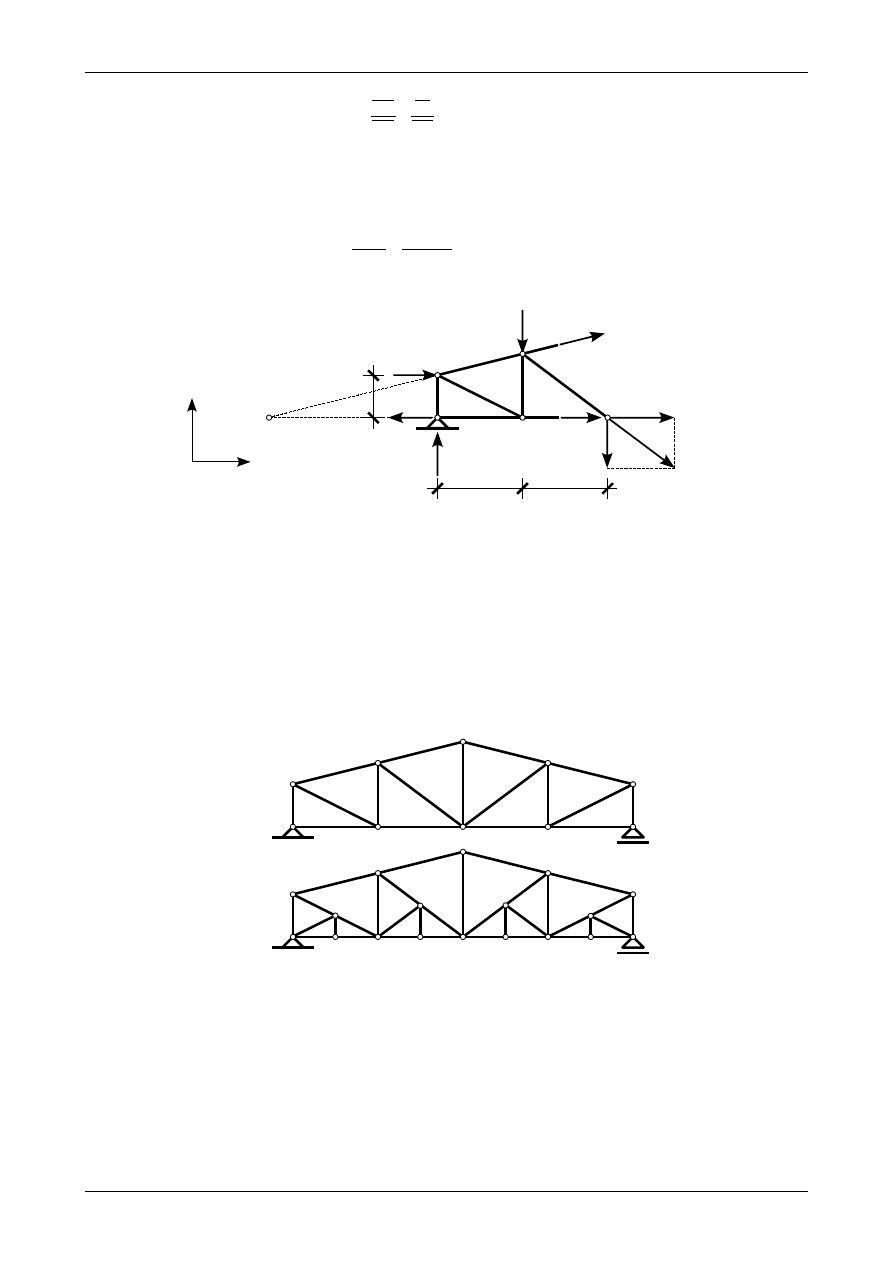
Punktem Rittera dla pręta numer 15 jest punkt przecięcia się kierunków prętów numer 2 i 6 czyli
punkt K. Aby znaleźć odległość x należy zastosować twierdzenie Talesa. Będzie ono miało postać
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
12
62'
22'
=
65
5K
.
(3.29)
Ostatecznie będzie on miał postać
b
−
c
2
⋅
a
=
b
x
2
⋅
a
.
(3.30)
1
1
2
5
6
9
10
14
15
2
3
5
4
P
1
P
2
V
1
H
1
a
a
N
6
c
N
15
N
2
X
Y
N
15X
N
15Y
K
Rys. 3.26. Siły działające na lewą część kratownicy płaskiej
Najwygodniej siłę normalną w pręcie numer 15 jest przyłożyć w węźle numer 5, który znajduje się na
jednej linii z punktem Rittera K. Następnie siłę N
15
rozkładamy na dwie siły składowe po kierunkach osi X i
Y. Kierunki obu sił składowych przecinają się w punkcie 5 znajdującym się na kierunku siły N
15
. Chcąc
wyznaczyć siłę normalną w pręcie numer 15 stosujemy równanie sumy momentów wszystkich sił
działających na lewą część kratownicy płaskiej względem punktu K. Przyłożenie sił składowych N
15X
oraz
N
15Y
powoduje to, że od siły składowej poziomej N
15X
moment wynosi zero i w równaniu równowagi
będziemy mieli tylko siłę składową N
15Y
.
a)
b)
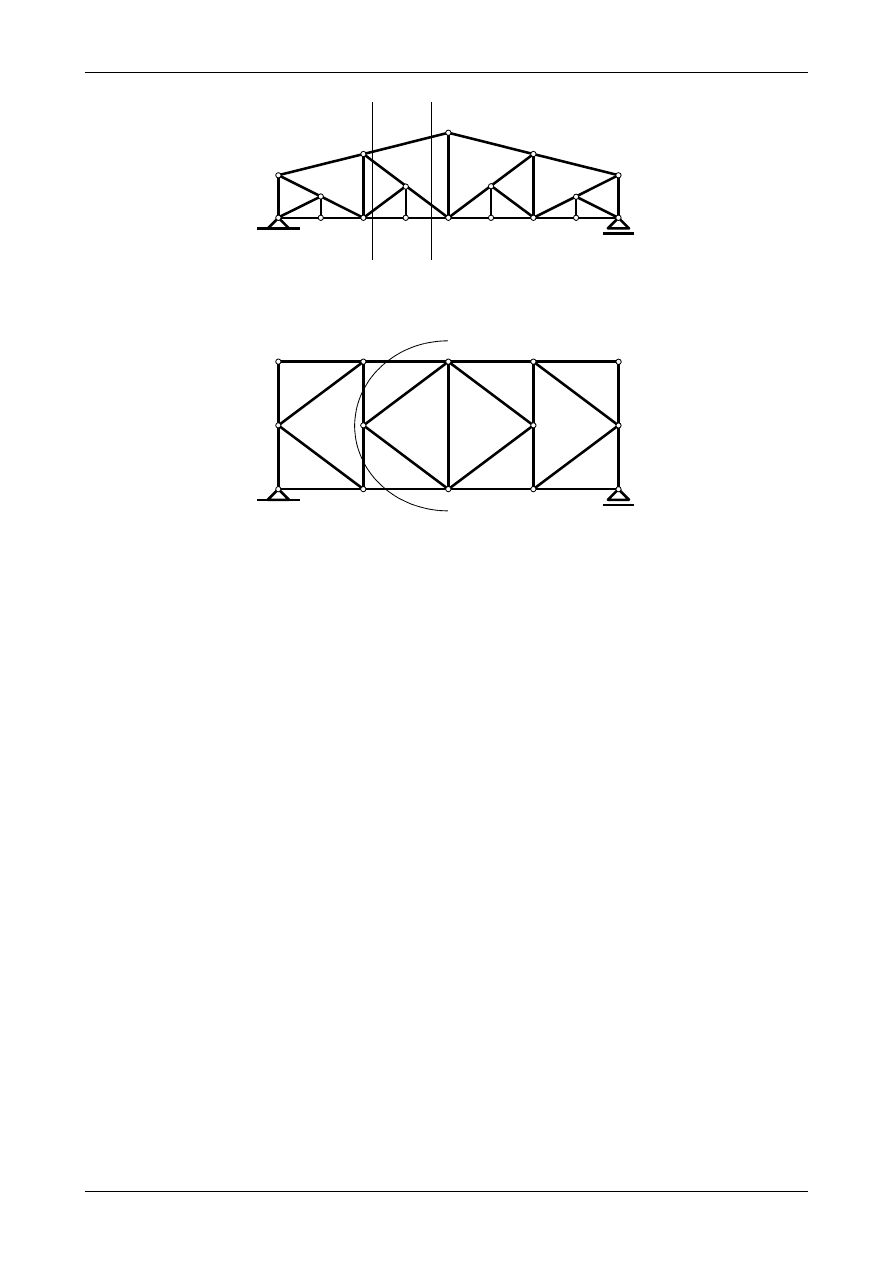
Rys. 3.27. Kratownica płaska. a) pierwszorzędne zakratowanie, b) pierwszorzędne i drugorzędne zakratowanie
Rysunek 3.27 b) przedstawia kratownicę płaską z drugorzędnym zakratowaniem. Rysunek 3.27 a)
przedstawia pierwszorzędne zakratowanie. Chcąc wyznaczyć siły normalne w prętach D
2
, K
1
oraz K
2
,
przedstawionych na rysunku 3.28, należy w pierwszej kolejności wyznaczyć siłę normalną w pręcie pasa
górnego G wykonując przekrój A-A. Znając już siłę normalną w tym pręcie przecinamy kratownicę z
drugorzędnym zakratowaniem przekrojem B-B, w którym nie znamy wartości sił normalnych już tylko w
trzech prętach czyli D
2
, K
1
oraz K
2
. Możemy więc siły normalne w tych prętach wyznaczyć stosując
klasyczną metodę Rittera. Zastosowaliśmy więc pośrednią metodę Rittera do wyznaczenia sił normalnych w
prętach D
2
, K
1
oraz K
2
.
Dr inż. Janusz Dębiński
Zaoczni
MO
3. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
13
K
1
G
D
1
D
2
K
2
A
A
B
B
Rys. 3.28. Przekroje kratownicy płaskiej z drugorzędnym zakratowaniem
G
D
A
A
S
1
S
2
4
5
6
Rys. 3.29. Kratownica półkrzyżulcowa
Rysunek 3.29 przedstawia kratownicę płaską nazywaną półkrzyżulcową. W kratownicy tej możemy
stosując metodę Rittera wyznaczyć siły normalne w pręcie pasa górnego G oraz pasa dolnego D. Aby to
uczynić należy wykonać przekrój A-A przedstawiony na rysunku 3.29. W przekroju A-A kierunki trzech sił
normalnych przecinają się w jednym punkcie. W węźle numer 4 przecinają się kierunki sił w prętach pasa
dolnego D oraz dwóch słupków S
1
i S
2
. W węźle numer 6 przecinają się kierunki sił w prętach pasa górnego
G oraz dwóch słupków S
1
i S
2
. Stosując równanie sumy momentów wszystkich sił działających na odciętą
część kratownicy półkrzyżulcowej względem punktu 4 wyznaczymy siłę normalną w pręcie pasa górnego G.
Stosując równanie sumy momentów wszystkich sił działających na odciętą część kratownicy półkrzy-
żulcowej względem punktu 6 wyznaczymy siłę normalną w pręcie pasa dolnego D.
Dr inż. Janusz Dębiński
Zaoczni
Document Outline
- 3.1. Definicja kratownicy płaskiej
- 3.2. Siła normalna w pręcie kratownicy
- 3.3. Metoda zrównoważenia węzłów
- 3.4. Pręty zerowe
- 3.5. Metoda Rittera
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron