
Wska´zniki nat ˛e˙zenia, wska´zniki struktury
PODSTAWOWE MIARY OPISU STRUKTURY
ZBIOROWO ´
SCI STATYSTYCZNEJ
Agnieszka Rossa
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Szkic wykładu
1
Wska´zniki nat ˛e˙zenia, wska´zniki struktury
2
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
3
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
4
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Analiza struktury zbiorowo ´sci
Analiza struktury polega na przetworzeniu szeregów
strukturalnych w syntetyczne miary opisowe takie, jak:
I.
Wska´zniki nat ˛e˙zenia i struktury
– wska´znik nat ˛e˙zenia
wyra˙za kształtowanie si ˛e wielko´sci jednego zjawiska na tle
innego, logicznie z nim zwi ˛
azanego; wska´zniki struktury
reprezentuj ˛
a z kolei liczebno´sci wzgl ˛edne wyst ˛epowania
okre´slonych warto´sci w badanej zbiorowo´sci.
II.
Miary ´srednie
(tendencji centralnej) – opisuj ˛
a przeci ˛etne
poło˙zenie warto´sci liczbowych danej cechy statystycznej.
III.
Miary zró˙znicowania
(dyspersji, rozrzutu, zmienno´sci,
rozproszenia) – opisuj ˛
a stopie ´n rozproszenia warto´sci
badanej cechy wokół ´sredniej.
IV.
Miary asymetrii
(sko´sno´sci) – informuj ˛
a, czy wi ˛eksza
cz ˛e´s´c jednostek zbiorowo´sci ma warto´sci cechy wi ˛eksze
czy te˙z mniejsze od warto´sci centralnej.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´zniki nat ˛e˙zenia
Wska´znik nat ˛e˙zenia
jest ilorazem liczebno´sci jednej
zbiorowo´sci do liczebno´sci innej zbiorowo´sci, logicznie
z ni ˛
a zwi ˛
azanej.
Typowym wska´znikiem nat ˛e˙zenia jest wska´znik g ˛esto´sci
zaludnienia, obliczany jako iloraz liczby mieszka ´nców do
powierzchni danego obszaru (na przykład, w Łodzi g ˛esto´s´c
zaludnienia w 2008 roku była na poziomie ok. 2548 osób
na kilometr kwadratowy).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´zniki nat ˛e˙zenia
Wska´znik nat ˛e˙zenia
jest ilorazem liczebno´sci jednej
zbiorowo´sci do liczebno´sci innej zbiorowo´sci, logicznie
z ni ˛
a zwi ˛
azanej.
Typowym wska´znikiem nat ˛e˙zenia jest wska´znik g ˛esto´sci
zaludnienia, obliczany jako iloraz liczby mieszka ´nców do
powierzchni danego obszaru (na przykład, w Łodzi g ˛esto´s´c
zaludnienia w 2008 roku była na poziomie ok. 2548 osób
na kilometr kwadratowy).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´zniki struktury
Załó˙zmy, ˙ze warto´sci badanej cechy w n-elementowej
zbiorowo´sci zostały pogrupowane w szereg rozdzielczy
(punktowy lub z przedziałami klasowymi).
Niech n
i
,
i = 1, 2, . . . , k b ˛ed ˛
a liczebno´sciami empirycznymi
poszczególnych klas szeregu.
Wska´znikiem struktury
w
i
nazywamy liczebno´s´c
wzgl ˛edn ˛
a i-tej klasy zdefiniowan ˛
a jako iloraz
w
i
=
n
i
n
,
przy czym
k
X
i=1
w
i
=
1.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´zniki struktury
Załó˙zmy, ˙ze warto´sci badanej cechy w n-elementowej
zbiorowo´sci zostały pogrupowane w szereg rozdzielczy
(punktowy lub z przedziałami klasowymi).
Niech n
i
,
i = 1, 2, . . . , k b ˛ed ˛
a liczebno´sciami empirycznymi
poszczególnych klas szeregu.
Wska´znikiem struktury
w
i
nazywamy liczebno´s´c
wzgl ˛edn ˛
a i-tej klasy zdefiniowan ˛
a jako iloraz
w
i
=
n
i
n
,
przy czym
k
X
i=1
w
i
=
1.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´zniki struktury
Załó˙zmy, ˙ze warto´sci badanej cechy w n-elementowej
zbiorowo´sci zostały pogrupowane w szereg rozdzielczy
(punktowy lub z przedziałami klasowymi).
Niech n
i
,
i = 1, 2, . . . , k b ˛ed ˛
a liczebno´sciami empirycznymi
poszczególnych klas szeregu.
Wska´znikiem struktury
w
i
nazywamy liczebno´s´c
wzgl ˛edn ˛
a i-tej klasy zdefiniowan ˛
a jako iloraz
w
i
=
n
i
n
,
przy czym
k
X
i=1
w
i
=
1.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´znik podobie ´
nstwa struktur
Wska´zniki struktury mo˙zna wykorzysta´c do oceny
podobie ´nstwa struktur zbiorowo´sci ze wzgl ˛edu na wybran ˛
a
cech ˛e.
Załó˙zmy, ˙ze warto´sci cechy w dwóch zbiorowo´sciach
pogrupowano w szeregi rozdzielcze o jednakowych
klasach. Niech w
1i
oraz w
2i
oznaczaj ˛
a wska´zniki struktury
dla i-tej klasy w obu szeregach.
Wówczas
wska´znik w
p
podobie ´
nstwa struktur
dla obu
zbiorowo´sci obliczamy ze wzoru
w
p
=
k
X
i=1
min(w
1i
,
w
2i
).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´znik podobie ´
nstwa struktur
Wska´zniki struktury mo˙zna wykorzysta´c do oceny
podobie ´nstwa struktur zbiorowo´sci ze wzgl ˛edu na wybran ˛
a
cech ˛e.
Załó˙zmy, ˙ze warto´sci cechy w dwóch zbiorowo´sciach
pogrupowano w szeregi rozdzielcze o jednakowych
klasach. Niech w
1i
oraz w
2i
oznaczaj ˛
a wska´zniki struktury
dla i-tej klasy w obu szeregach.
Wówczas
wska´znik w
p
podobie ´
nstwa struktur
dla obu
zbiorowo´sci obliczamy ze wzoru
w
p
=
k
X
i=1
min(w
1i
,
w
2i
).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´znik podobie ´
nstwa struktur
Wska´zniki struktury mo˙zna wykorzysta´c do oceny
podobie ´nstwa struktur zbiorowo´sci ze wzgl ˛edu na wybran ˛
a
cech ˛e.
Załó˙zmy, ˙ze warto´sci cechy w dwóch zbiorowo´sciach
pogrupowano w szeregi rozdzielcze o jednakowych
klasach. Niech w
1i
oraz w
2i
oznaczaj ˛
a wska´zniki struktury
dla i-tej klasy w obu szeregach.
Wówczas
wska´znik w
p
podobie ´
nstwa struktur
dla obu
zbiorowo´sci obliczamy ze wzoru
w
p
=
k
X
i=1
min(w
1i
,
w
2i
).
Agnieszka Rossa
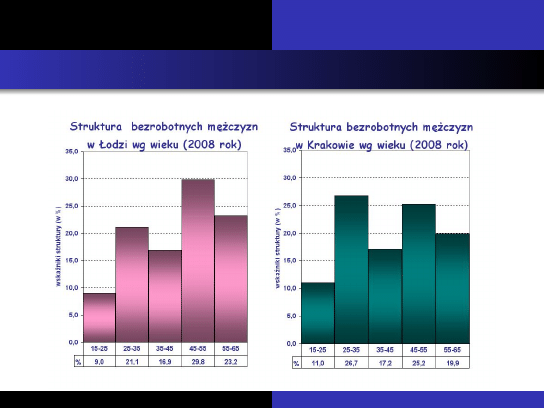
Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Wska´znik podobie ´
nstwa struktur
W tym przykładzie jest wysoki: w
p
=
9 + 21, 1 + 16, 9 + 25, 2 + 19, 9 = 92, 1%
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Obserwujemy zatem du˙ze podobie ´nstwo struktur wieku
bezrobotnych w obu miastach.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział
Miary ´srednie
dzielimy na:
1.
Miary ´srednie klasyczne.
S ˛
a to miary obliczane dla cechy
ilo´sciowej na podstawie jej warto´sci odnotowanych dla
wszystkich jednostek zbiorowo´sci. Do miar ´srednich
zaliczamy:
a.
´srednia arytmetyczna (oznaczana jako ¯
x ),
b.
´srednia harmoniczna (¯
x
h
) stosowana głównie w odniesieniu
do cech stosunkowych (np. wydajno´s´c, pr ˛edko´s´c itp.),
c.
´srednia geometryczna (G) stosowana np. w odniesieniu do
wska´zników dynamiki (b ˛edzie przedstawiona przy okazji
analizy dynamiki zjawisk).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział
Miary ´srednie
dzielimy na:
1.
Miary ´srednie klasyczne.
S ˛
a to miary obliczane dla cechy
ilo´sciowej na podstawie jej warto´sci odnotowanych dla
wszystkich jednostek zbiorowo´sci. Do miar ´srednich
zaliczamy:
a.
´srednia arytmetyczna (oznaczana jako ¯
x ),
b.
´srednia harmoniczna (¯
x
h
) stosowana głównie w odniesieniu
do cech stosunkowych (np. wydajno´s´c, pr ˛edko´s´c itp.),
c.
´srednia geometryczna (G) stosowana np. w odniesieniu do
wska´zników dynamiki (b ˛edzie przedstawiona przy okazji
analizy dynamiki zjawisk).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział
Miary ´srednie
dzielimy na:
1.
Miary ´srednie klasyczne.
S ˛
a to miary obliczane dla cechy
ilo´sciowej na podstawie jej warto´sci odnotowanych dla
wszystkich jednostek zbiorowo´sci. Do miar ´srednich
zaliczamy:
a.
´srednia arytmetyczna (oznaczana jako ¯
x ),
b.
´srednia harmoniczna (¯
x
h
) stosowana głównie w odniesieniu
do cech stosunkowych (np. wydajno´s´c, pr ˛edko´s´c itp.),
c.
´srednia geometryczna (G) stosowana np. w odniesieniu do
wska´zników dynamiki (b ˛edzie przedstawiona przy okazji
analizy dynamiki zjawisk).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział
Miary ´srednie
dzielimy na:
1.
Miary ´srednie klasyczne.
S ˛
a to miary obliczane dla cechy
ilo´sciowej na podstawie jej warto´sci odnotowanych dla
wszystkich jednostek zbiorowo´sci. Do miar ´srednich
zaliczamy:
a.
´srednia arytmetyczna (oznaczana jako ¯
x ),
b.
´srednia harmoniczna (¯
x
h
) stosowana głównie w odniesieniu
do cech stosunkowych (np. wydajno´s´c, pr ˛edko´s´c itp.),
c.
´srednia geometryczna (G) stosowana np. w odniesieniu do
wska´zników dynamiki (b ˛edzie przedstawiona przy okazji
analizy dynamiki zjawisk).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział
Miary ´srednie
dzielimy na:
1.
Miary ´srednie klasyczne.
S ˛
a to miary obliczane dla cechy
ilo´sciowej na podstawie jej warto´sci odnotowanych dla
wszystkich jednostek zbiorowo´sci. Do miar ´srednich
zaliczamy:
a.
´srednia arytmetyczna (oznaczana jako ¯
x ),
b.
´srednia harmoniczna (¯
x
h
) stosowana głównie w odniesieniu
do cech stosunkowych (np. wydajno´s´c, pr ˛edko´s´c itp.),
c.
´srednia geometryczna (G) stosowana np. w odniesieniu do
wska´zników dynamiki (b ˛edzie przedstawiona przy okazji
analizy dynamiki zjawisk).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział – c.d.
2.
Miary ´srednie pozycyjne.
Nazwa tych miar pochodzi
st ˛
ad, i˙z s ˛
a obliczane na podstawie warto´sci cechy tylko
tych jednostek, które zajmuj ˛
a okre´slon ˛
a pozycj ˛e w
uporz ˛
adkowanym szeregu lub które mog ˛
a by´c uznane za
szczególnie charakterystyczne dla danej zbiorowo´sci.
Do tej grupy miar zaliczamy:
a.
warto´s´c modaln ˛
a inaczej nazywana dominant ˛
a (Do),
b.
kwartyle, w tym: kwartyl pierwszy (Q
1
), kwartyl drugi (Q
2
),
kwartyl trzeci (Q
3
); szczególne znaczenie ma kwartyl drugi
zwany tak˙ze median ˛
a lub warto´sci ˛
a ´srodkow ˛
a i oznaczany
symbolem Me.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział – c.d.
2.
Miary ´srednie pozycyjne.
Nazwa tych miar pochodzi
st ˛
ad, i˙z s ˛
a obliczane na podstawie warto´sci cechy tylko
tych jednostek, które zajmuj ˛
a okre´slon ˛
a pozycj ˛e w
uporz ˛
adkowanym szeregu lub które mog ˛
a by´c uznane za
szczególnie charakterystyczne dla danej zbiorowo´sci.
Do tej grupy miar zaliczamy:
a.
warto´s´c modaln ˛
a inaczej nazywana dominant ˛
a (Do),
b.
kwartyle, w tym: kwartyl pierwszy (Q
1
), kwartyl drugi (Q
2
),
kwartyl trzeci (Q
3
); szczególne znaczenie ma kwartyl drugi
zwany tak˙ze median ˛
a lub warto´sci ˛
a ´srodkow ˛
a i oznaczany
symbolem Me.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Miary ´srednie
Podział – c.d.
2.
Miary ´srednie pozycyjne.
Nazwa tych miar pochodzi
st ˛
ad, i˙z s ˛
a obliczane na podstawie warto´sci cechy tylko
tych jednostek, które zajmuj ˛
a okre´slon ˛
a pozycj ˛e w
uporz ˛
adkowanym szeregu lub które mog ˛
a by´c uznane za
szczególnie charakterystyczne dla danej zbiorowo´sci.
Do tej grupy miar zaliczamy:
a.
warto´s´c modaln ˛
a inaczej nazywana dominant ˛
a (Do),
b.
kwartyle, w tym: kwartyl pierwszy (Q
1
), kwartyl drugi (Q
2
),
kwartyl trzeci (Q
3
); szczególne znaczenie ma kwartyl drugi
zwany tak˙ze median ˛
a lub warto´sci ˛
a ´srodkow ˛
a i oznaczany
symbolem Me.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna
´
Srednia arytmetyczna
jest sum ˛
a wszystkich warto´sci
badanej cechy, podzielon ˛
a przez ich liczb ˛e.
Przykładem mo˙ze by´c ´srednia ocen w indeksie (ka˙zdy
student z pewno´sci ˛
a j ˛
a obliczał).
Dla zapisu formalnego wzoru na ´sredni ˛
a arytmetyczn ˛
a
przyjmijmy nast ˛epuj ˛
ace oznaczenia. Niech x
1
,
x
2
, . . . ,
x
n
oznaczaj ˛
a kolejne warto´sci badanej cechy (np. kolejne
oceny w indeksie). Wówczas ´sredni ˛
a arytmetyczn ˛
a
zapiszemy wzorem:
¯
x =
x
1
+
x
2
+...+
x
n
n
lub krócej:
¯
x =
1
n
P
n
i=1
x
i
Przedstawiona ´sredni ˛
a, zwana jest ´sredni ˛
a arytmetyczn ˛
a
prost ˛
a, poniewa˙z oblicza si ˛e j ˛
a na podstawie szeregów
szczegółowych prostych.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna
´
Srednia arytmetyczna
jest sum ˛
a wszystkich warto´sci
badanej cechy, podzielon ˛
a przez ich liczb ˛e.
Przykładem mo˙ze by´c ´srednia ocen w indeksie (ka˙zdy
student z pewno´sci ˛
a j ˛
a obliczał).
Dla zapisu formalnego wzoru na ´sredni ˛
a arytmetyczn ˛
a
przyjmijmy nast ˛epuj ˛
ace oznaczenia. Niech x
1
,
x
2
, . . . ,
x
n
oznaczaj ˛
a kolejne warto´sci badanej cechy (np. kolejne
oceny w indeksie). Wówczas ´sredni ˛
a arytmetyczn ˛
a
zapiszemy wzorem:
¯
x =
x
1
+
x
2
+...+
x
n
n
lub krócej:
¯
x =
1
n
P
n
i=1
x
i
Przedstawiona ´sredni ˛
a, zwana jest ´sredni ˛
a arytmetyczn ˛
a
prost ˛
a, poniewa˙z oblicza si ˛e j ˛
a na podstawie szeregów
szczegółowych prostych.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna
´
Srednia arytmetyczna
jest sum ˛
a wszystkich warto´sci
badanej cechy, podzielon ˛
a przez ich liczb ˛e.
Przykładem mo˙ze by´c ´srednia ocen w indeksie (ka˙zdy
student z pewno´sci ˛
a j ˛
a obliczał).
Dla zapisu formalnego wzoru na ´sredni ˛
a arytmetyczn ˛
a
przyjmijmy nast ˛epuj ˛
ace oznaczenia. Niech x
1
,
x
2
, . . . ,
x
n
oznaczaj ˛
a kolejne warto´sci badanej cechy (np. kolejne
oceny w indeksie). Wówczas ´sredni ˛
a arytmetyczn ˛
a
zapiszemy wzorem:
¯
x =
x
1
+
x
2
+...+
x
n
n
lub krócej:
¯
x =
1
n
P
n
i=1
x
i
Przedstawiona ´sredni ˛
a, zwana jest ´sredni ˛
a arytmetyczn ˛
a
prost ˛
a, poniewa˙z oblicza si ˛e j ˛
a na podstawie szeregów
szczegółowych prostych.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna
´
Srednia arytmetyczna
jest sum ˛
a wszystkich warto´sci
badanej cechy, podzielon ˛
a przez ich liczb ˛e.
Przykładem mo˙ze by´c ´srednia ocen w indeksie (ka˙zdy
student z pewno´sci ˛
a j ˛
a obliczał).
Dla zapisu formalnego wzoru na ´sredni ˛
a arytmetyczn ˛
a
przyjmijmy nast ˛epuj ˛
ace oznaczenia. Niech x
1
,
x
2
, . . . ,
x
n
oznaczaj ˛
a kolejne warto´sci badanej cechy (np. kolejne
oceny w indeksie). Wówczas ´sredni ˛
a arytmetyczn ˛
a
zapiszemy wzorem:
¯
x =
x
1
+
x
2
+...+
x
n
n
lub krócej:
¯
x =
1
n
P
n
i=1
x
i
Przedstawiona ´sredni ˛
a, zwana jest ´sredni ˛
a arytmetyczn ˛
a
prost ˛
a, poniewa˙z oblicza si ˛e j ˛
a na podstawie szeregów
szczegółowych prostych.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – c.d.
W przypadku szeregów rozdzielczych korzystamy z
formuł
wa˙zonych
, w których rol ˛e wag pełni ˛
a liczebno´sci n
i
:
¯
x =
1
n
P
k
i=1
x
i
n
i
,
dla szeregu punktowego,
1
n
P
k
i=1
˙x
i
n
i
,
dla szeregu z przedziałami
klasowymi,
gdzie ˙x
i
dla i = 1, 2, . . . , k oznaczaj ˛
a ´srodki przedziałów
klasowych, natomiast k jest liczb ˛
a wierszy szeregu
rozdzielczego.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – wa˙zona ´srednia ze ´srednich
Formuł ˛e
´sredniej wa˙zonej
stosujemy tak˙ze w przypadku
obliczania ´sredniej ze ´srednich.
Przykład 1.
Załó˙zmy, ˙ze mamy trzy zbiory danych A, B, C:
A = {4, 6, 5} ,
B = {7, 9} ,
C = {5, 4, 5, 3, 3}
Mo˙zna sprawdzi´c, ˙ze ´srednie arytmetyczne wyznaczone z
danych ze zbiorów A, B, C równe s ˛
a odpowiednio: 5, 8, 4.
Pytanie:
Ile wynosi ´srednia arytmetyczna dla danych z
poł ˛
aczonych zbiorów?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – wa˙zona ´srednia ze ´srednich
Formuł ˛e
´sredniej wa˙zonej
stosujemy tak˙ze w przypadku
obliczania ´sredniej ze ´srednich.
Przykład 1.
Załó˙zmy, ˙ze mamy trzy zbiory danych A, B, C:
A = {4, 6, 5} ,
B = {7, 9} ,
C = {5, 4, 5, 3, 3}
Mo˙zna sprawdzi´c, ˙ze ´srednie arytmetyczne wyznaczone z
danych ze zbiorów A, B, C równe s ˛
a odpowiednio: 5, 8, 4.
Pytanie:
Ile wynosi ´srednia arytmetyczna dla danych z
poł ˛
aczonych zbiorów?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – wa˙zona ´srednia ze ´srednich
Formuł ˛e
´sredniej wa˙zonej
stosujemy tak˙ze w przypadku
obliczania ´sredniej ze ´srednich.
Przykład 1.
Załó˙zmy, ˙ze mamy trzy zbiory danych A, B, C:
A = {4, 6, 5} ,
B = {7, 9} ,
C = {5, 4, 5, 3, 3}
Mo˙zna sprawdzi´c, ˙ze ´srednie arytmetyczne wyznaczone z
danych ze zbiorów A, B, C równe s ˛
a odpowiednio: 5, 8, 4.
Pytanie:
Ile wynosi ´srednia arytmetyczna dla danych z
poł ˛
aczonych zbiorów?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – wa˙zona ´srednia ze ´srednich
Rozwi ˛
azanie:
Pierwszy sposób polega na poł ˛
aczeniu danych ze zbiorów
A, B, C i wyznaczeniu z nich ´sredniej arytmetycznej, czyli
4+6+5+7+9+5+4+5+3+3
10
=
5, 1.
Drugi sposób polega na wykorzystaniu ´srednich
cz ˛
astkowych obliczonych dla zbiorów A, B, C. Bł ˛edem
byłoby jednak obliczenie zwykłej ´sredniej ze ´srednich, tj.
5+8+4
3
. Otrzymany wynik (ok. 5, 7) nie zgadza si ˛e z
uzyskanym wy˙zej.
Poprawne rozwi ˛
azanie wymaga zastosowania formuły
´sredniej wa˙zonej, w której wagami s ˛
a liczebno´sci zbiorów:
5 · 3 + 8 · 2 + 4 · 5
10
=
15 + 16 + 20
10
=
5, 1.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – wa˙zona ´srednia ze ´srednich
Rozwi ˛
azanie:
Pierwszy sposób polega na poł ˛
aczeniu danych ze zbiorów
A, B, C i wyznaczeniu z nich ´sredniej arytmetycznej, czyli
4+6+5+7+9+5+4+5+3+3
10
=
5, 1.
Drugi sposób polega na wykorzystaniu ´srednich
cz ˛
astkowych obliczonych dla zbiorów A, B, C. Bł ˛edem
byłoby jednak obliczenie zwykłej ´sredniej ze ´srednich, tj.
5+8+4
3
. Otrzymany wynik (ok. 5, 7) nie zgadza si ˛e z
uzyskanym wy˙zej.
Poprawne rozwi ˛
azanie wymaga zastosowania formuły
´sredniej wa˙zonej, w której wagami s ˛
a liczebno´sci zbiorów:
5 · 3 + 8 · 2 + 4 · 5
10
=
15 + 16 + 20
10
=
5, 1.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia arytmetyczna – wa˙zona ´srednia ze ´srednich
Rozwi ˛
azanie:
Pierwszy sposób polega na poł ˛
aczeniu danych ze zbiorów
A, B, C i wyznaczeniu z nich ´sredniej arytmetycznej, czyli
4+6+5+7+9+5+4+5+3+3
10
=
5, 1.
Drugi sposób polega na wykorzystaniu ´srednich
cz ˛
astkowych obliczonych dla zbiorów A, B, C. Bł ˛edem
byłoby jednak obliczenie zwykłej ´sredniej ze ´srednich, tj.
5+8+4
3
. Otrzymany wynik (ok. 5, 7) nie zgadza si ˛e z
uzyskanym wy˙zej.
Poprawne rozwi ˛
azanie wymaga zastosowania formuły
´sredniej wa˙zonej, w której wagami s ˛
a liczebno´sci zbiorów:
5 · 3 + 8 · 2 + 4 · 5
10
=
15 + 16 + 20
10
=
5, 1.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej
1.
Spełnia relacj ˛e
x
min
< ¯
x < x
max
, gdzie x
min
, x
max
oznaczaj ˛
a
warto´s´c minimaln ˛
a i maksymaln ˛
a w zbiorze danych.
2.
Zachodz ˛
a nast ˛epuj ˛
ace równo´sci (wynikaj ˛
a z definicji):
-
dla szeregu szczegółowego
n
X
i=1
x
i
= ¯
x n,
-
dla szeregu rozdzielczego punktowego
n
X
i=1
x
i
n
i
= ¯
x
k
X
i=1
n
i
,
-
dla szeregu rozdzielczego z przedziałami klasowymi
n
X
i=1
˙x
i
n
i
= ¯
x
k
X
i=1
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej
1.
Spełnia relacj ˛e
x
min
< ¯
x < x
max
, gdzie x
min
, x
max
oznaczaj ˛
a
warto´s´c minimaln ˛
a i maksymaln ˛
a w zbiorze danych.
2.
Zachodz ˛
a nast ˛epuj ˛
ace równo´sci (wynikaj ˛
a z definicji):
-
dla szeregu szczegółowego
n
X
i=1
x
i
= ¯
x n,
-
dla szeregu rozdzielczego punktowego
n
X
i=1
x
i
n
i
= ¯
x
k
X
i=1
n
i
,
-
dla szeregu rozdzielczego z przedziałami klasowymi
n
X
i=1
˙x
i
n
i
= ¯
x
k
X
i=1
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej
1.
Spełnia relacj ˛e
x
min
< ¯
x < x
max
, gdzie x
min
, x
max
oznaczaj ˛
a
warto´s´c minimaln ˛
a i maksymaln ˛
a w zbiorze danych.
2.
Zachodz ˛
a nast ˛epuj ˛
ace równo´sci (wynikaj ˛
a z definicji):
-
dla szeregu szczegółowego
n
X
i=1
x
i
= ¯
x n,
-
dla szeregu rozdzielczego punktowego
n
X
i=1
x
i
n
i
= ¯
x
k
X
i=1
n
i
,
-
dla szeregu rozdzielczego z przedziałami klasowymi
n
X
i=1
˙x
i
n
i
= ¯
x
k
X
i=1
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej
1.
Spełnia relacj ˛e
x
min
< ¯
x < x
max
, gdzie x
min
, x
max
oznaczaj ˛
a
warto´s´c minimaln ˛
a i maksymaln ˛
a w zbiorze danych.
2.
Zachodz ˛
a nast ˛epuj ˛
ace równo´sci (wynikaj ˛
a z definicji):
-
dla szeregu szczegółowego
n
X
i=1
x
i
= ¯
x n,
-
dla szeregu rozdzielczego punktowego
n
X
i=1
x
i
n
i
= ¯
x
k
X
i=1
n
i
,
-
dla szeregu rozdzielczego z przedziałami klasowymi
n
X
i=1
˙x
i
n
i
= ¯
x
k
X
i=1
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej
1.
Spełnia relacj ˛e
x
min
< ¯
x < x
max
, gdzie x
min
, x
max
oznaczaj ˛
a
warto´s´c minimaln ˛
a i maksymaln ˛
a w zbiorze danych.
2.
Zachodz ˛
a nast ˛epuj ˛
ace równo´sci (wynikaj ˛
a z definicji):
-
dla szeregu szczegółowego
n
X
i=1
x
i
= ¯
x n,
-
dla szeregu rozdzielczego punktowego
n
X
i=1
x
i
n
i
= ¯
x
k
X
i=1
n
i
,
-
dla szeregu rozdzielczego z przedziałami klasowymi
n
X
i=1
˙x
i
n
i
= ¯
x
k
X
i=1
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
3.
Suma ochyle ´n poszczególnych warto´sci obserwowanej
cechy od jej ´sredniej arytmetycznej jest równa 0, czyli w
przypadku:
-
szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x ) = 0,
-
szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )n
i
=
0,
-
szeregu rozdzielczego z przedziałami klasowymi
k
X
i=1
( ˙
x
i
− ¯
x )n
i
=
0.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
3.
Suma ochyle ´n poszczególnych warto´sci obserwowanej
cechy od jej ´sredniej arytmetycznej jest równa 0, czyli w
przypadku:
-
szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x ) = 0,
-
szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )n
i
=
0,
-
szeregu rozdzielczego z przedziałami klasowymi
k
X
i=1
( ˙
x
i
− ¯
x )n
i
=
0.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
3.
Suma ochyle ´n poszczególnych warto´sci obserwowanej
cechy od jej ´sredniej arytmetycznej jest równa 0, czyli w
przypadku:
-
szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x ) = 0,
-
szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )n
i
=
0,
-
szeregu rozdzielczego z przedziałami klasowymi
k
X
i=1
( ˙
x
i
− ¯
x )n
i
=
0.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
3.
Suma ochyle ´n poszczególnych warto´sci obserwowanej
cechy od jej ´sredniej arytmetycznej jest równa 0, czyli w
przypadku:
-
szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x ) = 0,
-
szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )n
i
=
0,
-
szeregu rozdzielczego z przedziałami klasowymi
k
X
i=1
( ˙
x
i
− ¯
x )n
i
=
0.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
4.
Suma kwadratów ochyle ´n poszczególnych warto´sci cechy
od jej ´sredniej arytmetycznej jest minimalna, czyli dla
dowolnej stałej a spełnione s ˛
a nierówno´sci:
-
w przypadku szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x )
2
≤
n
X
i=1
(
x
i
− a)
2
,
-
w przypadku szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
(
x
i
− a)
2
n
i
,
-
w przypadku szeregu rozdzielczego z przedziałami kl.
k
X
i=1
( ˙
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
( ˙
x
i
− a)
2
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
4.
Suma kwadratów ochyle ´n poszczególnych warto´sci cechy
od jej ´sredniej arytmetycznej jest minimalna, czyli dla
dowolnej stałej a spełnione s ˛
a nierówno´sci:
-
w przypadku szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x )
2
≤
n
X
i=1
(
x
i
− a)
2
,
-
w przypadku szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
(
x
i
− a)
2
n
i
,
-
w przypadku szeregu rozdzielczego z przedziałami kl.
k
X
i=1
( ˙
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
( ˙
x
i
− a)
2
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
4.
Suma kwadratów ochyle ´n poszczególnych warto´sci cechy
od jej ´sredniej arytmetycznej jest minimalna, czyli dla
dowolnej stałej a spełnione s ˛
a nierówno´sci:
-
w przypadku szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x )
2
≤
n
X
i=1
(
x
i
− a)
2
,
-
w przypadku szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
(
x
i
− a)
2
n
i
,
-
w przypadku szeregu rozdzielczego z przedziałami kl.
k
X
i=1
( ˙
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
( ˙
x
i
− a)
2
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie – Własno ´sci ´sredniej arytmetycznej – c.d.
4.
Suma kwadratów ochyle ´n poszczególnych warto´sci cechy
od jej ´sredniej arytmetycznej jest minimalna, czyli dla
dowolnej stałej a spełnione s ˛
a nierówno´sci:
-
w przypadku szeregu szczegółowego
n
X
i=1
(
x
i
− ¯
x )
2
≤
n
X
i=1
(
x
i
− a)
2
,
-
w przypadku szeregu rozdzielczego punktowego
k
X
i=1
(
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
(
x
i
− a)
2
n
i
,
-
w przypadku szeregu rozdzielczego z przedziałami kl.
k
X
i=1
( ˙
x
i
− ¯
x )
2
n
i
≤
k
X
i=1
( ˙
x
i
− a)
2
n
i
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Własno ´sci ´sredniej arytmetycznej – c.d.
5.
´
Sredniej arytmetycznej nie mo˙zna obliczy´c dla szerego
rozdzielczego z otwartymi przedziałami klasowymi.
Je´sli otwarte przedziały klasowe maj ˛
a niewielkie liczebno´sci (do 5% ogólnej liczebno´sci), to przed
obliczeniem ´sredniej arytmetycznej mo˙zna je domkn ˛
a´c.
6.
´
Srednia arytmetyczna jest
”wra˙zliwa” na nietypowe
warto ´sci
cechy (tj. znacznie ró˙zni ˛
ace si ˛e od pozostałych
warto´sci w zbiorze); wielko´sci odstaj ˛
ace mog ˛
a
zniekształci´c (zawy˙zy´c lub zani˙zy´c) warto´s´c ´sredniej
arytmetycznej.
Istniej ˛
a jednak pewne sposoby radzenia sobie z tak ˛
a sytuacj ˛
a. Je´sli mamy podstawy przypuszcza´c, ˙ze
warto´s´c odstaj ˛
aca pojawiła si ˛e przypadkowo, wówczas przed obliczeniem ´sredniej usuwamy t ˛e warto´s´c ze
zbioru danych. Drugim sposobem jest przekształcenie wszystkich danych np. za pomoc ˛
a funkcji
logarytmicznej, dzi ˛eki czemu warto´sci w zbiorze po transformacji b ˛ed ˛
a do siebie bardziej zbli˙zone.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
Własno ´sci ´sredniej arytmetycznej – c.d.
5.
´
Sredniej arytmetycznej nie mo˙zna obliczy´c dla szerego
rozdzielczego z otwartymi przedziałami klasowymi.
Je´sli otwarte przedziały klasowe maj ˛
a niewielkie liczebno´sci (do 5% ogólnej liczebno´sci), to przed
obliczeniem ´sredniej arytmetycznej mo˙zna je domkn ˛
a´c.
6.
´
Srednia arytmetyczna jest
”wra˙zliwa” na nietypowe
warto ´sci
cechy (tj. znacznie ró˙zni ˛
ace si ˛e od pozostałych
warto´sci w zbiorze); wielko´sci odstaj ˛
ace mog ˛
a
zniekształci´c (zawy˙zy´c lub zani˙zy´c) warto´s´c ´sredniej
arytmetycznej.
Istniej ˛
a jednak pewne sposoby radzenia sobie z tak ˛
a sytuacj ˛
a. Je´sli mamy podstawy przypuszcza´c, ˙ze
warto´s´c odstaj ˛
aca pojawiła si ˛e przypadkowo, wówczas przed obliczeniem ´sredniej usuwamy t ˛e warto´s´c ze
zbioru danych. Drugim sposobem jest przekształcenie wszystkich danych np. za pomoc ˛
a funkcji
logarytmicznej, dzi ˛eki czemu warto´sci w zbiorze po transformacji b ˛ed ˛
a do siebie bardziej zbli˙zone.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna
´
Srednia harmoniczna
jest odwrotno´sci ˛
a ´sredniej
arytmetycznej z odwrotno´sci zaobserwowanych warto´sci
x
1
,
x
2
, . . . ,
x
n
cechy ilo´sciowej w badanej zbiorowo´sci.
Formalnie zapisujemy j ˛
a wzorem:
¯
x
h
=
n
P
n
i=1
1
x
i
Przedstawiona formuła odnosi si ˛e do szeregów prostych.
W przypadku szeregów rozdzielczych korzystamy z formuł
wa˙zonych:
¯
x
h
=
n
P
k
i=1
1
xi
n
i
,
dla szeregu punktowego,
n
P
k
i=1
1
˙
xi
n
i
,
dla szeregu z przedziałami klasowymi.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna
´
Srednia harmoniczna
jest odwrotno´sci ˛
a ´sredniej
arytmetycznej z odwrotno´sci zaobserwowanych warto´sci
x
1
,
x
2
, . . . ,
x
n
cechy ilo´sciowej w badanej zbiorowo´sci.
Formalnie zapisujemy j ˛
a wzorem:
¯
x
h
=
n
P
n
i=1
1
x
i
Przedstawiona formuła odnosi si ˛e do szeregów prostych.
W przypadku szeregów rozdzielczych korzystamy z formuł
wa˙zonych:
¯
x
h
=
n
P
k
i=1
1
xi
n
i
,
dla szeregu punktowego,
n
P
k
i=1
1
˙
xi
n
i
,
dla szeregu z przedziałami klasowymi.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna
´
Srednia harmoniczna
jest odwrotno´sci ˛
a ´sredniej
arytmetycznej z odwrotno´sci zaobserwowanych warto´sci
x
1
,
x
2
, . . . ,
x
n
cechy ilo´sciowej w badanej zbiorowo´sci.
Formalnie zapisujemy j ˛
a wzorem:
¯
x
h
=
n
P
n
i=1
1
x
i
Przedstawiona formuła odnosi si ˛e do szeregów prostych.
W przypadku szeregów rozdzielczych korzystamy z formuł
wa˙zonych:
¯
x
h
=
n
P
k
i=1
1
xi
n
i
,
dla szeregu punktowego,
n
P
k
i=1
1
˙
xi
n
i
,
dla szeregu z przedziałami klasowymi.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady
´
Srednie harmoniczne stosuje si ˛e do obliczania poziomu
´sredniego dla cechy o charakterze stosunkowym, takich jak:
wydajno´s´c, pr ˛edko´s´c, siła nabywcza pieni ˛
adza itp.
Przykład 2.
Długo´s´c linii kolejowej ł ˛
acz ˛
acej miasta A i B jest równa 100
km. Poci ˛
ag pospieszny jedzie z miasta A do miasta B
z pr ˛edko´sci ˛
a 100 km/h, a poci ˛
ag osobowy – z pr ˛edko´sci ˛
a
50 km/h.
Pytanie:
Jaka jest ´srednia pr ˛edko´s´c obu poci ˛
agów na tej
trasie?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady
´
Srednie harmoniczne stosuje si ˛e do obliczania poziomu
´sredniego dla cechy o charakterze stosunkowym, takich jak:
wydajno´s´c, pr ˛edko´s´c, siła nabywcza pieni ˛
adza itp.
Przykład 2.
Długo´s´c linii kolejowej ł ˛
acz ˛
acej miasta A i B jest równa 100
km. Poci ˛
ag pospieszny jedzie z miasta A do miasta B
z pr ˛edko´sci ˛
a 100 km/h, a poci ˛
ag osobowy – z pr ˛edko´sci ˛
a
50 km/h.
Pytanie:
Jaka jest ´srednia pr ˛edko´s´c obu poci ˛
agów na tej
trasie?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady
´
Srednie harmoniczne stosuje si ˛e do obliczania poziomu
´sredniego dla cechy o charakterze stosunkowym, takich jak:
wydajno´s´c, pr ˛edko´s´c, siła nabywcza pieni ˛
adza itp.
Przykład 2.
Długo´s´c linii kolejowej ł ˛
acz ˛
acej miasta A i B jest równa 100
km. Poci ˛
ag pospieszny jedzie z miasta A do miasta B
z pr ˛edko´sci ˛
a 100 km/h, a poci ˛
ag osobowy – z pr ˛edko´sci ˛
a
50 km/h.
Pytanie:
Jaka jest ´srednia pr ˛edko´s´c obu poci ˛
agów na tej
trasie?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Nasuwa si ˛e pozornie oczywista odpowied´z, ˙ze ´srednia
pr ˛edko´s´c obu poci ˛
agów jest równa
100+50
2
=
75 km/h.
Przygl ˛
adaj ˛
ac si ˛e jednak bli˙zej, zauwa˙zymy, ˙ze obydwa
poci ˛
agi pokonuj ˛
a ł ˛
acznie tras ˛e 200 km w czasie 3 godzin,
a zatem (poprawna) ´srednia pr ˛edko´s´c wynosi
200
3
≈ 66, 7
km/h.
Ten sam wynik uzyskamy, obliczaj ˛
ac ´sredni ˛
a harmoniczn ˛
a
z obu pr ˛edko´sci. Mamy bowiem
¯
x
h
=
2
1
100
+
1
50
=
2
1
100
+
2
100
=
2 · 100
3
≈ 66, 7 km/h.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Nasuwa si ˛e pozornie oczywista odpowied´z, ˙ze ´srednia
pr ˛edko´s´c obu poci ˛
agów jest równa
100+50
2
=
75 km/h.
Przygl ˛
adaj ˛
ac si ˛e jednak bli˙zej, zauwa˙zymy, ˙ze obydwa
poci ˛
agi pokonuj ˛
a ł ˛
acznie tras ˛e 200 km w czasie 3 godzin,
a zatem (poprawna) ´srednia pr ˛edko´s´c wynosi
200
3
≈ 66, 7
km/h.
Ten sam wynik uzyskamy, obliczaj ˛
ac ´sredni ˛
a harmoniczn ˛
a
z obu pr ˛edko´sci. Mamy bowiem
¯
x
h
=
2
1
100
+
1
50
=
2
1
100
+
2
100
=
2 · 100
3
≈ 66, 7 km/h.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Nasuwa si ˛e pozornie oczywista odpowied´z, ˙ze ´srednia
pr ˛edko´s´c obu poci ˛
agów jest równa
100+50
2
=
75 km/h.
Przygl ˛
adaj ˛
ac si ˛e jednak bli˙zej, zauwa˙zymy, ˙ze obydwa
poci ˛
agi pokonuj ˛
a ł ˛
acznie tras ˛e 200 km w czasie 3 godzin,
a zatem (poprawna) ´srednia pr ˛edko´s´c wynosi
200
3
≈ 66, 7
km/h.
Ten sam wynik uzyskamy, obliczaj ˛
ac ´sredni ˛
a harmoniczn ˛
a
z obu pr ˛edko´sci. Mamy bowiem
¯
x
h
=
2
1
100
+
1
50
=
2
1
100
+
2
100
=
2 · 100
3
≈ 66, 7 km/h.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Przykład 3.
W pewnym banku przy okienkach kasowych zatrudnionych
jest 10 pracowników.
Zmierzono czas obsługi klientów w ci ˛
agu wybranego
8-godzinnego dnia pracy.
Pi ˛eciu pracowników potrzebowało na realizacj ˛e transakcji
zleconych przez pojedynczego klienta po 20 min, trzech
pracowników – 15 min, a dwóch pracowników – 10 min.
Pytanie:
Jaki jest ´sredni czas obsługi klientów banku
w badanym dniu pracy?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Przykład 3.
W pewnym banku przy okienkach kasowych zatrudnionych
jest 10 pracowników.
Zmierzono czas obsługi klientów w ci ˛
agu wybranego
8-godzinnego dnia pracy.
Pi ˛eciu pracowników potrzebowało na realizacj ˛e transakcji
zleconych przez pojedynczego klienta po 20 min, trzech
pracowników – 15 min, a dwóch pracowników – 10 min.
Pytanie:
Jaki jest ´sredni czas obsługi klientów banku
w badanym dniu pracy?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Przykład 3.
W pewnym banku przy okienkach kasowych zatrudnionych
jest 10 pracowników.
Zmierzono czas obsługi klientów w ci ˛
agu wybranego
8-godzinnego dnia pracy.
Pi ˛eciu pracowników potrzebowało na realizacj ˛e transakcji
zleconych przez pojedynczego klienta po 20 min, trzech
pracowników – 15 min, a dwóch pracowników – 10 min.
Pytanie:
Jaki jest ´sredni czas obsługi klientów banku
w badanym dniu pracy?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary ´srednie
´
Srednia harmoniczna – przykłady c.d.
Przykład 3.
W pewnym banku przy okienkach kasowych zatrudnionych
jest 10 pracowników.
Zmierzono czas obsługi klientów w ci ˛
agu wybranego
8-godzinnego dnia pracy.
Pi ˛eciu pracowników potrzebowało na realizacj ˛e transakcji
zleconych przez pojedynczego klienta po 20 min, trzech
pracowników – 15 min, a dwóch pracowników – 10 min.
Pytanie:
Jaki jest ´sredni czas obsługi klientów banku
w badanym dniu pracy?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
´
Srednia harmoniczna – przykłady c.d.
Ze wzoru na wa˙zon ˛
a ´sredni ˛
a arytmetyczn ˛
a otrzymamy
w tym przypadku bł ˛edny wynik
20·5+15·3+10·2
10
=
16, 5 min.
Zauwa˙zymy, ˙ze pracownicy potrzebuj ˛
acy 20, 15 lub 10 min
na wykonanie operacji zleconych przez klienta, w ci ˛
agu
8-godzinnego dnia pracy zrealizuj ˛
a zlecenia odpowiednio
24 · 5, 32 · 3 i 48 · 2 klientów, obsługuj ˛
ac ł ˛
acznie 312 osób,
przy czym czas przepracowany w tym dniu przez
wszystkich pracowników wyniesie 8 · 60 · 10 = 4800 min.
´
Sredni czas obsługi klienta przy okienku w danym dniu jest
wi ˛ec równy
4800
312
≈ 15, 38
min.
Taki sam wynik otrzymamy ze wzoru na ´sredni ˛
a
harmoniczn ˛
a wa˙zon ˛
a:
10
1
20
· 5 +
1
15
· 3 +
1
10
· 2
=
10
0, 25 + 0, 2 + 0, 2
≈ 15, 38 min.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
´
Srednia harmoniczna – przykłady c.d.
Ze wzoru na wa˙zon ˛
a ´sredni ˛
a arytmetyczn ˛
a otrzymamy
w tym przypadku bł ˛edny wynik
20·5+15·3+10·2
10
=
16, 5 min.
Zauwa˙zymy, ˙ze pracownicy potrzebuj ˛
acy 20, 15 lub 10 min
na wykonanie operacji zleconych przez klienta, w ci ˛
agu
8-godzinnego dnia pracy zrealizuj ˛
a zlecenia odpowiednio
24 · 5, 32 · 3 i 48 · 2 klientów, obsługuj ˛
ac ł ˛
acznie 312 osób,
przy czym czas przepracowany w tym dniu przez
wszystkich pracowników wyniesie 8 · 60 · 10 = 4800 min.
´
Sredni czas obsługi klienta przy okienku w danym dniu jest
wi ˛ec równy
4800
312
≈ 15, 38
min.
Taki sam wynik otrzymamy ze wzoru na ´sredni ˛
a
harmoniczn ˛
a wa˙zon ˛
a:
10
1
20
· 5 +
1
15
· 3 +
1
10
· 2
=
10
0, 25 + 0, 2 + 0, 2
≈ 15, 38 min.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
´
Srednia harmoniczna – przykłady c.d.
Ze wzoru na wa˙zon ˛
a ´sredni ˛
a arytmetyczn ˛
a otrzymamy
w tym przypadku bł ˛edny wynik
20·5+15·3+10·2
10
=
16, 5 min.
Zauwa˙zymy, ˙ze pracownicy potrzebuj ˛
acy 20, 15 lub 10 min
na wykonanie operacji zleconych przez klienta, w ci ˛
agu
8-godzinnego dnia pracy zrealizuj ˛
a zlecenia odpowiednio
24 · 5, 32 · 3 i 48 · 2 klientów, obsługuj ˛
ac ł ˛
acznie 312 osób,
przy czym czas przepracowany w tym dniu przez
wszystkich pracowników wyniesie 8 · 60 · 10 = 4800 min.
´
Sredni czas obsługi klienta przy okienku w danym dniu jest
wi ˛ec równy
4800
312
≈ 15, 38
min.
Taki sam wynik otrzymamy ze wzoru na ´sredni ˛
a
harmoniczn ˛
a wa˙zon ˛
a:
10
1
20
· 5 +
1
15
· 3 +
1
10
· 2
=
10
0, 25 + 0, 2 + 0, 2
≈ 15, 38 min.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Dominanta (warto ´s ´c modalna)
Dominant ˛
a Do
nazywamy t ˛e warto´s´c cechy, która w
badanej zbiorowo´sci wyst ˛epuje najcz ˛e´sciej.
W szeregach szczegółowych lub rozdzielczych
punktowych dominant ˛e mo˙zna wskaza´c, odnajduj ˛
ac
warto´s´c najliczniej reprezentowan ˛
a przez jednostki
zbiorowo´sci.
W szeregach rozdzielczych z przedziałami klasowymi (a
wi ˛ec w przypadku cechy ilo´sciowej) mo˙zna okre´sli´c jedynie
przedział, w którym dominanta wyst ˛epuje. Jest to przedział
o najwi ˛ekszej liczebno´sci, oczywi´scie pod warunkiem, ˙ze
przedzial ten i przedziały bezpo´srednio s ˛
asiaduj ˛
ace maj ˛
a
tak ˛
a sam ˛
a rozpi ˛eto´s´c. Przedział taki nazywamy
przedziałem dominanty
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Dominanta (warto ´s ´c modalna)
Dominant ˛
a Do
nazywamy t ˛e warto´s´c cechy, która w
badanej zbiorowo´sci wyst ˛epuje najcz ˛e´sciej.
W szeregach szczegółowych lub rozdzielczych
punktowych dominant ˛e mo˙zna wskaza´c, odnajduj ˛
ac
warto´s´c najliczniej reprezentowan ˛
a przez jednostki
zbiorowo´sci.
W szeregach rozdzielczych z przedziałami klasowymi (a
wi ˛ec w przypadku cechy ilo´sciowej) mo˙zna okre´sli´c jedynie
przedział, w którym dominanta wyst ˛epuje. Jest to przedział
o najwi ˛ekszej liczebno´sci, oczywi´scie pod warunkiem, ˙ze
przedzial ten i przedziały bezpo´srednio s ˛
asiaduj ˛
ace maj ˛
a
tak ˛
a sam ˛
a rozpi ˛eto´s´c. Przedział taki nazywamy
przedziałem dominanty
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Dominanta (warto ´s ´c modalna)
Dominant ˛
a Do
nazywamy t ˛e warto´s´c cechy, która w
badanej zbiorowo´sci wyst ˛epuje najcz ˛e´sciej.
W szeregach szczegółowych lub rozdzielczych
punktowych dominant ˛e mo˙zna wskaza´c, odnajduj ˛
ac
warto´s´c najliczniej reprezentowan ˛
a przez jednostki
zbiorowo´sci.
W szeregach rozdzielczych z przedziałami klasowymi (a
wi ˛ec w przypadku cechy ilo´sciowej) mo˙zna okre´sli´c jedynie
przedział, w którym dominanta wyst ˛epuje. Jest to przedział
o najwi ˛ekszej liczebno´sci, oczywi´scie pod warunkiem, ˙ze
przedzial ten i przedziały bezpo´srednio s ˛
asiaduj ˛
ace maj ˛
a
tak ˛
a sam ˛
a rozpi ˛eto´s´c. Przedział taki nazywamy
przedziałem dominanty
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Dominanta (warto ´s ´c modalna) – c.d.
Przybli˙zon ˛
a warto´s´c dominanty w szeregu rozdzielczym
z przedziałami klasowymi wyznaczamy za pomoc ˛
a
nast ˛epuj ˛
acego wzoru interpolacyjnego
Do = x
s
+
h
s
n
s
− n
s−1
n
s
− n
s−1
+
n
s
− n
s+1
,
gdzie:
x
s
– pocz ˛
atek przedziału dominanty,
h
s
– rozpi ˛eto´s´c przedziału dominanty,
n
s
,
n
s−1
,
n
s+1
– liczebno´sci odpowiednio przedziału
dominanty, przedziału poprzedniego i nast ˛epnego.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Własno ´sci dominanty
1.
Charakteryzuje jednostki o typowym poziomie cechy, a
wi ˛ec nie wszystkie jednostki.
2.
W przeciwie ´nstwie do miar klasycznych dominant ˛e
mo˙zemy okre´sli´c tak˙ze dla cechy jako´sciowej.
W przypadku cechy ilo´sciowej wymieni´c mo˙zna dodatkowo
takie własno´sci dominanty, jak:
3.
W szeregu symetrycznym dominanta równa jest ´sredniej
arytmetycznej.
4.
Dominant ˛e mo˙zna wyznacza´c ze wzoru przybli˙zonego, gdy
przedział dominanty oraz przedziały poprzedni i nast ˛epny
maj ˛
a jednakow ˛
a rozpi ˛eto´s´c.
5.
Dominant ˛e mo˙zna wyznacza´c w szeregach rozdzielczych
z otwartymi przedziałami klasowymi (o ile przedziały te nie
s ˛
asiaduj ˛
a bezpo´srednio z przedziałem dominanty).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Własno ´sci dominanty
1.
Charakteryzuje jednostki o typowym poziomie cechy, a
wi ˛ec nie wszystkie jednostki.
2.
W przeciwie ´nstwie do miar klasycznych dominant ˛e
mo˙zemy okre´sli´c tak˙ze dla cechy jako´sciowej.
W przypadku cechy ilo´sciowej wymieni´c mo˙zna dodatkowo
takie własno´sci dominanty, jak:
3.
W szeregu symetrycznym dominanta równa jest ´sredniej
arytmetycznej.
4.
Dominant ˛e mo˙zna wyznacza´c ze wzoru przybli˙zonego, gdy
przedział dominanty oraz przedziały poprzedni i nast ˛epny
maj ˛
a jednakow ˛
a rozpi ˛eto´s´c.
5.
Dominant ˛e mo˙zna wyznacza´c w szeregach rozdzielczych
z otwartymi przedziałami klasowymi (o ile przedziały te nie
s ˛
asiaduj ˛
a bezpo´srednio z przedziałem dominanty).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Własno ´sci dominanty
1.
Charakteryzuje jednostki o typowym poziomie cechy, a
wi ˛ec nie wszystkie jednostki.
2.
W przeciwie ´nstwie do miar klasycznych dominant ˛e
mo˙zemy okre´sli´c tak˙ze dla cechy jako´sciowej.
W przypadku cechy ilo´sciowej wymieni´c mo˙zna dodatkowo
takie własno´sci dominanty, jak:
3.
W szeregu symetrycznym dominanta równa jest ´sredniej
arytmetycznej.
4.
Dominant ˛e mo˙zna wyznacza´c ze wzoru przybli˙zonego, gdy
przedział dominanty oraz przedziały poprzedni i nast ˛epny
maj ˛
a jednakow ˛
a rozpi ˛eto´s´c.
5.
Dominant ˛e mo˙zna wyznacza´c w szeregach rozdzielczych
z otwartymi przedziałami klasowymi (o ile przedziały te nie
s ˛
asiaduj ˛
a bezpo´srednio z przedziałem dominanty).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Własno ´sci dominanty
1.
Charakteryzuje jednostki o typowym poziomie cechy, a
wi ˛ec nie wszystkie jednostki.
2.
W przeciwie ´nstwie do miar klasycznych dominant ˛e
mo˙zemy okre´sli´c tak˙ze dla cechy jako´sciowej.
W przypadku cechy ilo´sciowej wymieni´c mo˙zna dodatkowo
takie własno´sci dominanty, jak:
3.
W szeregu symetrycznym dominanta równa jest ´sredniej
arytmetycznej.
4.
Dominant ˛e mo˙zna wyznacza´c ze wzoru przybli˙zonego, gdy
przedział dominanty oraz przedziały poprzedni i nast ˛epny
maj ˛
a jednakow ˛
a rozpi ˛eto´s´c.
5.
Dominant ˛e mo˙zna wyznacza´c w szeregach rozdzielczych
z otwartymi przedziałami klasowymi (o ile przedziały te nie
s ˛
asiaduj ˛
a bezpo´srednio z przedziałem dominanty).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Własno ´sci dominanty
1.
Charakteryzuje jednostki o typowym poziomie cechy, a
wi ˛ec nie wszystkie jednostki.
2.
W przeciwie ´nstwie do miar klasycznych dominant ˛e
mo˙zemy okre´sli´c tak˙ze dla cechy jako´sciowej.
W przypadku cechy ilo´sciowej wymieni´c mo˙zna dodatkowo
takie własno´sci dominanty, jak:
3.
W szeregu symetrycznym dominanta równa jest ´sredniej
arytmetycznej.
4.
Dominant ˛e mo˙zna wyznacza´c ze wzoru przybli˙zonego, gdy
przedział dominanty oraz przedziały poprzedni i nast ˛epny
maj ˛
a jednakow ˛
a rozpi ˛eto´s´c.
5.
Dominant ˛e mo˙zna wyznacza´c w szeregach rozdzielczych
z otwartymi przedziałami klasowymi (o ile przedziały te nie
s ˛
asiaduj ˛
a bezpo´srednio z przedziałem dominanty).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Dominanta (warto ´s ´c modalna)
Przykład 4.
Załó˙zmy, ˙ze badamy kolor oczu osób zamieszkuj ˛
acych
kraje skandynawskie i afryka ´nskie.
Wówczas prawdopodobnie oka˙ze si ˛e, ˙ze typowym (tj.
dominuj ˛
acym) kolorem oczu w´sród mieszka ´nców
Skandynawii jest kolor niebieski, a w´sród mieszka ´nców
Afryki – br ˛
azowy.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Dominanta (warto ´s ´c modalna)
Przykład 4.
Załó˙zmy, ˙ze badamy kolor oczu osób zamieszkuj ˛
acych
kraje skandynawskie i afryka ´nskie.
Wówczas prawdopodobnie oka˙ze si ˛e, ˙ze typowym (tj.
dominuj ˛
acym) kolorem oczu w´sród mieszka ´nców
Skandynawii jest kolor niebieski, a w´sród mieszka ´nców
Afryki – br ˛
azowy.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Kwartyle
Kwartyl pierwszy
Q
1
dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 25% jednostek
ma warto´sci cechy nie wi ˛eksze ni˙z kwartyl pierwszy Q
1
, a
75% jednostek ma warto´sci cechy nie mniejsze ni˙z Q
1
.
Kwartyl drugi
Q
2
(nazywany tak˙ze median ˛
a i oznaczany
symbolem Me) dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 50%
jednostek ma warto´sci cechy nie wi ˛eksze ni˙z mediana Me,
a pozostałe 50% jednostek ma warto´sci cechy nie
mniejsze ni˙z Me.
Kwartyl trzeci
Q
3
dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 75% jednostek
ma warto´sci cechy nie wi ˛eksze ni˙z kwartyl trzeci Q
3
, a 25%
jednostek ma warto´sci cechy nie mniejsze ni˙z Q
3
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Kwartyle
Kwartyl pierwszy
Q
1
dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 25% jednostek
ma warto´sci cechy nie wi ˛eksze ni˙z kwartyl pierwszy Q
1
, a
75% jednostek ma warto´sci cechy nie mniejsze ni˙z Q
1
.
Kwartyl drugi
Q
2
(nazywany tak˙ze median ˛
a i oznaczany
symbolem Me) dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 50%
jednostek ma warto´sci cechy nie wi ˛eksze ni˙z mediana Me,
a pozostałe 50% jednostek ma warto´sci cechy nie
mniejsze ni˙z Me.
Kwartyl trzeci
Q
3
dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 75% jednostek
ma warto´sci cechy nie wi ˛eksze ni˙z kwartyl trzeci Q
3
, a 25%
jednostek ma warto´sci cechy nie mniejsze ni˙z Q
3
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie – Kwartyle
Kwartyl pierwszy
Q
1
dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 25% jednostek
ma warto´sci cechy nie wi ˛eksze ni˙z kwartyl pierwszy Q
1
, a
75% jednostek ma warto´sci cechy nie mniejsze ni˙z Q
1
.
Kwartyl drugi
Q
2
(nazywany tak˙ze median ˛
a i oznaczany
symbolem Me) dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 50%
jednostek ma warto´sci cechy nie wi ˛eksze ni˙z mediana Me,
a pozostałe 50% jednostek ma warto´sci cechy nie
mniejsze ni˙z Me.
Kwartyl trzeci
Q
3
dzieli uporz ˛
adkowan ˛
a niemalej ˛
aco
zbiorowo´s´c na dwie cz ˛e´sci w ten sposób, ˙ze 75% jednostek
ma warto´sci cechy nie wi ˛eksze ni˙z kwartyl trzeci Q
3
, a 25%
jednostek ma warto´sci cechy nie mniejsze ni˙z Q
3
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle
W szeregach szczegółowych median ˛e obliczamy ze wzoru
Me =
x
n/2
+
x
(
n+2)/2
2
,
gdy
n
jest parzyste,
x
(
n+1)/2
,
gdy
n
jest nieparzyste,
gdzie x
(
n+1)/2
, x
n/2
, x
(
n+2)/2
oznaczaj ˛
a warto´sci cechy dla
tych jednostek zbiorowo´sci, które w uporz ˛
adkowanym
(niemalej ˛
aco lub nierosn ˛
aco) szeregu znajduj ˛
a si ˛e na
miejscach o numerach odpowiednio
n + 1
2
,
n
2
,
n + 2
2
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu szczegółowym i rozdzielczym punktowym
Wyznaczanie kwartyla pierwszego i trzeciego z szeregu
szczegółowego lub rozdzielczego punktowego
rozpoczynamy od znalezienia mediany, która dzieli
uporz ˛
adkowan ˛
a zbiorowo´s´c na połowy.
Dla pierwszej cze´sci (tj. dla połowy obserwacji nie
wi ˛ekszych od mediany) ponownie wyznaczamy median ˛e.
Wyznaczona warto´s´c b ˛edzie odpowiadała kwartylowi
pierwszemu Q
1
. Z kolei mediana wyznaczona dla drugiej
cz ˛e´sci – kwartylowi trzeciemu Q
3
.
W przypadku szeregu rozdzielczego punktowego
odnalezienie obserwacji reprezentuj ˛
acych kwartyle ułatwia
kumulacja liczebno´sci, która polega na sumowaniu
kolejnych liczno´sci n
i
w szeregu.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu szczegółowym i rozdzielczym punktowym
Wyznaczanie kwartyla pierwszego i trzeciego z szeregu
szczegółowego lub rozdzielczego punktowego
rozpoczynamy od znalezienia mediany, która dzieli
uporz ˛
adkowan ˛
a zbiorowo´s´c na połowy.
Dla pierwszej cze´sci (tj. dla połowy obserwacji nie
wi ˛ekszych od mediany) ponownie wyznaczamy median ˛e.
Wyznaczona warto´s´c b ˛edzie odpowiadała kwartylowi
pierwszemu Q
1
. Z kolei mediana wyznaczona dla drugiej
cz ˛e´sci – kwartylowi trzeciemu Q
3
.
W przypadku szeregu rozdzielczego punktowego
odnalezienie obserwacji reprezentuj ˛
acych kwartyle ułatwia
kumulacja liczebno´sci, która polega na sumowaniu
kolejnych liczno´sci n
i
w szeregu.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu szczegółowym i rozdzielczym punktowym
Wyznaczanie kwartyla pierwszego i trzeciego z szeregu
szczegółowego lub rozdzielczego punktowego
rozpoczynamy od znalezienia mediany, która dzieli
uporz ˛
adkowan ˛
a zbiorowo´s´c na połowy.
Dla pierwszej cze´sci (tj. dla połowy obserwacji nie
wi ˛ekszych od mediany) ponownie wyznaczamy median ˛e.
Wyznaczona warto´s´c b ˛edzie odpowiadała kwartylowi
pierwszemu Q
1
. Z kolei mediana wyznaczona dla drugiej
cz ˛e´sci – kwartylowi trzeciemu Q
3
.
W przypadku szeregu rozdzielczego punktowego
odnalezienie obserwacji reprezentuj ˛
acych kwartyle ułatwia
kumulacja liczebno´sci, która polega na sumowaniu
kolejnych liczno´sci n
i
w szeregu.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu rozdzielczym z przedziałami klasowymi
Obliczanie kwartyli w szeregach rozdzielczych
z przedziałami klasowymi opiera si ˛e na wzorach
przybli˙zonych.
W pierwszym kroku odnajdujemy przedziały, do których
nale˙z ˛
a jednostki o numerach
1
4
n,
1
2
n,
3
4
n. Przedziały te
nazywamy odpowiednio przedziałem kwartyla pierwszego,
przedziałem mediany i przedziałem kwartyla trzeciego.
W nast ˛epnym kroku obliczamy poszczególne kwartyle.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu rozdzielczym z przedziałami klasowymi
Obliczanie kwartyli w szeregach rozdzielczych
z przedziałami klasowymi opiera si ˛e na wzorach
przybli˙zonych.
W pierwszym kroku odnajdujemy przedziały, do których
nale˙z ˛
a jednostki o numerach
1
4
n,
1
2
n,
3
4
n. Przedziały te
nazywamy odpowiednio przedziałem kwartyla pierwszego,
przedziałem mediany i przedziałem kwartyla trzeciego.
W nast ˛epnym kroku obliczamy poszczególne kwartyle.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu rozdzielczym z przedziałami klasowymi
Obliczanie kwartyli w szeregach rozdzielczych
z przedziałami klasowymi opiera si ˛e na wzorach
przybli˙zonych.
W pierwszym kroku odnajdujemy przedziały, do których
nale˙z ˛
a jednostki o numerach
1
4
n,
1
2
n,
3
4
n. Przedziały te
nazywamy odpowiednio przedziałem kwartyla pierwszego,
przedziałem mediany i przedziałem kwartyla trzeciego.
W nast ˛epnym kroku obliczamy poszczególne kwartyle.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu rozdzielczym z przedziałami klasowymi – c.d.
Kwartyl pierwszy wyznaczamy z nast ˛epuj ˛
acego wzoru
przybli˙zonego
Q
1
=
x
s
+
h
s
n
s
1
4
n −
s−1
X
i=1
n
i
!
,
gdzie:
x
s
– pocz ˛
atek przedziału kwartyla pierwszego,
h
s
– rozpi ˛eto´s´c przedziału kwartyla pierwszego,
n
s
– liczebno´s´c przedziału kwartyla pierwszego,
P
s−1
i=1
n
i
– liczebno´s´c skumulowana od przedziału
pierwszego do przedziału poprzedzaj ˛
acego przedział
kwartyla pierwszego.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary ´srednie
Pozycyjne miary ´srednie
Kwartyle w szeregu rozdzielczym z przedziałami klasowymi – c.d.
W analogiczny sposób wyznaczamy Me i Q
3
Me = x
s
+
h
s
n
s
1
2
n −
s−1
X
i=1
n
i
!
,
Q
3
=
x
s
+
h
s
n
s
3
4
n −
s−1
X
i=1
n
i
!
,
przy czym x
s
,
h
s
,
n
s
w tych wzorach odnosz ˛
a si ˛e do
odpowiednio przedziału mediany lub przedziału kwartyla
trzeciego.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Przykład 5.
Wyobra´zmy sobie, ˙ze mamy przeprowadzi´c zaj ˛ecia
z matematyki w pewnej klasie uczniów licz ˛
acych 10 osób.
Od dyrektora szkoły wiemy, ˙ze ´sredni iloraz inteligencji
w tej klasie jest równy 100.
Mało obeznany metodologicznie nauczyciel mo˙ze uzna´c t ˛e
informacj ˛e za sygnał, ˙ze wystarczy przygotowa´c zadania
dla ”przeci ˛etniaków”.
Ale czy takie rozumowanie jest poprawne?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Przykład 5.
Wyobra´zmy sobie, ˙ze mamy przeprowadzi´c zaj ˛ecia
z matematyki w pewnej klasie uczniów licz ˛
acych 10 osób.
Od dyrektora szkoły wiemy, ˙ze ´sredni iloraz inteligencji
w tej klasie jest równy 100.
Mało obeznany metodologicznie nauczyciel mo˙ze uzna´c t ˛e
informacj ˛e za sygnał, ˙ze wystarczy przygotowa´c zadania
dla ”przeci ˛etniaków”.
Ale czy takie rozumowanie jest poprawne?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Przykład 5.
Wyobra´zmy sobie, ˙ze mamy przeprowadzi´c zaj ˛ecia
z matematyki w pewnej klasie uczniów licz ˛
acych 10 osób.
Od dyrektora szkoły wiemy, ˙ze ´sredni iloraz inteligencji
w tej klasie jest równy 100.
Mało obeznany metodologicznie nauczyciel mo˙ze uzna´c t ˛e
informacj ˛e za sygnał, ˙ze wystarczy przygotowa´c zadania
dla ”przeci ˛etniaków”.
Ale czy takie rozumowanie jest poprawne?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Przykład 5.
Wyobra´zmy sobie, ˙ze mamy przeprowadzi´c zaj ˛ecia
z matematyki w pewnej klasie uczniów licz ˛
acych 10 osób.
Od dyrektora szkoły wiemy, ˙ze ´sredni iloraz inteligencji
w tej klasie jest równy 100.
Mało obeznany metodologicznie nauczyciel mo˙ze uzna´c t ˛e
informacj ˛e za sygnał, ˙ze wystarczy przygotowa´c zadania
dla ”przeci ˛etniaków”.
Ale czy takie rozumowanie jest poprawne?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Wiemy, ˙ze ´srednia mo˙ze powsta´c z ró˙znych danych. Je´sli
w klasie wszyscy uczniowie maj ˛
a IQ równe 100, to ´srednia
te˙z wyniesie 100. Powiemy wówczas, ˙ze zbiorowo´s´c
uczniów jest
jednorodna
.
Ale ´sredni iloraz inteligencji równy 100 mo˙zna otrzyma´c
tak˙ze wtedy, gdy w klasie (przykładowo) połowa uczniów
ma iloraz 120, a druga połowa 80. Z prostych rachunków
wynika, ˙ze ´srednia jest tu te˙z równa 100:
120·5+80·5
10
=
100.
Tym razem jednak zbiorowo´s´c uczniów jest
heterogeniczna
.
Nauczyciel powinien zerkn ˛
a´c na indywidualne warto´sci IQ,
aby oceni´c, czy w klasie s ˛
a sami ”przeci ˛etniacy”, czy te˙z
zarówno ”geniusze”, jak i ”słabeusze”.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Wiemy, ˙ze ´srednia mo˙ze powsta´c z ró˙znych danych. Je´sli
w klasie wszyscy uczniowie maj ˛
a IQ równe 100, to ´srednia
te˙z wyniesie 100. Powiemy wówczas, ˙ze zbiorowo´s´c
uczniów jest
jednorodna
.
Ale ´sredni iloraz inteligencji równy 100 mo˙zna otrzyma´c
tak˙ze wtedy, gdy w klasie (przykładowo) połowa uczniów
ma iloraz 120, a druga połowa 80. Z prostych rachunków
wynika, ˙ze ´srednia jest tu te˙z równa 100:
120·5+80·5
10
=
100.
Tym razem jednak zbiorowo´s´c uczniów jest
heterogeniczna
.
Nauczyciel powinien zerkn ˛
a´c na indywidualne warto´sci IQ,
aby oceni´c, czy w klasie s ˛
a sami ”przeci ˛etniacy”, czy te˙z
zarówno ”geniusze”, jak i ”słabeusze”.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Wiemy, ˙ze ´srednia mo˙ze powsta´c z ró˙znych danych. Je´sli
w klasie wszyscy uczniowie maj ˛
a IQ równe 100, to ´srednia
te˙z wyniesie 100. Powiemy wówczas, ˙ze zbiorowo´s´c
uczniów jest
jednorodna
.
Ale ´sredni iloraz inteligencji równy 100 mo˙zna otrzyma´c
tak˙ze wtedy, gdy w klasie (przykładowo) połowa uczniów
ma iloraz 120, a druga połowa 80. Z prostych rachunków
wynika, ˙ze ´srednia jest tu te˙z równa 100:
120·5+80·5
10
=
100.
Tym razem jednak zbiorowo´s´c uczniów jest
heterogeniczna
.
Nauczyciel powinien zerkn ˛
a´c na indywidualne warto´sci IQ,
aby oceni´c, czy w klasie s ˛
a sami ”przeci ˛etniacy”, czy te˙z
zarówno ”geniusze”, jak i ”słabeusze”.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Dlaczego konieczne jest obliczanie miar zmienno ´sci dla zbioru danych?
Wiemy, ˙ze ´srednia mo˙ze powsta´c z ró˙znych danych. Je´sli
w klasie wszyscy uczniowie maj ˛
a IQ równe 100, to ´srednia
te˙z wyniesie 100. Powiemy wówczas, ˙ze zbiorowo´s´c
uczniów jest
jednorodna
.
Ale ´sredni iloraz inteligencji równy 100 mo˙zna otrzyma´c
tak˙ze wtedy, gdy w klasie (przykładowo) połowa uczniów
ma iloraz 120, a druga połowa 80. Z prostych rachunków
wynika, ˙ze ´srednia jest tu te˙z równa 100:
120·5+80·5
10
=
100.
Tym razem jednak zbiorowo´s´c uczniów jest
heterogeniczna
.
Nauczyciel powinien zerkn ˛
a´c na indywidualne warto´sci IQ,
aby oceni´c, czy w klasie s ˛
a sami ”przeci ˛etniacy”, czy te˙z
zarówno ”geniusze”, jak i ”słabeusze”.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział
Miary, które pozwalaj ˛
a oceni´c stopie ´n heterogeniczno´sci
danej zbiorowo´sci (czyli stopie ´n zró˙znicowania) nazywamy
miarami zmienno ´sci
lub zamiennie – miarami
zró˙znicowania, dyspersji, rozproszenia.
Miary zmienno´sci dzielimy na bezwzgl ˛edne i wzgl ˛edne.
Do
miar bezwzgl ˛ednych
zaliczamy:
1.
Klasyczne miary zró˙znicowania
, w tym:
a.
odchylenie przeci ˛etne d
x
,
b.
wariancj ˛e s
2
x
,
c.
odchylenie standardowe s
x
.
2.
Pozycyjne miary zró˙znicowania
, w tym:
a.
rozst ˛ep R
x
,
b.
odchylenie ´cwiartkowe Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Miary zmienno ´sci
Podział – c.d.
Do
miar wzgl ˛ednych
zaliczamy:
1.
Klasyczne współczynniki zmienno ´sci
, w tym:
a.
współczynnik zmienno´sci oparty na odchyleniu przeci ˛etnym
V
d
x
,
b.
współczynnik zmienno´sci oparty na odchyleniu
standardowym V
s
x
.
2.
Pozycyjny współczynnik zmienno ´sci
:
a.
współczynnik zmienno´sci oparty na odchyleniu
´cwiartkowym Q
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Jak obliczy ´c odchylenie przeci ˛etne?
Przykład 6.
W odniesieniu do przykładu 5 (dotycz ˛
acego IQ) załó˙zmy
dalej, ˙ze ilorazy inteligencji w 10-osobowej grupie uczniów
kształtował si ˛e nast ˛epuj ˛
aco:
85, 85, 95, 95, 95, 100, 105, 110, 115, 115.
´
Srednia warto´s´c IQ w tej grupie wynosi 100, ale ma tu
miejsce spore zró˙znicowanie pomi ˛edzy uczniami.
Oznaczmy poszczególne wyniki symbolami
x
1
,
x
2
, . . . ,
x
10
,
natomiast ´sredni ˛
a z tych wyników symbolem
¯
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Jak obliczy ´c odchylenie przeci ˛etne?
Przykład 6.
W odniesieniu do przykładu 5 (dotycz ˛
acego IQ) załó˙zmy
dalej, ˙ze ilorazy inteligencji w 10-osobowej grupie uczniów
kształtował si ˛e nast ˛epuj ˛
aco:
85, 85, 95, 95, 95, 100, 105, 110, 115, 115.
´
Srednia warto´s´c IQ w tej grupie wynosi 100, ale ma tu
miejsce spore zró˙znicowanie pomi ˛edzy uczniami.
Oznaczmy poszczególne wyniki symbolami
x
1
,
x
2
, . . . ,
x
10
,
natomiast ´sredni ˛
a z tych wyników symbolem
¯
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Jak obliczy ´c odchylenie przeci ˛etne?
Przykład 6.
W odniesieniu do przykładu 5 (dotycz ˛
acego IQ) załó˙zmy
dalej, ˙ze ilorazy inteligencji w 10-osobowej grupie uczniów
kształtował si ˛e nast ˛epuj ˛
aco:
85, 85, 95, 95, 95, 100, 105, 110, 115, 115.
´
Srednia warto´s´c IQ w tej grupie wynosi 100, ale ma tu
miejsce spore zró˙znicowanie pomi ˛edzy uczniami.
Oznaczmy poszczególne wyniki symbolami
x
1
,
x
2
, . . . ,
x
10
,
natomiast ´sredni ˛
a z tych wyników symbolem
¯
x
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Jak obliczy ´c odchylenie przeci ˛etne?
Mamy wi ˛ec nast ˛epuj ˛
ace warto´sci i ich odchylenia od ´sredniej
x
1
=
85,
x
1
− ¯
x = −15,
x
2
=
85,
x
2
− ¯
x = −15,
x
3
=
95,
x
3
− ¯
x = −5,
x
4
=
95,
x
4
− ¯
x = −5,
x
5
=
95,
x
5
− ¯
x = −5,
x
6
=
100,
x
6
− ¯
x =
0,
x
7
=
105,
x
7
− ¯
x =
5,
x
8
=
110,
x
8
− ¯
x = 10,
x
9
=
115,
x
9
− ¯
x = 15,
x
10
=
115,
x
10
− ¯
x = 15.
Ale suma wszystkich odchyle ´n jest równa
0
!
Mo˙zemy jednak obliczy´c sum ˛e odchyle ´n bezwzgl ˛ednych, która
w tym przykładzie wynosi
90
, a nast ˛epnie podzieli´c przez ich
liczb ˛e (tj. przez 10). W ten sposób otrzymamy odchylenie
przeci ˛etne d
x
równe
9
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Jak obliczy ´c odchylenie przeci ˛etne?
Mamy wi ˛ec nast ˛epuj ˛
ace warto´sci i ich odchylenia od ´sredniej
x
1
=
85,
x
1
− ¯
x = −15,
x
2
=
85,
x
2
− ¯
x = −15,
x
3
=
95,
x
3
− ¯
x = −5,
x
4
=
95,
x
4
− ¯
x = −5,
x
5
=
95,
x
5
− ¯
x = −5,
x
6
=
100,
x
6
− ¯
x =
0,
x
7
=
105,
x
7
− ¯
x =
5,
x
8
=
110,
x
8
− ¯
x = 10,
x
9
=
115,
x
9
− ¯
x = 15,
x
10
=
115,
x
10
− ¯
x = 15.
Ale suma wszystkich odchyle ´n jest równa
0
!
Mo˙zemy jednak obliczy´c sum ˛e odchyle ´n bezwzgl ˛ednych, która
w tym przykładzie wynosi
90
, a nast ˛epnie podzieli´c przez ich
liczb ˛e (tj. przez 10). W ten sposób otrzymamy odchylenie
przeci ˛etne d
x
równe
9
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Jak obliczy ´c odchylenie przeci ˛etne?
Mamy wi ˛ec nast ˛epuj ˛
ace warto´sci i ich odchylenia od ´sredniej
x
1
=
85,
x
1
− ¯
x = −15,
x
2
=
85,
x
2
− ¯
x = −15,
x
3
=
95,
x
3
− ¯
x = −5,
x
4
=
95,
x
4
− ¯
x = −5,
x
5
=
95,
x
5
− ¯
x = −5,
x
6
=
100,
x
6
− ¯
x =
0,
x
7
=
105,
x
7
− ¯
x =
5,
x
8
=
110,
x
8
− ¯
x = 10,
x
9
=
115,
x
9
− ¯
x = 15,
x
10
=
115,
x
10
− ¯
x = 15.
Ale suma wszystkich odchyle ´n jest równa
0
!
Mo˙zemy jednak obliczy´c sum ˛e odchyle ´n bezwzgl ˛ednych, która
w tym przykładzie wynosi
90
, a nast ˛epnie podzieli´c przez ich
liczb ˛e (tj. przez 10). W ten sposób otrzymamy odchylenie
przeci ˛etne d
x
równe
9
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu prostym
A zatem, je´sli dysponujemy zbiorem danych (o liczebno´sci n)
zestawionych w szereg szczegółowy, prosty, to
odchylenie
przeci ˛etne
obliczamy ze wzoru:
d
x
=
|x
1
− ¯
x | + |x
2
− ¯
x | + |x
3
− ¯
x | + . . . + |x
n
− ¯
x |
n
Formuł ˛e t ˛e zapisujemy w skrócie wzorem:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
Interpretacja:
Jest to ´srednia arytmetyczna z bezwzgl ˛ednych
odchyle ´n warto´sci cechy od jej ´sredniej arytmetycznej.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu prostym
A zatem, je´sli dysponujemy zbiorem danych (o liczebno´sci n)
zestawionych w szereg szczegółowy, prosty, to
odchylenie
przeci ˛etne
obliczamy ze wzoru:
d
x
=
|x
1
− ¯
x | + |x
2
− ¯
x | + |x
3
− ¯
x | + . . . + |x
n
− ¯
x |
n
Formuł ˛e t ˛e zapisujemy w skrócie wzorem:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
Interpretacja:
Jest to ´srednia arytmetyczna z bezwzgl ˛ednych
odchyle ´n warto´sci cechy od jej ´sredniej arytmetycznej.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu prostym
A zatem, je´sli dysponujemy zbiorem danych (o liczebno´sci n)
zestawionych w szereg szczegółowy, prosty, to
odchylenie
przeci ˛etne
obliczamy ze wzoru:
d
x
=
|x
1
− ¯
x | + |x
2
− ¯
x | + |x
3
− ¯
x | + . . . + |x
n
− ¯
x |
n
Formuł ˛e t ˛e zapisujemy w skrócie wzorem:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
Interpretacja:
Jest to ´srednia arytmetyczna z bezwzgl ˛ednych
odchyle ´n warto´sci cechy od jej ´sredniej arytmetycznej.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym punktowym – c.d. przykładu 6
Załó˙zmy, ˙ze dane z przykładu 6 pogrupowane zostały w szereg
rozdzielczy punktowy:
warto ´s ´c IQ
liczby
x
i
uczniów
n
i
85
2
95
3
100
1
105
1
110
1
115
2
Zauwa˙zymy, ˙ze s ˛
a to te same dane, ale inaczej przedstawione.
Odchylenie przeci ˛etne dla tego szeregu powinno pozosta´c wi ˛ec
bez zmian.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym punktowym – c.d. przykładu 6
Załó˙zmy, ˙ze dane z przykładu 6 pogrupowane zostały w szereg
rozdzielczy punktowy:
warto ´s ´c IQ
liczby
x
i
uczniów
n
i
85
2
95
3
100
1
105
1
110
1
115
2
Zauwa˙zymy, ˙ze s ˛
a to te same dane, ale inaczej przedstawione.
Odchylenie przeci ˛etne dla tego szeregu powinno pozosta´c wi ˛ec
bez zmian.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym punktowym – c.d. przykładu 6
Aby je obliczy´c, wygodnie jest przeprowadzi´c obliczenia
po´srednie w dodatkowych kolumnach tablicy.
warto ´s ´c
liczby
odchylenia
wa˙zone
IQ
uczniów
bezwzgl ˛edne
odchylenia
x
i
n
i
|x
i
− ¯
x |
|x
i
− ¯
x | · n
i
85
2
15
30
95
3
5
15
100
1
0
0
105
1
5
5
110
1
10
10
115
2
15
30
Razem
10
×
90
Mamy:
d
x
=
90
10
=
9.
Ogólny wzór:
d
x
=
1
n
P
k
i=1
|x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym punktowym – c.d. przykładu 6
Aby je obliczy´c, wygodnie jest przeprowadzi´c obliczenia
po´srednie w dodatkowych kolumnach tablicy.
warto ´s ´c
liczby
odchylenia
wa˙zone
IQ
uczniów
bezwzgl ˛edne
odchylenia
x
i
n
i
|x
i
− ¯
x |
|x
i
− ¯
x | · n
i
85
2
15
30
95
3
5
15
100
1
0
0
105
1
5
5
110
1
10
10
115
2
15
30
Razem
10
×
90
Mamy:
d
x
=
90
10
=
9.
Ogólny wzór:
d
x
=
1
n
P
k
i=1
|x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przykładu 6
Pogrupujmy dane z poprzedniego szeregu punktowego w
szereg rozdzielczy z przedziałami klasowymi o rozpi ˛eto´sci 10.
przedziały
liczby
warto ´sci IQ
x
i
uczniów
n
i
(85, 95]
5
(95,105]
2
(105,115]
3
W tym przypadku obliczona warto´s´c odchylenie przeci ˛etnego
b ˛edzie tylko
przybli˙zeniem
rzeczywistej warto´sci, poniewa˙z nie
mamy pełnej informacji o poziomie IQ dla wszystkich uczniów.
Aby znale´z´c d
x
musimy przyj ˛
a´c dla ka˙zdego przedziału
klasowego jak ˛
a´s u´srednion ˛
a warto´s´c IQ. Warto´sciami tymi
niech b ˛ed ˛
a ´srodki poszczególnych przedziałów.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przykładu 6
Pogrupujmy dane z poprzedniego szeregu punktowego w
szereg rozdzielczy z przedziałami klasowymi o rozpi ˛eto´sci 10.
przedziały
liczby
warto ´sci IQ
x
i
uczniów
n
i
(85, 95]
5
(95,105]
2
(105,115]
3
W tym przypadku obliczona warto´s´c odchylenie przeci ˛etnego
b ˛edzie tylko
przybli˙zeniem
rzeczywistej warto´sci, poniewa˙z nie
mamy pełnej informacji o poziomie IQ dla wszystkich uczniów.
Aby znale´z´c d
x
musimy przyj ˛
a´c dla ka˙zdego przedziału
klasowego jak ˛
a´s u´srednion ˛
a warto´s´c IQ. Warto´sciami tymi
niech b ˛ed ˛
a ´srodki poszczególnych przedziałów.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przykładu 6
Pogrupujmy dane z poprzedniego szeregu punktowego w
szereg rozdzielczy z przedziałami klasowymi o rozpi ˛eto´sci 10.
przedziały
liczby
warto ´sci IQ
x
i
uczniów
n
i
(85, 95]
5
(95,105]
2
(105,115]
3
W tym przypadku obliczona warto´s´c odchylenie przeci ˛etnego
b ˛edzie tylko
przybli˙zeniem
rzeczywistej warto´sci, poniewa˙z nie
mamy pełnej informacji o poziomie IQ dla wszystkich uczniów.
Aby znale´z´c d
x
musimy przyj ˛
a´c dla ka˙zdego przedziału
klasowego jak ˛
a´s u´srednion ˛
a warto´s´c IQ. Warto´sciami tymi
niech b ˛ed ˛
a ´srodki poszczególnych przedziałów.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przedziały
liczby
´srodki
odchylenia
wa˙zone
IQ
uczniów
przedz.
bezwzgl ˛edne
odchylenia
x
i
n
i
˙x
i
˙x
i
· n
i
| ˙x
i
− ¯
x |
| ˙x
i
− ¯
x | · n
i
85–95
5
90
450
8
40
95–105
2
100
200
2
4
105–115
3
110
330
12
36
Razem
10
×
980
×
80
´
Srednia arytmetyczna IQ obliczona na podstawie tego szeregu
wynosi
980
10
=
98, a zatem jest tylko przybli˙zeniem faktycznej
´sredniej. Dalej w obliczeniach przyj ˛eto to przybli˙zenie.
Uzyskujemy przybli˙zon ˛
a warto´s´c odchylenia przeci ˛etnego
80
10
=
8
. Ogólnie wzór:
d
x
=
1
n
P
k
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przedziały
liczby
´srodki
odchylenia
wa˙zone
IQ
uczniów
przedz.
bezwzgl ˛edne
odchylenia
x
i
n
i
˙x
i
˙x
i
· n
i
| ˙x
i
− ¯
x |
| ˙x
i
− ¯
x | · n
i
85–95
5
90
450
8
40
95–105
2
100
200
2
4
105–115
3
110
330
12
36
Razem
10
×
980
×
80
´
Srednia arytmetyczna IQ obliczona na podstawie tego szeregu
wynosi
980
10
=
98, a zatem jest tylko przybli˙zeniem faktycznej
´sredniej. Dalej w obliczeniach przyj ˛eto to przybli˙zenie.
Uzyskujemy przybli˙zon ˛
a warto´s´c odchylenia przeci ˛etnego
80
10
=
8
. Ogólnie wzór:
d
x
=
1
n
P
k
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przedziały
liczby
´srodki
odchylenia
wa˙zone
IQ
uczniów
przedz.
bezwzgl ˛edne
odchylenia
x
i
n
i
˙x
i
˙x
i
· n
i
| ˙x
i
− ¯
x |
| ˙x
i
− ¯
x | · n
i
85–95
5
90
450
8
40
95–105
2
100
200
2
4
105–115
3
110
330
12
36
Razem
10
×
980
×
80
´
Srednia arytmetyczna IQ obliczona na podstawie tego szeregu
wynosi
980
10
=
98, a zatem jest tylko przybli˙zeniem faktycznej
´sredniej. Dalej w obliczeniach przyj ˛eto to przybli˙zenie.
Uzyskujemy przybli˙zon ˛
a warto´s´c odchylenia przeci ˛etnego
80
10
=
8
. Ogólnie wzór:
d
x
=
1
n
P
k
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne – wzory
Podsumowanie:
Skorzystali´smy z trzech formuł na d
x
.
W szeregu szczegółowym:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
W szeregu rozdzielczym punktowym:
d
x
=
1
n
k
X
i=1
|x
i
− ¯
x | · n
i
W szeregu rozdzielczym z przedziałami klasowymi:
d
x
=
1
n
k
X
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne – wzory
Podsumowanie:
Skorzystali´smy z trzech formuł na d
x
.
W szeregu szczegółowym:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
W szeregu rozdzielczym punktowym:
d
x
=
1
n
k
X
i=1
|x
i
− ¯
x | · n
i
W szeregu rozdzielczym z przedziałami klasowymi:
d
x
=
1
n
k
X
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne – wzory
Podsumowanie:
Skorzystali´smy z trzech formuł na d
x
.
W szeregu szczegółowym:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
W szeregu rozdzielczym punktowym:
d
x
=
1
n
k
X
i=1
|x
i
− ¯
x | · n
i
W szeregu rozdzielczym z przedziałami klasowymi:
d
x
=
1
n
k
X
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Odchylenie przeci ˛etne – wzory
Podsumowanie:
Skorzystali´smy z trzech formuł na d
x
.
W szeregu szczegółowym:
d
x
=
1
n
n
X
i=1
|x
i
− ¯
x |
W szeregu rozdzielczym punktowym:
d
x
=
1
n
k
X
i=1
|x
i
− ¯
x | · n
i
W szeregu rozdzielczym z przedziałami klasowymi:
d
x
=
1
n
k
X
i=1
| ˙x
i
− ¯
x | · n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Wariancja
W analogiczny sposób konstruujemy wzory na inn ˛
a klasyczn ˛
a
miar ˛e zmienno´sci, zwan ˛
a
wariancj ˛
a
.
W szeregu szczegółowym:
s
2
x
=
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
2
x
=
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
2
x
=
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Wariancja
W analogiczny sposób konstruujemy wzory na inn ˛
a klasyczn ˛
a
miar ˛e zmienno´sci, zwan ˛
a
wariancj ˛
a
.
W szeregu szczegółowym:
s
2
x
=
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
2
x
=
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
2
x
=
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Wariancja
W analogiczny sposób konstruujemy wzory na inn ˛
a klasyczn ˛
a
miar ˛e zmienno´sci, zwan ˛
a
wariancj ˛
a
.
W szeregu szczegółowym:
s
2
x
=
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
2
x
=
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
2
x
=
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Wariancja
W analogiczny sposób konstruujemy wzory na inn ˛
a klasyczn ˛
a
miar ˛e zmienno´sci, zwan ˛
a
wariancj ˛
a
.
W szeregu szczegółowym:
s
2
x
=
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
2
x
=
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
2
x
=
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Odchylenie standardowe
Pierwiastek kw. z wariancji –
odchylenie standardowe.
W szeregu szczegółowym:
s
x
=
v
u
u
t
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
x
=
v
u
u
t
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
x
=
v
u
u
t
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Odchylenie standardowe
Pierwiastek kw. z wariancji –
odchylenie standardowe.
W szeregu szczegółowym:
s
x
=
v
u
u
t
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
x
=
v
u
u
t
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
x
=
v
u
u
t
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Odchylenie standardowe
Pierwiastek kw. z wariancji –
odchylenie standardowe.
W szeregu szczegółowym:
s
x
=
v
u
u
t
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
x
=
v
u
u
t
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
x
=
v
u
u
t
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci – Odchylenie standardowe
Pierwiastek kw. z wariancji –
odchylenie standardowe.
W szeregu szczegółowym:
s
x
=
v
u
u
t
1
n
n
X
i=1
(
x
i
− ¯
x )
2
W szeregu rozdzielczym punktowym:
s
x
=
v
u
u
t
1
n
k
X
i=1
(
x
i
− ¯
x )
2
· n
i
W szeregu rozdzielczym z przedziałami klasowymi:
s
x
=
v
u
u
t
1
n
k
X
i=1
( ˙
x
i
− ¯
x )
2
· n
i
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Wariancja i odch. stand. w szeregu szczegółowym – c.d. przykładu 6
W przypadku szeregu szczegółowego z przykładu 6 mamy
nast ˛epuj ˛
ace warto´sci IQ i kwadraty ich odchyle ´n od ´sredniej:
x
1
=
85,
(
x
1
− ¯
x )
2
=
225,
x
2
=
85,
(
x
2
− ¯
x )
2
=
225,
x
3
=
95,
(
x
3
− ¯
x )
2
=
25,
x
4
=
95,
(
x
4
− ¯
x )
2
=
25,
x
5
=
95,
(
x
5
− ¯
x )
2
=
25,
x
6
=
100,
(
x
6
− ¯
x )
2
=
0,
x
7
=
105,
(
x
7
− ¯
x )
2
=
25,
x
8
=
110,
(
x
8
− ¯
x )
2
=
100,
x
9
=
115,
(
x
9
− ¯
x )
2
=
225,
x
10
=
115,
(
x
10
− ¯
x )
2
=
225.
St ˛
ad otrzymujemy
s
2
x
=
1
10
P
10
i=1
(
x
i
− ¯
x )
2
=
1100
10
=
110,
s
x
=
√
110 ≈ 10, 5.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Wariancja i odch. stand. w szeregu rozdzielczym punktowym – c.d. przykładu 6
warto ´s ´c
liczby
kwadraty
wa˙zone kwadraty
IQ
uczniów
odchyle ´
n
odchyle ´
n
x
i
n
i
(
x
i
− ¯
x )
2
(
x
i
− ¯
x )
2
· n
i
85
2
225
450
95
3
25
75
100
1
0
0
105
1
25
25
110
1
100
100
115
2
225
450
Razem
10
×
1100
Wariancja równa jest wi ˛ec
s
2
x
=
1100
10
=
110,
a odchylenie
standardowe
s
x
=
√
110 ≈ 10, 5.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Wariancja i odch. stand. w szeregu rozdzielczym punktowym – c.d. przykładu 6
warto ´s ´c
liczby
kwadraty
wa˙zone kwadraty
IQ
uczniów
odchyle ´
n
odchyle ´
n
x
i
n
i
(
x
i
− ¯
x )
2
(
x
i
− ¯
x )
2
· n
i
85
2
225
450
95
3
25
75
100
1
0
0
105
1
25
25
110
1
100
100
115
2
225
450
Razem
10
×
1100
Wariancja równa jest wi ˛ec
s
2
x
=
1100
10
=
110,
a odchylenie
standardowe
s
x
=
√
110 ≈ 10, 5.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Wariancja i odch. stand. w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przykładu 6
przedziały
liczby
´srodki
kwadraty
wa˙zone kwadraty
IQ
uczniów
przedz.
odchyle ´
n
odchyle ´
n
x
i
n
i
˙x
i
( ˙
x
i
− ¯
x )
2
( ˙
x
i
− ¯
x )
2
· n
i
85– 95
5
90
64
320
95–105
2
100
4
8
105–115
3
110
144
432
Razem
10
×
×
760
W obliczeniach przyj ˛eto ´srednie IQ równe 98 (zamiast
dokładnej warto´sci 100).
Wariancja jest tu wyznaczona w przybli˙zeniu i wynosi
760
10
=
76.
Podobnie, przybli˙zeniem odchylenia standardowego jest liczba
√
76 ≈ 8, 7.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Wariancja i odch. stand. w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przykładu 6
przedziały
liczby
´srodki
kwadraty
wa˙zone kwadraty
IQ
uczniów
przedz.
odchyle ´
n
odchyle ´
n
x
i
n
i
˙x
i
( ˙
x
i
− ¯
x )
2
( ˙
x
i
− ¯
x )
2
· n
i
85– 95
5
90
64
320
95–105
2
100
4
8
105–115
3
110
144
432
Razem
10
×
×
760
W obliczeniach przyj ˛eto ´srednie IQ równe 98 (zamiast
dokładnej warto´sci 100).
Wariancja jest tu wyznaczona w przybli˙zeniu i wynosi
760
10
=
76.
Podobnie, przybli˙zeniem odchylenia standardowego jest liczba
√
76 ≈ 8, 7.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Klasyczne miary zmienno ´sci
Wariancja i odch. stand. w szeregu rozdzielczym z przedziałami klasowymi – c.d.
przykładu 6
przedziały
liczby
´srodki
kwadraty
wa˙zone kwadraty
IQ
uczniów
przedz.
odchyle ´
n
odchyle ´
n
x
i
n
i
˙x
i
( ˙
x
i
− ¯
x )
2
( ˙
x
i
− ¯
x )
2
· n
i
85– 95
5
90
64
320
95–105
2
100
4
8
105–115
3
110
144
432
Razem
10
×
×
760
W obliczeniach przyj ˛eto ´srednie IQ równe 98 (zamiast
dokładnej warto´sci 100).
Wariancja jest tu wyznaczona w przybli˙zeniu i wynosi
760
10
=
76.
Podobnie, przybli˙zeniem odchylenia standardowego jest liczba
√
76 ≈ 8, 7.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Kiedy obliczamy pozycyjne miary zmienno ´sci?
Wariancja i odchylenie standardowe s ˛
a miarami
zró˙znicowania, najcz ˛e´sciej stosowanymi w praktyce.
Jednak nie zawsze istnieje mo˙zliwo´s´c ich obliczenia.
Na przykład, gdy szereg rozdzielczy ma
otwarte
przedziały klasowe
i nie jest mo˙zliwe znalezienie ´sredniej
arytmetycznej, wówczas nie jest mo˙zliwe tak˙ze
wyznaczenie klasycznych miar zmienno´sci.
Innym przykładem jest wyst ˛epowanie w zbiorze danych
obserwacji nietypowych (odstaj ˛
acych)
. Wówczas
cz ˛esto nie jest wskazane obliczanie ´sredniej
arytmetycznej, a tym samym tak˙ze klasycznych miar
zmienno´sci.
W takich sytuacjach zamiast miar klasycznych obliczamy
miary pozycyjne
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Kiedy obliczamy pozycyjne miary zmienno ´sci?
Wariancja i odchylenie standardowe s ˛
a miarami
zró˙znicowania, najcz ˛e´sciej stosowanymi w praktyce.
Jednak nie zawsze istnieje mo˙zliwo´s´c ich obliczenia.
Na przykład, gdy szereg rozdzielczy ma
otwarte
przedziały klasowe
i nie jest mo˙zliwe znalezienie ´sredniej
arytmetycznej, wówczas nie jest mo˙zliwe tak˙ze
wyznaczenie klasycznych miar zmienno´sci.
Innym przykładem jest wyst ˛epowanie w zbiorze danych
obserwacji nietypowych (odstaj ˛
acych)
. Wówczas
cz ˛esto nie jest wskazane obliczanie ´sredniej
arytmetycznej, a tym samym tak˙ze klasycznych miar
zmienno´sci.
W takich sytuacjach zamiast miar klasycznych obliczamy
miary pozycyjne
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Kiedy obliczamy pozycyjne miary zmienno ´sci?
Wariancja i odchylenie standardowe s ˛
a miarami
zró˙znicowania, najcz ˛e´sciej stosowanymi w praktyce.
Jednak nie zawsze istnieje mo˙zliwo´s´c ich obliczenia.
Na przykład, gdy szereg rozdzielczy ma
otwarte
przedziały klasowe
i nie jest mo˙zliwe znalezienie ´sredniej
arytmetycznej, wówczas nie jest mo˙zliwe tak˙ze
wyznaczenie klasycznych miar zmienno´sci.
Innym przykładem jest wyst ˛epowanie w zbiorze danych
obserwacji nietypowych (odstaj ˛
acych)
. Wówczas
cz ˛esto nie jest wskazane obliczanie ´sredniej
arytmetycznej, a tym samym tak˙ze klasycznych miar
zmienno´sci.
W takich sytuacjach zamiast miar klasycznych obliczamy
miary pozycyjne
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Kiedy obliczamy pozycyjne miary zmienno ´sci?
Wariancja i odchylenie standardowe s ˛
a miarami
zró˙znicowania, najcz ˛e´sciej stosowanymi w praktyce.
Jednak nie zawsze istnieje mo˙zliwo´s´c ich obliczenia.
Na przykład, gdy szereg rozdzielczy ma
otwarte
przedziały klasowe
i nie jest mo˙zliwe znalezienie ´sredniej
arytmetycznej, wówczas nie jest mo˙zliwe tak˙ze
wyznaczenie klasycznych miar zmienno´sci.
Innym przykładem jest wyst ˛epowanie w zbiorze danych
obserwacji nietypowych (odstaj ˛
acych)
. Wówczas
cz ˛esto nie jest wskazane obliczanie ´sredniej
arytmetycznej, a tym samym tak˙ze klasycznych miar
zmienno´sci.
W takich sytuacjach zamiast miar klasycznych obliczamy
miary pozycyjne
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Kiedy obliczamy pozycyjne miary zmienno ´sci?
Wariancja i odchylenie standardowe s ˛
a miarami
zró˙znicowania, najcz ˛e´sciej stosowanymi w praktyce.
Jednak nie zawsze istnieje mo˙zliwo´s´c ich obliczenia.
Na przykład, gdy szereg rozdzielczy ma
otwarte
przedziały klasowe
i nie jest mo˙zliwe znalezienie ´sredniej
arytmetycznej, wówczas nie jest mo˙zliwe tak˙ze
wyznaczenie klasycznych miar zmienno´sci.
Innym przykładem jest wyst ˛epowanie w zbiorze danych
obserwacji nietypowych (odstaj ˛
acych)
. Wówczas
cz ˛esto nie jest wskazane obliczanie ´sredniej
arytmetycznej, a tym samym tak˙ze klasycznych miar
zmienno´sci.
W takich sytuacjach zamiast miar klasycznych obliczamy
miary pozycyjne
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Rozst ˛ep
Rozst ˛ep
definiujemy jako ró˙znic ˛e mi ˛edzy warto´sci ˛
a
najwi ˛eksz ˛
a i najmniejsz ˛
a badanej cechy w zbiorowo´sci,
czyli
R
x
=
x
max
− x
min
,
gdzie
x
max
=
max{x
1
,
x
2
, . . . ,
x
n
},
x
min
=
min{x
1
,
x
2
, . . . ,
x
n
}.
Na podstawie danych z przykładu 6 mamy: x
min
=
85,
x
max
=
115, zatem rozst ˛ep wynosi R
x
=
30.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Rozst ˛ep
Rozst ˛ep
definiujemy jako ró˙znic ˛e mi ˛edzy warto´sci ˛
a
najwi ˛eksz ˛
a i najmniejsz ˛
a badanej cechy w zbiorowo´sci,
czyli
R
x
=
x
max
− x
min
,
gdzie
x
max
=
max{x
1
,
x
2
, . . . ,
x
n
},
x
min
=
min{x
1
,
x
2
, . . . ,
x
n
}.
Na podstawie danych z przykładu 6 mamy: x
min
=
85,
x
max
=
115, zatem rozst ˛ep wynosi R
x
=
30.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
Ochylenie ´cwiatkowe
Q
x
jest miar ˛
a zró˙znicowania opart ˛
a
na kwartylach. Definiujemy je jako połowa ró˙znicy
pomi ˛edzy trzecim a pierwszym kwartylem
Q
x
=
Q
3
− Q
1
2
.
Odchylenie ´cwiartkowe interpretujemy jako połow ˛e
rozpi ˛eto´sci przedziału, w którym znajduje si ˛e 50%
jednostek skupionych najbli˙zej mediany.
Na warto´s´c odchylenia ´cwiartkowego nie maj ˛
a wpływu
warto´sci mniejsze od kwartyla pierwszego i warto´sci
wi ˛eksze od kwartyla trzeciego.
Miara ta zatem, w przeciwie ´nstwie do klasycznych miar
zró˙znicowania, nie jest wra˙zliwa na warto´sci skrajne.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
Ochylenie ´cwiatkowe
Q
x
jest miar ˛
a zró˙znicowania opart ˛
a
na kwartylach. Definiujemy je jako połowa ró˙znicy
pomi ˛edzy trzecim a pierwszym kwartylem
Q
x
=
Q
3
− Q
1
2
.
Odchylenie ´cwiartkowe interpretujemy jako połow ˛e
rozpi ˛eto´sci przedziału, w którym znajduje si ˛e 50%
jednostek skupionych najbli˙zej mediany.
Na warto´s´c odchylenia ´cwiartkowego nie maj ˛
a wpływu
warto´sci mniejsze od kwartyla pierwszego i warto´sci
wi ˛eksze od kwartyla trzeciego.
Miara ta zatem, w przeciwie ´nstwie do klasycznych miar
zró˙znicowania, nie jest wra˙zliwa na warto´sci skrajne.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
Ochylenie ´cwiatkowe
Q
x
jest miar ˛
a zró˙znicowania opart ˛
a
na kwartylach. Definiujemy je jako połowa ró˙znicy
pomi ˛edzy trzecim a pierwszym kwartylem
Q
x
=
Q
3
− Q
1
2
.
Odchylenie ´cwiartkowe interpretujemy jako połow ˛e
rozpi ˛eto´sci przedziału, w którym znajduje si ˛e 50%
jednostek skupionych najbli˙zej mediany.
Na warto´s´c odchylenia ´cwiartkowego nie maj ˛
a wpływu
warto´sci mniejsze od kwartyla pierwszego i warto´sci
wi ˛eksze od kwartyla trzeciego.
Miara ta zatem, w przeciwie ´nstwie do klasycznych miar
zró˙znicowania, nie jest wra˙zliwa na warto´sci skrajne.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
Ochylenie ´cwiatkowe
Q
x
jest miar ˛
a zró˙znicowania opart ˛
a
na kwartylach. Definiujemy je jako połowa ró˙znicy
pomi ˛edzy trzecim a pierwszym kwartylem
Q
x
=
Q
3
− Q
1
2
.
Odchylenie ´cwiartkowe interpretujemy jako połow ˛e
rozpi ˛eto´sci przedziału, w którym znajduje si ˛e 50%
jednostek skupionych najbli˙zej mediany.
Na warto´s´c odchylenia ´cwiartkowego nie maj ˛
a wpływu
warto´sci mniejsze od kwartyla pierwszego i warto´sci
wi ˛eksze od kwartyla trzeciego.
Miara ta zatem, w przeciwie ´nstwie do klasycznych miar
zró˙znicowania, nie jest wra˙zliwa na warto´sci skrajne.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
W przykładzie 6 mieli´smy nast ˛epuj ˛
ace dane:
85, 85, 95, 95, 95, 100, 105, 110, 115, 115.
Kwartyl pierwszy i trzeci s ˛
a tu równe odpowiednio:
Q
1
=
95, Q
3
=
110, a zatem odchylenie ´cwiartkowe wynosi
Q
x
=
110 − 95
2
=
7, 5
Mi ˛edzy miarami zró˙znicowania obliczonymi dla tego
samego szeregu zachodz ˛
a nierówno´sci
Q
x
<
d
x
<
s
x
.
Istotnie, w przykładzie Q
x
=
7, 5, d
x
=
9, s
x
=
10, 5.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
W przykładzie 6 mieli´smy nast ˛epuj ˛
ace dane:
85, 85, 95, 95, 95, 100, 105, 110, 115, 115.
Kwartyl pierwszy i trzeci s ˛
a tu równe odpowiednio:
Q
1
=
95, Q
3
=
110, a zatem odchylenie ´cwiartkowe wynosi
Q
x
=
110 − 95
2
=
7, 5
Mi ˛edzy miarami zró˙znicowania obliczonymi dla tego
samego szeregu zachodz ˛
a nierówno´sci
Q
x
<
d
x
<
s
x
.
Istotnie, w przykładzie Q
x
=
7, 5, d
x
=
9, s
x
=
10, 5.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Pozycyjne miary zmienno ´sci
Odchylenie ´cwiartkowe
W przykładzie 6 mieli´smy nast ˛epuj ˛
ace dane:
85, 85, 95, 95, 95, 100, 105, 110, 115, 115.
Kwartyl pierwszy i trzeci s ˛
a tu równe odpowiednio:
Q
1
=
95, Q
3
=
110, a zatem odchylenie ´cwiartkowe wynosi
Q
x
=
110 − 95
2
=
7, 5
Mi ˛edzy miarami zró˙znicowania obliczonymi dla tego
samego szeregu zachodz ˛
a nierówno´sci
Q
x
<
d
x
<
s
x
.
Istotnie, w przykładzie Q
x
=
7, 5, d
x
=
9, s
x
=
10, 5.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zmienno ´sci
Przykład 7.
Załó˙zmy, ˙ze dwóch skoczków narciarskich wykonało na
pewnych zawodach po 4 skoki (np. 2 podczas treningu
i 2 podczas konkursu).
´
Srednia długo´s´c skoków skoczka A wyniosła 130 m,
a skoczka B – 110 m (a zatem skoczek A był lepszy!)
Odchylenia standardowe długo´sci skoków dla obu
zawodników były jednakowe i wynosiły 2,5 m.
Pytanie:
Czy mo˙zna powiedzie´c, ˙ze pod wzgl ˛edem
regularno´sci skoków obydwaj zawodnicy byli podobni?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zmienno ´sci
Przykład 7.
Załó˙zmy, ˙ze dwóch skoczków narciarskich wykonało na
pewnych zawodach po 4 skoki (np. 2 podczas treningu
i 2 podczas konkursu).
´
Srednia długo´s´c skoków skoczka A wyniosła 130 m,
a skoczka B – 110 m (a zatem skoczek A był lepszy!)
Odchylenia standardowe długo´sci skoków dla obu
zawodników były jednakowe i wynosiły 2,5 m.
Pytanie:
Czy mo˙zna powiedzie´c, ˙ze pod wzgl ˛edem
regularno´sci skoków obydwaj zawodnicy byli podobni?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zmienno ´sci
Przykład 7.
Załó˙zmy, ˙ze dwóch skoczków narciarskich wykonało na
pewnych zawodach po 4 skoki (np. 2 podczas treningu
i 2 podczas konkursu).
´
Srednia długo´s´c skoków skoczka A wyniosła 130 m,
a skoczka B – 110 m (a zatem skoczek A był lepszy!)
Odchylenia standardowe długo´sci skoków dla obu
zawodników były jednakowe i wynosiły 2,5 m.
Pytanie:
Czy mo˙zna powiedzie´c, ˙ze pod wzgl ˛edem
regularno´sci skoków obydwaj zawodnicy byli podobni?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zmienno ´sci
Przykład 7.
Załó˙zmy, ˙ze dwóch skoczków narciarskich wykonało na
pewnych zawodach po 4 skoki (np. 2 podczas treningu
i 2 podczas konkursu).
´
Srednia długo´s´c skoków skoczka A wyniosła 130 m,
a skoczka B – 110 m (a zatem skoczek A był lepszy!)
Odchylenia standardowe długo´sci skoków dla obu
zawodników były jednakowe i wynosiły 2,5 m.
Pytanie:
Czy mo˙zna powiedzie´c, ˙ze pod wzgl ˛edem
regularno´sci skoków obydwaj zawodnicy byli podobni?
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zró˙znicowania
Wbrew pozorom odpowied´z, nie jest twierdz ˛
aca. Pod
wzgl ˛edem regularno´sci skoków zawodnik A tak˙ze okazuje
si ˛e by´c troch ˛e lepszym!
Odchylenie standardowe równe 2,5 m bowiem ”wi ˛ecej
znaczy” w przypadku, gdy ´srednia odległo´s´c skoku wynosi
110 m, ni˙z w przypadku ´sredniej równej 130 m.
Aby to liczbowo wykaza´c, wystarczy obliczy´c iloraz
odchylenia standardowego do ´sredniej.
Dla zawodnika A wspomniany iloraz wynosi
2,5
130
≈ 0, 019, a
dla zawodnika B
2,5
110
≈ 0, 023, a wi ˛ec dla zawodnika B
zmienno´s´c skoków stanowi wi ˛ekszy ułamek ´sredniej.
Obliczone ilorazy mo˙zna wyrazi´c w procentach
odpowiednio: 1, 9% i 2, 3%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zró˙znicowania
Wbrew pozorom odpowied´z, nie jest twierdz ˛
aca. Pod
wzgl ˛edem regularno´sci skoków zawodnik A tak˙ze okazuje
si ˛e by´c troch ˛e lepszym!
Odchylenie standardowe równe 2,5 m bowiem ”wi ˛ecej
znaczy” w przypadku, gdy ´srednia odległo´s´c skoku wynosi
110 m, ni˙z w przypadku ´sredniej równej 130 m.
Aby to liczbowo wykaza´c, wystarczy obliczy´c iloraz
odchylenia standardowego do ´sredniej.
Dla zawodnika A wspomniany iloraz wynosi
2,5
130
≈ 0, 019, a
dla zawodnika B
2,5
110
≈ 0, 023, a wi ˛ec dla zawodnika B
zmienno´s´c skoków stanowi wi ˛ekszy ułamek ´sredniej.
Obliczone ilorazy mo˙zna wyrazi´c w procentach
odpowiednio: 1, 9% i 2, 3%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zró˙znicowania
Wbrew pozorom odpowied´z, nie jest twierdz ˛
aca. Pod
wzgl ˛edem regularno´sci skoków zawodnik A tak˙ze okazuje
si ˛e by´c troch ˛e lepszym!
Odchylenie standardowe równe 2,5 m bowiem ”wi ˛ecej
znaczy” w przypadku, gdy ´srednia odległo´s´c skoku wynosi
110 m, ni˙z w przypadku ´sredniej równej 130 m.
Aby to liczbowo wykaza´c, wystarczy obliczy´c iloraz
odchylenia standardowego do ´sredniej.
Dla zawodnika A wspomniany iloraz wynosi
2,5
130
≈ 0, 019, a
dla zawodnika B
2,5
110
≈ 0, 023, a wi ˛ec dla zawodnika B
zmienno´s´c skoków stanowi wi ˛ekszy ułamek ´sredniej.
Obliczone ilorazy mo˙zna wyrazi´c w procentach
odpowiednio: 1, 9% i 2, 3%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zró˙znicowania
Wbrew pozorom odpowied´z, nie jest twierdz ˛
aca. Pod
wzgl ˛edem regularno´sci skoków zawodnik A tak˙ze okazuje
si ˛e by´c troch ˛e lepszym!
Odchylenie standardowe równe 2,5 m bowiem ”wi ˛ecej
znaczy” w przypadku, gdy ´srednia odległo´s´c skoku wynosi
110 m, ni˙z w przypadku ´sredniej równej 130 m.
Aby to liczbowo wykaza´c, wystarczy obliczy´c iloraz
odchylenia standardowego do ´sredniej.
Dla zawodnika A wspomniany iloraz wynosi
2,5
130
≈ 0, 019, a
dla zawodnika B
2,5
110
≈ 0, 023, a wi ˛ec dla zawodnika B
zmienno´s´c skoków stanowi wi ˛ekszy ułamek ´sredniej.
Obliczone ilorazy mo˙zna wyrazi´c w procentach
odpowiednio: 1, 9% i 2, 3%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zró˙znicowania
Współczynniki zmienno ´sci – czyli rzecz o porównywaniu zró˙znicowania
Wbrew pozorom odpowied´z, nie jest twierdz ˛
aca. Pod
wzgl ˛edem regularno´sci skoków zawodnik A tak˙ze okazuje
si ˛e by´c troch ˛e lepszym!
Odchylenie standardowe równe 2,5 m bowiem ”wi ˛ecej
znaczy” w przypadku, gdy ´srednia odległo´s´c skoku wynosi
110 m, ni˙z w przypadku ´sredniej równej 130 m.
Aby to liczbowo wykaza´c, wystarczy obliczy´c iloraz
odchylenia standardowego do ´sredniej.
Dla zawodnika A wspomniany iloraz wynosi
2,5
130
≈ 0, 019, a
dla zawodnika B
2,5
110
≈ 0, 023, a wi ˛ec dla zawodnika B
zmienno´s´c skoków stanowi wi ˛ekszy ułamek ´sredniej.
Obliczone ilorazy mo˙zna wyrazi´c w procentach
odpowiednio: 1, 9% i 2, 3%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zmienno ´sci – Współczynniki zmienno ´sci
Wzgl ˛edne miary zró˙znicowania (inaczej
współczynniki
zmienno ´sci
), definiujemy jako ilorazy bezwzgl ˛ednych miar
zró˙znicowania do odpowiednich miar ´srednich.
Współczynniki te stosujemy przy porównaniach.
-
współczynik zmienno´sci V
d
x
oparty na odchyleniu
przeci ˛etnym
V
d
x
=
d
x
¯
x
· 100%,
-
współczynik zmienno´sci V
s
x
oparty na odchyleniu
standardowym
V
s
x
=
s
x
¯
x
· 100%,
-
współczynik zmienno´sci V
Q
x
oparty na odch. ´cwiartkowym
V
Q
x
=
Q
x
Me
· 100%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zmienno ´sci – Współczynniki zmienno ´sci
Wzgl ˛edne miary zró˙znicowania (inaczej
współczynniki
zmienno ´sci
), definiujemy jako ilorazy bezwzgl ˛ednych miar
zró˙znicowania do odpowiednich miar ´srednich.
Współczynniki te stosujemy przy porównaniach.
-
współczynik zmienno´sci V
d
x
oparty na odchyleniu
przeci ˛etnym
V
d
x
=
d
x
¯
x
· 100%,
-
współczynik zmienno´sci V
s
x
oparty na odchyleniu
standardowym
V
s
x
=
s
x
¯
x
· 100%,
-
współczynik zmienno´sci V
Q
x
oparty na odch. ´cwiartkowym
V
Q
x
=
Q
x
Me
· 100%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zmienno ´sci – Współczynniki zmienno ´sci
Wzgl ˛edne miary zró˙znicowania (inaczej
współczynniki
zmienno ´sci
), definiujemy jako ilorazy bezwzgl ˛ednych miar
zró˙znicowania do odpowiednich miar ´srednich.
Współczynniki te stosujemy przy porównaniach.
-
współczynik zmienno´sci V
d
x
oparty na odchyleniu
przeci ˛etnym
V
d
x
=
d
x
¯
x
· 100%,
-
współczynik zmienno´sci V
s
x
oparty na odchyleniu
standardowym
V
s
x
=
s
x
¯
x
· 100%,
-
współczynik zmienno´sci V
Q
x
oparty na odch. ´cwiartkowym
V
Q
x
=
Q
x
Me
· 100%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zmienno ´sci – Współczynniki zmienno ´sci
Wzgl ˛edne miary zró˙znicowania (inaczej
współczynniki
zmienno ´sci
), definiujemy jako ilorazy bezwzgl ˛ednych miar
zró˙znicowania do odpowiednich miar ´srednich.
Współczynniki te stosujemy przy porównaniach.
-
współczynik zmienno´sci V
d
x
oparty na odchyleniu
przeci ˛etnym
V
d
x
=
d
x
¯
x
· 100%,
-
współczynik zmienno´sci V
s
x
oparty na odchyleniu
standardowym
V
s
x
=
s
x
¯
x
· 100%,
-
współczynik zmienno´sci V
Q
x
oparty na odch. ´cwiartkowym
V
Q
x
=
Q
x
Me
· 100%.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Podział
Klasyczne miary zmienno´sci
Pozycyjne miary zmienno´sci
Wzgl ˛edne miary zró˙znicowania
Wzgl ˛edne miary zmienno ´sci – Współczynniki zmienno ´sci
Wzgl ˛edne miary zró˙znicowania (inaczej
współczynniki
zmienno ´sci
), definiujemy jako ilorazy bezwzgl ˛ednych miar
zró˙znicowania do odpowiednich miar ´srednich.
Współczynniki te stosujemy przy porównaniach.
-
współczynik zmienno´sci V
d
x
oparty na odchyleniu
przeci ˛etnym
V
d
x
=
d
x
¯
x
· 100%,
-
współczynik zmienno´sci V
s
x
oparty na odchyleniu
standardowym
V
s
x
=
s
x
¯
x
· 100%,
-
współczynik zmienno´sci V
Q
x
oparty na odch. ´cwiartkowym
V
Q
x
=
Q
x
Me
· 100%.
Agnieszka Rossa
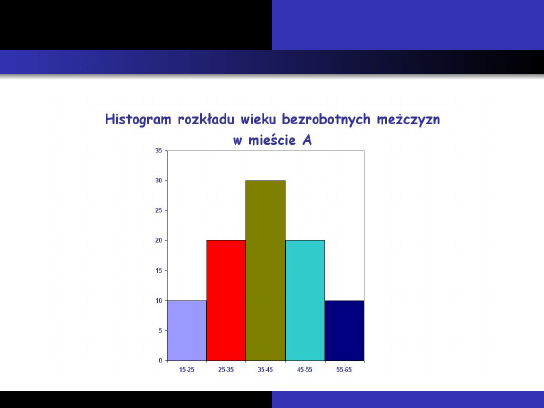
Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Analiza asymetrii – Przykład histogramu szeregu symetrycznego
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa
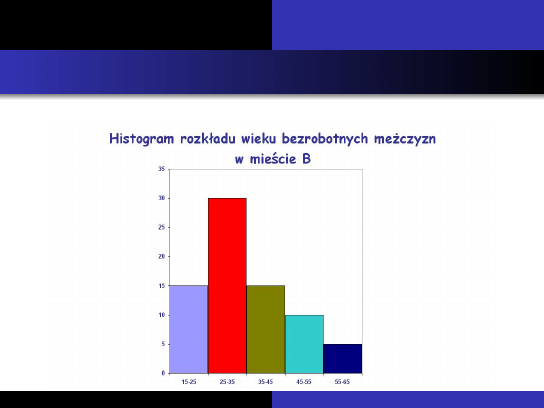
Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Analiza asymetrii – Przykład histogramu szeregu asymetrycznego
prawostronnie
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa
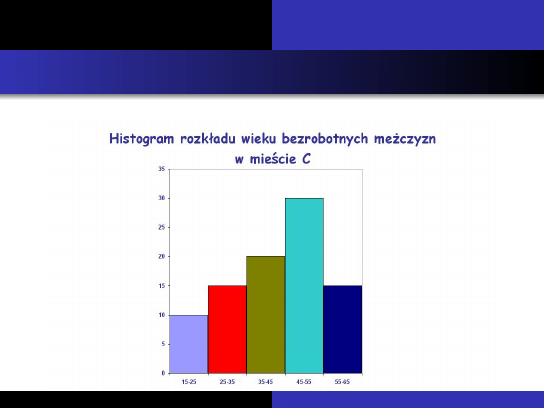
Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Analiza asymetrii – Przykład histogramu szeregu asymetrycznego
lewostronnie
Copyright Giorgio Krenkel and Alex Sandri, GNU Free Documentation License, Low Resolution
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii
W szeregach symetrycznych ´srednia arytmetyczna równa
jest medianie i dominancie, czyli
¯
x = Me = Do,
natomiast ró˙znica mi ˛edzy kwartylem trzecim a median ˛
a
równa jest ró˙znicy mi ˛edzy median ˛
a a kwartylem
pierwszym, czyli
Q
3
− Me = Me − Q
1
.
Przy asymetrii lewostronnej zachodz ˛
a nierówno´sci
¯
x ≤ Me ≤ Do,
(
Q
3
− Me) − (Me − Q
1
) <
0,
natomiast przy asymetrii prawostronnej maj ˛
a miejsce
nierówno´sci odwrotne.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii
W szeregach symetrycznych ´srednia arytmetyczna równa
jest medianie i dominancie, czyli
¯
x = Me = Do,
natomiast ró˙znica mi ˛edzy kwartylem trzecim a median ˛
a
równa jest ró˙znicy mi ˛edzy median ˛
a a kwartylem
pierwszym, czyli
Q
3
− Me = Me − Q
1
.
Przy asymetrii lewostronnej zachodz ˛
a nierówno´sci
¯
x ≤ Me ≤ Do,
(
Q
3
− Me) − (Me − Q
1
) <
0,
natomiast przy asymetrii prawostronnej maj ˛
a miejsce
nierówno´sci odwrotne.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Wska´znik sko ´sno ´sci
Własno´sci te wykorzystuje si ˛e przy konstrukcji wybranych
mierników asymetrii.
Wska´znik sko ´sno ´sci
definiujemy wzorem
M
s
= ¯
x − Do.
Znak tego wska´znika informuje o kierunku asymetrii:
znak
ujemny
oznacza asymetri ˛e lewostronn ˛
a (nazywan ˛
a tak˙ze
asymetri ˛
a ujemn ˛
a), natomiast
znak dodatni
oznacza
asymetri ˛e prawostronn ˛
a (dodatni ˛
a). W przypadku
szeregów symetrycznych mamy M
s
=
0.
Wska´znik M
s
jest
miar ˛
a mianowan ˛
a
, o jego warto´sci
decyduje nie tylko stopie ´n sko´sno´sci szeregu, ale równie˙z
ogólny poziom cechy w danej zbiorowo´sci. Z tego powodu
cz ˛e´sciej obliczany jest (wzgl ˛edny) współczynnik sko´sno´sci.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Wska´znik sko ´sno ´sci
Własno´sci te wykorzystuje si ˛e przy konstrukcji wybranych
mierników asymetrii.
Wska´znik sko ´sno ´sci
definiujemy wzorem
M
s
= ¯
x − Do.
Znak tego wska´znika informuje o kierunku asymetrii:
znak
ujemny
oznacza asymetri ˛e lewostronn ˛
a (nazywan ˛
a tak˙ze
asymetri ˛
a ujemn ˛
a), natomiast
znak dodatni
oznacza
asymetri ˛e prawostronn ˛
a (dodatni ˛
a). W przypadku
szeregów symetrycznych mamy M
s
=
0.
Wska´znik M
s
jest
miar ˛
a mianowan ˛
a
, o jego warto´sci
decyduje nie tylko stopie ´n sko´sno´sci szeregu, ale równie˙z
ogólny poziom cechy w danej zbiorowo´sci. Z tego powodu
cz ˛e´sciej obliczany jest (wzgl ˛edny) współczynnik sko´sno´sci.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Wska´znik sko ´sno ´sci
Własno´sci te wykorzystuje si ˛e przy konstrukcji wybranych
mierników asymetrii.
Wska´znik sko ´sno ´sci
definiujemy wzorem
M
s
= ¯
x − Do.
Znak tego wska´znika informuje o kierunku asymetrii:
znak
ujemny
oznacza asymetri ˛e lewostronn ˛
a (nazywan ˛
a tak˙ze
asymetri ˛
a ujemn ˛
a), natomiast
znak dodatni
oznacza
asymetri ˛e prawostronn ˛
a (dodatni ˛
a). W przypadku
szeregów symetrycznych mamy M
s
=
0.
Wska´znik M
s
jest
miar ˛
a mianowan ˛
a
, o jego warto´sci
decyduje nie tylko stopie ´n sko´sno´sci szeregu, ale równie˙z
ogólny poziom cechy w danej zbiorowo´sci. Z tego powodu
cz ˛e´sciej obliczany jest (wzgl ˛edny) współczynnik sko´sno´sci.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Wska´znik sko ´sno ´sci
Własno´sci te wykorzystuje si ˛e przy konstrukcji wybranych
mierników asymetrii.
Wska´znik sko ´sno ´sci
definiujemy wzorem
M
s
= ¯
x − Do.
Znak tego wska´znika informuje o kierunku asymetrii:
znak
ujemny
oznacza asymetri ˛e lewostronn ˛
a (nazywan ˛
a tak˙ze
asymetri ˛
a ujemn ˛
a), natomiast
znak dodatni
oznacza
asymetri ˛e prawostronn ˛
a (dodatni ˛
a). W przypadku
szeregów symetrycznych mamy M
s
=
0.
Wska´znik M
s
jest
miar ˛
a mianowan ˛
a
, o jego warto´sci
decyduje nie tylko stopie ´n sko´sno´sci szeregu, ale równie˙z
ogólny poziom cechy w danej zbiorowo´sci. Z tego powodu
cz ˛e´sciej obliczany jest (wzgl ˛edny) współczynnik sko´sno´sci.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Współczynnik sko ´sno ´sci
Współczynnik sko ´sno ´sci
obliczamy ze wzoru:
W
s
=
M
s
s
x
=
¯
x − Do
s
x
lub
W
s
=
M
s
d
x
=
¯
x − Do
d
x
.
Współczynnik W
s
przyjmuje na ogół warto´sci z przedziału
[−
1, 1]
(w przypadku skrajnej asymetrii mo˙ze si ˛e zdarzy´c,
˙ze jego warto´s´c wykroczy poza podany przedział).
Znak współczynnika W
s
informuje o
kierunku asymetrii
, a
warto´s´c bezwzgl ˛edna –
o sile asymetrii
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Współczynnik sko ´sno ´sci
Współczynnik sko ´sno ´sci
obliczamy ze wzoru:
W
s
=
M
s
s
x
=
¯
x − Do
s
x
lub
W
s
=
M
s
d
x
=
¯
x − Do
d
x
.
Współczynnik W
s
przyjmuje na ogół warto´sci z przedziału
[−
1, 1]
(w przypadku skrajnej asymetrii mo˙ze si ˛e zdarzy´c,
˙ze jego warto´s´c wykroczy poza podany przedział).
Znak współczynnika W
s
informuje o
kierunku asymetrii
, a
warto´s´c bezwzgl ˛edna –
o sile asymetrii
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Współczynnik sko ´sno ´sci
Współczynnik sko ´sno ´sci
obliczamy ze wzoru:
W
s
=
M
s
s
x
=
¯
x − Do
s
x
lub
W
s
=
M
s
d
x
=
¯
x − Do
d
x
.
Współczynnik W
s
przyjmuje na ogół warto´sci z przedziału
[−
1, 1]
(w przypadku skrajnej asymetrii mo˙ze si ˛e zdarzy´c,
˙ze jego warto´s´c wykroczy poza podany przedział).
Znak współczynnika W
s
informuje o
kierunku asymetrii
, a
warto´s´c bezwzgl ˛edna –
o sile asymetrii
.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Klasyczny współczynnik asymetrii
Klasyczny współczynnik asymetrii
jest cz ˛esto
stosowan ˛
a miar ˛
a asymetrii wyra˙zon ˛
a wzorem:
A
s
=
µ
3
s
3
x
,
gdzie s
x
oznacza odchylenie standardowe, natomiast µ
3
jest tzw. momentem centralnym trzeciego rz ˛edu, który
definiujemy nast ˛epuj ˛
aco:
µ
3
=
1
n
P
n
i=1
(
x
i
− ¯
x )
3
,
dla szeregu szczegółowego,
1
n
P
k
i=1
(
x
i
− ¯
x )
3
n
i
,
dla szeregu r. punktowego,
1
n
P
k
i=1
( ˙
x
i
− ¯
x )
3
n
i
,
dla szeregu r. z przedziałami.
Współczynnik A
s
przyjmuje na ogół warto´sci z przedziału
[−
2, 2]
(w przypadku skrajnej asymetrii jego warto´s´c mo˙ze
wykroczy´c poza ten przedział).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Klasyczny współczynnik asymetrii
Klasyczny współczynnik asymetrii
jest cz ˛esto
stosowan ˛
a miar ˛
a asymetrii wyra˙zon ˛
a wzorem:
A
s
=
µ
3
s
3
x
,
gdzie s
x
oznacza odchylenie standardowe, natomiast µ
3
jest tzw. momentem centralnym trzeciego rz ˛edu, który
definiujemy nast ˛epuj ˛
aco:
µ
3
=
1
n
P
n
i=1
(
x
i
− ¯
x )
3
,
dla szeregu szczegółowego,
1
n
P
k
i=1
(
x
i
− ¯
x )
3
n
i
,
dla szeregu r. punktowego,
1
n
P
k
i=1
( ˙
x
i
− ¯
x )
3
n
i
,
dla szeregu r. z przedziałami.
Współczynnik A
s
przyjmuje na ogół warto´sci z przedziału
[−
2, 2]
(w przypadku skrajnej asymetrii jego warto´s´c mo˙ze
wykroczy´c poza ten przedział).
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Pozycyjny współczynnik asymetrii
Pozycyjny współczynnik asymetrii
okre´sla sił ˛e i kierunek
asymetrii dla tych jednostek zbiorowo´sci, które znajduj ˛
a si ˛e
mi ˛edzy pierwszym i trzecim kwartylem, a wi ˛ec w
zaw ˛e˙zonym obszarze zmienno´sci cechy.
Definiujemy go wzorem
A
Q
=
(
Q
3
− Me) − (Me − Q
1
)
(
Q
3
− Me) + (Me − Q
1
)
=
=
Q
3
− 2Me + Q
1
Q
3
− Q
1
.
Współczynnik A
Q
przyjmuje warto´s´c z przedziału
[−
1, 1]
.
Podobnie, jak mierniki W
s
i A
s
, jego znak informuje o
kierunku, a warto´s´c bezwzgl ˛edna – o sile asymetrii.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Pozycyjny współczynnik asymetrii
Pozycyjny współczynnik asymetrii
okre´sla sił ˛e i kierunek
asymetrii dla tych jednostek zbiorowo´sci, które znajduj ˛
a si ˛e
mi ˛edzy pierwszym i trzecim kwartylem, a wi ˛ec w
zaw ˛e˙zonym obszarze zmienno´sci cechy.
Definiujemy go wzorem
A
Q
=
(
Q
3
− Me) − (Me − Q
1
)
(
Q
3
− Me) + (Me − Q
1
)
=
=
Q
3
− 2Me + Q
1
Q
3
− Q
1
.
Współczynnik A
Q
przyjmuje warto´s´c z przedziału
[−
1, 1]
.
Podobnie, jak mierniki W
s
i A
s
, jego znak informuje o
kierunku, a warto´s´c bezwzgl ˛edna – o sile asymetrii.
Agnieszka Rossa

Wska´zniki nat ˛e˙zenia, wska´zniki struktury
Miary asymetrii – Pozycyjny współczynnik asymetrii
Pozycyjny współczynnik asymetrii
okre´sla sił ˛e i kierunek
asymetrii dla tych jednostek zbiorowo´sci, które znajduj ˛
a si ˛e
mi ˛edzy pierwszym i trzecim kwartylem, a wi ˛ec w
zaw ˛e˙zonym obszarze zmienno´sci cechy.
Definiujemy go wzorem
A
Q
=
(
Q
3
− Me) − (Me − Q
1
)
(
Q
3
− Me) + (Me − Q
1
)
=
=
Q
3
− 2Me + Q
1
Q
3
− Q
1
.
Współczynnik A
Q
przyjmuje warto´s´c z przedziału
[−
1, 1]
.
Podobnie, jak mierniki W
s
i A
s
, jego znak informuje o
kierunku, a warto´s´c bezwzgl ˛edna – o sile asymetrii.
Agnieszka Rossa
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron