1
Plan wykładu
1. Wymagania do aparatury pomiarowej
2. Ograniczenia wyst
ę
puj
ą
ce podczas
pomiarów wielko
ś
ci elektrycznych.
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci.
4. Przykładowy schemat strukturalny
multimetru elektronicznego cyfrowego
(DMM - ang. Digital Multi-Meter).
1. Wymagania do aparatury pomiarowej
Podstawowymi wymaganiami s
ą
:
• Mo
ż
liwo
ść
pomiaru warto
ś
ci wielko
ś
ci w zadanym
zakresie (tak małych jak i du
ż
ych warto
ś
ci), jest to
wymagania amplitudowe;
• Mo
ż
liwo
ść
pomiarów wielokanałowych – kilka wielko
ś
ci
jednego lub ró
ż
nego rodzaju
• Brak obci
ąż
enia obiektu badanego – odpowiednia
warto
ść
rezystancji wej
ś
ciowej
• Zadana dokładno
ść
pomiarów, zapewnia si
ę
odpowiedni
ą
klas
ą
dokładno
ś
ci woltomierza oraz innymi
warto
ś
ciami jego parametrów: stabilno
ś
ci
ą
temperaturow
ą
oraz czasow
ą
, odporno
ś
ci
ą
na inne wielko
ś
ci wpływaj
ą
ce
1. Wymagania do aparatury pomiarowej
• Odporno
ść
na oddziaływania zakłóce
ń
tak regularnych
jak i losowych wpływu zakłóce
ń
to wymaganie jest wa
ż
ne
przy pomiarach wielko
ś
ci niskiego poziomu, w warunkach
przemysłowych
• Szybko
ść
pomiaru – to wymaganie jest wa
ż
ne przy
pomiarach wielko
ś
ci szybko zmiennych (dynamicznych),.
• Mo
ż
liwo
ść
współpracy z PC – jest to wa
ż
ne przy
automatyzacji pomiarów
• Mo
ż
liwo
ść
opracowania wyników wg zadanego
algorytmu
• Łatwo
ść
obsługi
• Niska cena oraz niski koszty pomiarów
2. Ograniczenia wyst
ę
puj
ą
ce podczas
pomiarów wielko
ś
ci elektrycznych.
Fundamentalnym czynnikiem ograniczaj
ą
cym jest szum cieplny lub
szum Jonson’a.
Na dowolnej rezystancji R energia cieplna powoduje ruch no
ś
ników
ładunków elektrycznych, który z kolei powoduj
ą
szum
elektryczny.
Moc tego szumu opisuje si
ę
wzorem
P=4kTB,
gdzie: k=1.38·10
-23
J/K- stała Boltsmana;
T –temperatura (K);
B – pasmo cz
ę
stotliwo
ś
ciowe szumu (Hz).
Warto
ść
skuteczna szumu Jonsona U
sz
na rezystancji (R) równa si
ę
:
a warto
ść
pr
ą
du szumu Jonsona I
sz
:
kBTR
PR
U
sz
4
=
=
R
kBT
R
P
I
sz
4
=
=
2. Ograniczenia wyst
ę
puj
ą
ce podczas
pomiarów wielko
ś
ci elektrycznych.
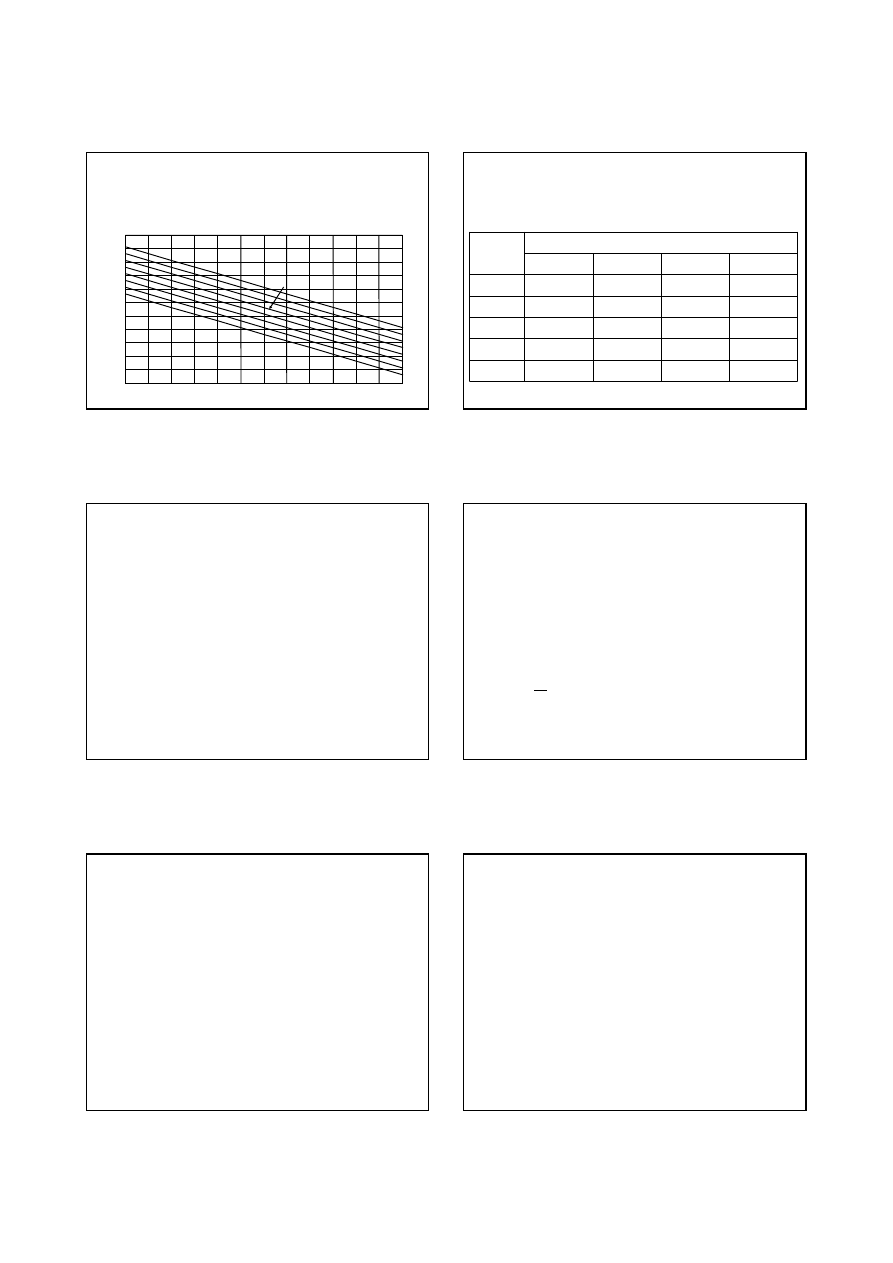
Zale
ż
no
ś
ci warto
ś
ci napi
ę
cia oraz pr
ą
du szumu cieplnego przy
T=295 K (22
o
C) jako funkcje rezystancji oraz szeroko
ś
ci pasma
pokazane ni
ż
ej
1
Ω
1 k
Ω
0.01
0.1
10
100
10
100
B=0,1 Hz
B=1 MHz
1 µV
B=1 kHz
1 mV
1 V
1 nV
0.01
0.1
1 M
Ω
1 G
Ω
2. Ograniczenia wyst
ę
puj
ą
ce podczas
pomiarów wielko
ś
ci elektrycznych.
Teoretyczna granica czuło
ś
ci pomiaru napi
ę
cia
100 mV
3 mV
100 µV
30 µV
1 TΩ
3 mV
100 µV
3 µV
1 µV
1 GΩ
100 µV
3 µV
0,1 µV
30 nV
1 MΩ
3 µV
0,1 µV
3 nV
1 nV
1 kΩ
0,1 µV
3 nV
0,1 nV
0,03 nV
1 Ω
1 MHz
1 kHz
1 Hz
0,1 Hz
Pasmo częstotliwości
Rezystancja
2
2. Ograniczenia wyst
ę
puj
ą
ce podczas
pomiarów wielko
ś
ci elektrycznych.
Zale
ż
no
ś
ci warto
ś
ci skutecznej pr
ą
du szumu cieplnego przy T=295 K
(22
o
C) jako funkcje rezystancji oraz szeroko
ś
ci pasma
1
Ω
1 k
Ω
0.01
0.1
10
100
10
100
0,1 Hz
1 MHz
1 kHz
1 pA
1 nA
1 µA
1 fA
0.01
0.1
1 M
Ω
1 G
Ω
T
Ω
2. Wymagania do woltomierzy DC. Zakresy
Teoretyczna granica czuło
ś
ci pomiaru pr
ą
du
0,1 pA
3 fA
0,1 fA
0,03 fA
1 TOhm
3 pA
0,1 pA
3 fA
1 fA
1 GOhm
100 pA
3 pA
0,1 pA
0,03 pA
1 MOhm
3 nA
100 pA
3 pA
1 pA
1 kOhm
100 nA
3 nA
100 pA
30 pA
1 Ohm
1 MHz
1 kHz
1 Hz
0,1 Hz
Pasmo częstotliwości
Rezystancja
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
W zale
ż
no
ś
ci od zakresów i warunków pomiaru (wła
ś
ciwo
ś
ci obiektu –
rezystancja, pasmo cz
ę
stotliwo
ś
ci) rozró
ż
nia si
ę
:
•
multimetry;
•
elektrometry,
•
nanowoltomierzy,
•
pikoamperomierzy,
•
mikro-omomierzy,
•
przyrz
ą
dy
ź
ródła – mierniki,
• oraz inne.
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
Multimetry
s
ą
to przyrz
ą
dy dla pomiarów:
- napi
ęć
powy
ż
ej 1 mkV ;
- pr
ą
dów powy
ż
ej 1 mkA, oraz
- rezystancji poni
ż
ej 1 GOhm.
Rezystancja wej
ś
ciowa woltomierza (Rv) DMM stanowi od
około (1-10-100) MOhm do maksymalnie (1-10) GOhm
Rozdzielczo
ść
DMM wynosi od 3½ cyfr dziesi
ą
tkowych
(bardzo tanie) a
ż
do drogich 6½-7½ cyfr dziesi
ą
tkowych.
Maksymalna czuło
ść
DMM stanowi do (0,1-0,01) mkV (do
10 nV).
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
Elektrometry
S
ą
to przyrz
ą
dy pomiarowe dla pomiarów napi
ęć
, pr
ą
dów, ładunku i
rezystancji przy nast
ę
pnych warunkach:
–
pr
ą
dów poni
ż
ej 1 µA do 100 pA, napi
ę
cie
ź
ródła przy
pomiarach pr
ą
du jest poni
ż
ej kilku set mV;
–
napi
ę
cia poni
ż
ej 1 µV,
ź
ródło napi
ę
cia ma rezystancj
ą
wyj
ś
ciow
ą
rz
ę
du 1 M
Ω
i wy
ż
ej do 10 T
Ω
;
–
rezystancji powy
ż
ej 1 G
Ω
;
–
pomiar ładunku;
–
pomiary przy porównywalnych warto
ś
ciach szumów cieplnych
oraz innych.
Rezystancja wej
ś
ciowa woltomierza elektrometru stanowi typowo od
około 100 T
Ω
nawet do około 100 P
Ω
.
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
Nanowoltomierzy
S
ą
to bardzo czułe, pracuj
ą
cy w pobli
ż
u teoretycznej granicy
czuło
ś
ci w porównaniu do elektrometrów.
Nanowoltomierzy
zapewniaj
ą
te
ż
inne wła
ś
ciwo
ś
ci, np.
lepsz
ą
szybko
ść
pomiaru, liepsze tłumienie szumów i
zakłóce
ń
.
3
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
Pikoamperomierze
S
ą
to bardzo czułe, pracuj
ą
cy w pobli
ż
u teoretycznej granicy
czuło
ś
ci
oraz przy mniejszych warto
ś
ciach spadku
napi
ę
cia
(tzw. votage
burden) w porównaniu do
elektrometrów.
Pikoamperomierze zapewniaj
ą
te
ż
inne wła
ś
ciwo
ś
ci, np.
lepsz
ą
szybko
ść
pomiaru lub mo
ż
liwo
ść
logarytmicznej
charakterystyki.
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
Mikro-omomierzy
Mikro-omomierz jest to specjalny omomierz przeznaczony do
pomiaru bardzo niskich warto
ś
ci rezystancji.
Typowy mikro-omomierz ma czuło
ść
do około 10 µ
Ω
.
Pomiar małych rezystancji odbywa si
ę
przez 4-przewodowe
podł
ą
czenie obiektu badanego (w celu eliminacji wpływu
rezystancji przewodów) oraz charakteryzuj
ą
si
ę
dodatkowymi (w porównaniu do DMM) funkcjami.
Z po
ś
ród nich jest to mo
ż
liwo
ść
kompensacji napi
ę
cia
przesuni
ę
cia (offset), spowodowanego przykładowo
termoelektryczn
ą
SEM, mo
ż
liwo
ść
ograniczenia napi
ę
cia
wzdłu
ż
badanej rezystancji do bardzo niskiego poziomu
(typowo poni
ż
ej 20 mV), co jest bardzo wa
ż
ne przy
testowaniu takich elementów jak kontakty przeł
ą
czników,
kluczy oraz (rele) kontaktronów.
3. Klasyfikacja przyrz
ą
dów pomiarowych
według ich funkcji i wła
ś
ciwo
ś
ci
Przyrz
ą
dy
ź
ródła – mierniki
Sourse-Measure Unit - SMU
s
ą
to przyrz
ą
dy, funkcjami których s
ą
:
- pomiar napi
ę
cia;
- pomiar pr
ą
du;
-
ź
ródło napi
ę
cia;
-
ź
ródło pr
ą
du.
SMU pozwalaj
ą
na jednoczesne dokładne (o zadanej
warto
ś
ci):
- wymuszanie obiektu napi
ę
ciowe i pomiar pr
ą
du odpowiedzi
oraz
- wymuszanie obiektu pr
ą
dowe i pomiar napi
ę
cia odpowiedzi.
4. Przykładowy schemat strukturalny
multimetru elektronicznego cyfrowego
(DMM - ang. Digital Multi-Meter)
AC
Wzmacniacz/
dzielnik
AC
przetwornik
DC
Wzmacniacz/
dzielnik
Ohms
przetwornik
AC
DC
Ohms
I
→
→
→
→
U
przetw
ornik
HI
LO
W
e
j
ś
c
ie
AC
DC
Ohms
V
A
A
A/C
przetwornik
(+procesor)
Odczyt
Cyfrowy
(display)
Wyj
ś
cie
Cyfrowe
(RS 232,
GPIB,
USB)
Plan wykładu
1. Wymagania do woltomierzy DC.
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
3. Układy wej
ś
ciowe woltomierza.
4. Układ wej
ś
ciowy woltomierza ze
wzmacniaczem instrumentalnym.
1. Wymagania do woltomierzy DC.
Ogólnymi wymaganiami do woltomierze przy pomiarach warto
ś
ci napi
ę
cia
DC s
ą
:
1.
Mo
ż
liwo
ść
pomiaru warto
ś
ci napi
ę
cia w zadanym zakresie
(małych jak i du
ż
ych warto
ś
ci napi
ę
cia),
jest to wymagania amplitudowe;
2.
Brak obci
ąż
enia obiektu badanego – odpowiednia warto
ść
rezystancji wej
ś
ciowej;
4
1. Wymagania do woltomierzy DC.
Ogólnymi wymaganiami do woltomierze przy pomiarach warto
ś
ci napi
ę
cia
DC s
ą
:
3.
Zadana dokładno
ść
pomiaru, zapewnia si
ę
odpowiedni
ą
klas
ą
dokładno
ś
ci woltomierza oraz innymi warto
ś
ciami jego parametrów:
stabilno
ś
ci
ą
temperaturow
ą
oraz czasow
ą
, odporno
ś
ci
ą
na inne
wielko
ś
ci wpływaj
ą
ce min. Zakłócenia;
4.
Szybko
ść
pomiaru – ten problem jest wa
ż
ny przy pomiarach
wielko
ś
ci szybko zmiennych (dynamicznych), jest zwi
ą
zany z
odporno
ś
ci
ą
do wpływu zakłóce
ń
;
5.
Mo
ż
liwo
ść
przesyłania danych pomiarowych do PC – jest to
wa
ż
ne przy automatyzacji pomiarów oraz opracowania wyników.
Ograniczenia szumowe wyst
ę
puj
ą
ce podczas
pomiarów napi
ę
cia
Fundamentalnym czynnikiem ograniczaj
ą
cym jest szum cieplny lub
szum Jonson’a.
Na dowolnej rezystancji R energia cieplna powoduje ruch no
ś
ników
ładunków elektrycznych, który z kolei powoduj
ą
szum
elektryczny.
Moc tego szumu opisuje si
ę
wzorem
P=4kTB,
gdzie: k=1.38·10
-23
J/K- stała Boltsmana;
T –temperatura (K);
B – pasmo cz
ę
stotliwo
ś
ciowe szumu (Hz).
Warto
ść
skuteczna szumu Jonsona U
sz
na rezystancji (R) równa si
ę
:
kBTR
PR
U
sz
4
=
=
Ograniczenia szumowe wyst
ę
puj
ą
ce podczas
pomiarów napi
ę
cia
Zale
ż
no
ś
ci warto
ś
ci napi
ę
cia szumu cieplnego przy T=295 K (22
o
C)
jako funkcje rezystancji oraz szeroko
ś
ci pasma
1
Ω
1 k
Ω
0.01
0.1
10
100
10
100
B=0,1 Hz
B=1 MHz
1 µV
B=1 kHz
1 mV
1 V
1 nV
0.01
0.1
1 M
Ω
1 G
Ω
Teoretyczna szumowa granica przy
pomiarach napi
ę
cia
100 mV
3 mV
100 µV
30 µV
1 TΩ
3 mV
100 µV
3 µV
1 µV
1 GΩ
100 µV
3 µV
0,1 µV
30 nV
1 MΩ
3 µV
0,1 µV
3 nV
1 nV
1 kΩ
0,1 µV
3 nV
0,1 nV
0,03 nV
1 Ω
1 MHz
1 kHz
1 Hz
0,1 Hz
Pasmo częstotliwości
Rezystancja
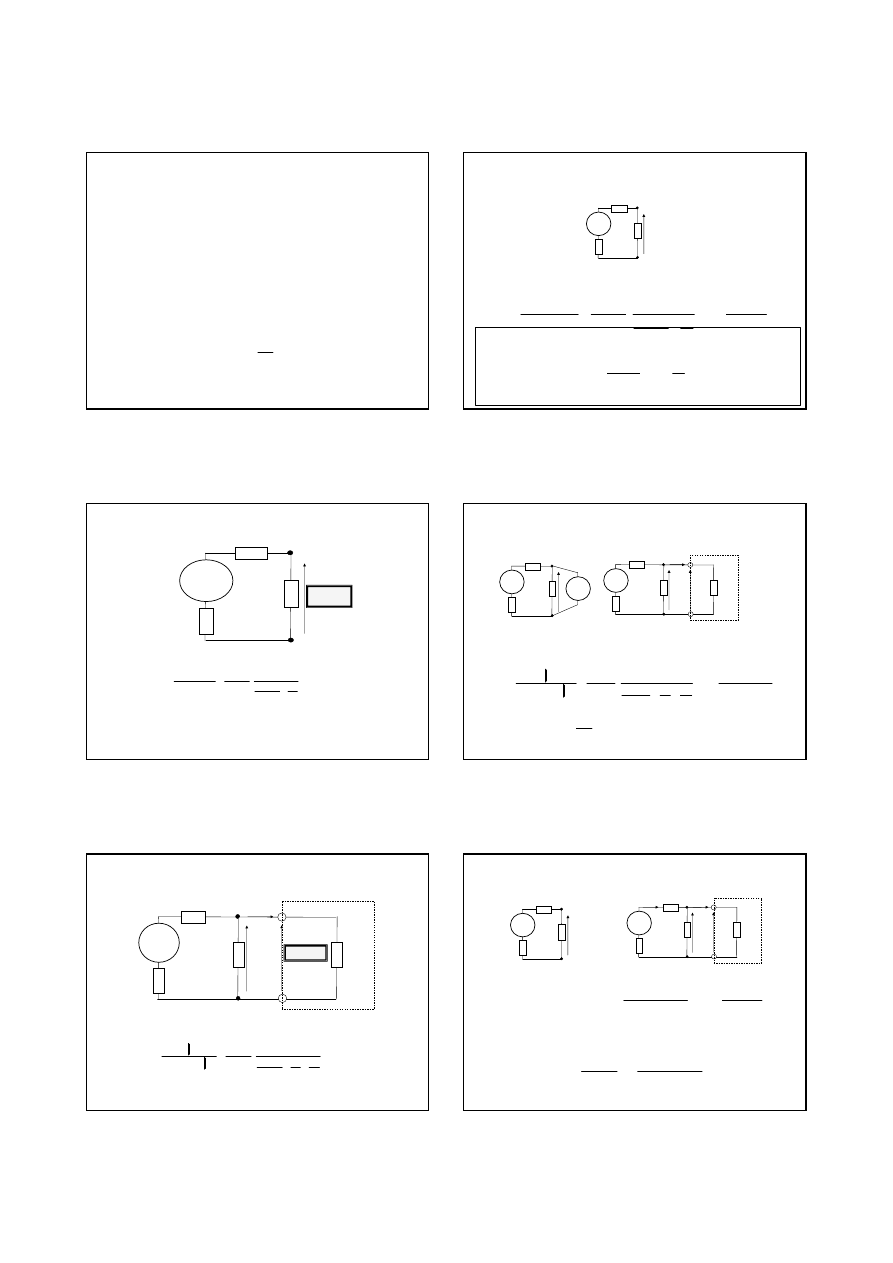
1. Wymagania do woltomierzy DC.
Zakresy
Mo
ż
liwo
ść
pomiaru warto
ś
ci napi
ę
cia w ró
ż
nych zakresach zapewnia si
ę
wykorzystaniem na wej
ś
ciu woltomierza
- wzmacniacza - dla małych warto
ś
ci napi
ęć
;
- dzielnika – dla du
ż
ych warto
ś
ci napi
ęć
.
8.937
mV
mV
mV
mV
0,1 mV 1 mV 10 mV 100mV
1 V 10 V 100 V 1000 V
1. Wymagania do woltomierzy DC.
Zakresy
Typowe zakresy woltomierzy s
ą
krotne:
warto
ś
ciom 10
n
, gdzie n – liczba całkowita, ujemna i
dodatnia, na przykład
0,001 V (1 mV) 0,01 V (10 mV); 0,1 V (100 mV); 1 V, 10 V,
100 V; 1000 V,
lub krotne warto
ś
ciom 2·10
n
, na przykład :
0,002 V (2 mV) 0,02 V (20 mV); 0,2 V (200 mV); 2 V, 20 V,
200 V.
5
1. Wymagania do woltomierzy DC.
Zakresy
Z zakresami pomiarowymi s
ą
powi
ą
zane liczba cyfr (miejsc
znacz
ą
cych) wskazania oraz warto
ść
cyfry najmniej
znacz
ą
cej.
W woltomierze cyfrowym z liczb
ą
cyfr dziesi
ą
tkowych n z
zakresem 10
n
krotnym istnieje ró
ż
nych wskaza
ń
od do ,
przy tym warto
ś
ci cyfry najmniej znacz
ą
cej – CNZ (ang. LSB)
równa si
ę
:
3
2
1
n
0
...
00
3
2
1
n
9
...
99
n
z
U
LSB
CNZ
10
=
=
1. Wymagania do woltomierzy DC.
Rezystancja wej
ś
ciowa
Do podł
ą
czenia woltomierza warto
ść
tego napi
ę
cia wynosi
Po podł
ą
czeniu woltomierza wynik pomiaru tego napi
ę
cia
wynosi
R
0
U
x
U
0
R
1
R
2
V
V
V
V
R
R
R
R
R
R
U
R
R
R
R
R
R
U
U
1
1
1
1
2
1
0
1
0
0
2
1
0
2
0
+
+
+
⋅
+
=
+
+
=
2
01
01
0
2
1
0
1
0
0
2
1
0
2
0
1
1
1
G
G
G
U
R
R
R
R
R
U
R
R
R
R
U
U
x
+
⋅
=
+
+
⋅
+
=
+
+
=
2
2
1
0
01
1
,
1
R
G
R
R
G
=
+
=
1. Wymagania do woltomierzy DC.
Rezystancja
wej
ś
ciowa
Do podł
ą
czenia woltomierza warto
ść
tego napi
ę
cia wynosi
V
R
R
R
R
R
U
R
R
R
R
U
U
x
9975
.
4
1
1
1
2
1
0
1
0
0
2
1
0
2
0
=
+
+
⋅
+
=
+
+
=
100
Ω
10V
100k
Ω
100k
Ω
4.9975V
1. Wymagania do woltomierzy DC.
Rezystancja wej
ś
ciowa
Po podł
ą
czeniu woltomierza wynik pomiaru tego napi
ę
cia
wynosi
I
V
R
0
U
V
U
0
R
1
R
2
R
V
V
U
x’
R
0
U
x
U
0
R
1
R
2
V
V
V
V
V
V
G
G
G
G
U
R
R
R
R
R
R
U
R
R
R
R
R
R
U
U
+
+
⋅
=
+
+
+
⋅
+
=
+
+
=
2
01
01
0
2
1
0
1
0
0
2
1
0
2
0
1
1
1
1
V
V
R
G
1
=
1. Wymagania do woltomierzy DC.
Rezystancja wej
ś
ciowa
Po podł
ą
czeniu woltomierza wynik pomiaru tego napi
ę
cia
wynosi
V
R
R
R
R
R
R
U
R
R
R
R
R
R
U
U
V
V
V
V
97263
.
4
1
1
1
1
2
1
0
1
0
0
2
1
0
2
0
=
+
+
+
⋅
+
=
+
+
=
I
V
100
Ω
4.97263V
10V
100k
Ω
100k
Ω
10M
Ω
V
U’
x
U
V
1. Wymagania do woltomierzy
DC.
Rezystancja wej
ś
ciowa
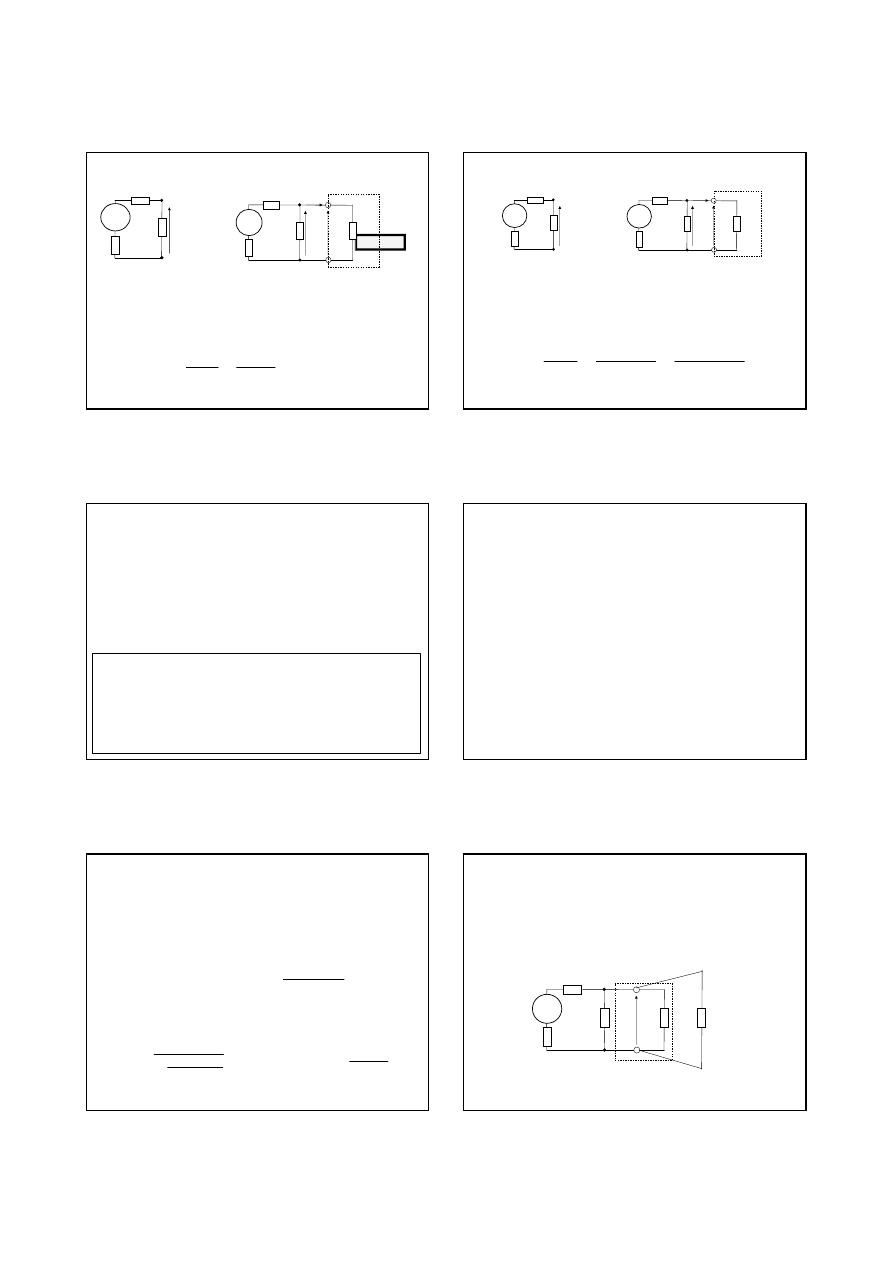
Zmniejszenie napi
ę
cia pomiarowego wynosi
Jest to bł
ą
d systematyczny!
Wzgl
ę
dny bł
ą
d systematyczny
R
0
U
x
U
0
R
1
R
2
I
V
R
0
U
V
U
0
R
1
R
2
R
V
V
U’
x
I
0
2
01
2
01
)
(
G
G
G
U
G
G
G
G
U
U
U
U
V
V
V
V
x
x
V
R
v
+
−
=
+
+
−
=
−
=
∆
V
V
x
R
R
G
G
G
G
U
U
V
v
+
+
−
=
∆
=
2
01
)
(
δ
6
1. Wymagania do woltomierzy
DC.
Rezystancja wej
ś
ciowa
Zmniejszenie napi
ę
cia pomiarowego (warto
ść
bł
ę
du systematycznego)
wynosi
Warto
ść
wzgl
ę
dnego bł
ę
du systematycznego:
100
Ω
U
x
=
=4.9975V
10V
100k
Ω
100k
Ω
I
V
100
Ω
4.97263V
10V
100k
Ω
100k
Ω
10M
Ω
V
U’
x
V
V
V
U
U
U
x
V
R
v
025
.
0
9975
.
4
97263
.
4
)
(
−
≈
−
=
−
=
∆
%
5
.
0
%
100
9975
.
4
025
.
0
)
(
≈
−
=
∆
=
V
V
U
U
x
R
R
V
v
δ
1. Wymagania do woltomierzy
DC.
Rezystancja wej
ś
ciowa
Otó
ż
warto
ść
bł
ę
du systematycznego (metodycznego), spowodowanego
ograniczonej warto
ś
ci
ą
rezystancji wej
ś
ciowej woltomierza zale
ż
y od
stosunku ekwiwalentnej rezystancji obwodu ze strony
ź
ródła (R
0
+R
1
) i
rezystancji wej
ś
ciowej woltomierza R
V
.
Zwi
ę
kszenie
rezystancji
wej
ś
ciowej
woltomierza
R
V
zapewnia
zmniejszenie bł
ę
du metodycznego
R
0
U
x
U
0
R
1
R
2
I
V
R
0
U
V
U
0
R
1
R
2
R
V
V
U
x’
1
)
(
1
)
(
2
01
2
01
+
+
−
=
+
+
−
=
∆
=
G
G
R
G
G
G
G
U
U
V
V
V
x
R
R
V
v
δ
1. Wymagania do woltomierzy DC.
Rezystancja wej
ś
ciowa
Przykład 2.
Je
ż
eli warto
ś
ci rezystancji obiektu badanego b
ę
d
ą
o 10 razy wi
ę
ksze
R
1
=1 MOhm , R
2
=1 MOhm otrzymuje si
ę
:
- wskazanie woltomierza
- Bł
ą
d systematyczny bezwzgl
ę
dny:
-
bł
ą
d systematyczny wzgl
ę
dny:
Przy warto
ś
ci rezystancji obiektu badanego porównywalnej do rezystancji
woltomierza R1=10 MOhm, R2=10 MOhm otrzymuje si
ę
bł
ą
d
systematyczny wzgl
ę
dny: .
Dla zmniejszenia tego bł
ę
du nale
ż
y wykorzysta
ć
elektrometr z wi
ę
ksz
ą
rezystancj
ę
wej
ś
ciow
ą
, na przykład RV=1 TOhm lub wi
ę
kszej, wtedy w
ostatnim przypadku bł
ą
d metodyczny wzgl
ę
dny:
V
U
x
4,99975
=
V
U
V
4,761655
=
V
U
v
R
0,24
)
(
−
≈
∆
%
8
,
4
−
≈
v
R
δ
%
33
−
≈
v
R
δ
%
5
,
0
−
≈
v
R
δ
1. Wymagania do woltomierzy DC.
Rezystancja wej
ś
ciowa
Przykład 2.
Je
ż
eli warto
ś
ci rezystancji obiektu badanego b
ę
d
ą
o 10 razy wi
ę
ksze
R
1
=1 MOhm , R
2
=1 MOhm otrzymuje si
ę
:
- wskazanie woltomierza
- Bł
ą
d systematyczny bezwzgl
ę
dny:
-
bł
ą
d systematyczny wzgl
ę
dny:
Przy warto
ś
ci rezystancji obiektu badanego porównywalnej do rezystancji
woltomierza R1=10 MOhm, R2=10 MOhm otrzymuje si
ę
bł
ą
d
systematyczny wzgl
ę
dny: .
Dla zmniejszenia tego bł
ę
du nale
ż
y wykorzysta
ć
elektrometr z wi
ę
ksz
ą
rezystancj
ę
wej
ś
ciow
ą
, na przykład RV=1 TOhm lub wi
ę
kszej, wtedy w
ostatnim przypadku bł
ą
d metodyczny wzgl
ę
dny:
V
U
x
4,99975
=
V
U
V
4,761655
=
V
U
v
R
0,24
)
(
−
≈
∆
%
8
,
4
−
≈
v
R
δ
%
33
−
≈
v
R
δ
%
5
,
0
−
≈
v
R
δ
2.Korekcja wpływu rezystancji wej
ś
ciowej
woltomierza
• Je
ż
eli warto
ś
ci parametrów obwodu pomiarowego nie s
ą
znane, wtedy w eksperymentalny sposób mo
ż
na
oszacowa
ć
warto
ść
bł
ę
du systematycznego a nawet jego
skorygowa
ć
!
•
Ze wzoru podstawowego dla bł
ę
du systematycznego
•
wynika,
ż
e skorygowana warto
ść
napi
ę
cia równa si
ę
•
lub
V
V
x
x
V
R
G
G
G
G
U
U
U
U
v
+
+
−
=
−
=
∆
2
01
)
(
V
V
V
x
G
G
G
G
U
U
+
+
−
=
2
01
1
+
+
⋅
=
2
01
1
G
G
G
U
U
V
V
x
2.Korekcja wpływu rezystancji wej
ś
ciowej
woltomierza
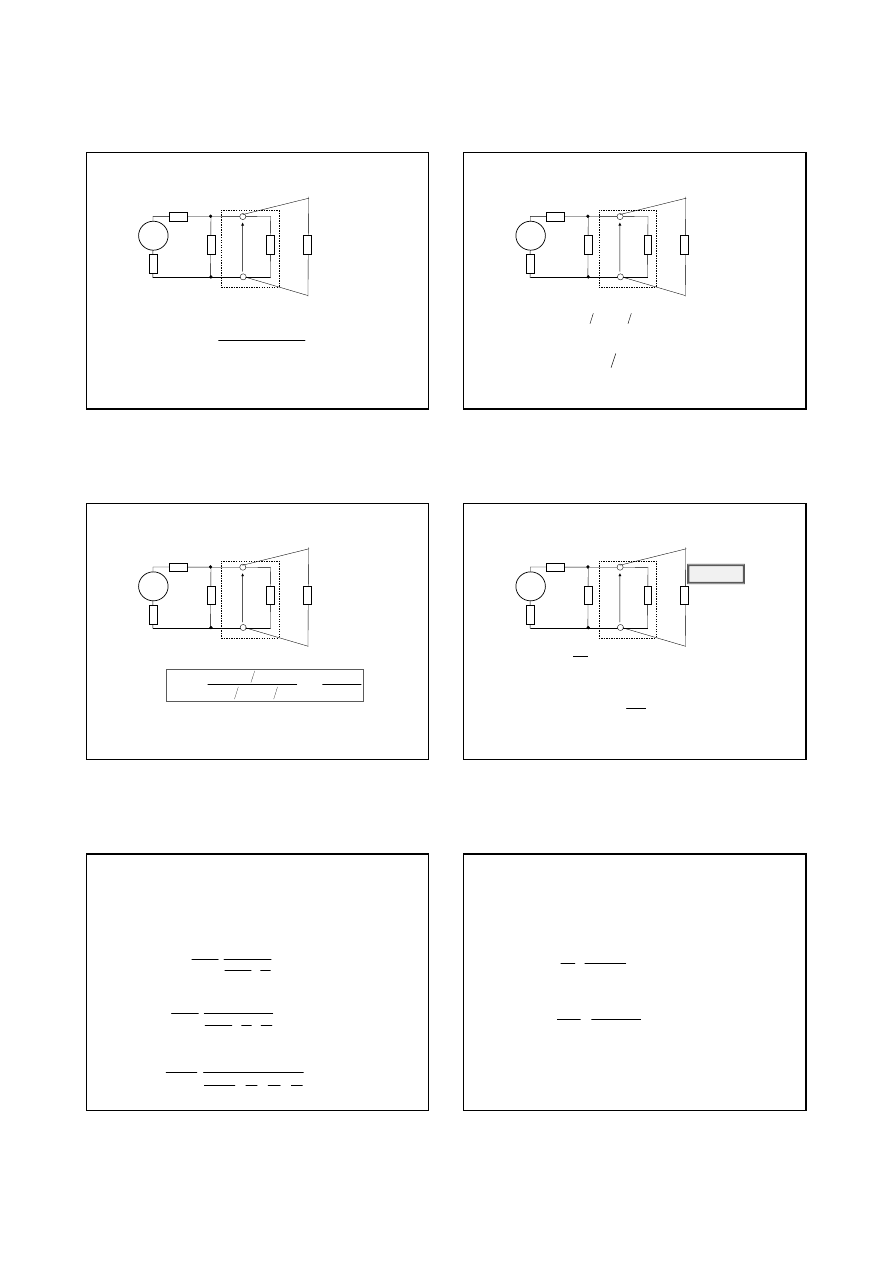
•
W celu jej wyznaczania i dalej dla korekcji wpływ rezystancji
woltomierza R
V
na wynik pomiaru napi
ę
cia nale
ż
y przeprowadzi
ć
dodatkowy pomiar napi
ę
cia z dodatkowym (znanym!) obci
ąż
eniem
gał
ę
zi, na której jest mierzono napi
ę
cie. W tym celu mo
ż
na wł
ą
czy
ć
równolegle do woltomierza bocznik Rb o znanej warto
ś
ci rezystancji,
na przykład R
b
=R
V
R
0
U
Vb
U
0
R
1
R
2
R
V
V
R
b
7
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
•
Jest oczywistym,
ż
e wskazanie woltomierza si
ę
zmieni (zimniejsze si
ę
)
i wskazanie woltomierza w drugim pomiarze jest równy:
R
0
U
Vb
U
0
R
1
R
2
R
V
V
R
b
b
V
Vb
G
G
G
G
G
U
U
+
+
+
⋅
=
2
01
01
0
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
•
Je
ś
li stosunek rezystancji poznaczy
ć
jako:
•
Oraz stosunek wskaza
ń
woltomierza - jako
100
U
Vb
10V
100k
100k
R
V
=
=1M
V
R
b
= R
V
=1M
b
V
V
b
R
R
G
G
=
=
β
b
,
V
V
U
U
=
γ
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
•
Wtedy skorygowana warto
ść
napi
ę
cia
γ
β
β
−
+
=
−
+
=
1
1
V
b
,
V
V
b
V
b
V
V
sk
U
U
U
R
R
R
R
U
U
R
0
U
Vb
U
0
R
1
R
2
R
V
V
R
b
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
•
Przy R
b
=R
v
•
Wtedy skorygowana warto
ść
napi
ę
cia
γ
−
=
2
V
sk
U
U
R
0
U
Vb
U
0
R
1
R
2
R
V
V
R
b
1
=
=
b
V
R
R
β
V
4,54521
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
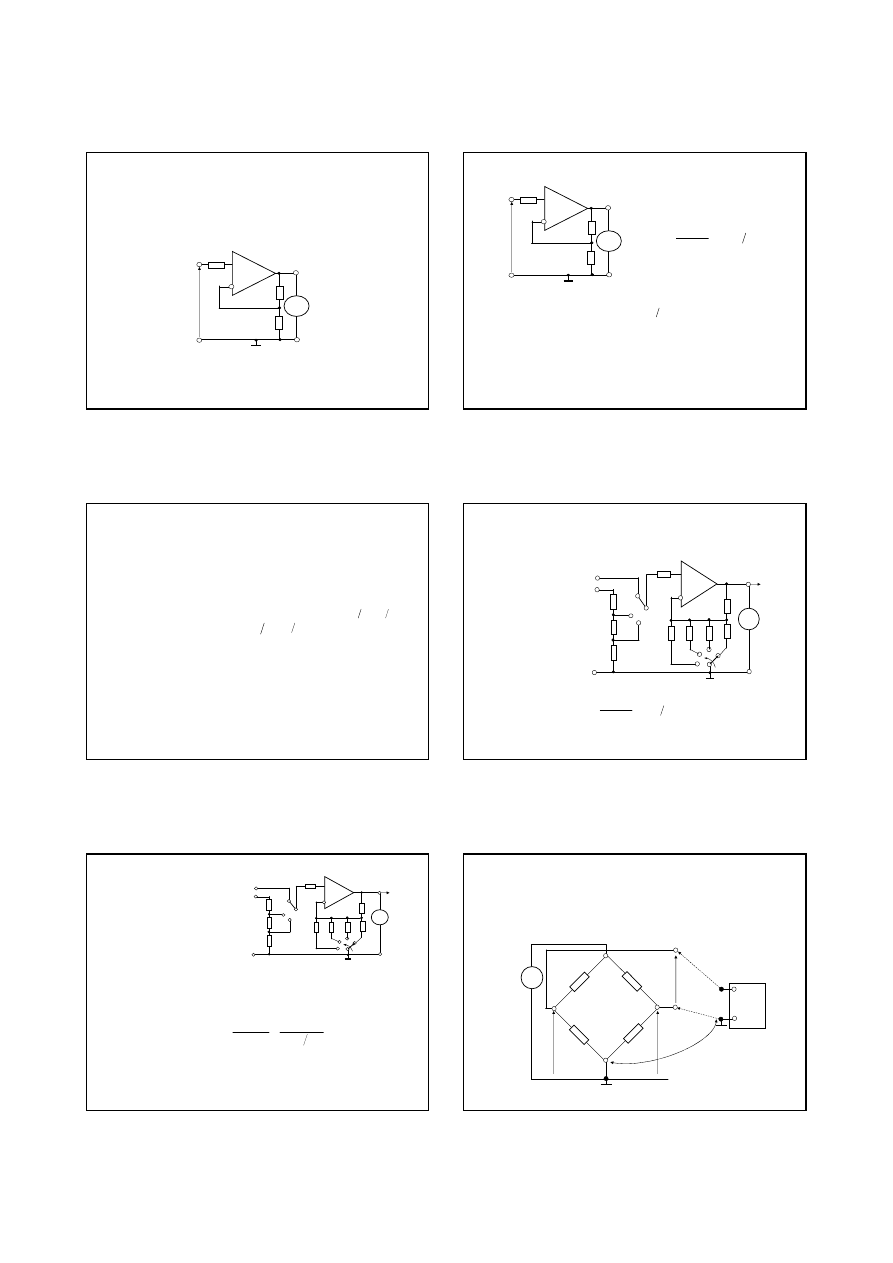
•
Przykład 1d. U
0
=10 V, R
0
=100 Ohm, R
1
=1 MOhm, R
2
=1 MOhm,
R
V
=10 MOhm
1. Warto
ść
rzeczywista napi
ę
cia
2. Wynik pierwszego pomiaru
3. Wynik drugiego pomiaru przy R
b
=R
v
(
β
=1)
V
4,99975
1
1
1
2
1
0
1
0
0
=
+
+
⋅
+
=
R
R
R
R
R
U
U
x
V
4,76166
1
1
1
1
2
1
0
1
0
0
=
+
+
+
⋅
+
=
V
V
R
R
R
R
R
R
U
U
V
4,54521
1
1
1
1
1
2
1
0
1
0
0
=
+
+
+
+
⋅
+
=
b
V
Vb
R
R
R
R
R
R
R
U
U
2.Korekcja wpływu rezystancji
wej
ś
ciowej woltomierza
•
Przykład 1d. U
0
=10 V, R
0
=100 Ohm, R
1
=1 MOhm, R
2
=1 MOhm,
R
V
=10 MOhm
4. Warto
ść
współczynnika
5. Skorygowany wynik pomiaru
Co odpowiada rzeczywistej warto
ś
ci napi
ę
cia
1,04762
V
4,54521
V
4,76166
≈
=
=
Vb
V
U
U
β
V
4,99975
1,04762
2
V
4,76166
2
=
−
=
−
=
β
V
x
U
U
8
3.Układy wej
ś
ciowe woltomierza
W celu zapewnienia du
ż
ej rezystancji wej
ś
ciowej na wej
ś
ciu woltomierza
wykorzystuje wzmacniacz nieodwracaj
ą
cy, zbudowany na
wzmacniaczu operacyjnym (WO) ze spr
ęż
eniem zwrotnym z
dzielnikiem napi
ę
cia na rezystorach R
1
oraz R
2
.
Do wyj
ś
cia wzmacniacza jest podł
ą
czony przetwornik A/C (lub analogowy
woltomierz).
Równanie przetwarzania dla struktury bazowej:
U
v
=U
x
⋅
K
wu
,
gdzie K
wu
- współczynnik wzmocnienia napi
ę
cia
U
x
WO
U
wy
+
-
R
1
R
2
V
HI
R
3
LO
3.Układy wej
ś
ciowe woltomierza
Rezystancja wej
ś
ciowa woltomierza równa si
ę
rezystancji wej
ś
ciowej
wzmacniacza:
gdzie R
we,WO
- jest rezystancj
ą
wej
ś
ciow
ą
wzmacniacza operacyjnego,
A
0
- współczynnik wzmocnienia rozwartego WO
U
x
WO
U
wy
+
-
R
1
R
2
V
HI
R
3
LO
2
1
2
1
2
1
R
R
R
R
R
K
wu
+
=
+
=
(
)
w
WO
we
we
V
K
A
R
R
R
R
0
,
3
1
+
≥
+
=
3.Układy wej
ś
ciowe woltomierza
Wpływ zmian wej
ś
ciowego napi
ę
cia przesuwu e
we
:
Wpływ zmian wej
ś
ciowego pr
ą
du przesuwu
∆
i
we
:
Wzgl
ę
dny wpływ warto
ś
ci współczynnika wzmocnienia WO A
0
:
Rezystancja wyj
ś
ciowa:
Wymagania do WO:
•
du
ż
a rezystancj
ą
wej
ś
ciow
ą
wzmacniacza operacyjnego ,
•
małe warto
ś
ci wej
ś
ciowego napi
ę
cia przesuwu oraz
•
wej
ś
ciowego pr
ą
du przesuwu,
•
du
ż
a warto
ść
współczynnika A
0
wzmocnienia WO
we
we
e
e
U
=
∆
)
(
3
)
(
R
I
I
U
we
we
∆
=
∆
∆
(
)
wu
I
K
A
A
0
0
1
1
)
(
+
=
δ
(
)
wu
WO
wy
wy
K
A
R
R
0
,
1
+
≅
2.Układy wej
ś
ciowe woltomierza
W celu zapewnienia rozszerzenia zakresów w stron
ę
napi
ęć
mniejszych
(poni
ż
ej około 1 V) wykorzystuje kilku rezystorów R
2j
w obwodzie
spr
ęż
enia zwrotnego WO.
Wtedy współczynnik wzmocnienia równa si
ę
:
zwykle maksymalne wzmocnienie stanowi 10
3
-10
4
razy.
WO
U
wy
+
-
R
1
R
2,1
V
R
3
R
2,2
R
2,3
R
4,1
R
4,2
R
5
200V
20V
2V
200mV
20mV
2mV
LO
HI
2mV-2V
20V, 200V
(do A/C)
R
2,4
j
j
j
j
w
R
R
R
R
R
K
,
2
1
,
2
1
,
2
,
1
+
=
+
=
3.Układy wej
ś
ciowe woltomierza
W celu zapewnienia rozszerzenia zakresów w stron
ę
napi
ęć
wi
ę
kszych
(ponad około 10 V) jak w DMM wykorzystuje si
ę
dzielnik wej
ś
ciowy
Równanie przetwarzania dla struktury na rys:
Uv=Ux
⋅
K
d,i
⋅
K
w,j
,
gdzie K
d,i
⋅
- współczynnik podziału napi
ę
cia wej
ś
ciowego dzielnika
Rezystancja wej
ś
ciowa woltomierza w tym przypadku równa si
ę
rezystancji dzielnika Rd (przyjmuj
ą
c ze rezystancja wej
ś
ciowa
wzmacniacza W0 jest w du
ż
ym stopniu wi
ę
ksza od rezystancji
dzielnika):
WO
U
wy
+
-
R
1
R
2,1
V
R
3
R
2,2
R
2,3
R
4,1
R
4,2
R
5
200V
20V
2V
200mV
20mV
2mV
LO
HI
2mV-2V
20V, 200V
(do A/C)
R
2,4
i
i
i
i
d
R
R
R
R
R
K
,
4
5
5
,
4
,
4
,
1
1
+
=
+
=
d
V
R
R
R
R
R
=
+
+
+
=
...
2
,
4
1
,
4
5
4. Układ wej
ś
ciowy woltomierza ze
wzmacniaczem instrumentalnym.
Przy pomiarach napi
ęć
z obiektów, wyj
ś
cia którego s
ą
odseparowani od
masy wspólnej (ziemi), podł
ą
czenie tych wyj
ść
do wej
ść
woltomierza z
uziemionym wej
ś
ciem „LO” mo
ż
e powodowa
ć
sytuacj
ę
konfliktow
ą
.
E
R
1
R
4
R
3
R
2
U
x
=U
1
-U
2
U
2
U
1
„0(
ź
)”
V
HI
LO
?
Konflikt!
„0(
V
)”
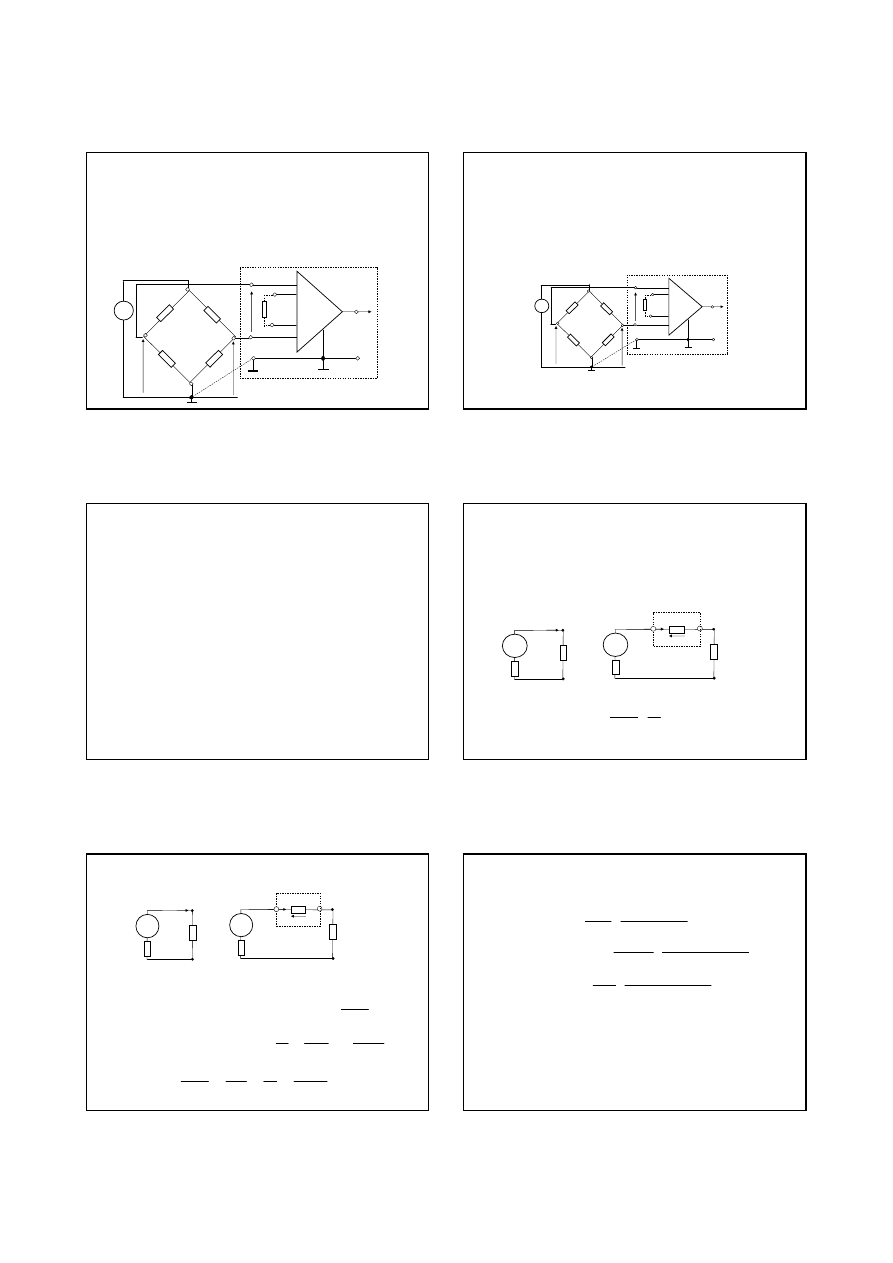
9
3. Układ wej
ś
ciowy woltomierza ze
wzmacniaczem instrumentalnym.
W celu unikni
ę
cia takiej sytuacji układ woltomierza powinien mie
ć
symetryczne (odseparowane od masy) wej
ś
cia. Taki warunki mog
ą
by
ć
spełnione przy wykorzystaniu wzmacniacza instrumentalnego.
W takim układzie woltomierz jest wyposa
ż
ony w trzy wej
ś
cia (sygnałowe
wysokie – „HI” i niskie „LO” oraz mas
ę
„0”).
Do sygnałowych wej
ść
s
ą
doł
ą
czone punkty obwodu obiektu, ró
ż
nic
ę
potencjałów nale
ż
y zmierzy
ć
. Wej
ś
cie masy mog
ę
by
ć
podł
ą
czone do
masy obiektu.
R
G
WI
-
+
HI
Do A/C
LO
0
Ref
U
x
=U
1
-U
2
E
R
1
R
4
R
3
R
2
U
1
„0(
ź
)
”
U
2
4. Układ wej
ś
ciowy woltomierza ze
wzmacniaczem instrumentalnym.
Równanie przetwarzania dla struktury woltomierza ze wzmacniaczem
instrumentalnym:
gdzie K
g
=K
WI
- współczynnik wzmocnienia wzmacniacza instrumentalnego.
Rezystancja wej
ś
ciowa takiego układu równa si
ę
rezystancji wej
ś
ciowej
wzmacniacza instrumentalnego.
R
G
WI
-
+
HI
Do A/C
L
O
0
Ref
U
x
=U
1
-U
2
E
R
1
R
4
R
3
R
2
U
1
„0(
ź
)
”
U
2
WI
x
V
K
U
U
=
Plan wykładu
1. Wymagania do amperomierze
2. Układy wej
ś
ciowe amperomierze.
1. Wymagania do amperomierze
Ogólnym wymaganiem do amperomierze jest zapewnienie małej
rezystancji wej
ś
ciowej , poniewa
ż
ona decyduje o bł
ę
dzie
metodycznym pomiaru pr
ą
du oraz o spadku napi
ę
cia pomiarowego
na wej
ś
ciu amperomierza (tzw. Burden Volage).
Na rys. pokazano obwód elektryczny, w którym nale
ż
y zmierzy
ć
warto
ść
pr
ą
du Ix.
Do wprowadzenia amperomierza warto
ść
tego pr
ą
du wynosi
R
0
I
x
U
0
R
1
I
A
R
0
U
0
R
A
R
1
A
U
A
01
0
1
0
0
R
U
R
R
U
I
x
=
+
=
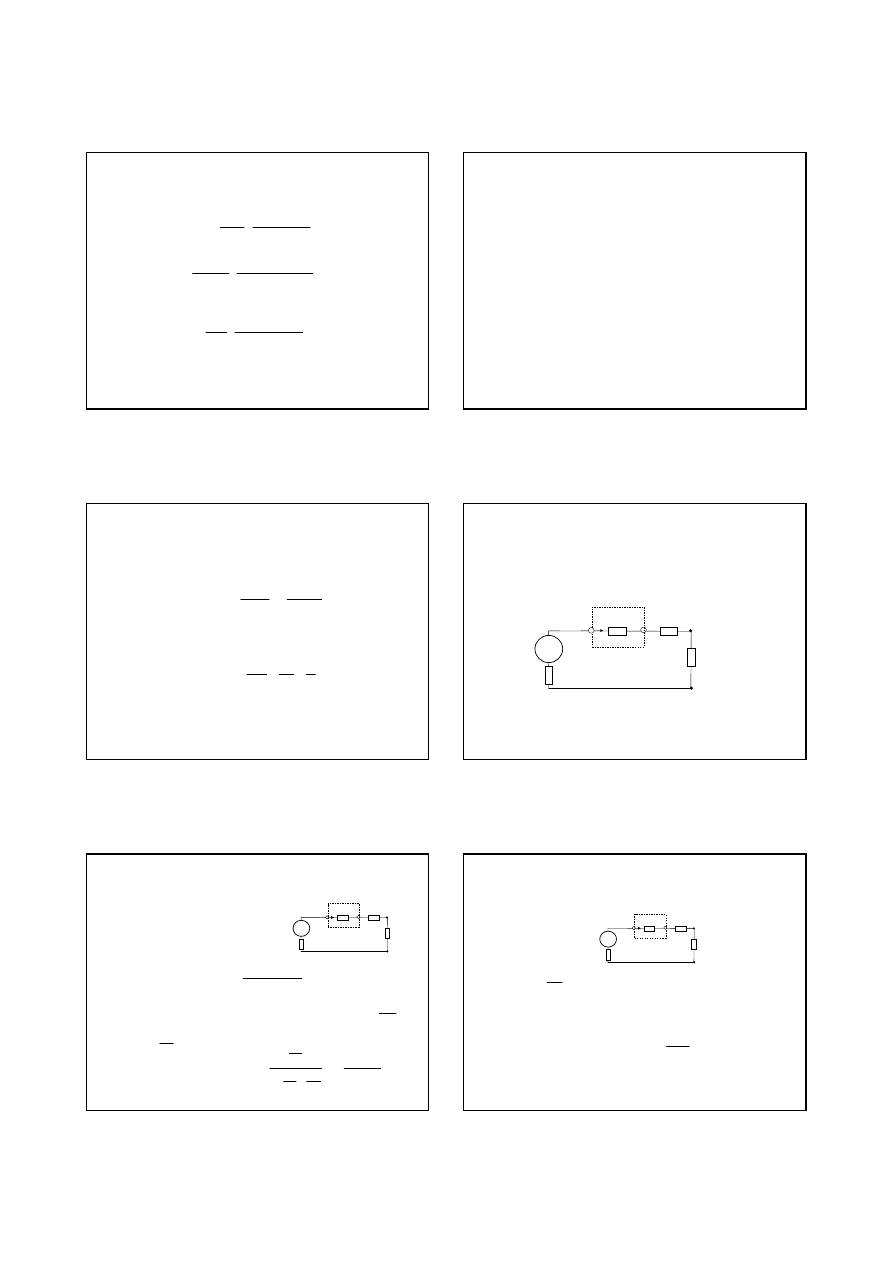
1. Wymagania do amperomierze
Po szeregowym wł
ą
czeniu amperomierza z rezystancj
ą
wej
ś
ciowej RA
zmieni si
ę
ekwiwalentna rezystancja obwodu, w wyniku czego
zmieni si
ę
pr
ą
d mierzony (wskazanie amperomierza)
Zmniejszenie pr
ą
du pomiarowego wynosi
Wzgl
ę
dny bł
ą
d
R
0
I
x
U
0
R
1
I
A
R
0
U
0
R
A
R
1
A
U
A
A
x
A
R
R
U
I
I
+
=
=
′
01
0
( )
x
A
A
x
A
A
A
A
x
A
R
I
R
R
R
I
U
R
I
R
R
I
I
I
I
A
+
−
=
⋅
−
=
−
=
−
=
∆
01
0
01
A
A
A
A
A
x
R
R
R
R
R
U
U
U
R
I
I
I
A
A
+
−
=
−
=
−
=
∆
=
01
0
0
)
(
δ
1. Wymagania do amperomierze
Przykład 1a. Przy R0=100 Ohm, R1=1 kOhm oraz RA=1 Ohm, U0=1 V
otrzymuje si
ę
:
Wskazanie mikroamperomierza:
Bł
ą
d metodyczny wzgl
ę
dny:
Przykład 1b. Je
ż
eli warto
ś
ci rezystancji obiektu badanego b
ę
d
ą
o 10 razy
mniejsza R1=100 Ohm , otrzymuje si
ę
:
wskazanie amperomierza ;
bł
ą
d metodyczny wzgl
ę
dny:
mA
kOhm
Ohm
V
R
R
U
I
x
90909
,
0
1
100
1
1
0
0
=
+
=
+
=
mA
Ohm
kOhm
Ohm
V
R
R
R
U
I
A
A
90827
,
0
1
1
100
1
1
0
0
=
+
+
=
+
+
=
%
091
,
0
%
100
90909
,
0
90909
,
0
90827
,
0
−
≈
−
=
−
=
mA
mA
mA
I
I
I
x
x
A
R
v
δ
mA
I
x
5
=
mA
I
A
4.97512
=
%
5
,
0
−
≈
A
R
δ
10
1. Wymagania do amperomierze
Przykład 1c. Przy R0=10 Ohm, R1=10 Ohm oraz RA=1 Ohm, U0=1 V
otrzymuje si
ę
:
Wskazanie miliamperomierza:
Bł
ą
d metodyczny wzgl
ę
dny:
mA
Ohm
Ohm
V
R
R
U
I
x
00
,
50
10
10
1
1
0
0
=
+
=
+
=
mA
Ohm
Ohm
Ohm
V
R
R
R
U
I
A
A
47,619
1
10
10
1
1
0
0
=
+
+
=
+
+
=
%
8
,
4
%
100
00
,
50
00
,
50
47,619
−
≈
−
=
−
=
mA
mA
mA
I
I
I
x
x
A
R
v
δ
1. Wymagania do amperomierze
Dla zmniejszenia tego bł
ę
du nale
ż
y wykorzysta
ć
miliamperomierz z
mniejsz
ą
rezystancj
ę
wej
ś
ciow
ą
, na przykład RA=0,01 Ohm lub
jeszcze mniejszej, wtedy w ostatnim przypadku bł
ą
d metodyczny
wzgl
ę
dny:
%
005
,
0
−
≈
A
R
δ
1. Wymagania do amperomierze
Otó
ż
warto
ść
bł
ę
du metodycznego, spowodowanego ograniczonej
warto
ś
ci
ą
rezystancji wej
ś
ciowej amperomierza zale
ż
y od stosunku
rezystancji wej
ś
ciowej amperomierza RA i ekwiwalentnej rezystancji
obwodu ze strony pomi
ę
dzy punktami wł
ą
czenia amperomierza
Zmniejszenie rezystancji wej
ś
ciowej amperomierza R
A
zapewnia
zmniejszenie bł
ę
du metodycznego.
Z innej strony, warto
ść
bł
ę
du metodycznego wyznacza si
ę
stosunkiem
spadku napi
ę
cia na amperomierze (Burden Voltage) do napi
ę
cia
obwodu.
Napi
ę
cie na amperomierze wynosi
jego warto
ść
powinna by
ć
ograniczona.
A
A
A
R
I
U
=
A
A
x
R
R
R
R
R
I
I
A
A
+
−
=
∆
=
01
)
(
δ
0
0
)
(
U
U
U
R
I
I
I
A
A
A
x
R
R
A
A
−
=
−
=
∆
=
δ
Korekcja bł
ę
du od wpływu rezystancji
amperomierza R
A
.
Wpływ rezystancji amperomierza R
A
na wynik pomiaru pr
ą
du mo
ż
e by
ć
skorygowany przez dodatkowy pomiar pr
ą
du z wł
ą
czeniem
dodatkowej rezystancji R
d
o znanej warto
ś
ci, na przykład taki samy
amperomierz: R
d
=R
A
.
I
A2
R
0
U
0
R
A
R
1
A
R
d
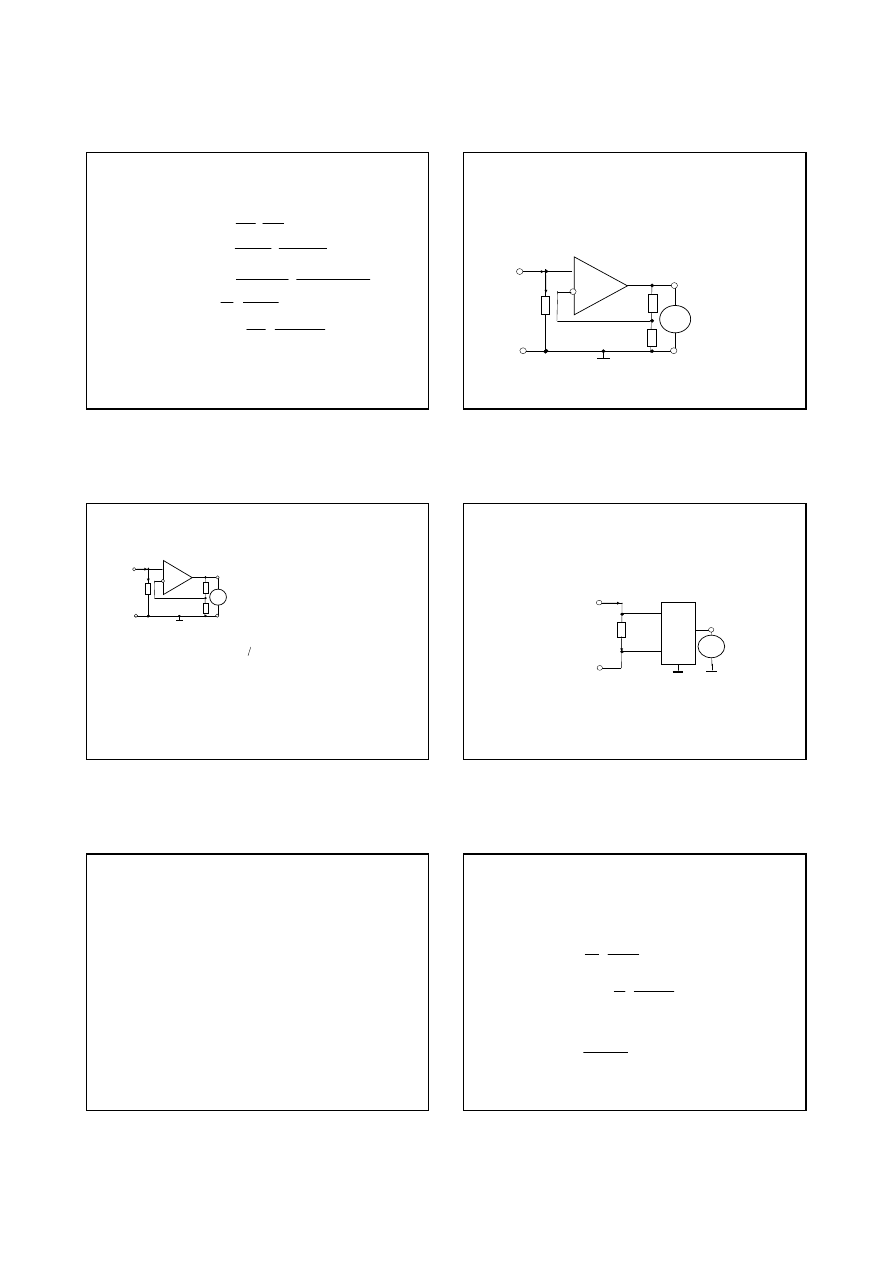
Korekcja bł
ę
du od wpływu rezystancji
amperomierza R
A
.
Wtedy wynik pomiaru pr
ą
du w drugim pomiarze
W tym celu poprzednio wprowadzimy dodatkowe zmienne
Oraz
St
ą
d skorygowana warto
ść
pr
ą
du
d
A
A
R
R
R
U
I
+
+
=
01
0
2
1
2
>
=
A
A
I
I
γ
d
A
R
R
=
β
I
A2
R
0
U
0
R
A
R
1
A
R
d
γ
β
β
−
+
=
−
+
=
1
1
2
A
A
A
d
A
d
A
A
I
I
I
R
R
R
R
I
I
Korekcja bł
ę
du od wpływu rezystancji
amperomierza R
A
.
Lub przy
skorygowana warto
ść
pr
ą
du
γ
−
=
=
2
1
A
sk
x
I
I
I
I
A2
R
0
U
0
R
A
R
1
A
R
d
1
=
=
d
A
R
R
β
11
Korekcja bł
ę
du od wpływu rezystancji
amperomierza R
A
.
Przykład 1d. U0=10 V, R0+R1=10 Ohm, RA=1 Ohm.
Warto
ść
rzeczywista pr
ą
du
Wynik pierwszego pomiaru
Wynik drugiego pomiaru
Warto
ść
współczynnika
Skorygowana warto
ść
pr
ą
du
Co odpowiada rzeczywistej warto
ś
ci pr
ą
du.
A
Ohm
V
R
R
U
I
x
000
,
1
10
10
1
0
0
=
=
+
=
A
Ohm
Ohm
V
R
R
R
U
I
A
A
909091
,
0
1
10
10
1
0
0
=
+
=
+
+
=
A
,
Ohm
Ohm
Ohm
V
R
R
R
R
U
I
A
A
A
8333333
0
1
1
10
10
1
0
0
2
=
+
+
=
+
+
+
=
0909091
1
833333
0
909091
0
2
,
,
,
I
I
A
A
≈
=
=
γ
A
,
,
,
I
I
A
x
000
1
0909091
1
2
909091
0
2
=
−
=
−
=
γ
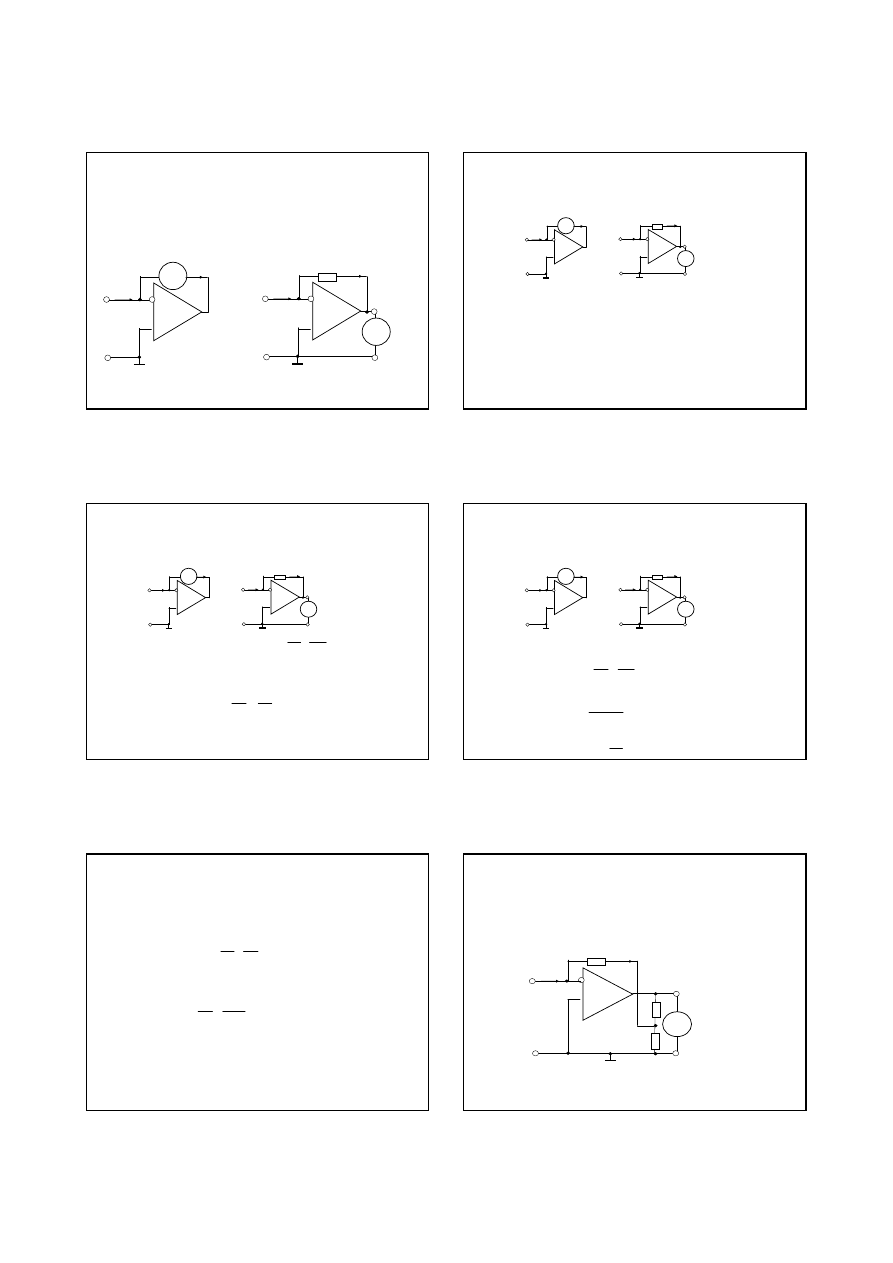
2. Układy wej
ś
ciowy amperomierze
2.1. Układy wej
ś
ciowe amperomierza z bocznikiem
Dla pomiarów pr
ą
dów o du
ż
ej warto
ś
ci (od kilku miliamperów i wy
ż
ej)
wykorzystuje si
ę
układ pomiarowy amperomierza z bocznikiem na
wej
ś
ciu
WO
-
I
x
R
b
I
x
U
v
=Ix
⋅
R
b
⋅
K
wu
R
1
R
2
V
+
2. Układy wej
ś
ciowy amperomierze
2.1. Układy wej
ś
ciowe amperomierza z bocznikiem
Dla takiego układu napi
ę
cie wyj
ś
ciowe wynosi
Rb - jest rezystancj
ą
bocznika, Kwu- jest współczynnikiem wzmocnienia
wzmacniacza
WO
-
I
x
R
b
I
x
U
v
=Ix
⋅
R
b
⋅
K
wu
R
1
R
2
V
+
(
)
wu
b
x
b
x
wy
v
K
R
I
R
R
R
I
U
U
=
+
=
=
2
1
1
2. Układy wej
ś
ciowy amperomierze
2.1. Układ wej
ś
ciowy amperomierza z bocznikiem
Lepsze charakterystyki mo
ż
na uzyska
ć
stosuj
ą
c wzmacniacz
instrumentalny (WI), zwłaszcza w przypadkach kiedy obiekt mierzony
jest odseparowany od masy wspólnej.
Dla takiego układu napi
ę
cie wyj
ś
ciowe wynosi
Kwi- jest współczynnikiem wzmocnienia WI
I
x
R
b
I
x
U
v
=Ix
⋅
R
b
⋅
K
wi
V
WI
K
wi
wi
b
x
wy
v
K
R
I
U
U
=
=
2. Układy wej
ś
ciowy amperomierze
2.1. Układy wej
ś
ciowe amperomierza z bocznikiem
Dla takich układów wej
ś
ciowych:
Rezystancja wej
ś
ciowa amperomierza : R
A
=Rb
Warto
ść
napi
ę
cia na amperomierze: U
A
=I
x
·R
b
Dokładno
ść
takiej struktury amperomierza wyznacza si
ę
dokładno
ś
ci
ą
:
•
bocznika - bł
ą
d
δ
b
;
•
wzmacniacza - bł
ą
d
δ
w
oraz ;
•
przetwornika analogowo-cyfrowego (na wyj
ś
ciu) – bł
ą
d
δ
A/C
:
δ
A
=
δ
b
+
δ
W
+
δ
A/C
2. Układy wej
ś
ciowy amperomierze
2.1. Układ wej
ś
ciowy amperomierza z bocznikiem
Przy ograniczeniu warto
ś
ci współczynnika wzmocnienia na poziomie
Kw=10
3
-10
4
, oraz napi
ę
ciu wyj
ś
ciowym około Uwy=1V, warto
ść
spadku napi
ę
cia na amperomierze wynosi około
Wtedy warto
ść
rezystancji bocznika równa si
ę
:
Przykład 2. Przy zakresach pr
ą
du mierzonego Ix od 1mA do 1 A oraz
Kw=10
4
warto
ś
ci rezystancji bocznika równaj
ą
si
ę
mV
V
K
U
U
w
wy
A
)
1
1
,
0
(
10
10
1
4
3
−
=
÷
=
=
x
x
A
A
b
I
mV
I
U
R
R
)
1
1
,
0
(
−
=
=
=
Ohm
mOhm
A
mA
mV
R
R
A
b
1
,
0
01
,
0
10
1
1
,
0
÷
=
÷
=
=
12
2. Układy wej
ś
ciowy amperomierze
2.2. Bazowa konfiguracja układu wej
ś
ciowego mikroamperomierze
z przetwarzaniem bezpo
ś
rednim
Do pomiarów pr
ą
dów, których warto
ś
ci s
ą
z zakresie mikroamperów i
ni
ż
ej, wykorzystuj
ą
si
ę
układy z bezpo
ś
rednim przetwarzaniem
pr
ą
du.
I
x
WO
-
+
V
R
F
I
x
U
wy
=-Ix
⋅
R
F
LO
HI
I
x
WO
-
+
µ
A
HI
I
µ
A
=I
x
LO
2. Układy wej
ś
ciowy amperomierze
2.2. Bazowa konfiguracja układu wej
ś
ciowego mikroamperomierze
z przetwarzaniem bezpo
ś
rednim
W układzie z przetwarzaniem bezpo
ś
rednim pr
ą
du napi
ę
cie wyj
ś
ciowe
równa si
ę
:
gdzie R
F
- rezystancja spr
ęż
enia zwrotnego.
I
x
WO
-
+
V
R
F
I
x
U
wy
=-Ix
⋅
R
F
LO
HI
I
x
WO
-
+
µ
A
HI
I
µ
A
=I
x
LO
F
x
wy
v
R
I
U
U
−
=
=
2. Układy wej
ś
ciowy amperomierze
2.2. Bazowa konfiguracja układu wej
ś
ciowego mikroamperomierze
z przetwarzaniem bezpo
ś
rednim
Spadek napi
ę
cia na amperomierze:
Otó
ż
w pierwszym przybli
ż
eniu rezystancja wej
ś
ciowa
mikroamperomierza:
I
x
WO
-
+
V
R
F
I
x
U
wy
=-Ix
⋅
R
F
LO
HI
I
x
WO
-
+
µ
A
HI
I
µ
A
=I
x
LO
WO
F
x
wy
A
A
R
I
A
U
U
=
≈
0
0
A
R
I
U
R
F
x
A
A
≈
=
µ
2. Układy wej
ś
ciowy amperomierze
2.2. Bazowa konfiguracja układu wej
ś
ciowego mikroamperomierze
z przetwarzaniem bezpo
ś
rednim
Przykład 3. Je
ż
eli Ix=1 µA i na wyj
ś
ciu przetwornika chcemy otrzyma
ć
Uwy=1 V wtedy warto
ść
rezystancji spr
ęż
enia zwrotnego :
Przy wzmocnienie WO A0=10
5
-10
6
warto
ść
rezystancji wej
ś
ciowej równa
si
ę
:
przy tym spadek napi
ę
cia na amperomierzu równa si
ę
:
I
x
WO
-
+
V
R
F
I
x
U
wy
=-Ix
⋅
R
F
LO
HI
I
x
WO
-
+
µ
A
HI
I
µ
A
=I
x
LO
MOhm
A
V
I
U
R
x
wy
F
1
1
1
=
=
=
µ
Ohm
MOhm
R
A
)
10
1
(
10
10
1
6
5
÷
=
÷
≈
µ
mkV
A
U
I
R
U
wy
x
A
A
)
10
1
(
0
÷
=
=
=
µ
2. Układy wej
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
Je
ż
eli zakres pomiaru pr
ą
du ma by
ć
1 nA wtedy warto
ść
rezystancji
spr
ęż
enia zwrotnego ma by
ć
równ
ą
:
a przy zakresie pomiaru pr
ą
du 10 pA warto
ść
rezystancji spr
ęż
enia
zwrotnego ma by
ć
100 razy wi
ę
ksz
ą
Rezystory z takimi warto
ś
ciami rezystancji nie mog
ą
by
ć
wykorzystywane w precyzyjnych obwodach pomiarowych,
poniewa
ż
te warto
ś
ci s
ą
porównywalne s
ą
do warto
ś
ci rezystancji
izolacji płytek, na których oni s
ą
umocowani.
GOhm
nA
V
I
U
R
x
wy
F
1
1
1
=
=
=
GOhm
pA
V
I
U
R
x
wy
F
100
10
1
=
=
=
2. Układy wej
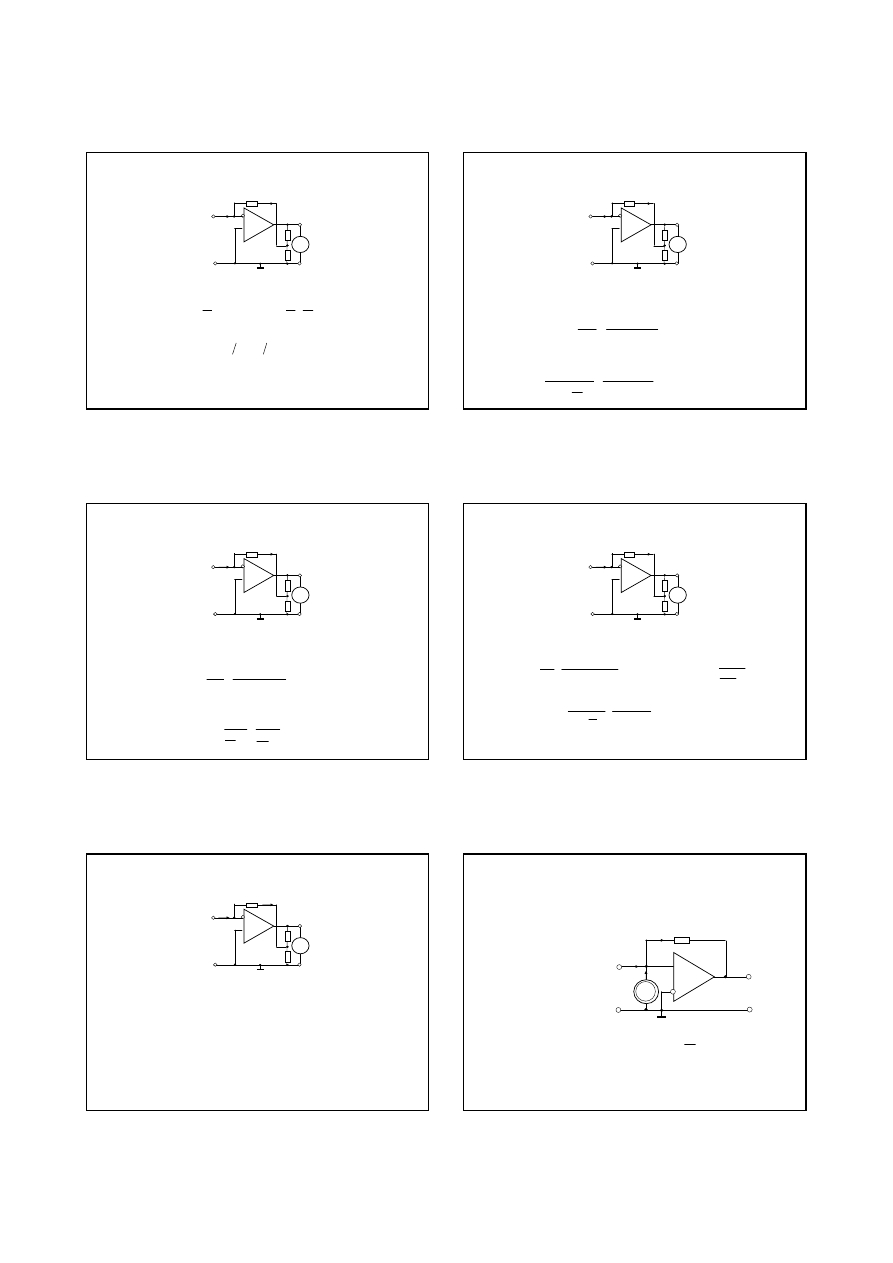
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
Ten problem jest usuni
ę
ty poprzez wykorzystania wła
ś
ciwo
ś
ci
„wzmacniania” rezystancji obwodu gwiazdowego.
W tym obwodzie odbywa si
ę
przetwarzanie pr
ą
d-napi
ę
cie (R
F
) z
nast
ę
pnym wzmocnieniem napi
ę
cia (rezystory R
1
oraz R
2
).
WO
I
x
-
R
F
I
x
U
wy
=-I
x
⋅
R
F
⋅
K
i
R
1
R
2
V
+
13
2. Układy wej
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
W układzie ze wzmocnieniem napi
ę
cia wyj
ś
ciowego (rys.4,b) napi
ę
cie
wyj
ś
ciowe równa si
ę
:
Gdzie wzmocnienie pr
ą
du wynosi
WO
I
x
-
R
F
I
x
U
wy
=-I
x
⋅
R
F
⋅
K
wi
R
1
R
2
V
+
I
F
x
F
F
x
F
x
wy
v
K
R
I
R
R
R
R
I
R
R
R
R
I
U
U
−
=
+
+
−
=
+
+
−
=
=
1
1
1
1
2
1
1
2
1
(
)
F
I
R
R
R
K
1
1
1
2
1
+
+
=
2. Układy wej
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
Przykład 4a. Je
ż
eli Ix=1 nA i na wyj
ś
ciu przetwornika dalej chcemy
otrzyma
ć
Uwy=1 V przy ograniczonej warto
ś
ci rezystancji
spr
ęż
enia zwrotnego , wtedy warto
ść
współczynnika wzmocnienia
pr
ą
du powinna równa
ć
si
ę
:
Dlatego przy oraz zakładaj
ą
c ograniczon
ą
warto
ść
rezystancji
otrzymuje si
ę
warto
ść
rezystancji R2
WO
I
x
-
R
F
I
x
U
wy
=-I
x
⋅
R
F
⋅
K
wi
R
1
R
2
V
+
1000
1
1
1
=
⋅
=
=
MOhm
nA
V
R
I
U
K
F
x
wy
I
(
)
(
)
kOhm
MOhm
R
R
K
R
R
F
I
F
002
,
1
1
1
1
1000
1
1
1
1
2
=
−
⋅
−
=
−
−
=
2. Układy wej
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
Przykład 4b. Je
ż
eli Ix=10 pA i na wyj
ś
ciu przetwornika dalej chcemy
otrzyma
ć
Uwy=1 V przy ograniczonej warto
ś
ci rezystancji
spr
ęż
enia zwrotnego , wtedy warto
ść
współczynnika wzmocnienia
pr
ą
du powinna równa
ć
si
ę
:
Jest to zbyt du
ż
a warto
ść
, dlatego ze przy współczynniku wzmocnienia
W0 A
0
=10
6
bł
ą
d statyczny b
ę
dzie równa
ć
si
ę
:
WO
I
x
-
R
F
I
x
U
wy
=-I
x
⋅
R
F
⋅
K
wi
R
1
R
2
V
+
100000
1
10
1
=
⋅
=
=
MOhm
pA
V
R
I
U
K
F
x
wy
I
%
9
1
10
10
1
1
1
5
6
0
0
≈
+
=
+
≈
I
A
K
A
δ
2. Układy wej
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
Przykład 4b. Ix=10 pA i Uwy=1 V :
Dlatego nale
ż
y zwi
ę
kszy
ć
warto
ść
rezystancji R
1
=R
F
=33,333 MOhm,
wtedy warto
ść
współczynnika wzmocnienia pr
ą
du powinna równa
ć
si
ę
i warto
ść
rezystancji R2 b
ę
dzie równa
ć
si
ę
:
WO
I
x
-
R
F
I
x
U
wy
=-I
x
⋅
R
F
⋅
K
wi
R
1
R
2
V
+
3000
33
,
33
10
1
=
⋅
=
=
MOhm
pA
V
R
I
U
K
F
x
wy
I
%
3
,
0
1
10
3
10
1
3
6
0
≈
+
⋅
≈
A
δ
(
)
(
)
kOhm
MOhm
R
R
K
R
R
F
I
F
1185
,
11
1
1
1
3000
33
,
33
1
1
1
2
≈
−
⋅
−
=
−
−
=
2. Układy wej
ś
ciowy amperomierze
2.3. Bazowa konfiguracja układu wej
ś
ciowego nano – i
pikoamperomierze
Przykład 4b. Ix=10 pA i Uwy=1 V :
S
ą
to bardzo dobre wyniki, poniewa
ż
przy ograniczonych warto
ś
ciach
rezystancji do (1-33) MOhm (zamiast 100 GOhm) otrzymuje si
ę
na
wyj
ś
ciu napi
ę
cie 1 V przy pr
ą
dzie 10 pA.
WO
I
x
-
R
F
I
x
U
wy
=-I
x
⋅
R
F
⋅
K
wi
R
1
R
2
V
+
2. Układy wej
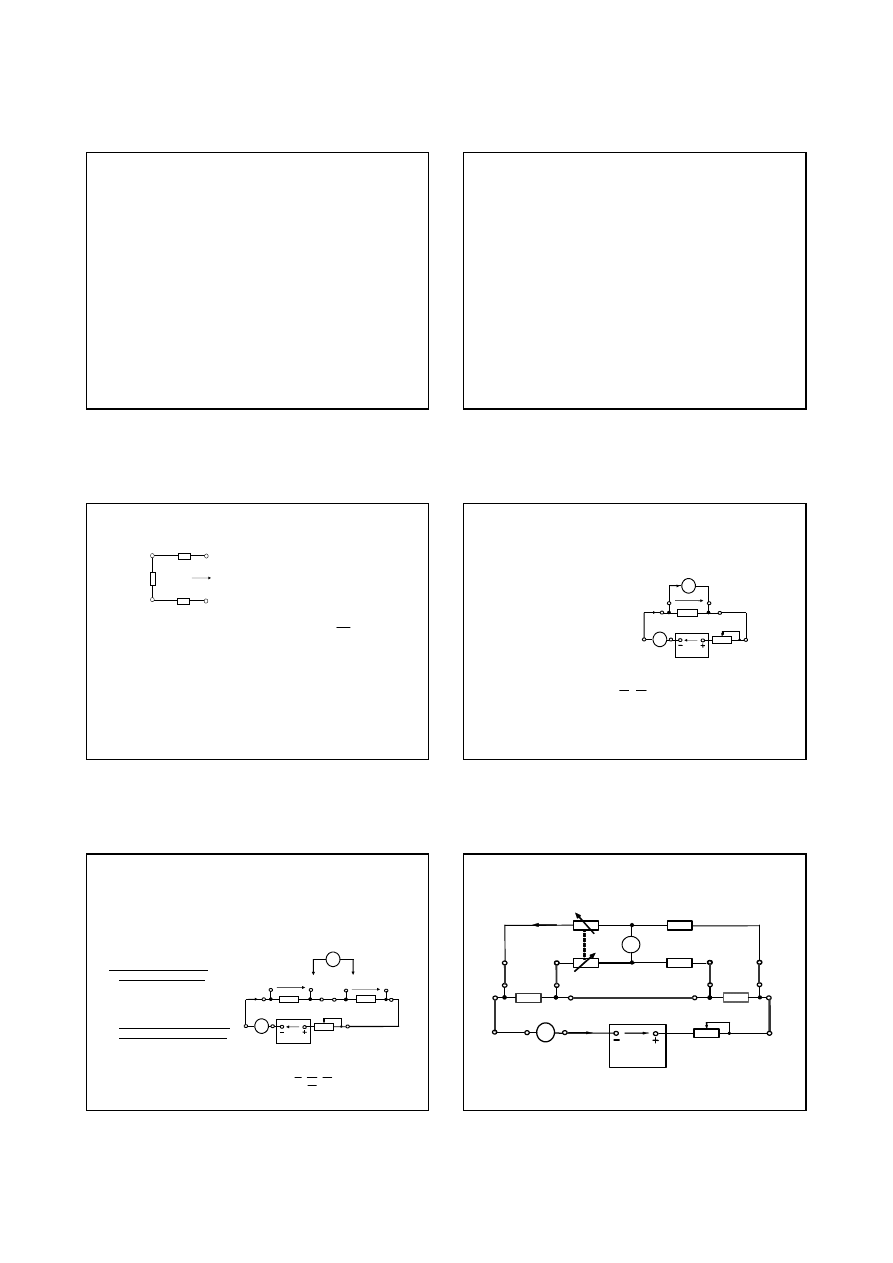
ś
ciowy amperomierze
2.4. Podstawowym problemem układów nano- i pikoamperomierzy jest
wpływ wej
ś
ciowego pr
ą
du wzmacniacza operacyjnego (Iwe), który
zniekształca pr
ą
d mierzony bezpo
ś
rednio, poniewa
ż
pr
ą
d przez
rezystancj
ę
RF równa si
ę
sumie pr
ą
du mierzonego Ix oraz prz
ą
du
wej o
ś
ciowego WO Iwe:
I
F
=I
x
+I
we
.
St
ą
d napi
ę
cie na wyj
ś
ciu układu
U
wy
=I
F
·R
F
=(I
x
+I
we
)·R
F
Wzgl
ę
dny bł
ą
d przetwarzania równa si
ę
Dlatego wymagany jest WO o niskim poziomie pr
ą
dów wej
ś
ciowych
niezrównowa
ż
enia oraz zabezpieczenia przeciw oddziaływa
ń
innych pr
ą
dów upływu przez rezystancje izolacji płytki monta
ż
owej.
U
wy
WO
-
+
R
F
I
F
=I
x
+I
we
I
x
I
we
x
we
Iwe
I
I
=
δ
14
Cel: Zapozna
ć
si
ę
z podstawowymi schematami układów
elektronicznych omomierze.
Plan:
1. Wst
ę
p.
2. Pomiary małych rezystancji
3. Pomiary du
ż
ych rezystancji
1. Wst
ę
p. Problemy pomiaru małych
rezystancji
Rozró
ż
nia si
ę
układy do pomiaru małych,
ś
rednich oraz
du
ż
ych rezystancji (impedancji).
Przy pomiarach małych rezystancji (poni
ż
ej ok.
10
Ω
...100
Ω
) na wynik pomiaru wpływaj
ą
rezystancji
przewodów (rys. 1,a). Im mniejsza rezystancja
pomiarowa tym wi
ę
kszy wpływ rezystancji przewodów.
Przy pomiarach du
ż
ych rezystancji (powy
ż
ej ok.
10 M
Ω
...100 M
Ω
) na wynik pomiaru wpływaj
ą
rezystancji
wej
ś
ciowe przetwornika, izolacja, pr
ą
dy upływów i t.p.
(rys. 1,b).
2. Do wpływu rezystancji przewodów linii
• Wpływ rezystancji przewodów
• Dla warto
ś
ci
ś
rednich (od ok. 1 k
Ω
do ok. 10 M
Ω
)
wpływ przewodów z rezystancj
ą
ok. R
l
=0,1
Ω
Ω
Ω
Ω
jest
mniejszy od 0,01%
R
x
Do miernika
rezystancji
R
l
R
l
x
l
Rl
R
R
2
=
δ
3. Do pomiaru małych rezystancji
4- przewodowe podł
ą
czenie
badanego rezystora do układu
pomiarowego:
Rozdzielone obwody:
pr
ą
dowy (wymuszenie) i
napi
ę
ciowy (pomiar)
Zas.
R
X
A
R
reg
R
L1
U
0
I
x
V
U
x
I
V
<<I
x
R
L2
R
L3
R
L4
I
V
Jeśli R
V
>> R
x
wtedy I
V
<< R
x
i I
A
= I
x
stąd
praktycznie U
V
=U
x
=I
x
×R
x
A
V
x
x
x
I
U
I
U
R
=
=
3. Do pomiaru małych rezystancji
4- przewodowe podł
ą
czenie
badanego rezystora do układu
pomiarowego:
Rozdzielone obwody:
pr
ą
dowy (wymuszenie) i
napi
ę
ciowy (pomiar).
Zwi
ę
kszenie dokładno
ś
ci:
Po
ś
redni pomiar pr
ą
du poprzez
pomiar spadku napi
ę
cia na
rezystorze wzorcowym Rn
Zas.
R
x
A
R
reg
R
L1
U
0
I
x
R
L3
R
L4
U
x
R
L2
R
n
V
U
n
R
L2
1 pomiar
2 pomiar
1 pomiar
: U
V1
=I
x
×R
x
;
2 pomiar
: U
V2
=I
x
×R
n
Wynik
n
V
V
n
V
V
x
x
x
R
U
U
R
U
U
I
U
R
2
1
2
1
=
=
=
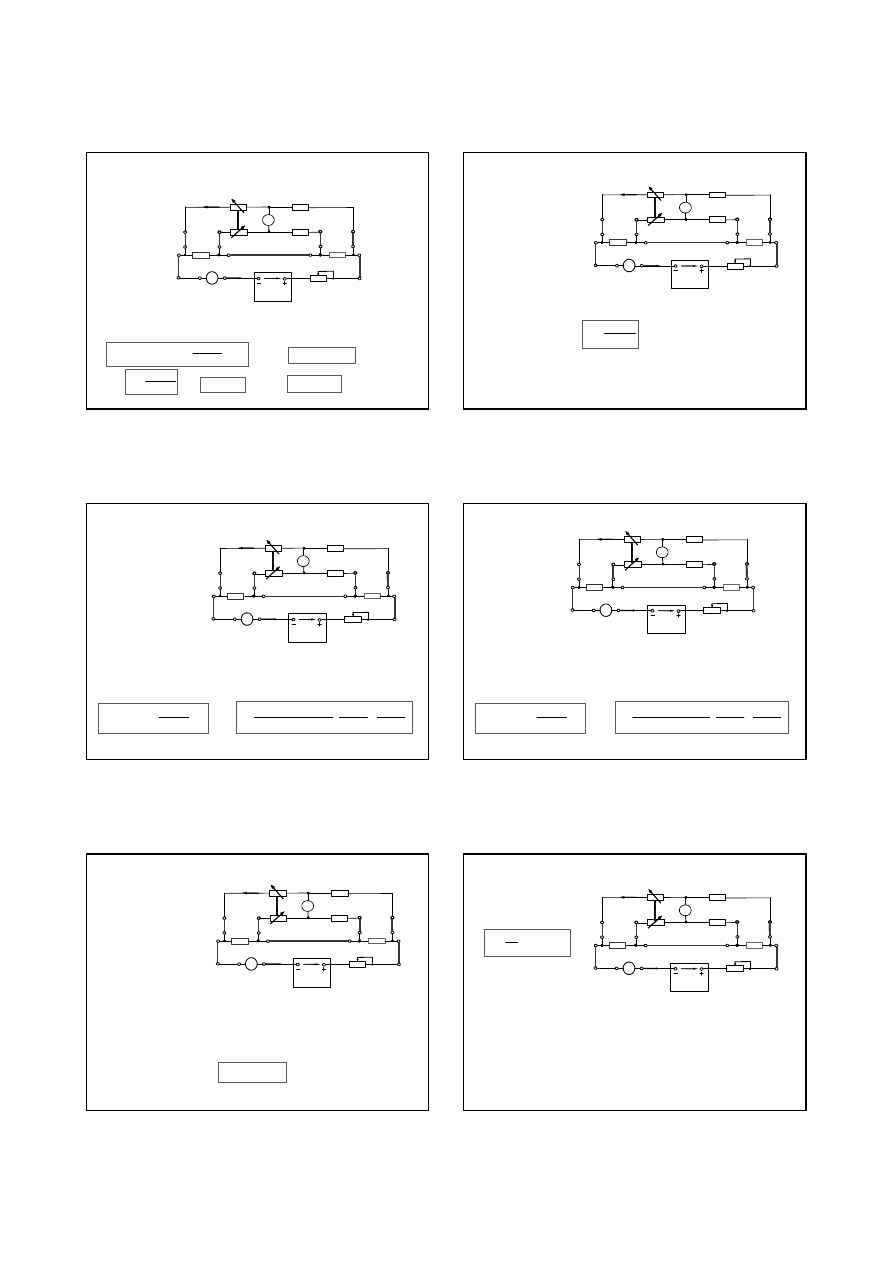
4. Do pomiaru małych rezystancji
Mostek Thomsona
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
15
4.
Do pomiaru małych rezystancji: Mostek Thomsona
Warunkiem zrównowa
ż
enia mostka (przy bardzo małej rezystancji (r=0)
przewodu pomi
ę
dzy punktami a-c) – pr
ą
d przez galwanometr równa
si
ę
zeru (Ig=0) jest równanie
0
=
+
+
−
=
⋅
−
=
zr
A
zr
N
x
X
zr
M
x
g
R
R
R
U
U
U
R
I
U
U
zr
N
B
x
R
U
R
U
⋅
=
A
zr
N
x
M
R
R
U
U
I
+
+
=
x
x
R
I
U
⋅
=
N
N
R
I
U
⋅
=
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
4.
Do pomiaru małych rezystancji: Mostek Thomsona
Warunkiem zrównowa
ż
enia mostka – równanie pomiaru
A
zr
N
x
R
R
R
R
⋅
=
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
Do pomiaru małych rezystancji: Mostek Thomsona
Start 5.12.2011
Na ogół przy pomiarach bardzo małych warto
ś
ci rezystancji nale
ż
y
uwzgl
ę
dnia
ć
niezerowe warto
ś
ci rezystancji przewodów, którymi
podł
ą
cza si
ę
rezystor mierzony R
x
, wzorcowy R
N
oraz elementy
mostka. Wtedy równanie mostka ma posta
ć
:
d
r
R
R
r
R
R
B
N
zr
x
+
+
+
=
2
1
)
(
+
+
′
−
+
+
+
+
+
+
⋅
+
=
4
3
2
1
4
3
/
4
)
(
r
R
r
R
r
R
r
R
r
r
r
R
R
r
r
R
d
А
z
B
zr
zr
A
A
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
Do pomiaru małych rezystancji: Mostek Thomsona
Na ogół przy pomiarach bardzo małych warto
ś
ci rezystancji nale
ż
y
uwzgl
ę
dnia
ć
niezerowe warto
ś
ci rezystancji przewodów, którymi
podł
ą
cza si
ę
rezystor mierzony R
x
, wzorcowy R
N
oraz elementy
mostka. Wtedy równanie mostka ma posta
ć
:
d
r
R
R
r
R
R
A
N
zr
x
+
+
+
=
2
1
)
(
+
+
′
−
+
+
+
+
+
+
⋅
+
=
4
3
2
1
4
3
/
4
)
(
r
R
r
R
r
R
r
R
r
r
r
R
R
r
r
R
d
B
z
A
zr
zr
B
B
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
Do pomiaru małych rezystancji: Mostek Thomsona
Zwykle rezystancja rezystora wzorcowego R
N
=10
k
, gdzie k
jest liczb
ą
całkowit
ą
ujemn
ą
lub dodatni
ą
, oraz rezystancja
rezystora te
ż
krotna 10: R
A
=10
m
, gdzie m jest liczb
ą
dodatni
ą
(R
A
=10; 100; 1000; 10000
Ω
), dlatego stosunek
R
N
/R
A
=10
n
– jest krotny 10 (n liczba całkowita) i
uproszczony wzór na warto
ść
rezystancji mierzonej ma
posta
ć
:
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
zr
n
x
R
R
⋅
=
10
Do pomiaru małych rezystancji: Mostek Thomsona
Mostki Thomsona wykorzystuj
ą
si
ę
do pomiaru małych warto
ś
ci
rezystancji: w zakresie od 10
-8
do 10
2
Ω
, jest to mo
ż
liwie dzi
ę
ki małym
warto
ś
ciom rezystancji R
N
od 10
-5
…do 10
Ω
.
Zas.
r
3
r
r
4
r
1
r
2
R
N
R
B
R
A
R
X
A
R
reg
r
5
R`
zr
R
zr
G
U
0
I
a
c
b
r
6
I
G
=0
g
I
M
zr
n
zr
A
N
x
R
R
R
R
R
⋅
=
=
10
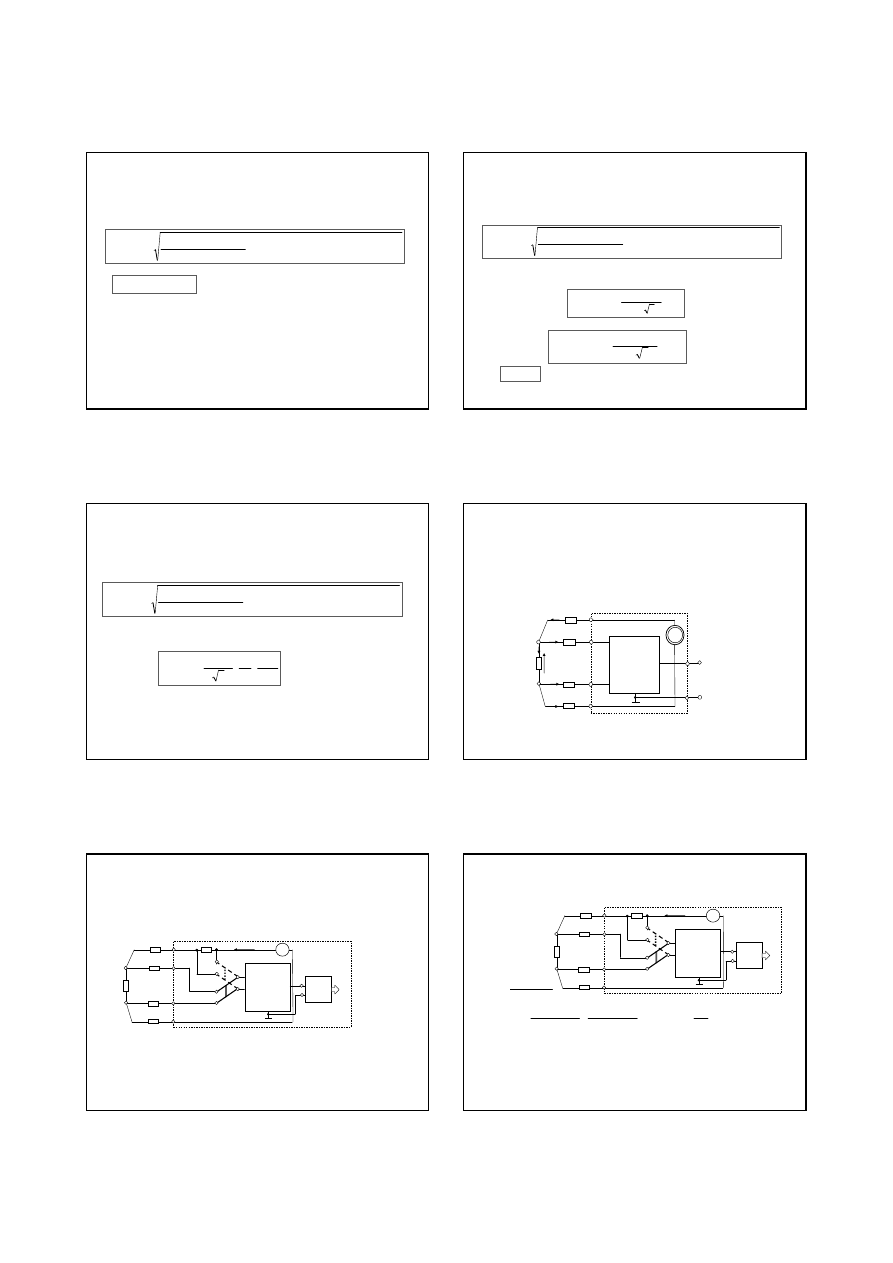
16
5. Niepewno
ść
wyniku pomiaru mostkiem
Thomsona
Wzgl
ę
dna zło
ż
ona niepewno
ść
standardowa wyniku pomiaru rezystancji,
obliczona metod
ą
typu B:
- wzgl
ę
dne graniczne (dopuszczalne) odchylenia
odpowiednich rezystancji mostka od warto
ś
ci nominalnych;
( )
(d)
u
)
(R
u
)
(R
u
3
2
rel
B,
nc
x,
2
rel
B,
kw
zr,
2
rel
B,
2
2
2
+
+
+
+
+
=
gr
,
R
gr
,
R
gr
,
R
x
rel
,
B
N
A
zr
R
u
δ
δ
δ
gr
,
R
gr
,
R
gr
,
R
N
A
zr
;
;
δ
δ
δ
5. Niepewno
ść
wyniku pomiaru mostkiem
Thomsona
Wzgl
ę
dna zło
ż
ona niepewno
ść
standardowa wyniku pomiaru rezystancji,
obliczona metod
ą
typu B:
Wzgl
ę
dna niepewno
ść
od kwantowania (dyskretno
ś
ci) rezystancji
zrównowa
ż
enia R
zr
oblicza si
ę
z wzoru
Wzgl
ę
dna niepewno
ść
od nieczuło
ś
ci oblicza si
ę
z wzoru
gdzie
- zmiana rezystancji zrównowa
ż
enia wywołuj
ą
ca odchylenie
wska
ź
nika galwanometru o 0,1 podzialki
( )
(d)
u
)
(R
u
)
(R
u
3
2
rel
B,
nc
x,
2
rel
B,
kw
zr,
2
rel
B,
2
2
2
+
+
+
+
+
=
gr
,
R
gr
,
R
gr
,
R
x
rel
,
B
N
A
zr
R
u
δ
δ
δ
%
100
3
)
(
)
(R
u
1
,
0
nc
x,
rel
cB,
zr
dz
zr
R
R
∆
=
%
100
3
5
,
0
)
(R
u
,
kw
zr,
rel
B,
⋅
∆
⋅
=
zr
kw
zr
R
R
dz
zr
R
1
,
0
)
(
∆
5. Niepewno
ść
wyniku pomiaru mostkiem
Thomsona
Wzgl
ę
dna zło
ż
ona niepewno
ść
standardowa wyniku pomiaru rezystancji,
obliczona metod
ą
typu B:
Wzgl
ę
dna niepewno
ść
od członu d (niezerowej warto
ś
ci rezystancji r
≠
0)
k=R
x
/R
N
( )
(d)
u
)
(R
u
)
(R
u
3
2
rel
B,
nc
x,
2
rel
B,
kw
zr,
2
rel
B,
2
2
2
+
+
+
+
+
=
gr
,
R
gr
,
R
gr
,
R
x
rel
,
B
N
A
zr
R
u
δ
δ
δ
( )
k
k
R
r
d
u
x
R
rel
,
B
gr
.
zr
+
⋅
⋅
=
1
3
4
δ
6. Omomierz z 4-przewodowym podł
ą
czeniem
rezystora badanego.
-
Przetwornik rezystancji ze
ź
ródłem pr
ą
dowym oraz wzmacniaczem
instrumentalnym.
Podstawowy problem polega na eliminacji wpływu rezystancji
przewodów linii. W tym celu wykorzystuje si
ę
poł
ą
czenia
czteroprzewodowe (rys.2).
Do schematu przetwarzania małej warto
ś
ci rezystancji
Wzmacniacz
instrumentalny
K
WI
R
l2
R
l3
R
l1
R
l4
U
wy
=
=K
wi
⋅
I
0
⋅
R
x
I
0
WE
WY
1
2
3
4
R
x
U
x
I
0
I
0
I
0
I
we2
=0
I
we3
=0
7. Omomierz z 4-przewodowym podł
ą
czeniem rezystora
badanego (
ze
ź
ródłem napi
ę
ciowym oraz rezystorem
referencyjnym i wzmacniaczem instrumentalnym
).
Eliminacja wpływu rezystancji przewodów linii bazuje na pomiarze pr
ą
du
wymuszaj
ą
cego, poprzez pomiar spadku napi
ę
cia na rezystorze
referencyjnym
Schemat pomiaru małej warto
ś
ci rezystancji w układzie ze
ź
ródłem napi
ę
ciowym
oraz rezystorem referencyjnym i wzmacniaczem instrumentalnym
R
x
Wzmacniacz
instrumentalny
K
WI
R
l2
R
l3
R
l1
R
l4
N
x
=I
pom
⋅
R
x
K
wi
⋅
k
ADC
WE
WY
1
2
3
3
4
U
0
I
pom
R
ref
U
Rref
U
x
1
2
ADC
k
ADC
N
ref
=I
pom
⋅
R
ref
K
wi
⋅
k
ADC
7. Omomierz z 4-przewodowym podł
ą
czeniem
rezystora badanego (
ze
ź
ródłem napi
ę
ciowym oraz
rezystorem referencyjnym i wzmacniaczem
instrumentalnym
).
Otó
ż
wynik pomiaru jest niezale
ż
ny od warto
ś
ci napi
ę
cia zasilaj
ą
cego
(pr
ą
du wymuszaj
ą
cego) oraz rezystancji przewodów linii. Wymagano
jest tylko krótko czasowa stabilno
ść
wszystkich parametrów układu
pomiarowego.
R
x
Wzmacniacz
instrumentalny
K
WI
R
l2
R
l3
R
l1
R
l4
N
x
=I
pom
⋅
R
x
K
wi
⋅
k
ADC
WE
WY
1
2
3
3
4
U
0
I
pom
R
ref
U
Rref
U
x
1
2
ADC
k
ADC
N
ref
=I
pom
⋅
R
ref
K
wi
⋅
k
ADC
ADC
wi
ref
ref
pom
k
K
R
N
I
=
ref
ref
x
ADC
WI
ref
ADC
WI
ref
x
ADC
WI
pom
x
x
R
N
N
k
K
R
k
K
N
N
k
K
I
N
R
=
⋅
⋅
⋅
⋅
=
⋅
⋅
=
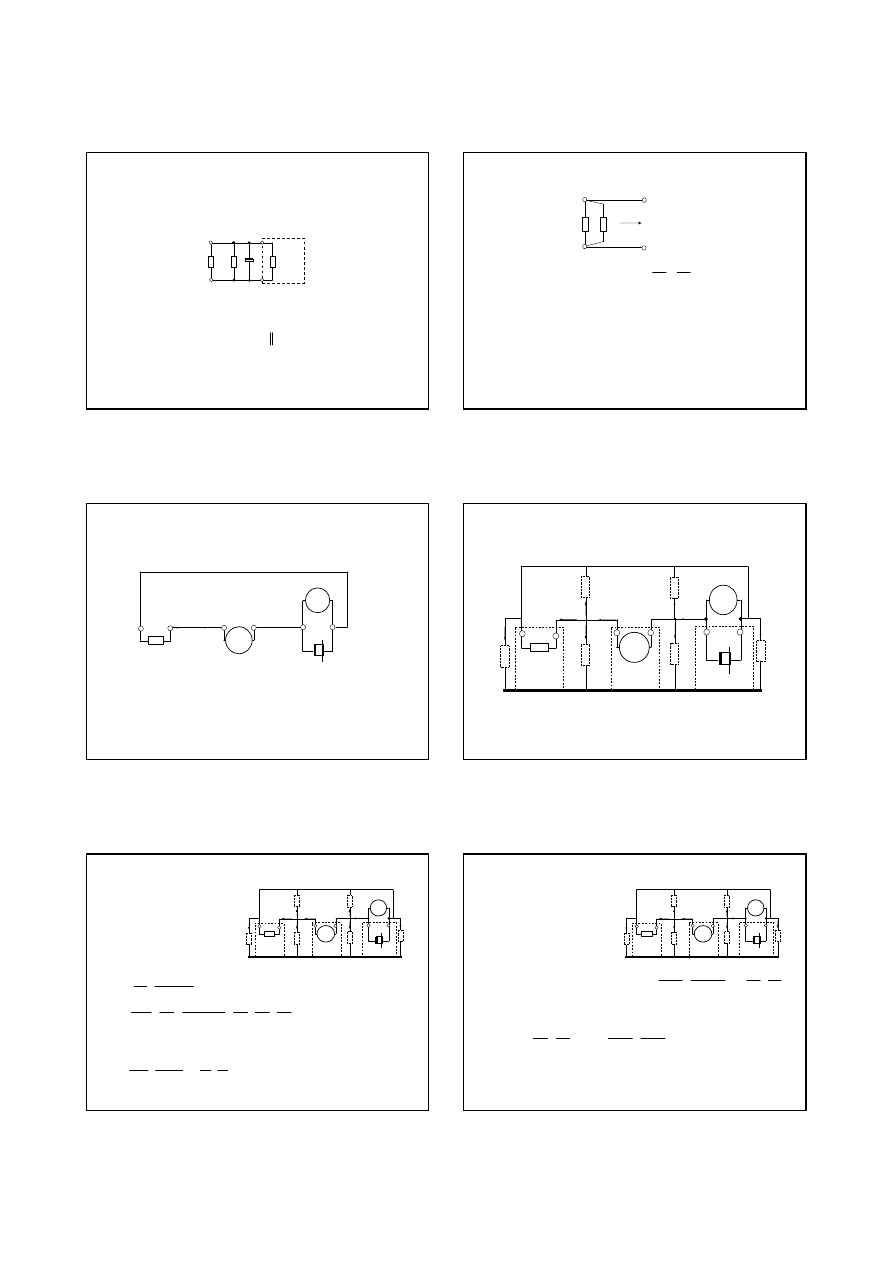
17
8. Pomiary du
ż
ych rezystancji
Problem pomiarów (przetworników) du
ż
ych rezystancji
polega we wpływie rezystancji izolacji R
k
i pojemno
ś
ci C
k
kabla oraz wzmacniacze operacyjnych.
Te parametry bocznikuj
ą
rezystancj
ą
mierzon
ą
, wskutek
czego wynik pomiaru równa si
ę
rezystancji równoległego
poł
ą
czenia mierzonego i kabla
Pojemno
ść
kabla powoduje zwi
ę
kszenie czasu pomiaru
poniewa
ż
wzrasta stała czasowa obwodu pomiarowego
R
x
R
we
R
k
kabel
Miernik
C
k
k
x
pom
R
R
R
=
k
x
x
C
R
⋅
≈
τ
8. Pomiary du
ż
ych rezystancji
Wpływ rezystancji izolacji kable
• wpływ izolacji z rezystancj
ą
powy
ż
ej R
iz
=100 G
Ω
Ω
Ω
Ω
przy
R
x
<100M
Ω
Ω
Ω
Ω
jest mniejszy od 0,1%.
Do miernika
rezystancji
R
x
R
iz
iz
x
x
iz
iz
R
R
G
G
≅
≅
δ
8. Pomiary du
ż
ych rezystancji
Rys.5. Zasada pomiaru rezystancji rezystancji
I
nA
R
x
U
zas
nA
I
x
V
8. Pomiary du
ż
ych rezystancji
Rys. Układ zast
ę
pczy uwzgl
ę
dniaj
ą
cy wpływ rezystancji izolacji
R
k2
I
nA
R
x
R
iz2
R
iz1
U
zas
nA
R
k1
I
x
I
zas
I
izU
I
izx
I
k2
I
iz2
I
iz1
I
k1
V
R
izU
R
izx
3. Pomiary du
ż
ych rezystancji
Wynik pomiaru pr
ą
du:
I
nA
=I
x
+I
iz2
+I
k2
Zamiast I
nA
=I
x
Pr
ą
dy przez izolacje I
iz2
=U
zas
/R
iz2
oraz kabel I
k2
=U
zas
/R
k2
powoduj
ą
powstanie bł
ę
du:
R
k2
I
nA
R
x
R
iz2
R
iz1
U
zas
nA
R
k1
I
x
I
zas
I
izU
I
izx
I
k2
I
iz2
I
iz1
I
k1
V
R
iz
U
R
iz
x
2
2
k
iz
x
zas
nA
zas
pom
,
x
I
I
I
U
I
U
R
+
+
=
=
2
2
2
2
2
2
1
k
iz
x
zas
k
zas
iz
zas
x
zas
k
iz
x
zas
nA
pom
,
x
pom
,
x
G
G
G
U
I
U
I
U
I
U
I
I
I
U
I
R
G
+
+
=
+
+
=
+
+
=
=
=
2
2
k
iz
pom
,
x
pom
,
x
G
G
G
G
G
pom
,
x
+
=
−
=
∆
∆∆
∆
+
=
+
=
=
2
2
2
2
1
1
k
iz
x
x
k
iz
x
G
G
R
R
R
G
G
G
G
pom
,
x
pom
,
x
∆
∆∆
∆
δ
8. Pomiary du
ż
ych rezystancji
Pr
ą
dy przez izolacje I
iz2
=U
zas
/R
iz2
oraz kabel I
k2
=U
zas
/R
k2
powoduj
ą
powstanie bł
ę
du:
R
k2
I
nA
R
x
R
iz2
R
iz1
U
zas
nA
R
k1
I
x
I
zas
I
izU
I
izx
I
k2
I
iz2
I
iz1
I
k1
V
R
iz
U
R
iz
x
2
2
k
iz
pom
,
x
pom
,
x
G
G
G
G
G
pom
,
x
+
=
−
=
∆
∆∆
∆
+
=
+
=
=
2
2
2
2
1
1
k
iz
x
x
k
iz
x
G
G
R
R
R
G
G
G
G
pom
,
x
pom
,
x
∆
∆∆
∆
δ
Przykład: R
x
=1 G
Ω
; R
iz2
=R
k2
=10 G
Ω
=10
10
Ω
%
,
R
R
R
k
iz
x
G
pom
,
x
20
2
0
10
1
10
1
10
1
1
10
10
9
2
2
=
=
+
=
+
=
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
δ
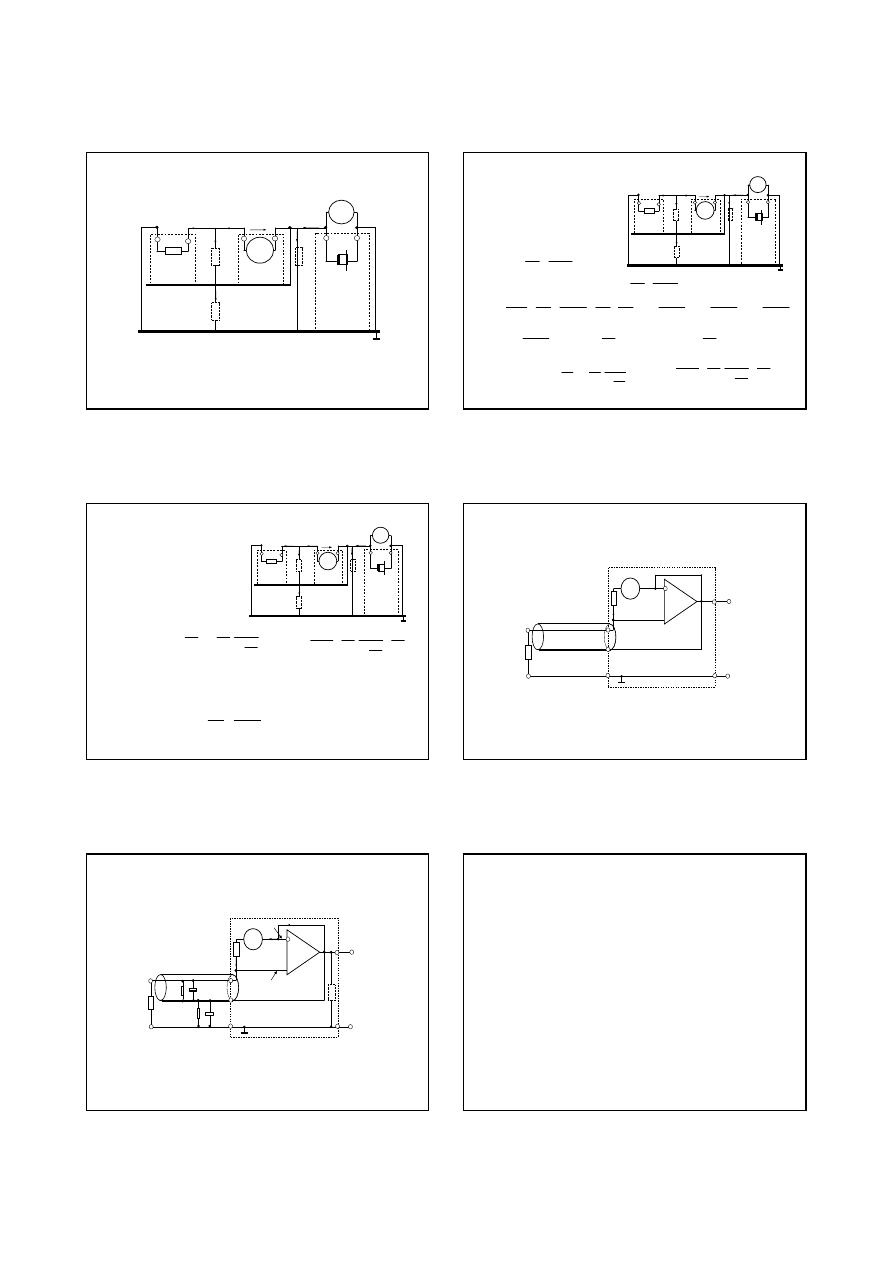
18
8. Pomiary du
ż
ych rezystancji
Rys. zasada ekwipotencjalnego zabezpieczenia podczas pomiaru
du
ż
ych rezystancji.
R
iz3
I
nA
R
x
R
iz2
R
iz1
U
zas
nA
I
x
I
zas
I'
iz2
I
iz3
I
iz1
V
U
nA
Ekran ekwipotencjalny
8. Pomiary du
ż
ych rezystancji
Wynik pomiaru pr
ą
du: I
nA
=I
x
+I'
iz2
Pr
ą
d przez izolacj
ę
Wynik pomiaru rezystancji:
Bł
ą
d
R
iz3
I
nA
R
x
R
iz2
R
iz1
U
zas
nA
I
x
I
zas
I'
iz2
I
iz3
I
iz1
V
U
nA
Ekran ekwipotencjalny
2
2
2
iz
nA
nA
iz
nA
iz
R
R
I
R
U
I
=
=
′
2
iz
x
zas
nA
zas
pom
,
x
I
I
U
I
U
R
′
+
=
=
zas
iz
nA
nA
x
zas
iz
nA
x
zas
nA
nA
x
zas
iz
zas
x
zas
iz
x
zas
nA
pom
,
x
pom
,
x
U
R
I
R
G
U
R
U
G
U
R
U
G
U
I
U
I
U
I
I
U
I
R
G
3
3
2
2
1
+
=
+
=
+
=
′
+
=
′
+
=
=
=
pom
,
x
iz
nA
x
pom
,
x
zas
iz
nA
nA
x
pom
,
x
G
R
R
G
G
U
R
I
R
G
G
3
3
+
=
=
+
=
−
=
3
1
iz
nA
pom
,
x
x
R
R
G
G
3
3
3
1
1
iz
nA
iz
nA
x
iz
nA
pom
,
x
x
pom
,
x
G
R
R
R
R
G
R
R
G
G
G
pom
,
x
−
⋅
=
=
−
=
∆
∆∆
∆
3
3
3
1
1
iz
nA
iz
nA
iz
nA
x
G
G
R
R
R
R
R
R
G
pom
,
x
pom
,
x
≅
−
⋅
=
=
∆
∆∆
∆
δ
8. Pomiary du
ż
ych rezystancji
Bł
ą
d:
R
nA
<<R
iz3
Przykład: R
nA
=100
Ω
; R
iz3
=10 G
Ω
=10
10
Ω
R
iz3
I
nA
R
x
R
iz2
R
iz1
U
zas
nA
I
x
I
zas
I'
iz2
I
iz3
I
iz1
V
U
nA
Ekran ekwipotencjalny
3
3
3
1
1
iz
nA
iz
nA
x
iz
nA
pom
,
x
x
pom
,
x
G
R
R
R
R
G
R
R
G
G
G
pom
,
x
−
⋅
=
=
−
=
∆
∆∆
∆
3
3
3
1
1
iz
nA
iz
nA
iz
nA
x
G
G
R
R
R
R
R
R
G
pom
,
x
pom
,
x
≅
−
⋅
=
=
∆
∆∆
∆
δ
%
R
R
iz
nA
G
pom
,
x
6
8
10
3
10
10
10
100
−
−
=
=
=
≅
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
δ
9. Omomierz do pomiaru du
ż
ych rezystancji
Przetwornik rezystancji z ekranowaniem ekwipotencjalnym
Rys.8. Schemat przetwarzania du
ż
ej warto
ś
ci rezystancji
R
n
WO
-
+
I
x
U
wy
U
ref
R
x
Ekran
ekwipotencjalny
HI
LO
E -Ekran
Do A/C
WY
WE
9. Omomierz do pomiaru du
ż
ych rezystancji
-
Przetwornik rezystancji z ekranowaniem ekwipotencjalnym
Rys.8. Schemat przetwarzania du
ż
ej warto
ś
ci rezystancji
R
n
WO
-
+
I
x
=I
n
U
wy
U
ref
I
n
=U
ref
/R
n
R
x
I
n
Ekran
ekwipotencjalny
U
e
=U
wy
=U
-
=U
+
=U
HI
R
iz
R
wy
C
iz
HI
LO
U
HI
E -Ekran
Do A/C
I
we+
=0
I
we-
=0
WY
WE
R
k
C
k
10. Pomiary parametrów izolacji
Podstawowymi obiektywnymi parametrami materiałów
dielektrycznych (izolacji) w stałym polu elektrycznym
s
ą
:
rezystywno
ść
skro
ś
na
ρ
s
oraz
powierzchniowa
ρ
p
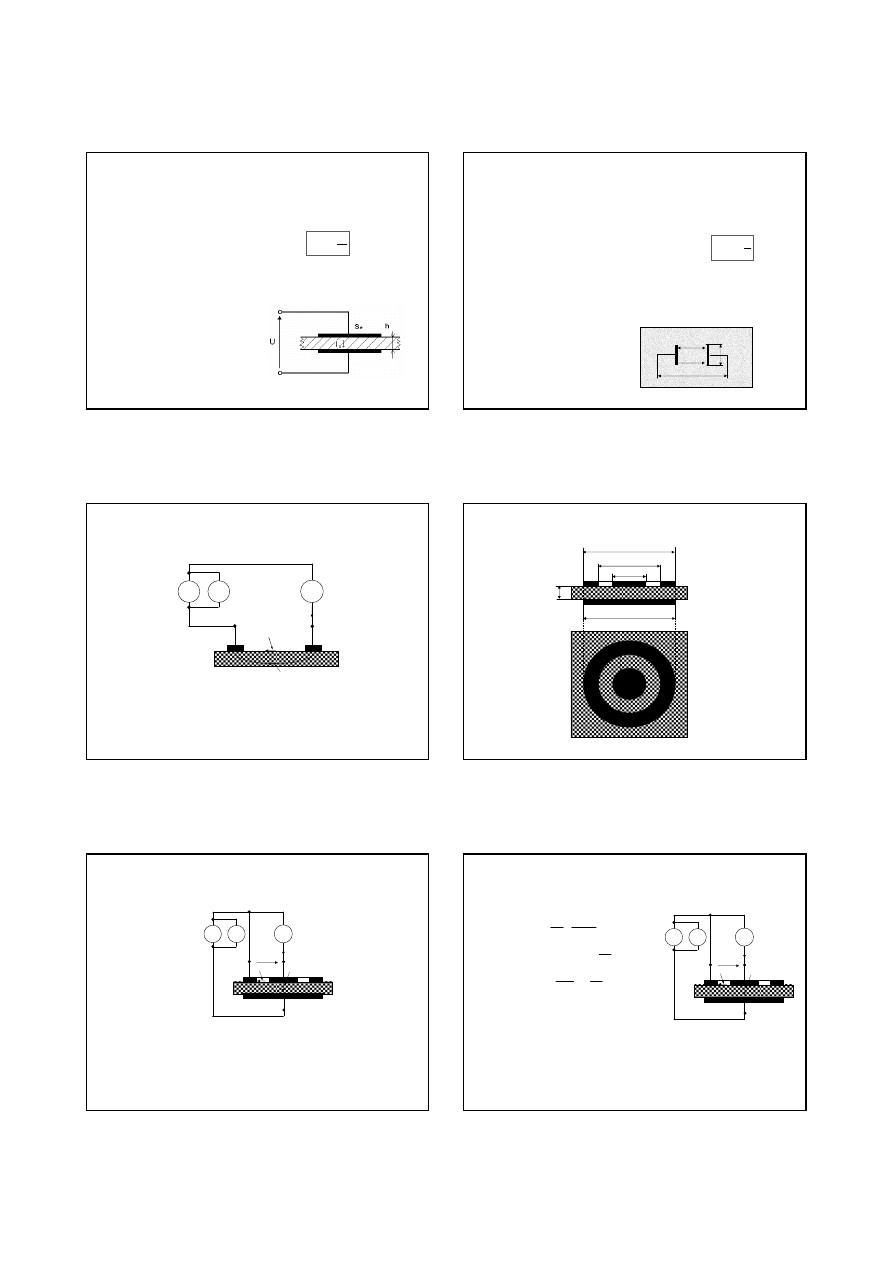
19
10. Pomiary parametrów izolacji
Rezystywno
ść
skro
ś
na
ρ
s
odwzoruje własno
ś
ci przepływu pr
ą
du wewn
ą
trz
obj
ę
to
ś
ci dielektryka umieszczonego pomi
ę
dzy dwoma elektrodami (o
zadanej powierzchni), do których doprowadzone jest napi
ę
cie stałe.
Rezystywno
ść
skro
ś
na
ρ
s
wyznaczana jest ze wzoru:
[
Ω
·m] lub [
Ω
·cm]
gdzie R
s
=U/I
s
jest zmierzona warto
ść
rezystancji skro
ś
nej przez pomiar
warto
ś
ci doprowadzonego do elektrod napi
ę
cia U oraz warto
ść
płyn
ą
cego
wewn
ą
trz obj
ę
to
ś
ci dielektryka pr
ą
d I
s
;
S
e
jest efektywn
ą
powierzchni
ą
elektrod;
h – jest grubo
ś
ci
ą
izolacji (dielektryka).
h
S
R
e
s
s
=
ρ
10. Pomiary parametrów izolacji
Rezystywno
ść
powierzchniowa
ρ
p
odwzoruje własno
ś
ci przepływu pr
ą
du
po powierzchni dielektryka pomi
ę
dzy dwoma elektrodami o zadanych
wymiarach i odst
ę
pie usytuowanymi na jego powierzchni, do których
doprowadzone jest napi
ę
cie stałe .
Rezystywno
ść
powierzchniowa
ρ
p
wyznaczana jest ze wzoru: [
Ω
]
gdzie R
p
=U/I
p
jest zmierzona warto
ść
rezystancji powierzchniowej przez
pomiar warto
ś
ci doprowadzonego do elektrod napi
ę
cia U oraz warto
ść
płyn
ą
cego po powierzchni dielektryka pr
ą
d I
p
;
L jest odległo
ś
ci
ą
pomi
ę
dzy elektrodami;
g – jest odst
ę
pem pomi
ę
dzy elektrodami
g
L
R
p
p
=
ρ
L
g
I
p
U
10. Pomiary parametrów izolacji
Przez materiał dielektryczny, do którego za pomoc
ą
elektrod pomiarowych zostało
podane napi
ę
cie, płyn
ą
jednocze
ś
nie pr
ą
dy wewn
ą
trz jego obj
ę
to
ś
ci (I
s
) oraz po
powierzchnie (I
p
).
Dlatego zmierzona warto
ść
rezystancji jest wypadkow
ą
rezystancj
ą
skro
ś
nej i
powierzchniowej: I
pom
=I
s
+I
p
.
W celu niezale
ż
nego pomiaru rezystancji skro
ś
nej i powierzchniowej (i dalej
odpowiednich rezystywno
ś
ci) wykorzystuje si
ę
specjalne elektrody pomiarowe
(komórka pomiarowa)
U
V
µA
2
1
I
pom
I
s
I
p
10. Pomiary parametrów izolacji
Układ elektrod pomiarowych (komórka pomiarowa) do niezale
ż
nego pomiaru
rezystancji skro
ś
nej i powierzchniowej
d
4
d
3
d
1
d
2
h
10. Pomiary parametrów izolacji
Pomiar rezystancji i rezystywno
ś
ci skro
ś
nej
2
E
U
V
µ
A
3
1
I
pom
I
s
I
p
U
µ
A
10. Pomiary parametrów izolacji
Pomiar rezystancji i rezystywno
ś
ci skro
ś
nej
Warto
ść
pr
ą
du powierzchniowego (powoduj
ą
cego bł
ą
d)
Bł
ą
d
R
µ
A
<<R
p
2
E
U
V
µ
A
3
1
I
pom
I
s
I
p
U
µ
A
p
A
pom
p
A
p
R
R
I
R
U
I
µ
µ
=
=
−
=
−
=
p
A
pom
p
pom
pom
R
R
I
I
I
I
µ
1
∆
∆∆
∆
( )
p
A
pom
pom
p
pom
R
R
I
I
I
I
µ
δ
−
=
=
1
∆
∆∆
∆
( )
0
→
p
pom
I
I
δ
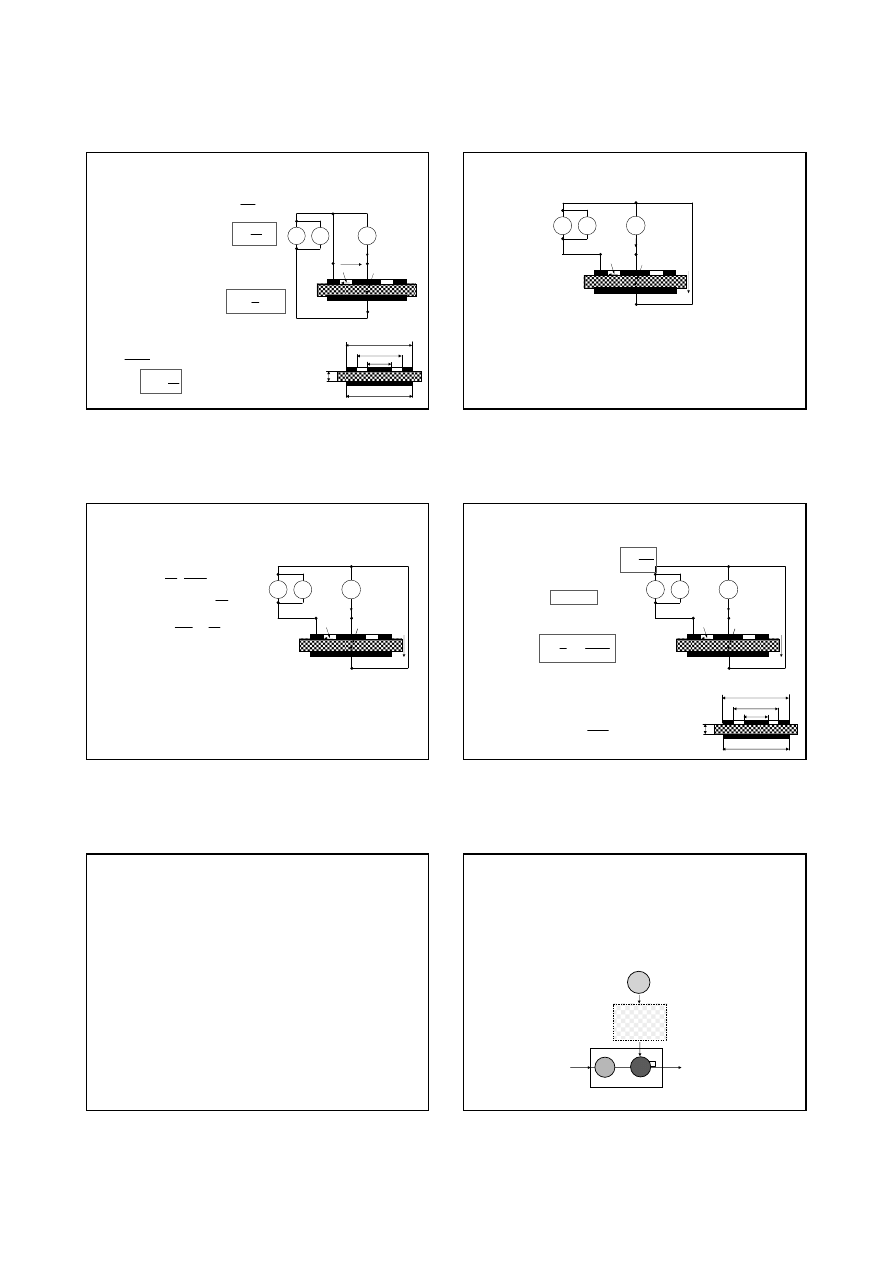
20
10. Pomiary parametrów izolacji
Pomiar rezystancji i rezystywno
ś
ci skro
ś
nej
Warto
ść
rezystancji skro
ś
nej
Warto
ść
rezystywno
ś
ci skro
ś
nej
Warto
ść
stałej K
s
komórki pomiarowej
z okr
ą
głymi elektrodami pomiarowymi
do pomiaru rezystywno
ś
ci skro
ś
nej
ρ
s
wyznaczana jest ze wzoru:
gdzie B jest współczynnikiem efektywnej powierzchni elektrody pomiarowej
(mo
ż
na przyj
ąć
B=0);
- jest połow
ą
odległo
ś
ci
elektrody wewn
ę
trznej i zewn
ę
trznej.
Otó
ż
2
E
U
V
µ
A
3
1
I
pom
I
s
I
p
U
µ
A
pom
i
I
U
R
=
s
s
s
R
h
K
⋅
=
ρ
2
1
2
⋅
+
=
g
B
d
K
s
π
2
1
2
d
d
g
−
=
4
2
1
d
K
s
π
≅
d
4
d
3
d
1
d
2
h
10. Pomiary parametrów izolacji
Pomiar rezystancji i rezystywno
ś
ci powierzchniowej
2
E
U
V
µ
A
3
1
I
pom
I
s
I
p
U
µA
10. Pomiary parametrów izolacji
Pomiar rezystancji i rezystywno
ś
ci powierzchniowej
Warto
ść
pr
ą
du skro
ś
nego (powoduj
ą
cego bł
ą
d)
Bł
ą
d
R
µ
A
<<R
s
2
E
U
V
µ
A
3
1
I
pom
I
s
I
p
U
µA
s
A
pom
s
A
s
R
R
I
R
U
I
µ
µ
=
=
−
=
−
=
s
A
pom
s
pom
pom
R
R
I
I
I
I
µ
1
∆
∆∆
∆
s
A
pom
pom
pom
R
R
I
I
I
µ
δ
−
=
=
1
∆
∆∆
∆
( )
0
→
s
pom
I
I
δ
10. Pomiary parametrów izolacji
Pomiar rezystancji i rezystywno
ś
ci powierzchniowej
Warto
ść
rezystancji powierzchniowej
Warto
ść
rezystywno
ś
ci powierzchniowej
Warto
ść
stałej K
p
komórki pomiarowej
do pomiaru rezystywno
ś
ci powierzchniowej
gdzie P jest efektywnym obwodem elektrody ekranuj
ą
cej:
g - jest połow
ą
odległo
ś
ci elektrody wewn
ę
trznej i zewn
ę
trznej:
2
E
U
V
µ
A
3
1
I
pom
I
s
I
p
U
µA
pom
p
I
U
R
=
p
p
p
R
K
⋅
=
ρ
−
+
=
=
1
2
2
1
d
d
d
d
g
P
K
p
π
(
)
g
d
d
P
+
=
=
1
0
π
π
2
1
2
d
d
g
−
=
d
4
d
3
d
1
d
2
h
Plan wykładu
Plan:
3.1. Wst
ę
p
3.2. Metody konstrukcyjno-technologiczne
zmniejszenia wpływu zakłóce
ń
3.2.1. Ekranowanie
3.2.2. Skr
ę
canie par przewodów
3.2.3. Prawidłowe uziemienie
3.2.4. Ekwipotencjalne ekranowanie
3.3. Zabezpieczenie (ekranowanie) ekwipotencjalne
3.3.1. Niektóry przykłady analizy wpływu zakłóce
ń
wspólnych
3.3.2. Współczynnik tłumienia zakłócenia wspólnego
3.3.3. Ekranowanie ekwipotencjalne
Cel: Zapozna
ć
si
ę
z rodzajami zakłóce
ń
w obwodach pomiarowych
3.1. Wst
ę
p
Zakłócenia, wyst
ę
puj
ą
ce w torze pomiarowym, powoduj
ą
powstanie dodatkowej
niepewno
ś
ci wyników pomiaru. Przy tym warto
ść
na niepewno
ś
ci,
spowodowanej zakłóceniami, zale
ż
y od wielu czynników. Przy rozpatrywaniu
zagadnie
ń
wpływu zakłóce
ń
na wyniki pomiaru nale
ż
y uwzgl
ę
dnia
ć
trzy
podstawowe składowe (rys. 1):
-
ź
ródło zakłóce
ń
;
- kanał przenikania zakłócenia w tor pomiarowy oraz
- obwód pomiarowy wraz z urz
ą
dzeniami pomiarowymi i metod
ą
przetwarzania
sygnału pomiarowego.
Kanał
przenikania
zakłócenia -
wra
ż
liwo
ść ξ
z
Ź
ródło
zakłócenia
U
x
Obwód pomiarowy
U
z
Ź
ródło sygnału
pomiarowego
Z
z
Wynik pomiaru X i
jego niepewno
ść
u
z
(Z)
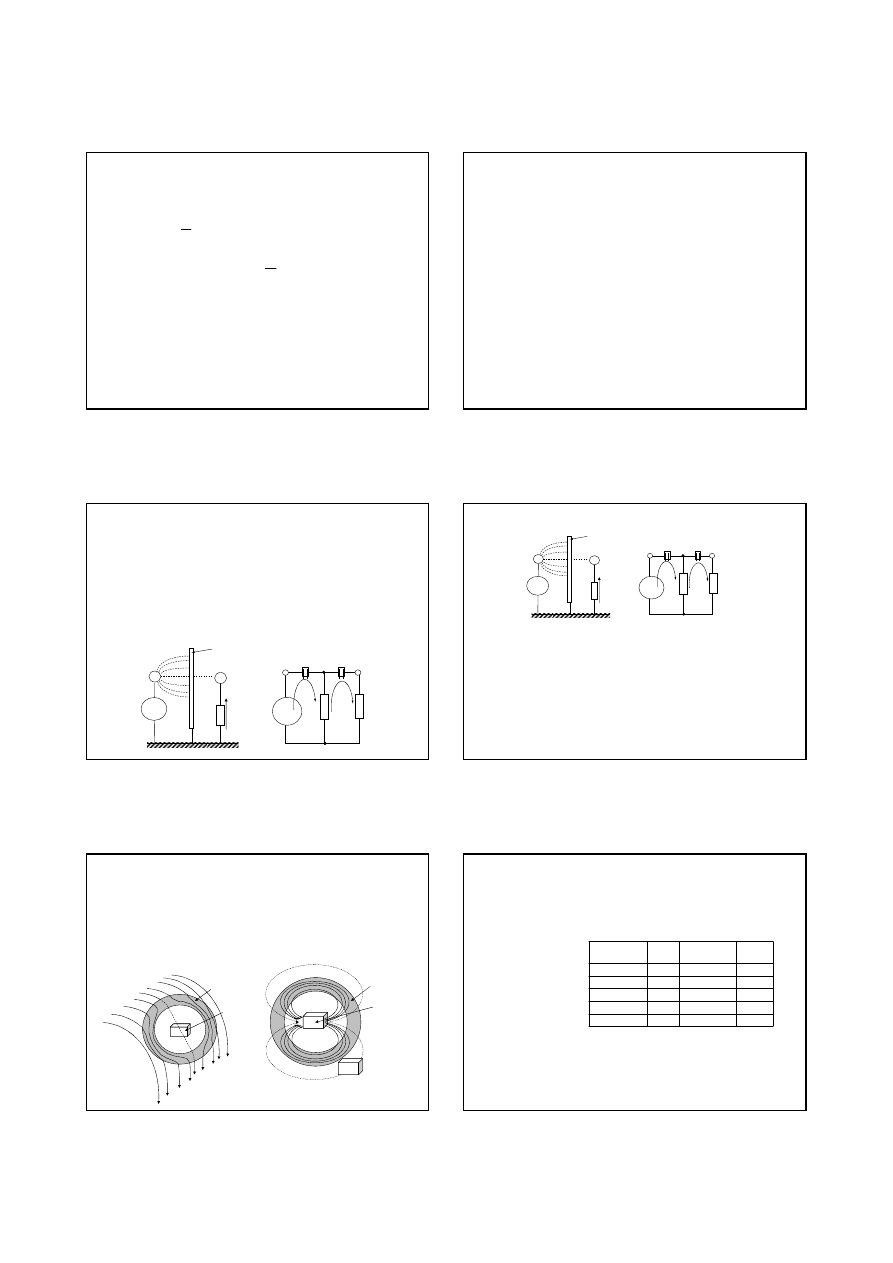
21
3.1. Wst
ę
p
W ogólnym podej
ś
ciu niepewno
ść
wyniku pomiaru wielko
ś
ci od wpływu
zakłócenia z zale
ż
y od
-
jego intensywno
ś
ci Z,
-
wra
ż
liwo
ś
ci
obwodu pomiarowego na zakłócenie oraz
-
operatora (algorytmu)
opracowania sygnału:
Dlatego mo
ż
na wyró
ż
ni
ć
trzy podstawowe sposoby zwalczania zakłóce
ń
w układach pomiarowych:
1. Tłumienie zakłóce
ń
w miejscu ich powstania (tłumienie „
ź
ródła”);
2. Utrudnienie przenikania zakłóce
ń
w obwód pomiarowy – zmniejszenia
wra
ż
liwo
ś
ci obwodu na zakłócenia;
3. Podwy
ż
szenie odporno
ś
ci sygnałów i układów pomiarowych na
zakłócenia – zmniejszenie skutku oddziaływania zakłócenia.
z
X
z
∂
∂
=
ξ
{
}
Z
L
z
⋅
ξ
( ) {
}
⋅
∂
∂
=
⋅
=
Z
z
X
L
Z
L
z
X
u
z
ξ
,
3.2. Konstrukcyjno-technologiczne metody
zmniejszenia wpływu zakłóce
ń
Pierwszy dwie metody s
ą
metodami konstrukcyjno-technologicznymi, a
trzecia metoda jest powi
ą
zana z odpowiednimi odpornym na
zakłócenia przetwarzaniami sygnałów pomiarowych.
Podstawowymi konstrukcyjno-technologicznymi metodami zwalczania wpływu
zakłóce
ń
s
ą
:
- ekranowanie oraz
- prawidłowe uziemienie,
a dla zmniejszenia przenikania zakłóce
ń
tak
ż
e wykorzystanie
- skr
ę
conych par przewodów linii.
3.2.1. Ekranowanie
W zale
ż
no
ś
ci od rodzaju pola elektrostatycznego, magnetostatycznego i
elektromagnetycznego rozró
ż
nia si
ę
ekrany:
•
elektrostatyczne;
•
magnetostatyczne;
•
elektromagnetyczne.
Ekran elektrostatyczny.
Pole elektrostatyczne indukuje na powierzchni ekranu ładunki
elektryczne, na których ko
ń
cz
ą
si
ę
linii pola, które spowodowało
powstanie tych ładunków. Przez co pole nie wnika za ekran.
+
U
e
-
Uz
C
1e
C
e2
Ekran
γ
e
, (r
e
)
C
1e
Uz
U
e
I
1e
1
2
C
e2
I
e2
Z
Z
e
3.2.1. Ekranowanie
Skuteczno
ść
ekranu zale
ż
y od przewodno
ś
ci materiału ekranu. Ona musi by
ć
du
ż
a
(materiał: mied
ź
, aluminium, srebro, złoto, itp.).
Przy obecno
ś
ci ekranu pr
ą
d I
e1
płyn
ą
c b
ę
dzie tylko w obwodzie
ź
ródło – pojemno
ść
paso
ż
ytnicza C
e1
– ekran, powoduj
ą
c napi
ę
cie na rezystancji na ekranie (gdzie
uwzgl
ę
dniono,
ż
e rezystancja ekranu jest w du
ż
ym stopniu mniejsza impedancj
ą
pojemno
ś
ci C
e1
(r
e
<<1/
ω
C
e1
).
Napi
ę
cie U
ez
jest
ź
ródłem wtórnego pr
ą
du płyn
ą
cego przez pojemno
ść
paso
ż
ytnicza C
e2
do
impedancji wej
ś
ciowej Z, wywołuj
ą
c na niej napi
ę
cie zakłócaj
ą
ce , gdzie C
e
=C
e1
≈
C
e2
.
Przykładowo, dla Us=230V, f=50Hz; C
e
=25pF (zwi
ę
kszenie pojemno
ś
ci wskutek
zwi
ę
kszenia powierzchni ekranu); r
e
=2,5
Ω
,
Z
=1M
Ω
warto
ść
napi
ę
cia zakłócenia
wynosi około U
z
≈
0,035
µ
V.
Skuteczno
ść
ekranowania zale
ż
y od przewodno
ś
ci materiału ekranu i jej zmniejszenie
powoduje pogorszenie skuteczno
ś
ci ekranowania. Ekran mo
ż
e by
ć
jako siatka.
+
U
ez
-
Uz
C
1e
C
e2
Ekran
γ
e
, (r
e
)
C
1e
Uz
U
ez
I
1e
1
2
C
e2
I
e2
Z
Z
e
Magnetostatyczne ekranowanie
Linii pola magnetostatycznego trafiaj
ą
c na ekran z materiału
ferromagnetycznego wnikaj
ą
we
ń
i zbieraj
ą
si
ę
w materiale ekranu
malej
ą
c wewn
ą
trz niego.
Ekranowany mo
ż
e by
ć
obwód pomiarowy (a) lub
ź
ródło zakłócenia (b).
Skuteczno
ść
takiego ekranu tym wi
ę
ksza im mniejszy opór magnetyczny
ekranu (im wi
ę
ksza przenikalno
ść
magnetyczna i grubo
ść
ekranu).
Ekran musi by
ć
jednolity, bez dziur.
Ekran
magnetyczny
Układ
pomiarowy
Pole
magnetostatyczn
e zewn
ę
trzne
Ekran
magnetyczny
Układ
pomiarowy
Ź
ródło zakłócenia
magnetycznego
wewn
ę
trznego
Ekranowanie elektromagnetyczne
Pole elektromagnetyczne (EMP) zwykle przyjmuje si
ę
zmiennym sinusoidalnym,
ono powoduje powstanie siły elektromotorycznej (EMS) oraz pr
ą
dów
wirowych w materiale przewodz
ą
cym.
Te pr
ą
dy wywołuj
ą
c pole magnetyczne, które przeciwdziała polu zewn
ę
trznemu.
Efektywno
ść
ekranu zale
ż
y od przewodno
ś
ci i przenikalno
ś
ci magnetycznej
materiału, grubo
ś
ci ekranu oraz długo
ś
ci fali (cz
ę
stotliwo
ś
ci) EMP
Przenikalno
ść
EMP, mm
Grubo
ść
ekranu musi by
ć
co najmniej równa trzykrotnej gł
ę
boko
ś
ci wnikania fali
elektromagnetycznej.
Wymiary szczelin i dziur w ekranie te
ż
musz
ą
by
ć
kilka razy mniejszymi od
długo
ś
ci fali elektromagnetycznej. Im wi
ę
ksza cz
ę
stotliwo
ść
EMP tym cie
ń
szy
wymagany jest ekran.
0.008
0.08
0.08
100000=1MHz
0.08
0.84
0.66
10000=10kHz
0.20
2.7
2.1
1000=1kHz
0.66
8.5
6.6
100
0.91
11.5
9
50
Stal
Aluminium
Miedź
Częstotliwość,
Hz
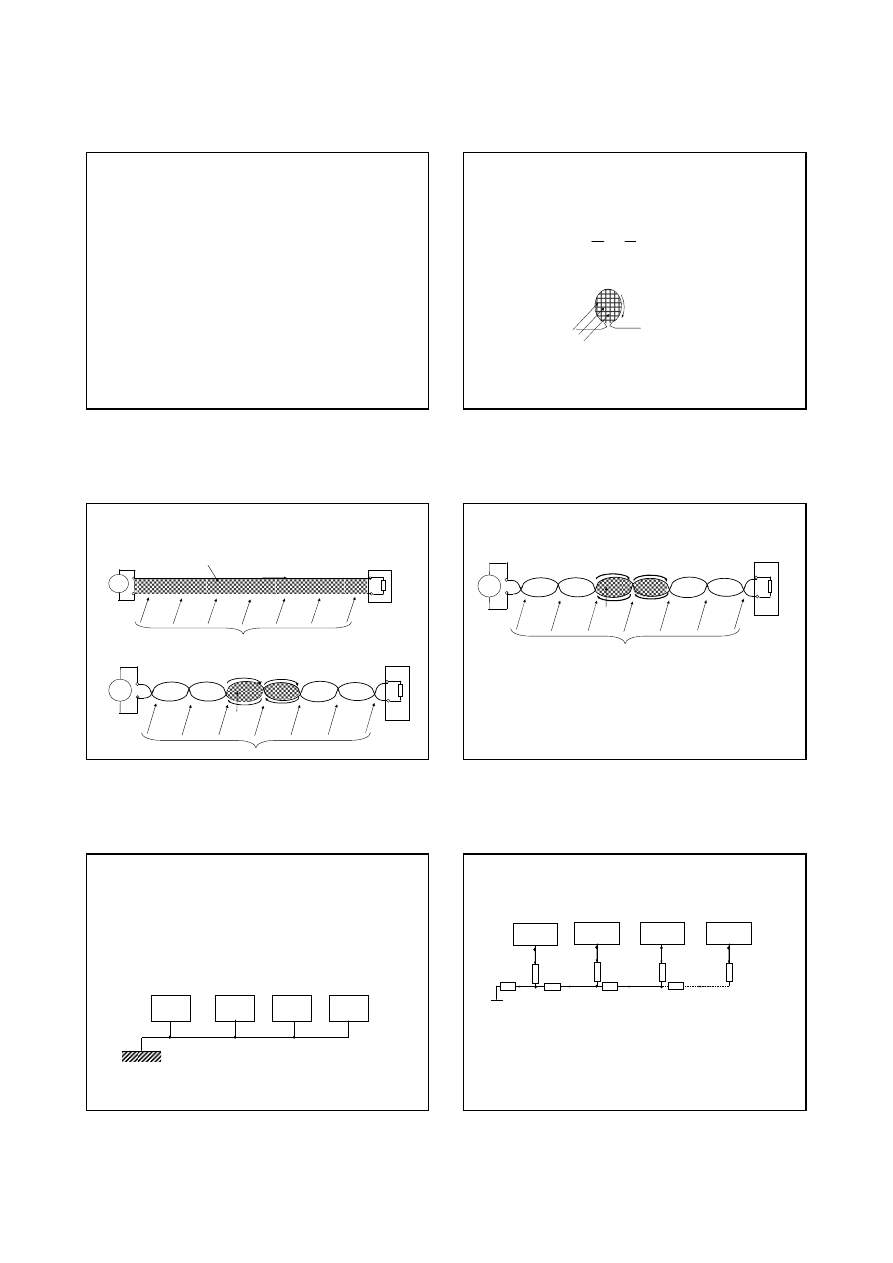
22
Rekomendacje
Je
ż
eli obudowa przyrz
ą
du pomiarowego jest zrobiona z tworzywa wtedy jako
ekran mo
ż
e si
ę
wykorzystywa
ć
zewn
ę
trzne przewodz
ą
ce pokrycia obudowy.
Dla zapewnienia zmniejszenia wpływu pól ró
ż
nego rodzaju na praktyce cz
ę
sto
stosuje si
ę
wielu warstwowe ekrany z ró
ż
nych materiałów.
W niektórych przypadkach mog
ą
by
ć
ekranowany ka
ż
dy element układu
pomiarowego lub najwa
ż
niejszy jego podzespoły.
W takich przypadkach ekrany powinny by
ć
doł
ą
czone do masy lub punktu
odniesienia
Rekomendacje [ZwAE]:
- Ekran elektrostatyczny: wysoka przewodno
ść
materiału, mo
ż
e by
ć
jako siatka.
- Ekran magnetostatyczny: wysoka przenikalno
ść
materiału, musi by
ć
bez dziur
lub z niewielkimi dziurami. Dla zwi
ę
kszenia skuteczno
ś
ci ekran mo
ż
e by
ć
kilku warstwowym.
- Ekran elektromagnetyczny: efektywno
ść
ekranu zale
ż
y od przewodno
ś
ci i
przenikalno
ś
ci magnetycznej materiału, grubo
ś
ci ekranu oraz długo
ś
ci fali
(cz
ę
stotliwo
ś
ci) EMP. Grubo
ść
ekranu musi by
ć
co najmniej równa trzykrotnej
gł
ę
boko
ś
ci wnikania fali elektromagnetycznej.
- Dla zapewnienia zmniejszenia wpływu pól ró
ż
nego rodzaju na praktyce cz
ę
sto
stosuje si
ę
wielu warstwowe ekrany z ró
ż
nych materiałów.
3.2.2.Tłumienie pola magnetycznego
przez skr
ę
canie par przewodów
Pole zmienne magnetyczne o indukcyjno
ś
ci B powoduje powstanie w obwodzie o
powierzchnie S siły elektro motorycznej
gdzie
Ф
– jest strumie
ń
magnetyczny, B – jest g
ę
sto
ść
strumieniu
magnetycznego. To znaczy,
ż
e wpływ zmiennego pola magnetycznego jest
proporcjonalny do powierzchni obwodu.
Dla zmniejszenia wpływu takiego pola nale
ż
y unika
ć
p
ę
tli przewodów oraz
długich dwu przewodowych kabli.
dt
dB
S
dt
d
e
B
−
=
−
=
Φ
Φ
Φ
Φ
S
e
B
=-SdB/dt
B
3.2.2.Tłumienie pola magnetycznego
przez skr
ę
canie par przewodów
Skutecznym przeciwdziałaniem wpływu pola magnetycznego jest skr
ę
canie par
dwu przewodowych kabli
S
p
e
z
=S
⋅
dB/dt
Z
we
U
z
B
e
B
=-SdB/dt
S
S
i
e
zi
=S
i
⋅
dB/dt
Z
we
U
z
B
e
zi+1
=-S
i+1
⋅
dB/dt
3.2.2.Tłumienie pola magnetycznego
przez skr
ę
canie par przewodów
Rekomendacje:
- Unika
ć
długi kabli
- Unika
ć
p
ę
tli
- Separowa
ć
linii zasilania od linii sygnałów pomiarowych
-
Wykorzystanie skr
ę
conych par przewodów
Efektywno
ść
skr
ę
cania zale
ż
y od jednakowo
ś
ci powierzchni p
ę
tli, liczba
p
ę
tli musi by
ć
du
żą
i parzyst
ą
.
S
i
e
zi
=S
i
⋅
dB/dt
Z
we
U
z
B
e
zi+1
=-S
i+1
⋅
dB/dt
3.2.3. Uziemienie
Dla prawidłowej transmisji, przetwarzania i wykorzystania sygnałów pomiarowych
elektrycznych wymaganie jest istnienie punktów lub płaszczyzn
ekwipotencjalnych (stałych w czasie i niezale
ż
nych od przepływaj
ą
cych
pr
ą
dów).
Te punkty lub płaszczyzny odniesienia w danym układzie, zespole lub systemie
pomiarowym stanowi
ą
tzw. mas
ę
.
Nazywa si
ę
ona równie
ż
uziemieniami dla sygnałów pomiarowych.
W praktyce płaszczyzny odniesienia posiada niezerow
ą
impedancj
ą
(rezystywno
ś
ci
ą
) (zale
ż
n
ą
od materiału, jej długo
ś
ci, szeroko
ś
ci i grubo
ś
ci
oraz cz
ę
stotliwo
ś
ci sygnałów) i dla tego płaszczyzna odniesienia przy
obecno
ś
ci przepływaj
ą
cych pr
ą
dów nie jest ekwipotencjaln
ą
.
W takiej sytuacji przy doł
ą
czeniu
ź
ródła sygnału oraz odbiornika do takiej
płaszczyzny w dostatecznych odległych punktach pomi
ę
dzy tymi punktami
powstaje ró
ż
nica potencjałów, która powoduje blendy transmisji
(przetwarzania) sygnału pomiarowego.
Układ 1
Układ 2
Układ 3
Układ 4
Masa
3.2.3. Uziemienie
Przykładem powstania nieekwipotencjalno
ś
ci jest uziemienie jedno
punktowe szeregowe, układ zast
ę
pczy jest pokazany ni
ż
ej.
Własny potencjał odniesienia pierwszego układu wynosi:
gdzie
- potencjał punkcie w pierwszym punkcie uziemienia.
Podobnie, własne potencjały odniesienia drugiego i trzeciego punktów
wynosz
ą
:
Układ 1
Układ 2
Układ 3
Układ n
I
un
I
u1
I
u2
I
u3
Z
zn
Z
z1
Z
z2
Z
z3
U
1
U
2
U
3
U
n
Z
01
Z
02
Z
03
Z
0n
I
Σ
3
I
Σ
2
I
Σ
n
I
Σ
1
U
01
U
02
U
03
U
0n
1
1
1
01
z
u
Z
I
U
U
+
=
(
)
01
3
2
1
01
1
1
...
Z
I
I
I
I
Z
I
U
un
u
u
u
+
+
+
+
=
=
Σ
2
2
2
02
z
u
Z
I
U
U
+
=
3
3
3
03
z
u
Z
I
U
U
+
=
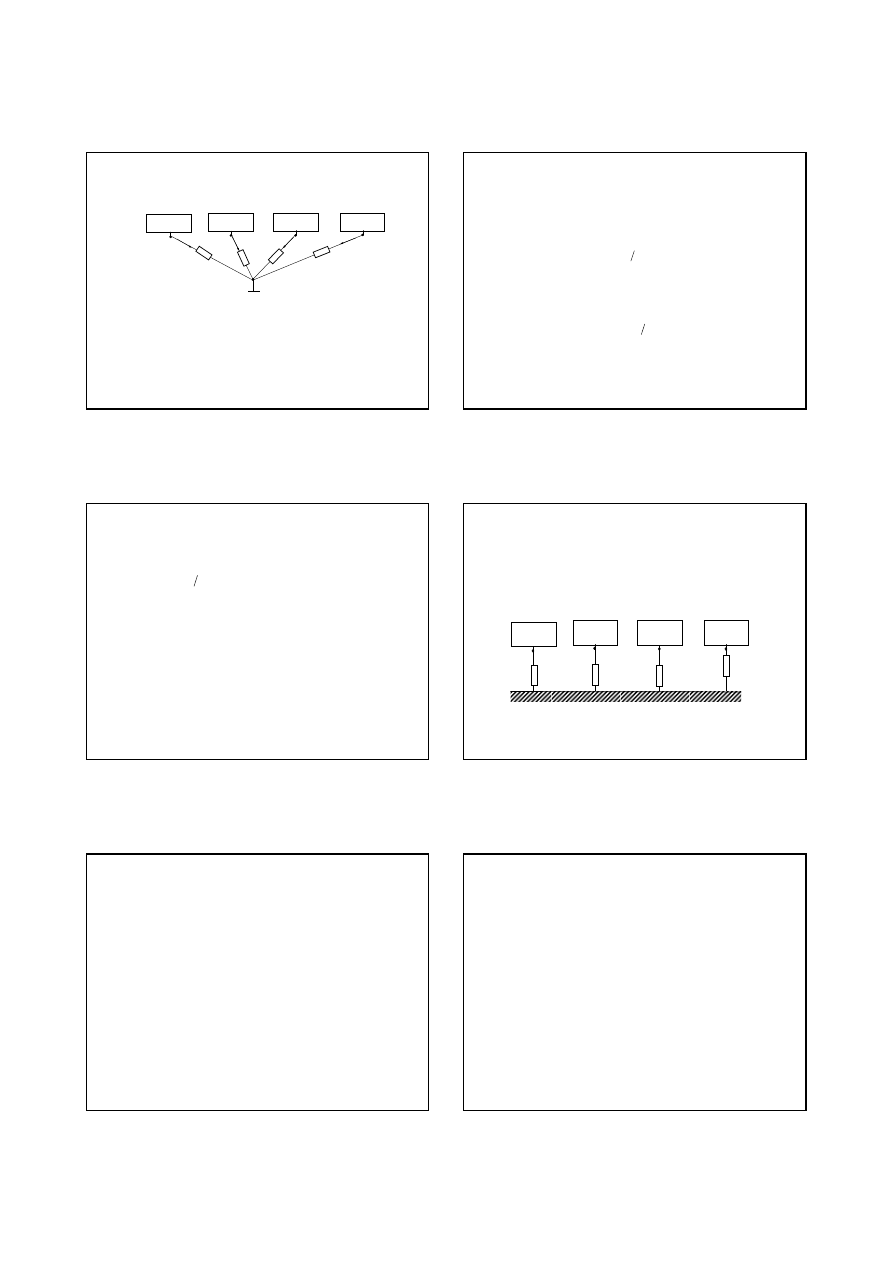
23
3.2.3. Uziemienie
Dla unikni
ę
cia wzajemnych wpływów pr
ą
dów od ró
ż
nych układów nale
ż
y
wykorzysta
ć
jednopunktowe uziemienie równoległe
Przy takim uziemieniu potencjały odniesienia układów (U
01
, U
02
, U
03
,..., U
0n
) s
ą
zale
ż
ny tylko od warto
ś
ci własnych pr
ą
dów oraz rezystancji uziemienia (Z
z1
,
Z
z2
, Z
z3
,..., Z
zn
).
Mog
ą
by
ć
stosowane jednopunktowe uziemienia mieszane (szeregowo-
równolegle).
Układ 1
Układ 2
Układ 3
Układ n
I
un
I
u1
I
u2
I
u3
Z
zn
Z
z1
Z
z2
Z
z3
U
01
U
02
U
03
U
0n
3.2.3. Uziemienie
Nale
ż
y pami
ę
ta
ć ż
e rezystancja uziemienia zale
ż
y nie tylko od materiału i
wymiarów geometrycznych (szeroko
ść
, długo
ść
, grubo
ść
) jednak tak
ż
e w
du
ż
ym stopniu od cz
ę
stotliwo
ś
ci (długo
ś
ci fali) sygnałów w danym obwodzie
pomiarowym.
Przy stosunkowo małych (w porównaniu do długo
ś
ci fali) odległo
ś
ciach
pomi
ę
dzy punktami płaszczyzny (L/
λ
<1/20=0.05) warto
ść
impedancji
równa si
ę
:
, [
Ω
/
],
gdzie R
DC
, [
Ω
/
] - rezystancja powierzchniowa dla pr
ą
du stałego;
k=R
RF
/R
DC
– współczynnik, wyra
ż
aj
ą
cy stosunek rezystancji na pr
ą
dzie
zmiennym oraz stałym.
Przy L/
λ
=1/8=0,125 warto
ść
impedancji równa si
ę
:
, [
Ω
/
].
A przy L/
λ
>1/8=0,125 warto
ść
impedancji mo
ż
e mie
ć
znacznie wi
ę
ksze
warto
ś
ci.
W
L
R
k
Z
DC
⋅
≅
W
L
R
k
Z
DC
⋅
=
2
3.2.3. Uziemienie
Przykładowo, dla płaszczyzny odniesienia (uziemienia) wykonanej z
miedzi przy L
≅
0,5 m, szeroko
ś
ci W
≅
5 mm, cz
ę
stotliwo
ś
ci f
≅
100 kHz
(
λ≅
3 km) obliczamy [
Ω
/
], L/
λ
=0.17
⋅
10
-3
<1/20, dla tego
Taka sama płaszczyzna wykonana ze stali (
µ
w
≅
1000,
σ
w
≅
0.1) ma
impedancj
ę
o warto
ś
ci 100 razy wi
ę
ksz
ą
.
Przy cz
ę
stotliwo
ś
ci powy
ż
ej 10 MHz oraz du
ż
ej odległo
ś
ci układów od
wspólnego punktu uziemienia mo
ż
e okaza
ć
si
ę ż
e niektóre z
rezystancji uziemienia (Z
z1
, Z
z2
, Z
z3
,..., Z
zn
) s
ą
du
ż
e (wzrost długo
ś
ci
powoduje wzrost wpływu składowej indukcyjno
ś
ciowej) .
Ω
=
⋅
⋅
=
≅
−
m
W
L
R
Z
RF
22
.
8
005
.
0
/
5
.
0
10
22
.
8
5
3.2.3. Uziemienie
W takich przypadkach jest rekomendowane uziemienie wielopunktowe.
Przy tym płaszczyzny uziemienia obecnie s
ą
wykonywane z cienkiej
warstwy srebra lub nawet złota pokrywaj
ą
cej praktycznie w cało
ś
ci
elementy konstrukcyjne (tak zwane chassis) układu.
Uziemienie jest wykonywane krótkimi przewodami o malej indukcyjno
ś
ci.
Układ 1
Układ 2
Układ 3
Układ n
Z
zn
Z
z1
Z
z2
Z
z3
Chassi
s
3.2.3. Uziemienie
Dla zapewnienia skuteczno
ś
ci uziemienia w szerokim zakresie
cz
ę
stotliwo
ś
ci wykorzystuje si
ę
uziemienie kombinowane:
jednopunktowe dla składowych niskocz
ę
stotliwo
ś
ciowych, oraz przez
kondensatory (o pomijalnie małych indukcyjno
ś
ciach wyprowadze
ń
)
wielopunktowe do chassis.
Rekomendacje:
- W realizacjach praktycznych systemów pomiarowych
powinny by
ć
przewidywane co najmniej trzy oddzielne
systemy uziemienia:
dla sygnałów (obwodów) analogowych pomiarowych;
dla sygnałów (obwodów) cyfrowych;
dla uziemienia ochronnego,
które mog
ą
mie
ć
poł
ą
czenie tylko w jednym punkcie.
3.2.3. Uziemienie
Dla zapewnienia skuteczno
ś
ci uziemienia w szerokim zakresie
cz
ę
stotliwo
ś
ci wykorzystuje si
ę
uziemienie kombinowane:
jednopunktowe dla składowych niskocz
ę
stotliwo
ś
ciowych, oraz przez
kondensatory (o pomijalnie małych indukcyjno
ś
ciach wyprowadze
ń
)
wielopunktowe do chassis.
Rekomendacje:
- Rezystancja przewodów oraz warstw uziemiaj
ą
cych zale
ż
y
od ich materiału i parametrów geometrycznych oraz
cz
ę
stotliwo
ś
ci sygnałów.
- W zakresie małych cz
ę
stotliwo
ś
ci (do ok. 1 MHz)
rekomenduje si
ę
uziemienie jednopunktowe równoległe.
- W zakresie du
ż
ych cz
ę
stotliwo
ś
ci (powy
ż
ej ok. 10 MHz)
rekomenduje si
ę
uziemienie wielopunktowe krótkimi
przewodami do płaszczyzny odniesienia w postaci cienkiej
warstwy srebra lub nawet złota pokrywaj
ą
cej praktycznie
w cało
ś
ci elementy konstrukcyjne (tak zwane chassis)
układu.
24
3.3. Zabezpieczenie (ekranowanie)
ekwipotencjalne
3.3.1.Typowe poł
ą
czenie obiektu oraz narz
ę
dzi pomiarowego
•
R
x
- rezystancja
ź
ródła sygnału,
•
R
l1
, R
l2
- rezystancja przewodów,
•
R
we
- rezystancja wej
ś
ciowa odbiornika sygnału
•
R
iz
– rezystancja izolacji pomi
ę
dzy wej
ś
ciami sygnałowymi i obudow
ą
przyrz
ą
du
R
l2
R
we
U
x
R
iz
Układ 2
R
z
R
l1
ZU
Z
Ź
ZO
R
x
Układ 1
U
cm
U
z
ZU – “ziemia” układu
ZO – “ziemia” odbiornika
Z
Ż
– “ziemia”
ź
rudła
U
cm
– napi
ę
cie wspólne
U
z
– napi
ę
cie uziemienia
3.3.1.Analiza wpływu zakłócenia wspólnego przez R
iz
Typowy lub najgorsze warto
ś
ci:
R
x
≈
1…100
Ω
;
R
l1
=R
l2
≈
1…1000
Ω
; R
z
≈
1…100
Ω
R
we
≈
>1…10 M
Ω
; R
iz
≈
>1…10 G
Ω
; U
cm
≈
230 V; U
z
≈
10V
Uproszczenia: R
we
=10 M
Ω
>>R
l2
+R
x
=1000
Ω
+100
Ω
R
1sum
=R
we
+R
l2
+R
x
≈
R
we
=
10 M
Ω
; R
l1
||
R
1sum
≅
R
l1
R
iz
>>R
l1
||
R
1sum
+R
z
R
l2
≈
<1000
Ω
R
we
=10M
Ω
U
x
R
iz
≈
10 G
Ω
Układ 2
R
z
≈
10
Ω
R
l1
≈
<1000
Ω
ZU
Z
Ź
ZO
R
x
≈
100
Ω
Układ 1
U
cm
≈
230V
U
z
≈
10V
3.3.1.Analiza wpływu zakłócenia wspólnego
I
2
=I
1
/10
4
<<I
1
R
l2
≈
1000
Ω
R
we
=10M
Ω
U
x
I
Riz
=I
1
+I
2
≈
25nA
R
iz
≈
10 G
Ω
Układ 2
R
z
≈
10
Ω
R
l1
≈
1000
Ω
ZU
Z
Ź
ZO
R
x
≈
100
Ω
I
1
≅
I
Riz
≅
25nA
Układ 1
U
cm
≈
230V
U
l1
=I
1
R
l1
≅
25
µ
V
U
z
≈
10V
iz
z
cm
sum
z
iz
z
cm
Riz
R
U
U
R
R
R
R
U
U
I
I
+
≅
+
+
+
=
≅
2
1
1
(
)
nA
G
V
I
Riz
25
10
10
230
≈
Ω
+
≅
U
l1
=25 nA
⋅
1000
Ω
=25
µ
V
3.3.1.Analiza wpływu zakłócenia wspólnego przez C
iz
Jeszcze gorsza sytuacja wyst
ę
puje w skutek działania pojemno
ś
ci
paso
ż
ytniczej C
iz
pomi
ę
dzy obudow
ą
odbiornika a obwodem wspólnym
Typowa warto
ść
pojemno
ś
ci wynosi około kilku dziesi
ęć
pikofarad:
przyjmiemy C
iz
≈
32 pF.
Wtedy na cz
ę
stotliwo
ś
ci sieciowej (f=50 Hz) impedancja tej pojemno
ś
ci
wynosi
U
z
≈
10V
R
l2
≈
1000
Ω
R
we
=10M
Ω
U
x
I
c
=I
1
+I
2
≈
2,4
µ
A
C
iz
≈
32pF
Układ 2
U
z
R
z
≈
10
Ω
R
l1
≈
1000
Ω
ZU
Z
Ź
ZO
R
x
≈
100
Ω
I
1
≅
I
c
≅
2,4
µ
A
Układ 1
U
cm
≈
230V
U
l1c
=I
1
R
l1
≅
2,4mV
I
2
=I
1
/10
4
<<I
1
(
)
(
)
Ω
≅
⋅
⋅
≅
=
−
M
fC
Z
iz
Ciz
100
10
32
314
1
2
1
12
π
3.3.1.Analiza wpływu zakłócenia wspólnego przez C
iz
Warto
ść
napi
ę
cia zakłócaj
ą
cego normalnego wynosi
U
l1
≈
2,4
µ
A
⋅
1000
Ω
≈
2,4 mV.
U
z
≈
10V
R
l2
≈
1000
Ω
R
we
=10M
Ω
U
x
I
c
=I
1
+I
2
≈
2,4
µ
A
C
iz
≈
32pF
Układ 2
U
z
R
z
≈
10
Ω
R
l1
≈
1000
Ω
ZU
Z
Ź
ZO
R
x
≈
100
Ω
I
1
≅
I
ciz
≅
2,4
µ
A
Układ 1
U
cm
≈
230V
U
l1c
=I
1
R
l1
≅
2,4mV
I
2
=I
1iz
/10
4
<<I
1
(
)
iz
z
cm
Ciz
z
cm
sum
z
Ciz
z
cm
Ciz
fC
U
U
Z
U
U
R
R
R
Z
U
U
I
I
π
2
2
1
1
+
=
+
≅
+
+
+
=
≅
A
Sm
V
I
I
Ciz
l
µ
4
,
2
10
240
8
1
≈
⋅
≅
≅
−
3.2.2. Współczynnik tłumienia zakłócenia
wspólnego
Stopie
ń
szkodliwo
ś
ci zakłócenia wspólnego zale
ż
y od stopnia jego
przekształcenia w zakłócenie normalne.
•Stopie
ń
takiego przekształcenia charakteryzuje si
ę
przez współczynnik
tłumienia zakłócenia wspólnego (Common Mode Rejection Ratio,
CMRR).
•CMRR jest to stosunek warto
ś
ci maksymalnej zakłócenia wspólnego do
warto
ś
ci maksymalnej spowodowanego nim zakłócenia normalnego
obecnie wyra
ż
ana w decybeli
( )
cm
nm
cm
U
U
U
CMRR
max
,
max
,
lg
20
=
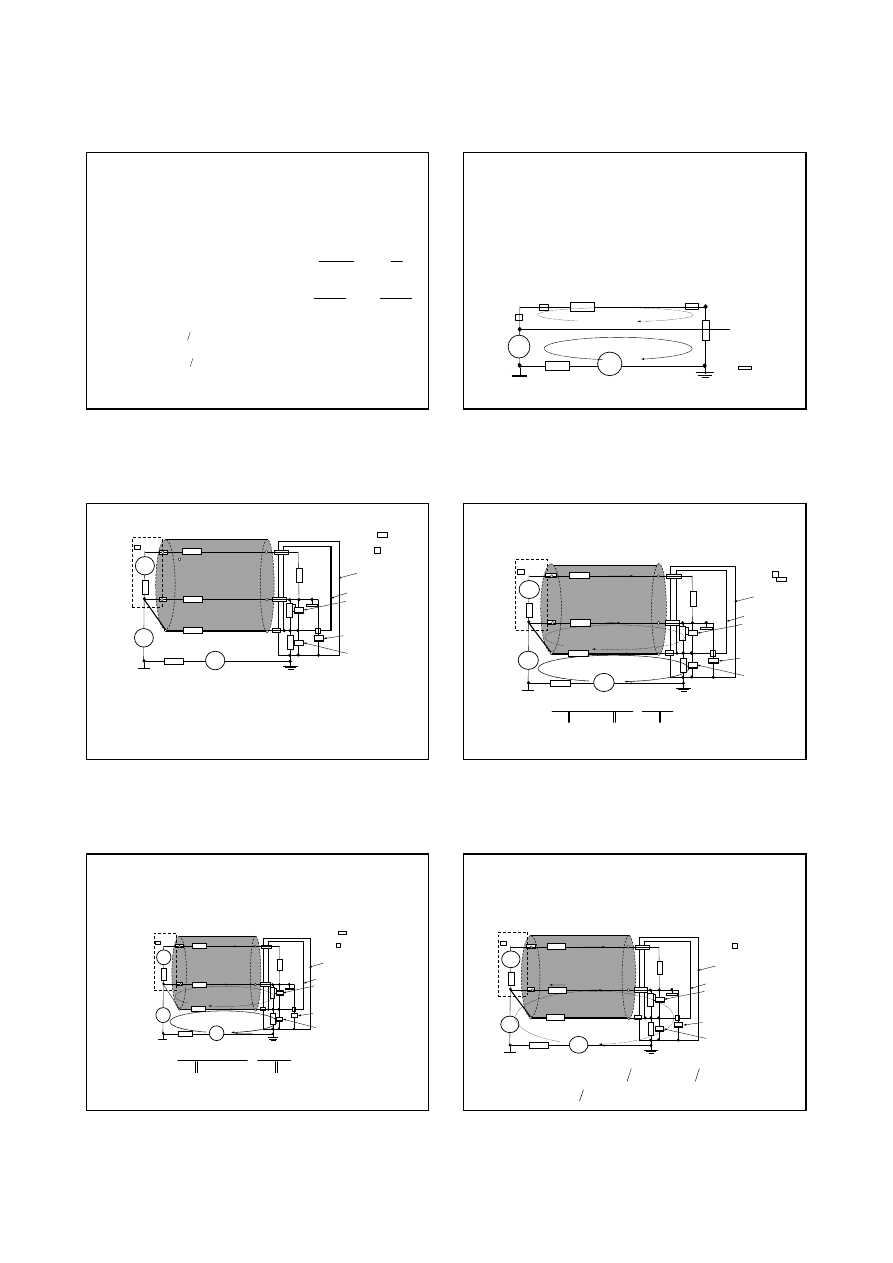
25
3.2.2. Współczynnik tłumienia zakłócenia
wspólnego
•
Współczynniki tłumienia zakłóce
ń
wspólnych s
ą
wyra
ż
any tylko przez
warto
ś
ci rezystancji oraz pojemno
ś
ci izolacji (z jednej strony ) i
rezystancji linii pomi
ę
dzy
ź
ródłem odbiornikiem sygnału (z innej strony)
parametry, a mianowicie:
•
na pr
ą
dzie stałym:
•
na pr
ą
dzie przemiennym
•
(tłumienie 5 mln razy),
•
(tłumienie 100 tys. razy).
≈
+
=
1
,
lg
20
lg
20
l
iz
n
Riz
z
cm
Riz
R
R
U
U
U
CMRR
≈
+
=
1
,
2
1
lg
20
lg
20
l
iz
n
Ciz
z
cm
Ciz
R
fC
U
U
U
CMRR
π
(
)
(
)
dB
G
CMRR
Riz
134
10
5
lg
20
1000
5
lg
20
6
≈
⋅
=
Ω
Ω
≅
[
]
(
)
dB
M
CMRR
Ciz
100
100000
lg
20
1000
100
lg
20
≈
=
Ω
Ω
≅
3.3.3. Ekranowanie ekwipotencjalne
•
Je
ż
eli za po
ś
rednictwem przewodu z zerowa rezystancj
ą
(R
E
=0)
poł
ą
czy
ć
punkt A (punkt oddziaływania zakłócenia wspólnego) z
płaszczyzn
ą
B (która tez ma zerow
ą
rezystancj
ę
i przecina izolacj
ę
pomi
ę
dzy obudow
ą
i nisko potencjalnym wej
ś
ciem), jak jest pokazano na
rys. , wtedy pr
ą
d (I
Riz2
) od
ź
ródeł zakłócaj
ą
cych b
ę
dzie płyn
ąć
w
obwodzie utworzonym tymi przewodem i płaszczyzn
ą
, omijaj
ą
c obwód z
przewodem sygnałowym (I
l1
=0).
R
iz1
I
1
≅
0
U
cm
U
R1
≅
0
I
Riz2
R
z
Z
Ź
ZO
U
z
A
B
R
iz2
R
l1
R
AB
=R
E
≅
0
U
AB
≅
0
3.3.3. Ekranowanie ekwipotencjalne
•
W układzie z ekranowaniem ekwipotencjalnym ma miejsce
dwustopniowe tłumienie przy przekształceniu zakłócenia wspólnego w
zakłócenie normalne.
Ekran
Z
Ź
C
iz
, R
iz
R
l2
U
x
C
iz
, R
iz
Układ 2
R
l1
R
x
Układ 1
LO
HI
C
p
=1...2pF
R
we
ZU
1
2
3
Ekran
Obudowa
U
z
R
z
ZO
U
uz
E
R
e
3.3.3. Ekranowanie ekwipotencjalne
•
Na pierwszym stopniu zakłócenia wspólne powoduj
ą
pr
ą
d zakłócaj
ą
cy przez
rezystancj
ę
ekranu R
e
zale
ż
ny tylko od warto
ś
ci impedancji poł
ą
czenia poprzez pojemno
ść
izolacji C
iz1
(C
iz1
=2·C
iz
≈
64 pF) oraz rezystancj
ę
izolacji R
iz1
C
p
=1...2pF
Obudowa
C
iz1
, R
iz1
R
l2
≈
1000
Ω
U
x
C
iz2
, R
iz2
Układ 2
R
l1
≈
1000
Ω
R
x
≈
100
Ω
I
2
<<I
1
Układ 1
LO
HI
R
we
=10M
Ω
ZU
1
2
3
U
e
≈
5mV
Ekran
I
iz
≈
5
µ
A
Uz=10 V
R
z
≈
10
Ω
Z
Ź
ZO
U
uz
≈
230V
I
e
≅
I
iz
≅
5
µ
A
E
R
e
≈
1000
Ω
I
Rle
≅
U
e
/Z
iz2
≅
0,1nA
U
e1
≈
0,1
µ
V
(
)
A
fC
U
U
R
Z
U
U
R
R
R
R
Z
U
U
I
I
iz
z
cm
iz
Ciz
z
cm
sum
z
iz
Ciz
z
cm
iz
e
µ
π
5
2
1
1
1
2
1
1
1
≈
+
≈
+
≅
+
+
+
=
=
Warto
ść
spadku napi
ę
cia na ekranie: U
e
=5
µ
A
⋅
1000
Ω
=5 mV
3.3.3. Ekranowanie ekwipotencjalne
Na drugim stopniu zakłóceniem wspólnym staje si
ę
spadek napi
ę
cia
na ekranie, które powoduje pr
ą
d zakłócaj
ą
cy przez rezystancj
ę
linii R
l1
zale
ż
ny od warto
ś
ci impedancji poł
ą
czenia poprzez pojemno
ść
izolacji
C
iz2
oraz rezystancj
ę
izolacji R
iz2
U
l1
=0,1 nA
⋅
1000
Ω
=0,1
µ
V
C
iz1
, R
iz1
R
l2
≈
1000
Ω
U
x
C
iz2
, R
iz2
Układ 2
R
l1
≈
1000
Ω
R
x
≈
100
Ω
I
2
<<I
1
Układ 1
LO
HI
C
p
=1...2pF
R
we
=10M
Ω
ZU
1
2
3
U
e
≈
5mV
Ekran
Obudowa
I
iz
≈
5
µ
A
Uz=10 V
R
z
≈
10
Ω
Z
Ź
ZO
U
uz
≈
230V
I
e
≅
I
iz
≅
5
µ
A
E
R
e
≈
1000
Ω
I
Rle
≅
U
e
/Z
iz2
≅
0,1nA
U
e1
≈
0,1
µ
V
2
2
2
1
2
2
1
2
iz
e
iz
Ciz
e
l
e
iz
Ciz
e
e
Rl
fC
U
R
Z
U
R
R
R
Z
U
I
π
≈
≅
+
+
=
nA
Sm
mV
I
e
Rl
1
,
0
10
2
5
8
1
≈
⋅
⋅
≅
−
3.3.3. Ekranowanie ekwipotencjalne
Jednak w tym przypadku oprócz rezystancji i pojemno
ś
ci izolacji pomi
ę
dzy
lini
ą
sygnałow
ą
a ekranem (R
iz2
, C
iz2
) oraz pomi
ę
dzy ekranem i obwodami
ź
ródeł
zakłócaj
ą
cych (R
iz1
, C
iz1
) wyst
ę
puje paso
ż
ytnicza (przej
ś
ciowa) pojemno
ść
C
p
)
pomi
ę
dzy lini
ą
sygnałow
ą
a obwodami
ź
ródeł zakłócaj
ą
cych (obudow
ą
).
(
)
[
]
(
)
1
2
1
20
20
l
p
n
,
Cp
z
cm
Cp
R
fC
lg
U
U
U
lg
CMRR
π
=
+
=
C
iz2
,
R
iz2
R
l2
≈
1000
Ω
U
x
C
iz1
,
R
iz1
Układ 2
R
l1
≈
1000
Ω
R
x
I
2
<<I
1
Układ 1
LO
HI
C
p
=1...2pF
R
we
=10M
Ω
ZU
1
2
3
I
Cp
≅
(U
uz
+U
z
)/Z
cp
≈
0,15
µ
A
U
Rl1Cp
≅
I
Cp
R
l1
≈
0,15mV
Ekran
Obudowa
Uz
≈
10 V
R
z
≈
10
Ω
Z
Ź
ZO
U
uz
≈
230V
E
R
e
≈
1000
Ω
I
Cp
(
)
[
]
dB
Sm
,
lg
CMRR
Cp
125
1000
10
28
6
1
20
10
≈
⋅
⋅
≈
−
Ω
Ω
Ω
Ω
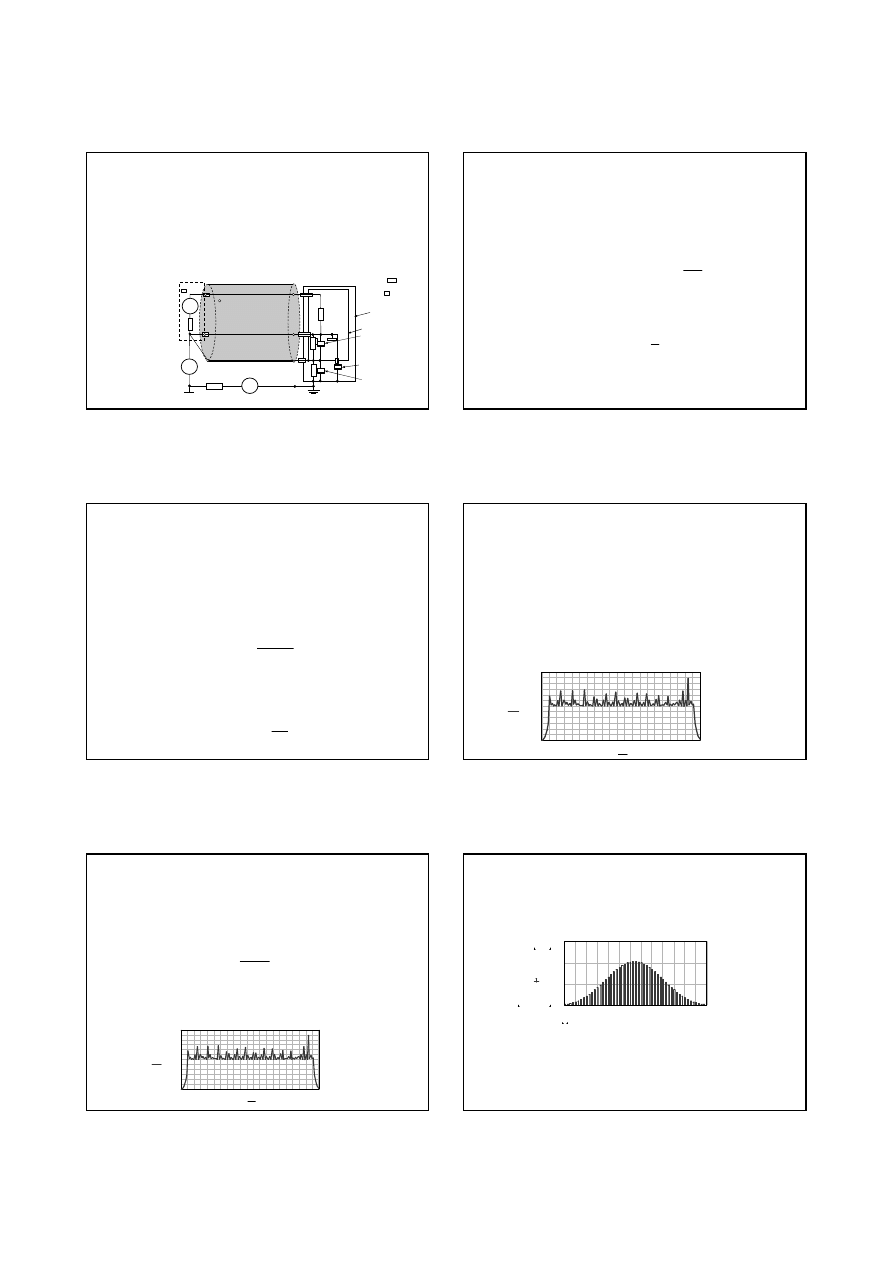
26
Nieprawidłowe poł
ą
czenie obiektu i miernika
Rekomendacj
ę
:
- w celu skutecznego tłumienia zakłóce
ń
wspólnych nale
ż
y stosowa
ć
ekranowanie ekwipotencjalne;
- na obiekcie badanym ekran nale
ż
y podł
ą
cza
ć
w jak najbli
ż
szym
punkcie do oddziaływania zakłócenia wspólnego;
- po stronie miernika nie mo
ż
na ł
ą
czy
ć
zaciski LO (potencjał niski)
oraz E (ekran), w wyniku czego traci si
ę
skuteczno
ść
ekranowania
ekwipotencjalnego.
Z
Ź
C
iz2
, R
iz2
U
x
C
iz1
, R
iz1
Układ 2
R
x
Układ 1
LO
HI
C
p
=1...2pF
R
we
ZU
1
2
3
Ekran
Obudowa
Uz
R
z
ZO
U
uz
E
Ekran
Obliczanie warto
ś
ci bł
ę
du przez ograniczona
warto
ś
ci
ą
współczynnika tłumienia zakłócenia
wspólnego
Je
ż
eli warto
ść
maksymalna sygnału wspólnego wynosi
wtedy przy współczynniku tłumienia CMRR maksymalna
warto
ść
napi
ę
cia normalnego , w które zostało
transformowane napi
ę
cie wspólne równa si
ę
Na przykład, przy oraz CMRR=100 dB
maksymalna warto
ść
napi
ę
cia normalnego , w
które zostało transformowane napi
ę
cie wspólne równa
si
ę
wsp
U
max,
norm
U
max,
20
max,
max,
10
CMRR
wsp
norm
U
U
−
⋅
=
V
U
wsp
230
max,
=
norm
U
max,
mV
V
U
norm
3
,
2
10
230
20
100
max,
=
⋅
=
−
Sumaryczny współczynnik tłumienia
zakłócenia (napi
ę
cia) wspólnego
Je
ż
eli karta pomiarowa zapewnia tłumienie napi
ęć
wspólnego oraz normalnego (szeregowego) wtedy
sumaryczny współczynnik napi
ę
cia wspólnego równa si
ę
sumie współczynników
CMMR+NMRR
dla którego maksymalna warto
ść
bł
ę
du, spowodowanego
tym zakłóceniem równa si
ę
Na przykład, przy oraz CMMR=100 dB i
NMRR=40 dB maksymalna warto
ść
maksymalna
warto
ść
bł
ę
du, spowodowanego zakłóceniem wspólnym
równa si
ę
20
max,
max
10
NMRR
CMRR
wsp
U
+
−
⋅
=
∆
V
U
wsp
230
max,
=
mkV
V
23
10
230
20
40
100
max
=
⋅
=
∆
+
−
Tłumienie składowych harmonicznych
szerokim pa
ś
mie cz
ę
stotliwo
ś
ciowym. Funkcja
wagowa (okno) Dolpha-Czebyszewa
Dla tłumienia składowych harmonicznych o nieznanych cz
ę
stotliwo
ś
ciach
oraz przy ich zmianie w szerokim zakresie – co ma miejsce przy cyfrowych
pomiarach parametrów sygnałów (warto
ś
ci
ś
rednia wyprostowana,
skuteczna, moc czynna oraz bierna itp.) najlepszy efekt daje zastosowanie
funkcji wagowej (okna) Dolpha- Czebyszewa.
Z po
ś
ród innych funkcji wagowych jest to “najlepsza” funkcja wagowa
(okno). Jej wykorzystanie zapewnia zadany poziom tłumienia Ktl zakłóce
ń
w zadanym sko
ń
czonym zakresie cz
ę
stotliwo
ś
ci od dolnej fd do górnej fg.
przy minimalnie mo
ż
liwym czasie u
ś
redniania Tus.
0
20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420
0
10
20
30
40
50
60
70
80
90
100
110
120
120
0
Ktl_dB
x
( )
420
0
x fd
⋅
v0
Funkcja wagowa (okno) Dolpha-Czebyszewa
•Na tym rysunku funkcja wagowa zapewnia tłumienie 60 dB (1000 razy) w
zakresie cz
ę
stotliwo
ś
ci od dolnej fd =20 Hz do górnej fg=400 Hz.
•Trwało
ść
u
ś
redniania praktycznie zale
ż
y tylko od poziomu tłumienia oraz
warto
ś
ci fd i jest minimalnie mo
ż
liw
ą
:
•i równa si
ę
około 121 ms dla zadanych wy
ż
ej parametrów.
•Nie istnieje innej funkcji wagowej, która zapewni tłumienie minimalnie 60 dB w
interwale czasowym mniej ni
ż
eli 121 ms.
0
20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420
0
10
20
30
40
50
60
70
80
90
100
110
120
120
0
Ktl_dB
x
( )
420
0
x fd
⋅
v0
d
tl
us
f
K
T
π
)
2
ln(
≅
Funkcja wagowa (okno) Dolpha-Czebyszewa
•Charakterystyczny widok FW Dolpha-Czebyszewa jest pokazana na
rysunku ni
ż
ej
0
4
8
12 16 20 24 28 32 36 40 44 48 52
0
0.02
0.04
0.06
0.041
8.791 10
4
−
×
g
in
N
0
in
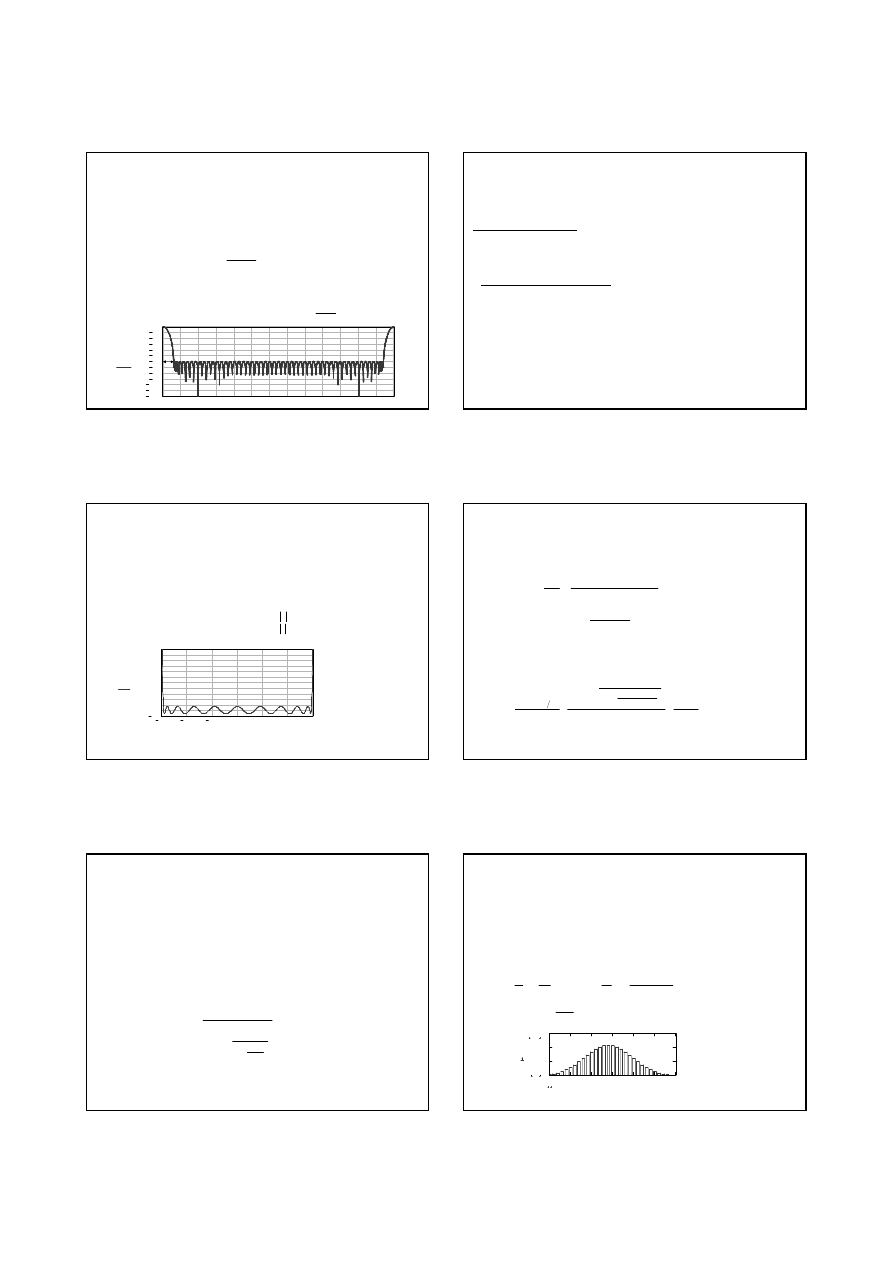
27
Funkcja wagowa (okno) Dolpha-Czebyszewa
v0
ln 2Ktl
(
)
π
:=
v0
2.419
=
•W dziedzinie cz
ę
stotliwo
ś
ci FW Dolpha-Czebyszewa minimalizuje si
ę
szeroko
ść
listka głównego widma przy zało
ż
eniu okre
ś
lonej długo
ś
ci okna
oraz przy ograniczeniu dopuszczalnej wysoko
ś
ci maksymalnego listka
bocznego widma .
•
•Przykładowo na rys. ni
ż
ej pokazano moduł widma FW Dolpha-
Czebyszewa zapewniaj
ą
cej stały minimalny poziom tłumienia 60 dB (1
tysi
ą
c razy) w pa
ś
mie cz
ę
stotliwo
ś
ci od 20 Hz do 400 Hz warto
ść
szeroko
ś
ci głównego listka równa si
ę
:
π
)
2
ln(
0
tl
K
v
≅
0
4
8
12
16
20
24
28
32
36
40
44
48
52
120
110
100
90
80
70
60
50
40
30
20
10
0
0
120
−
WF_dB
x
(
)
n
0
x
v0
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Z punktu widzenia realizacji praktycznej u
ś
redniania wagowego
zadanymi parametrami s
ą
:
1)
poziom tłumienia Ktl oraz
2)
pasmo cz
ę
stotliwo
ś
ci od fd do fg;
a poszukiwanymi parametrami s
ą
:
1)
Rz
ą
d FW n;
2)
liczba N (długo
ść
) współczynników FW;
3)
warto
ś
ci współczynników w
i
(i=1,2,…,N),
4)
cz
ę
stotliwo
ść
próbkowania fs oraz
5)
czas u
ś
redniania Tus.
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Charakterystyka widmowa funkcji wagowej Dolpha-Czebyszewa o N
współczynnikach gi jest konstruowana na podstawie wielomiana
Czebyszewa rz
ę
du
n=N-1:
(
)
(
)
1
1
,
)
(
h
arccos
cosh
,
)
arccos(
cos
)
(
>
≤
⋅
⋅
=
x
x
dla
dla
x
n
x
n
x
T
n
1.02
0.68
0.34
0
0.34
0.68
1.02
1.5
0
1.5
3
4.5
6
7.5
9
10.5
12
13.5
15
16.5
16.5
1.5
−
Tcheb 20 x
,
(
)
1.025
1.025
−
x
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Warto
ś
ci współczynników tej FW mo
ż
na obliczy
ć
wg wzoru
Gdzie:
parametr, który jest powi
ą
zany z szeroko
ś
ci
ą
głównego listka widma
zale
ż
no
ś
ci
ą
:
( )
∑
−
=
−
−
−
+
−
−
−
−
−
=
1
0
2
0
2
0
)!
1
(
)!
1
(
!
)!
1
(
1
2
i
j
j
j
tl
i
j
i
i
j
n
j
x
j
n
n
K
x
g
=
n
K
x
tl
)
(
h
arccos
cosh
0
( )
π
π
π
ν
)
2
ln(
)
(
h
arccos
cosh
1
arccos
1
arccos
0
0
tl
tl
K
n
K
n
x
n
≅
⋅
=
⋅
=
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Cz
ę
stotliwo
ść
próbkowania sygnału równa si
ę
:
fs=fd+fg=fd (D+1)
gdzie
D=fg/fd
jest wzgl
ę
dnym zakresem cz
ę
stotliwo
ś
ci
Rz
ą
d WF wyznacza si
ę
wg. wzoru:
(
)
( )
+
=
+
=
1
cos
1
h
arccos
h
arccos
1
0
D
K
D
n
tl
π
ν
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Liczba próbek FW Dolpha-Czebyszewa równa si
ę
:
N=n+1
Lepsza dokładno
ść
oblicze
ń
(zwłaszcza przy du
ż
ych N) otrzymuje si
ę
wykorzystuj
ąć
odwrotne przekształcenie Fouriera wielomianu
Czebyszowa
−
+
=
∑
=
−
N
M
m
k
N
k
x
T
K
N
w
M
k
N
tl
in
)
(
2
cos
cos
2
1
1
0
1
1
π
π
2
1
−
=
N
M
1
2
0
−
=
≤
≤
N
M
m
0
5
10
15
20
25
30
0
1
2
3
2.135
0.04
w
in
n 1
+
(
)
⋅
N 1
+
0
in
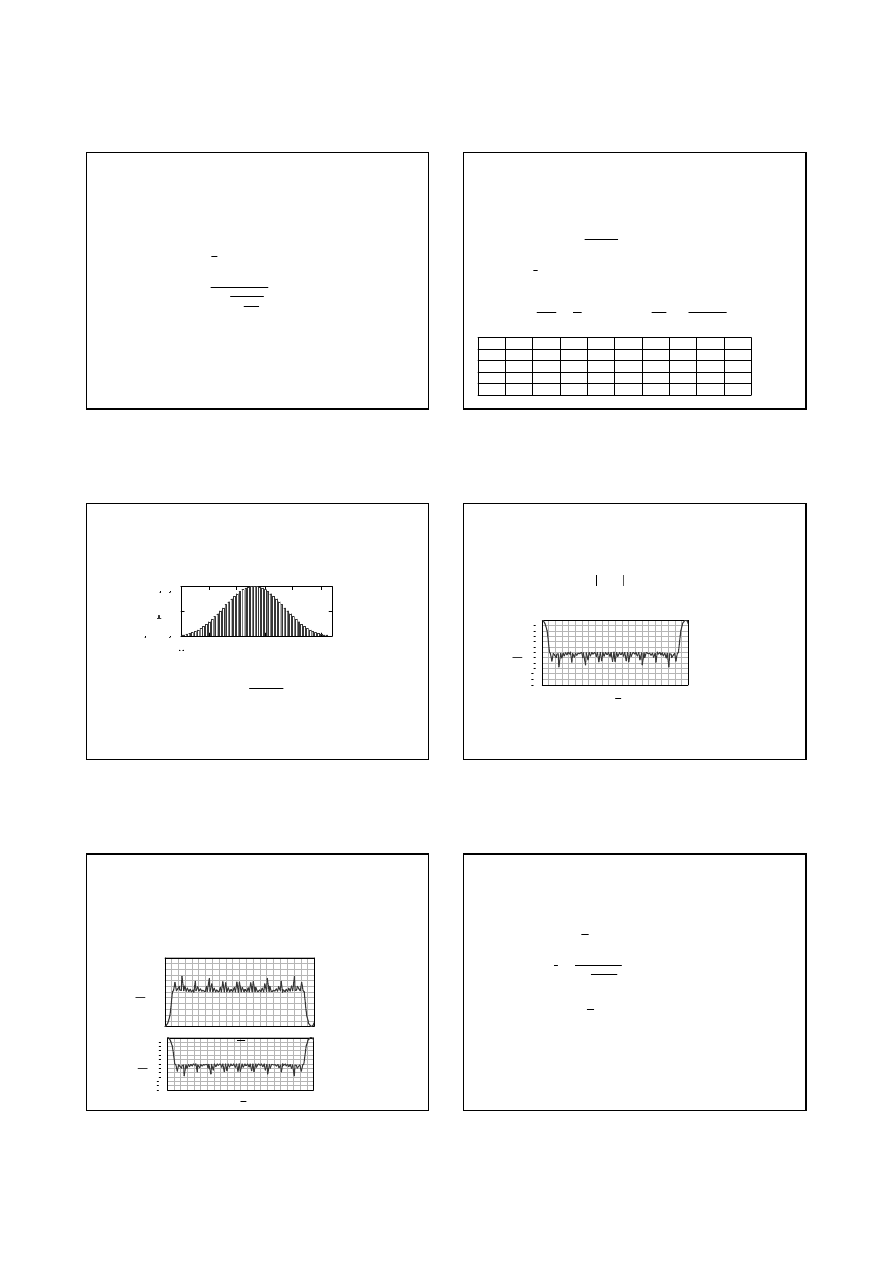
28
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
1)
Zadano:
2)
Obliczanie wzgl
ę
dnej szeroko
ś
ci pasma tłumienia
3)
Obliczanie rz
ę
du wielomianu Czebyszewa
Po zaokr
ą
gleniu do warto
ś
ci całkowitej wi
ę
kszej
n=51
4)
Obliczanie długo
ś
ci (liczby próbek) FW Dolpha-Czebyszewa
Ktl
1000
:=
fd
20
:=
fg
400
:=
D
fg
fd
:=
D
20
=
n
acosh Ktl
(
)
acosh
1
cos
π
D
1
+
:=
N
1
n
+
:=
N
52
=
5)
Obliczanie warto
ś
ci parametru x0
6)
Obliczanie warto
ś
ci współczynników FW Dolpha-Czebyszewa
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
x0
cosh
acosh Ktl
(
)
n
:=
x0
1.011
=
M
n
2
:=
M
26
=
in
0 n
..
:=
w
in
1
n
1
+
(
)
1
2
Ktl
1
M
k
Tcheb n x0 cos
π
k
n
1
+
⋅
⋅
,
cos
2
π
⋅
k
⋅
in
M
−
(
)
⋅
n
1
+
⋅
∑
=
⋅
+
⋅
:=
0.046
0.050
0.077
0.110
0.152
0.202
0.262
0.332
0.412
0.602
0.710
0.825
0.947
1.073
1.201
1.329
1.456
1.578
1.692
1.891
1.970
2.034
2.081
2.109
2.119
2.109
2.081
2.034
1.970
1.797
1.692
1.578
1.456
1.329
1.201
1.073
0.947
0.825
0.710
0.502
0.412
0.332
0.262
0.202
0.152
0.110
0.077
0.050
0.046
7)
Wykres funkcji wagowej
8)
Obliczanie charakterystyki widmowej: x=f·T
us
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
0
10
20
30
40
50
0
0.02
0.04
0.04
8.697 10
4
−
×
gin
N 1
+
0
in
WF x
( )
0
n
in
w
in
cos 2
π
x in
M
−
(
)
⋅
n
⋅
⋅
∑
=
:=
9)
Obliczanie charakterystyki widmowej w decybeli
10)
Wykres charakterystyki widmowej
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
WF_dB x
( )
20 log
WF x
( )
0.0000001
+
(
)
⋅
:=
0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420 440
120
110
100
90
80
70
60
50
40
30
20
10
0
0
120
−
WF_dB x
( )
440
0
x
fd
v0
⋅
11) Obliczanie współczynnika tłumienia w decybeli
12)
Wykres współczynnika tłumienia
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
0
20
40
60
80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420 440
120
110
100
90
80
70
60
50
40
30
20
10
0
0
120
−
WF_dB
x
( )
440
0
x
fd
v0
⋅
Ktl_dB x
( )
WF_dB x
( )
−
:=
0 20 40 60 80 100120140160180200220240260280300320340360380400420440
0
10
20
30
40
50
60
70
80
90
100
110
120
120
0
Ktl_dB x
( )
440
0
x fd
⋅
v0
13) Obliczanie wzgl
ę
dnej trwało
ś
ci u
ś
redniania FW Dolpha-Czebyszewa
14) Obliczanie trwało
ś
ci u
ś
redniania FW Dolpha-Czebyszewa
15) Obliczanie cz
ę
stotliwo
ś
ci próbkowania
16) Obliczanie wyniku przetwarzania je
ż
eli x
1
,x
2
, x
3
,…,x
N
s
ą
warto
ś
ciami
zarejestrowanymi sygnału badanego
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
v0
n
π
acos
1
cosh
acosh Ktl
(
)
n
⋅
:=
v0
2.411
=
Tus
v0
fd
:=
Tus
0.121
=
fp
n
fd
v0
⋅
:=
fp
431.379
=
∑
=
=
N
i
i
i
X
w
x
N
1
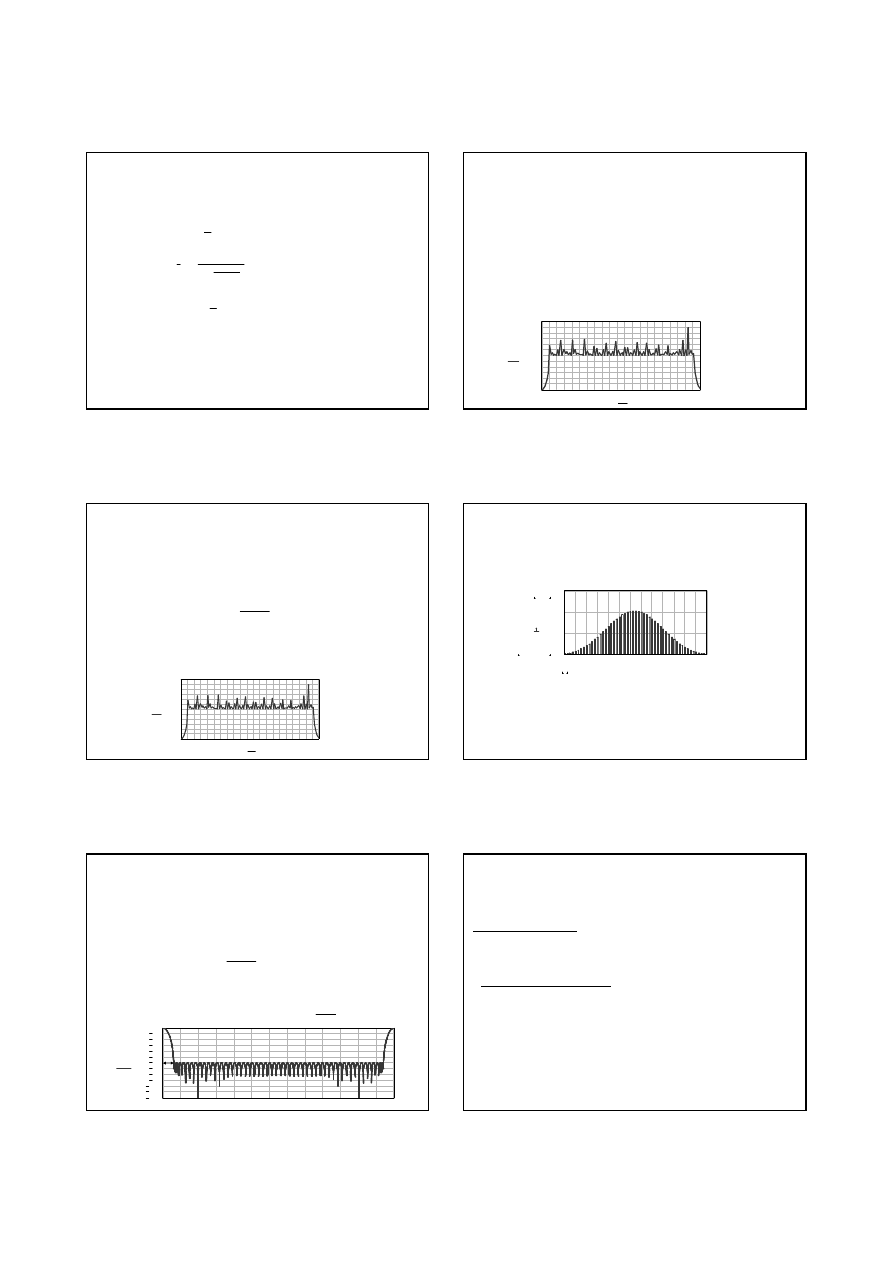
29
13) Obliczanie wzgl
ę
dnej trwało
ś
ci u
ś
redniania FW Dolpha-Czebyszewa
14) Obliczanie trwało
ś
ci u
ś
redniania FW Dolpha-Czebyszewa
15) Obliczanie cz
ę
stotliwo
ś
ci próbkowania
16) Obliczanie wyniku przetwarzania je
ż
eli x
1
,x
2
, x
3
,…,x
N
s
ą
warto
ś
ciami
zarejestrowanymi sygnału badanego
3. Algorytm obliczania współczynników funkcji
(okna) Dolpha-Czebyszewa z przykaładem
v0
n
π
acos
1
cosh
acosh Ktl
(
)
n
⋅
:=
v0
2.411
=
Tus
v0
fd
:=
Tus
0.121
=
fp
n
fd
v0
⋅
:=
fp
431.379
=
∑
=
=
N
i
i
i
X
w
x
N
1
Tłumienie składowych harmonicznych
szerokim pa
ś
mie cz
ę
stotliwo
ś
ciowym. Funkcja
wagowa (okno) Dolpha-Czebyszewa
Dla tłumienia składowych harmonicznych o nieznanych cz
ę
stotliwo
ś
ciach
oraz przy ich zmianie w szerokim zakresie – co ma miejsce przy cyfrowych
pomiarach parametrów sygnałów (warto
ś
ci
ś
rednia wyprostowana,
skuteczna, moc czynna oraz bierna itp.) najlepszy efekt daje zastosowanie
funkcji wagowej (okna) Dolpha- Czebyszewa.
Z po
ś
ród innych funkcji wagowych jest to “najlepsza” funkcja wagowa
(okno). Jej wykorzystanie zapewnia zadany poziom tłumienia Ktl zakłóce
ń
w zadanym sko
ń
czonym zakresie cz
ę
stotliwo
ś
ci od dolnej fd do górnej fg.
przy minimalnie mo
ż
liwym czasie u
ś
redniania Tus.
0
20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420
0
10
20
30
40
50
60
70
80
90
100
110
120
120
0
Ktl_dB
x
( )
420
0
x fd
⋅
v0
Funkcja wagowa (okno) Dolpha-Czebyszewa
•Na tym rysunku funkcja wagowa zapewnia tłumienie 60 dB (1000 razy) w
zakresie cz
ę
stotliwo
ś
ci od dolnej fd =20 Hz do górnej fg=400 Hz.
•Trwało
ść
u
ś
redniania praktycznie zale
ż
y tylko od poziomu tłumienia oraz
warto
ś
ci fd i jest minimalnie mo
ż
liw
ą
:
•i równa si
ę
około 121 ms dla zadanych wy
ż
ej parametrów.
•Nie istnieje innej funkcji wagowej, która zapewni tłumienie minimalnie 60 dB w
interwale czasowym mniej ni
ż
eli 121 ms.
0
20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420
0
10
20
30
40
50
60
70
80
90
100
110
120
120
0
Ktl_dB
x
( )
420
0
x fd
⋅
v0
d
tl
us
f
K
T
π
)
2
ln(
≅
Funkcja wagowa (okno) Dolpha-Czebyszewa
•Charakterystyczny widok FW Dolpha-Czebyszewa jest pokazana na
rysunku ni
ż
ej
0
4
8
12 16 20 24 28 32 36 40 44 48 52
0
0.02
0.04
0.06
0.041
8.791 10
4
−
×
g
in
N
0
in
Funkcja wagowa (okno) Dolpha-Czebyszewa
v0
ln 2Ktl
(
)
π
:=
v0
2.419
=
•W dziedzinie cz
ę
stotliwo
ś
ci FW Dolpha-Czebyszewa minimalizuje si
ę
szeroko
ść
listka głównego widma przy zało
ż
eniu okre
ś
lonej długo
ś
ci okna
oraz przy ograniczeniu dopuszczalnej wysoko
ś
ci maksymalnego listka
bocznego widma .
•
•Przykładowo na rys. ni
ż
ej pokazano moduł widma FW Dolpha-
Czebyszewa zapewniaj
ą
cej stały minimalny poziom tłumienia 60 dB (1
tysi
ą
c razy) w pa
ś
mie cz
ę
stotliwo
ś
ci od 20 Hz do 400 Hz warto
ść
szeroko
ś
ci głównego listka równa si
ę
:
π
)
2
ln(
0
tl
K
v
≅
0
4
8
12
16
20
24
28
32
36
40
44
48
52
120
110
100
90
80
70
60
50
40
30
20
10
0
0
120
−
WF_dB
x
(
)
n
0
x
v0
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Z punktu widzenia realizacji praktycznej u
ś
redniania wagowego
zadanymi parametrami s
ą
:
1)
poziom tłumienia Ktl oraz
2)
pasmo cz
ę
stotliwo
ś
ci od fd do fg;
a poszukiwanymi parametrami s
ą
:
1)
Rz
ą
d FW n;
2)
liczba N (długo
ść
) współczynników FW;
3)
warto
ś
ci współczynników w
i
(i=1,2,…,N),
4)
cz
ę
stotliwo
ść
próbkowania fs oraz
5)
czas u
ś
redniania Tus.
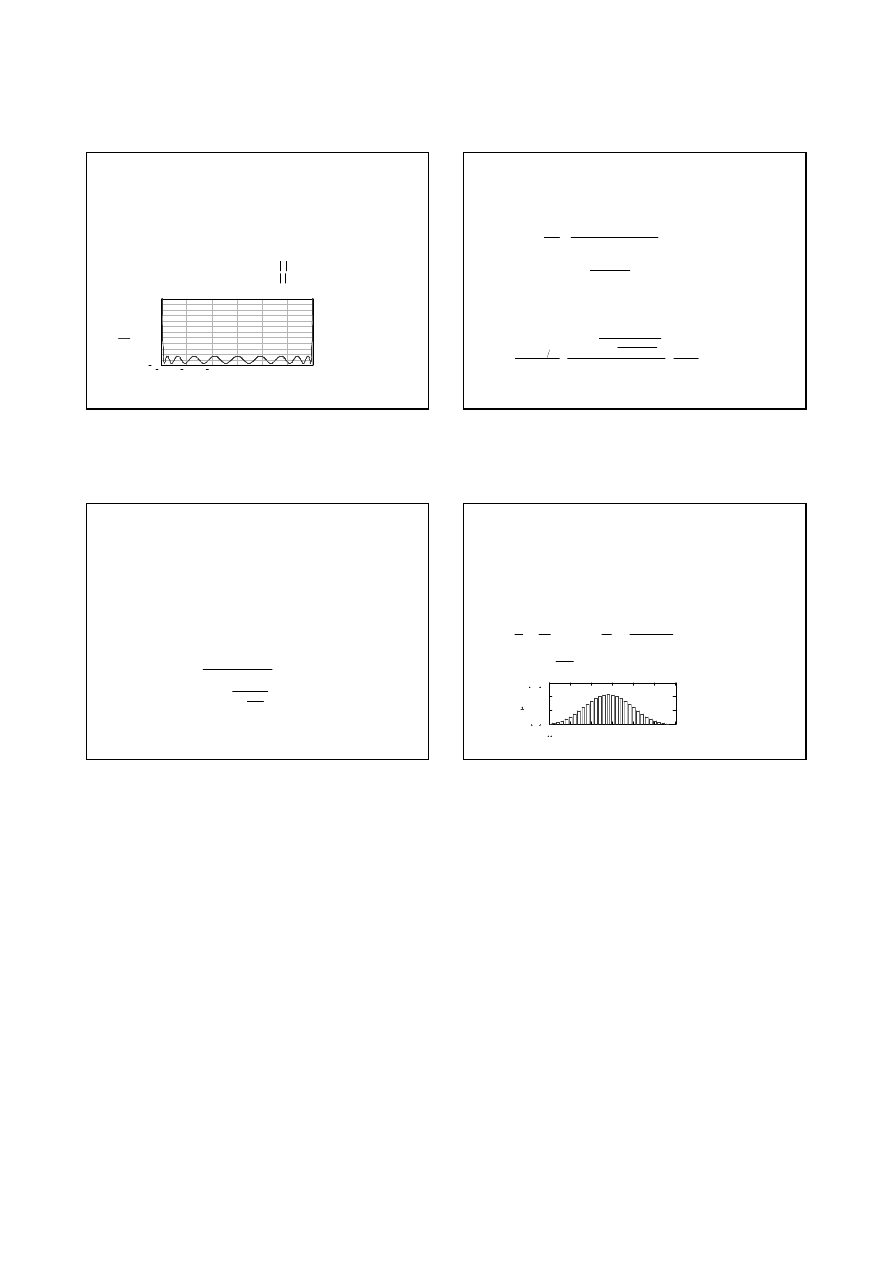
30
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Charakterystyka widmowa funkcji wagowej Dolpha-Czebyszewa o N
współczynnikach gi jest konstruowana na podstawie wielomiana
Czebyszewa rz
ę
du
n=N-1:
(
)
(
)
1
1
,
)
(
h
arccos
cosh
,
)
arccos(
cos
)
(
>
≤
⋅
⋅
=
x
x
dla
dla
x
n
x
n
x
T
n
1.02
0.68
0.34
0
0.34
0.68
1.02
1.5
0
1.5
3
4.5
6
7.5
9
10.5
12
13.5
15
16.5
16.5
1.5
−
Tcheb 20 x
,
(
)
1.025
1.025
−
x
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Warto
ś
ci współczynników tej FW mo
ż
na obliczy
ć
wg wzoru
Gdzie:
parametr, który jest powi
ą
zany z szeroko
ś
ci
ą
głównego listka widma
zale
ż
no
ś
ci
ą
:
( )
∑
−
=
−
−
−
+
−
−
−
−
−
=
1
0
2
0
2
0
)!
1
(
)!
1
(
!
)!
1
(
1
2
i
j
j
j
tl
i
j
i
i
j
n
j
x
j
n
n
K
x
g
=
n
K
x
tl
)
(
h
arccos
cosh
0
( )
π
π
π
ν
)
2
ln(
)
(
h
arccos
cosh
1
arccos
1
arccos
0
0
tl
tl
K
n
K
n
x
n
≅
⋅
=
⋅
=
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Cz
ę
stotliwo
ść
próbkowania sygnału równa si
ę
:
fs=fd+fg=fd (D+1)
gdzie
D=fg/fd
jest wzgl
ę
dnym zakresem cz
ę
stotliwo
ś
ci
Rz
ą
d WF wyznacza si
ę
wg. wzoru:
(
)
( )
+
=
+
=
1
cos
1
h
arccos
h
arccos
1
0
D
K
D
n
tl
π
ν
2. Projektowanie optymalnej
FW Dolpha–Czebyszewa
Liczba próbek FW Dolpha-Czebyszewa równa si
ę
:
N=n+1
Lepsza dokładno
ść
oblicze
ń
(zwłaszcza przy du
ż
ych N) otrzymuje si
ę
wykorzystuj
ąć
odwrotne przekształcenie Fouriera wielomianu
Czebyszowa
−
+
=
∑
=
−
N
M
m
k
N
k
x
T
K
N
w
M
k
N
tl
in
)
(
2
cos
cos
2
1
1
0
1
1
π
π
2
1
−
=
N
M
1
2
0
−
=
≤
≤
N
M
m
0
5
10
15
20
25
30
0
1
2
3
2.135
0.04
w
in
n 1
+
(
)
⋅
N 1
+
0
in
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron