PROBLEM NIEPEWNOŚCI W DZIAŁALNOŚCI
INŻYNIERSKIEJ

• Niedoskonałość człowieka
• Ograniczona wiedza

Niepewność wyników rozumowania, obliczeń inżynierskich,
trafności decyzji

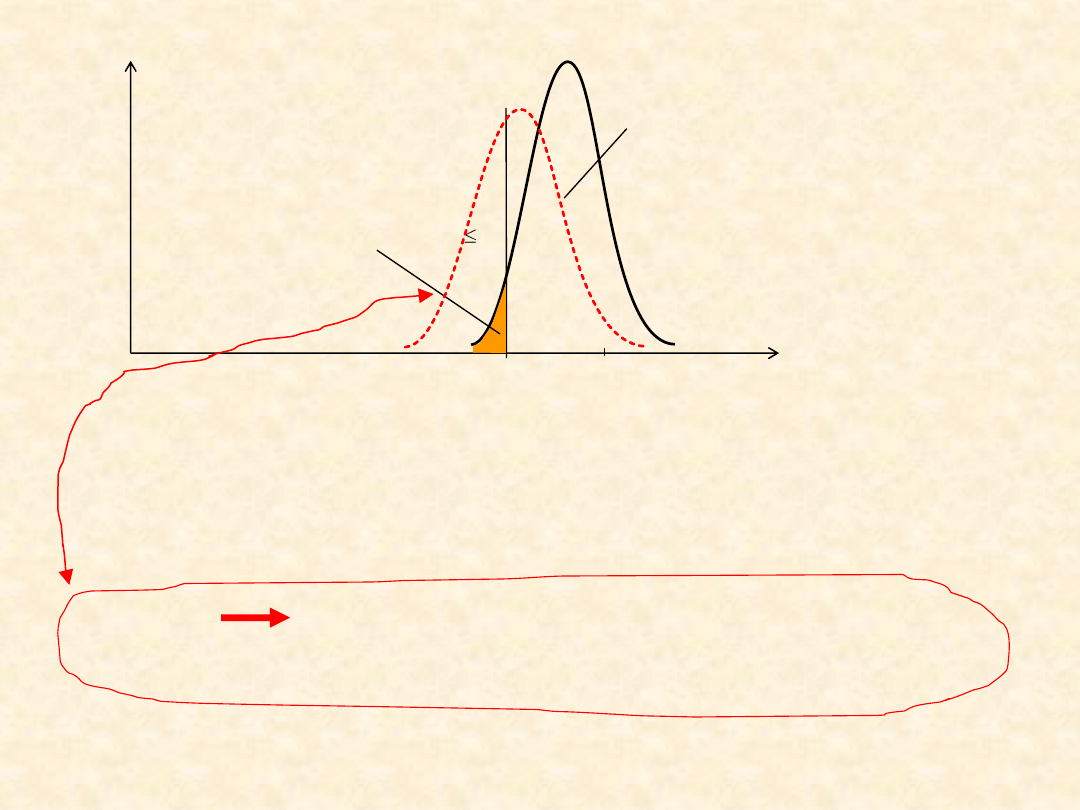
Np. niepewność dotycząca naprężeń σ i naprężeń krytycznych

σ

kr

1

σ ≤ σ

dop

gdzie

σ

dop

= σ

kr

/n

wym

σ

kr

R

e

, R

m

, Z, …

Świadome pomijanie mniej istotnych
czynników, np. uproszczenia w
modelach obliczeniowych

Nierozpoznanie niektórych czynników,
w szczególności - ważnych

2

Niepewność dotycząca obliczeń, zwłaszcza wytrzymałościowych,
jest szczególnie istotna . Może być przyczyną uszkodzeń, awarii i
katastrof strat.

Zajście niesprawności, gdy
T ≤ t

wym

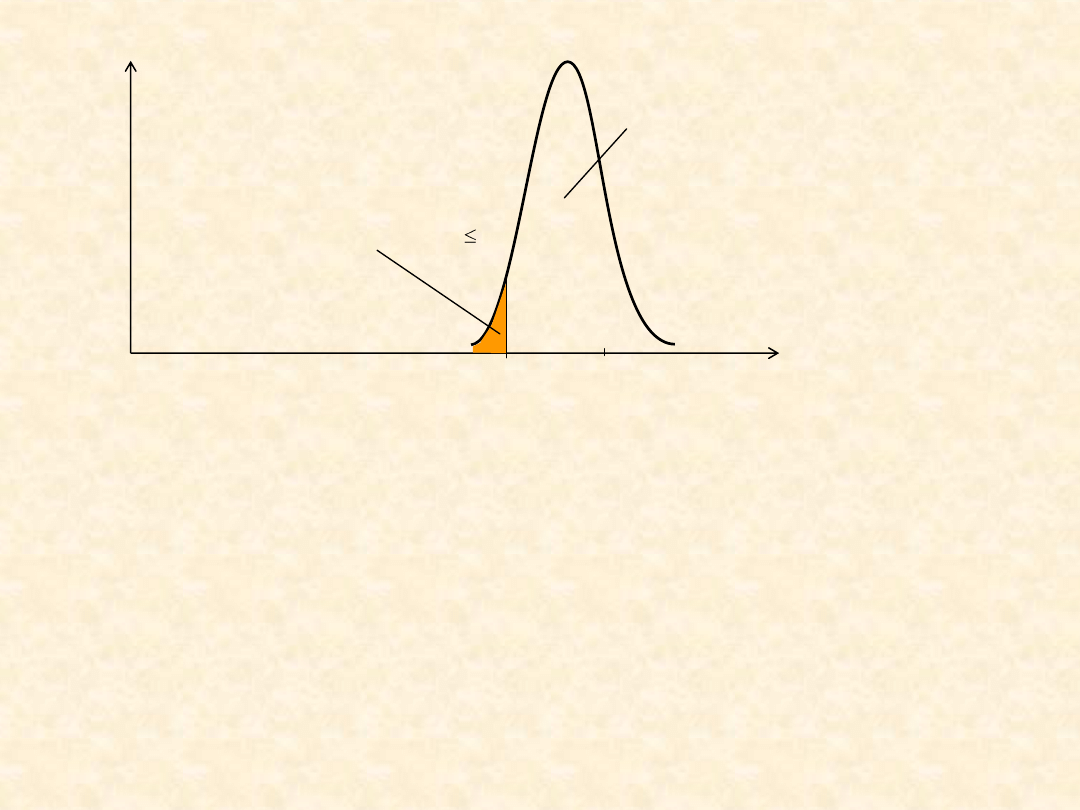
Im większa niepewność, tym może być większe prawdopodobieństwo
Q(t

wym

) zajścia niesprawności

Q(t

wym

) = P(

T ≤ t

wym

)

t

wym

t

T

niesprawność, np. uszkodzenie

3

τ

t

ET

Q(t) = P{T t }

R(t) = P{T > t }

f

R(t) = P{ T > t} -

funkcja niezawodności

Q(t) = P{ T ≤ t} - funkcja zawodności

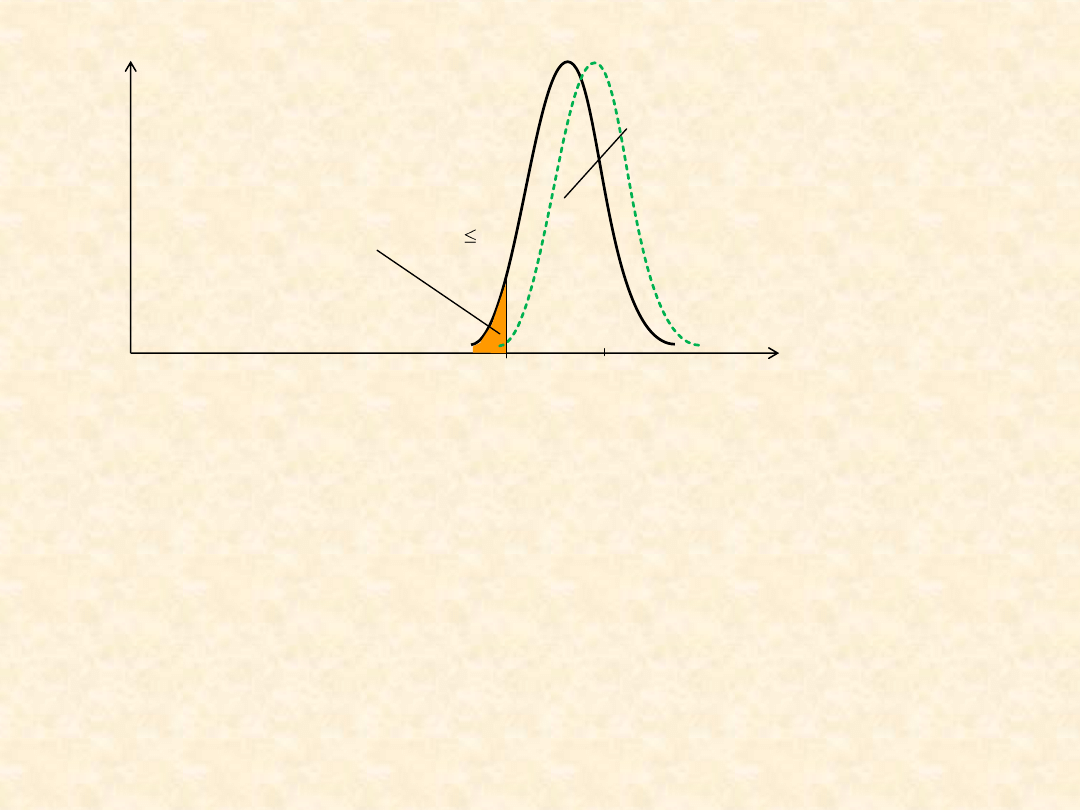
4

τ

t

ET

Q(t) = P{T t }

R(t) = P{T > t }

f

R(t) = P{ T > t} -

funkcja niezawodności

Q(t) = P{ T ≤ t} - funkcja zawodności

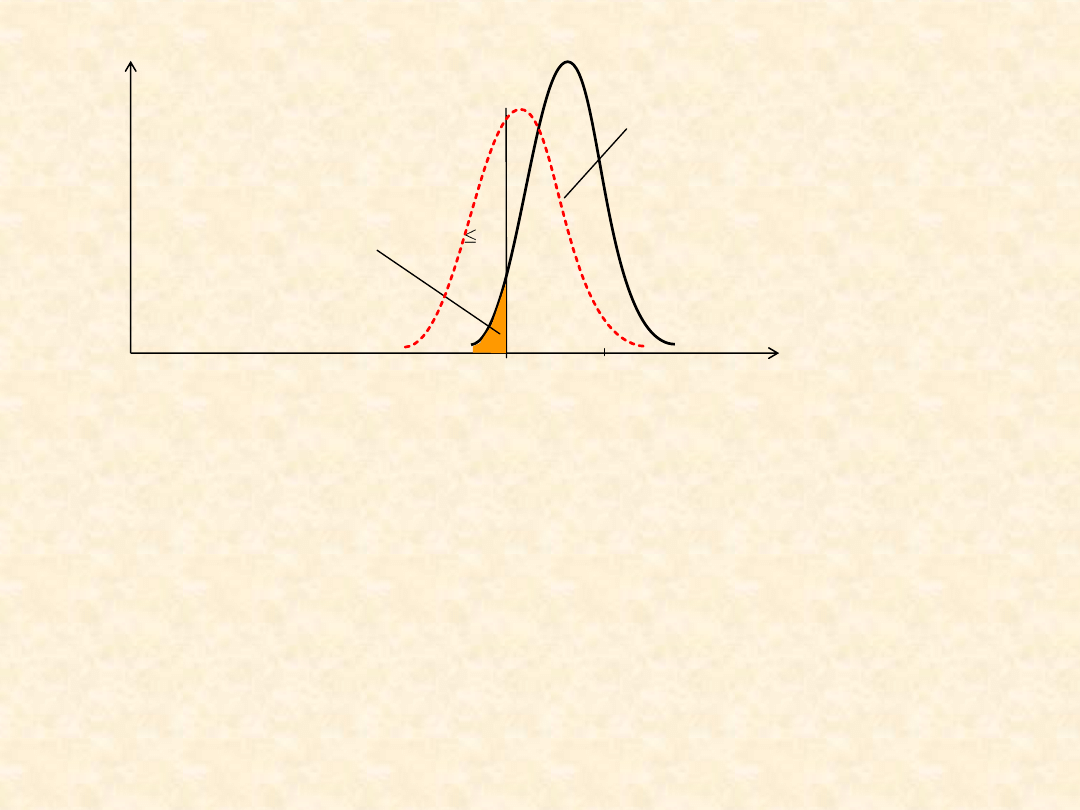
5

τ

t

ET

Q(t) = P{T t }

R(t) = P{T > t }

f

R(t) = P{ T > t} -

funkcja niezawodności

Q(t) = P{ T ≤ t} - funkcja zawodności

!

6

τ

t

ET

Q(t) = P{T t }

R(t) = P{T > t }

f

R(t) = P{ T > t} -

funkcja niezawodności

Q(t) = P{ T ≤ t} - funkcja zawodności

!

Powód : nierozpoznanie istotnego czynnika (np. zjawiska
zmęczenia wywołanego nieprzewidzianymi drganiami)

Zmniejszanie niepewności
w procesie projektowania

• stosowanie w obliczeniach współczynników
bezpieczeństwa

• wykorzystywanie do obliczeń dokładniejszych modeli,
w tym modeli probabilistycznych, np. naprężeń
i naprężeń krytycznych

• przeprowadzanie badań prototypu i serii informacyjnej

7

Obliczenia probabilistyczne

Probabilistyczna forma warunków ograniczających

σ

sup

≤ R

e

σ

max

≤ Z

X(t) ≤ X

kr

y ≤ y

kr

.

. .

P{ …} ≡ R(t) - funkcja niezawodności

Np. R = P{σ

sup

≤ R

e

}

σ

sup

, σ

max

, R

e

,

Z, …

zmienne losowe

8

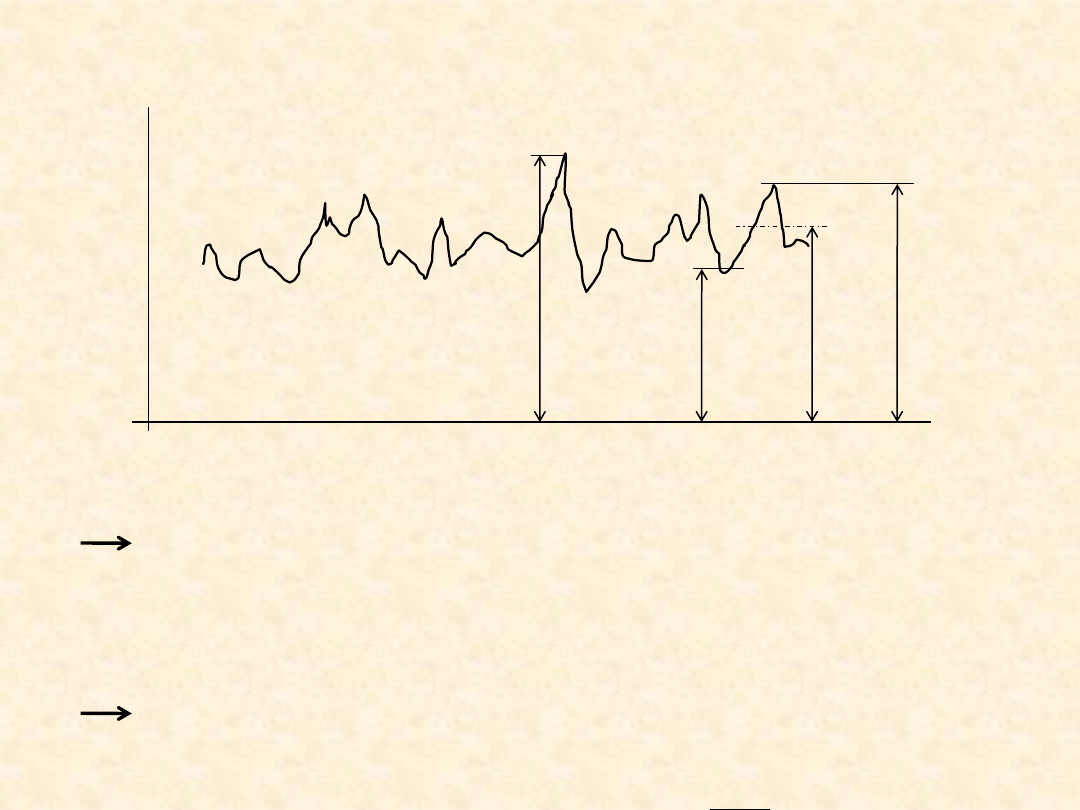
Probabilistyczny opis naprężeń

σ

sup

σ

max,i

σ

m,i

σ

min,i

t

σ

Do probabilistycznych obliczeń na wytrzymałość doraźną
rozkład prawdopodobieństwa σ

sup

w postaci na przykład

gęstości prawdopodobieństwa f (σ

sup

)

Do probabilistycznych obliczeń na wytrzymałość zmęczeniową
rozkłady prawdopodobieństwa σ

max

i σ

m

9

Duże rozrzuty cech, właściwości także właściwości
obiektów technicznych mechanicznych

R

e

, R

m

, Z , H , h , t

rw

, …,wymiary

Probabilistyczny opis właściwości mechanicznych

P{R

e

> R

e min

} ≈ 0,98- 0,99

10

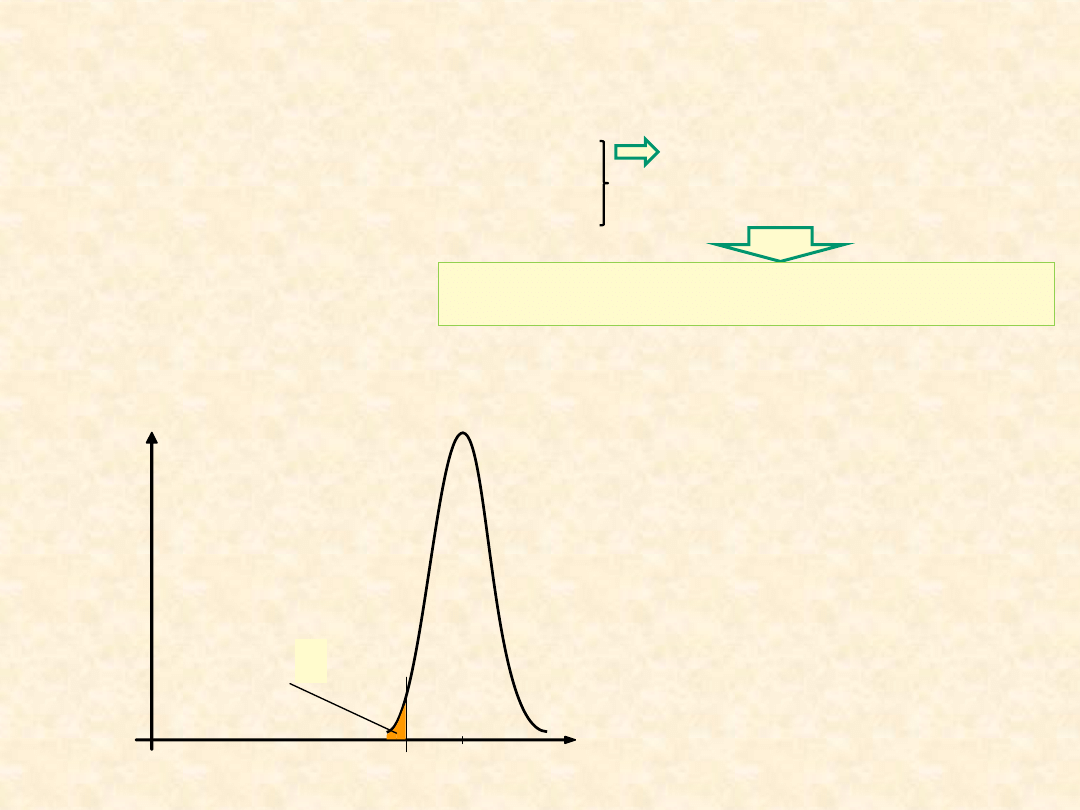
f

R

e

ER

e

R

e

P{R

e

≤ R

emin

}

R

emin

≤

Np.

probabilistyczny opis wytrzymałości doraźnej

Uwzględnianie losowości w obliczeniach
inżynierskich

•

operowanie opisami probabilistycznymi naprężeń (lub obciążeń)

oraz cech i właściwości (np.mechanicznych)

P{war. ograniczający} ≡ R(t)
R(t) = 1- Q(t)

11

R = P{σ

sup

≤ R

e

},

gdzie

σ ≡ σ

sup

σ

kr

≡ R

e

albo

R = P{σ

max k

≤ Z }

Np.

12

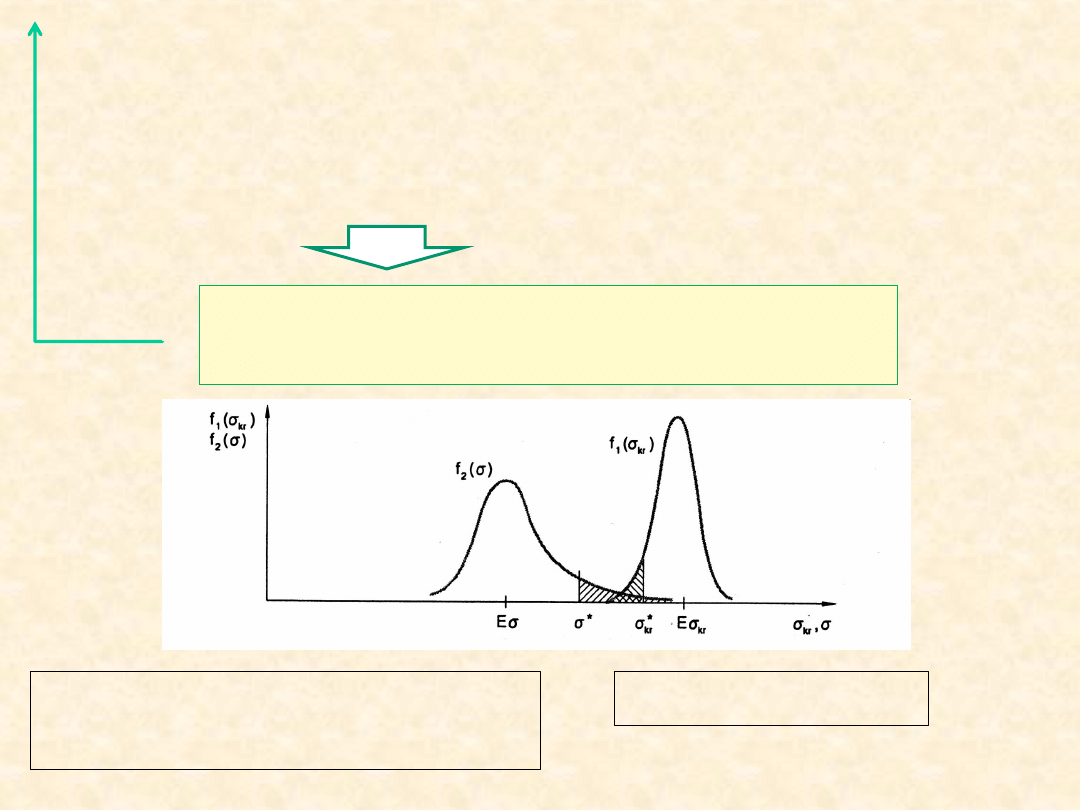
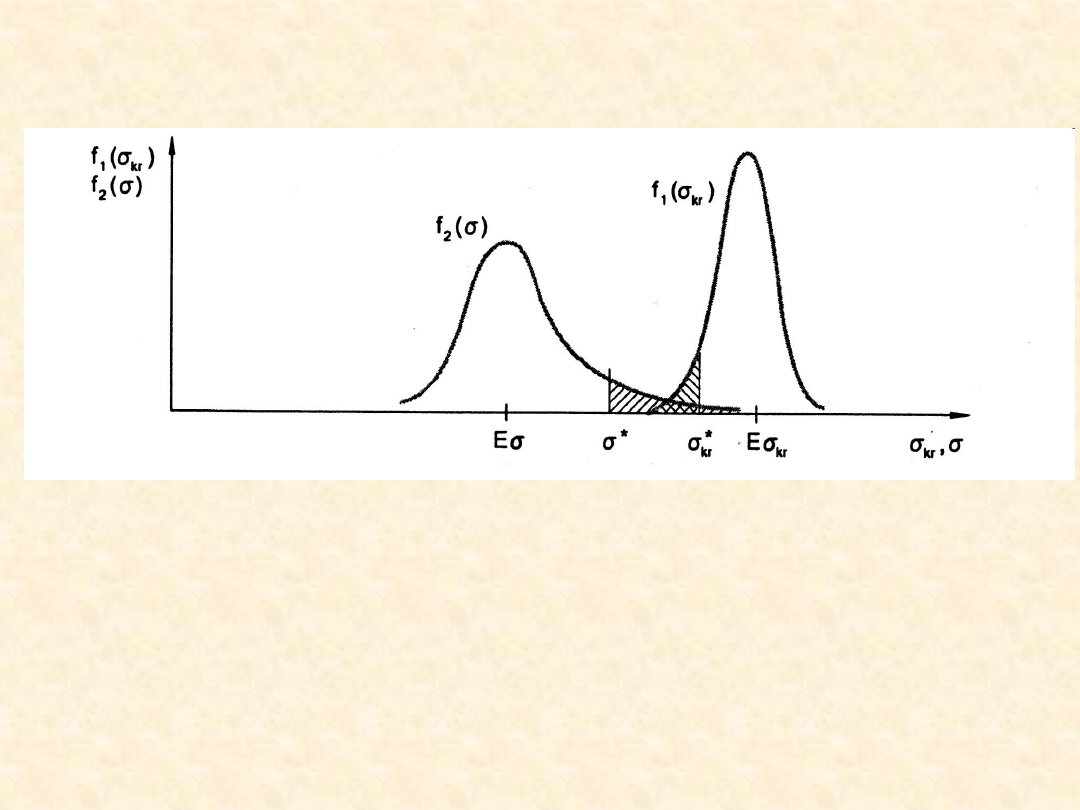
Gdy probabilistyczny opis σ i σ

kr

Prawdopodobieństwo uszkodzenia
Q = P{σ – σ

kr

> 0}

Q = f(n)

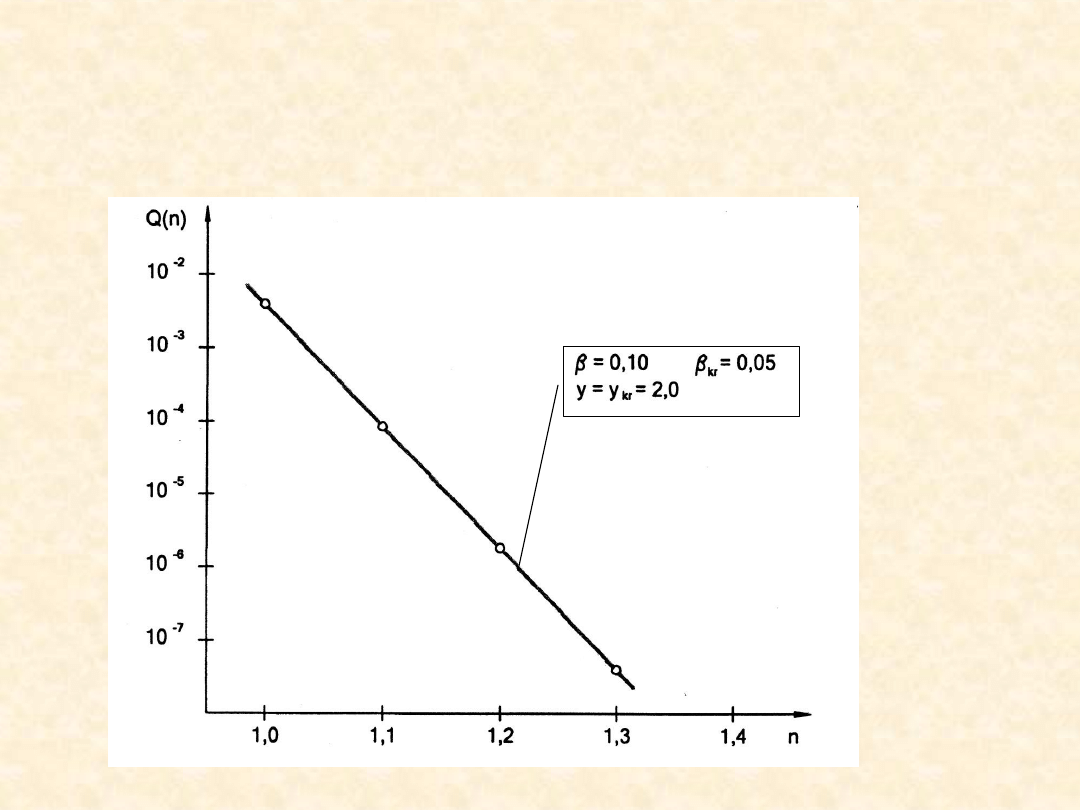
13

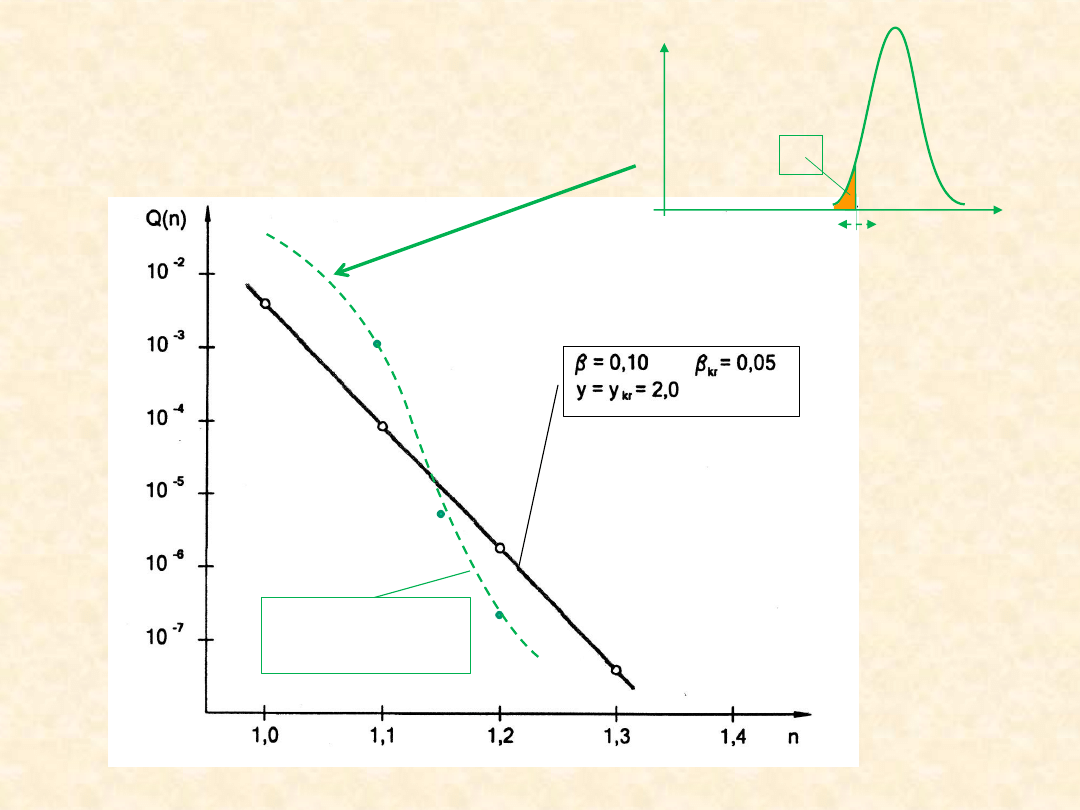
14

β = 0 β

kr

= 0,05

y

kr

= 2,0

Q

f

R

e

σ

σ -zdeterminowane

(β = 0)

15

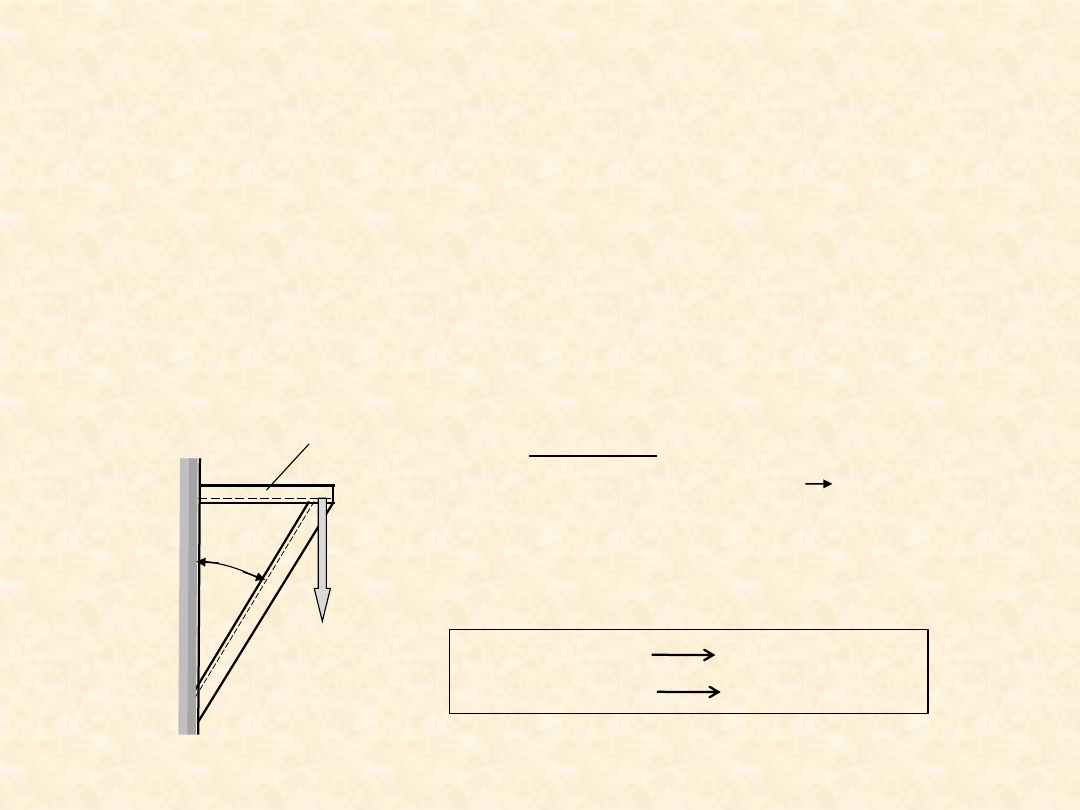
a

α

F

Wspornik przedstawiony na rysunku jest zespawany z ceownik

ów.

• Zdefiniuj współczynnik bezpieczeństwa ze względu na doraźne rozciąganie
pręta a.
• Wyznacz siłę rozciągającą ten pręt, a następnie oblicz wartość współczynnika
bezpieczeństwa, gdy α = 30

° i gdy α = 35°.

• Opierając się na wykresie Q = f(n), oszacuj dla obu przypadków wartości
prawdopodobieństwa uszkodzenia pręta.

Dane: F = 140kN, R

e

= 185MPa,

pole przekroju pręta a A = 7,1cm

2

.

Zadanie

Odp.: n = 1,62 Q ≈ 10

-11

n = 1,34 Q ≈ 10

-8

!!

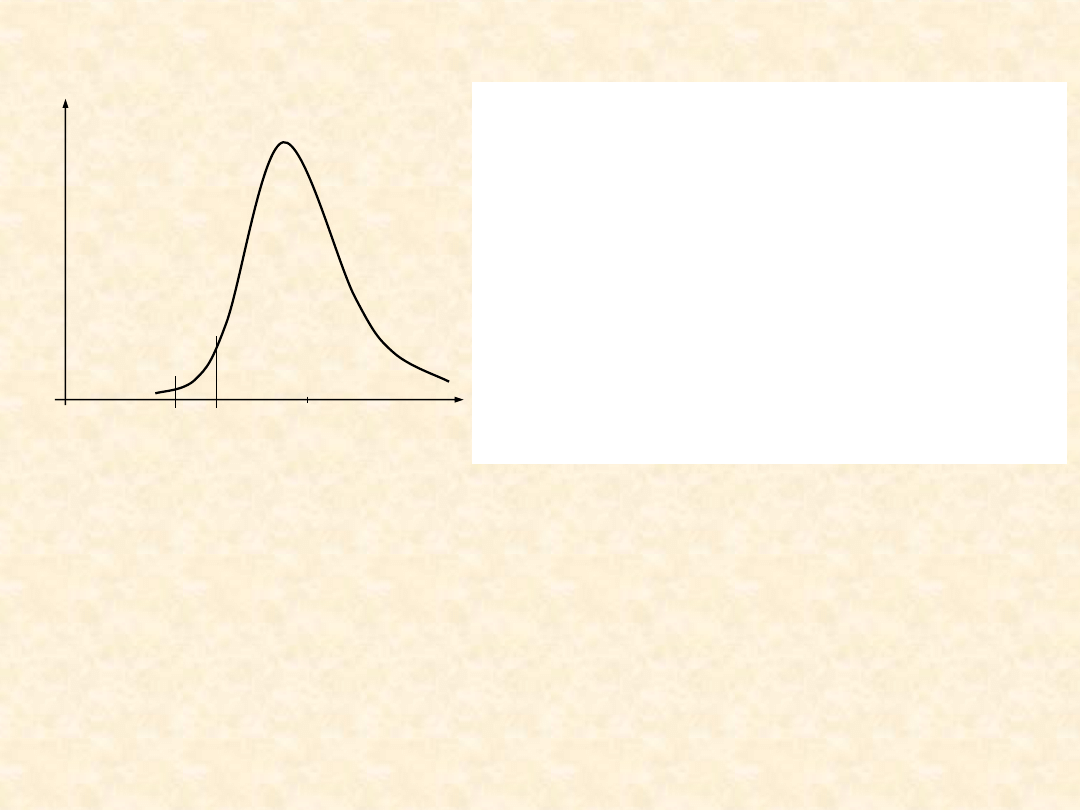
16

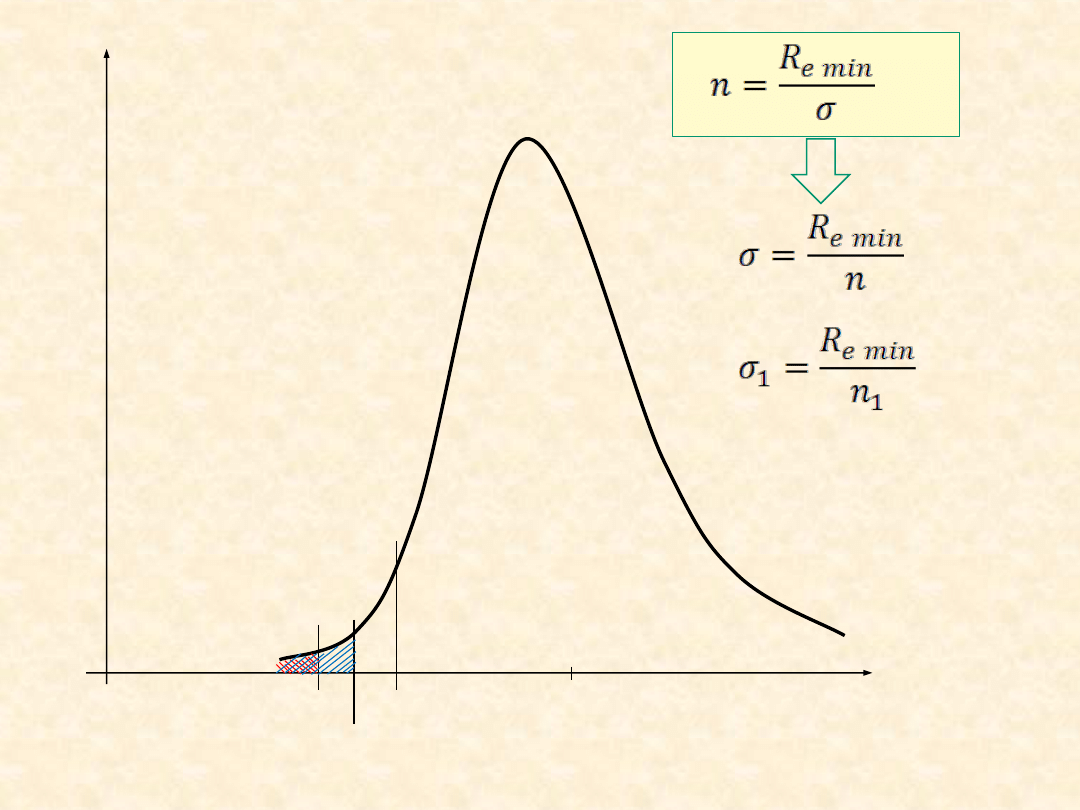
Na wykresie jest przedstawiona gęstość
prawdopodobieństwa granicy plastyczności R

e

materiału, z którego wykonano pręt obciążony
siłą wzdłużną wywołującą w nim naprężenia σ.
Posługując się wykresem, należy określić, jaki
wpływ na prawdopodobieństwo uszkodzenia
pręta mogłoby mieć zmniejszenie wartości
wsp

ółczynnika bezpieczeństwa w stosunku do

wartości wynikającej z wykresu

.

f

R

e

ER

e

R

emin

σ

Zadanie

Rozwiązanie

Uszkodzenie, gdy σ > R

e

σ – wielkość zdeterminowana (określona
wartość)
R

e

– zmienna losowa o gęstości f

Prawdopodobieństwo uszkodzenia Q = P{σ > R

e

}

17

f

R

e

ER

e

R

emin

σ

σ

1

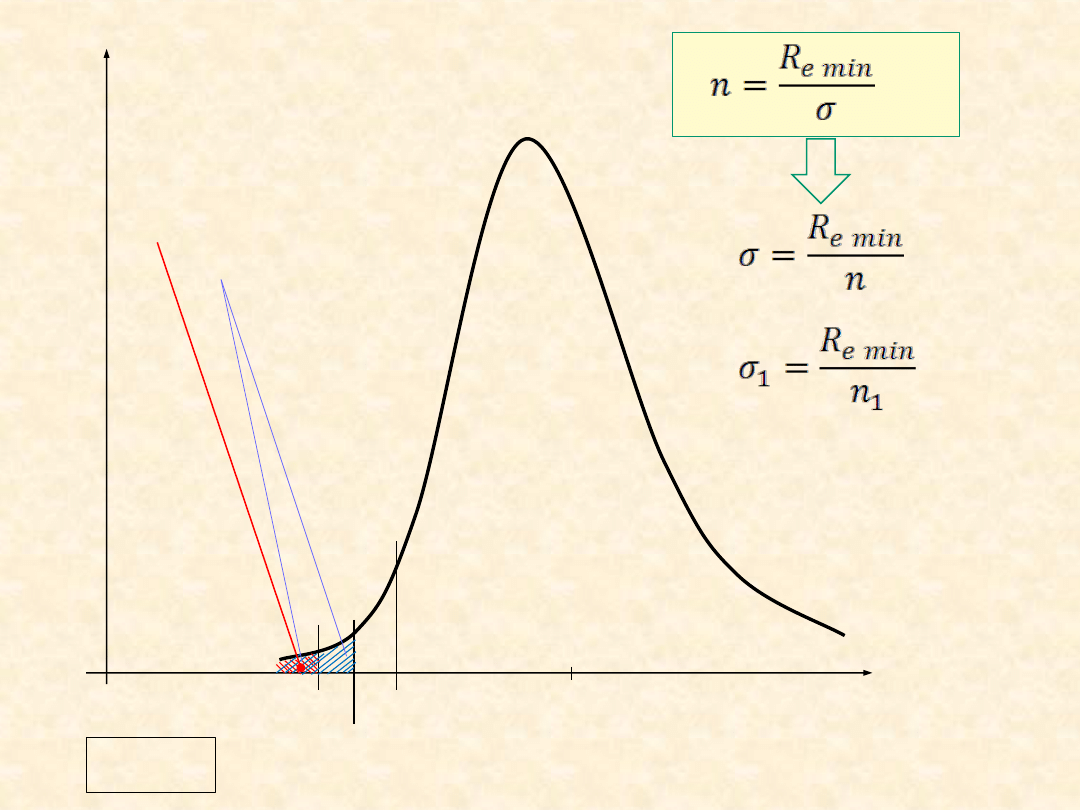
18

f

R

e

ER

e

R

emin

σ

σ

1

Prawdopodobieństwo
uszkodzenia
Q = P{ R

e

< σ }

Q

1

= P{R

e

< σ

1

}

Q

1

>

Q

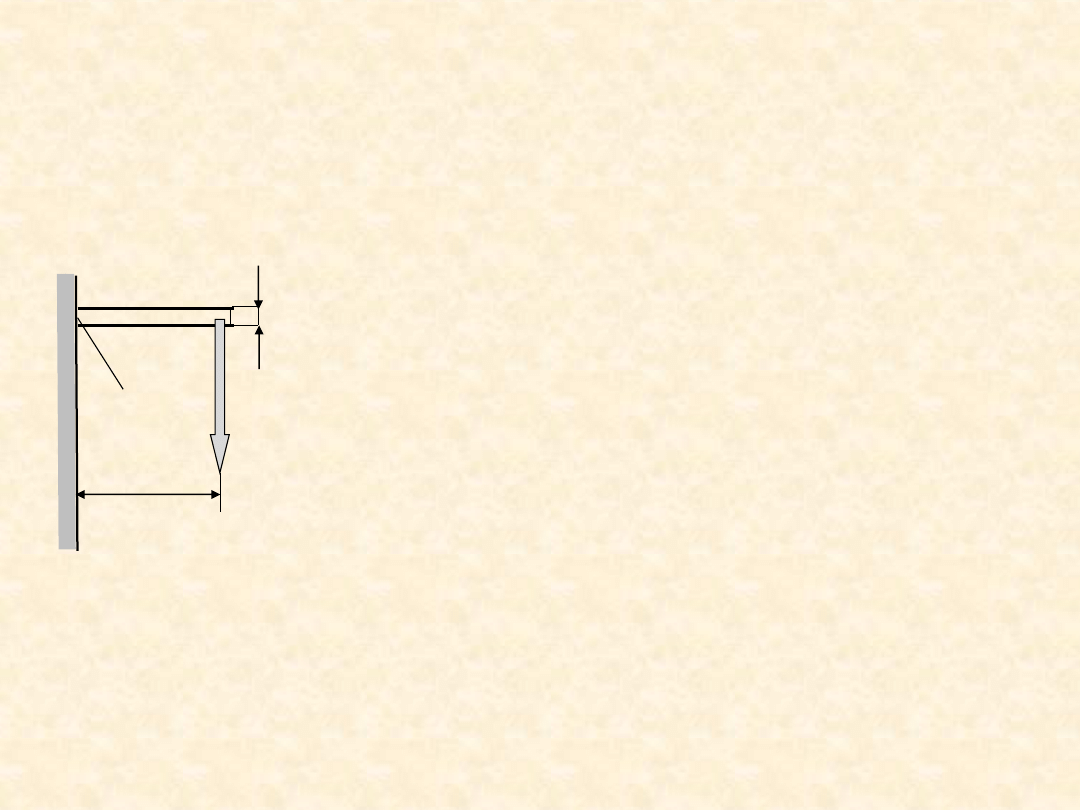
19

• Zdefiniuj współczynnik bezpieczeństwa ze względu
na doraźne zginanie pręta.
• Uzależnij ten współczynnik, określany dla przekroju
K, od wielkości podanych w temacie.
• Przedstaw w postaci poglądowej wykres gęstości
prawdopodobieństwa granicy plastyczności wspom-

nianej stali konstrukcyjnej. Zaznacz na nim położenie
granicy plastyczności stosowanej w obliczeniach
deterministycznych, a także – prawdopodobieństwo
uszkodzenia wspornika w przypadku, gdy
współczynnik bezpieczeństwa n > 1 i w przypadku,
gdy n = 1.

Belka wspornikowa wystająca z konstrukcji jest pełnym prętem o przekroju
kwadratowym wykonanym ze stali konstrukcyjnej o granicy plastyczności

R

e

.

Zadanie

a

F

K

l

Uwzględnianie losowości w obliczeniach
inżynierskich

•

operowanie opisami probabilistycznymi naprężeń (lub obciążeń)

oraz cech i właściwości (np.mechanicznych) – obliczenia
probabilistyczne

• stosowanie w obliczeniach deterministycznych współczynników
uwzględniających rozrzuty losowe właściwości materiału lub
elementu (wymagany poziom „niezawodności”), np.
- c

r

w obliczeniach zmęczeniowych

- a

R

w obliczeniach łożysk tocznych

oraz kwantyli wytrzymałości materiału określanych dla
- r = 0,99 w obliczeniach zmęczeniowych kół zębatych
- r ≈ 0,98 (R

e

, R

m

) w obliczeniach ze względu na

wytrzymałość doraźną

20

Częściej

21

Z∙c

r

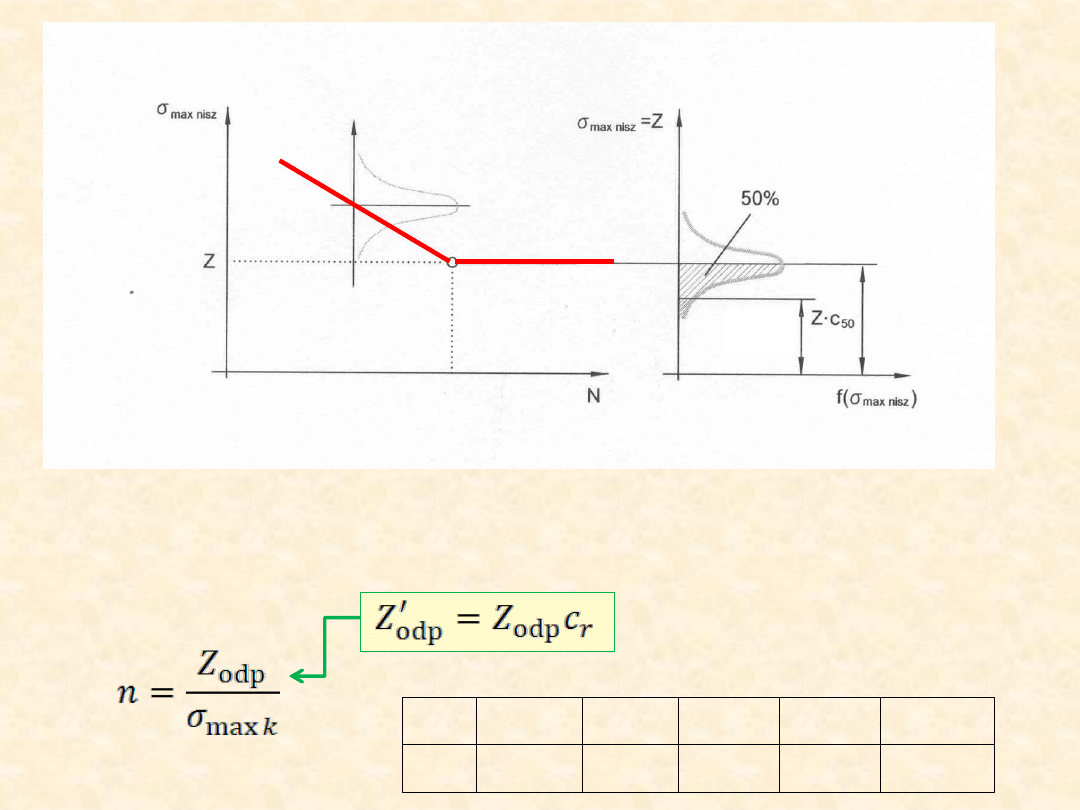
Probabilistyczny opis wytrzymałości zmęczeniowej

Podawana i stosowana w obliczeniach deterministycznych granica
zmęczenia Z = EZ .
P{Z < Z} = 0,50 , a współcz. „niezawodności” c

r

= 1.

r

0,5000 0,9000 0,9900 0,9990 0,9999

c

r

1,000 0,897 0,814 0,753 0,702

22

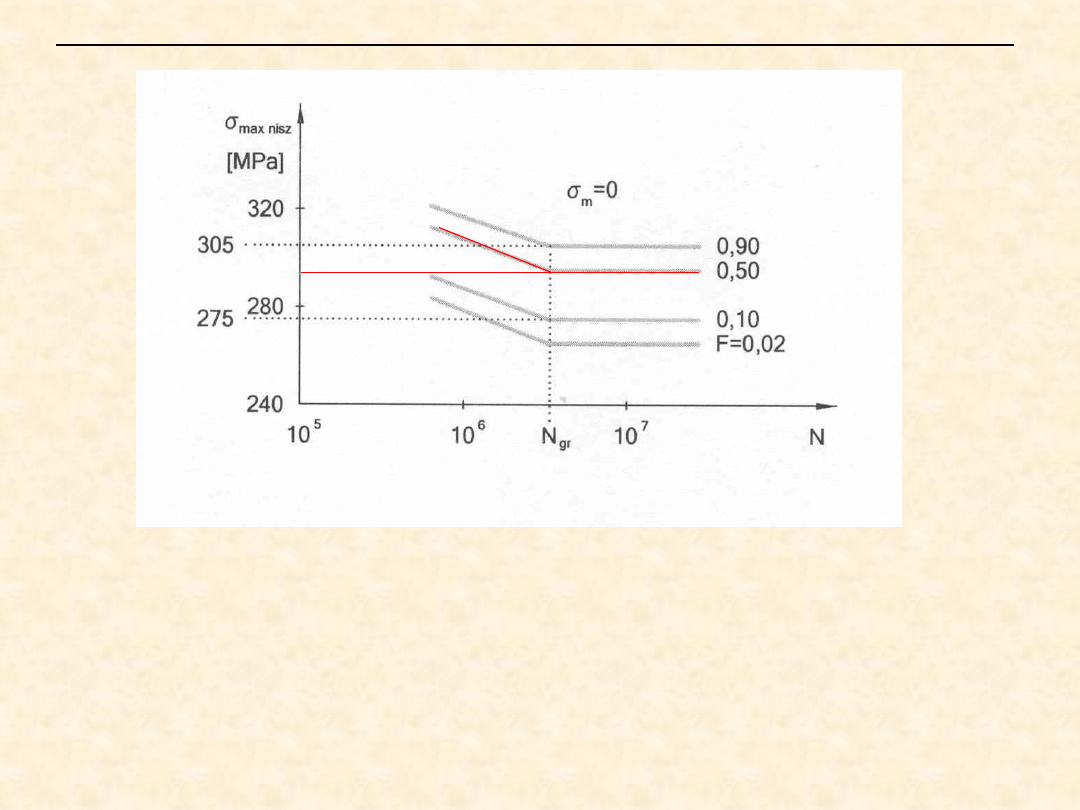
Inna ilustracja graficzna rozrzutów losowych granicy zmęczenia Z

Zmniejszenie naprężeń σ

maxk

z 305 MPa do 275 MPa powoduje

wzrost prawdopodobieństwa przeżycia N

gr

P{N > N

gr

} = P{σ

maxk

< Z} = 1-F

z wartości 0,10 do 0,90.

Jedna ze stali
węglowych do
ulepszania cieplnego

Z =

Z =

F = P{Z < Z} – dystrybuanta zmiennej losowej Z

23

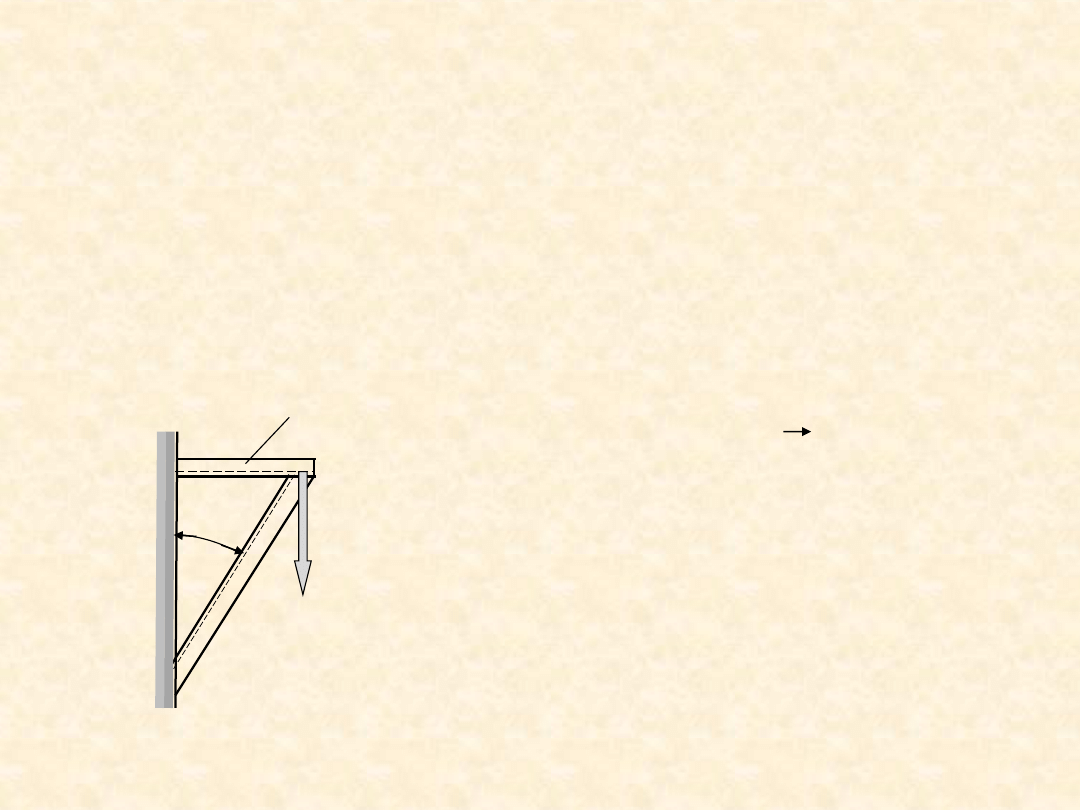
a

α

F

Wspornik przedstawiony na rysunku jest zespawany z ceownik

ów wykononych ze

stali niskowęglowej C22R. Siła F obciążająca wspornik zmienia się w czasie w
zakresie wartości od 0 do 140 MPa. W okresie przewidywanej jego trwałości
liczba obciążeń jest duża, mianowicie N ≈ 8∙10

5

.

• Zdefiniuj współczynnik bezpieczeństwa ze względu na zmęczenie pręta a.
• Oblicz wartość współczynnika bezpieczeństwa ze względu na zmęczenie w
przekroju tego pręta oddalonego od zamocowań, gdy α = 30

° i gdy α = 35°.

Pozostałe dane: R

e

= 390 MPa, R

m

= 470 MPa, pole

przekroju pręta a A = 7,1cm

2

.

Zadanie

24

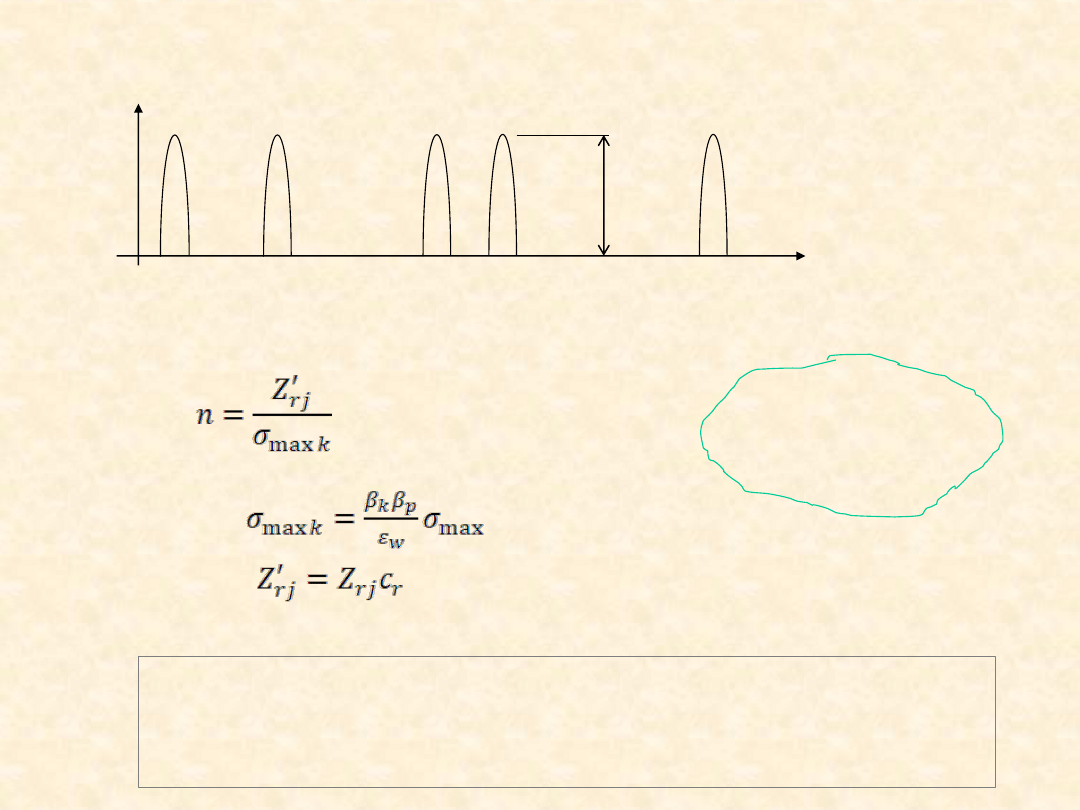
• Naprężenia w pręcie – rozciągające, odzerowo tętniące.

Zatem współcz. bezpiecz.



gdzie

σ

t

…

σ

max

= σ

max

Z

rj

≈ 0,60

R

m

, R

m

– na poziomie prawdopodobieństwa ~ 0,98,

zatem także c

r

na poziomie r = 0,98, czyli

c

r

≈ 0,820 .

Wykres Smitha
(Haigha, Goodmana)
- zbędny

Rozwiązanie

25

L

l

A

F

ω

D

d

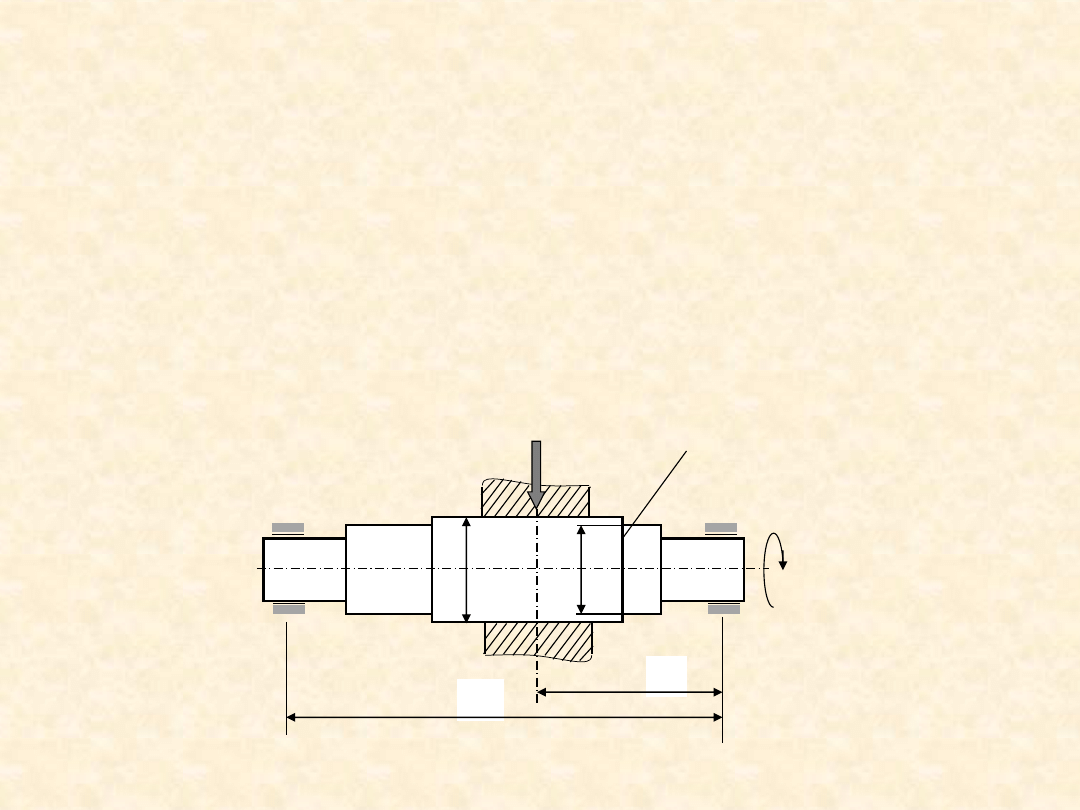
Zdefiniuj matematycznie, a następnie wyznacz współczynnik
bezpieczeństwa n ze względu na zginanie doraźne i ze względu na
zginanie zmęczeniowe w przekroju A wałka pośredniego przekładni
zębatej, pokazanego na rysunku. Znane są między innymi wartości
wielkości: siły F, odległości l i L, średnic D i d, a także – R

m

, R

e

, Z

go

,

Z

gj

materiału wałka.

Zadanie

26

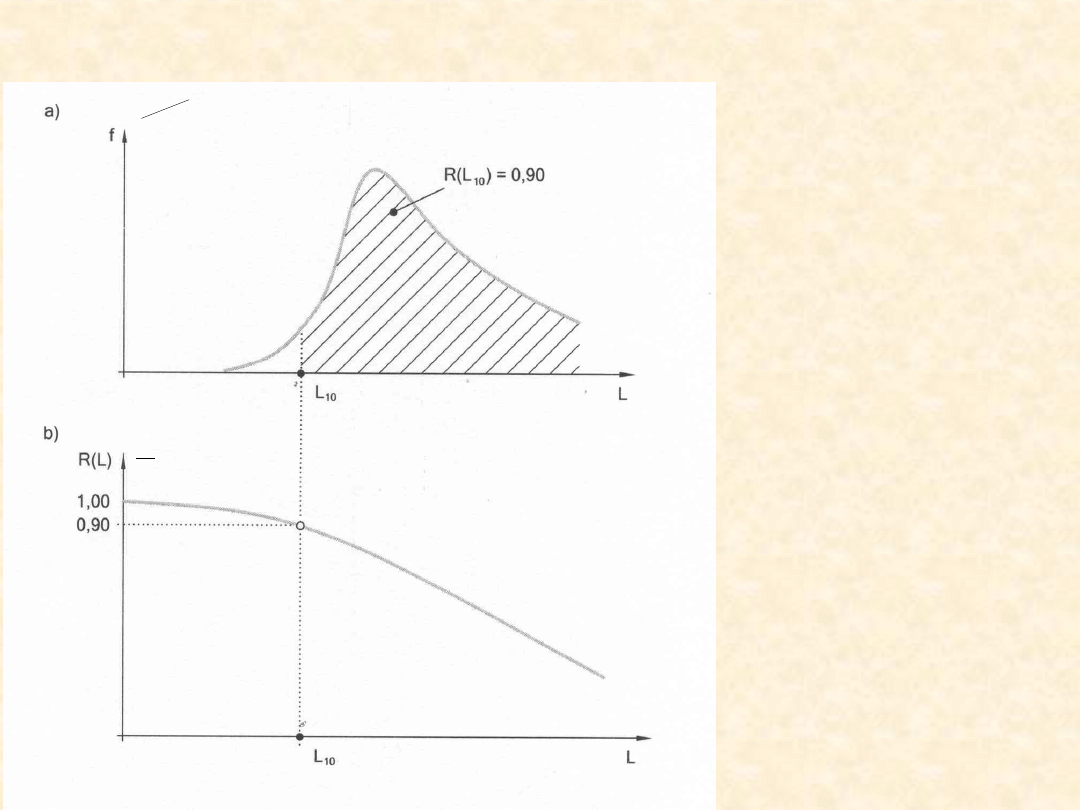
Probabilistyczny opis trwałości łożyska tocznego

gęstość prawdopodobieństwa zmiennej losowej L

funkcja niezawodności łożyska

27

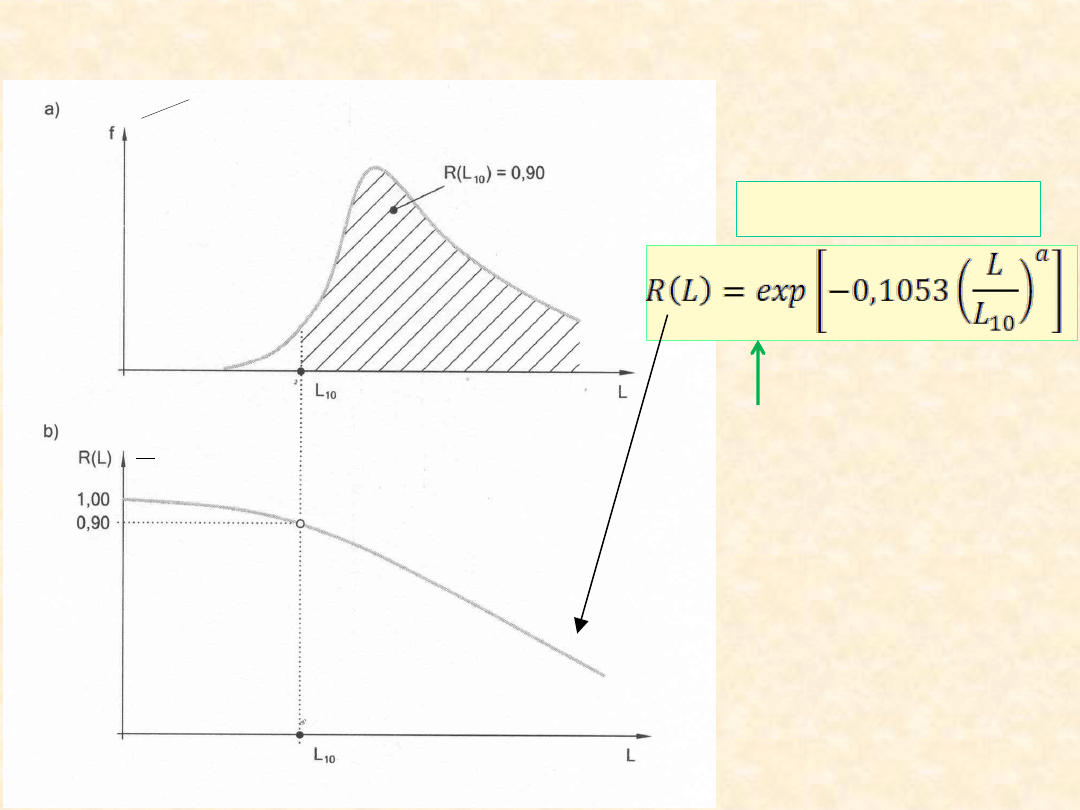
Probabilistyczny opis trwałości łożyska tocznego

R(L) = P{ L ≥ L}

rozkład Weibulla zm. L

a = 10/9 dla łoż. kulk.;
a = 9/8 dla łoż.wałeczk.

F(L) = 1- R(L)

gęstość prawdopodobieństwa zmiennej losowej L

funkcja niezawodności łożyska

R(L)
1,00
0,90 L

68

≈ 10 L

10

0,32



L

10

L

68

L[mln obr.]

R(L)

1,00
0,90

0,32

28

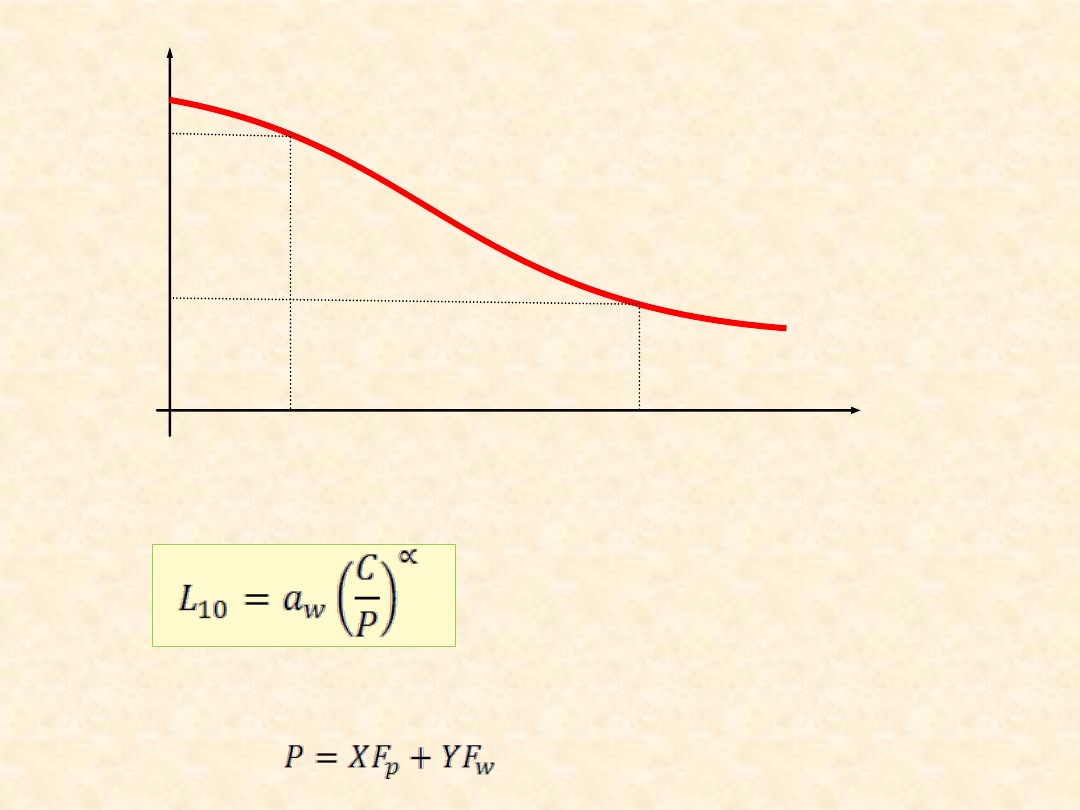
Trwałość umowna ( katalogowa)

α = 3 dla łoż. kulk.;
α = 10/3 dla łoż. wałeczk.

C – nośność dynamiczna (ruchowa)
P – obciążenie zastępcze

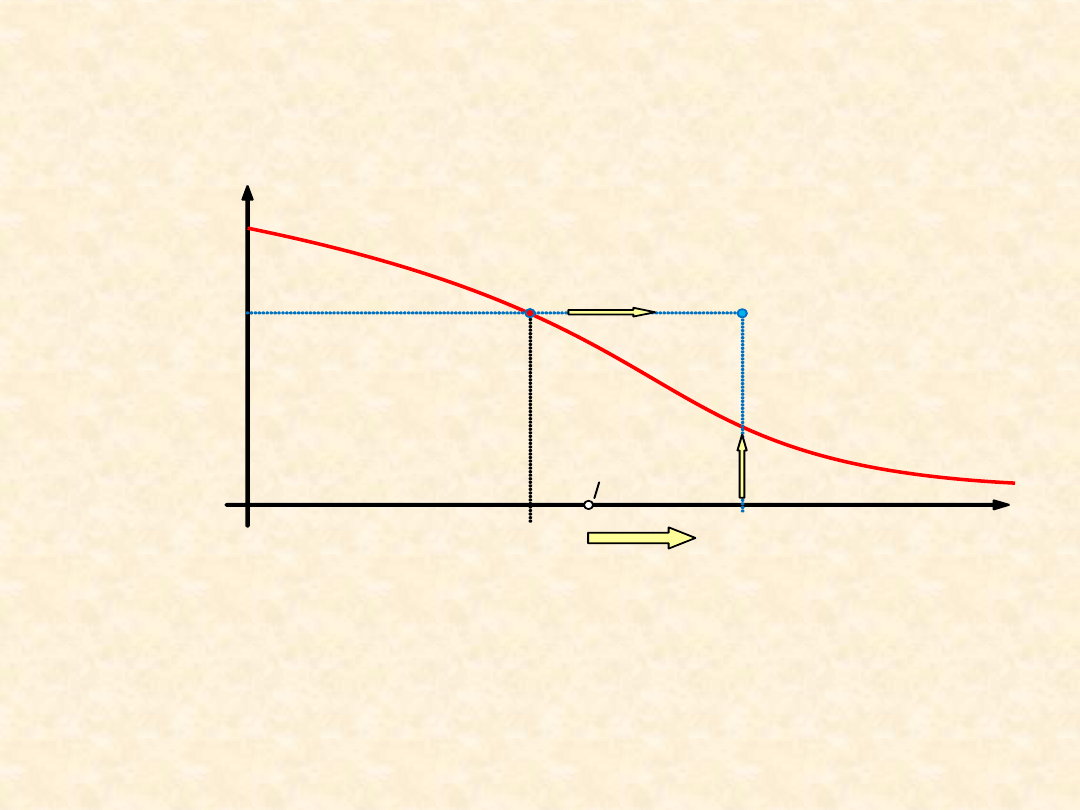
L

10

L

10

R(L)

0,90

L

1,00

0,60

L

wym

29

a

w

= 0,1 – 50 współczynnik warunków pracy (temperatura, lepkość i

czystość smaru, obciążenie itd.)

L

10

L

10

R(L)

0,90

L

1,00

0,60

L

wym

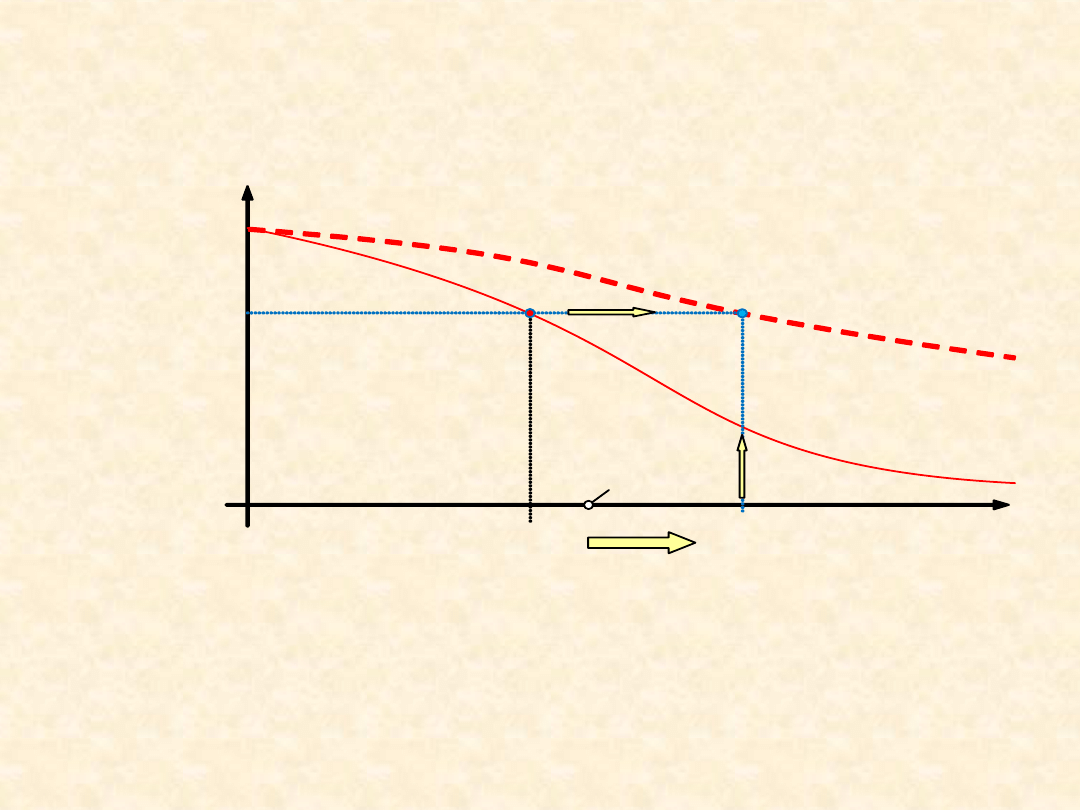
30

a

w

= 0,1 – 50 współczynnik warunków pracy (temperatura, lepkość i

czystość smaru, obciążenie itd.)

L

10

L

10

R(L)

0,90

L

1,00

0,60

L

wym

R(L

wym

)

R(L

wym

) ≥ R

wym

, - warunek doboru wielkości łożyska (C,…)

gdzie R

wym

= …. (np. R

wym

= 0,98 )

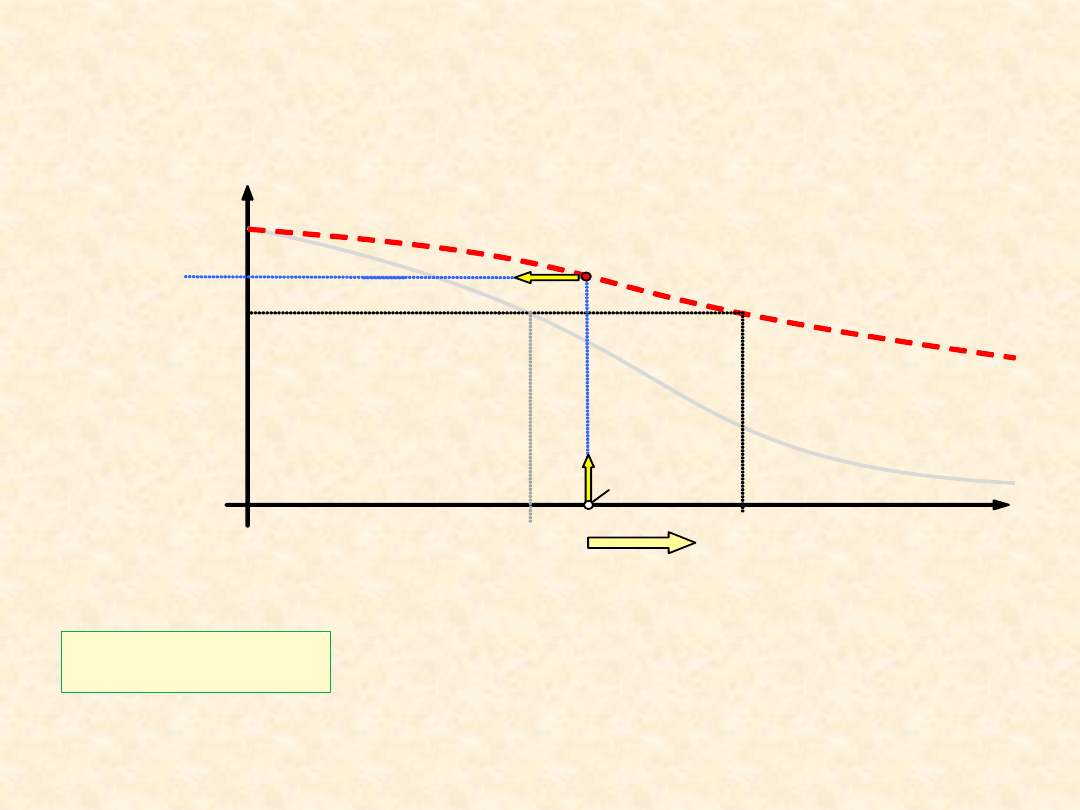
31

a

w

= 0,1 – 50 współczynnik warunków pracy (temperatura, lepkość i

czystość smaru, obciążenie itd.)

L

10

R(L)

L

1,00

0,70

L(R

wym

)

R

wym

L

wym

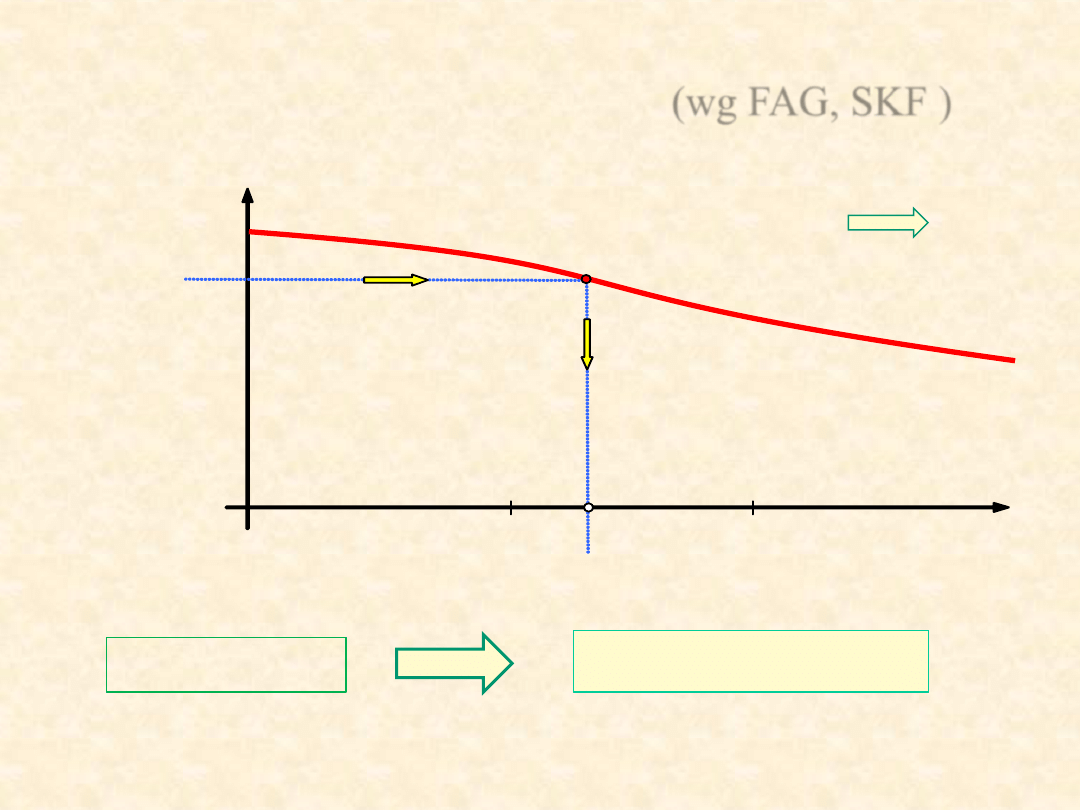
32

Deterministyczny opis trwałości łożyska tocznego
uwzględniający jej rozrzut losowy (wg FAG, SKF )

Jeśli R(L),to L(R)

L(R

wym

) ≥ L

wym

gdzie L(R

wym

) =

a

R

L

10

R(L

wym

) ≥ R

wym

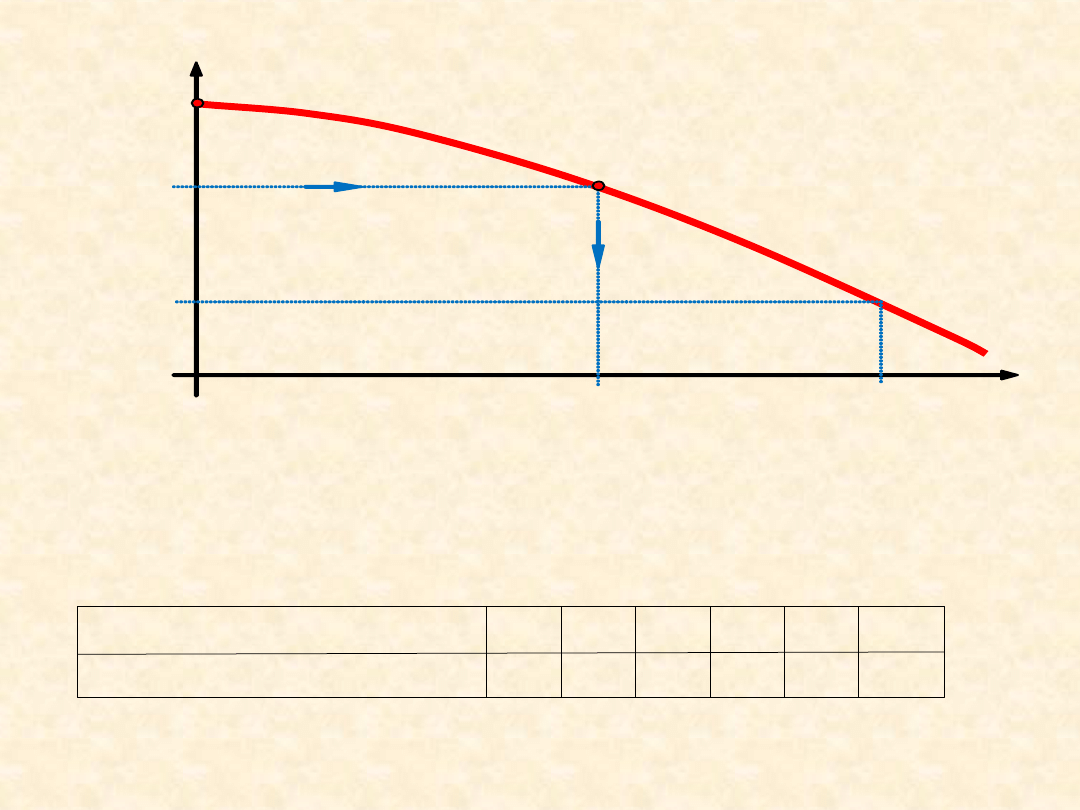
R(L)

L

R

L(R)

0,90

L

10

1,00

a

R

= L(R) ∕ L

10

33

Funkcja „niezawodności” R 0,90 0,95 0,96 0,97 0,98 0,99
Współczynnik a

R

1 0,62 0,53 0,44 0,33 0,21

34

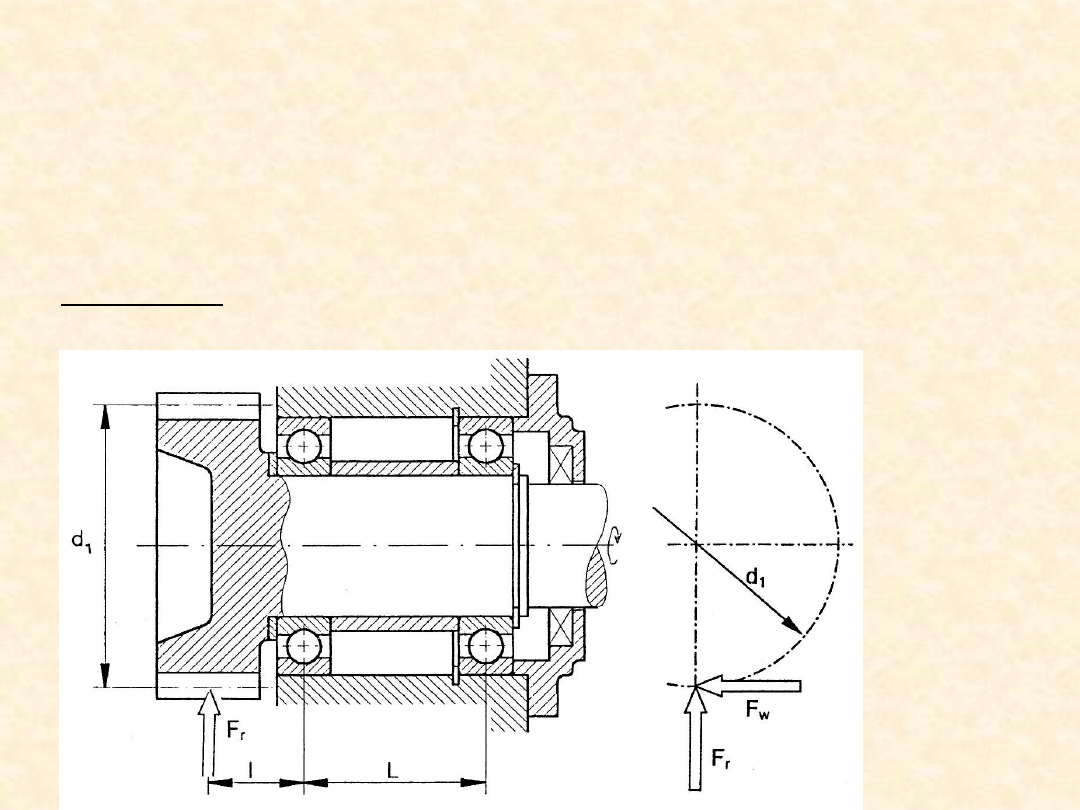
Zadanie

Do podparcia wałka przekładni zębatej (p. rysunek) użyto dwóch jednakowych łożysk
poprzecznych kulkowych zwykłych 6208 o nośnościach ruchowych każdego z nich
C = 32,5 kN. W strefie zazębienia występuje obciążenie poprzeczne o dwóch składowych,
związanych relacją F

r

= 0,364 F

w

, przy czym F

w

= 8 kN.

Przewidywana trwałość

pojedynczego łożyska L

wym

= 120 mln obr., a wymagana wartość funkcji jego niezawodności

w tym okresie powinna być nie mniejsza niż R

wym

= 0,98. Sprawdzić prawidłowość doboru

łożysk do tych warunków.
Pozostałe dane: d

1

= 80 mm, l = 30 mm, L = 60 mm, oraz niektóre informacje potrzebne do

doboru z katalogu wartości współczynnika warunków pracy łożyska – P

u

= 0,80 kN,

n = 1000 obr/min, t = 30

o

C, olej niefiltrowany o lepk. kinemat. ν

z

= 10 mm

2

/s (w 40

o

C),

d = 40 mm,
D = 80 mm.

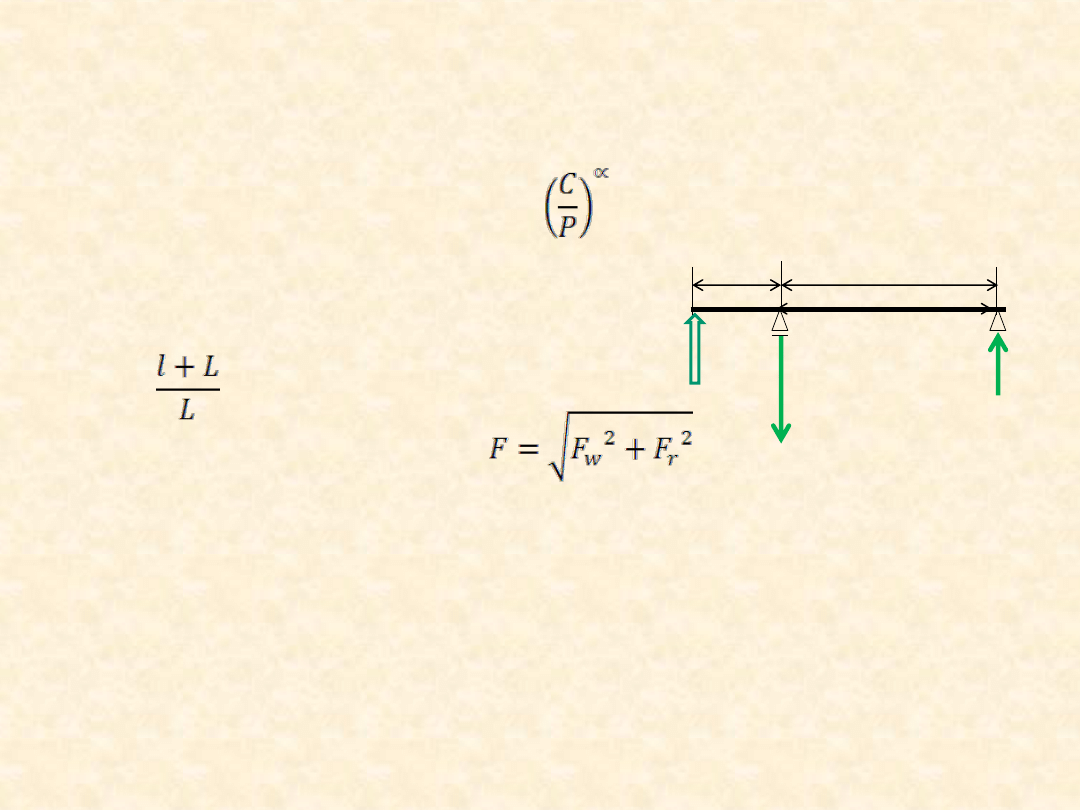
35

Rozwiązanie

Sprawdzenie przy użyciu warunku

L(R

wym

) ≥ L

wym

gdzie L(R

wym

) = a

R

L

10

, L

10

= a

w

P = XP

p

+ YP

w

P = P

p

P

p

= F

L

l

F

P

p

36

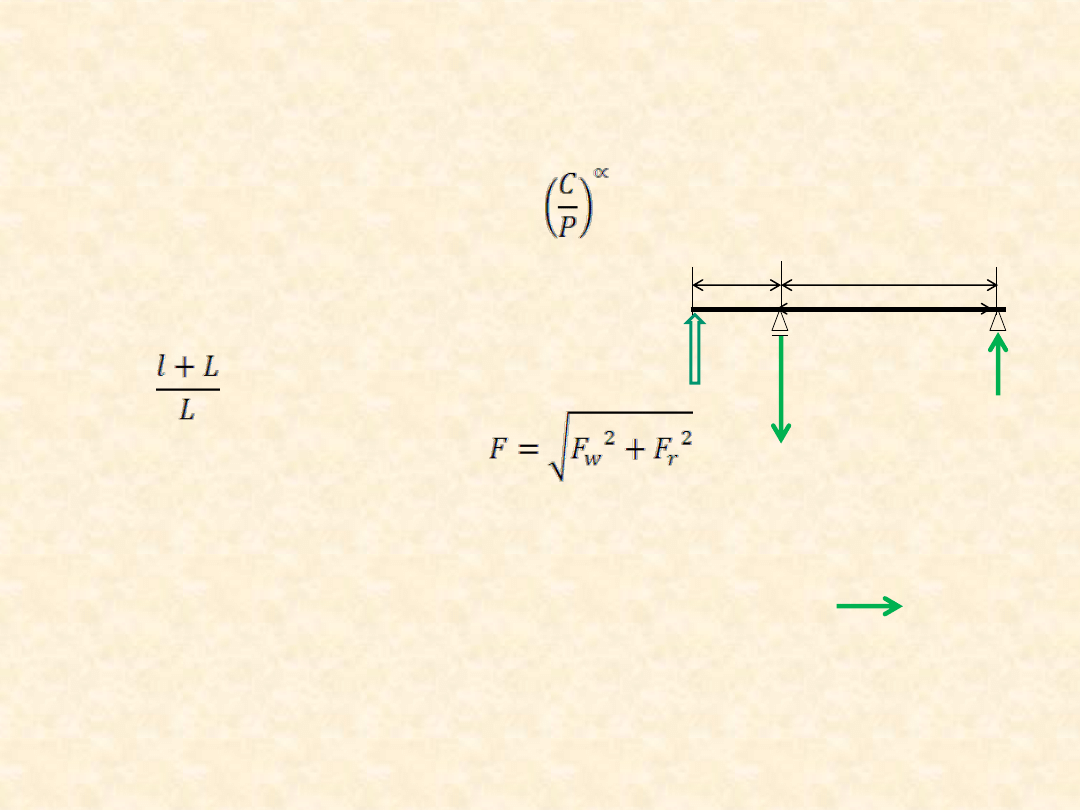
Rozwiązanie

Sprawdzenie przy użyciu warunku

L(R

wym

) ≥ L

wym

gdzie L(R

wym

) = a

R

L

10

, L

10

= a

w

Warunki pracy niedobre: lepkość oleju zbyt mała w stosunku do zalecanej
(SKF), łożyska niechronione przed zanieczyszczeniami itd. na
podstawie wykresów w SKF
a

w

≈ 0,55 !

P = XP

p

+ YP

w

P = P

p

P

p

= F

L

l

F

P

p

37

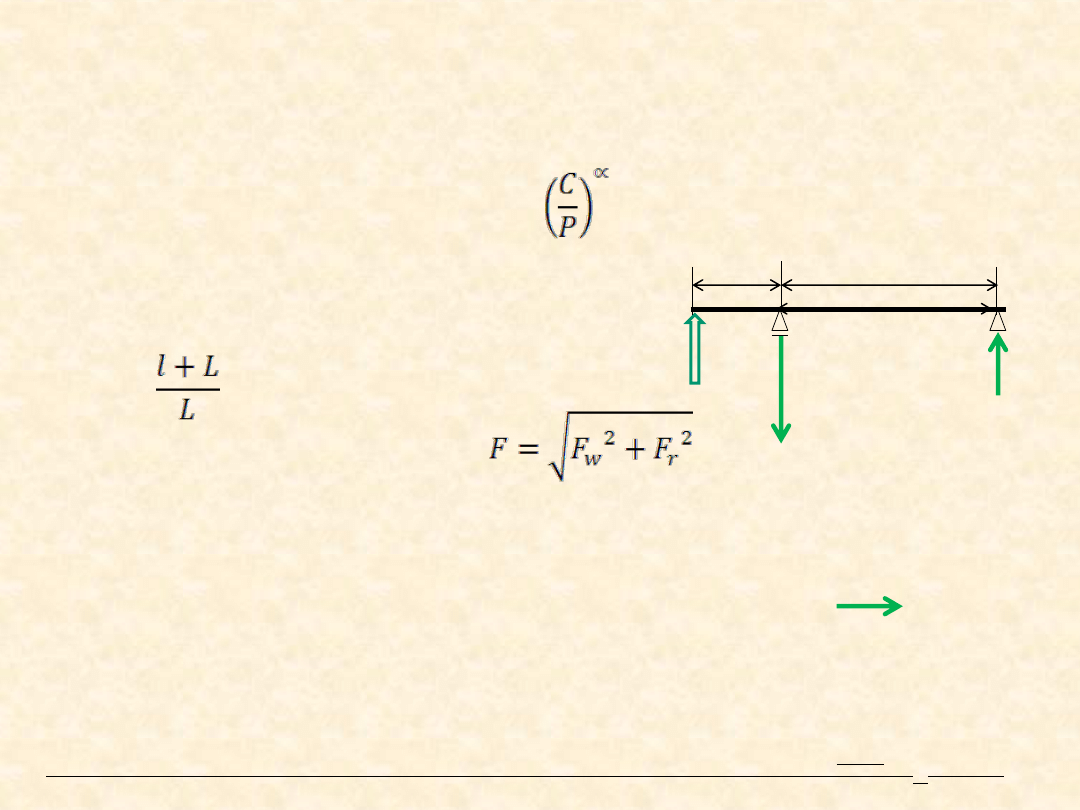
Rozwiązanie

Sprawdzenie przy użyciu warunku

L(R

wym

) ≥ L

wym

gdzie L(R

wym

) = a

R

L

10

, L

10

= a

w

Warunki pracy niedobre: lepkość oleju zbyt mała w stosunku do zalecanej
(SKF), łożyska niechronione przed zanieczyszczeniami itd. na
podstawie wykresów w SKF
a

w

≈ 0,55 !

Zmiana łożyska na uszczelnione (wewnętrznie) 6208-RS1 a

w

≈ 12.

P = XP

p

+ YP

w

P = P

p

P

p

= F

L

l

F

P

p

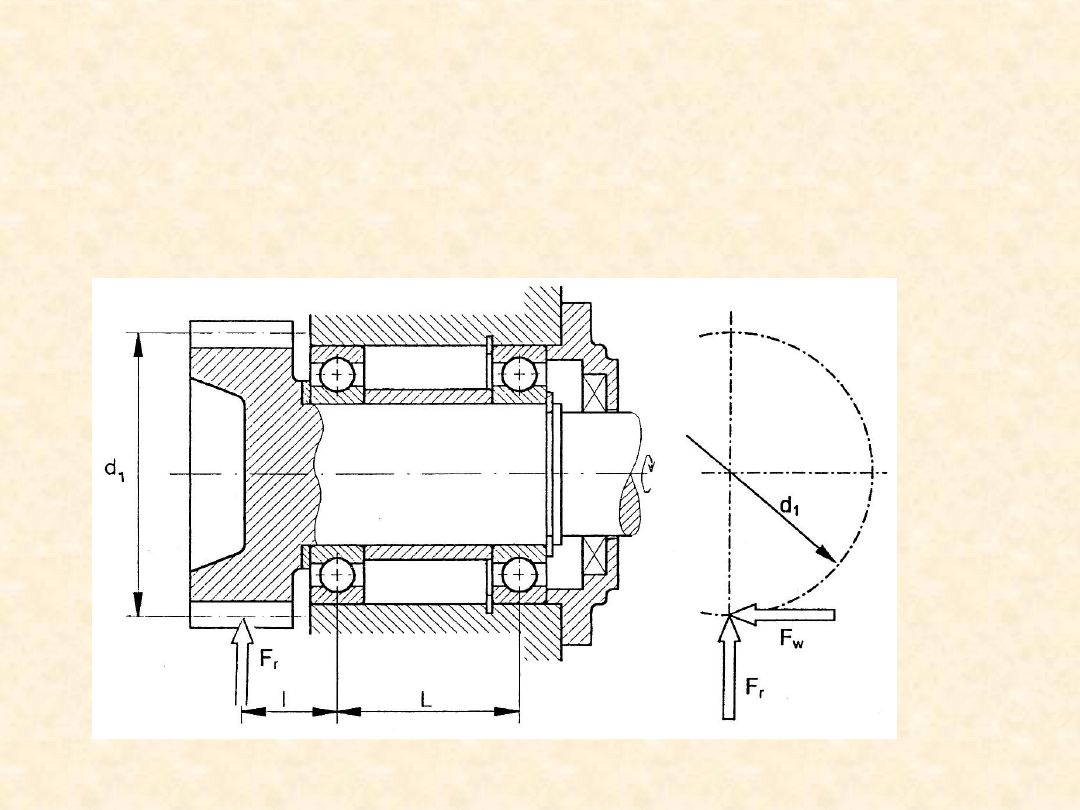
Zadanie

Narysować wykres funkcji niezawodności łożyska bardziej obciążonego
z dwóch łożysk, o których mowa w poprzednim zadaniu i funkcjonujących
w opisanych warunkach. Jakie są dwa dominujące zjawiska fizyczne
prowadzące do uszkodzeń łożysk tocznych?

38

Zadanie

Łożysko wałeczkowe walcowe, podpierające czop końcowy
wałka ma nośność ruchową równą C. Siła zastępcza P,
obciążająca to łożysko, jest równa jego nośności ruchowej.
Należy porównać prawdopodobieństwa nieuszkodzenia tego
łożyska w okresie L

wym

= 10

6

obrotów dla dwóch następujących

przypadków:
• przedstawionego powyżej,
• gdy siła zastępcza jest równa 80% nośności ruchowej.
W obu przypadkach łożysko i warunki jego pracy są zbliżone
(współczynnik a

w

warunków pracy jest w przybliżeniu taki sam).

Wyniki zilustrować na wykresach funkcji niezawodności łożyska.

39

40

F

L

l

A

B

Wałek pośredni przekładni zębatej podparty jest dwoma jednakowymi łożyskami
kulkowymi poprzecznymi o nośności dynamicznej każdego z nich C = 5,85 kN.
Wałek jest obciążony siłą poprzeczną F = 4 kN wynikającą z oddziaływania
zamocowanego na nim koła zębatego. Koło może być usytuowane w stosunku do
wałka w dwóch wariantach:
1. l = 0,25 L,
2. l = 0,50 L.
W obu wariantach warunki pracy przyjąć jako zbliżone (a

w

≈ 5) . Należy:

- dla obu tych wariant

ów narysować w jednym układzie współrzędnych

wykresy funkcji niezawodności zespołu łożysk podpierających wałek (przez co
najmniej trzy punkty),
- wskazać wariant lepszy ze względu na niezawodność podparcia wałka.

Zadanie