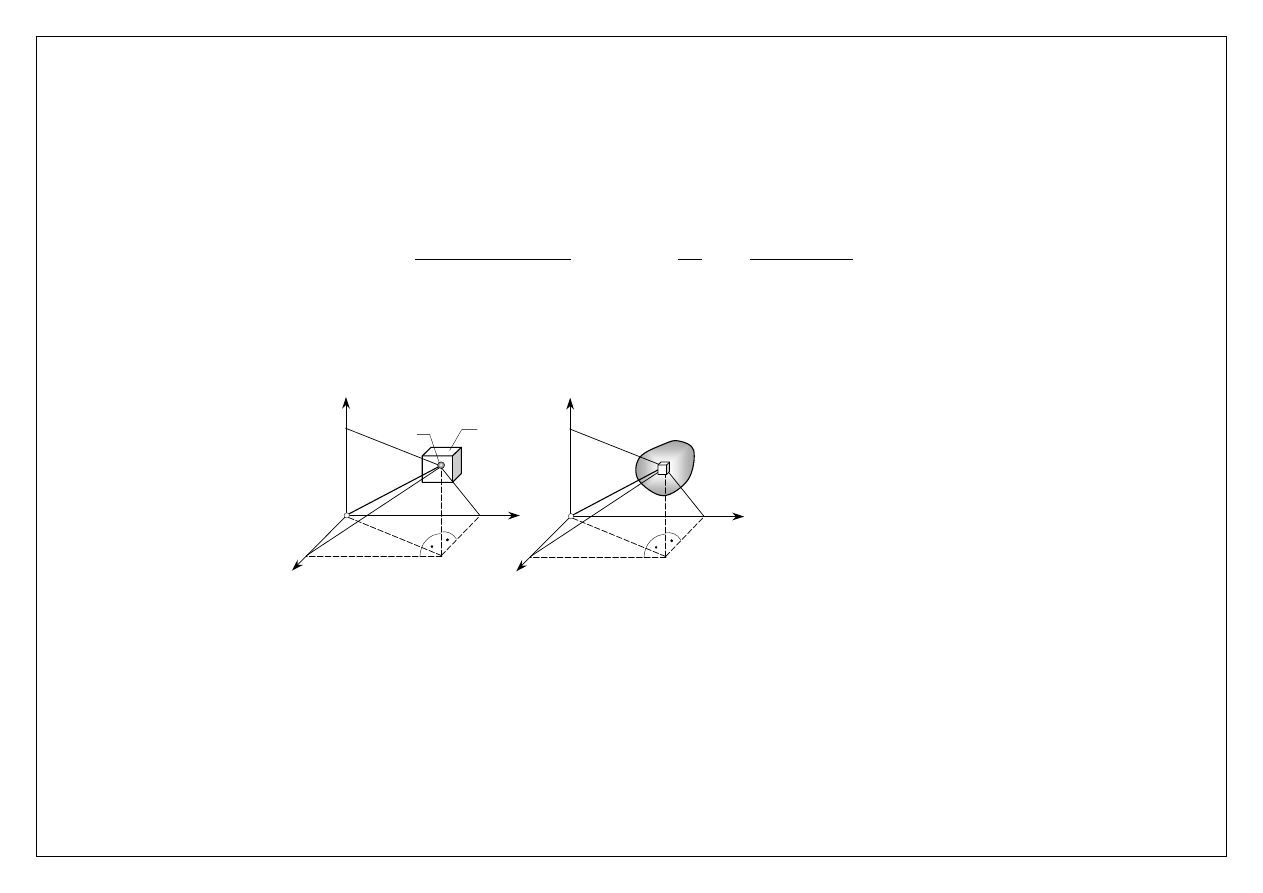
Prof. Edmund Wittbrodt
Geometria mas
Masowe momenty bezwładności
Rozkład masy ciała (układu ciał) względem punktu (bieguna), osi lub płaszczyzny charakteryzują masowe momenty
bezwładności.
Masowy moment bezwładności względem punktu, osi lub płaszczyzny jest sumą (całką) iloczynów mas przez kwadraty ich
odległości od punktu, osi lub płaszczyzny.
Odległości od punktu, osi i płaszczyzny: a) środka masy
bryły o masie m
i
i o skończonych wymiarach, b) masy
elementarnej dm bryły o masie rozłożonej
z
dm
O
x
y
b)
ρ
z
ρ
y
ρ
x
r
z
i
x
y
y
z
m
i
O
x
a)
ρ
zi
ρ
yi
ρ
xi
r
i
z
i
x
i
y
i
C
i

Prof. Edmund Wittbrodt
Biegunowy moment bezwładności obliczamy z zależności
2
1
=
=
∑
n
O
i
i
i
J
r m
lub
( )
2
=
∫
O
m
J
r dm
,
(4.51)
natomiast osiowe momenty bezwładności:
2
1
ρ
=
=
∑
n
x
xi
i
i
J
m
lub
( )
2
ρ
=
∫
x
x
m
J
dm
,
2
1
ρ
=
=
∑
n
y
yi
i
i
J
m
lub
( )
2
ρ
=
∫
y
y
m
J
dm
,
(4.52)
2
1
ρ
=
=
∑
n
z
zi
i
i
J
m
lub
( )
2
ρ
=
∫
z
z
m
J
dm
,
zaś płaszczyznowe momenty bezwładności:
2
1
=
=
∑
n
xy
i
i
i
J
z m
lub
( )
2
=
∫
xy
m
J
z dm
,
2
1
=
=
∑
n
yz
i
i
i
J
x m
lub
( )
2
=
∫
yz
m
J
x dm
,
(4.53)
2
1
=
=
∑
n
xz
i
i
i
J
y m
lub
( )
2
=
∫
xz
m
J
y dm
.

Prof. Edmund Wittbrodt
Ponadto rozkład mas charakteryzują momenty iloczynowe zwane momentami dewiacyjnymi lub momentami zboczenia.
Określa się je z zależności:
1
=
=
∑
n
xy
i i
i
i
D
x y m
lub
( )
=
∫
xy
m
D
xydm
,
1
=
=
∑
n
yz
i i
i
i
D
y z m
lub
( )
=
∫
yz
m
D
yzdm
,
(4.54)
1
=
=
∑
n
xz
i i
i
i
D
x z m
lub
( )
=
∫
xz
m
D
xzdm
.
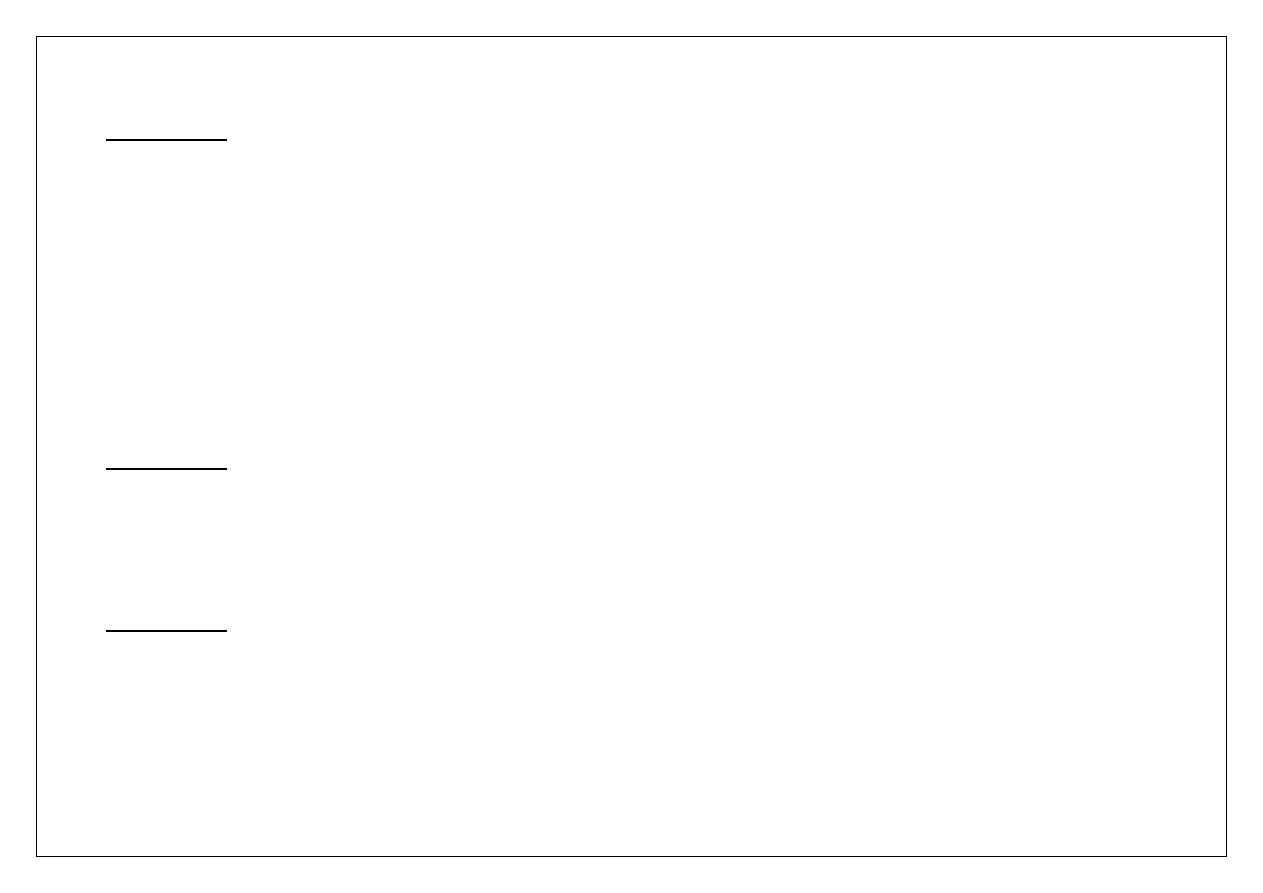
Prof. Edmund Wittbrodt
Twierdzenie 1
Masowy moment bezwładności względem osi równy jest sumie masowych momentów bezwładności względem dwóch
wzajemnie prostopadłych płaszczyzn tworzących tę oś
x
xy
xz
J
J
J
=
+
.
(4.55)
Dowód:
2
2
2
2
2
1
1
1
1
(
)
ρ
=
=
=
=
=
=
+
=
+
=
+
∑
∑
∑
∑
n
n
n
n
x
xi
i
i
i
i
i
i
i
i
xy
xz
i
i
i
i
J
m
z
y m
z m
y m
J
J
.
Twierdzenie 2
Biegunowy, masowy moment bezwładności jest równy sumie masowych momentów bezwładności względem trzech
wzajemnie prostopadłych płaszczyzn przechodzących przez biegun
O
xy
yz
xz
J
J
J
J
=
+
+
.
(4.56)
Twierdzenie 3
Podwójny biegunowy, masowy moment bezwładności bryły jest równy sumie masowych momentów bezwładności
względem trzech, wzajemnie prostopadłych osi, przechodzących przez biegun
2
O
x
y
z
J
J
J
J
=
+
+
.
(4.57)

Prof. Edmund Wittbrodt
Masowe momenty bezwładności przy transformacji układu współrzędnych
Translacja układu. Jeżeli osie układu odniesienia x,y,z są przesunięte równolegle względem osi x
1
,y
1
,z
1
przechodzących
przez środek masy bryły, wówczas słuszne są zależności:
Układ współrzędnych x, y, z
i przesunięty równolegle względem niego układ współrzędnych x
1
, y
1
, z
1
2
x
xC
x
J
J
ma
=
+
,
2
y
yC
y
J
J
ma
=
+
,
(4.58)
2
z
zC
z
J
J
ma
=
+
,
oraz:
xy
xyC
C
C
D
D
mx y
=
+
,
yz
yzC
C C
D
D
my z
=
+
,
(4.59)
zx
zxC
C C
D
D
mz x
=
+
.
z
dm
x
y
C(x
C
, y
C
, z
C
)
a
x
y
1
z
1
x
1
x
C
a
z
y
C
a
y
z
C
y
z
x
y
1
z
1
x
1
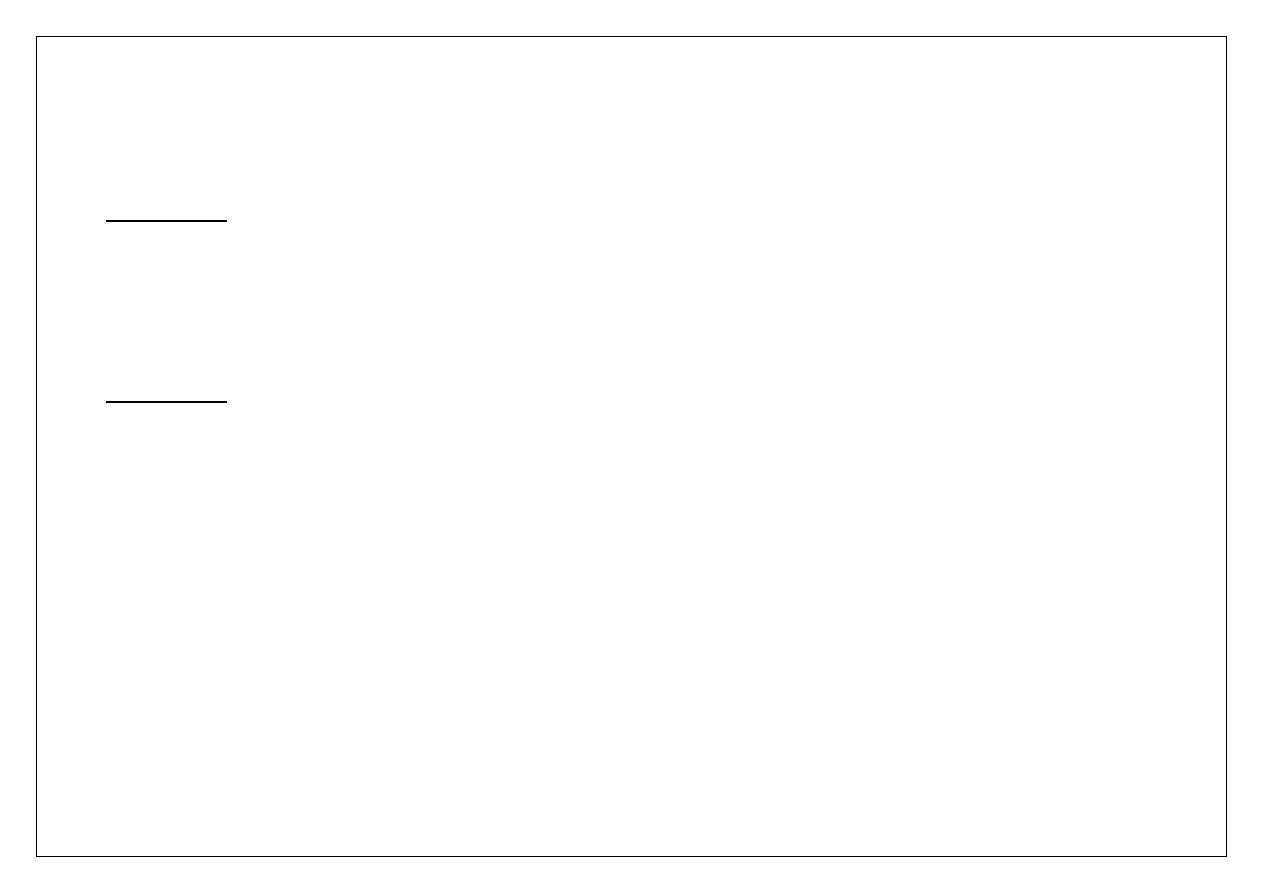
Prof. Edmund Wittbrodt
Twierdzenia Steinera:
Twierdzenie 1
Masowy moment bezwładności względem osi równoległej do osi przechodzącej przez środek masy bryły jest równy
masowemu momentowi bezwładności względem osi przechodzącej przez środek masy powiększonemu o iloczyn masy
i kwadratu odległości pomiędzy osiami.
Twierdzenie 2
Masowy, dewiacyjny moment bezwładności względem układu osi równoległych do osi przechodzących przez środek
masy bryły jest równy masowemu, dewiacyjnemu momentowi bezwładności względem osi przechodzących przez
środek masy powiększonemu o iloczyn masy przez odpowiednie odległości pomiędzy płaszczyznami.
Dowód twierdzenia 1:
( )
2
2
1
1
[(
)
(
) ]
x
C
C
m
J
y
y
z
z
dm
=
+
+
+
=
∫
( )
( )
( )
( )
2
2
2
2
2
1
1
1
1
(
)
(
)
2
2
=
+
+
+
+
+
=
+
∫
∫
∫
∫
C
C
C
C
xC
x
m
m
m
m
y
z
dm
y
z
dm
y
y dm
z
z dm
J
ma
,
gdyż:
( )
1
0
m
y dm
=
∫
oraz
( )
1
0
m
z dm
=
∫
, ze względu na to, że środek masy C ma w układzie x
1
,y
1
,z
1
współrzędne zerowe.

Prof. Edmund Wittbrodt
Rotacja układu. Moment bezwładności względem dowolnej prostej u, wychodzącej z bieguna O, gdy dane są momenty
bezwładności względem układu x,y,z, obliczamy
Dowolna półprosta u określona za pomocą kątów
α
x
,
α
y
,
α
z
cos
cos
cos
cos
cos
cos
T
x
xy
xz
x
x
u
y
xy
y
yz
y
z
xz
yz
z
z
J
D
D
J
D
J
D
D
D
J
α
α
α
α
α
α
−
−
=
⋅ −
−
⋅
−
−
.
(4.60)
Korzystając z zależności (4.60) możemy obliczyć momenty bezwładności względem osi x
1
, y
1
układu płaskiego, obróconego
względem osi x, y o kąt
α
. Są one równe
J
1
= T
⋅⋅⋅⋅J,
(4.61)
gdzie:
1
1
1
1 1
col(
,
,
)
x
y
x y
J
J
D
=
J
,
col(
,
,
)
x
y
xy
J
J
D
=
J
,
zaś
2
2
2
2
cos
sin
sin 2
sin
cos
sin 2
sin
cos
sin
cos
cos 2
α
α
α
α
α
α
α
α
α
α
α
−
=
−
T
– macierz rotacji.
Płaski układ współrzędnych x, y i obrócony względem niego układ współrzędnych x
1
, y
1
O
x
y
z
α
x
α
y
α
z
u
O
y
1
x
y
x
α
dm
x
1
y
x
1
y
1
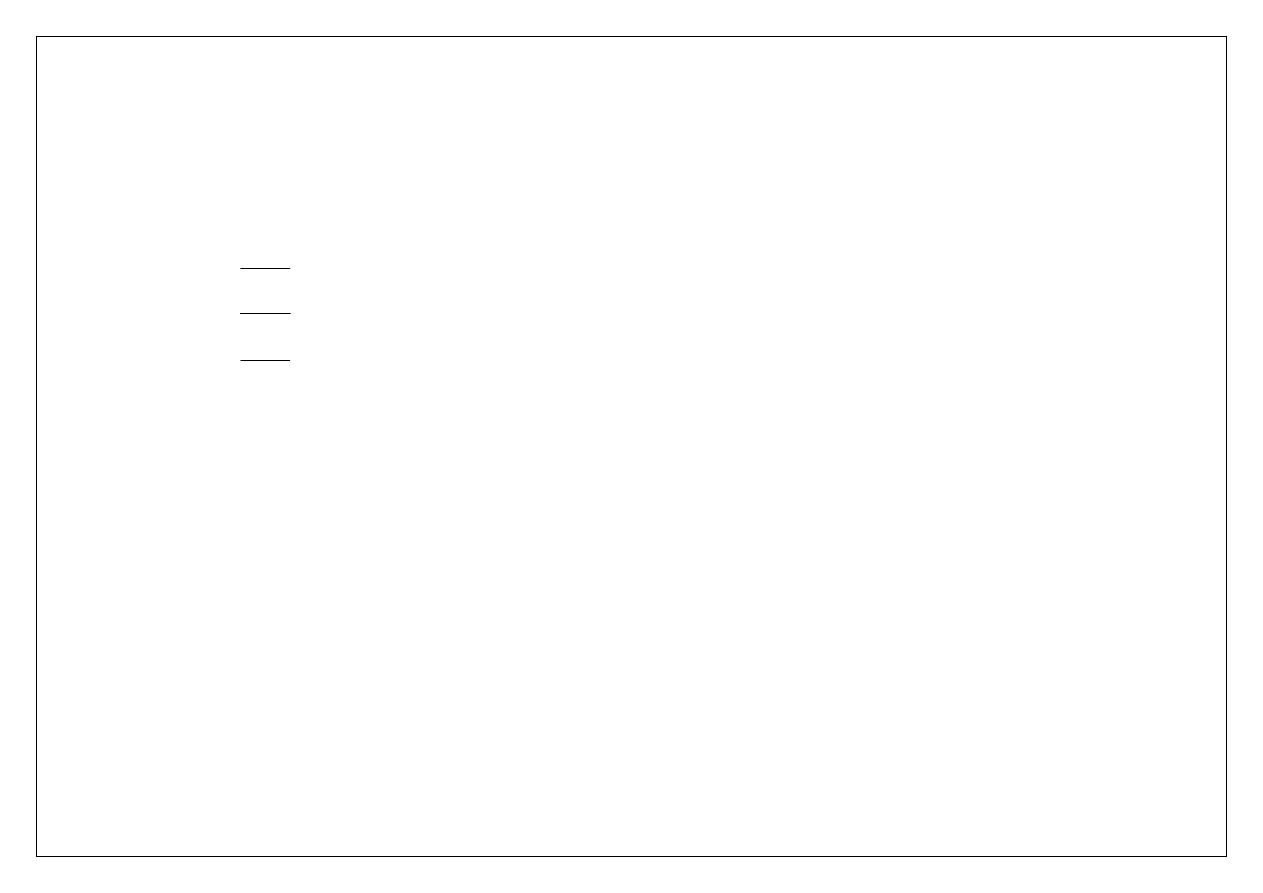
Prof. Edmund Wittbrodt
Główne i centralne masowe momenty bezwładności
Dla określenia takiej prostej u, dla której masowy moment bezwładności J
u
osiąga wartość ekstremalną oraz dla określenia
tej wartości ekstremalnej należy obliczyć różniczkę dJ
u
(względem:
α
x
,
α
y
,
α
z
) i przyrównać ją do zera. Zatem
cos
cos
cos
cos
cos
cos
u
x
x
xy
xz
x
u
u
xy
y
yz
y
y
xz
yz
z
z
u
z
J
J
J
D
D
J
dJ
D
J
J
D
D
D
J
J
J
α
α
α
α
α
α
∂
∂
−
−
−
∂
=
= −
−
−
⋅
=
∂
−
−
−
∂
∂
0
,
(4.62)
gdzie
J
– wartość ekstremalna momentu bezwładności.
Równanie (4.62) ma rozwiązania nietrywialne wtedy i tylko wtedy, gdy wyznacznik z macierzy zawierającej wartości
momentów bezwładności jest równy zero, tj.
det
(
)(
)(
)
x
xy
xz
xy
y
yz
x
y
z
xy
yz
xz
xz
xz
yz
xz
yz
z
J
J
D
D
D
J
J
D
J
J J
J J
J
D D D
D D D
D
D
J
J
−
−
−
−
−
−
=
−
−
−
−
−
−
−
−
−
2
2
2
(
)
(
)
(
)
0
y
xz
z
xy
x
yz
J
J D
J
J D
J
J D
−
−
−
−
−
−
=
.
(4.63)
Z rozwiązania (4.63) otrzymamy trzy pierwiastki J
′, J″, J′′′, które są głównymi momentami bezwładności. Mają one wartości
maksymalną, minimalną i pośrednią. Położenia prostych odpowiadającym momentom głównym obliczamy podstawiając do
(4.62) kolejne wartości: J
′, J″ oraz J′′′, otrzymując:
,
,
x
y
z
α
α
α
′
′
′
;
,
,
x
y
z
α
α
α
′′
′′
′′
;
,
,
x
y
z
α
α
α
′′′
′′′
′′′
.
Prof. Edmund Wittbrodt
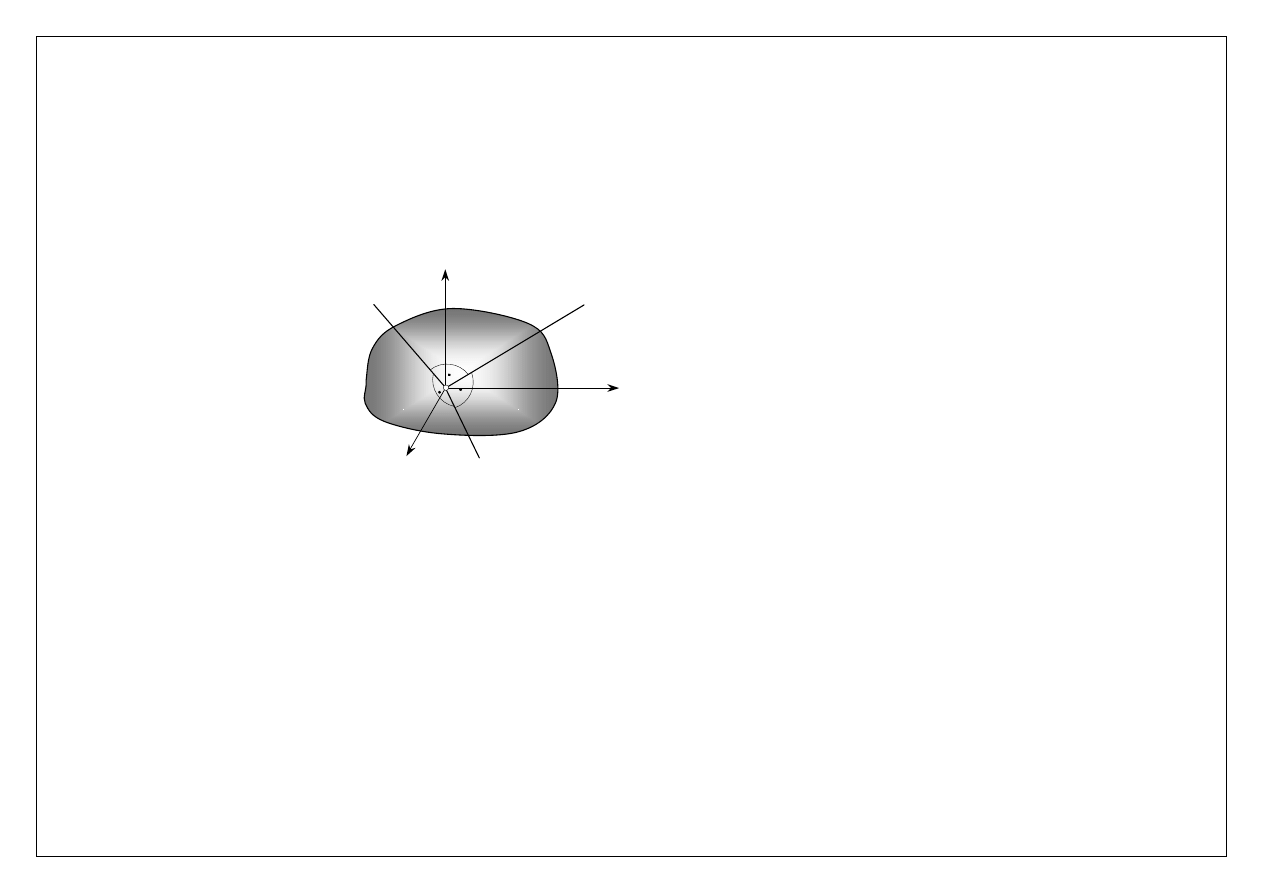
Jeżeli rozważany układ osi x, y, z ma swój początek w środku masy bryły, to momenty J
′, J″ oraz J′′′ nazywamy głównymi,
centralnymi momentami bezwładności
.
Główne, centralne momenty bezwładności
Masowe momenty dewiacyjne względem osi, dla których momenty są głównymi, centralnymi osiami bezwładności są
równe zeru.
Masowe momenty bezwładności są zawsze większe od zera, natomiast masowe momenty dewiacyjne mogą być zarówno
dodatnie jak i ujemne.
C
x
y
z
J’
J’’’
J’’
Prof. Edmund Wittbrodt
=
=
12
2
y
z
ml
I
I
=
x
I
0
m – masa pręta
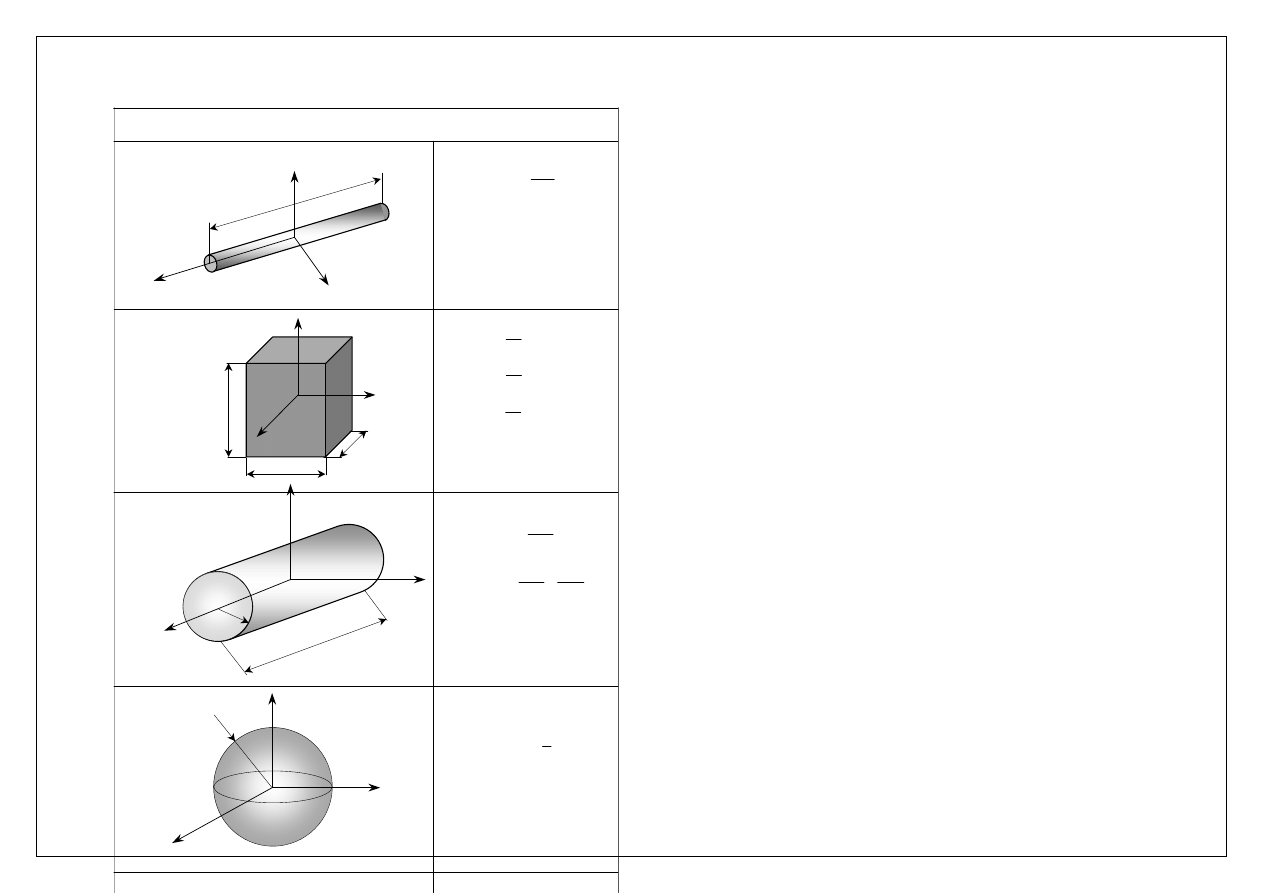
Masowe momenty bezwładności
pręt cienki
z
y
x
C
l
=
+
=
+
=
+
12
12
12
2
2
x
2
2
y
2
2
z
m
I
(a
c )
m
I
(b
c )
m
I
(a
b )
m – masa prostopadłościanu
z
y
x
C
a
b
c
prostopadłościan
=
=
=
2
5
2
x
y
z
I
I
I
mr
m – masa kuli
z
y
x
r
kula
=
2
2
x
mr
I
=
=
+
4
12
2
2
y
z
mr
mh
I
I
m – masa walca
C
z
y
x
h
walec
r
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron