Multipleksery i demultipleksery służą do transmisji informacji.
Są to układy funkcjonalnie odpowiadające przełącznikom z kodowanym wyborem pozycji, za
pomocą dekodera adresu.
W multipleksowanym systemie transmisji informacji, po stronie nadawczej umieszczamy
multiplekser, a po stronie odbiorczej demultiplekser. Adres bazuje na naturalnym kodzie
dwójkowym. Jeżeli linia przesyłowa jest dłuższa od 50 cm to stosujemy pomocnicze układy
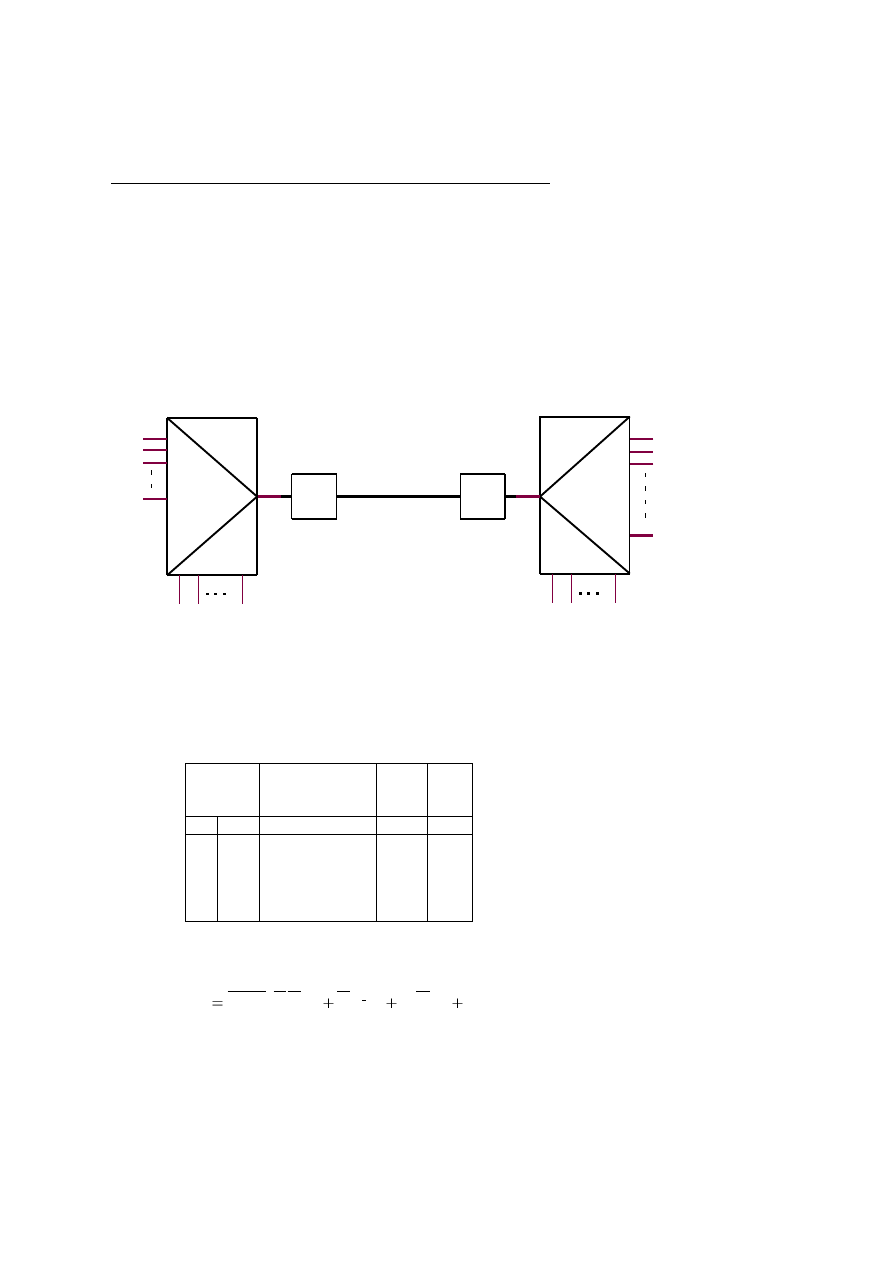
transmisji sygnałów cyfrowych. Linia taka wygląda następująca:
Wejścia
adresow
e
Wejścia
informacyjne
We
Strob
Wy
A
2
A
1
W
1
W
2
W
3
W
4
Str.
Wy
X
0
0
1
1
X
0
1
0
1
X X X X
1 X X X
X 1 1 1
X X 1 X
X X X 1
1
0
0
0
0
0
1
1
1
1
y Strob a a d
a a d
a a d
a a d
(
)
1 0
0
1 0
1
1 0
2
1 0
3
0
1
n
W
W
W
W
W y
1
2
3
n
A
A
A
1
0
3
n
2
n
W y
W
d
1
A
A
A
W y
W y
W y
N a d
O d b
L in ia
p r z e s y ło w a
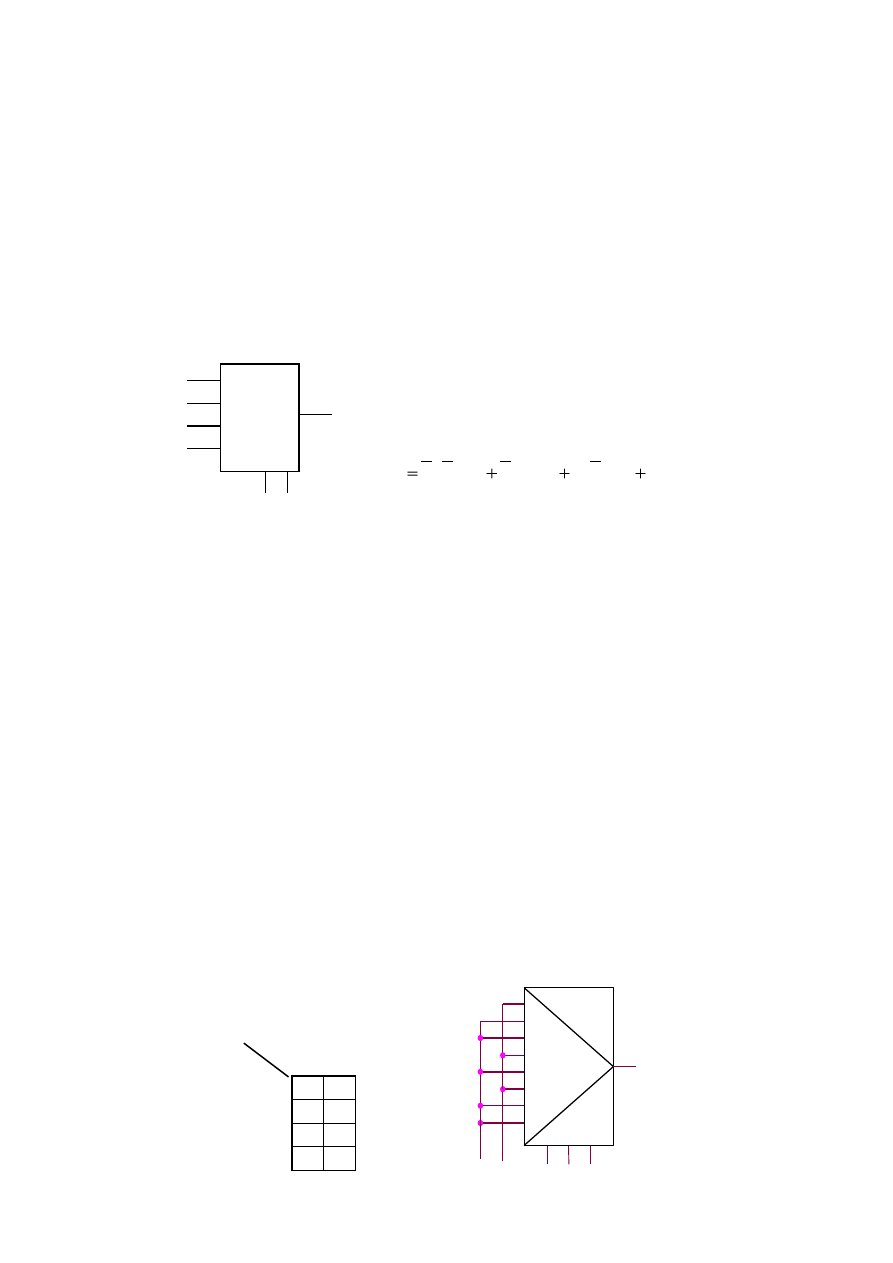
Zastosowanie multiplekserów
do syntezy układów
kombinacyjnych
Podstawowym zastosowaniem multipleksera jest użycie go jako wybieraka, czyli układu
umożliwiającego przesłanie na wyjście wybranego sygnału informacyjnego D
i
, przy czym
wyboru dokonują sygnały na wejściach adresowych A
k
.
Jeżeli jednak napisać funkcję przełączającą realizowaną przez układ
multipleksera
i potraktować wejścia informacyjne D
i
jako współczynniki, którym mogą być przypisane
wartości 0 i 1, to stwierdza się, że układ ten potrafi wygenerować wszystkie składniki
postaci kanonicznej sumy funkcji logicznej.
Na przykład funkcja przełączająca określająca sygnał
wyjściowy multipleksera 4-wejściowego jest następująca:
3
0
1
2
0
1
1
0
1
0
0
1
D
A
A
D
A
A
D
A
A
D
A
A
Y
Przez dobór odpowiednich sygnałów (0 lub 1) na wejściach informacyjnych D
i
można
określić każdą funkcję dwóch zmiennych wejściowych A
1
i A
0
realizowaną przez ten
multiplekser.
Realizacja funkcji przełączających przy pomocy multiplekserów polega więc na
zastosowaniu wejść adresowych A
i
jako właściwych wejść układu, a wejść informacyjnych
multipleksera jako wejść bramkujących, określających typ realizowanej funkcji.
Pierwszym krokiem przy projektowaniu układów logicznych budowanych za
pomocą multiplekserów jest wyrażenie funkcji logicznej w postaci kanonicznej sumy.
Realizacja t
echniczna układu polega na wyeliminowaniu zbędnych składników sygnałami D
i
=0
i pozostawieniu składników wchodzących do postaci kanonicznej sumy przez podanie na
odpowiednie wejścia D
i
sygnałów logicznych 1.
Za pomocą multipleksera z adresem n-bitowym można zrealizować dowolną funkcję
przełączającą n zmiennych. Realizacja funkcji n zmiennych nie wymaga dodatkowych
elementów.
Rozważmy realizację funkcji przełączającej trzech zmiennych A, B, C.
C
Y
BA
0
1
00 0
1
01 1
0
11 0
1
10 1
1
1
A
A
A
D
0
0
D
1
0
W
2
A
3
1
D
D
1
D
2
D
3
0
D
D
Y
C B
A
0
1
2
3
4
5
6
7
A
A A
2
1
0
0
1

Zmie
nne wejściowe są podane na wejścia adresowe multipleksera. Na wejścia informacyjne
podane są sygnały 0 lub 1 , w zależności od tego, jaką wartość przyjmuje realizowana funkcja
dla danej kombinacji sygnałów wejściowych.
Korzyści wynikające ze stosowania multiplekserów do realizacji funkcji przełączających są
najbardziej widoczne, gdy liczba składników jest duża.
Multipleksery można stosować również wtedy, gdy liczba argumentów funkcji
przełączającej przewyższa liczbę wejść adresowych multipleksera. Argumenty dodatkowe, nie
mające odpowiednika w wejściach adresowych multipleksera należy podać na wejścia
informacyjne.
Realizacja tych dodatkowych sygnałów może wymagać zastosowania bramek logicznych.
Jeżeli liczba wejść projektowanego układu logicznego jest o jeden większa od liczby
wejść adresowych multipleksera, to realizacja nie wymaga dodatkowych elementów, z tym że
bramkowanie wejść informacyjnych odbywa się również sygnałem nadmiarowym.
Sposób określania sygnałów bramkujących
Analityczne przedstawienie postaci kanonicznej sumy
(liczba wejść projektowanego układu jest o 1 większa)
Postępowanie przy syntezie jest następujące:
1.
Wybieramy multiplekser o liczbie n-
1 wejść adresowych (mniejszej o 1 od liczby zmiennych zadanej
funkcji przełączającej).
2.
Dla wygody oznaczamy zmienne x zgodnie z pozycjami n-bitowego kodu NB (np. X=x
3
x
2
x
1
x
0
) i
podajemy zmienne x na wejścia adresowe o tych samych indeksach (x
0
na a
0
).
3.
Przedstawiamy funkcję przełączającą taką formą sumacyjną f, której składniki stanowią lub zawierają
il
oczyny pełne (mintermy) w odniesieniu do zmiennych x
n-1
, x
n-2
, ... , x
0
.
4.
Wyznaczamy wejścia
k
d
, do których ma być przyłączony stan 1. Numery k tych wejść są określone
przez równoważniki dziesiętne tych składników formy f, które nie zawierają zmiennej x
n.
5.
Wyznaczamy numery wejść
k
d
, do których ma być przyłączona zmienna
n
x
. Są one określone
przez równoważniki dziesiętne k tych iloczynów, które w danej formie są mnożone z
n
x
.
Do tych wejść, do których już poprzednio przyłączono stan 1, nie przyłącza się zmiennej
n
x
,
ponieważ
x 1 = 1.
6.
Podobnie określa się numery
k
d
, dla zmiennej x
n ,
a na tych wejściach na których wyznaczono stany
n
x
i
n
x
u
stala się stan 1.
7.
Na pozostałych wejściach ustala się stan 0.
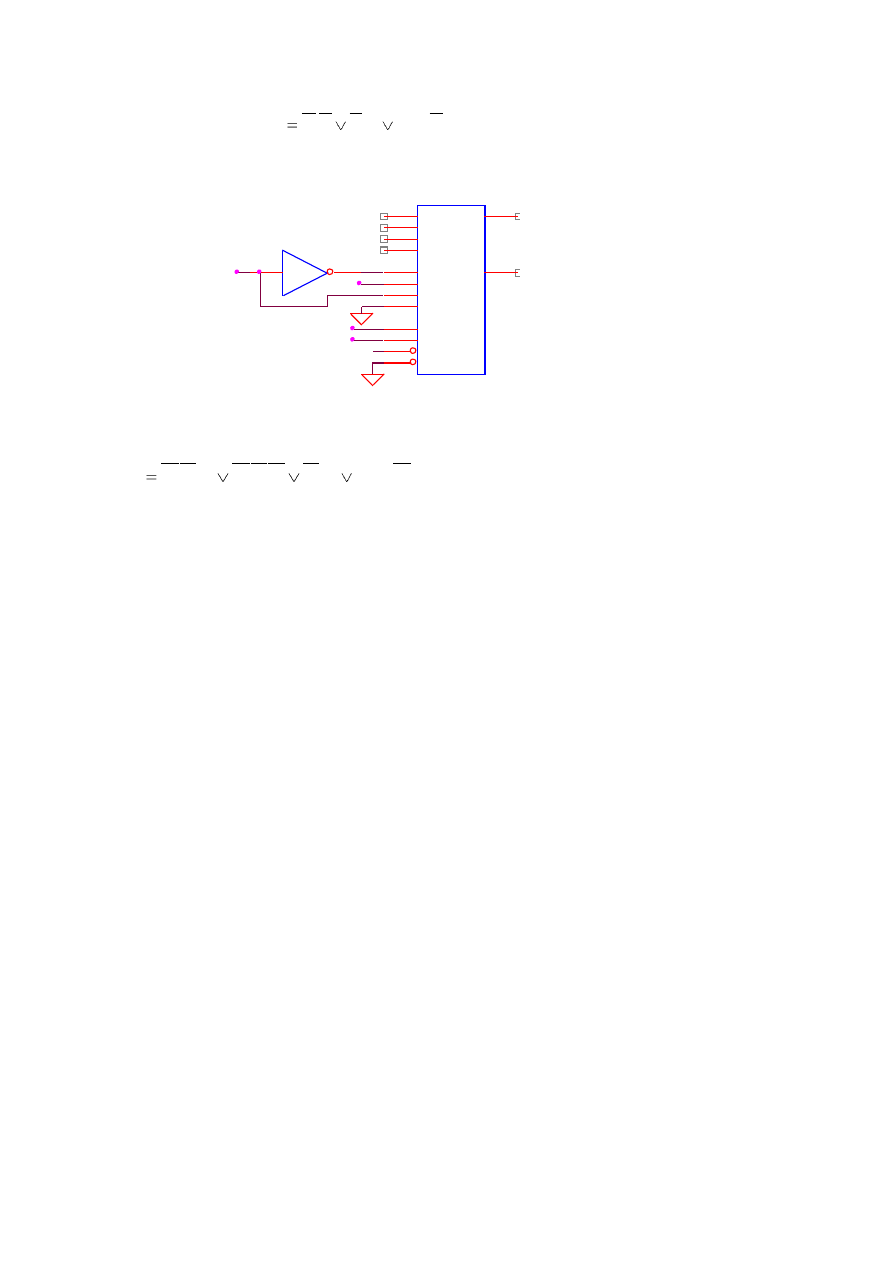
Korzystając z powyższego algorytmu określić połączenia multipleksera realizującego funkcję
przełączającą:
y
x x
x x
x x x
2 1
1 0
2 1 0
1 i 2) wybieramy multiplekser o dwóch wejściach adresowych (1/2 ‘153)
1
x
x
x
2
0
1
74153
1C0
6
1C1
5
1C2
4
1C3
3
2C0
10
2C1
11
2C2
12
2C3
13
A
14
B
2
1G
1
2G
15
1Y
7
2Y
9
7404
1
2
Na wejścia adresowe podajemy zmienne x
0
i x
1
3)
x
x
x
x
x
x
x
x
x
x
x
y
0
1
2
0
1
0
1
2
0
1
2
4) wejście o stanie „1” jest wyznaczone przez trzeci składnik: L(01) = 1;
5)
wejścia zmiennej /x
2
są wyznaczane przez pierwszy i drugi składnik: L(01) = 1 i L(00) = 0,
przy czym we
jście 1 zostało już przyłączone poprzednio do stanu 1;
6)
wejście zmiennej x
2
jest wyznaczone przez czwarty składnik: L(10) = 2;
7)
„pozostałe wejście 3 łączymy ze stanem „0”.
Sposób określania sygnałów bramkujących
Metoda graficzna
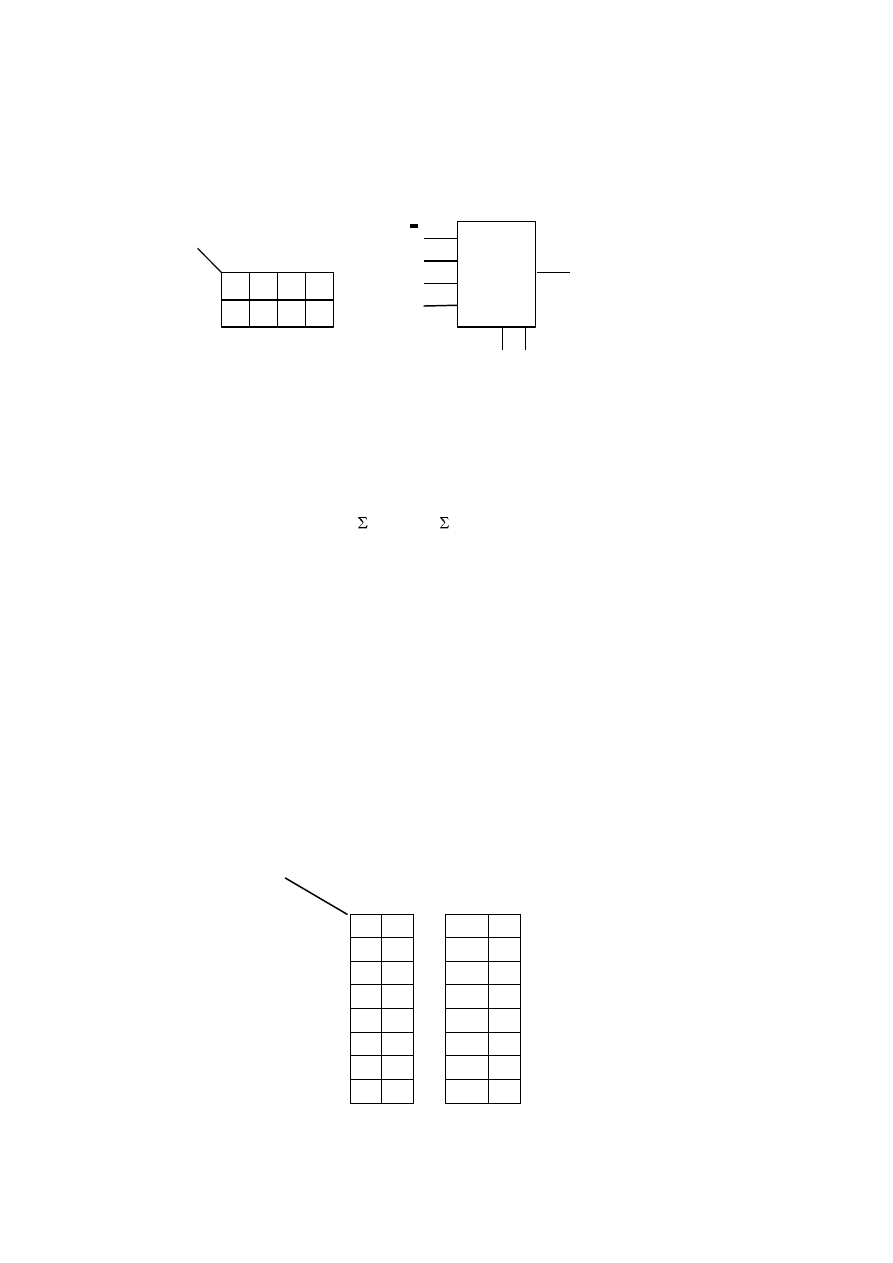
Na poniższym rysunku przedstawiona jest tablica Karnaugha funkcji W, którą należy
zrealizować przy pomocy 4 - wejściowego multipleksera.
1
0
0
0 0
0
1
0 1
1
0
1 1 1 0
1
1
0
B
1
0
A A
D
0
D
1
D
2
D
3
B
B
A
1
A
0
W
0
1
W
0
1
3
2
A
A
1
0
Ponieważ funkcja jest 3 - argumentowa, a multiplekser posiada dwa wejścia adresowe, należy
określić sygnały bramkujące wejścia informacyjne multipleksera z uwzględnieniem trzeciego,
nadmiarowego argumentu funkcji.
Przyjmując, że tym dodatkowym argumentem jest zmienna B, rozpatrywaną funkcję można
zapisać w postaci
W = (0,3)
B=0
+ (1,3)
B=1
Na podstawie tego opisu można określić sposób bramkowania wejść multipleksera:
-
Jeżeli stan występuje w obu zbiorach dla B = 0 i B = 1, to na odpowiadające mu
wejścia informacyjne multipleksera należy podać sygnał logiczny 1; w przykładzie D
3
= 1.
-
Jeżeli stan nie występuje w żadnym zbiorze, to na odpowiadające mu wejście należy
podać sygnał logiczny 0; w przykładzie D
2
= 0.
-
Na wejścia bramkujące związane ze stanami występującymi tylko w jednym zbiorze,
należy podać sygnał /B lub B - w zależności od tego, w którym zbiorze one występują;
w przykładzie D
0
= /B, a D
1
= B.
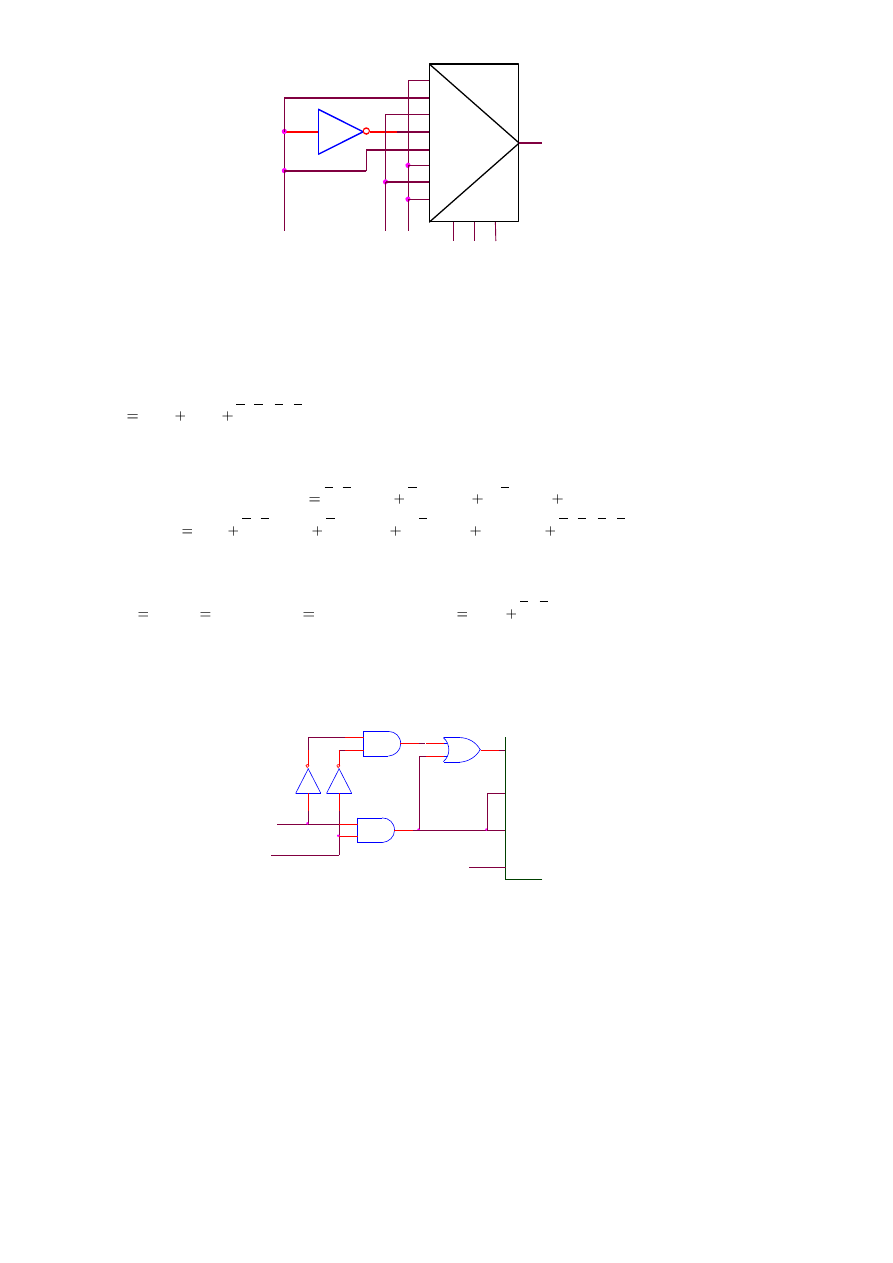
W następnym przykładzie pokazane jest, jak przy użyciu 8 - wejściowego multipleksera można
zrealizować funkcję czterech zmiennych.
Tablica funkcji
D
Y
Y
CBA
0
1
CBA
0
000
0
0
000
0
1
001
0
1
001
D
3
011
1
0
011 /D
2
010
1
1
010
1
6
110
1
1
110
1
7
111
0
0
111
0
5
101
0
0
101
0
4
100
0
1
100
D
0
2
A
7
A
4
2
5
B
0
Y
0
1
1
A
3
A
6
1
C
D
7 4 0 4
1
2
Przy danych wartościach zmiennych A, B, C, funkcja może przyjmować wartości 0, 1, D lub /D;
odpowiedni sygnał jest więc podawany na wejście multipleksera.
Przykład
4
3
2
1
4
3
2
1
x
x
x
x
x
x
x
x
y
Funkcję przełączającą y przekształcamy w sposób przedstawiony poniżej.
Iloczyn pełny wyrażenia
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
czyli
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
Stosując znany algorytm otrzymujemy
1
3
D
4
3
2
x
x
D
4
3
1
x
x
D
4
3
4
3
0
x
x
x
x
D
0
1
2
3
X
3
4
X
1
1
2
3
1
2
3
1
2
3
1
2
1
2
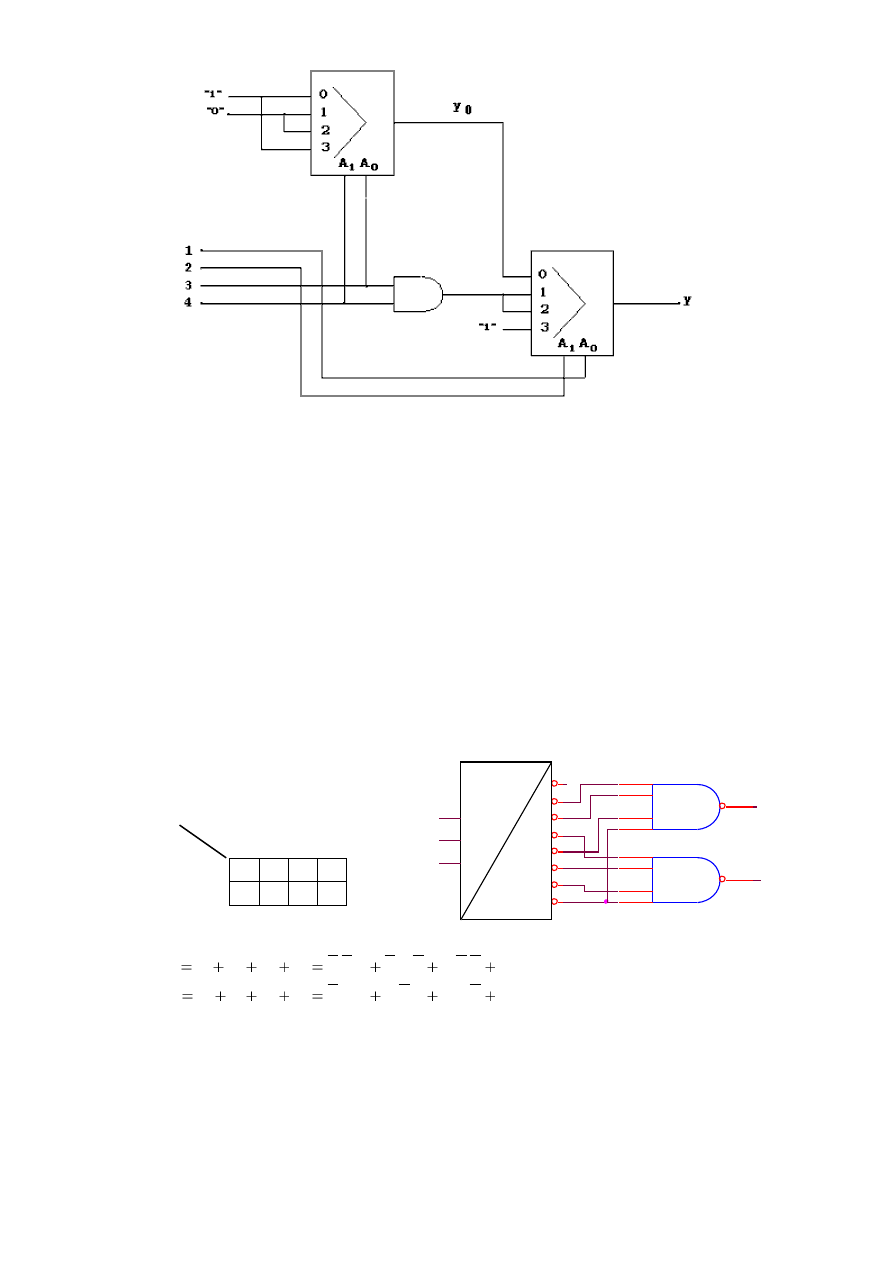
Schemat układu zrealizowanego przy użyciu multiplekserów
Chcąc zrealizować kilka funkcji przełączających tych samych zmiennych (układ
kombinacyjny wielowyjściowy), trzeba użyć osobnego multipleksera dla każdej funkcji.
W tej sytuacji korzystniejszy może być układ zbudowany na bazie dekodera np.
S Y
Y
Y
Y
C B A C B A C B A C B A
1
2
4
7
Z Y
Y
Y
Y
C B A C B A C B A C B A
3
5
6
7
A
5
1
2
1
7
A
0
0
3
A
2
4
6
S
Z
A
B
C
7420
1
2
4
5
6
7420
1
2
4
5
6
BA
C
00 01 11 10
0
00 01 10 01
1
01 10 11 10
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron