RELACJE I ODWZOROWANIA

Definicja 1.

Dwuargumentową relacją określoną w iloczynie kartezjańskim X×Y ,
X≠∅ ∧ Y≠∅ nazywamy uporządkowaną trójkę R = ( X, grR , Y ) , gdzie
grR ⊂ X×Y .
Zbiór X nazywamy naddziedziną relacji.
Zbiór Y nazywamy zapasem relacji.
grR to wykres relacji.

Mówimy, że dwa elementy x ∈ X ∧ y∈Y są w relacji R ⇔ ( x, y ) ∈ grR

Definicja 2.

R = ( X, grR, Y )
Dziedzinę relacji oznaczamy D

R

D

R

: = { x∈X: ∃ y∈Y: xRy }

Przeciwdziedzinę relacji oznaczamy

R :={y∈Y: ∃x∈X: xRy}

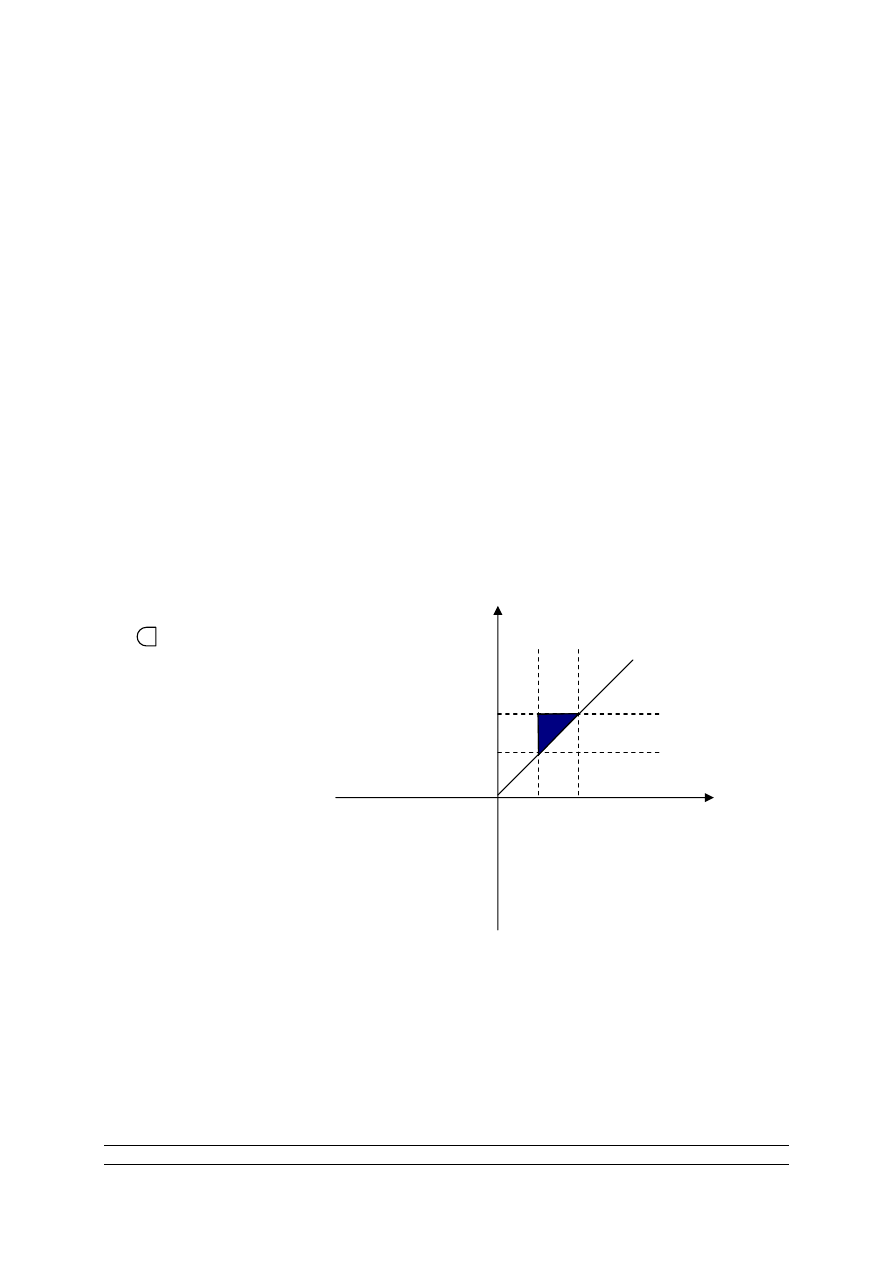
PRZYKŁAD 1.

X=[1,2] , Y=[1,2]
grR = {(x,y): x ≤ y }

1

2

2

1

Definicja 3.

R= (X, grR, Y)

Relacją odwrotną do relacji R nazywamy relację

R

-1

= (Y, grR

-1

, X)

,

gdzie

grR

-1

= {(x,y)∈Y×X: (y,x)∈grR }

Wykład dr Magdaleny Sękowskiej

strona 1 z 9

Część 2 - Relacje i odwzorowania

Definicja 4.
Niech R i S to następujące relacje:

R= (X, grR, U)
S= (U, grS, Y)

Złożeniem relacji R z relacją S nazywamy relację

(

)

(

)

(

)

(

)

{

}

S R :

,gr S R ,

, gdzie

gr S R : ( , )

:

:

u U

X

Y

x y

X Y

xRu uSy

∈

=

=

∈

×

∃

∧

D

D

D

PRZYKŁAD 2.

( ) (

) (

) ( )

( ) (

) (

) (

)

(

) ( ) (

)

( )

( ,

, )

{(2,1), 3,1 , 4,2 , 4,5 , 5,3 }

( ,

, )

{(1,3), 4,1 , 3,6 , 6,8 , 6,7 }

{2,3,4,5}

{1,2,3,5}

( ,

(

), )

(

) { 2,3 , 3,3 , 5,6 }

( ,

(

), )

(

) { 1,1 }

R

R

R

grR

grR
S

grS

grS
D

S R

gr S R

gr S R
R S

gr R S

gr R S

=

=

=

=

=

⊂

=

⊂

=

∧

=

=

∧

=

`

`

`

`

`

`

D

`

D

`

D

D

`

D

`

D

Definicja 5.

R = ( X, grR , Y ) ∧ X=Y ≠ ∅ relacje, czyli

R = ( X, grR , X )

Relacja jest relacją równoważności, gdy spełnione są warunki:

1° Relację nazywamy zwrotną: ⇔ ∀x∈X: xRx
2° Relację nazywamy symetryczną: ⇔ ∀x,y∈X: xRy ⇒ yRx
3° Relację nazywamy przechodnią: ⇔ ∀x,y,z∈X: xRy ∧ yRz ⇒ xRz
Przyjmujemy oznaczenie (X,R)

Definicja 6.

Jeżeli (X,R) jest zbiorem z relacją równoważności i x∈ X to klasą
równoważności elementu x nazywamy zbiór:

[x]:={y∈X: xRy }

Wykład dr Magdaleny Sękowskiej

strona 2 z 9

Część 2 - Relacje i odwzorowania

PRZYKŁAD 3.
R jest relacją równości w zbiorze liczb rzeczywistych.
R=(R,=), xRy ⇔ x=y

1° ∀x∈R x=x ⇒ xRx

2° ∀x,y∈R xRy ⇒ x=y ⇒ y=x ⇒ yRx

3° ∀x,y,z∈R xRy ∧ yRz⇒ x=y ∧ y=z⇒x=z⇒ xRz

PRZYKŁAD 4.

(

)

{

}

ˆˆ

R

||

wektory są zgodnie równolegŁe

Z wasnos

ˆˆ

1°

R

, gdyż

||

2°

R

R

X

AB

AB

CD

AB

CD

AB

CD

ci wektorów

AB

AB

AB

AB

AB

AB

AB

CD

CD

AB

=

⇔

=

∧

=

∧

⇒

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

3°

R

R

R

{ :

R }

W tej relacji klasą równoważnoci

jest wektor swobodny.

AB

CD

CD

EF

AB

CD

AB

CD AB

CD

AB

∧

⇒



 =





JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG

JJJG JJJG

JJJG

JJJG

Definicja 7.

(X,R) – zbiór z relacją równoważności
Zbiór klas równoważności relacji nazywamy zbiorem ilorazowym i

oznaczamy X/

R

:={[x]: x∈X }

TWIERDZENIE 1.
Z: (X,R) – zbiór z relacją równoważności
T:

1° ∀x∈X: [x]≠∅
2° ∀[x], [y]∈X/

R

: [x]≠[y]⇒[x]∩[y]=∅

3° ∀[x]∈ X/

R

: x=X

Wykład dr Magdaleny Sękowskiej

strona 3 z 9

Część 2 - Relacje i odwzorowania

WNIOSEK

Relacja równoważności w zbiorze X dzieli ten zbiór na podzbiory niepuste,
rozłączne, dające w sumie cały zbiór X.

Definicja 8.

(X,R) – zbiór z relacją równoważności

1° Relację nazywamy antysymetryczną: ⇔ ∀x,y∈X: xRy ∧ yRx ⇒ x=y
2° Relacja nazywamy asymetryczną: ⇔ ∀x,y∈X: xRy ⇒ ¬(yRx)
3° Relacja nazywamy spójną: ⇔ ∀x,y∈X: xRy ∨ yRx ∨ x=y

Definicja 9.

A) Jeśli dwuelementowa relacja (X,R) jest zwrotna, antysymetryczna i

przechodnia to nazywamy ją relacją słabego porządku częściowego.
Jeżeli dodatkowo jest spójna to nazywamy ją relacją słabego
porządku totalnego albo liniowego.

B) Jeżeli dwuelementowa relacja (X,R) jest asymetryczna i

przechodnia to nazywamy ją relacją silnego porządku częściowego,
jeżeli ponadto jest spójna to jest to relacja silnego porządku
liniowego lub totalnego.

C) Jeżeli w zbiorze X określona jest którakolwiek z powyższych relacji,

to zbiór nazywamy uporządkowanym

• Częściowo, jeżeli R jest relacją porządku częściowego,

• Totalnie, jeżeli R jest relacją porządku liniowego.

PRZYKŁAD 5.

(

)

(

)

x

x,y

x,y,z

x,y

,

, xRy:

x

y

Sprawdzamy, czy relacja

,

jest relacją porządku.

Z własnosci liczb rzeczywistych

1°

2°

3°

4°

Re

jest relacją słabego porz

R

x

x

x

y

y

x

x

y

x

y

y

z

x

z

x

y

y

x

x

y

lacja

∈

∈

∈

∈

⇔

≤

≤

∀

≤

∀

≤

∧

≤

⇒

=

∀

≤

∧

≤

⇒

≤

∀

≤

∨

≤

∨

=

R

R

R

R

R

R

ądku liniowego.

Wykład dr Magdaleny Sękowskiej

strona 4 z 9

Część 2 - Relacje i odwzorowania

PRZYKŁAD 6.

(

)

∈

∈

∈

⇔

⊂

∀

⊂

∀

⊂

∧

⊂

⇒

=

∀

⊂

∧

⊂

⇒

⊂

E

E

E

A 2

A,B 2

A,B,c 2

2 ,

A R B

A

B

1°

A

A

2°

A

3°

A

Jest to relacja slabego porządku częsciowego.

E

R

B B

A

A

B

B B

C

A

B

Relacja nie jest spójna na przykład dla zbiorów z

B

A

ELEMENTY WYRÓŻNIONE ZBIORU UPORZĄDKOWANEGO

Definicja 10.
(X,R) –zbiór uporządkowany

1° M∈X , M nazywamy elementem największym zbioru
słabouporządkowanego: ⇔ ∀x∈X xRM (dla silnego porządku M≠x)

2° m∈X, m nazywamy elementem najmniejszym zbioru
słabouporządkowanego: ⇔ ∀x∈X mRx (dla silnego porządku m≠x)

TWIERDZENIE 2.

(X,R) – zbiór uporządkowany
Jeżeli w zbiorze X istnieje element największy (najmniejszy) to jest on
jedyny.

Definicja 11.
(X,R) – zbiór uporządkowany

1° ξ∈X ∧ ξ≠x, ξ nazywamy elementem maksymalnym zbioru
słabouporządkowanego: ⇔ ¬(∃x∈X: ξRx) (dla silnego porządku ξ≠x)

2° η∈X ∧ η≠x, η nazywamy elementem minimalnym zbioru
uporządkowanego: ⇔ ¬(∃x∈X: xRη) (dla silnego porządku η≠x)

Wykład dr Magdaleny Sękowskiej

strona 5 z 9

Część 2 - Relacje i odwzorowania

PRZYKŁAD 8.

( )

*

1

2

*

x

1

k

2

k

1

1 2

1 2

1 2

2

y

,| x|y:

:

x

1°

x|x bo x=1x

2° x|y

y|x

x=y

ten jest w formie twierdzenia

Z:

:

:

T: x=y
D:

y=

1

k

k

y

kx

Warunek

y

k x

x

k y

k x

y

k k y

k k

k k

k

x

k y

∈

∈

∈

∈

⇔ ∃

=

⇔

=

∀

∧

⇒

∃

=

∃

=



⇒

=

∧

∈

⇒

= ⇒



=



`

`

`

`

`

`

1

2

3

1

2

1

k

2

k

3

k

2

2 1

3

3

2 1

1

1

3° x|y y|z

x|z

Z:

: y=

:

T:

:

D: z=k
z=

k

elacja nie jest spójna, bo na przykład dla liczb 2

k

x

k x

x

k y

z

k x

y

k k x

z

k x

k k

R

∈

∈

∈

y

= ∧

= ⇒

=

∧

⇒

∃

∃

=

∃

=

=

=

∈

`

`

`

`

*

1

,

3

(2|3)

(3|2)

(2 3)

| | x=y

Jest to więc relacja słabego porządku częściowego.

x y

x y

y x

∈

∧

¬

∧ ¬

∧ ¬

=

′

∀

∪

∪

`

PRZYKŁAD 9.

a) (A, | ) – relacja podzielności w zbiorze A tzn. x,y∈A :xRy ⇔ x|y

Wykład dr Magdaleny Sękowskiej

strona 6 z 9

Część 2 - Relacje i odwzorowania

A={1,2,4,8,16}

m=1 bo 1|2, 1|4, 1|8, 1|16

M=16 bo 1|16 ,2|16, 4|16, 8|16

b) (B, | )

B={1,2,3,4,5,6,7,8}

m=1

η=1

ξ=8
ξ=7
ξ=6
ξ=5

Definicja 12.

(X,R) –zbiór uporządkowany , A⊂X, A≠∅

1° ν∈X ν nazywamy majorantą zbioru uporządkowanego A: ⇔ ∀x∈A: xRν

-1

5

(R,≤) Majorantą jest np. 6

2° ζ∈X, ζ nazywamy minorantą zbioru uporządkowanego A: ⇔ ∀x∈A: ζRx

Definicja 13.

Jeżeli zbiór A posiada co najmniej jedną majorantę, to mówimy, że jest on
ograniczony od góry.

Jeżeli zbiór A posiada co najmniej jedną minorantę, to mówimy, że jest
on ograniczony od dołu.

(X,R), A⊂X, (A,R)
Kresem górnym zbioru A w zbiorze X nazywamy, o ile istnieje, element
najmniejszy zbioru majorant i oznaczamy go supA.

Wykład dr Magdaleny Sękowskiej

strona 7 z 9

Część 2 - Relacje i odwzorowania

(X,R), A⊂X, (A,R)
Kresem dolnym zbioru A w zbiorze X nazywamy, o ile istnieje, element
największy zbioru minorant i oznaczamy go infA.



Definicja 14.
R=(X,grR,Y) - relacja

1° relację nazywamy relacją prawostronnie jednoznaczną (funkcją):⇔
∀x∈X ∧ ∀y

1

,y

2

∈Y: xRy

1

∧ xRy

2

⇒ y

1

=y

2

2° relację nazywamy relacją lewostronnie jednoznaczną (injektywną) :⇔
∀x

1

,x

2

∈X ∧ ∀y∈Y: x

1

Ry ∧ x

2

Ry ⇒ x

1

=x

2

3° relację R nazywamy surjektywną: ⇔

R

=Y

4° relację R nazywamy wszędzie określoną: ⇔ D

R

=X

5° relację wszędzie określoną i prawostronnie jednoznaczną (funkcję
wszędzie określoną) nazywamy odwzorowaniem.

6° odwzorowanie, które jest injektywne i surjektywne nazywamy
odwzorowaniem bijektywnym.

Wykład dr Magdaleny Sękowskiej

strona 8 z 9

Część 2 - Relacje i odwzorowania

Wykład dr Magdaleny Sękowskiej

strona 9 z 9

Część 2 - Relacje i odwzorowania