Matematyka wyrównawcza – ćwiczenia z 20.11.2009r.

1.

Zbadaj własności i narysuj wykres funkcji

a)

݂ሺݔሻ = sin

ଶ

ݔ

- dziedzina, przeciwdziedzina

D:

ܦ = ܴ

Dziedziną funckji trygonometrycznych są liczby rzeczywiste.

ܻ =< 0; 1 >

Przedział wartości

sin ݔ =< −1; 1 >, więc wykres funkcji sin

ଶ

ݔ =< 0; 1 >

- parzystość, nieparzystość

Cosinus jest funkcją parzystą, pozostałe funkcje trygonometryc zne są funkcjami nieparzystymi,

oznacza to że

sinሺ−ݔሻ = −sin ሺݔሻ. W miejsce każdzego ݔ we wzorze funkcji podstawiamy ሺ−ݔሻ i

sprawdzamy czy spełniony jest warunek parzystości

݂ሺ−ݔሻ = ݂ሺݔሻ lub warunek nieparzystości

݂ሺ−ݔሻ = −݂ሺݔሻ

݂ሺ−ݔሻ = sin

ଶ

ሺ−ݔሻ = ሺ− sin ݔሻ^2 = sin

ଶ

ݔ = ݂ሺݔሻ funkcja jest parzysta

- punkty przecięcia z osiami

sin ݔ ma miejsca zerowe ݇ߨ ሺ݌ݎݖݕ ܿݖݕ݉ ݇ ∈ ܥሻ, sin

ଶ

ݔ również zachowuje tę zależność

sin

ଶ

ݔ = 0 ⇔ ݔ = ݇ߨ, ݇ ∈ ܥ

W celu obliczenia punktu przecięcia z osią OY podstawiamy

ݔ = 0

݂ሺ0ሻ = sin

ଶ

0 = 0

- granice na końcach przedziału określoności

Granica

lim

௫→ஶ

sin ݔ nie istnieje, tak samo jest z sin

ଶ

ݔ

lim

௫→ஶ

sin

ଶ

ݔ = lim sin

ଶ

∞ nie istnieje

lim

௫→ିஶ

sin

ଶ

ݔ = lim ݏ݅݊

ଶ

−∞ nie istnieje

- asymptoty

Jakoż, że dziedziną funkcji jest zbiór liczb rzeczywistych, nie istnieje asymptota pionowa.

Asymptota pozioma nie istnieje, gdyż funkcja nie dąży cały czas do jednej wartości.

Brak asymptoty poziomej, pionowej

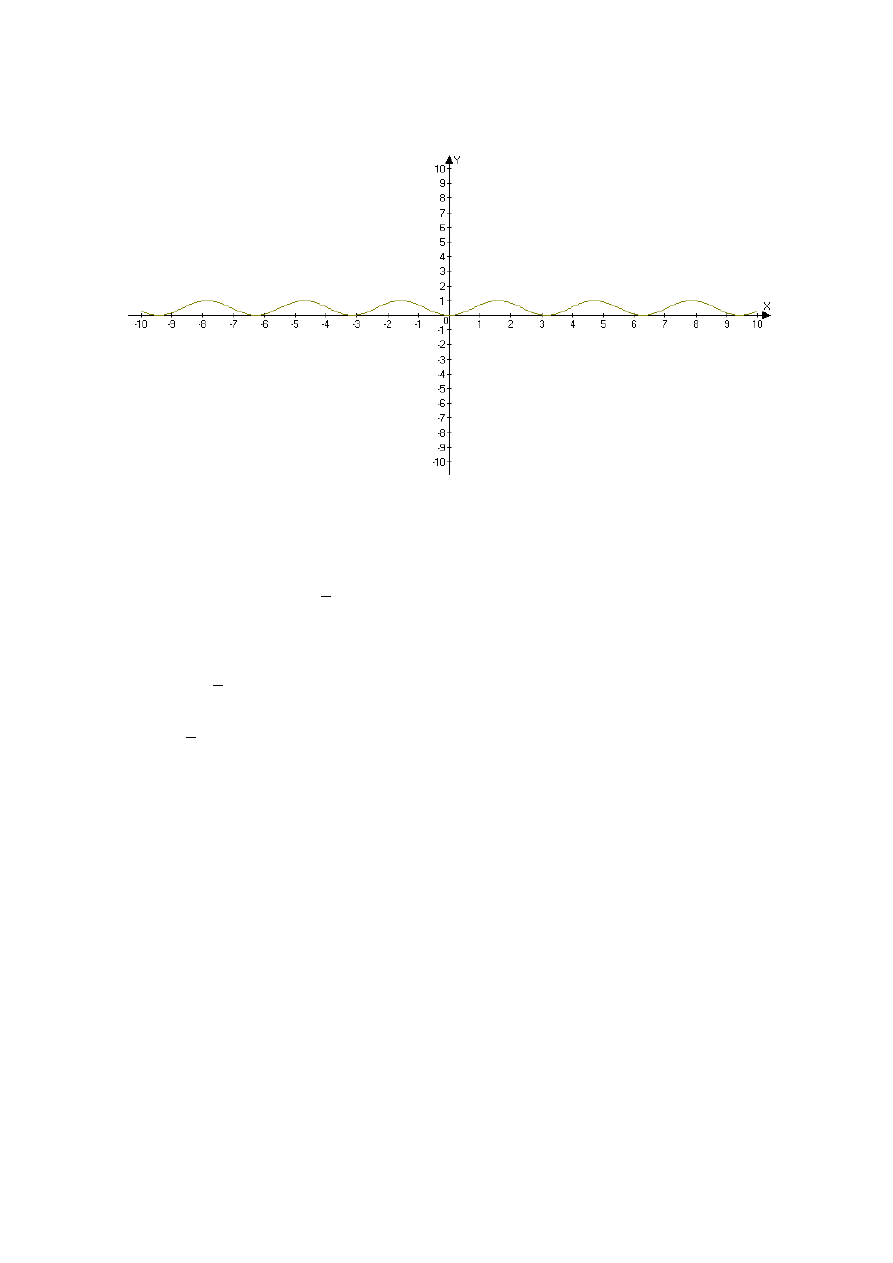
- szkic wykresu

Funkcja okresowa

ܶ = ߨ

- maksimum, minimum

maksimum lokalne ݕ = 1, ݔ =

ߨ

2 + ݇ߨ

minimum lokalne ݕ = 0, x = kπ

݂

↑

݈݀ܽ ݔ ∈ ሺ݇ߨ;

ߨ

2 + ݇ߨሻ

݂

↓

݈݀ܽ ݔ ∈ ሺ

ߨ

2 + ݇ߨ; ݇ߨሻ

b)

݂ሺݔሻ = ݔ ∗ sin ݔ

-dziedzina, przeciwdziedzina

ܦ = ܴ

Z dziedziną tak samo jak przy funkcji poprzedniej.

ܻ = ሺ−∞, ∞ሻ

Jak to zostało wspomniane wcześniej, zbiór wartości funkcji

sin ݔ =< −1; 1 >. Przy mnożeniu tego

przedziału przez

ݔ ∈ ܴ, wzrasta on do ሺ−∞, ∞ሻ

- punkty przecięcia z osiami

0 = ݔ ∗ sin ݔ

ݔ = ݇ߨ

݂ሺ0ሻ = 0

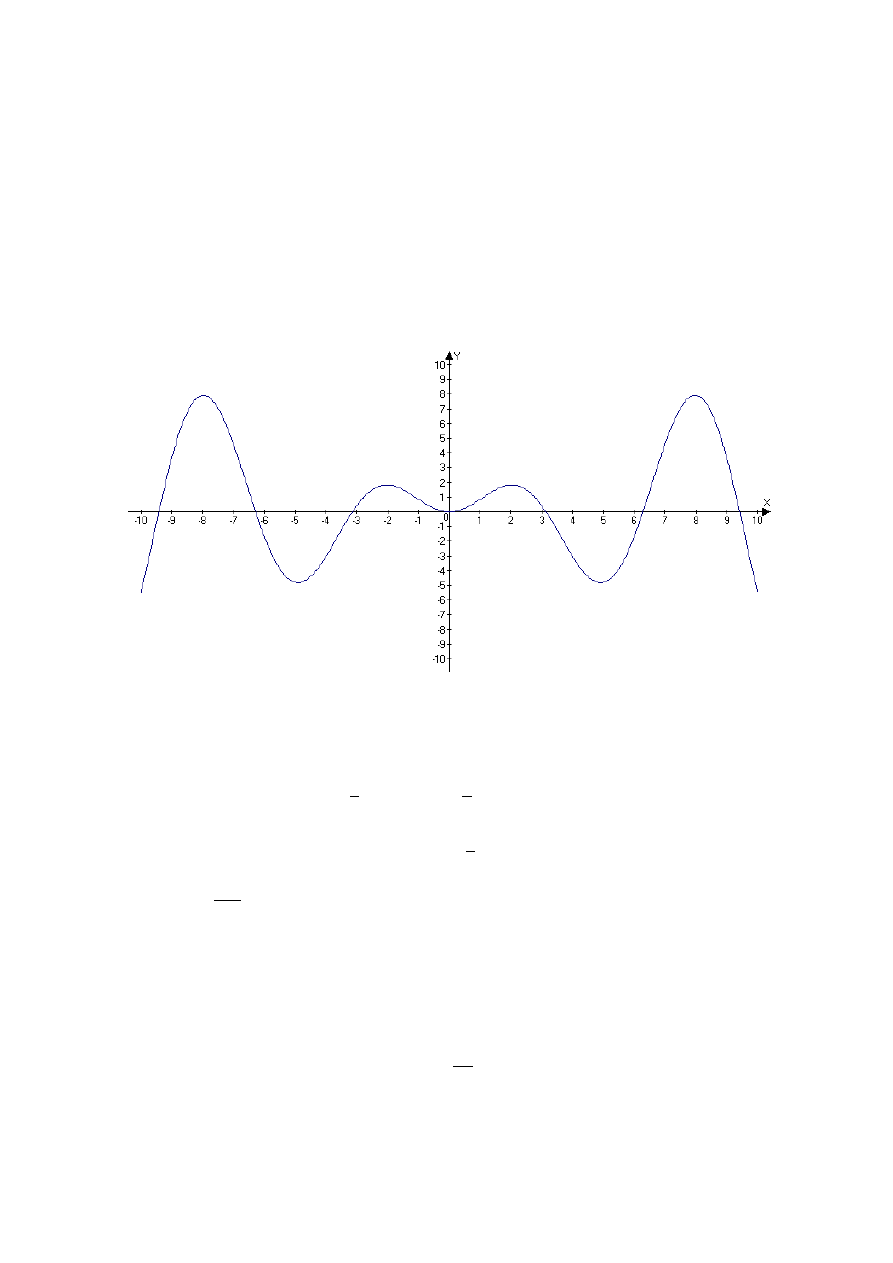
- granice na przedziałach określoności

lim

௫→ஶ

ݔ ∗ sin ݔ nie istnieje

lim

௫→ିஶ

ݔ ∗ sin ݔ nie istnieje

- asymptoty

Brak asymptoty pionowej, poziomej

- szkic wykresu funkcji

݂ okresowa ܶ = 2ߨ

-minimum, maksimum

݉ =

3

2 ߨ + 2݇ߨ, ܯ =

1

2 ߨ + 2݇ߨ, ݇ ∈ ܥ

݂

↑

݈݀ܽ ݔ ∈ ሺ݇ߨ;

1

2 ߨ + ݇ߨሻ

c)

݂ሺݔሻ =

ୱ୧୬ ௫

௫

-dziedzina i przeciwdziedzina

ܦ = ܴ\{0}

Dziedziną są liczby rzeczywiste oprócz 0, gdyż 0 nie może znajdować się w mianowniku.

ܻ =< −

2

3ߨ ; 1ሻ

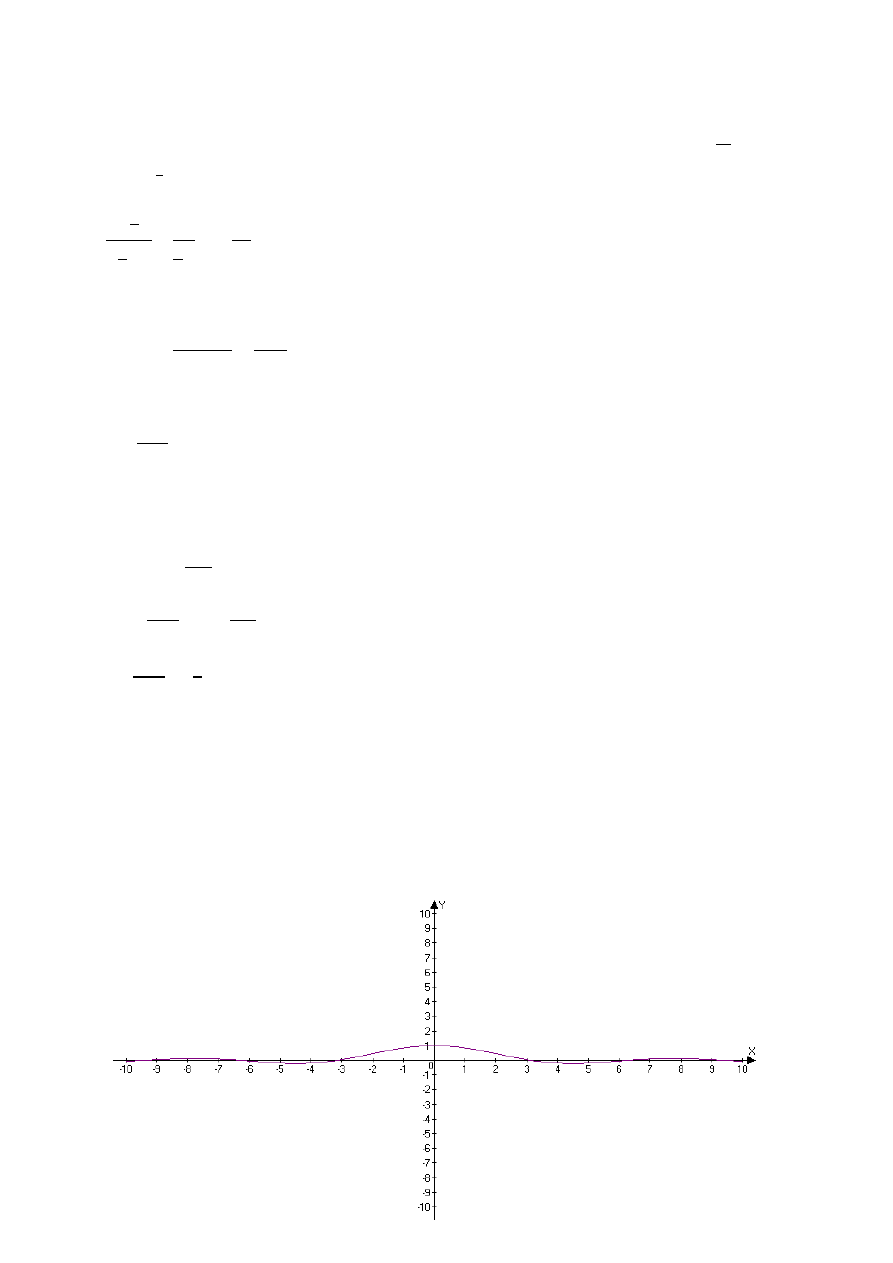
Ogólnie zbiór wartości tej funkcji wyznaczamy później, mając dany wykres. Górną wartością jest

1ሻ,

która występuje w punkcie

ሺ0,0ሻ ∉ ܦ, dlatego przedział otwarty. Wartością dolną jest < −

ଶ

ଷగ

dla

ݔ = ±

ଷ
ଶ

ߨ. Podstawiając do wzoru mamy:

sin 32ߨ

3

2 ߨ

=

−1

3

2 ߨ

= −

2

3ߨ

- parzystość, nieparzystość

݂ሺ−ݔሻ =

sin ሺ−ݔሻ

−ݔ =

sin ݔ

ݔ funkcja jest parzysta

- punkty przecięcia z osiami

0 =

ݏ݅݊ݔ

ݔ ⇔ ሺsin ݔሻሺݔሻ = 0 ⇔ ݔ = ݇ߨ\{0}

݂ሺ0ሻ = 0

- granice na przedziałach określoności

Granica dla

ୱ୧୬ ௫

௫

= 1

lim

௫→±ஶ

sin ݔ

ݔ = lim[

±ܿ

±∞] = 0

lim

௫→଴

ݏ݅݊ݔ

ݔ = ൤

0

0൨ = 1

-asymptoty

Asymptotą poziomą w tym przypadku jest 0. Pomimo faktu, że wykres funkcji wielokrotnie przez 0

przechodzi, w nieskończoności funkcja do niego dąży.

asymptota pozioma ݕ = 0

brak asymptoty pionowej

- szkic wykresu

d)

݂ሺݔሻ = ݏ݅݊ݔ ∗ ܿ݋ݏݔ

- dziedzina, przeciwdziedzina

ܦ = ܴ

Dziedziną zarówno

sin ݔ , cos ݔ = ܴ, więc dziedzina funkcji sin ݔ ∗ cos ݔ = ܴ

ܻ =< −

1

2 ;

1

2 >

- parzystość, nieparzystość

Jak już wspomniałem wcześniej

cos ݔ jest jedyną parzystą funkcją trygonometryczną, a iloczyn funkcji

nieparzystej i parzystej jest funkcją nieparzystą.

݂ሺ−ݔሻ = sinሺ−ݔሻ ∗ cosሺ−ݔሻ = −sin ݔ ∗ cosሺ−ݔሻ funkcja jest nieparzysta

- punkty przecięcia z osiami współrzędnych

cos ሺݔሻ ma miejsca zerowe w ݔ =

గ

ଶ

+ ݇ߨ, sinሺݔሻ w ݔ = ݇ߨ, więc miejsca zerowe funkcji

występowałyby w

ݔ =

గ

ଶ

, ߨ,

ଷగ

ଶ

, 2ߨ, więc widać że występują one co

௞గ

ଶ

0 = sinሺݔሻ ∗ cosሺݔሻ ⇔ sinሺݔሻ = 0 ∨ cosሺݔሻ = 0 ⇔ ݔ = ݇ߨ⋁ݔ =

ߨ

2 + ݇ߨ

ݔ = ݇ ∗

ߨ

2

݂ሺ0ሻ = 0

- granice na przedziałach określoności

lim

௫→±ஶ

sin ݔ cos ݔ nie istnieje

- szkic wykresu

-minimum, maksimum

ܯ =

1

2 , ݔ ∈

ߨ

4 + ݇ߨ

݉ = −

1

2 , ݔ ∈

3

4 ߨ + ݇ߨ

ܶ = ߨ

݂ ↑ ݔ ∈ ሺ

2

3 ߨ + ݇ߨ;

1

3 ߨ + ݇ߨሻ

݂ ↓ ݔ ∈ ሺ

1

3 ߨ + ݇ߨ;

2

3 ߨ + ݇ߨሻ

2.

Sprawdź czy funkcja jest parzysta bądź nieparzysta

a)

݂ሺݔሻ =

ଷ௦௜௡௫

ଵାଶ ୱ୧୬

ర

௫

݂ሺ−ݔሻ =

−3 sin ݔ

1 + 2 sin

ସ

ݔ = −݂ሺݔሻ funkcja jest nieparzysta

b)

݂ሺݔሻ = ݔ

ଷ

∗ ݐ݃ሺ2ݔሻ

݂ሺ−ݔሻ = ሺ−ݔሻ

ଷ

∗ ݐ݃ሺ−2ݔሻ = −ݔ

ଷ

∗ −ݐ݃ሺ2ݔሻ ⇔ ݔ

ଷ

∗ ݐ݃ሺ2ݔሻ = ݂ሺݔሻ funkcja parzysta

Autor:

shenlon