
ZAKŁAD OCHRONY I KSZTAŁTOWANIA
ŚRODOWISKA
WYDZIAŁ INŻYNIERII ŚRODOWISKA
PRZEDMIOT:
HYDROLOGIA
PROWADZĄCY:
Dr inż. Bogdan Ozga-Zieliński
Dla:
Inżynieria Środowiska sem. III

ĆWICZENIA AUDYTORYJNE:
13
TEMAT :
Transformacja przepływu w korycie rzecznym – metoda
Muskingum
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Idea metody Muskingum
Odcinek koryta rzecznego
Przekrój wejściowy z mierzonym
z krokiem czasowym ∆t
dopływem o natężeniu I
j
Przekrój wyjściowy z obliczanym
z krokiem czasowym ∆t
odpływem o natężeniu Q
j
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Idea metody Muskingum
Odcinek koryta rzecznego
Przekrój wejściowy z mierzonym
z krokiem czasowym ∆t
dopływem o natężeniu I
j
Przekrój wyjściowy z obliczanym
z krokiem czasowym ∆t
odpływem o natężeniu Q
j
j
Q
j
I
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Idea metody Muskingum
Odcinek koryta rzecznego
j
Q
j
I
Przepływ ustalony
j
j
I
Q
=
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Idea metody Muskingum
Odcinek koryta rzecznego
j
Q
j
I
Przepływ nieustalony
j
j
I
Q
≠
j
Q
j
j
Q
I
−
j
j
I
Q
i
<
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
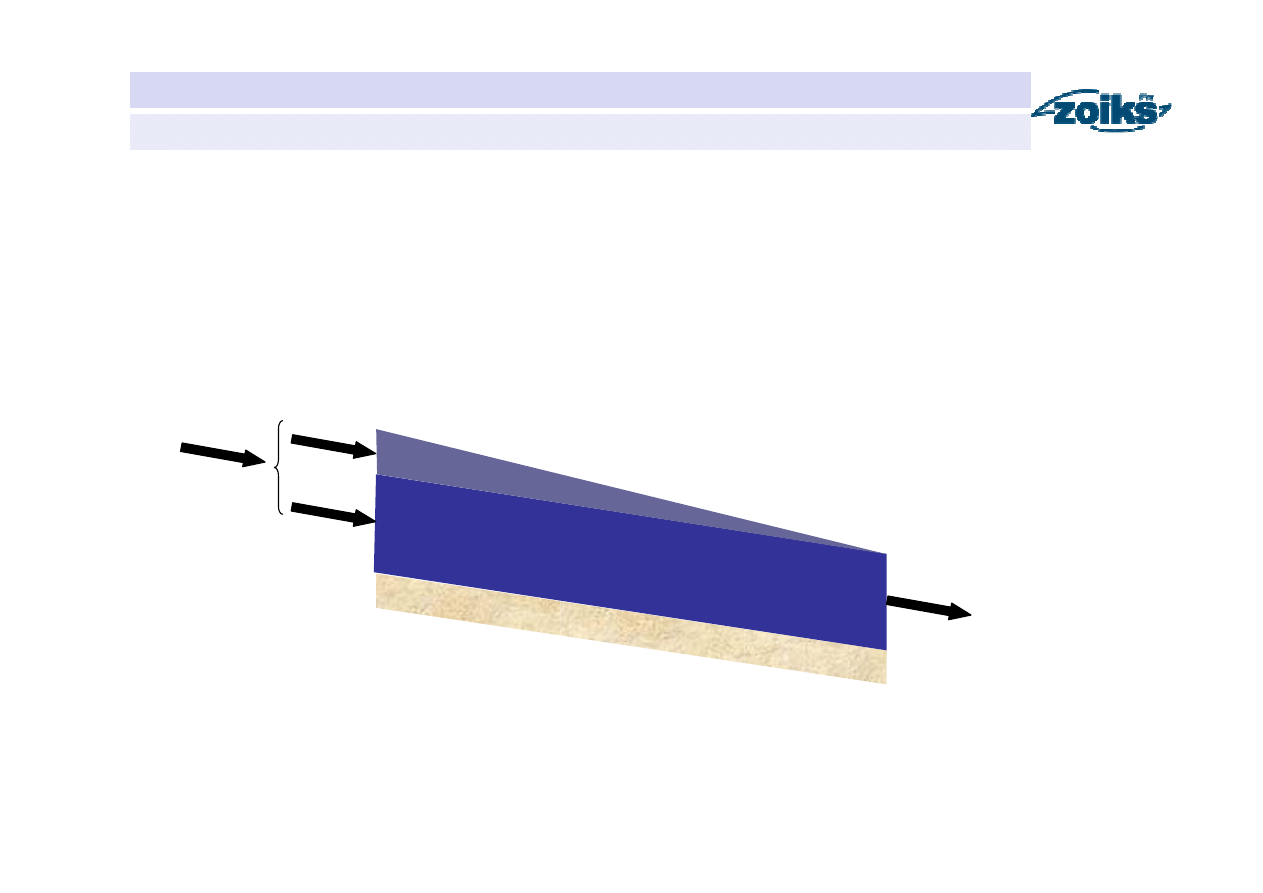
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
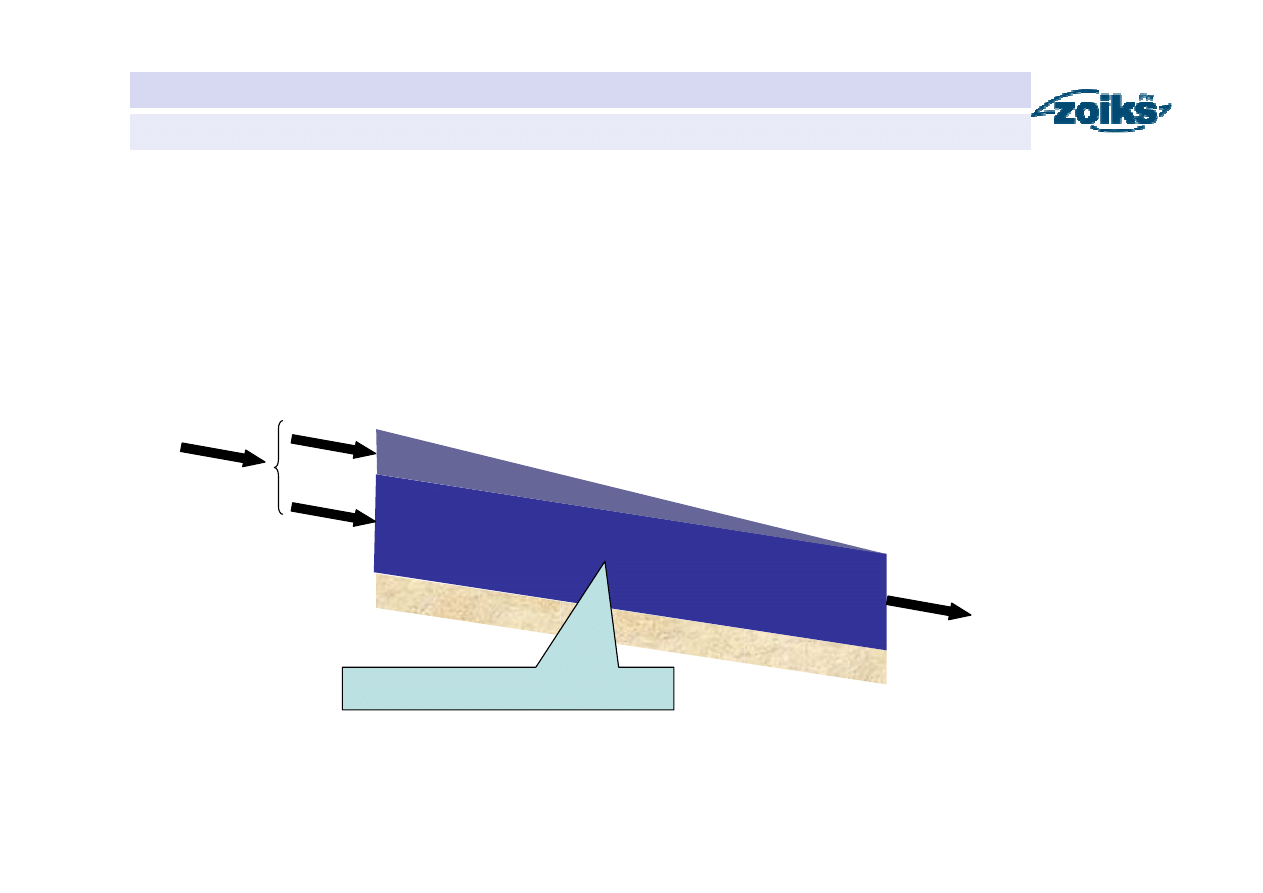
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
Retencja pryzmatyczna S
pr
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
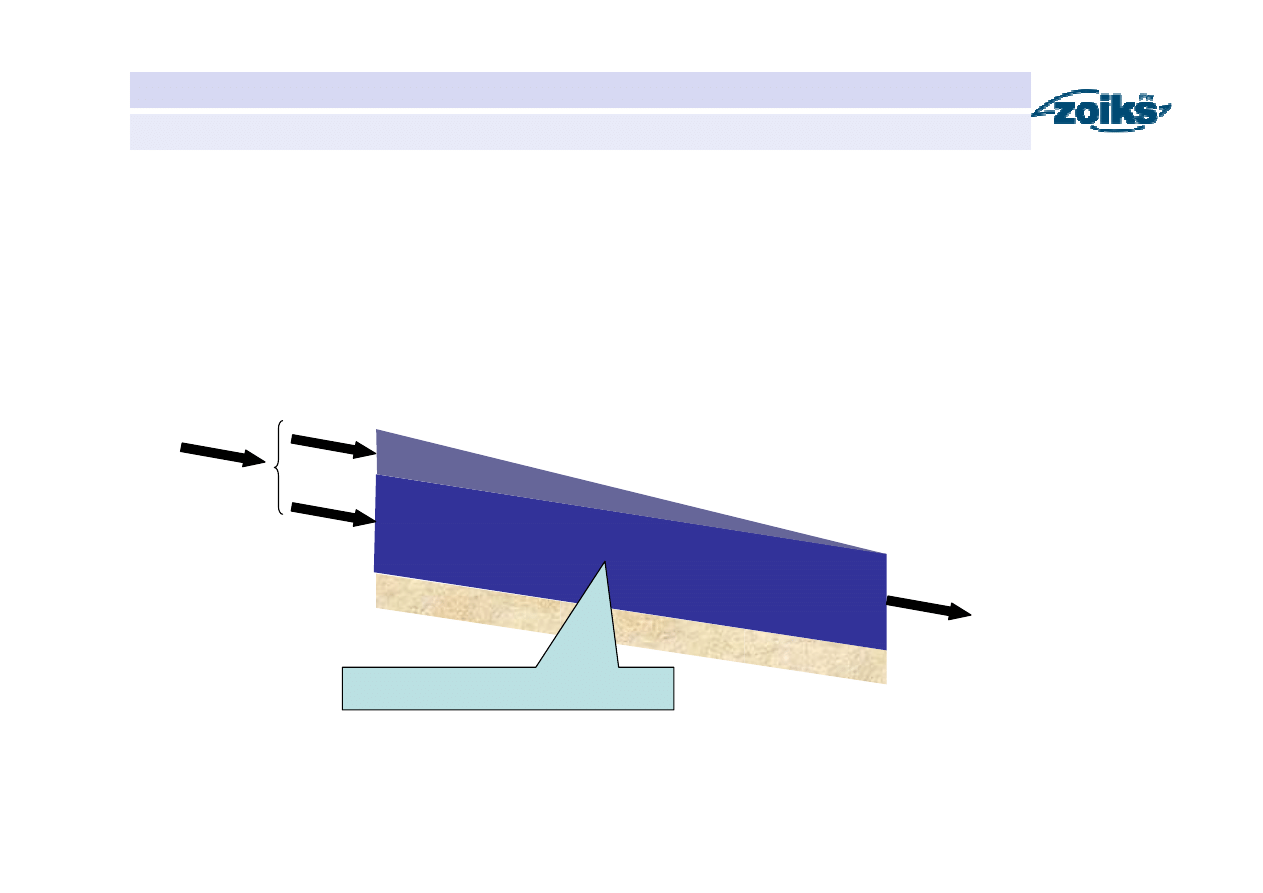
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
Retencja pryzmatyczna S
pr
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
j
kQ
S
=
pr
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
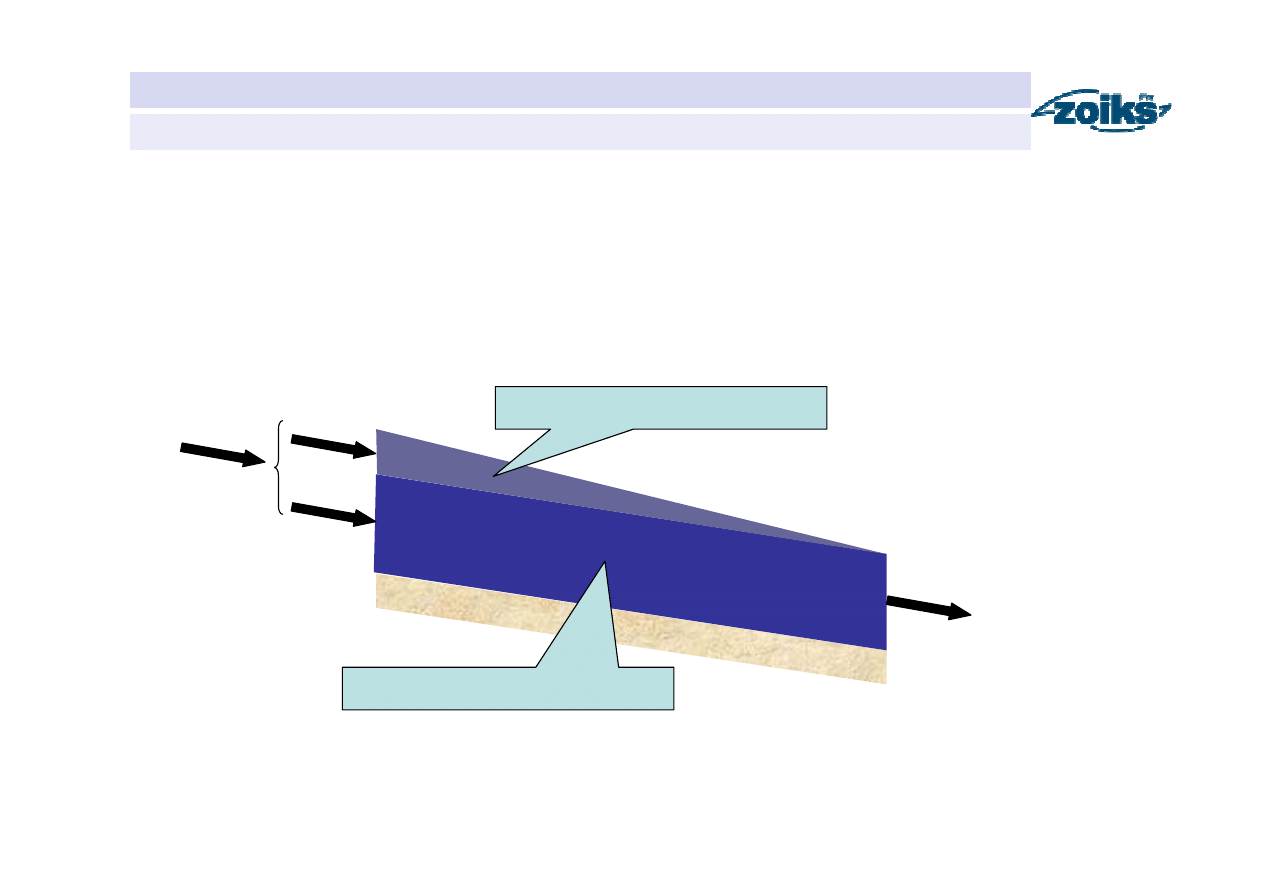
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
Retencja pryzmatyczna S
pr
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
j
kQ
S
=
pr
Retencja klinowa S
kl
x – współczynnik wagowy
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
Retencja pryzmatyczna S
pr
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
j
kQ
S
=
pr
Retencja klinowa S
kl
)
(
kl
j
j
Q
I
kx
S
−
=
x – współczynnik wagowy
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
x – współczynnik wagowy
)
(
j
j
j
j
Q
I
kx
kQ
S
−
+
=
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Retencja odcinka koryta rzecznego
j
Q
j
I
j
Q
j
j
Q
I
−
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
x – współczynnik wagowy
)
(
j
j
j
j
Q
I
kx
kQ
S
−
+
=
]
)
1
(
[
j
j
j
Q
x
xI
k
S
−
+
=

Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Równanie ciągłości
)
(
)
(
d
)
(
d
t
Q
t
I
t
t
S
−
=

Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Równanie ciągłości
)
(
)
(
d
)
(
d
t
Q
t
I
t
t
S
−
=
∆t – krok czasowy pomiaru i obliczania przepływu

Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Równanie ciągłości
)
(
)
(
d
)
(
d
t
Q
t
I
t
t
S
−
=
∆t – krok czasowy pomiaru i obliczania przepływu
2
2
1
1
1
−
−
−
+
−
+
=
∆
−
j
j
j
j
j
j
Q
Q
I
I
t
S
S

Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Podstawowe równania metody Muskingum
2
2
1
1
1
−
−
−
+
−
+
=
∆
−
j
j
j
j
j
j
Q
Q
I
I
t
S
S
Równanie ciągłości
]
)
1
(
[
j
j
j
Q
x
xI
k
S
−
+
=
Równanie retencji

Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Podstawowe równania metody Muskingum
2
2
1
1
1
−
−
−
+
−
+
=
∆
−
j
j
j
j
j
j
Q
Q
I
I
t
S
S
Równanie ciągłości
]
)
1
(
[
j
j
j
Q
x
xI
k
S
−
+
=
Równanie retencji
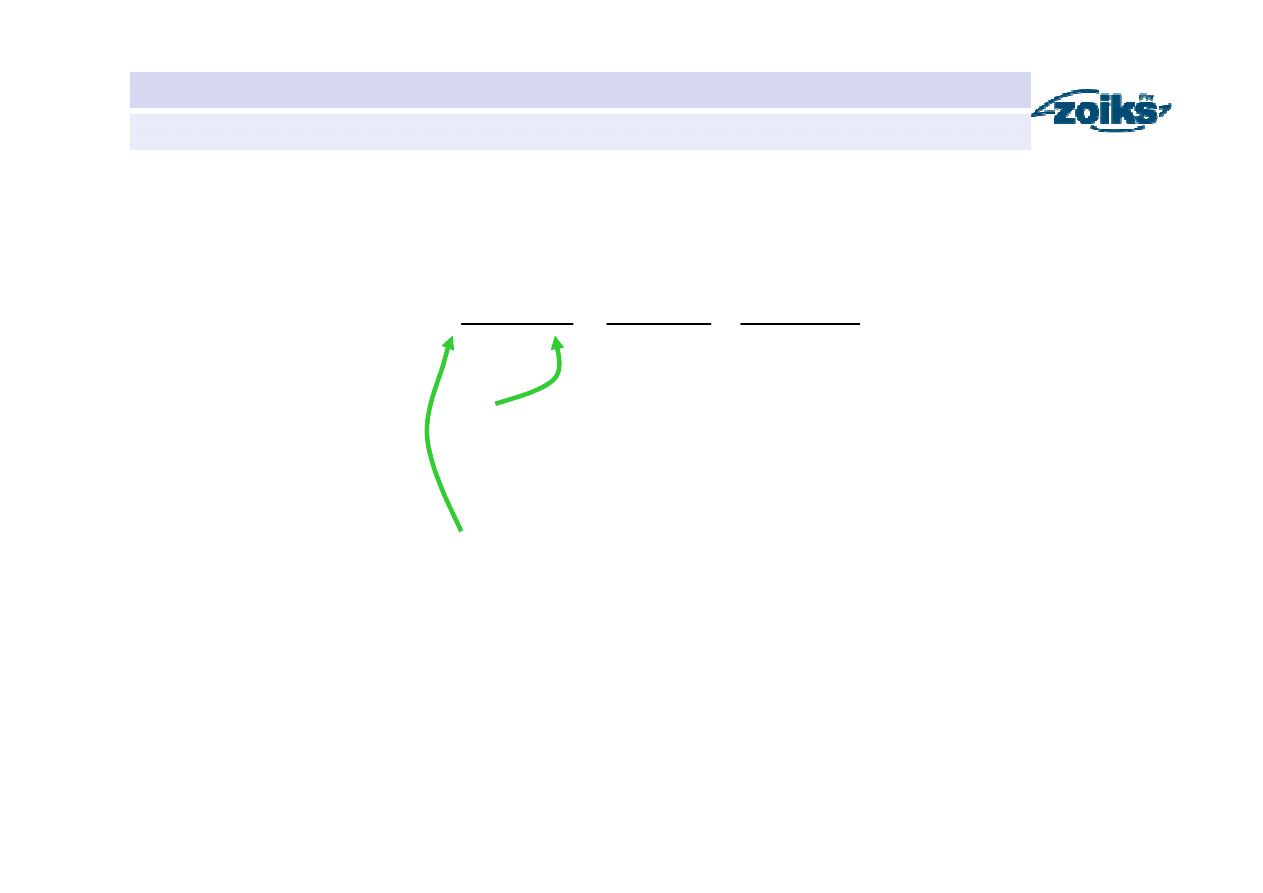
Eliminacja retencji
]
)
1
(
[
1
1
1
−
−
−
−
+
=
j
j
j
Q
x
xI
k
S
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Podstawowe równania metody Muskingum
2
2
1
1
1
−
−
−
+
−
+
=
∆
−
j
j
j
j
j
j
Q
Q
I
I
t
S
S
Równanie ciągłości
]
)
1
(
[
j
j
j
Q
x
xI
k
S
−
+
=
Równanie retencji
Eliminacja retencji
]
)
1
(
[
1
1
1
−
−
−
−
+
=
j
j
j
Q
x
xI
k
S
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
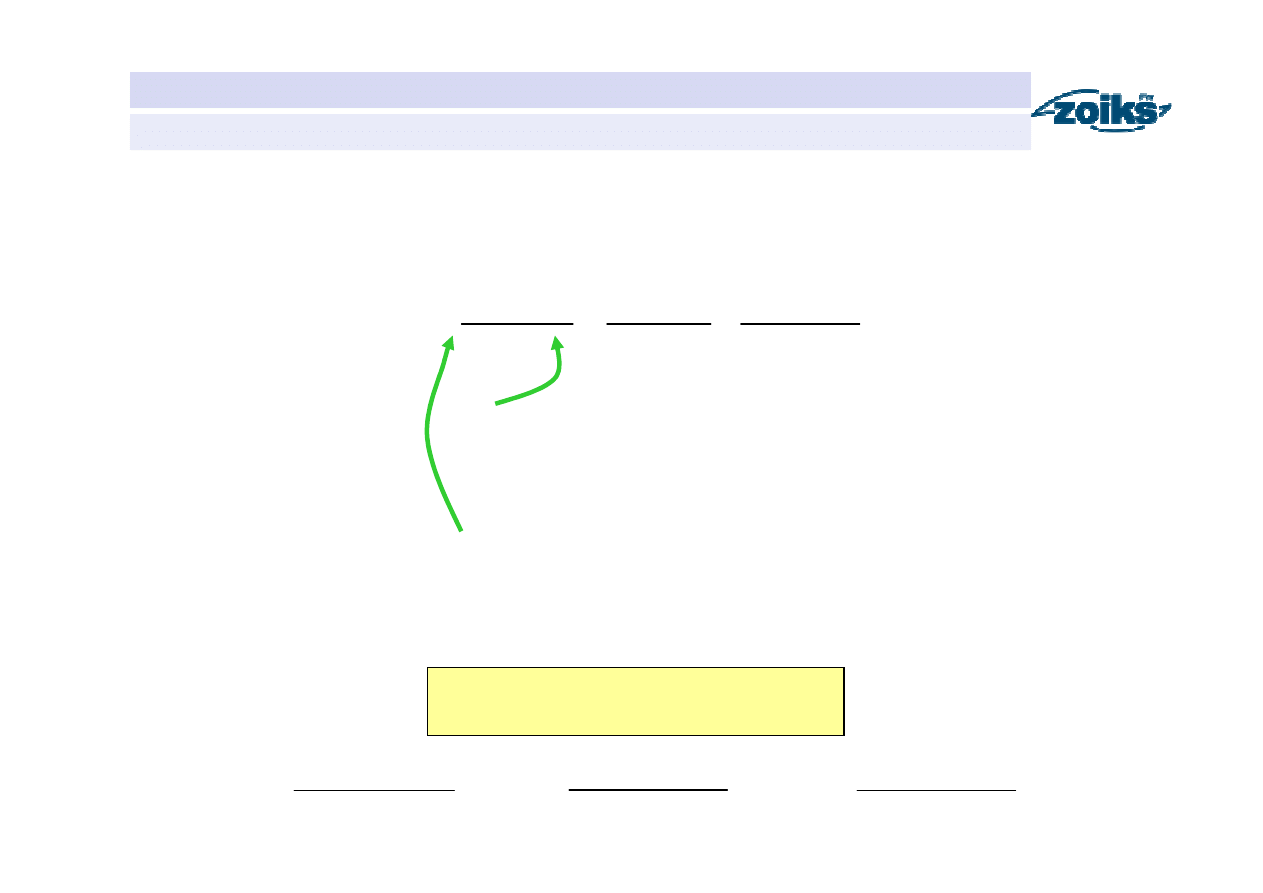
Podstawowe równania metody Muskingum
2
2
1
1
1
−
−
−
+
−
+
=
∆
−
j
j
j
j
j
j
Q
Q
I
I
t
S
S
Równanie ciągłości
]
)
1
(
[
j
j
j
Q
x
xI
k
S
−
+
=
Równanie retencji
Eliminacja retencji
]
)
1
(
[
1
1
1
−
−
−
−
+
=
j
j
j
Q
x
xI
k
S
Wzór rekurencyjny
1
3
1
2
1
−
−
+
+
=
j
j
j
j
Q
C
I
C
I
C
Q
t
x
k
kx
t
C
∆
+
−
−
∆
=
)
1
(
2
2
1
t
x
k
kx
t
C
∆
+
−
+
∆
=
)
1
(
2
2
2
t
x
k
t
x
k
C
∆
+
−
∆
−
−
=
)
1
(
2
)
1
(
2
3
2.0
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
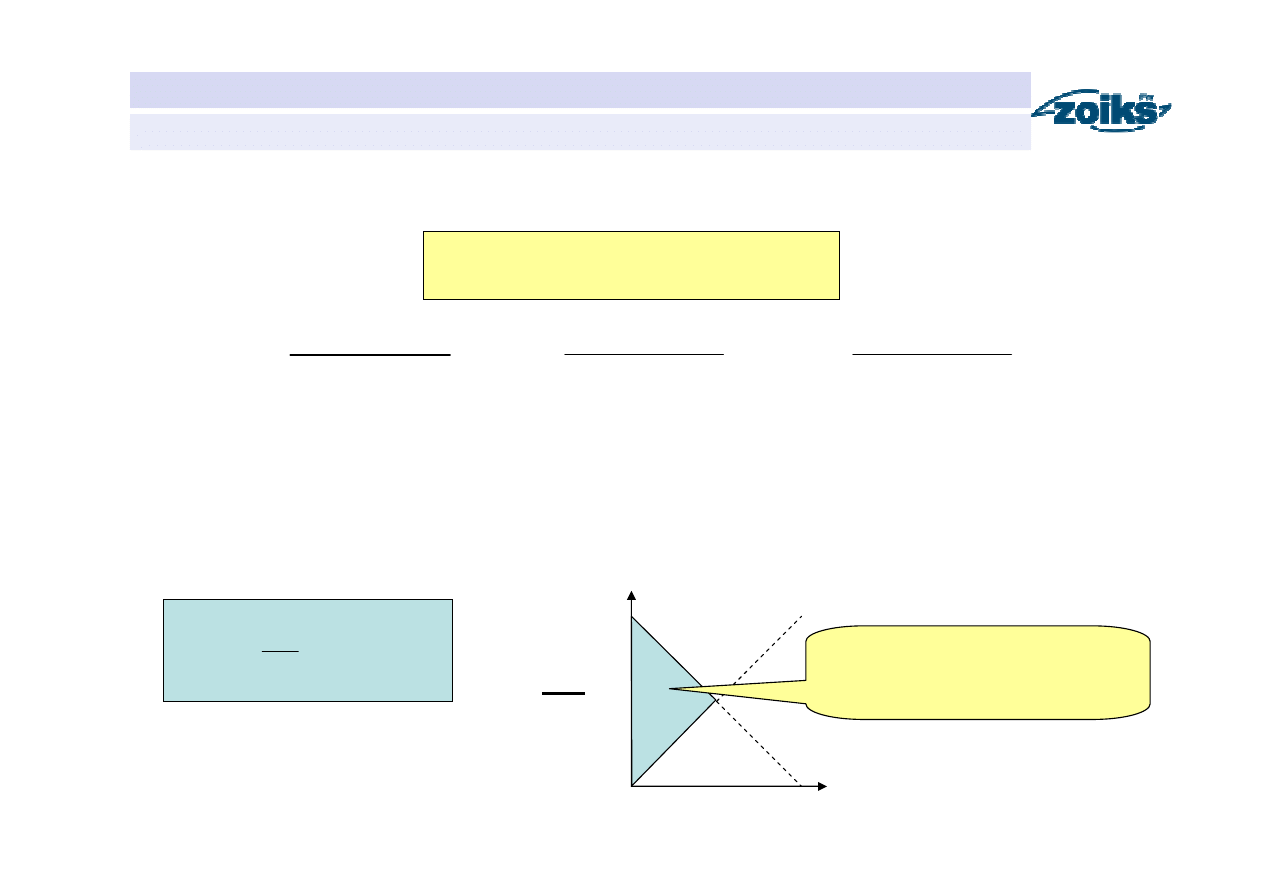
Wzór obliczeniowy w metodzie Muskingum
1
3
1
2
1
−
−
+
+
=
j
j
j
j
Q
C
I
C
I
C
Q
t
x
k
kx
t
C
∆
+
−
−
∆
=
)
1
(
2
2
1
t
x
k
kx
t
C
∆
+
−
+
∆
=
)
1
(
2
2
2
t
x
k
t
x
k
C
∆
+
−
∆
−
−
=
)
1
(
2
)
1
(
2
3
k – czas przepływu wody od przekroju pomiarowego do przekroju obliczeniowego
x – współczynnik wagowy
∆t – krok czasowy pomiaru i obliczania przepływu
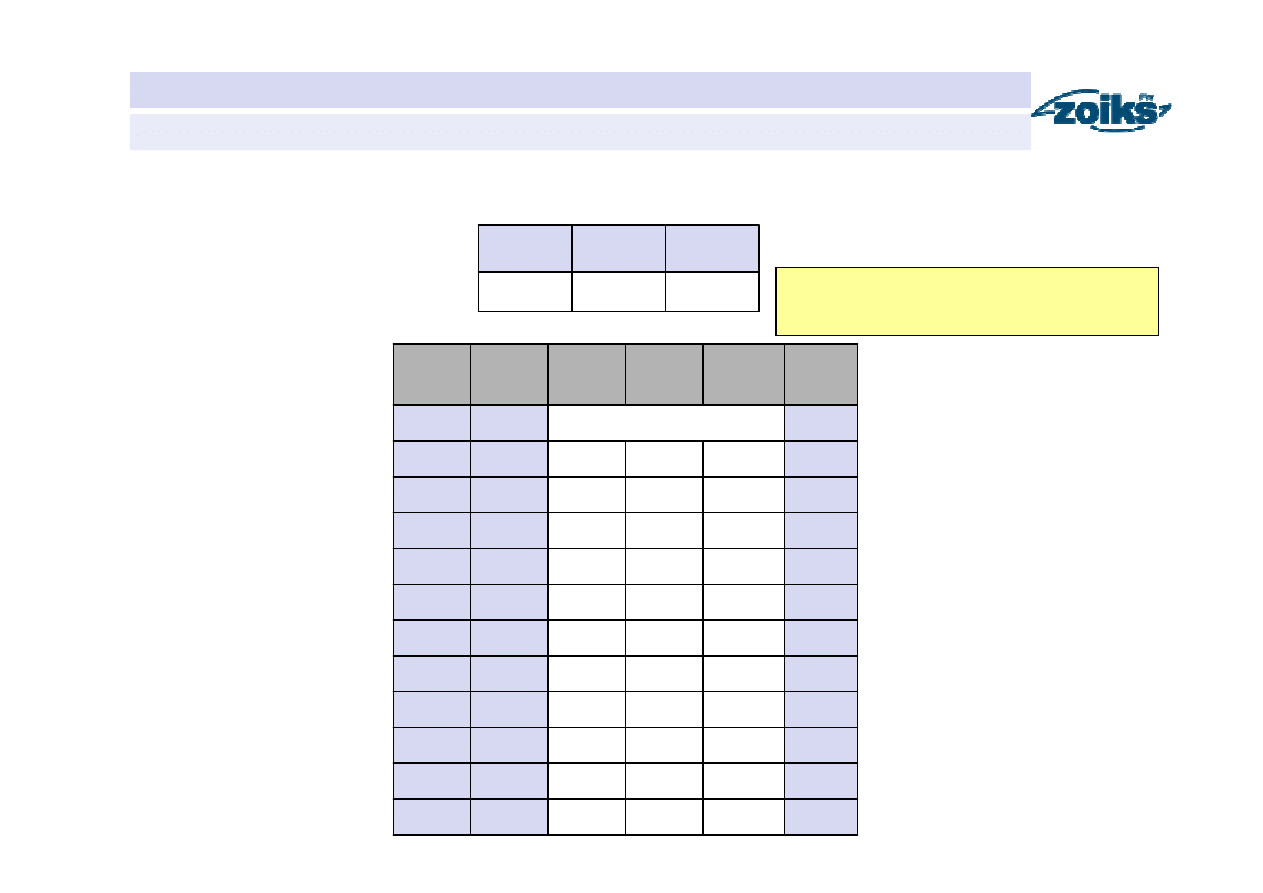
Warunek prawidłowego działania dla naturalnych koryt rzecznych
0
0
0.5
1.0
1.0
x
∆t
k
Obszar prawidłowej
transformacji przepływu na
odcinku koryta rzecznego
)
1
(
2
2
x
k
t
x
−
≤
∆
≤
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
Przykład obliczeniowy
k = 2 doby
x = 0.2
∆t = 1 doba
0.5238
0.4286
0.0476
C
3
C
2
C
1
8.50
5.54
2.67
0.29
6.08
24
10.59
6.93
3.36
0.30
6.23
23
…
…
…
…
…
…
34.94
12.37
19.71
2.86
60.00
8
23.62
10.03
11.40
2.19
46.00
7
19.15
8.88
9.00
1.27
26.60
6
16.96
6.70
9.26
1.00
21.00
5
12.80
4.61
7.16
1.03
21.60
4
8.81
3.21
4.80
0.80
16.70
3
6.13
2.32
3.28
0.53
11.20
2
4.42
2.23
1.83
0.36
7.65
1
4.26
Przepływ ustalony
4.26
0
Nr
doby
j
I
j
I
C
1
1
2
−
j
I
C
1
3
−
j
Q
C
j
Q
1
3
1
2
1
−
−
+
+
=
j
j
j
j
Q
C
I
C
I
C
Q
Transformacja przepływu w korycie rzecznym – metoda Muskingum
HYDROLOGIA
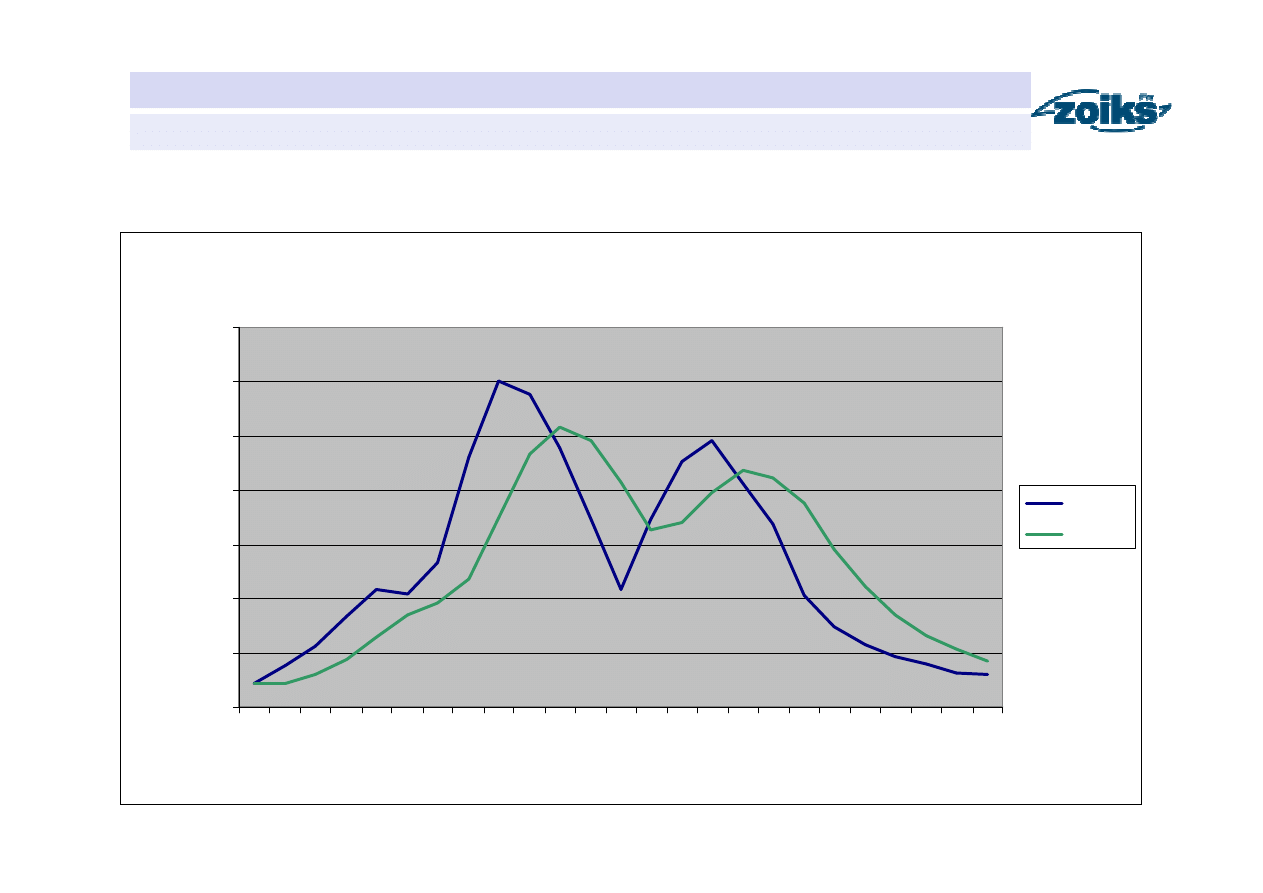
Wynik obliczeń
Transformacja przepływu
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Numer doby
N
a
t
ę
ż
e
n
ie
p
rz
e
p
ły
w
u
[
m
3
/s
]
Dopływ
Odpływ

ĆWICZENIA AUDYTORYJNE:
14
TEMAT :
Maksymalne wiarygodne wezbranie MWW. Strefy zagrożenia
powodziowego i ochrony przeciwpowodziowej
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
Maksymalne Wiarygodne Wezbranie
Maksymalne wiarygodne wezbranie (
MWW) jest
definiowane jako największe wezbranie, które może wystąpić
w ekstremalnych warunkach sprzyjających jednoczesnemu
wystąpieniu ekstremalnie wysokiego opadu, tj. maksymalnego
wiarygodnego opadu (MWO) i ekstremalnie korzystnych
warunków jego spływu na obszarze zlewni, tzn. przy
najmniejszych stratach wody zależnych od lokalnych warunków
fizjograficznych i sposobu zagospodarowania zlewni.
Ozga-Zielińska M., Kupczyk E., Ozga-Zieliński B., Suligowski K., Niedbała J., Brzeziński J.,
2003. Powodziogenność rzek pod kątem bezpieczeństwa budowli hydrotechnicznych i
zagrożenia powodziowego. Materiały Badawcze IMGW, seria: Hydrologia i Oceanologia, nr 29.
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
Maksymalny Wiarygodny Opad
Maksymalny wiarygodny opad (
MWO) definiowany jest jako
teoretycznie największy opad o określonym czasie trwania
(minuty, godzina, kilka godzin, doba, wielokrotność doby itp.),
którego wystąpienie jest fizycznie możliwe na obszarze o danej
wielkości, w danych warunkach geograficznych i w określonej
porze roku, a zatem dotyczy górnego limitu wysokości opadu
określanego na podstawie charakterystyk fizycznych mechanizmu
tworzenia się opadów.
Metody obliczania MWO są dostosowane do:
• charakterystycznych warunków meteorologicznych w danym
regionie,
• skali przestrzennej i czasowej,
• charakterystyk zlewni dla której będzie on transformowany
w maksymalne wiarygodne wezbranie.

Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
Maksymalny Wiarygodny Opad
Podstawą obliczania MWO jest opad potencjalny PP
jako suma wilgotności właściwej w kolumnie atmosfery
- wysokość [m]
- gęstość powietrza [kg m
-3
]
- gęstość pary wodnej [kg m
-3
]
- wilgotność właściwa [g kg
-1
]
- ciśnienie atmosferyczne [hPa·10
-2
]
- przyspieszenie ziemskie [m s
-2
]
∫
∫
∫
=
ρ
ρ
−
=
ρ
=
z
z
p
p
a
w
z
w
dp
g
q
dp
dz
0
0
0
PP
z
a
ρ
w
ρ
q
p
g
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
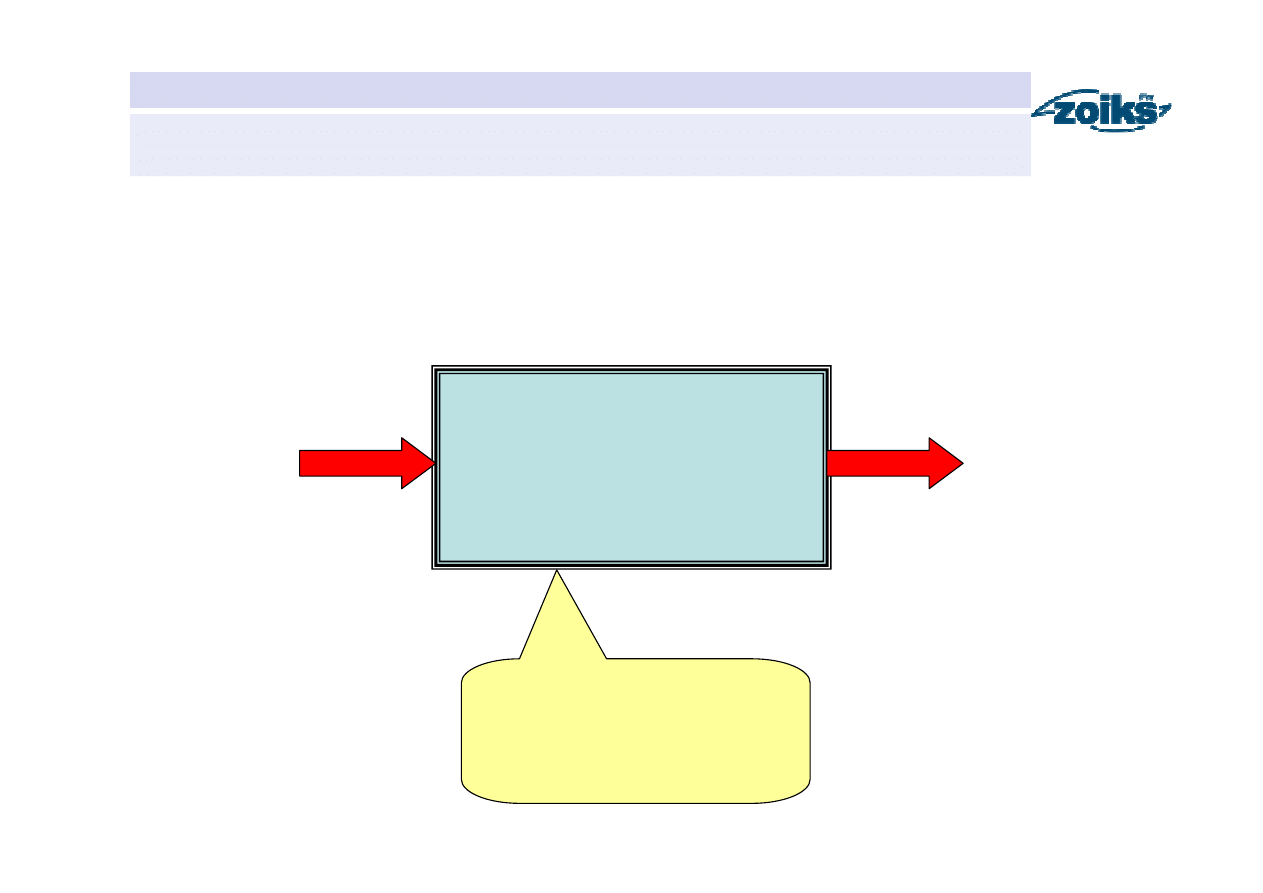
Koncepcja obliczania MWW
Matematyczny model
zlewni hydrologicznej
MWO
MWW
Parametry modelu
określające stan
maksymalnego nawilżenia
zlewni przed wystąpieniem
MWO
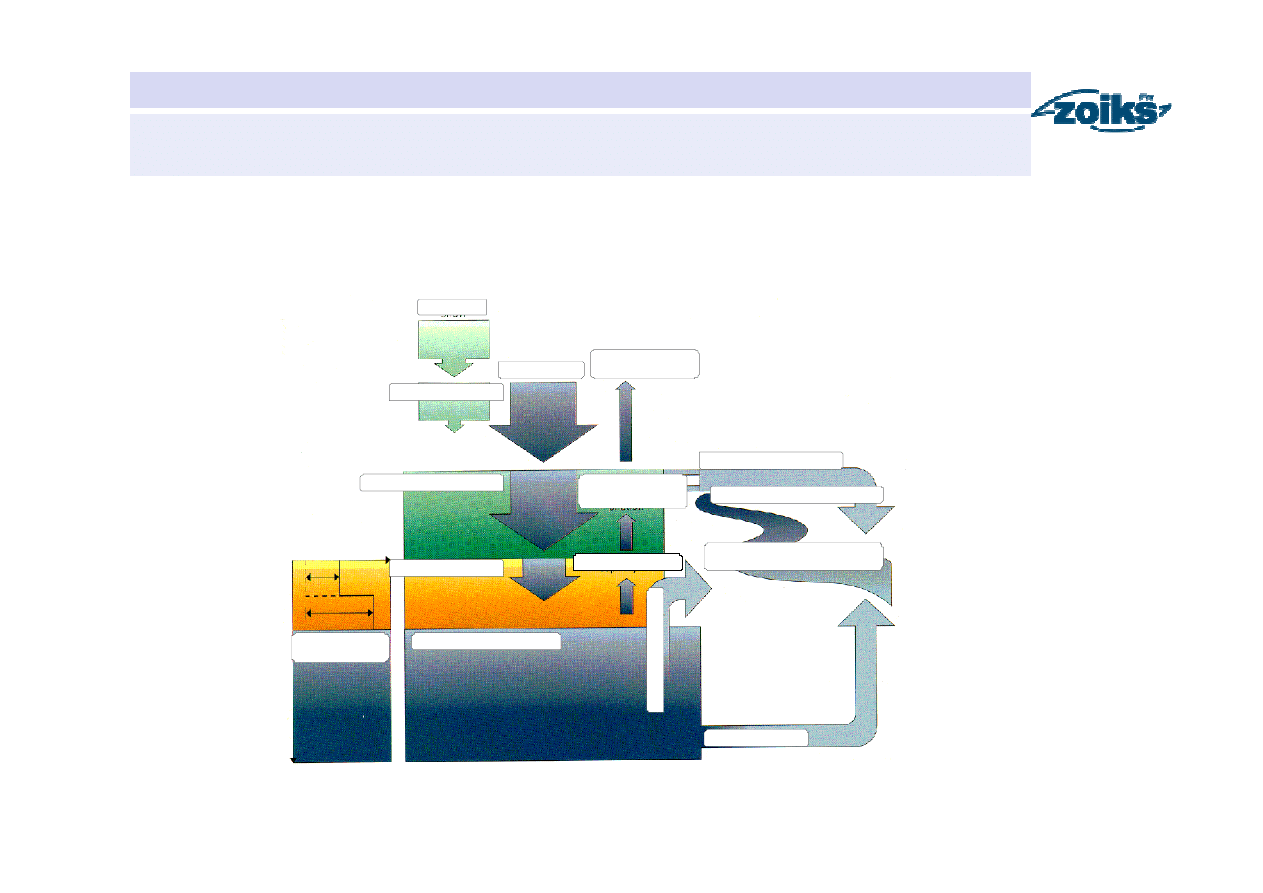
ś
nieg
p okrywa
ś
n ie
ż
n a
stref a powierzch nio wa
strefa ko rzenio wa
st refa wód pod ziem nych
po ziom wód
g runt owych
o dp ływ b azo wy
o pad d eszc zu
ewap otransp iracja
p ot encjalna
po dsi
ą
k
ka pilarny
ewapo transp iracja
aktualn a
mo delo wan y
przep ływ
spływ po wierzchn iowy
o dp ływ po dp owierzchn iowy
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
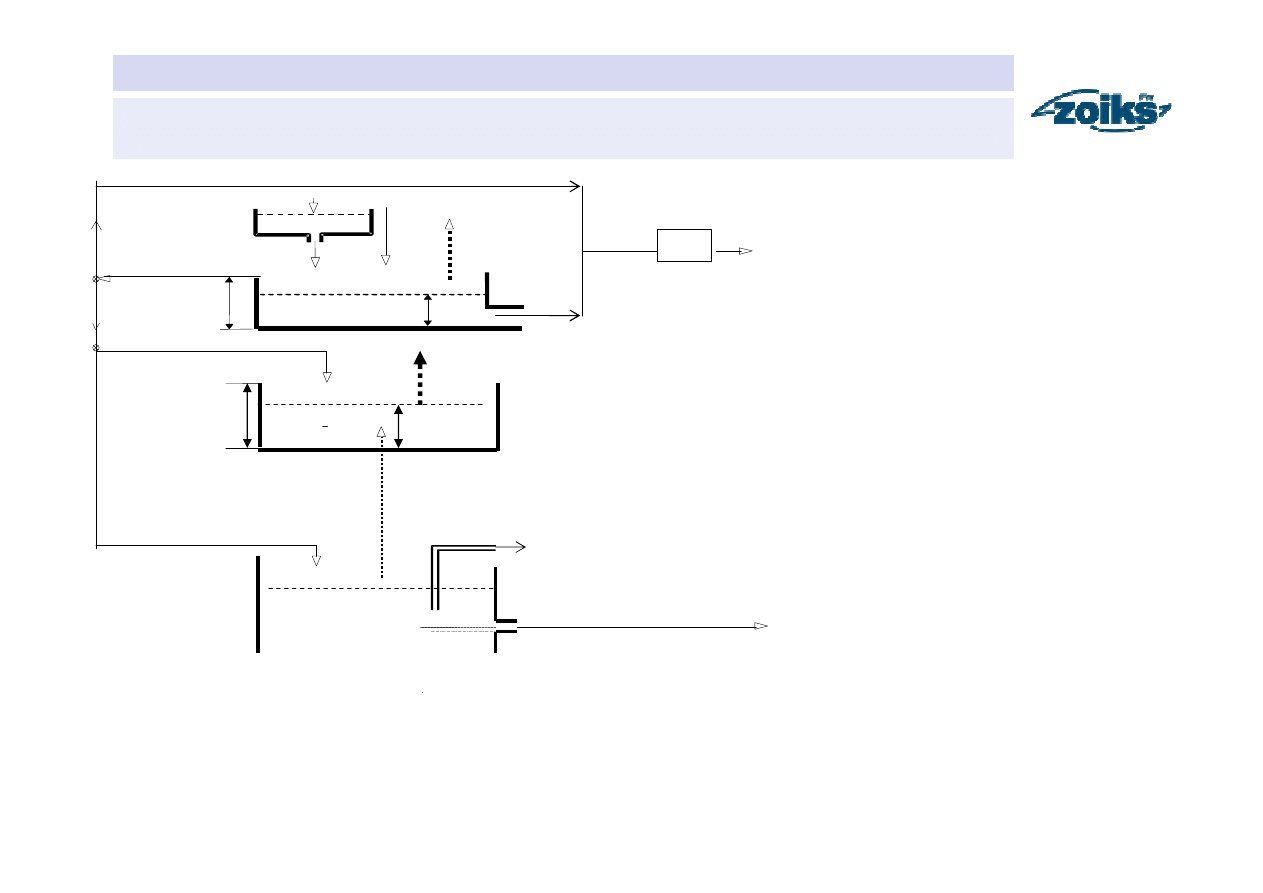
Przykład modelu OPAD-ODPŁYW
p
o
b
ó
r
w
ó
d
Ogólna koncepcja modelu NAM
ŚNIEG
PAROWANIE
ODPŁYW POWIERZCHNIOWY
STAŁA
CZASOWA
STAŁA
CZASOWA
ODPŁYW PODPOWIERZCHNIOWY
ZBIORNIK ŚNIEGOWY
ZBIORNIK POWIERZCHNIOWY
U
Ea
P
Ps
P
N
U
max
DL
Ea
Q
IF
Q
OF
L
max
ZBIORNIK GRUNTOWY
L
C
AF
DESZCZ
PODSIĄK KAPILARNY
G
G
WPUMP
G
WL
L
ZBIORNIK PODZIEMNY
G
WLBFo
ODPŁYW PODSTAWOWY
B
F
OF
IF
G
CK
1
CK
2
Struktura modelu NAM „opad–odpływ”
HYDROLOGIA
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
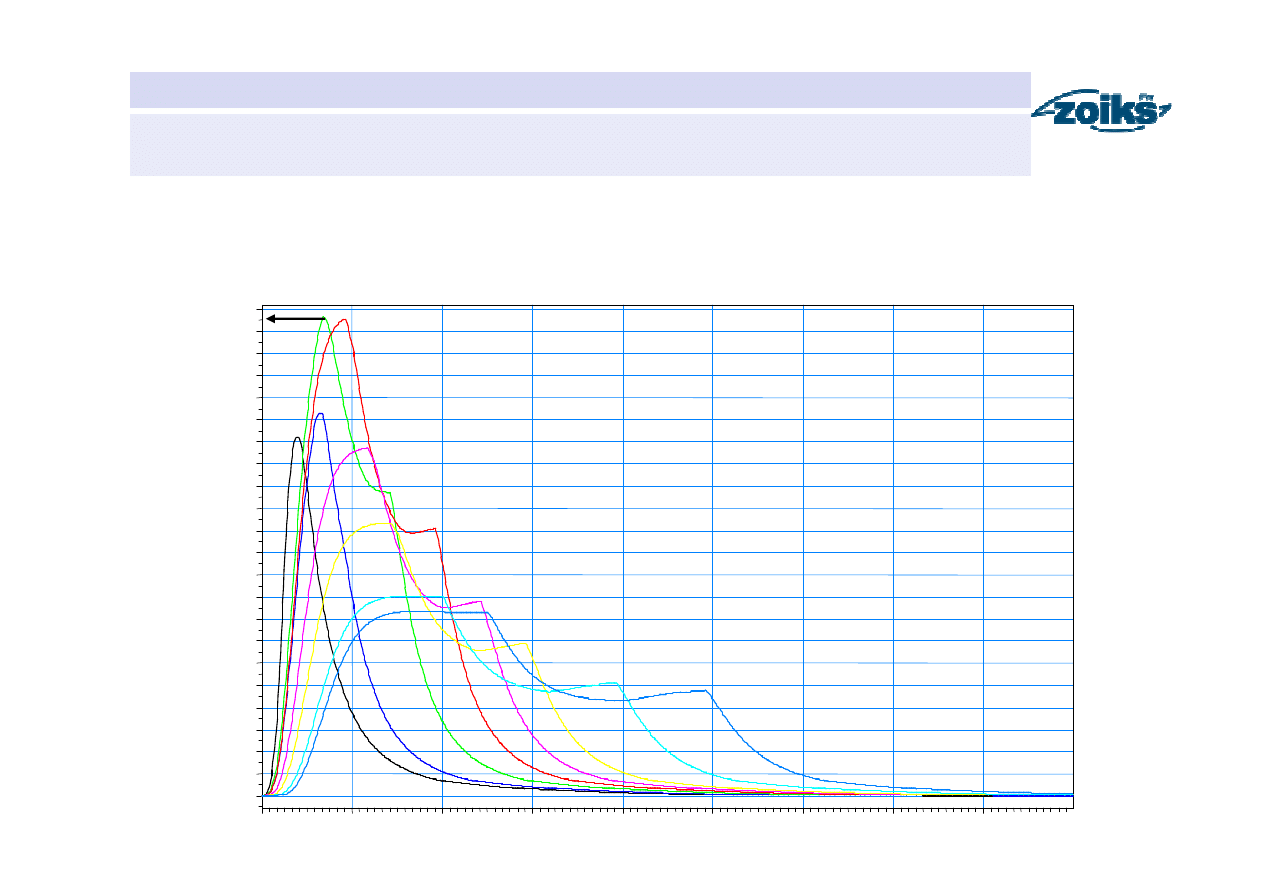
Przykład modelowania MWW dla MWO o różnych czasach trwania
(zlewnia rzeki Leśnianki)
06:00:00
1-7-2001
08:00:00
10:00:00
12:00:00
14:00:00
16:00:00
18:00:00
20:00:00
22:00:00
0.0
10.0
20.0
30.0
40.0
50.0
60.0
70.0
80.0
90.0
100.0
110.0
120.0
130.0
140.0
150.0
160.0
170.0
180.0
190.0
200.0
210.0
220
.0
[
m
3
/s]
MWW
m
3
/s

HYDROLOGIA
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
Strefy zagrożenia powodziowego określa się w czterech podstawowych
celach:
• utworzenia planu kompleksowej ochrony życia ludzi oraz ich dobytku przed powodzią,
• minimalizacji wszelkiego rodzaju zniszczeń i strat materialnych oraz problemów społecznych
wywołanych powodzią,
• utworzenia planów rozwoju i zagospodarowania zlewni oraz uzyskania poparcia administracji
terenowej dla realizacji tych planów,
• podjęcia i koordynacji niezbędnych inwestycji dla potrzeb gospodarki wodnej oraz towarzyszącej
infrastruktury.
Istotnym elementem dotyczącym zapewnienia bezpieczeństwa w odniesieniu do budowli
hydrotechnicznych i ochrony przeciwpowodziowej jest
znajomość możliwych maksymalnych wartości zagrożeń
oraz
znajomość aktualnego stopnia zabezpieczenia przed zagrożeniami
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
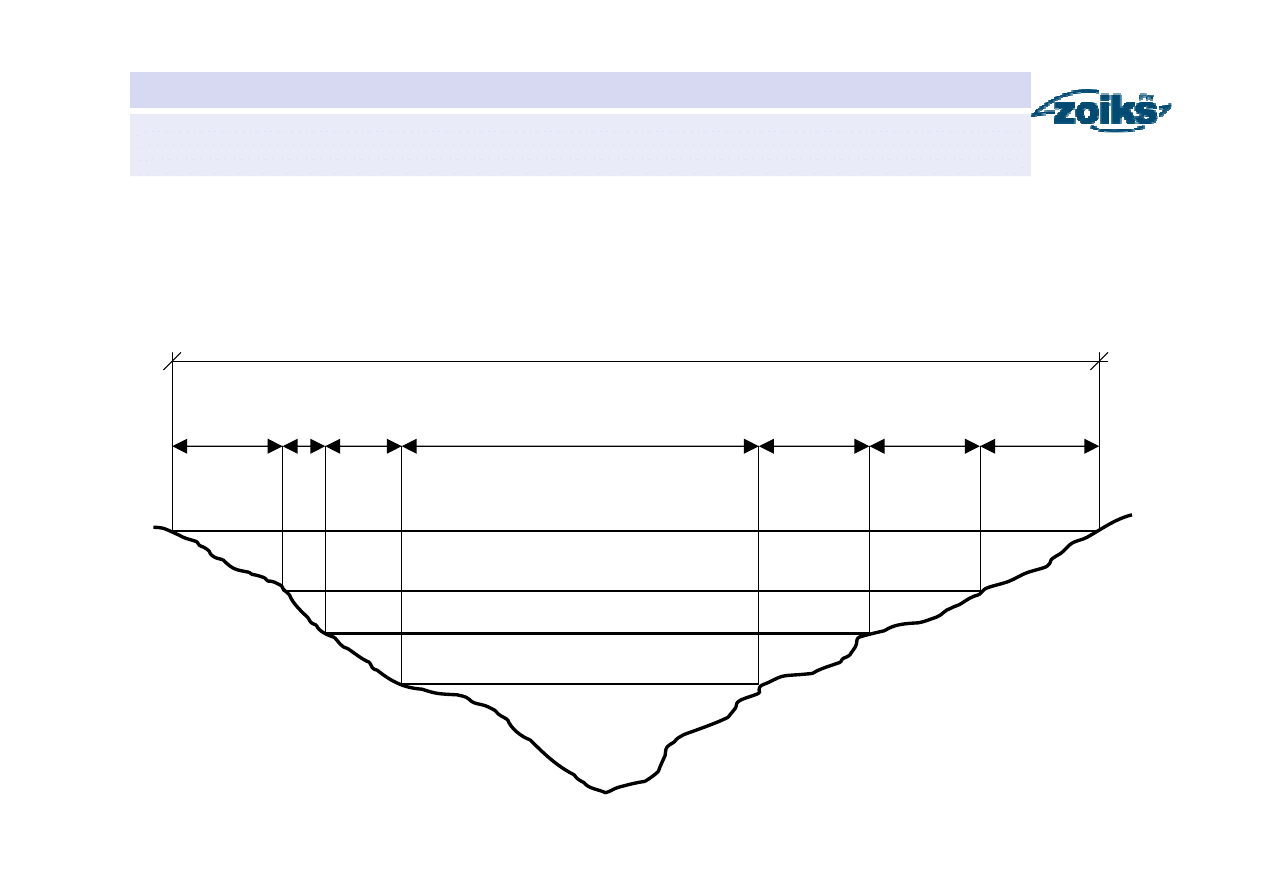
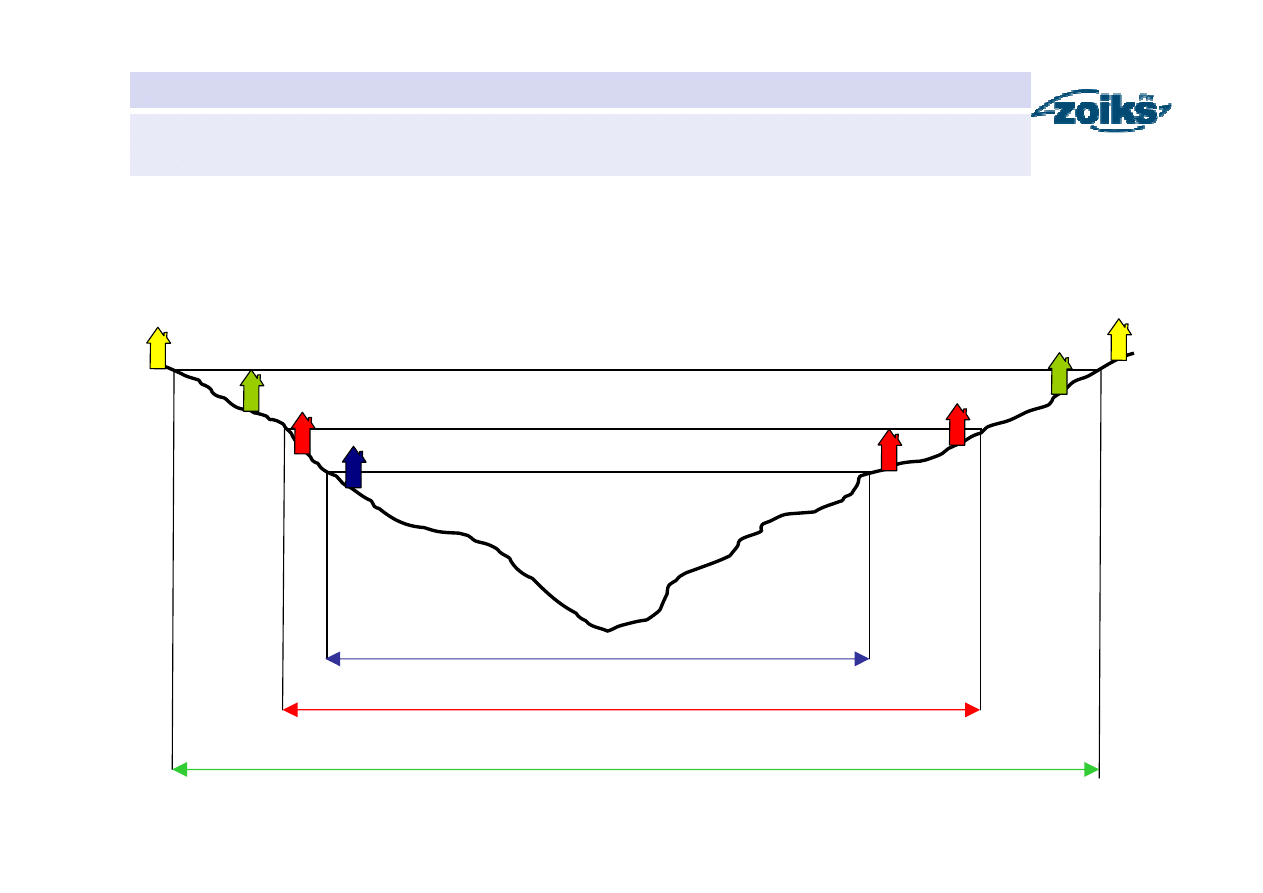
Strefy zagrożenia powodziowego
MWW
½ MWW
Q
max,p=1%
SWQ
ZM
ZM
ZZ
ZZ
ZW
ZW
ZS
ZS – zagrożenie stałe
ZW – zagrożenie wysokie
ZZ – zagrożenie znaczne
ZM – zagrożenie małe
Maksymalny zasięg zagrożenia powodziowego
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
Strefy ochrony przeciwpowodziowej
MWW
½ MWW
Q
max,p=1%
Strefa podstawowa
Strefa nadzwyczajna
Strefa ekstremalna
S
tr
e
fa
S
tr
e
fa
b
e
z
p
ie
c
z
n
a
b
e
z
p
ie
c
z
n
a
S
tr
e
fa
b
e
z
p
ie
c
z
n
a
S
tr
e
fa
b
e
z
p
ie
c
z
n
a

Powodziogenność pod kątem bezpieczeństwa obiektów hydrotechnicznych
Wskaźnik gwarancji bezpieczeństwa
MWW
m
Q
WGB
=
Q
m
– przepływ miarodajny, tzn. przepływ, na który został zaprojektowany rozpatrywany obiekt
hydrotechniczny
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA

Powodziogenność pod kątem zagrożenia powodziowego
Wskaźnik zagrożenia powodziowego
Q
doz
– przepływ dozwolony
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
MWW
MWW
doz
Q
WZP
−
=

Powodziogenność pod kątem największego dotychczas zaobserwowanego przepływu
Wskaźnik komplementarnej powodziogenności
WWQ – największy obserwowany przepływ w wieloleciu
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
MWW
WWQ
MWW
−
=
WKP

Wskaźniki powodziogenności obliczone dla przekroju Żywiec na Sole
Wskaźnik gwarancji bezpieczeństwa obiektów hydrotechnicznych
64
.
0
MWW
m
=
=
Q
WGB
Q
m
= Q
max,p=1%
= 1170 m
3
/s
MWW = 1833 m
3
/s
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
Oznacza to, że obiekty podstawowej ochrony przeciwpowodziowej gwarantują bezpieczeństwo
na obszarach chronionych tylko w 64%. Istnieje znaczne zagrożenie w przypadku wystąpienia
przepływów większych, które mogą uszkodzić lub zniszczyć te obiekty, lub też woda może się
przez nie przelać i zatopić obszary chronione

Wskaźnik zagrożenia powodziowego
Q
doz
– wartość jego jest określana na podstawie sytuacji topograficznej doliny rzecznej i
stopnia jej zagospodarowania, bądź w sposób przybliżony, np. jako SWQ lub Q
max,p=50%
. W
niniejszym przykładzie przyjęto dla przekroju Żywiec jako Q
doz
wielkość Q
max,p=50%
=215
m
3
/s
MWW = 1833 m
3
/s
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
86
.
0
MWW
MWW
=
−
=
doz
Q
WZP
Oznacza to, że obszary położone poniżej przekroju Żywiec mają bardzo wysoki wskaźnik zagrożenia
powodziowego, na których nie powinni mieszkać ludzie, ani nie powinno lokalizować się żadnych
stałych obiektów gospodarczych bez zabezpieczeń przeciwpowodziowych

Wskaźnik komplementarnej powodziogenności
WWQ = 1250 m
3
/s (zaobserwowany w 1958 roku)
MWW = 1833 m
3
/s
Maksymalne wiarygodne wezbranie MWW
Strefy zagrożenia powodziowego i ochrony przeciwpowodziowej
HYDROLOGIA
34
.
0
MWW
WWQ
MWW
=
−
=
WKP
Oznacza to, że w przekroju Żywiec przepływ, który wystąpił w 1958 roku, był bardzo duży
i tylko o 34% był mniejszy od największego z możliwych, czyli od MWW

DZIĘKUJĘ ZA UWAGĘ
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron