2011-09-27
1
Z. KASPERSKI - t.1
1
ALGEBRA Z GEOMETRIĄ
2 godz. wykładów +2godz. ćwiczeń + EGZAMIN
LITERATURA
1.
T. Jurlewicz, Z. Skoczylas, Algebra liniowa I. Definicje,
twierdzenia, wzory
, Matematyka dla studentów politechnik, Oficyna
Wydawnicza GiS
, Wrocław 2007.
2.
T. Jurlewicz, Z. Skoczylas,
Algebra liniowa I. Przykłady i zadania,
Matematyka dla studentów politechnik, Oficyna Wydawnicza GiS,
Wrocław 2007.
3.
M. Lassak,
Matematyka dla studiów technicznych, SUPREMUM
2002,
4.
R. Grzymkowski,
Matematyka dla studentów wyższych uczelni
technicznych, Gliwice 1999,
5.
R. Leitner, J. Zacharski,
Zarys matematyki wyższej dla studiów
technicznych, WNT Warszawa,1990
6.
----------------------------------------------.
DR ZYGMUNT KASPERSKI
Katedra Matematyki i Zastosowao Informatyki
Z. KASPERSKI - t.1
2
ELEMENTY LOGIKI
Def.1. Zdaniem w sensie logiki nazywamy wypowiedź, która jest prawdziwa
albo fałszywa.
Wartości logiczne zdao:
1- wartość prawdziwa
0 -wartość fałszywa
PRZYKŁADY:
SPÓJNIKI (OPERATORY) LOGICZNE:
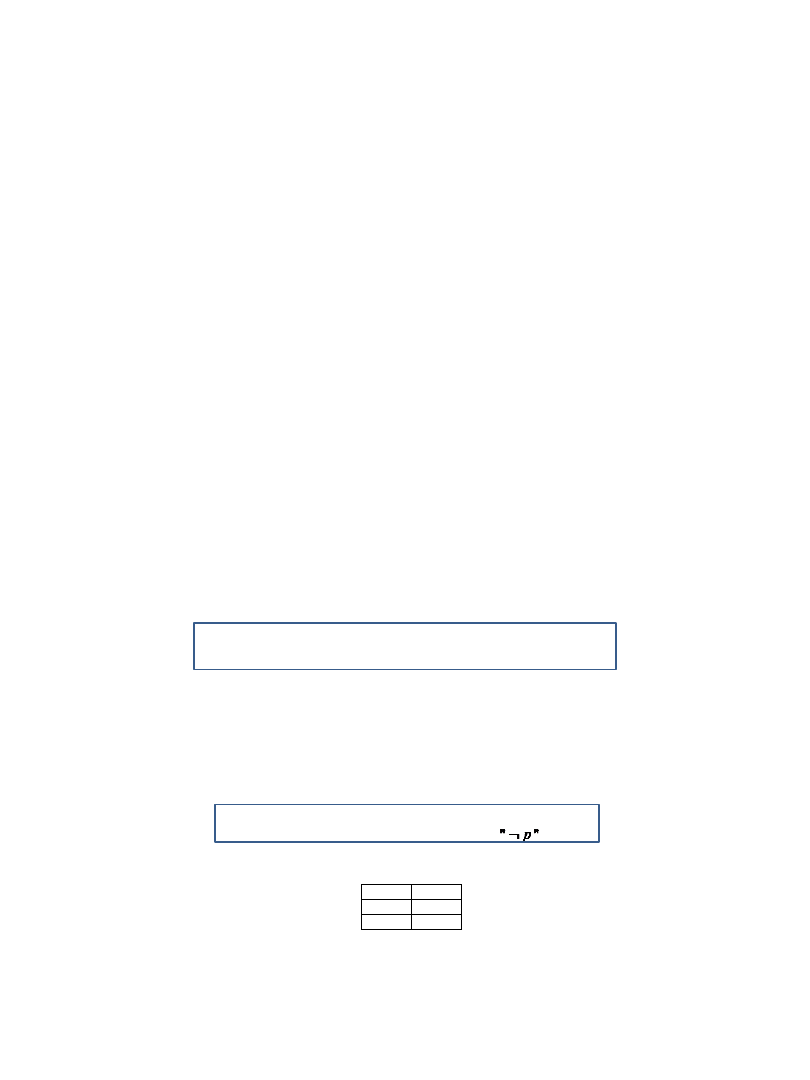
Def.2. Negacją (zaprzeczeniem) zdania p nazywamy zdanie „Nie p”
lub „Nieprawda, że p”, co zapisujemy symbolicznie .
Wartość logiczna negacji:
p
p
0
1
1
0
2011-09-27
2
Z. KASPERSKI - t.1
3
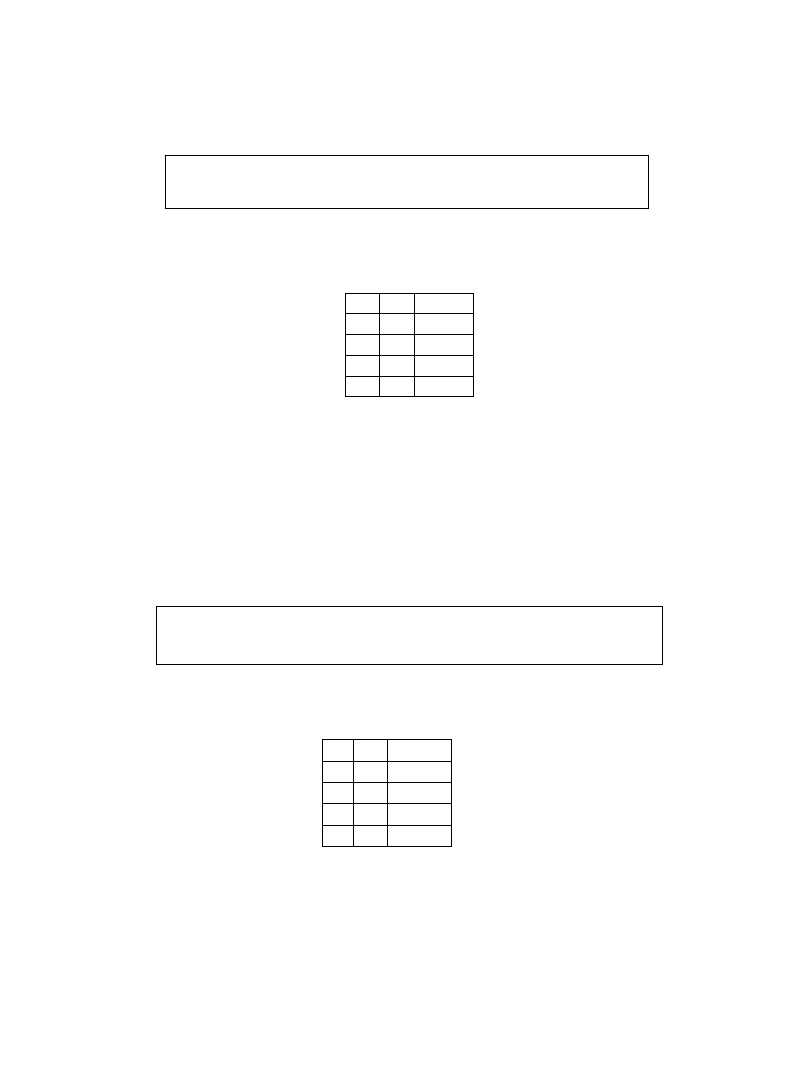
Def.3.
Koniunkcją(iloczynem logicznym) zdań p oraz q nazywamy zdanie „p i
q”, co zapisujemy symbolicznie
"
"
q
p
.
p
q
q
p
0
0
0
0
1
0
1
0
0
1
1
1
Wartość logiczna koniunkcji:
Z. KASPERSKI - t.1
4
Def.4
. Alternatywą (sumą logiczną) zdań p oraz q nazywamy zdanie „ p
lub q”, co zapisujemy symbolicznie
"
"
q
p
.
Wartość logiczna alternatywy:
p
q
q
p
0
0
0
0
1
1
1
0
1
1
1
1
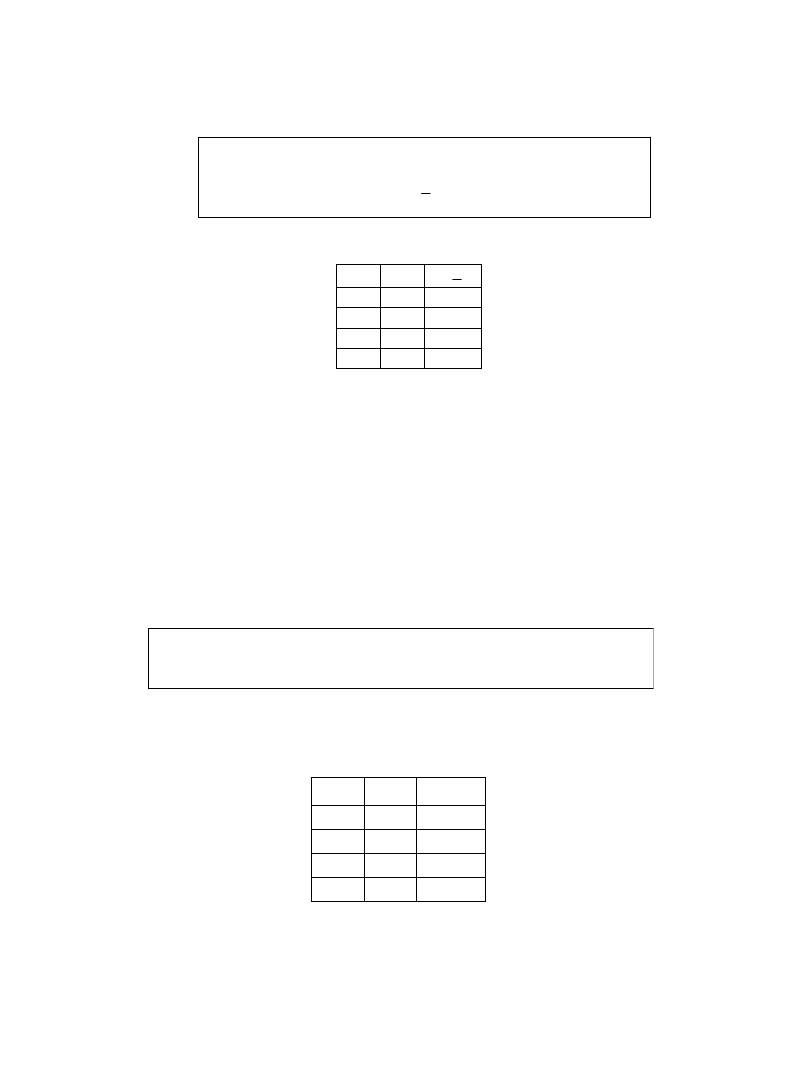
2011-09-27
3
Z. KASPERSKI - t.1
5
Def.5.
Alternatywą wykluczającą zdań p oraz q nazywamy zdanie „p albo
q”, co zapisujemy symbolicznie
"
"
q
p
.
Wartość logiczna alternatywy wykluczającej:
p
q
q
p
0
0
0
0
1
1
1
0
1
1
1
0
Z. KASPERSKI - t.1
6
Def.6.
Implikacją nazywamy zdanie postaci „Jeżeli p, to q”, co
zapisujemy symbolicznie
"
"
q
p
.
Wartość logiczna implikacji:
p
q
q
p
0
0
1
0
1
1
1
0
0
1
1
1

2011-09-27
4
Z. KASPERSKI - t.1
7
Def.7.
Równoważnością zdań p oraz q nazywamy zdanie „p wtedy i tylko wtedy, gdy q”,
co symbolicznie zapisujemy
"
"
q
p
lub
"
"
q
p
.
Wartość logiczna równoważności:
p
q
q
p
0
0
1
0
1
0
1
0
0
1
1
1
Z. KASPERSKI - t.1
8
Def.8.
Nazwę (literę) w miejsce której możemy podstawić dowolne zdanie nazywamy
zmienną zdaniową, a wyrażenie zbudowane ze zmiennych zdaniowych i spójników
logicznych nazywamy formułą rachunku zdań.
KOLEJNOŚĆ DZIAŁANIA OPERATORÓW LOGICZNYCH:
.
5
.
4
.
3
.
2
.
1
oraz
- (
kolejność ustalają nawiasy)
Def.9.
Formułę rachunku zdań, która staje się zdaniem prawdziwym, niezależnie od
tego jakie zdania, prawdziwe czy fałszywe podstawimy za zmienne zdaniowe
nazywamy tautologią lub prawem rachunku zdań.

2011-09-27
5
Z. KASPERSKI - t.1
9
NAJWAŻNIEJSZE TAUTOLOGIE RACHUNKU ZDAŃ:
1.
p
p
)
(
podwójna negacja
4.
)
(
)
(
q
p
q
p
zaprz.koniunkcji
–prawo de Morgana
2.
p
q
q
p
przemienność koniunkcji
3.
p
q
q
p
przemienność alternatywy
5.
)
(
)
(
q
p
q
p
zaprz.alternatywy
–prawo de Morgana
6.
)
(
)
(
q
p
q
p
zaprzeczenie implikacji
7.
)
(
)]
(
)
[(
r
p
r
q
q
p
przechodniośc implikacji
8.
)
(
)]
(
)
[(
q
p
p
q
q
p
związek implikacji z równoważnością
DOWÓD ( SPRAWDZENIE ZEROJEDYNKOWE )
Z. KASPERSKI - t.1
10
Def.10.
Zmienną nazywamy dowolną nazwę, np. x, w miejsce której możemy wstawić
dowolny element danego zbioru, np. zbioru D, który nazywamy dziedziną albo
zakresem zmiennej x. Piszemy
.
D
x
Def.11.
Warunkiem albo formą zdaniową zmiennej x
D nazywamy wypowiedź p(x) ze
zmienną x, która staje się zdaniem, jeżeli w miejsce x wstawimy dowolny element z
dziedziny D.
Def.12.
Warunkiem (formą zdaniową) wielu zmiennych
n
n
D
x
D
x
D
x
,...,
,
2
2
1
1
nazywamy wypowiedź
)
,...,
,
(
2
1
n
x
x
x
p
zawierające te zmienne, która staje się
zdaniem jeżeli w miejsce każdej zmiennej wstawimy dowolny element z jej dziedziny.
MAKSYMALNA
DOMYŚLNA DZIEDZINA.

2011-09-27
6
Z. KASPERSKI - t.1
11
Zbiór prawdziwości warunku p(x), x
D
– zbiór tych x, które wstawione do p(x) dają
zdania prawdziwe, czyli spełniają warunek
.
Zbiór ten zapisujemy na jeden z dwóch sposobów:
1.
)}
(
:
{
x
p
D
x
czytamy „
Zbiór x
D takich, że p(x)”,
2.
}
),
(
:
{
D
x
x
p
x
czytamy
„
Zbiór x takich, że p(x), gdzie x
D”
.
ANALOGICZNIE DLA FORMY ZDANIOWEJ WIELU ZMIENNYCH.
Z. KASPERSKI - t.1
12
KWANTYFIKATORY
1. Kwantyfikator ogólny:
D
x
„dla każdego x
D” lub „dla dowolnego x
D
”;
2. Kwantyfikator szczegółowy:
D
x
„ istnieje x
D” ;
D
x
1
„ istnieje dokładnie jeden x
D”.
ZDANIA ZAPI
SANE Z POMOCĄ KWANTYFIKATORÓW:
)
(
;
x
p
D
x
-
„Dla każdego x
D, p(x)
”(przy dziedzinie domyślnej
)
(
;
x
p
x
) ;
)
(
;
x
p
D
x
-
„ Istnieje x
D takie, że p(x)” (przy dziedzinie domyślnej
)
(
;
x
p
x
) ;
PRZYKŁADY:

2011-09-27
7
Z. KASPERSKI - t.1
13
Prawa de Morgana dla
kwantyfikatorów
:
1.
)
(
;
)
(
;
x
p
D
x
x
p
D
x
;
2.
)
(
;
)
(
;
x
p
D
x
x
p
D
x
.
PRZYKŁADY
Z. KASPERSKI - t.1
14
Zdania zbudowane za pomocą dwóch kwantyfikatorów:
1.
0
3
;
y
x
y
x
-
zdanie fałszywe;
2.
0
3
;
y
x
x
y
-
zdanie fałszywe;
3.
0
3
;
y
x
y
x
- zdanie prawdziwe;
4.
0
3
;
y
x
x
y
-
zdanie fałszywe.
UWAGA:
Zmiana kolejności kwantyfikatorów tego samego rodzaju nie zmienia
wartości logicznej zdania.
Można skracać zapisy:
)
,
(
;
,
)
,
(
;
y
x
p
D
y
D
x
y
x
p
D
y
D
x
y
x
y
x
)
,
(
;
,
)
,
(
;
y
x
p
D
y
D
x
y
x
p
D
y
D
x
y
x
y
x
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron