WYBÓR ANALITYCZNEJ

POSTACI MODELU

EKONOMETRYCZNEGO

WYBÓR ANALITYCZNEJ POSTACI

MODELU EKONOMETRYCZNEGO



Na podstawie poza statystycznych informacji o typie

związku, który łączy zmienną objaśnianą ze zmiennymi

objaśniającymi, a zatem na podstawie apriorycznej
wiedzy o prawidłowościach występujących w badanym
fragmencie rzeczywistości gospodarczej.

a priori
a posteriori


Metodą heurystyczną tj. metodą prób polegającą na
zastosowaniu różnych postaci analitycznych do opisu
wybranego fragmentu rzeczywistości gospodarczej i
wyborze jednego z nich na podstawie przyjętego
kryterium

„dobroci”

dopasowania

modelu

do

rzeczywistości.

WYBÓR ANALITYCZNEJ POSTACI

MODELU EKONOMETRYCZNEGO

 Metodą oceny wzrokowej wykresów rozrzutu

(tylko dla modeli z jedną zmienną objaśniającą).
Szczególnym przypadkiem oceny wzrokowej jest
metoda aproksymacji segmentowej.

 Metodą badania przyrostów (tylko dla modeli

tendencji rozwojowej). Metoda ta zakłada, że
model ma postać wielomianu, a wybór dotyczy
tylko stopnia wielomianu.

WYBÓR ANALITYCZNEJ POSTACI

MODELU EKONOMETRYCZNEGO

Żadna z wymienionych metod nie jest uniwersalna,

ponieważ nie zapewnia obiektywnych narzędzi
wyboru klasy modelu lub zakres ich zastosowań jest
ograniczony. Podjęto próby konstrukcji tzw. modeli
adaptacyjnych, w których nie zakłada się a priori
postaci analitycznej lecz wynika z zastosowania
pewnych

algorytmów

„wygładzających”

obserwowany

faktycznie

związek zmiennej

objaśnianej

ze

zmiennymi

objaśniającymi.

Przykładem modeli adaptacyjnych jest metoda
trendu pełzającego.

WYBÓR ANALITYCZNEJ POSTACI

MODELU EKONOMETRYCZNEGO

Funkcje najczęściej spotykane w badaniach

empirycznych, a obrazujące typy związków

pomiędzy zjawiskami ekonomicznymi.

Funkcja liniowa

Funkcja hiperboliczna

t

t

t

X

Y













1

0

t

t

t

X

Y













1

1

0

WYBÓR ANALITYCZNEJ POSTACI

MODELU EKONOMETRYCZNEGO

Funkcja wielomianowa


Parabola jako szczególny zapis funkcji

wielomianowej drugiego stopnia

t

n

t

n

t

t

t

X

X

X

Y























...

2

2

1

0

t

t

t

t

X

X

Y

















2

2

1

0

WYBÓR ANALITYCZNEJ POSTACI

MODELU EKONOMETRYCZNEGO

Funkcja potęgowa

Funkcja wykładnicza

Funkcja logarytmiczna

t

t

t

X

Y







10

1

0





t

t

e

Y

x

t













1

0

t

t

t

X

Y













2

0

log

ESTYMACJA PARAMETRÓW

STRUKTURALNYCH

Algorytm estymacji parametrów strukturalnych w konwencji

macierzowej. Przyjmując, że dokonano n obserwacji na zmiennych
Y

t

, X

1t

,X

2t

,…,X

kt

Y = Xa + u

Gdzie

wektor zaobserwowanych zmiennych endogenicznych Yt

t

k

i

it

i

t

X

Y

















1

0

;

2

1



























n

y

y

y



y

ESTYMACJA PARAMETRÓW

STRUKTURALNYCH

macierz realizacji zmiennych objaśniających

W modelu występuje zmienna X

0i

=1 przy parametrze α

0

dla t=1,2,..,n

wektor estymatorów parametrów strukturalnych



























kn

n

k

k

x

x

x

x

x

x













1

2

12

1

11

1

1

1

X

;

1























K









wektor reszt u

t



























n

u

u

u

u



2

1

Zestaw założeń 1) – 5) nazywamy Klasycznym Modelem

Regresji Liniowej (KMRL).

Model liniowy w notacji macierzowo-wektorowej wraz ze

sformułowanymi werbalnie założeniami można zapisać:

• 1)

(model którego parametry szacujemy jest

modelem liniowym)

• 2) Zmienne objaśniające są zmiennymi nielosowymi

(ustalonymi w powtarzanych próbach dla każdego
na poziomie ) , zatem macierz X jest macierzą

nielosową i

nie występuje współliniowość zmiennych

objaśniających); liczba zmiennych objaśniających jest
mniejsza od liczby obserwacji (K<n).

1

1











N

K

N

N

u



X

y

n

t

,...,

1



tK

t

x

x ,...,

1

• 3) Wartość oczekiwana składnika losowego jest równa zero,

czyli (odchylenia losowe in plus i in minus redukują
się).

• 4) wariancja składnika losowego jest stała dla wszystkich

obserwacji dla każdego t (własność ta
nazywana jest także jednorodnością lub
homoskedastycznością wariancji),

• 5) obserwacje są niezależne, składniki losowe

poszczególnych obserwacji są nieskorelowane (nie
występuje autokorelacja składników losowych).

1

)

(





n

0



E

2

2







t

SCHEMAT ESTYMACJI FUNKCJI LINIOWEJ

Zakładając, że zależność ma charakter liniowy, oszacujemy parametry modelu:

y

X

X

X

a

T

T

1

)

(





t

t

t

t

X

X

Y

















2

2

1

1

0

.





































































n

n

n

y

y

y

y

y

x

x

x

x

x

x

x

x

X







3

2

1

2

1

32

31

22

21

12

11

1

1

1

1

1







































































































































n

t

t

n

t

t

t

n

t

t

n

t

t

t

n

t

t

n

t

t

n

t

t

n

t

t

n

n

n

n

x

x

x

x

x

x

x

x

x

x

n

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

1

2

2

1

1

2

1

2

1

2

1

1

2

1

1

1

1

2

1

1

2

1

32

31

22

21

12

11

2

32

22

12

1

31

21

11

1

1

1

1

1

1

1

1

1

1









X

X

T











































































































n

t

t

t

n

t

t

t

n

t

t

n

n

n

y

x

y

x

y

y

y

y

y

x

x

x

x

x

x

x

x

1

2

1

1

1

3

2

1

2

32

22

12

1

31

21

11

1

1

1

1

1







y

X

T

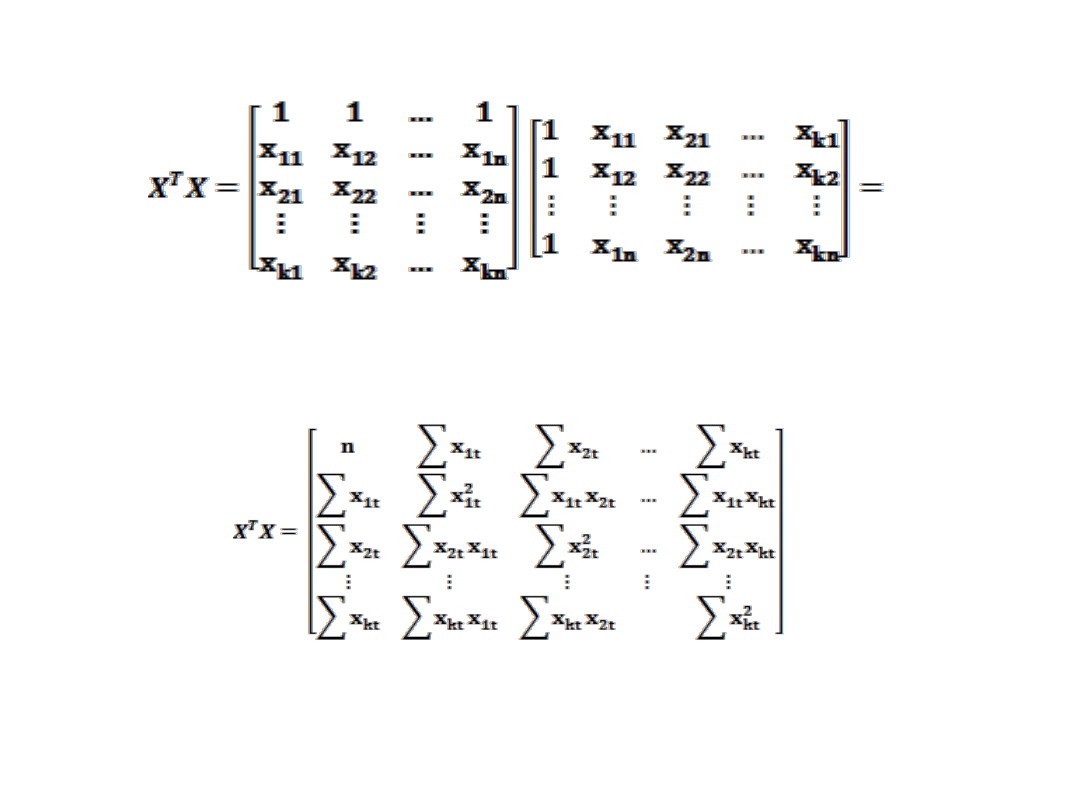
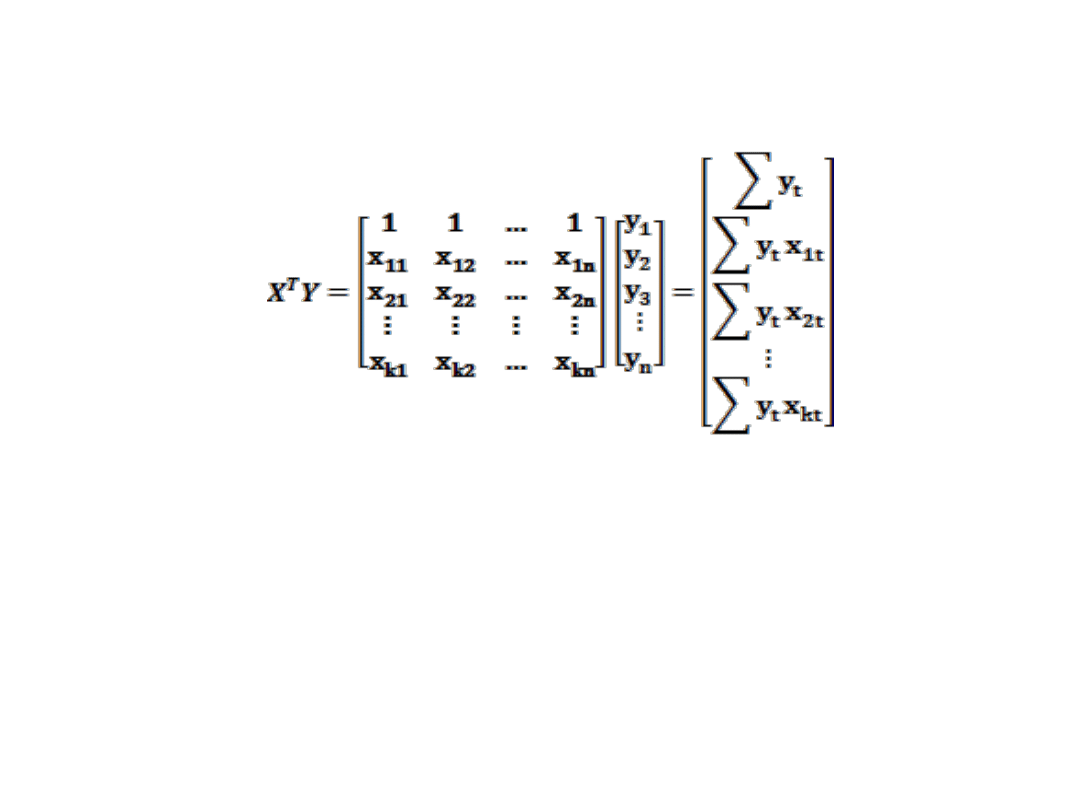
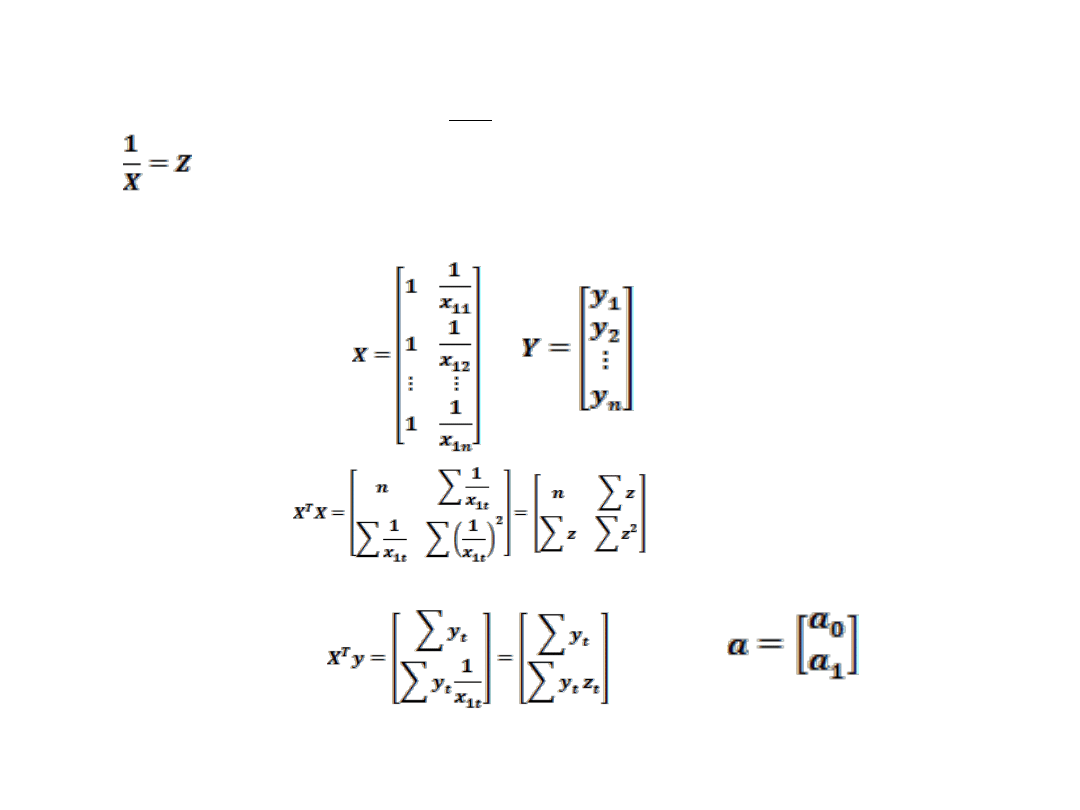
SCHEMAT ESTYMACJI FUNKCJI HIPERBOLICZNEJ

Wtedy zmienna endogeniczna Y jest funkcją liniową zmiennej Z

t

t

t

X

Y













1

1

0

t

t

z

Y













1

0

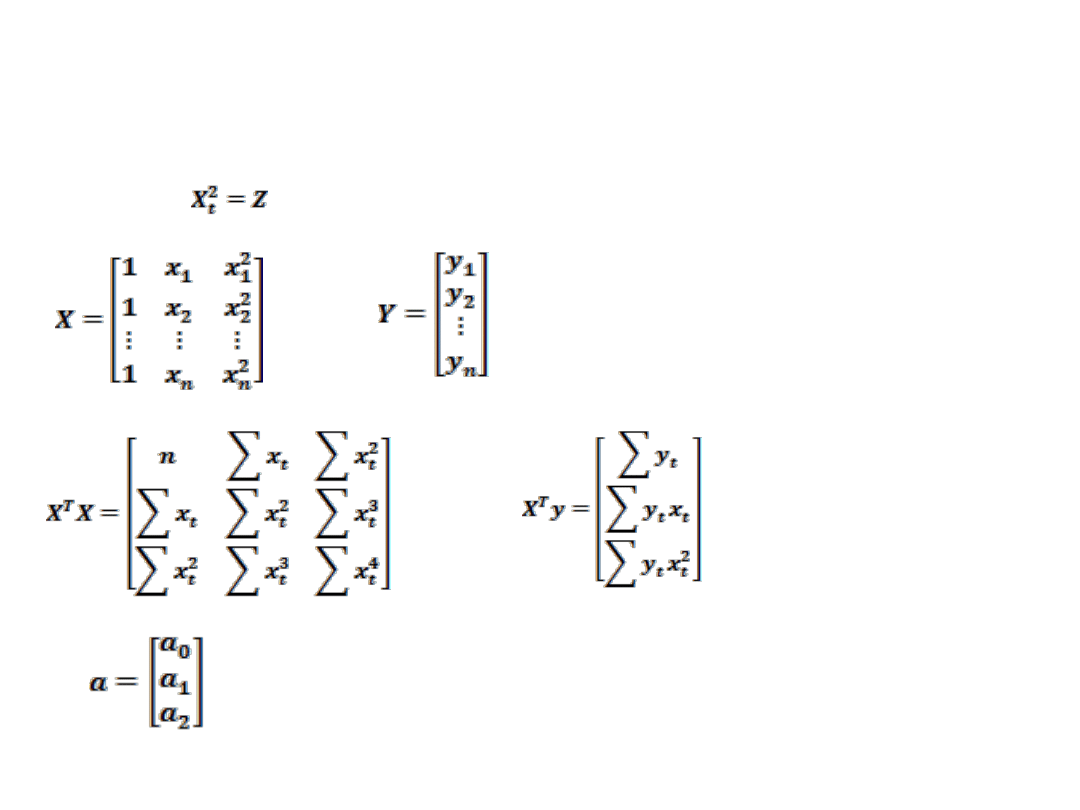
Po podstawieniu funkcja nieliniowa ze względu na X jest funkcją liniową ze względu na X i Z

SCHEMAT ESTYMACJI FUNKCJI PARABOLICZNEJ

t

t

t

t

X

X

Y

















2

1

1

0

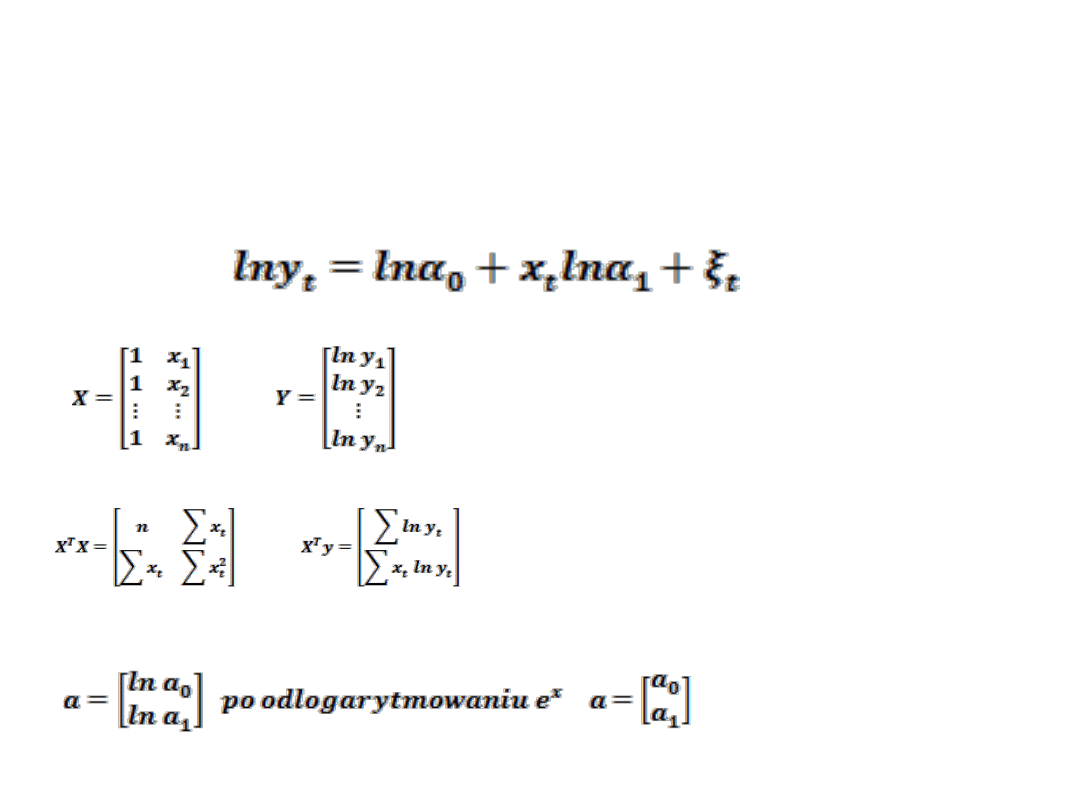
SCHEMAT ESTYMACJI FUNKCJI WYKŁADNICZEJ

t

t

e

Y

x

t













1

0

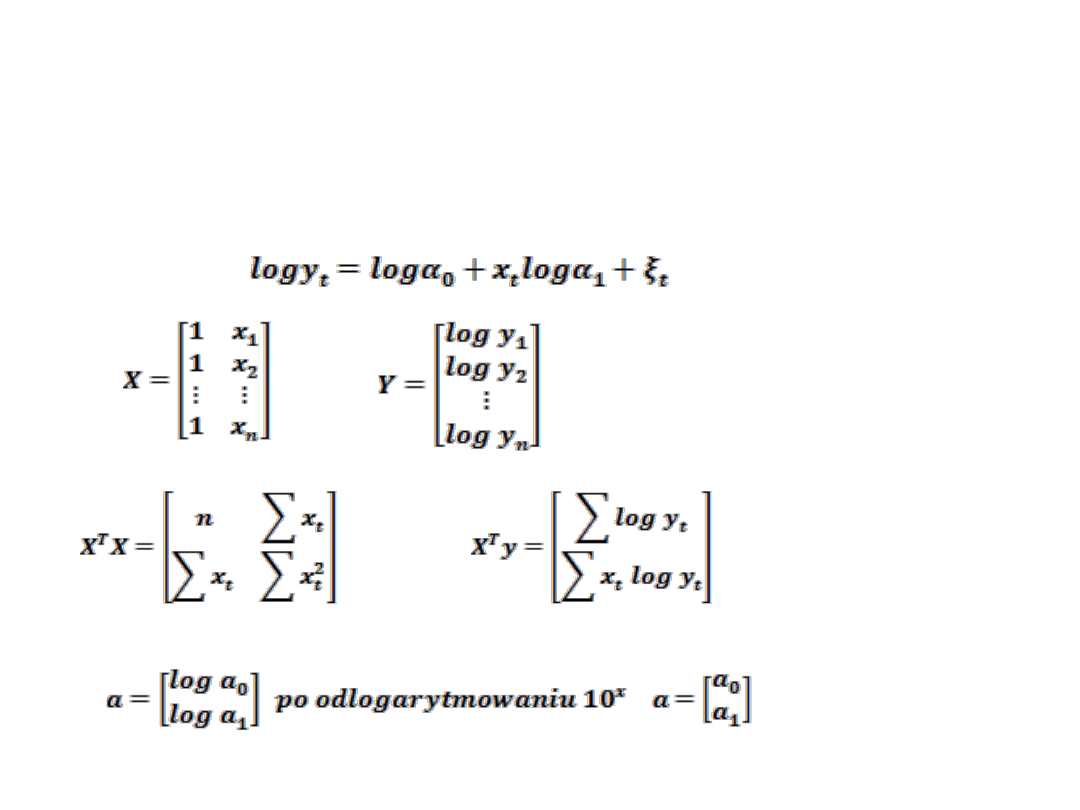
SCHEMAT ESTYMACJI FUNKCJI WYKŁADNICZEJ

t

t

x

t

Y







10

1

0







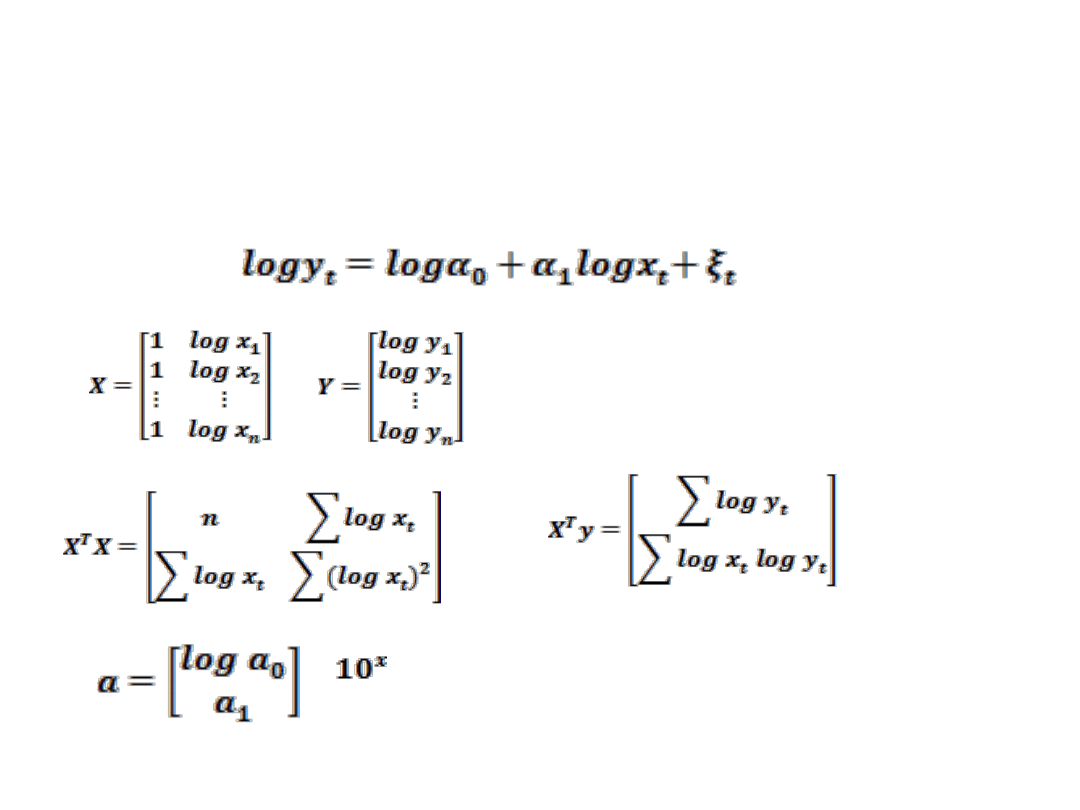
SCHEMAT ESTYMACJI FUNKCJI POTĘGOWEJ

t

t

t

X

Y







10

1

0





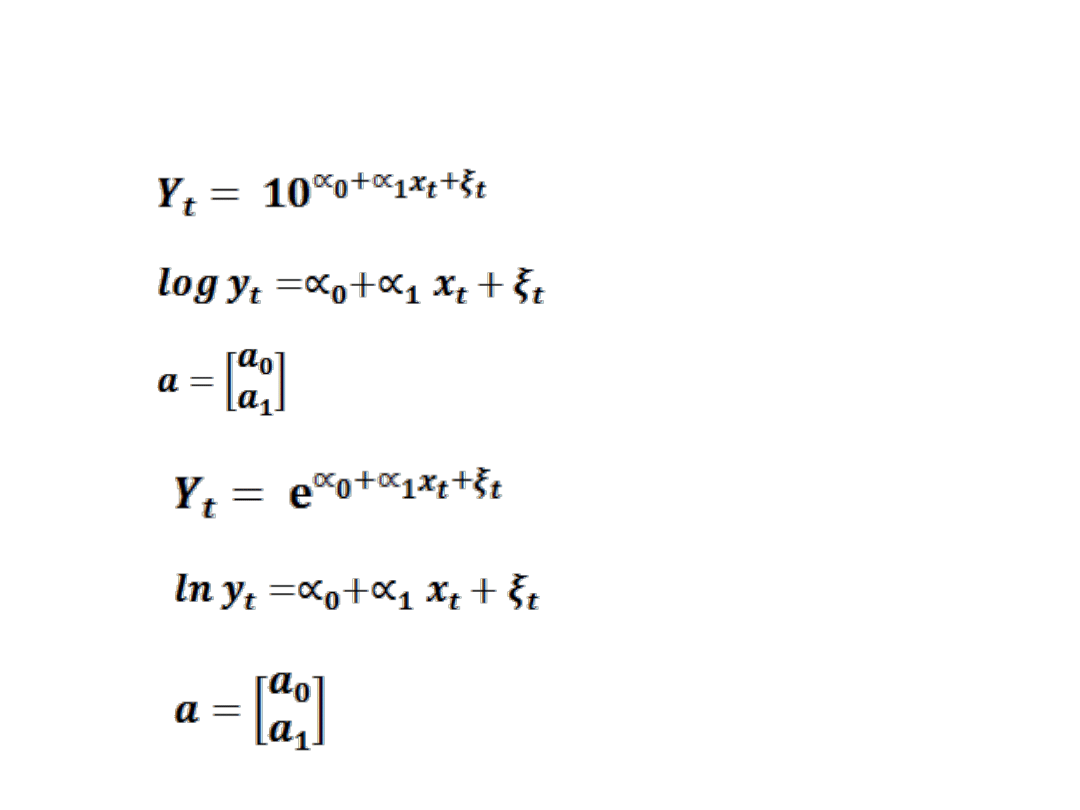
W praktyce mogą występować jeszcze inne postacie funkcji wykładniczej.

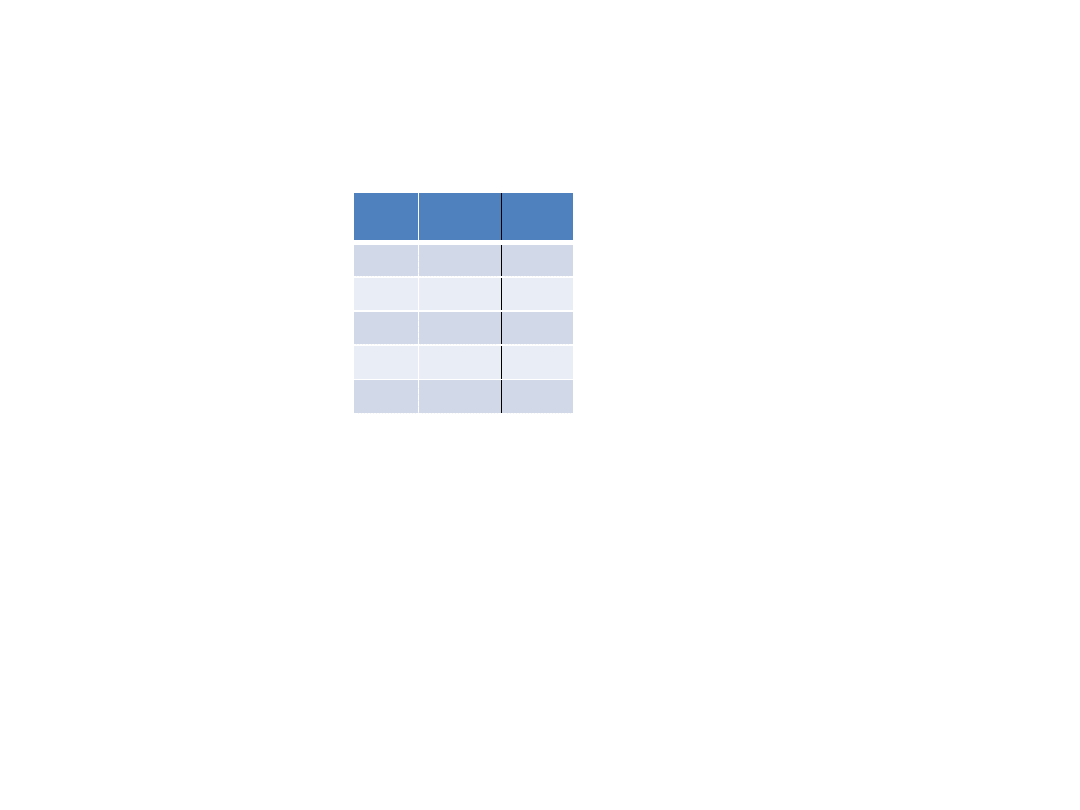
Mając dane dotyczące 5 pracowników bezpośrednio produkcyjnych:

gdzie:
y

i

- ilość braków wytwarzanych przez pracownika (w szt. rocznie),

x

1i

– staż pracy (w latach,)

x

2i

– liczba dni przepracowanych przez pracownika w warunkach szkodliwych dla zdrowia

Nalęży:
Oszacować parametry strukturalne funkcji liniowej
y

i

= a

0

+a

1

x

1i

+a

2

x

2i

+e

i

opisującej badaną zależność
b. Zweryfikować statystyczną istotność otrzymanych estymatorów parametrów (t

a

= 2,156),

c. zinterpretować otrzymane wyniki,
d. wyznaczyć prognozę y gdy x

1i

= 5 i x

2i

= 7;

d. Dokonać oceny dokładności predykcji (wariancja predykcji, błąd średni predykcji, względny błąd średni

predykcji)

e. zbudować 95% przedział ufności.

Y

i

X

1i

X

2i

35

5

2

50

3

3

62

2

4

72

1

5

82

0

6



 





 



)

(

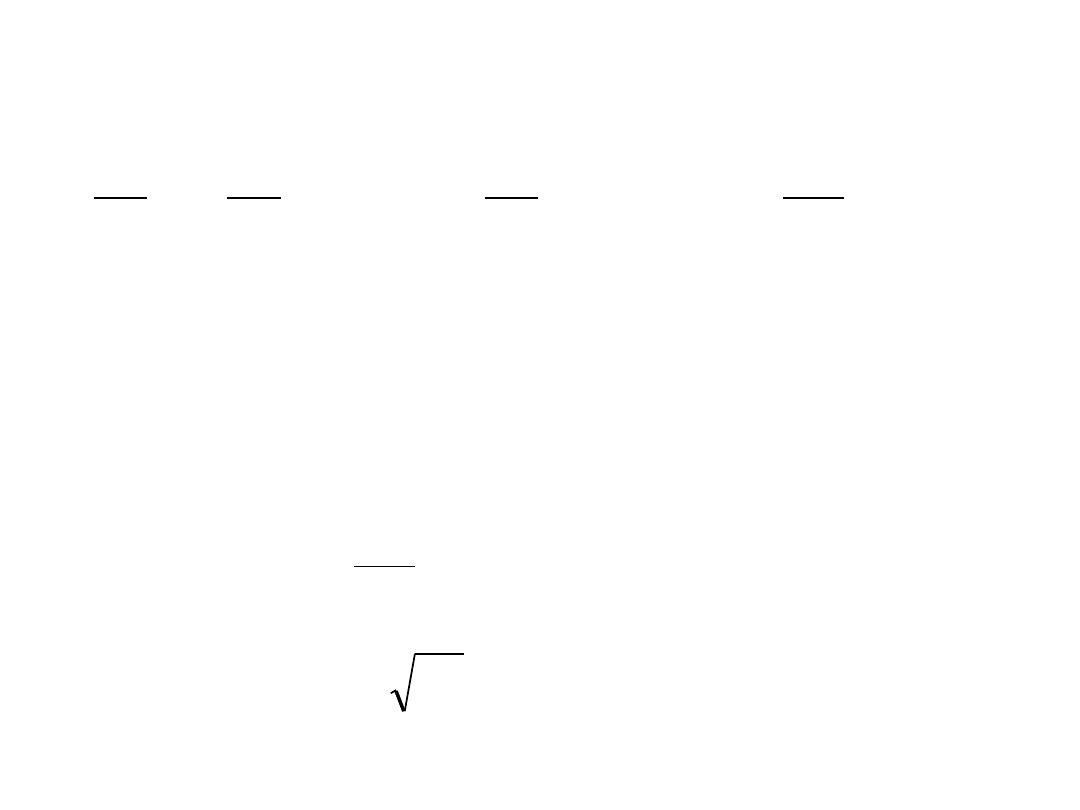
1

ˆ

ˆ

1

1

1

2

y

X

a

y

y

Xa

y

Xa

y

y

y

y

y

T

T

T



























k

n

u

u

S

T

T

T

e

k

n

k

n

k

n

Xa

y



ˆ

y

y

ˆ





u

gdzie: n

— liczba obserwacji

k

— liczba szacowanych parametrów strukturalnych

n-k

— liczba stopni swobody

— wektor reszt

— wektor wartości teoretycznych

lub w zapisie skalarnym:









N

t

t

e

u

k

n

S

1

2

2

1

2

e

e

S

S



Parametry struktury stochastycznej

WARIANCJA RESZTOWA

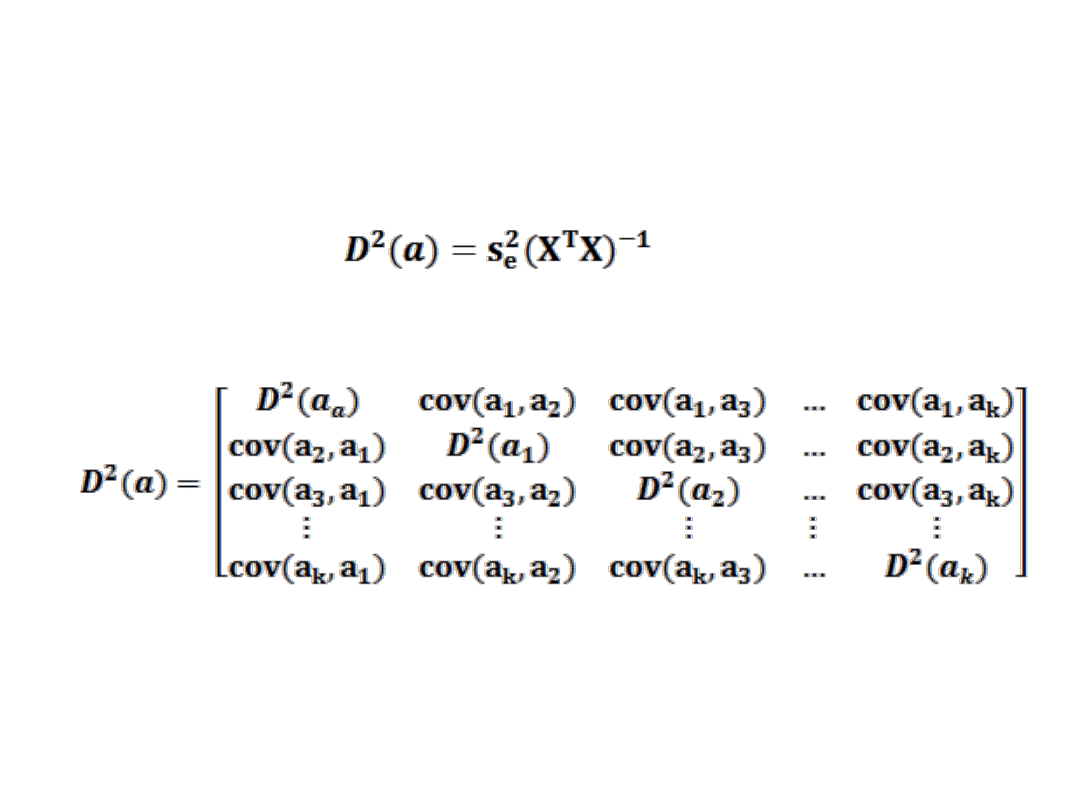
BŁĘDY ŚREDNIE SZACUNKU

Błędy średnie szacunku parametrów strukturalnych określają rząd

dokładności szacunku tych parametrów.

MACIERZ WARIANCJI I KOWARIANCJI

Elementy diagonalne znajdujące się na

przekątnej głównej macierzy wariancji i

kowariancji są wariancjami estymatorów

parametrów strukturalnych.

Pierwiastki kwadratowe z elementów

znajdujących się na przekątnej głównej

stanowią błędy średnie szacunku.

Natomiast poza przekątną główną znajdują

się kowariancje estymatorów parametrów

strukturalnych określających stopień

skorelowania dwóch estymatorów.

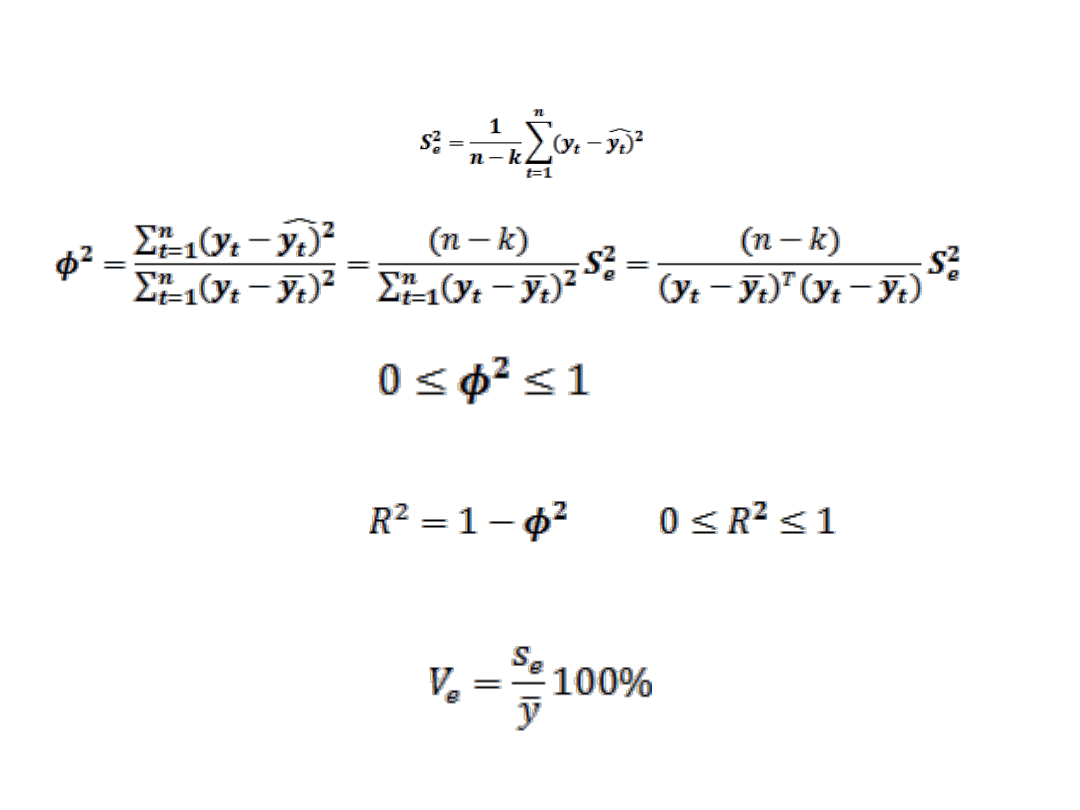
WSPÓŁCZYNNIK DETERMINACJI

WSPÓŁCZYNNIK ZBIEŻNOŚCI

WSPÓŁCZYNNIK ZMIENNOŚCI LOSOWEJ

WERYFIKACJA MODELI EKONOMETRYCZNYCH

Model z oszacowanymi parametrami strukturalnymi i parametrami
struktury

stochastycznej

trzeba

poddać procedurze weryfikacyjnej

dotyczącej:

1. Prawidłowego doboru zmiennych objaśniających do modelu i

siły oddziaływania tych zmiennych na zmienną endogeniczną

(objaśnianą).

2. Stopnia dopasowania modelu do opisywanego fragmentu

rzeczywistości gospodarczej.

3. Rozkładu reszt w aspekcie spełnienia apriorycznych założeń

poczynionych przy wyborze metody estymacji parametrów
modelu.

WERYFIKACJA MODELI EKONOMETRYCZNYCH

Pozytywny rezultat procedury weryfikacyjnej modelu ekonometrycznego

umożliwia właściwą realizację celów, dla których podjęto badania
ekonometryczne.
Możemy przyjąć, że model ekonometryczny będzie spełniał warunki
praktycznego wykorzystania wtedy, gdy:

•

Estymatory parametrów strukturalnych są statystycznie istotne.

•

Wybrane parametry struktury stochastycznej przyjmują wartości

arbitralnie uznane za dopuszczalne czyli spełniony będzie warunek

φ

2

< φ

0

2

, lub R

2

> R

0

2

lub V<V

0

gdzie φ

0

2

, R

0

2

, V

0

to tzw. wartości

krytyczne.

•

Reszty modelu charakteryzują się pożądanymi własnościami (losowością,

symetrią, brakiem autokorelacji.

BADANIE STATYSTYCZNEJ ISTOTNOŚCI

ESTYMATORÓW PARAMETRÓW STRUKTURALNYCH

Po etapie estymacji parametrów modelu ekonometrycznego
musimy zweryfikować statystyczną istotność estymatorów
parametrów strukturalnych tzn. zbadać a posteriori czy
poszczególne zmienne objaśniające mają istotny wpływ na
kształtowanie się zmiennej endogenicznej (objaśnianej).

Algorytm postępowania jest następujący:

 Przyjmujemy,

że

spełnione

są

założenia

metody

najmniejszych kwadratów

 Zakładamy, że składniki losowe ξ

t

(dla t=1,2,…,n) mają

wielowymiarowy rozkład normalny ξ-N(0,

𝛔

2

I

n

)

BADANIE STATYSTYCZNEJ ISTOTNOŚCI

ESTYMATORÓW PARAMETRÓW STRUKTURALNYCH

 Stawiamy hipotezę zerową

H

0

: α

i

= 0

Wobec hipotezy alternatywnej

H

1

: α

i

≠ 0

 Hipoteza zerowa zakłada, że parametr α

i

nieistotnie różni

się od zera tzn. że zmienna x

i

przy której ten parametr się

znajduje wywiera nieistotny wpływ na zmienną objaśnianą

 W przypadku odrzucenia hipotezy H

0

przyjmujemy

hipotezę alternatywną H

1

, która mówi że wartość

parametru istotnie różni się od zera czyli badana zmienna
objaśniająca ma istotny wpływ na zmienną endogeniczną.

BADANIE STATYSTYCZNEJ ISTOTNOŚCI

ESTYMATORÓW PARAMETRÓW STRUKTURALNYCH

 Weryfikację hipotez dotyczących istotności parametrów

strukturalnych prowadzi się korzystając z testu opartego na

rozkładzie statystyki t-studenta określonej wzorem:

Gdzie: ma rozkład studenta o n-k stopniach swobody

a

i

estymator i-tego parametru strukturalnego

α

i

prawdziwa wartość i-tego parametru (zgodnie z

hipotezą zerową α

i

= 0

D(a

i

)

błąd średni szacunku parametru.

BADANIE STATYSTYCZNEJ ISTOTNOŚCI

ESTYMATORÓW PARAMETRÓW STRUKTURALNYCH

 Dla każdego parametru strukturalnego wyznaczamy wartość statystyki t

empirycznego (tzw. t

emp

).

 Następnie z tablic rozkładu t-studenta dla przyjętego poziomu istotności

α oraz dla n-k stopni swobody odczytujemy wartość krytyczną t

α

.

 WNIOSKOWANIE:
Jeżeli spełniona jest nierówność

|t

emp

|>t

α

to hipotezę H

0

należy odrzucić na korzyść hipotezy alternatywnej H

1

.

Oznacza to, że badany parametr jest statystycznie istotny i zmienna
objaśniająca przy której ten parametr się znajduje ma istotny wpływ na
kształtowanie się zmiennej endogenicznej.
W przypadku gdy

|t

emp

|≤t

α

Nie ma podstaw do odrzucenia hipotezy zerowej. Zmienna objaśniająca przy
której ten parametr się znajduje wywiera istotny wpływ na zmienną Y.

BADANIE STATYSTYCZNEJ ISTOTNOŚCI

ESTYMATORÓW PARAMETRÓW STRUKTURALNYCH

 Weryfikację modelu można uznać za pozytywną w

przypadku istotności wszystkich parametrów strukturalnych
modelu ekonometrycznego i można przejść do analizy
dopuszczalności modelu ze względu na wartość wybranych
parametrów struktury stochastycznej, a zatem wybranych
własności rozkładu reszt.

 W przypadku, gdy przynajmniej jeden z parametrów

strukturalnych

jest

statystycznie

nieistotny

model

ekonometryczny należy odrzucić w całości i rozpocząć
procedurę badań ekonometrycznych od nowa w kolejnych
etapach badań.

BADANIE WYBRANYCH WŁASNOŚCI SKŁADNIKA

RESZTOWEGO MODELU.

Poprawność konstrukcji modelu i jego przydatność
praktyczną determinują także pewne własności, którymi
powinny się charakteryzować rozkłady reszt modelu jako
realizacje składnika losowego.

 W procesie weryfikacji niezbędne jest zbadanie

 Losowości reszt

 Symetrii reszt

 Autokorelacji reszt

BADANIE LOSOWOŚCI RESZT MODELU

.

1. Dla ciągu n obserwacji wyznaczamy reszty u

t

= y

t

- , które

są różnicą pomiędzy rzeczywiście zaobserwowaną wartością
zmiennej objaśnianej, a jej wartością wyznaczoną z modelu.

2. Następnie resztom dodatnim u

t

> 0 przypisuje się symbole A

zaś resztom ujemnym u

t

< 0 przypisuje się symbole B

wartości u

t

= 0 nie bierze się pod uwagę

3. Tworzymy w ten sposób ciąg złożony z symboli A i B. W

utworzonym ciągu elementy jednego rodzaju (podciągi) A lub
B następujące bezpośrednio po sobie noszą nazwę serii.

4. Na podstawie ciągu empirycznego określamy liczbę serii tzw.

k

emp

empiryczne.

BADANIE LOSOWOŚCI RESZT MODELU.

5. Testem wykorzystywanym do weryfikacji hipotezy o

losowości reszt jest

tzw. test liczby serii.

Dla n

1

(liczba

symboli A) i dla n

2

(liczba symboli B) oraz przyjętego

poziomu istotności α odczytujemy z Tablic liczby serii taką

wartość krytyczną kα, że P{k ≤ kα} = α

6. WNIOSKOWANIE
Jeżeli
k

emp

> k

α

nie ma podstaw do odrzucenia hipotezy o losowości

reszt, a więc reszty mają charakter losowy

k

emp

≤k

α

to hipotezę o losowości reszt należy odrzucić co

powinno skutkować modyfikacją postaci analitycznej

modelu, powtórnym szacowaniem parametrów i kolejną

weryfikacją.

BADANIE LOSOWOŚCI RESZT MODELU.

• Przykład.
Ciąg reszt ma postać

BBAABAAAB

K

emp

= 5

Z Tablic liczby serii dla n

1

= 5 i n

2

= 4

K

α=0,05

= 2

K

emp

= 5 > k

α

= 2

Nie ma podstaw do odrzucenia hipotezy o losowości reszt

(reszty modelu mają charakter losowy).

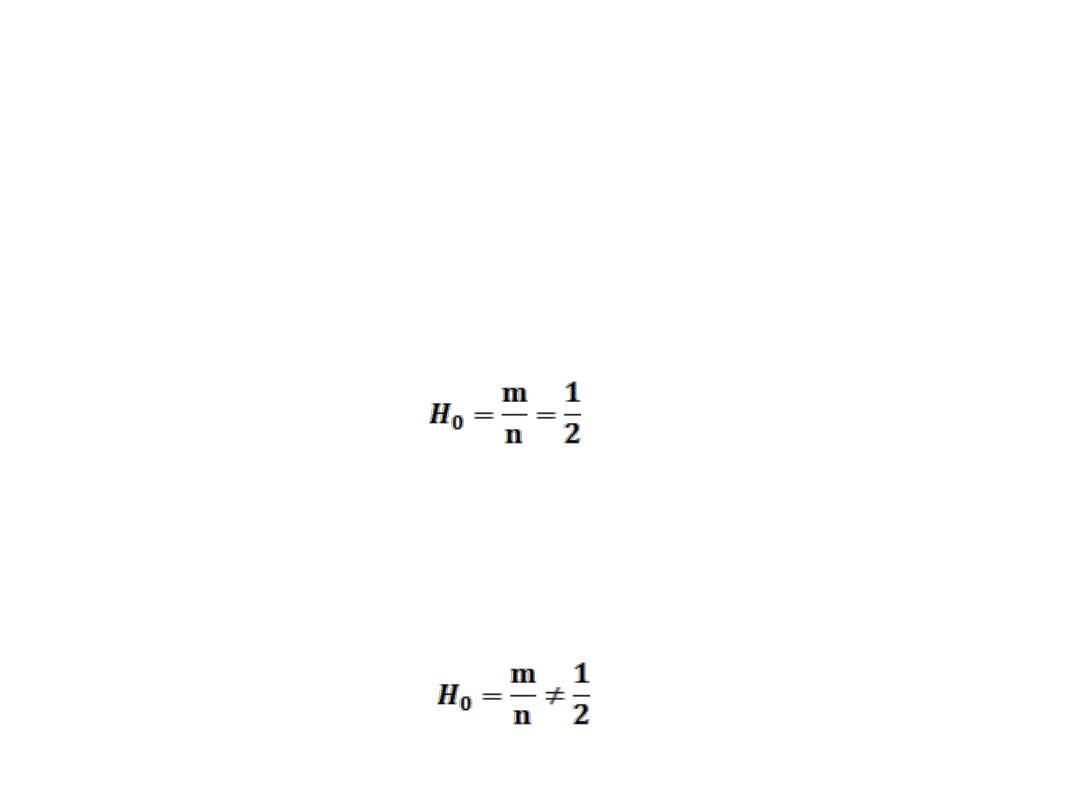
BADANIE SYMETRII SKŁADNIKA RESZTOWEGO.

Symetria rozkładu reszt jest rozumiana jako równość częstości
występowania obserwacji odchylających się in plus bądź in
minus od wartości modelowych.
• Weryfikując symetrię składnika resztowego formułujemy

hipotezę zerową, która mówi, że składnik resztowy ma
rozkład symetryczny

gdzie : m jest liczbą reszt dodatnich (odchylających się in

plus)

wobec hipotezy alternatywnej, mówiącej że rozkład składnika
resztowego jest niesymetryczny

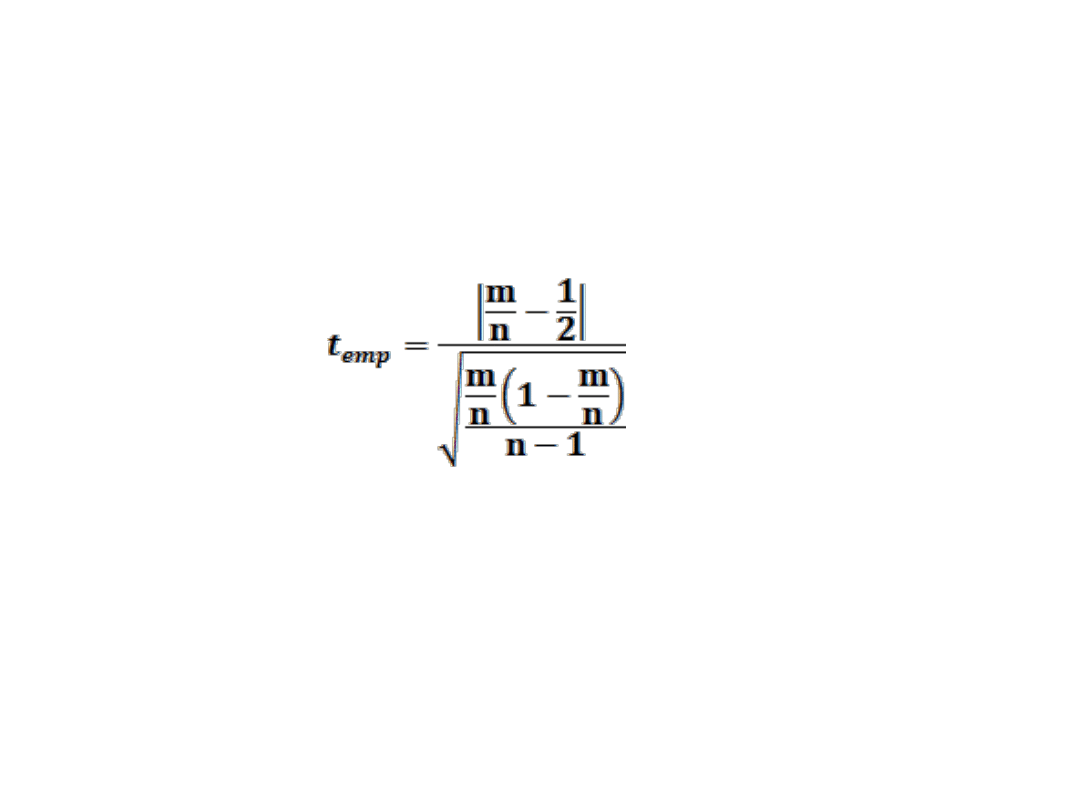
BADANIE SYMETRII SKŁADNIKA RESZTOWEGO.

• Statystyka weryfikująca hipotezę H

0

jest następująca

dla małej próby liczba obserwacji n ≤ 30 statystyka t ma
rozkład t-studenta o n-1 stopniach swobody

dla n > 30 (duża próba) ma rozkład normalny

BADANIE SYMETRII SKŁADNIKA RESZTOWEGO.

Jeżeli

t

emp

≤ t

α

Dla przyjętego poziomu istotności α oraz n-1 stopni swobody
Nie ma podstaw do odrzucenia hipotezy H

0

, a zatem można

wyprowadzić wniosek o symetrii składnika resztowego
Jeżeli

t

emp

> t

α

Hipotezę H

0

należy odrzucić na korzyść hipotezy

alternatywnej co oznacza powrót do etapu konstrukcji
modelu w tym w szczególności jego postaci analitycznej.

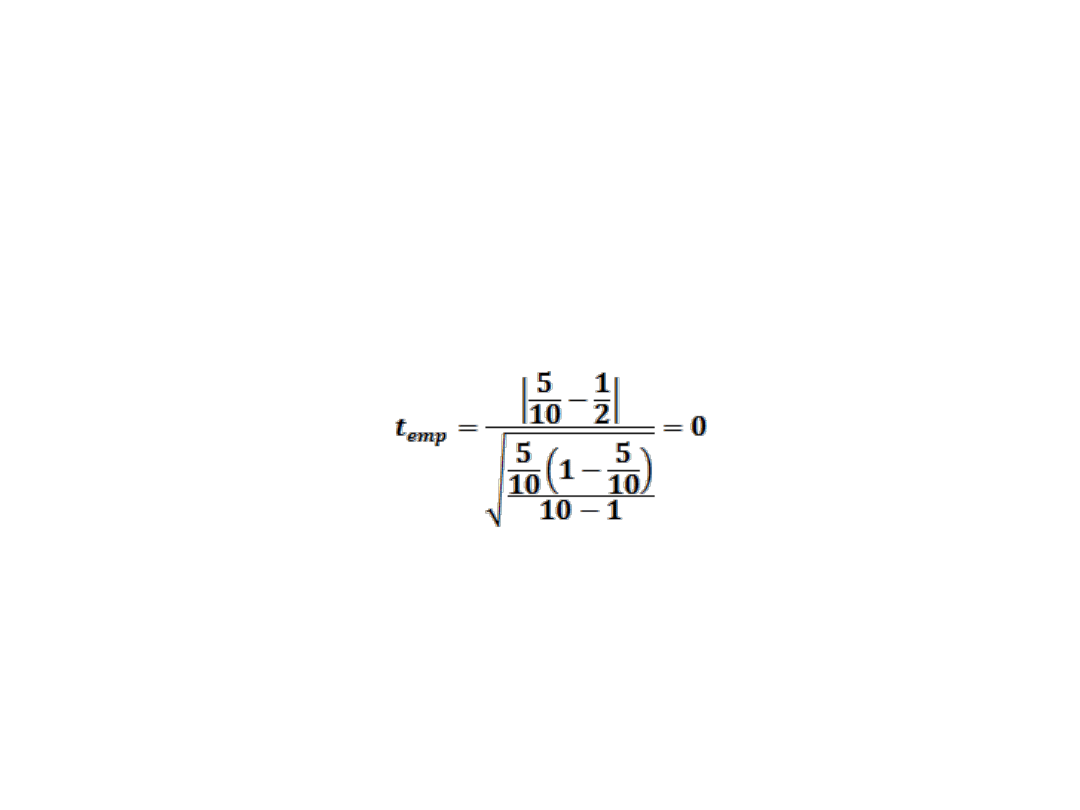
BADANIE SYMETRII SKŁADNIKA RESZTOWEGO

 Przykład
m=5 liczba reszt dodatnich

n=10 liczba wszystkich reszt

t

emp

=0 < t

α=0,05;9

=2,262

nie ma podstaw do odrzucenia hipotezy H

0

o symetrii

składnika resztowego.

BADANIE AUTOKORELACJI RESZT.

Autokorelacja składnika resztowego to korelacja pomiędzy zmienną

losową ξ

t

oraz ξ

t-τ

gdzie τ jest liczbą okresów oddalenia

0 ≤ τ < n

Podstawowe przyczyny występowania autokorelacji składników
losowych to:

1.

Działanie czynników przypadkowych przez okres czasu dłuższy

niż okres przyjęty za jednostkę.

2.

Błędy konstrukcyjne modelu polegające na:

•

pominięcie

zmiennej

(zmiennych)

objaśniającej

istotnie

oddziałującej na zmienną endogeniczną (objaśnianą),

•

wprowadzenie do modelu zmiennej z niewłaściwym opóźnieniem
czasowym,

•

źle dobrana postać analityczna modelu.

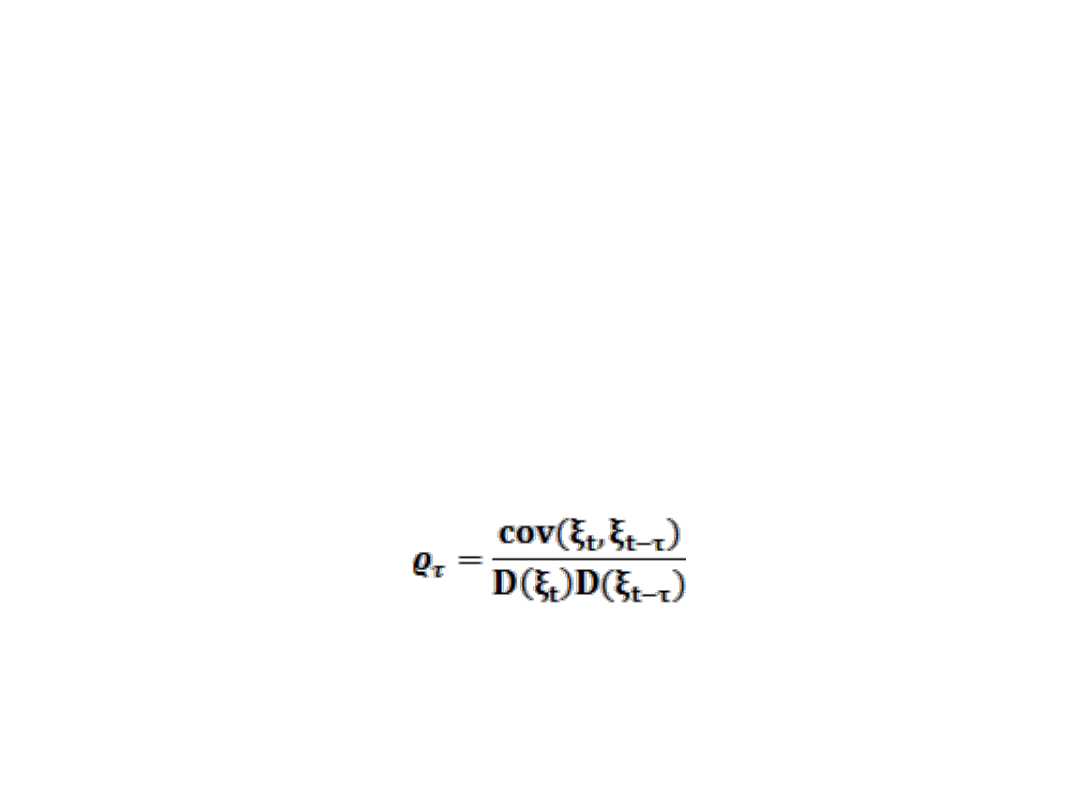
BADANIE AUTOKORELACJI RESZT.

• Miernikami autokorelacji są tzw. współczynniki autokorelacji

ρ. Współczynnik autokorelacji rzędu pierwszego mierzy
zależność pomiędzy bezpośrednio po sobie następującymi
zmiennymi, współczynnik rzędu drugiego mierzy zależność
między zmiennymi odległymi o dwie jednostki wskaźnika t
itd..

• Współczynnik autokorelacji rzędu τ wyraża się wzorem

• Współczynnik autokorelacji rzędu zerowego zawsze jest równy

1, zaś wyższych rzędów w przedziale [-1,1]

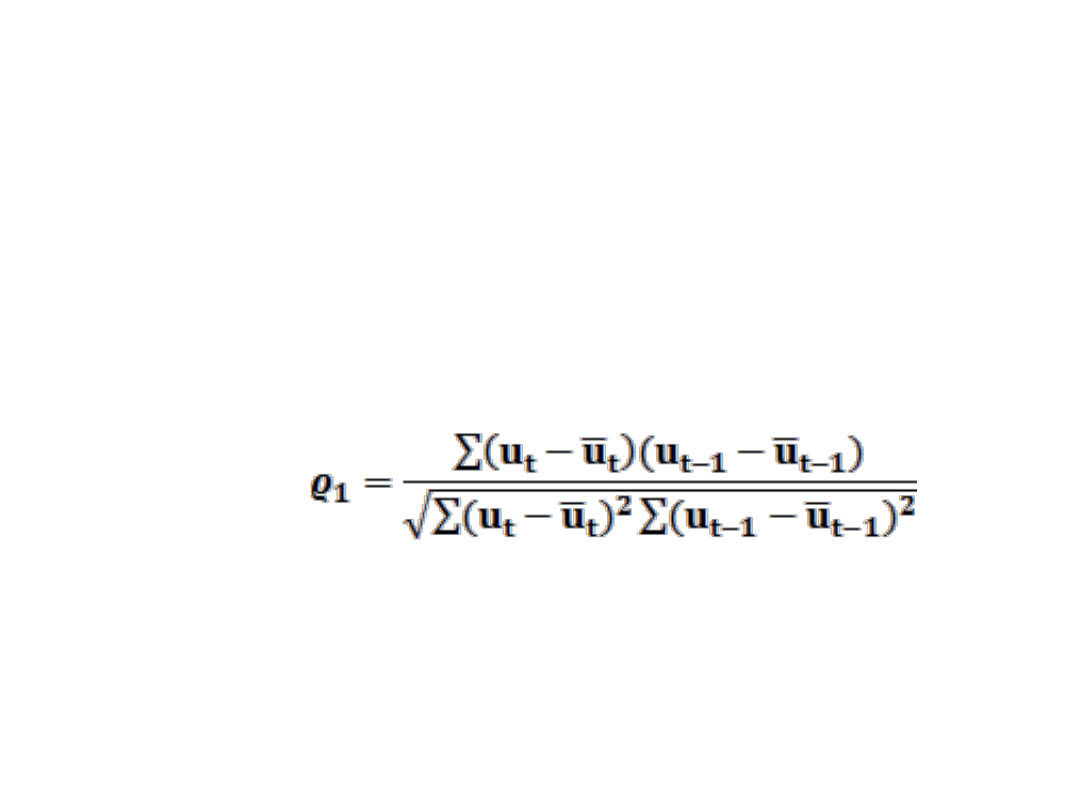
BADANIE AUTOKORELACJI RESZT.

W praktyce nie znamy współczynnika autokorelacji
składnika losowego i stąd wyznaczamy współczynniki
autokorelacji

składnika

resztowego.

Współczynnik

autokorelacji reszt rzędu pierwszego tj. pomiędzy u

t

i u

t-1

wynosi:

Wartości ϱ1 bliskie zeru mówią o braku autokorelacji
składnika resztowego (losowego) rzędu pierwszego.

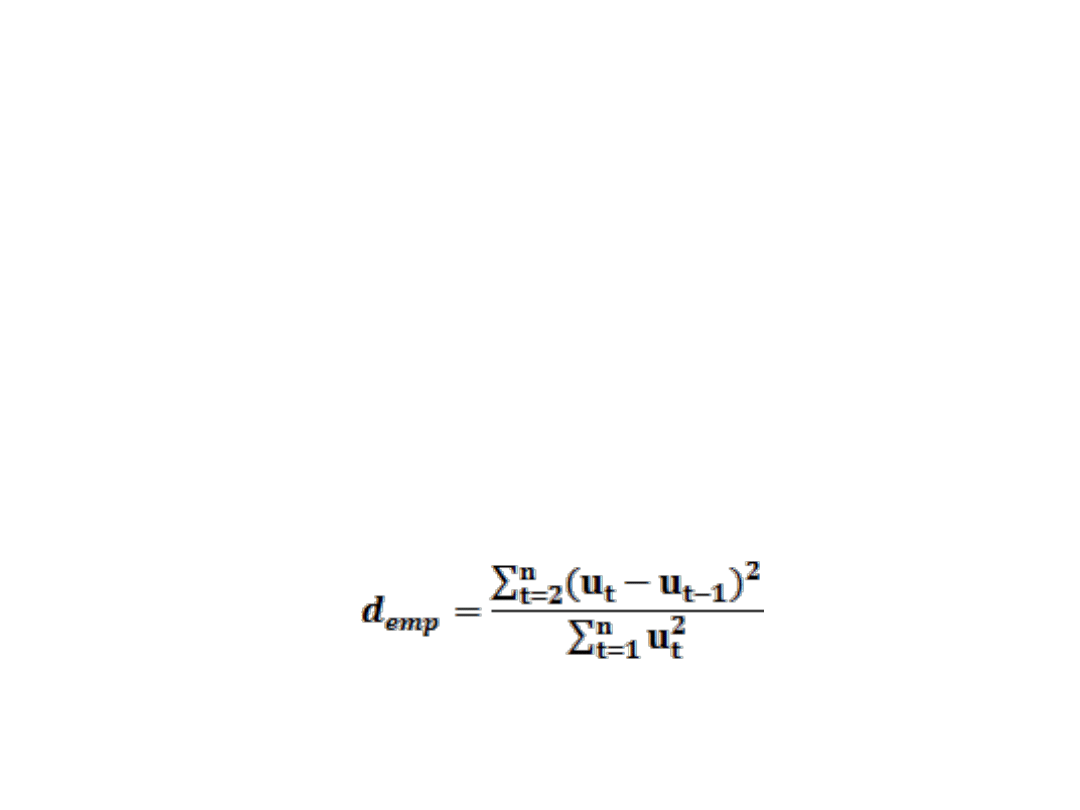
BADANIE AUTOKORELACJI RESZT.

Badamy istotność współczynnika autokorelacji, weryfikują
hipotezę

H

0

: ϱ

1

= 0

mówiącej o braku autokorelacji reszt modelu wobec hipotezy
alternatywnej

H

1

: ϱ

1

≠ 0

informującej o występowaniu autokorelacji reszt.
Statystyka za pomocą której prowadzi się weryfikację ma postać:

BADANIE AUTOKORELACJI RESZT.

Statystyka d ma rozkład Durbina - Watsona, który jest funkcją
dwóch parametrów: n – liczba obserwacji; k – liczba zmiennych
objaśniających

Dla przyjętego poziomu istotności α oraz n i k stopni swobody z
tablic Durbina-Watsaona odczytujemy dwie wartości krytyczne
d

L

(wartość dolna) oraz d

U

(wartość górna).

Jeżeli d

emp

< d

L

odrzucamy hipotezę zerową,

Jeżeli d

emp

> d

U

nie ma podstaw do odrzucenia hipotezy zerowej.

W przypadku jeżeli d

L

≤ d

emp

≤ d

U

nie można podjąć żadnej

decyzji i trzeba stosować inne testy istotności.

BADANIE AUTOKORELACJI RESZT.

Hipoteza alternatywna potwierdza występowanie

autokorelacji dodatniej (H

1

: ϱ

1

> 0) dla d

emp

<2

autokorelacji ujemnej (H

1

: ϱ

1

< 0) dla d

emp

>2

a sprawdzianem jest statystyka d’ = 4 – d

emp

Stwierdzenie

autokorelacji

skłania

do

zastosowania

uogólnionej MNK przy estymacji modelu.

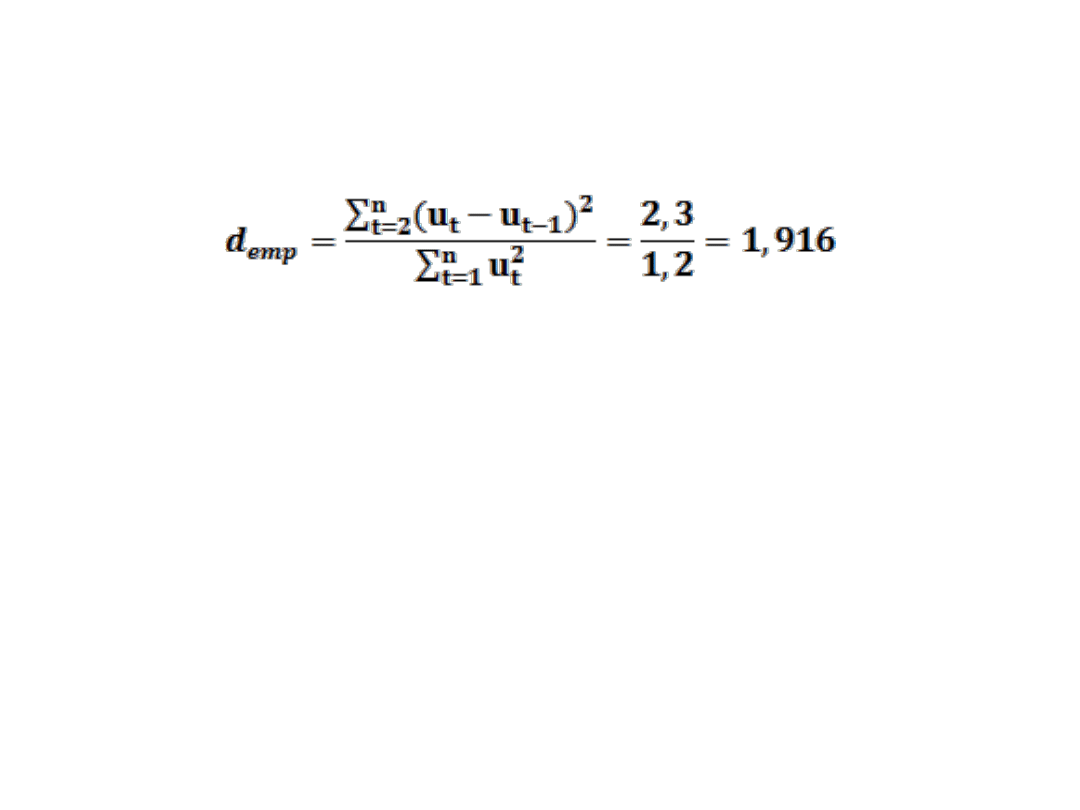
BADANIE AUTOKORELACJI RESZT.

Dla n=10
α = 0,05 k = 2
d

L

= 0,697

d

U

= 1,641

d

emp

= 1,916 > d

U

= 1,641

Nie ma podstaw do odrzucenia hipotezy H

0

o braku

autokorelacji czyli autokorelacja składnika resztowego nie

występuje.