Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
71
35
Pochodna funkcji
Niech funkcja f b dzie okre lona przynajmniej na otoczeniu punktu
0
x
.
Ilorazem ró nicowym
funkcji f w
punkcie
0
x
odpowiadaj cym przyrostowi x
∆ zmiennej niezale nej nazywamy liczb
(
) ( )
x
x
f
x
x
f
x
f
∆
−
∆
+
=
∆
∆
0
0
.
Definicja.
Pochodn funkcji
f w punkcie x nazywamy granic (0 ile ta granica istnieje)
(
) ( )
x
x
f
x
x
f
x
f
x
∆
−
∆
+
=
′
→
∆
0
lim
)
(
.
Je li granica ta jest sko czona (wła ciwa), to mówimy, e funkcja jest ró niczkowalna w punkcie.
Do obliczania pochodnej w konkretnym punkcie wygodniejszy jest wzór
( )
( ) ( )
0
0
0
0
lim
x
x
x
f
x
f
x
f
x
x
−
−
=
′
→
.
Zadanie 1.
Korzystaj c z definicji obliczy pochodn funkcji
5
2
)
(
+
=
x
x
f
.
Rozwi zanie.
=
−
+
=
′
→
h
x
f
h
x
f
x
f
h
)
(
)
(
lim
)
(
0
=
+
−
+
+
→
h
x
h
x
h
5
2
5
)
(
2
lim
0
b
a
b
a
b
a
+
−
=
−
2
2
wzoru
ze
korzystamy
=
+
+
+
+
+
−
+
+
=
→
)
5
2
5
)
(
2
(
)
5
2
(
5
)
(
2
lim
0
x
h
x
h
x
h
x
h
=
+
+
+
+
→
)
5
2
5
)
(
2
(
2
lim
0
x
h
x
h
h
h
=
+
+
+
+
→
5
2
5
)
(
2
2
lim
0
x
h
x
h
=
+
=
5
2
2
2
x
5
2
1
+
x
Zadanie 2.
Korzystaj c z definicji obliczy pochodn funkcji
1
)
(
2
+
= x
x
f
w punkcie
1
0
−
=
x
.
Rozwi zanie.
1
)
1
(
)
(
lim
)
1
(
1
+
−
−
=
−
′
−
→
x
f
x
f
f
x
=
+
−
+
=
−
→
1
2
1
lim
2
1
x
x
x
=
+
−
−
→
1
1
lim
2
1
x
x
x
=
+
+
−
−
→
1
)
1
)(
1
(
lim
1
x
x
x
x
2
)
1
(
lim
1
−
=
−
−
→
x
x
Definicja.
Pochodn lewostronn funkcji
f w punkcie
0
x nazywamy granic
( )
( ) ( )
0
0
0
0
lim
x
x
x
f
x
f
x
f
x
x
−
−
=
′
−
→
−
.
Pochodn prawostronn funkcji
f w punkcie
0
x nazywamy granic
( )
( ) ( )
0
0
0
0
lim
x
x
x
f
x
f
x
f
x
x
−
−
=
′
+
→
+
.
Fakt.
Warunkiem istnienia pochodnej funkcji f w punkcie
0
x jest istnienie i równo pochodnych jednostronnych funkcji w
tym punkcie:
( )
( )
0
0
x
f
x
f
+
−
′
=
′
.
Zadanie 3.
Korzystaj c z definicji obliczy pochodn w punkcie
0
0
=
x
funkcji
<
−
≥
=
0
0
)
(
2
2
x
x
x
x
x
f
dla
dla
.
Rozwi zanie.
Warunkiem istnienia pochodnej funkcji f w punkcie
0
0
=
x
jest istnienie i równo pochodnych jednostronnych funkcji
w tym punkcie. Je li s one przy tym wła ciwe – funkcja f jest ró niczkowalna w punkcie
0
0
=
x
.
Pochodna lewostronna:
x
f
x
f
f
x
)
0
(
)
(
lim
)
0
(
0
−
=
′
−
→
−
x
x
x
0
lim
2
0
−
−
=
−
→
0
)
(
lim
0
=
−
=
−
→
x
x
.
Pochodna prawostronna:
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
72
x
f
x
f
f
x
)
0
(
)
(
lim
)
0
(
0
−
=
′
+
→
+
x
x
x
0
lim
2
0
−
=
+
→
0
lim
0
=
=
+
→
x
x
.
Pochodne jednostronne s równe, wi c
0
)
0
(
=
′
f
.
Zadanie 4.
Korzystaj c z definicji obliczy pochodn funkcji
<
+
≥
=
0
1
0
cos
)
(
x
x
x
x
x
f
dla
dla
w punkcie
0
0
=
x
.
Rozwi zanie.
x
f
x
f
f
x
)
0
(
)
(
lim
)
0
(
0
−
=
′
−
→
−
x
x
x
1
cos
lim
0
−
=
−
→
x
x
x
0
cos
cos
lim
0
−
=
−
→
2
sin
2
sin
2
cos
cos
α
+
β
⋅
α
−
β
=
β
−
α
wzoru
ze
korzystamy
=
=
⋅
−
=
−
→
x
x
x
x
2
sin
2
sin
2
lim
0
=
−
⋅
=
−
−
→
→
2
sin
lim
2
2
sin
lim
0
0
x
x
x
x
x
1
sin
lim
0
=
→
t
t
t
wzoru
ze
korzystamy
0
0
1
=
⋅
=
x
f
x
f
f
x
)
0
(
)
(
lim
)
0
(
0
−
=
′
+
→
+
x
x
x
1
1
lim
0
−
+
=
+
→
1
lim
0
=
=
+
→
x
x
x
.
Pochodne jednostronne s ró ne, wi c
)
0
(
f ′
nie istnieje.
Fakt.
Je eli funkcja f jest ró niczkowalna w punkcie, to jest ci gła w tym punkcie.
(Ci gło funkcji w punkcie jest warunkiem koniecznym istnienia jej pochodnej w tym punkcie)
Ci gło nie jest warunkiem wystarczaj cym dla istnienia pochodnej.
Zadanie 5.
Zbada ci gło i ró niczkowalno funkcji
1
)
(
+
= x
x
f
w punkcie
1
0
−
=
x
.
Rozwi zanie.
Funkcja f jest ci gła, gdy jest funkcj elementarn (
2
)
1
(
1
)
(
+
=
+
=
x
x
x
f
) – jest wi c ci gła w punkcie
1
0
−
=
x
.
Ponadto
−
<
−
−
−
≥
+
=
1
1
1
1
)
(
x
x
x
x
x
f
dla
dla
Funkcja nie ma pochodnej (i dlatego nie jest ró niczkowalna) w punkcie
1
0
−
=
x
, gdy
1
)
1
(
)
(
lim
)
1
(
1
+
−
−
=
−
′
−
−
→
−
x
f
x
f
f
x
1
1
)
1
(
lim
1
0
1
lim
1
1
−
=
+
+
−
=
+
−
−
−
=
−
−
−
→
−
→
x
x
x
x
x
x
;
1
)
1
(
)
(
lim
)
1
(
1
+
−
−
=
−
′
+
−
→
+
x
f
x
f
f
x
1
1
0
1
lim
1
=
+
−
+
=
+
−
→
x
x
x
.
Zadanie 6.
Zbada ci gło i ró niczkowalno funkcji
3
)
(
x
x
f
=
w punkcie
0
0
=
x
.
Rozwi zanie.
Funkcja
3
)
(
x
x
f
=
jest – jako funkcja elementarna – ci gła w całej dziedzinie, równej R. Dlatego w punkcie
0
0
=
x
jest
ci gła.
∞
=
=
=
−
=
−
−
=
′′
→
→
→
→
3 2
0
3
0
3
0
0
1
lim
lim
0
lim
0
)
0
(
)
(
lim
)
0
(
x
x
x
x
x
x
f
x
f
f
x
x
x
x
Funkcja
3
)
(
x
x
f
=
ma w punkcie
0
0
=
x
pochodn niewła ciw . Zatem nie jest ró niczkowalna w tym punkcie.
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
73
Definicja.
Niech funkcja f b dzie ró niczkowaln w ka dym punkcie x
∈(a, b) (przedział otwarty).
Pochodn funkcji f na przedziale (a, b) nazywamy funkcj f ′ , przyjmuj c w ka dym punkcie x przedziału
(a, b) warto
)
(x
f ′
.
Je eli przedział [a, b] jest domkni ty – na ko cach przedziału rozpatrujemy pochodne jednostronne.
•
Twierdzenie (o działaniach arytmetycznych na pochodnych):
Je li funkcje f i g s ró niczkowalne w punkcie x, to
[
]
)
(
)
(
)
(
)
(
x
g
x
f
x
g
x
f
′
+
′
=
′
+
[
]
)
(
)
(
)
(
)
(
x
g
x
f
x
g
x
f
′
−
′
=
′
−
[
]
)
(
)
(
)
(
)
(
)
(
)
(
x
g
x
f
x
g
x
f
x
g
x
f
′
⋅
+
⋅
′
=
′
⋅
[ ]
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
x
g
x
g
x
f
x
g
x
f
x
g
x
f
′
⋅
−
⋅
′
=
′
•
Twierdzenie (o pochodnej funkcji zło onej):
Je li funkcja f jest ró niczkowalna w punkcie x, za funkcja g jest ró niczkowalna w punkcie y = f(x), to ró niczkowalna
w punkcie x jest funkcja
f
g
i ponadto
(
)
)
(
)
(
)
(
)
(
x
f
x
f
g
x
f
g
′
⋅
′
=
′
•
Twierdzenie (o pochodnej funkcji odwrotnej):
Je li funkcja odwracalna (ró nowarto ciowa) f jest ró niczkowalna w przedziale (a, b) oraz
0
)
(
≠
′ x
f
w ka dym punkcie
tego przedziału, to funkcja
1
−
f
jest te ró niczkowalna i przy tym
(
)
)
(
1
)
(
1
)
(
)
(
1
1
x
f
f
y
f
x
f
−
−
′
=
′
=
′
Pochodne obliczamy przy pomocy wzorów.
′
⋅
⋅
=
−1
)
(
k
k
dx
d
k
2
)
(
′
=
dx
d
n n
n
dx
d
n
1
)
(
−
′
=
′
⋅
=
)
(cos
)
(sin
dx
d
′
⋅
−
=
)
sin
(
)
(cos
dx
d
2
cos
)
(
′
=
tg
dx
d
2
sin
)
(
′
−
=
ctg
dx
d
2
1
)
(
−
′
=
arcsin
dx
d
2
1
)
(
−
′
−
=
arccos
dx
d
2
1
)
(
+
′
=
arctg
dx
d
2
1
)
(
+
′
−
=
arcctg
dx
d
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
74
′
⋅
=
a
a
a
dx
d
ln
)
(
′
⋅
= e
e
dx
d
)
(
a
a
dx
d
ln
)
(lg
⋅
′
=
′
=
)
(ln
dx
d
Zadanie 7.
Obliczy pochodn funkcji
1
)
(
+
= x
x
f
.
Rozwi zanie.
−
<
−
−
−
≥
+
=
1
1
1
1
)
(
x
x
x
x
x
f
dla
dla
−
<
−
−
>
=
′
1
1
1
1
)
(
x
x
x
f
dla
dla
Funkcja nie jest ró niczkowalna w punkcie
1
0
−
=
x
, gdy
1
)
1
(
)
(
lim
)
1
(
1
+
−
−
=
−
′
−
−
→
−
x
f
x
f
f
x
1
1
0
1
lim
1
=
+
−
+
=
−
−
→
x
x
x
;
1
)
1
(
)
(
lim
)
1
(
1
+
−
−
=
−
′
+
−
→
+
x
f
x
f
f
x
1
1
0
1
lim
1
−
=
+
−
−
−
=
+
−
→
x
x
x
.
Zadanie 8.
Obliczy pochodn funkcji
x
x
x
f
3
)
(
2
−
=
.
Rozwi zanie.
Funkcja okre lona jest przez wzór
∈
+
−
∞
∪
−∞
∈
−
=
−
=
)
3
,
0
(
3
)
,
3
[
]
0
,
(
3
3
)
(
2
2
2
x
x
x
x
x
x
x
x
x
f
dla
dla
Jej pochodna jest równa
∈
+
−
∞
∪
−∞
∈
−
=
′
)
3
,
0
(
3
2
)
,
3
(
)
0
,
(
3
2
)
(
x
x
x
x
x
f
dla
dla
)
0
(
f ′
nie istnieje, gdy
3
)
3
2
(
lim
)
0
(
0
−
=
−
=
′
−
→
−
x
f
x
,
3
)
3
2
(
lim
)
0
(
0
=
+
−
=
′
+
→
+
x
f
x
;
)
3
(
f ′
nie istnieje, gdy
3
)
3
2
(
lim
)
3
(
3
−
=
+
−
=
′
−
→
−
x
f
x
,
3
)
3
2
(
lim
)
3
(
3
=
−
=
′
−
→
+
x
f
x
.
Zadanie 9.
Obliczy pochodn funkcji
≤
>
=
0
0
0
ln
)
(
x
x
x
x
f
dla
dla
.
Rozwi zanie.
<
>
=
′
0
0
0
)
(
1
x
x
x
f
x
dla
dla
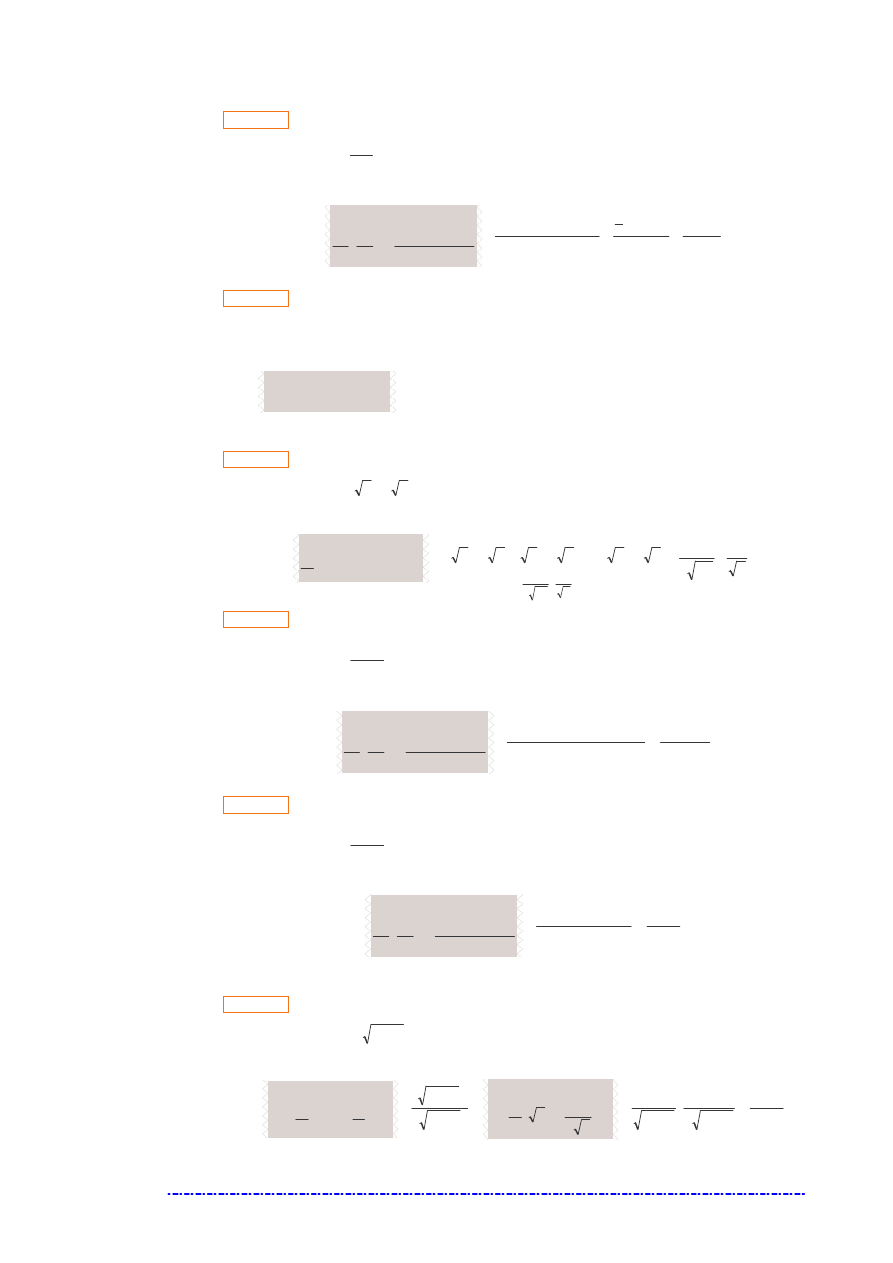
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
75
Pochodna
)
0
(
f ′
nie istnieje, gdy funkcja f nie jest ci gła w punkcie
0
=
x
.
Zadanie 10.
Oblicz pochodn funkcji
x
x
x
f
ln
)
(
=
.
Rozwi zanie.
=
′ )
(x
f
2
M
M
L
M
L
M
L
dx
d
′
⋅
−
⋅′
=
wzoru
ze
korzystamy
2
2
1
2
ln
1
ln
)
(
ln
)
(ln
x
x
x
x
x
x
x
x
x
x
x
−
=
−
⋅
=
′
⋅
−
⋅′
=
Zadanie 11.
Oblicz pochodn funkcji
x
e
x
x
f
−
=
3
)
(
.
Rozwi zanie.
=
′ )
(x
f
g
f
g
f
g
f
′
⋅
+
⋅′
=
′
⋅ )
(
wzoru
ze
korzystamy
=
′
⋅
+
⋅′
=
−
−
)
(
)
(
3
3
x
x
e
x
e
x
=
−
⋅
+
⋅
−
−
)
(
3
3
2
x
x
e
x
e
x
)
3
(
2
x
e
x
x
−
−
Zadanie 12.
Oblicz pochodn funkcji
3
3
)
2
(
)
(
x
x
x
f
−
=
.
Rozwi zanie.
=
′ )
(x
f
′
⋅
⋅
=
−1
)
(
k
k
dx
d
k
wzoru
ze
korzystamy
(
) (
)
′
−
−
=
−
x
x
x
x
x
x
1
3
1
3
2
3
3
2
2
2
3
(
)
−
−
=
x
x
x
x
1
3
1
2
3
3 2
2
3
Zadanie 13.
Oblicz pochodn funkcji
1
1
)
(
2
2
+
−
=
x
x
x
f
Rozwi zanie.
=
′ )
(x
f
2
M
M
L
M
L
M
L
dx
d
′
⋅
−
⋅′
=
wzoru
ze
korzystamy
2
2
2
2
2
2
)
1
(
4
)
1
(
2
)
1
(
)
1
(
2
+
=
+
⋅
−
−
+
⋅
=
x
x
x
x
x
x
x
Zadanie 14.
Oblicz pochodn funkcji
x
x
x
f
2
1
)
(
+
=
Rozwi zanie.
=
′ )
(x
f
2
M
M
L
M
L
M
L
dx
d
′
⋅
−
⋅′
=
wzoru
ze
korzystamy
2
2
2
2
1
1
)
1
(
2
x
x
x
x
x
x
−
=
⋅
+
−
⋅
=
Zadanie 15.
Oblicz pochodn funkcji
2
1
ln
)
(
x
x
f
+
=
Rozwi zanie.
=
′ )
(x
f
′
=
)
(ln
dx
d
wzoru
ze
korzystamy
=
+
′
+
=
2
2
1
)
1
(
x
x
2
)
(
′
=
dx
d
wzoru
ze
korzystamy
1
1
2
2
1
1
2
2
2
+
=
+
⋅
+
=
x
x
x
x
x
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
76
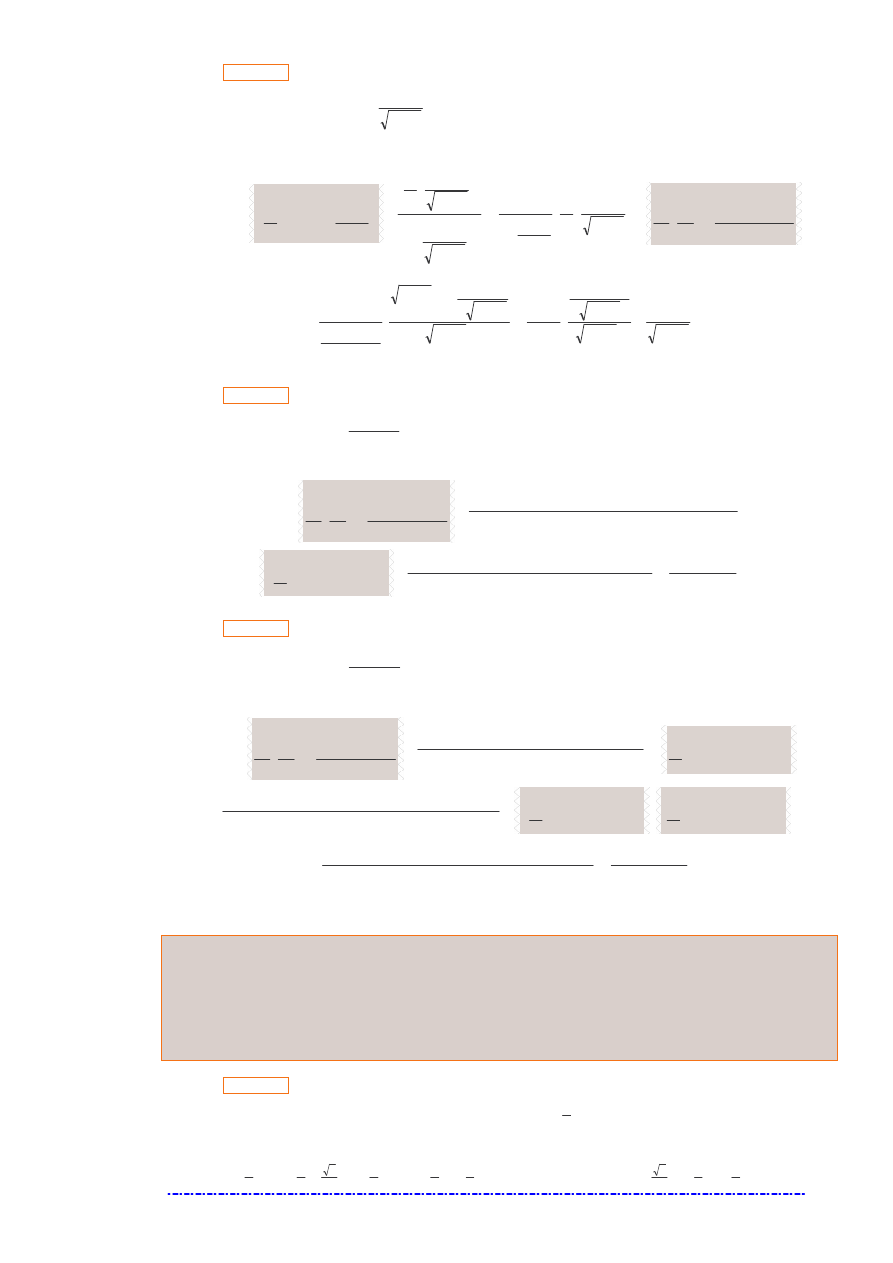
Zadanie 16.
Oblicz pochodn funkcji
2
1
)
(
x
x
x
f
−
= arctg
=
′ )
(x
f
2
1
)
(
+
′
=
arctg
wzoru
ze
korzystamy
dx
d
=
−
+
−
=
2
2
2
1
1
1
x
x
x
x
dx
d
=
−
⋅
−
+
2
2
2
1
1
1
1
x
x
x
x
dx
d
2
M
M
L
M
L
M
L
dx
d
′
⋅
−
⋅′
=
wzoru
ze
korzystamy
2
2
2
2
2
2
2
)
1
(
1
2
2
1
1
1
1
x
x
x
x
x
x
x
x
−
−
−
⋅
−
−
⋅
−
+
−
=
2
2
2
2
2
2
2
1
1
)
1
(
1
1
1
1
x
x
x
x
x
x
−
=
−
−
+
−
⋅
−
=
Zadanie 17.
Oblicz pochodn funkcji
x
x
x
f
2
sin
1
2
sin
1
)
(
−
+
=
=
′ )
(x
f
2
M
M
L
M
L
M
L
dx
d
′
⋅
−
⋅′
=
wzoru
ze
korzystamy
=
−
′
−
⋅
+
−
−
⋅′
+
=
2
)
2
sin
1
(
)
2
sin
1
(
)
2
sin
1
(
)
2
sin
1
(
)
2
sin
1
(
x
x
x
x
x
cos
)
(sin
⋅′
=
dx
d
wzoru
ze
korzystamy
=
−
−
⋅
+
−
−
⋅
=
2
)
2
sin
1
(
)
2
cos
2
(
)
2
sin
1
(
)
2
sin
1
(
2
cos
2
x
x
x
x
x
2
)
2
sin
1
(
2
cos
4
x
x
−
⋅
Zadanie 18.
Oblicz pochodn funkcji
x
x
x
f
2
2
sin
1
cos
)
(
+
=
=
′ )
(x
f
2
M
M
L
M
L
M
L
dx
d
′
⋅
−
⋅′
=
wzoru
ze
korzystamy
=
+
′
+
⋅
−
+
⋅′
=
2
2
2
2
2
2
)
sin
1
(
)
sin
1
(
cos
)
sin
1
(
)
(cos
x
x
x
x
x
′
⋅
⋅
=
−1
)
(
k
k
dx
d
k
wzoru
ze
korzystamy
,
=
+
′
⋅
⋅
−
+
⋅′
⋅
=
2
2
2
2
)
sin
1
(
)
(sin
sin
2
cos
)
sin
1
(
)
(cos
cos
2
x
x
x
x
x
x
x
cos
)
(sin
⋅′
=
dx
d
wzoru
ze
korzystamy
,
sin
)
(cos
⋅′
−
=
dx
d
wzoru
ze
korzystamy
=
+
⋅
⋅
−
+
⋅
−
⋅
=
2
2
2
2
)
sin
1
(
cos
sin
2
cos
)
sin
1
(
)
sin
(
cos
2
x
x
x
x
x
x
x
2
2
)
sin
1
(
cos
sin
4
x
x
x
+
⋅
−
Fakt.
Funkcja f jest ró niczkowalna w punkcie wtedy i tylko wtedy, gdy istnieje styczna do wykresu funkcji w tym punkcie.
Równanie stycznej do wykresu funkcji f ró niczkowalnej w punkcie (x
0
, f(x
0
)) ma w tym punkcie posta
)
)(
(
)
(
0
0
0
x
x
x
f
x
f
y
−
′
+
=
.
Je li w punkcie x = x
0
funkcja f ma pochodn niewła ciw , to styczna do wykresu funkcji w tym punkcie jest postaci
x = x
0
.
Zadanie 19.
Wyznacz równania stycznych do wykresu funkcji
x
x
f
cos
)
(
=
w
6
0
π
=
x
.
Rozwi zanie.
Poniewa
2
3
6
6
cos
)
(
=
=
π
π
f
,
2
1
6
6
sin
)
(
−
=
−
=
′
π
π
f
, wi c styczna ma równanie
)
(
6
2
1
2
3
π
−
−
=
−
x
y
.
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
77
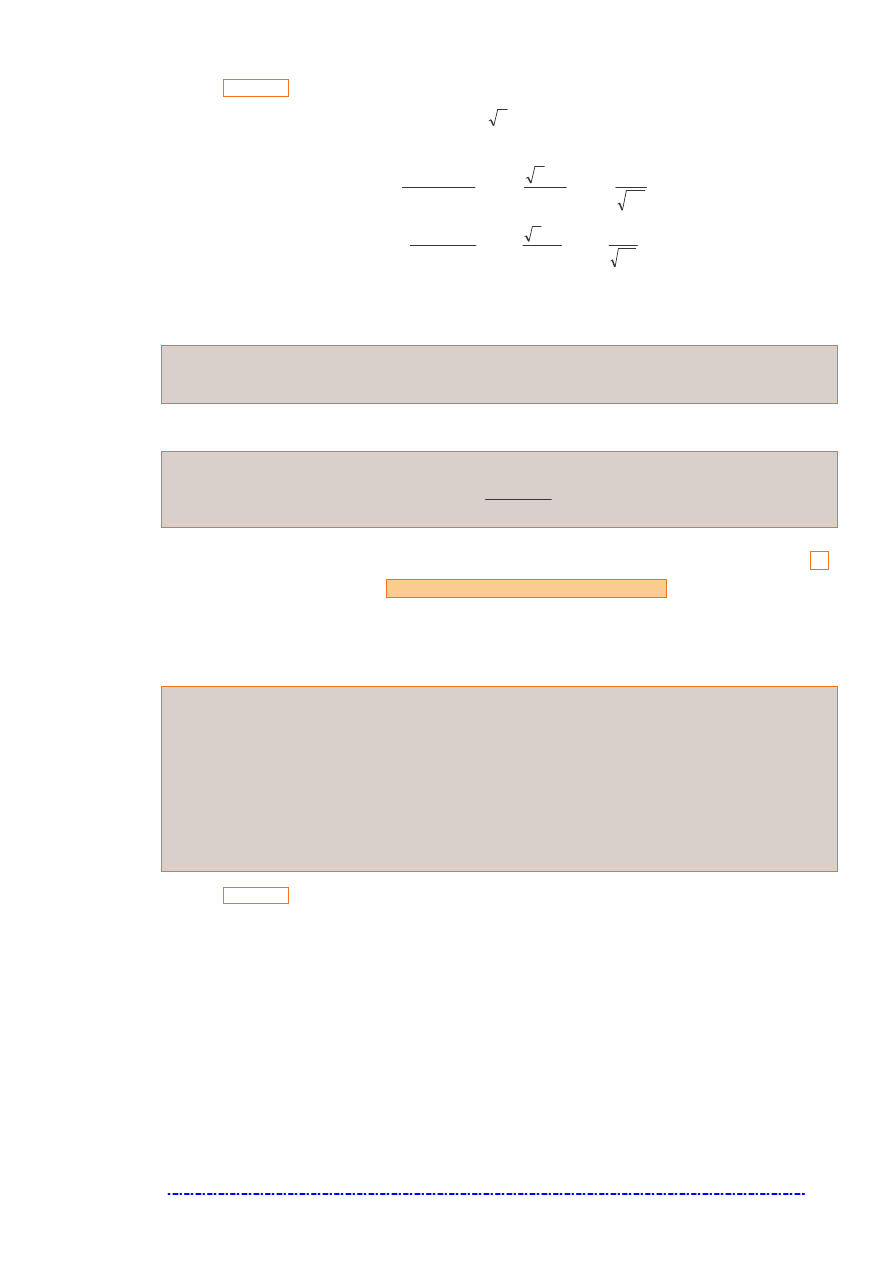
Zadanie 20.
Wyznacz równania stycznych do wykresu funkcji
3
)
(
x
x
f
=
w
0
0
=
x
.
Rozwi zanie.
x
f
x
f
f
x
)
0
(
)
(
lim
)
0
(
0
−
=
′
−
→
−
x
x
x
0
lim
3
0
−
=
−
→
∞
=
=
−
→
3
2
0
1
lim
x
x
,
x
f
x
f
f
x
)
0
(
)
(
lim
)
0
(
0
−
=
′
+
→
+
x
x
x
0
lim
3
0
−
=
+
→
∞
=
=
+
→
3 2
0
1
lim
x
x
.
Styczna ma równanie
0
=
x
.
•
Twierdzenie Rolle’a (o warto ci redniej).
Niech funkcja f b dzie ci gła w [a, b] i ró niczkowalna w (a, b) oraz
)
(
)
(
b
f
a
f
=
. Wówczas istnieje
)
,
( b
a
c
∈
taki, e
0
)
(
=
′ c
f
.
•
Tw. Lagrange’a (o warto ci redniej).
Niech funkcja f b dzie ci gła w [a, b] i ró niczkowalna w (a, b). Wówczas istnieje
)
,
( b
a
c
∈
taki, e
a
b
a
f
b
f
c
f
−
−
=
′
)
(
)
(
)
(
.
36
Badanie monotoniczno ci funkcji
Praktyczne badanie monotoniczno ci funkcji ró niczkowalnej na zbiorze A, zawartym w dziedzinie funkcji,
sprowadza si do wyznaczenia przedziałów (zawartych w A), na których pochodna funkcji przyjmuje ró ne znaki) jest
dodatnia, ujemna, równa zero). Korzystamy przy tym z twierdzenia:
>
′
∀
Γ
∈
0
)
(x
f
x
funkcja f jest rosn ca na
)
,
( b
a
=
Γ
;
≥
′
∀
Γ
∈
0
)
(x
f
x
funkcja f jest niemalej ca na
)
,
( b
a
=
Γ
;
=
′
∀
Γ
∈
0
)
(x
f
x
funkcja f jest stała na
)
,
( b
a
=
Γ
;
≤
′
∀
Γ
∈
0
)
(x
f
x
funkcja f jest nierosn ca na
)
,
( b
a
=
Γ
;
<
′
∀
Γ
∈
0
)
(x
f
x
funkcja f jest malej ca na
)
,
( b
a
=
Γ
.
Zadanie 21.
Wyznaczymy przedziały monotoniczno ci funkcji
3
12
)
(
3
−
+
−
=
x
x
x
f
.
Rozwi zanie.
Funkcja
3
12
)
(
3
−
+
−
=
x
x
x
f
jest funkcj ró niczkowaln . Wyznaczamy jej pochodn :
12
3
)
(
2
+
−
=
′
x
x
f
.
W celu wyznaczenia przedziałów monotoniczno ci podanej funkcji badamy znak jej pochodnej:
{
}
2
,
2
0
)
2
)(
2
(
0
12
3
0
)
(
2
−
∈
⇔
=
+
−
⇔
=
+
−
⇔
=
′
x
x
x
x
x
f
)
2
;
2
(
0
)
2
)(
2
(
0
12
3
0
)
(
2
−
∈
⇔
<
+
−
⇔
>
+
−
⇔
>
′
x
x
x
x
x
f
)
;
2
(
)
2
;
(
0
)
2
)(
2
(
0
12
3
0
)
(
2
∞
∪
−
−∞
∈
⇔
>
+
−
⇔
<
+
−
⇔
<
′
x
x
x
x
x
f
Funkcja
3
12
)
(
3
−
+
−
=
x
x
x
f
maleje w przedziale
)
2
,
(
−
−∞
, ro nie w przedziale
)
2
,
2
(
−
, maleje w przedziale
)
,
2
(
∞ .

Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
78
Uwaga. Punkty
2
−
=
x
i
2
=
x
mo na doł czy do przedziałów, ale nie jest to konieczne! Poniewa wymaga-
łoby to dodatkowej analizy, wi c wygodniej jest takie punkty pomin .
Zadanie 22.
Wyznaczymy przedziały monotoniczno ci funkcji
1
)
(
+
=
x
x
x
f
.
Rozwi zanie
Dziedzin funkcji
1
)
(
+
=
x
x
x
f
jest zbiór
)
∞
= ,
0
[
D
. Funkcja ta jest ró niczkowalna i jej pochodna wynosi:
2
2
2
2
)
1
(
2
1
)
1
(
2
2
1
)
1
(
2
1
)
1
(
)
1
(
)
1
(
)
(
)
(
+
−
=
+
−
+
=
+
−
+
=
+
′
+
⋅
−
+
⋅′
=
′
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f
Badamy znak pochodnej podanej funkcji. Poniewa mianownik jest dodatni dla ka dego
)
;
0
(
∞
∈
x
, wi c o znaku po-
chodnej decyduje wyra enie w liczniku. Dlatego:
1
0
1
0
)
(
=
⇔
=
−
⇔
=
′
x
x
x
f
,
)
1
;
0
(
0
1
0
)
(
∈
⇔
>
−
⇔
>
′
x
x
x
f
,
)
;
1
(
0
1
0
)
(
∞
∈
⇔
<
−
⇔
<
′
x
x
x
f
.
Funkcja
1
)
(
+
=
x
x
x
f
ro nie w przedziale
)
1
,
0
(
, maleje w przedziale
)
,
1
(
∞ .
Zadanie 23.
Wyznaczymy przedziały monotoniczno ci funkcji
x
x
x
f
−
= sin
)
(
,
π
∈
2
,
0
x
.
Rozwi zanie
Funkcja
x
x
x
f
−
= sin
)
(
jest ró niczkowalna i jej pochodna wyra a si wzorem
1
cos
)
(
−
=
′
x
x
f
,
)
2
;
0
(
π
∈
x
.
Badamy znak pochodnej:
)
2
;
0
(
0
1
cos
0
)
(
π
∈
⇔
<
−
⇔
<
′
x
x
x
f
.
Funkcja
x
x
x
f
−
= sin
)
(
maleje w przedziale
π
2
,
0
.
Zadanie 24.
Wyznaczymy przedziały monotoniczno ci funkcji
2
1
ln
)
(
x
x
f
+
=
.
Rozwi zanie
Funkcja
2
1
ln
)
(
x
x
f
+
=
jest okre lona i ró niczkowalna w swojej dziedzinie, tzn. w zbiorze R. Monotoniczno tej
funkcji okre lamy na podstawie znaku jej pochodnej (zobacz zadanie 15):
2
1
)
(
x
x
x
f
+
=
′
Poniewa mianownik jest dodatni dla ka dej liczby rzeczywistej, wi c o znaku pochodnej decyduje wyra enie w liczni-
ku. Zatem
0
0
)
(
>
⇔
>
′
x
x
f
,
0
0
)
(
<
⇔
<
′
x
x
f
.
Funkcja maleje w przedziale
)
0
,
(
−∞
, ro nie w przedziale
)
,
0
(
∞ .
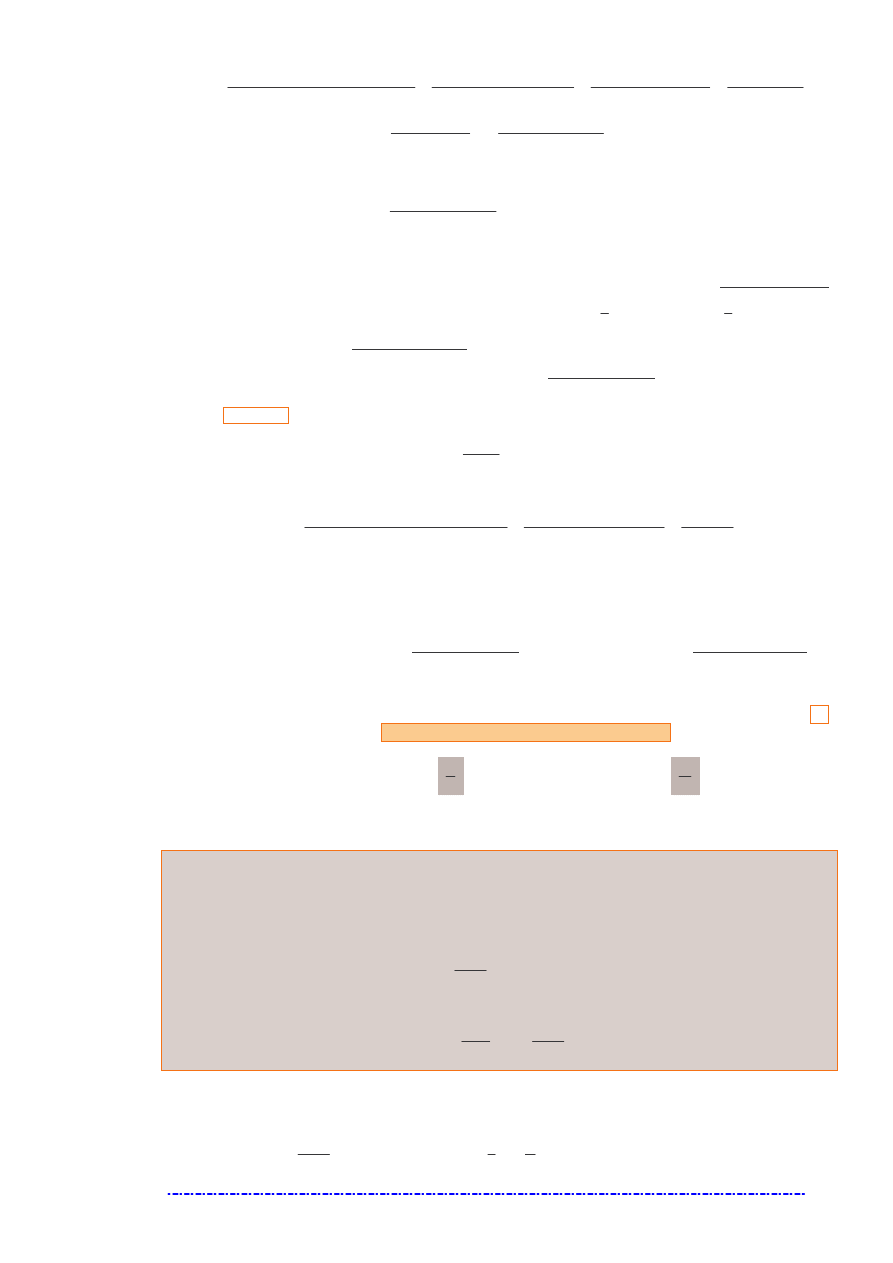
Zadanie 25.
Wyznacz przedziały monotoniczno ci funkcji
1
2
)
(
2
3
+
−
=
x
x
x
f
.
Rozwi zanie
Mamy
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
79
=
+
′
+
−
−
+
′
−
=
′
2
2
2
3
2
3
)
1
(
)
1
)(
2
(
)
1
(
)
2
(
)
(
x
x
x
x
x
x
f
=
+
⋅
−
−
+
2
2
3
2
2
)
1
(
2
)
2
(
)
1
(
3
x
x
x
x
x
=
+
+
−
+
2
2
4
2
4
)
1
(
4
2
3
3
x
x
x
x
x
=
+
+
+
2
2
2
4
)
1
(
4
3
x
x
x
x
=
+
+
+
2
2
3
)
1
(
)
4
3
(
x
x
x
x
2
2
2
)
1
(
)
4
)(
1
(
+
+
−
+
=
x
x
x
x
x
.
Najwygodniej jest zacz od równania:
0
)
(
=
′ x
f
⇔
0
)
1
(
)
4
)(
1
(
2
2
2
=
+
+
−
+
x
x
x
x
x
⇔
0
)
1
(
=
+
x
x
⇔
}
0
,
1
{
−
∈
x
.
Funkcja f ′ jest ci gła na zbiorze
)
,
(
∞
−∞
=
R
, warto 0 przyjmuje w punktach
−1 oraz 0. Wybierzmy dowolny punkt
półprostej
)
1
,
(
−
−∞
, np.
2
−
=
x
. Poniewa
0
)
2
(
>
−
′
f
, wi c
0
)
(
>
′ x
f
dla
)
1
,
(
−
−∞
∈
x
. Dlatego funkcja jest rosn ca
na przedziale
)
1
,
(
−
−∞
. Wybieraj c dowolny punkt odcinka
)
0
,
1
(
−
, np.
2
1
−
=
x
, otrzymujemy
0
)
(
2
1
<
−
′
f
, co pozwala
stwierdzi : na przedziale
)
0
,
1
(
−
funkcja jest malej ca. Wybieraj c dowolny punkt odcinka półprostej
)
,
0
(
∞ , np.
1
=
x
,
otrzymujemy
0
)
1
(
>
′
f
, co pozwala stwierdzi : na przedziale
)
,
0
(
∞ funkcja jest rosn ca.
Zadanie 26.
Wyznacz przedziały monotoniczno ci funkcji
4
1
)
(
2
2
−
+
=
x
x
x
f
.
Rozwi zanie
=
−
′
−
⋅
+
−
−
⋅′
+
=
′
2
2
2
2
2
2
)
4
(
)
4
(
)
1
(
)
4
(
)
1
(
)
(
x
x
x
x
x
x
f
=
−
⋅
+
−
−
⋅
2
2
2
2
)
4
(
2
)
1
(
)
4
(
2
x
x
x
x
x
2
2
)
4
(
10
−
−
x
x
.
Łatwo wida , e
0
)
(
>
′ x
f
⇔
0
2
<
≠
−
x
,
0
)
(
<
′ x
f
⇔
0
2
>
≠ x
.
Dlatego: na przedziałach
)
2
,
(
−
−∞
,
)
0
,
2
(
−
funkcja jest rosn ca, na przedziałach
)
2
,
0
(
,
)
,
2
(
∞ funkcja jest malej ca.
37
Obliczanie granic nieoznaczonych
Do obliczania granic nieoznaczonych
0
0
(ilorazu niesko czenie małych) lub
∞
∞
(ilorazu niesko czenie
wielkich) bardzo przydatna jest
•
Reguła de L’Hospitala.
Je li funkcje f i g oraz punkt x
0
spełniaj zało enia:
1
° x
0
jest punktem skupienia dziedzin obu funkcji,
2
° f i g s niesko czenie małe (niesko czenie wielkie) w s siedztwie tego punktu,
3
° f i g s ró niczkowalne w s siedztwie tego punktu,
4
° istnieje granica (wła ciwa lub niewła ciwa)
)
(
)
(
lim
0
x
g
x
f
x
x
′
′
→
to
)
(
)
(
lim
)
(
)
(
lim
0
0
x
g
x
f
x
g
x
f
x
x
x
x
′
′
=
→
→
•
Reguł de L’Hospitala mo na stosowa te do granic jednostronnych.
•
Reguł de L’Hospitala mo na stosowa te do granic niewła ciwych.
•
Je li granica
)
(
)
(
lim
0
x
g
x
f
x
x
′
′
→
jest nieoznaczono ci typu
0
0
lub
∞
∞
, reguł de L’Hospitala mo emy stosowa ponownie.
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
80
Zadanie 27.
Obliczy
1
1
lim
3
1
−
−
→
x
x
x
.
Rozwi zanie.
Skorzystamy z reguły de L’Hospitala.
=
−
−
→
1
1
lim
3
1
x
x
x
0
0
=
′
−
′
−
=
→
)
1
(
)
1
(
lim
3
1
x
x
x
H
3
1
3
lim
2
1
=
→
x
x
Zadanie 28.
=
−
→
x
x
x
ln
1
lim
3
1
0
0
=
′
′
−
=
→
)
(ln
)
1
(
lim
3
1
x
x
x
H
3
3
lim
1
2
1
=
→
x
x
x
Zadanie 29.
=
→
x
x
x
5
)
10
sin(
lim
0
0
0
=
′
′
=
→
)
5
(
)
10
(sin
lim
0
x
x
x
H
2
5
10
cos
10
lim
0
=
⋅
→
x
x
Zadanie 30.
=
→∞ 2
lim
x
e
x
x
∞
∞
=
′
′
=
∞
→
)
(
)
(
lim
2
x
e
x
x
H
=
∞
→
x
e
x
x
2
lim
∞
∞
=
′
′
=
→∞
)
2
(
)
(
lim
x
e
x
x
H
∞
=
∞
→
2
lim
x
x
e
Zadanie 31.
=
+
+
→
x
x
x
)
1
ln(
lim
0
0
0
=
′
′
+
=
+
→
)
(
]
)
1
[ln(
lim
0
x
x
x
H
1
1
lim
1
1
0
=
+
→
+
x
x
Zadanie 32.
=
−
−
+
→
x
x
x
x
5
2
2
lim
0
0
0
)
5
(
)
2
2
(
lim
0
′
′
−
−
+
=
→
x
x
x
x
H
10
2
2
5
1
2
2
1
2
2
1
0
5
lim
=
=
+
=
−
+
→
x
x
x
Zadanie 33.
=
−
+
−
→
x
x
x
2
2
1
3
lim
4
0
0
)
2
(
)
2
1
3
(
lim
4
′
−
′
+
−
=
→
x
x
x
H
3
4
lim
2
1
2
1
1
4
=
=
−
+
−
→
x
x
x
38
Pochodne wy szych rz dów
Definicja.
Pochodn f ′ funkcji f nazywamy
pochodn pierwszego rz du
tej funkcji. Pochodn rz du n+1 funkcji f nazywamy
pochodn pochodnej rz du n tej funkcji:
]
)
(
[
)
(
)
1
(
)
(
′
=
−
x
f
x
f
n
n
Funkcja f jest klasy
)
(n
C
w punkcie x (na zbiorze
A), je li pochodna n-tego rz du funkcji f jest ci gła w punkcie
x (na zbiorze
A).
Zadanie 34.
Oblicz
)
(
)
(
n
x
e
.
Rozwi zanie.
Poniewa funkcja eksponencjalna
x
e nie zmienia si przy ró niczkowaniu, wi c
x
n
x
e
e
=
)
(
)
(
.
Zadanie 35.
Oblicz
)
(
)
(ln
n
x
.
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
81
Rozwi zanie.
Mamy kolejno:
x
x
1
)
(ln
=
′
,
2
1
2
1
1
)
1
(
)
(
)
(
]
)
[(ln
)
(ln
x
x
x
x
x
x
−
=
⋅
−
=
′
=
′
=
′
′
=
′′
−
−
,
3
2
2
1
2
3
2
1
)
1
(
)
2
(
)
1
(
)
(
)
(
]
)
[(ln
)
(ln
x
x
x
x
x
x
⋅
−
−
−
=
⋅
−
⋅
−
=
′
−
=
′
−
=
′
′′
=
′′′
,
4
3
2
1
3
4
2
3
2
)
4
(
)
1
(
)
3
(
2
1
)
1
(
]
2
1
)
1
[(
]
)
[(ln
)
(ln
x
x
x
x
x
⋅
⋅
−
−
−
=
⋅
−
⋅
⋅
⋅
−
=
′
⋅
⋅
⋅
−
=
′
′′′
=
Twierdzimy, e
n
n
n
x
n
x
)!
1
(
)
1
(
)
(ln
1
)
(
−
−
=
−
.
Zadanie 36.
Oblicz
)
(
)
(sin
n
x
.
Rozwi zanie.
Obliczamy kolejne pochodne:
)
sin(
cos
)
(sin
2
π
+
=
=
′
x
x
x
,
)
2
sin(
sin
)
cos
(
]
)
[(sin
)
(sin
2
π
⋅
+
=
−
=
′
=
′
′
=
′′
x
x
x
x
x
,
)
3
sin(
cos
)
sin
(
]
)
[(sin
)
(sin
2
π
⋅
+
=
−
=
′
−
=
′
′′
=
′′′
x
x
x
x
x
,
)
4
sin(
sin
)
cos
(
]
)
[(sin
)
(sin
2
)
4
(
π
⋅
+
=
=
′
−
=
′
′′′
=
x
x
x
x
x
,
)
5
sin(
cos
)
sin
(
]
)
[(sin
)
(sin
2
)
4
(
)
5
(
π
⋅
+
=
=
′
=
′
=
x
x
x
x
x
.
Twierdzimy, e
)
sin(
)
(sin
2
)
(
π
⋅
+
=
n
x
x
n
.
Jak widzieli my, poj cie pochodnej jest blisko zwi zane z poj ciem stycznej do wykresu funkcji. Fakt ten
mo na zinterpretowa nast puj co:
Funkcja
)
(
)
(
)
(
)
(
a
x
a
f
a
f
x
w
−
⋅
′
+
=
jest tym spo ród wielomianów stopnia co najwy ej pierwszego, który najlepiej przybli a funkcj f lokalnie w punkcie a.
Zagadnienie Taylora polega na pytaniu, czy istniej inne proste funkcje, które jeszcze lepiej przybli aj lokalnie dowoln
funkcj ró niczkowaln .
•
Wzór Taylora.
Niech funkcja f w przedziale domkni tym
]
,
[ x
a
ma n
−1 pochodnych
)
1
(
,
,
,
−
′′
′
n
f
f
f
; w przedziale otwartym
)
,
( x
a
istnieje te
)
(n
f
. Wówczas istnieje punkt c taki, e
x
c
a
<
<
oraz
n
n
n
a
x
n
a
f
a
x
a
f
a
x
a
f
a
f
x
f
ℜ
+
−
−
+
+
−
′′
+
−
′
+
=
−
−
1
)
1
(
2
)
(
)!
1
(
)
(
...
)
(
!
2
)
(
)
(
!
1
)
(
)
(
)
(
.
Je li
n
n
n
a
x
n
c
f
)
(
!
)
(
)
(
−
=
ℜ
, to
n
ℜ nazywa si reszt Lagrange’a.
Dla a = 0 wzór ten nazywa si wzorem Maclaurina i przyjmuje posta
n
n
n
n
n
x
n
c
f
x
n
f
x
f
x
f
f
x
f
ℜ
−
−
−
+
−
+
+
′′
+
′
+
=
!
)
(
)!
1
(
)
0
(
...
!
2
)
0
(
!
1
)
0
(
)
0
(
)
(
)
1
(
1
)
1
(
2
,
x
c
<
<
0
.
...
!
...
!
2
!
1
1
2
+
+
+
+
+
=
n
x
x
x
e
n
x
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
82
...
)!
1
2
(
)
1
(
...
!
5
!
3
sin
1
2
1
5
3
+
−
−
+
−
+
−
=
−
−
n
x
x
x
x
x
n
n
...
)!
2
2
(
)
1
(
...
!
4
!
2
1
cos
2
2
1
4
2
+
−
−
+
−
+
−
=
−
−
n
x
x
x
x
n
n
∞
=
−
−
=
+
1
1
)
1
(
)
1
ln(
k
k
k
x
k
x
Zadanie 37.
Oszacowa bł d przybli enia
3
6
1
2
2
1
1
x
x
x
e
x
+
+
+
≈
na przedziale
]
,
0
[
2
1
.
Rozwi zanie.
Poniewa
(
)
4
4
24
1
4
3
6
1
2
2
1
1
x
e
x
x
x
e
x
=
ℜ
=
+
+
+
−
oraz funkcja
4
4
24
1
4
x
e
=
ℜ
jest rosn ca na przedziale
]
,
0
[
2
1
, wi c
bł d przybli enia nie przekroczy warto ci
14218
,
1
)
(
|
|
4
384
1
4
2
1
4
24
1
4
≈
=
≤
ℜ
=
∆
e
e
.
Zadanie 38.
Oszacowa bł d przybli enia funkcji
x
x
f
sin
)
(
=
na przedziale
]
,
0
[
10
1
.
Rozwi zanie.
1.
x
x
≈
sin
3
6
1
3
)
cos
(
x
c
⋅
−
=
ℜ
3
3
6
1
3
6
1
3
10
)
1
,
0
(
)
1
,
0
(
|
cos
|
|
|
−
<
≤
⋅
−
≤
ℜ
=
∆
c
2.
3
6
1
sin
x
x
x
−
≈
5
!
5
1
5
)
(cos
x
c
⋅
=
ℜ
7
5
120
1
5
120
1
5
10
)
1
,
0
(
)
1
,
0
(
|
cos
|
|
|
−
<
≤
⋅
≤
ℜ
=
∆
c
3.
5
120
1
3
6
1
sin
x
x
x
x
+
−
≈
7
!
7
1
7
)
cos
(
x
c
⋅
−
=
ℜ
10
7
5040
1
7
5040
1
3
10
)
1
,
0
(
)
1
,
0
(
|
cos
|
|
|
−
<
≤
⋅
−
≤
ℜ
=
∆
c
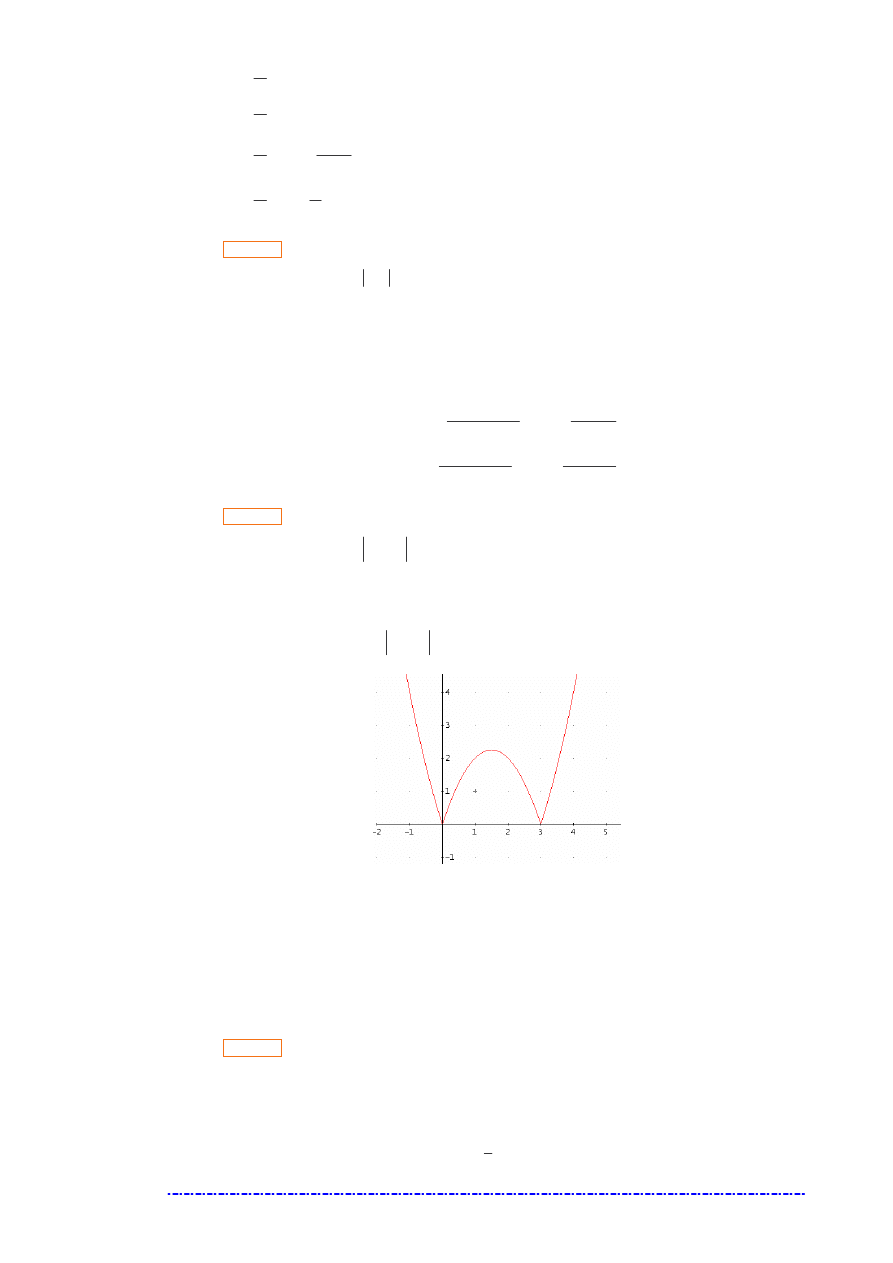
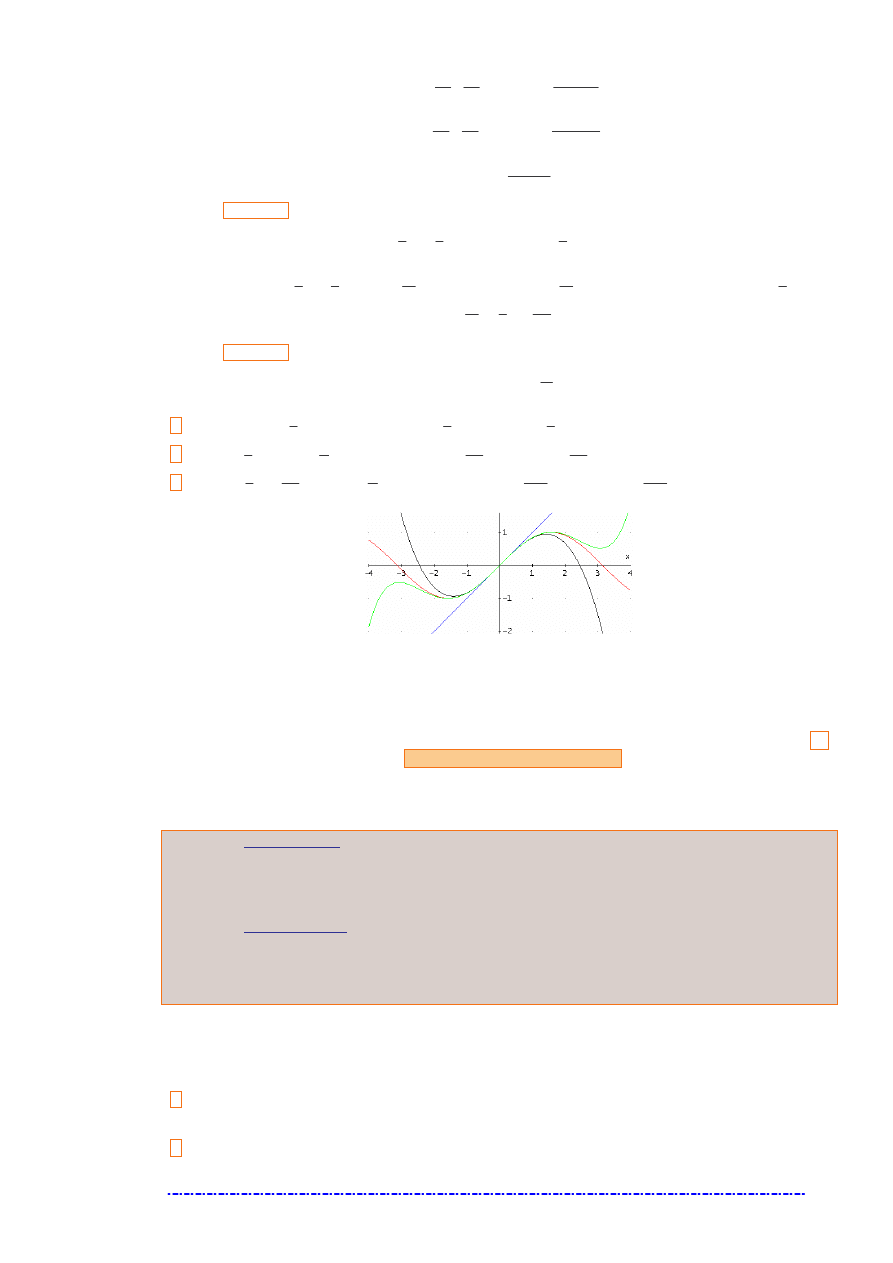
Ilustracja wykresu funkcji
x
x
f
sin
)
(
=
oraz trzech pierwszych przybli e (z zadania).
39
Ekstrema lokalne funkcji
Definicja.
Funkcja f ma
minimum lokalne
w punkcie
f
D
a Int
∈
, je li jest spełniony warunek
(istnieje s siedztwo
f
a
D
S
⊂
takie, e dla ka dego
a
S
x
∈
):
)
(
)
(
a
f
x
f
≥
.
Je li nierówno jest ostra dla
a
x
≠ - minimum nazywamy wła ciwym.
Funkcja f ma
maksimum lokalne
w punkcie
f
D
a Int
∈
, je li jest spełniony warunek
(istnieje s siedztwo
f
a
D
S
⊂
takie, e dla ka dego
a
S
x
∈
):
)
(
)
(
a
f
x
f
≤
Je li nierówno jest ostra dla
a
x
≠ - maksimum nazywamy wła ciwym.
Funkcja mo e mie ekstrema lokalne tylko w tych punktach swej dziedziny, w których b d nie jest ró nicz-
kowalna, b d ma pochodn równ zero.
Przy wyznaczaniu ekstremów lokalnych funkcji wykonuje si nast puj ce czynno ci:
1. W punktach, które nie nale do dziedziny pochodnej (w nich funkcja nie jest ró niczkowalna) szukamy ekstremów
bezpo rednio z definicji.
2. Rozwi zujemy równanie
0
)
(
=
′ x
f
. Punkty, b d ce rozwi zaniami tej równo ci s jedynymi, w których ekstremum
mo e, ale nie musi, si znajdowa .
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
83
3. W punktach, w których
0
)
(
=
′ x
f
mo emy sprawdzi czy jest ekstremum na jeden z dwu sposobów:
a)
Badaj c zmian monotoniczno ci funkcji w s siedztwie punktu,
b)
Licz c, o ile istniej , kolejne pochodne funkcji w punkcie.
Fakt.
Je li
0
)
(
...
)
(
)
(
0
)
1
(
0
0
=
=
=
′′
=
′
−
x
f
x
f
x
f
n
,
0
)
(
0
)
(
≠
x
f
n
, to
gdy n jest liczb nieparzyst – w
0
x nie ma ekstremum;
gdy n jest liczb parzyst i
0
)
(
0
)
(
>
x
f
n
– w
0
x jest minimum lokalne wła ciwe;
gdy n jest liczb parzyst i
0
)
(
0
)
(
<
x
f
n
– w
0
x jest maksimum lokalne wła ciwe.
Zadanie 39.
Wyznaczymy ekstrema lokalne funkcji
4
9
6
)
(
2
3
−
+
−
=
x
x
x
x
f
.
Rozwi zanie
Funkcja
4
9
6
)
(
2
3
−
+
−
=
x
x
x
x
f
jako wielomian jest ró niczkowalna w zbiorze R. Ekstremum funkcji poszukujemy w
punktach, w których pochodna funkcji si zeruje lub w punktach, w których funkcja nie jest ró niczkowalna. Wyznacza-
my pochodn funkcji i jej miejsca zerowe.
9
12
3
)
(
2
+
−
=
′
x
x
x
f
,
}
3
,
1
{
0
9
12
3
0
)
(
2
∈
⇔
=
+
−
⇔
=
′
x
x
x
x
f
.
Zatem funkcja mo e mie ekstremum dla x = 1 lub x = 3 (warunek konieczny istnienia ekstremum funkcji). Sprawdzamy,
czy jest spełniony warunek wystarczaj cy istnienia ekstremum. Obliczamy pochodn drugiego rz du i jej warto ci w
punktach stacjonarnych
12
6
)
(
−
=
′′
x
x
f
.
Poniewa warto drugiej pochodnej w punkcie x = 1 jest ujemna,
6
)
1
(
−
=
′′
f
, wi c funkcja osi ga w tym punkcie mak-
simum lokalne. Natomiast warto drugiej pochodnej w punkcie x = 3 jest dodatnia,
6
)
3
(
=
′′
f
, st d funkcja osi ga w
tym punkcie minimum lokalne.
Zadanie 40.
Wyznaczymy ekstrema lokalne funkcji
x
x
x
f
2
cos
2
sin
)
(
+
=
,
π
∈
2
,
0
x
.
Rozwi zanie
Wyznaczamy punkty, w których pochodna si zeruje (punkty stacjonarne)
}
,
{
2
sin
2
cos
0
)
2
sin
2
(cos
2
0
)
(
8
5
8
π
π
∈
⇔
=
⇔
=
−
⇔
=
′
x
x
x
x
x
x
f
Obliczamy pochodn drugiego rz du i jej warto ci w punktach stacjonarnych
)
2
cos
2
(sin
4
)
(
x
x
x
f
+
−
=
′′
.
Poniewa warto drugiej pochodnej w punkcie
8
π
=
x
jest ujemna, wi c funkcja osi ga w tym punkcie maksimum
lokalne. Natomiast w punkcie
8
5
π
=
x
druga pochodna przyjmuje warto dodatni , st d funkcja osi ga w tym punkcie
minimum lokalne.
Zadanie 41.
Dana jest funkcja
π
∈
−
=
2
,
0
,
cos
2
sin
)
(
x
x
x
x
f
. Wyznaczymy jej ekstrema lokalne.
Rozwi zanie
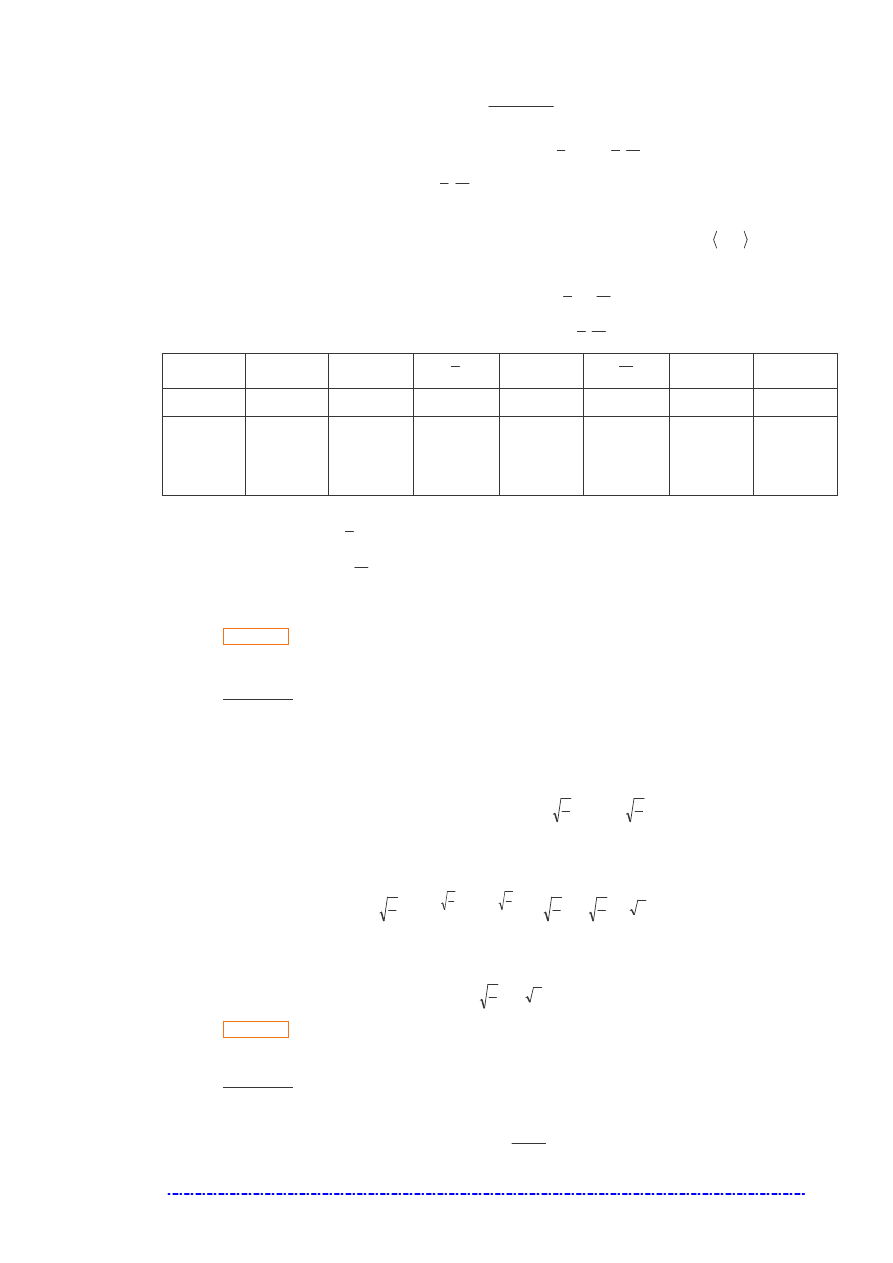
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
84
Wyznaczamy pochodn funkcji i jej miejsca zerowe.
2
)
cos
2
(
1
cos
2
)
(
x
x
x
f
−
−
=
′
}
,
{
cos
0
1
cos
2
0
)
(
3
5
3
2
1
π
π
∈
⇔
=
⇔
=
−
⇔
=
′
x
x
x
x
f
Zatem funkcja mo e mie ekstremum dla
}
,
{
3
5
3
π
π
∈
x
(w tych punktach jest spełniony warunek konieczny istnienia
ekstremum funkcji). Sprawdzamy, czy jest spełniony warunek dostateczny istnienia ekstremum, tzn. czy w otoczeniu
punktów stacjonarnych pochodna zmienia znak. Poniewa mianownik jest dodatni dla ka dego
π
∈
2
,
0
x
, wi c o znaku
pochodnej decyduje wyra enie w liczniku. St d
)
2
,
(
)
,
0
(
0
1
cos
2
0
)
(
3
5
3
π
∪
∈
⇔
>
−
⇔
>
′
π
π
x
x
x
f
,
)
,
(
0
1
cos
2
0
)
(
3
5
3
π
π
∈
⇔
<
−
⇔
<
′
x
x
x
f
.
x
0
…
3
π
…
3
5
π
…
π
2
f ′
+
0
−−−−
0
+
f
Ro nie
Maksimum
lokalne
Maleje
Minimum
lokalne
Ro nie
Zatem w otoczeniu punktu
3
π
=
x
pochodna zmienia znak z „+” na „
−”, wi c w tym punkcie funkcja osi ga maksimum
lokalne. W otoczeniu punktu
3
5
π
=
x
pochodna zmienia znak z „
−” na „+”, wi c w tym punkcie funkcja osi ga minimum
lokalne.
Zadanie 42.
Wyznaczymy minimum i maksimum funkcji
x
x
e
e
x
f
−
+
=
3
2
)
(
.
Rozwi zanie
Funkcja
x
x
e
e
x
f
−
+
=
3
2
)
(
jest okre lona i ró niczkowalna w zbiorze R. Wyznaczamy pochodn funkcji i jej miejsca
zerowe.
x
x
e
e
x
f
−
−
=
′
3
2
)
(
,
2
3
2
3
ln
0
3
2
0
)
(
=
⇔
=
⇔
=
−
⇔
=
′
−
x
e
e
e
x
f
x
x
x
Obliczamy pochodn drugiego rz du i jej warto w punkcie stacjonarnym.
x
x
e
e
x
f
−
+
=
′′
3
2
)
(
6
2
3
2
3
2
)
(ln
3
2
2
3
ln
ln
2
3
2
3
2
3
=
⋅
+
⋅
=
+
=
′′
−
e
e
f
.
Poniewa druga pochodna w punkcie stacjonarnym przyjmuje warto dodatni , to funkcja ma w tym punkcie minimum
lokalne. Obliczamy warto minimum
6
2
)
(ln
2
3
=
f
.
Zadanie 43.
Wyznaczymy ekstrema funkcji
x
x
x
f
arctg
2
)
(
−
=
.
Rozwi zanie
Funkcja jest ró niczkowalna dla ka dego
R
x
∈ . Ekstremów nale y szuka tam, gdzie
0
)
(
=
′ x
f
.
2
1
2
1
)
(
x
x
f
+
−
=
′
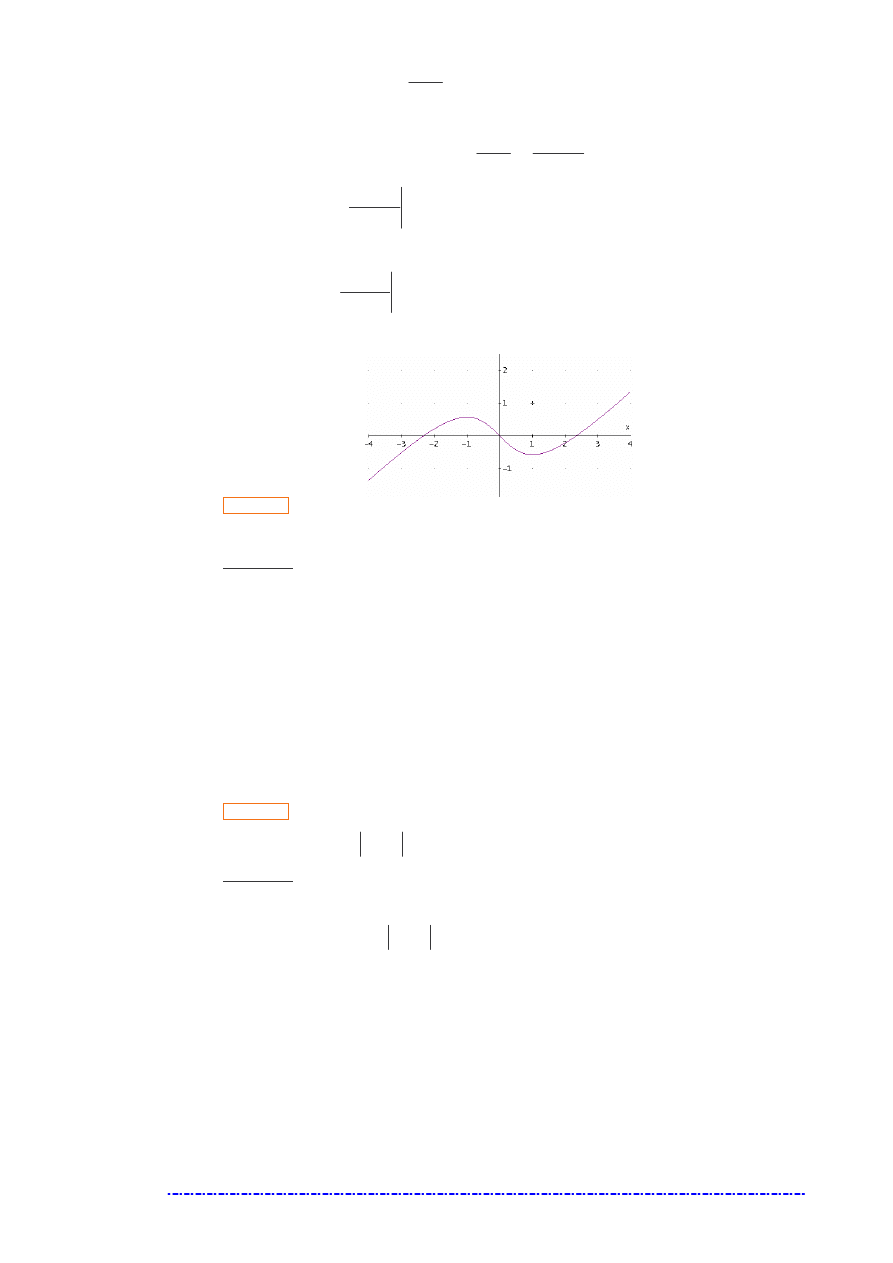
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
85
0
)
(
=
′ x
f
⇔
0
1
2
1
2
=
+
−
x
⇔
2
1
2
=
+ x
⇔
1
2
=
x
⇔
}
1
,
1
{
−
∈
x
.
Obliczymy drug pochodn
2
2
2
)
1
(
4
)
1
2
1
(
)
(
x
x
x
x
f
+
=
′
+
−
=
′′
.
Poniewa
0
)
1
(
=
−
′
f
,
0
1
)
1
(
4
)
1
(
1
2
2
<
−
=
+
=
−
′′
−
=
x
x
x
f
, wi c w punkcie
1
−
=
x
jest maksimum lokalne wła ciwe rów-
ne
1
)
1
(
2
1
)
1
(
−
π
=
−
⋅
−
−
=
−
arctg
f
.
Poniewa
0
)
1
(
=
′
f
,
0
1
)
1
(
4
)
1
(
1
2
2
>
=
+
=
′′
=
x
x
x
f
, wi c w punkcie
1
=
x
jest minimum lokalne wła ciwe równe
π
−
=
⋅
−
=
1
1
2
1
)
1
(
arctg
f
.
Zadanie 44.
Wyznaczymy ekstrema funkcji
x
e
x
x
f
−
=
3
)
(
.
Rozwi zanie
Funkcja jest ró niczkowalna dla ka dego
R
x
∈ . Ekstremów nale y szuka tam, gdzie
0
)
(
=
′ x
f
.
)
3
(
3
)
(
2
3
2
x
e
x
e
x
e
x
x
f
x
x
x
−
=
−
=
′
−
−
−
0
)
(
=
′ x
f
⇔
0
)
3
(
2
=
−
−
x
e
x
x
⇔
}
3
,
0
{
∈
x
.
Poniewa w s siedztwie punktu
0
=
x
pochodna nie zmienia znaku (funkcja nie zmienia monotoniczno ci), wi c w
punkcie
0
=
x
nie ma ekstremum lokalnego.
Poniewa w s siedztwie punktu
3
=
x
pochodna zmienia znak z dodatniego na ujemny (funkcja zmienia si z rosn cej na
malej c ), wi c w punkcie
3
=
x
jest maksimum lokalne wła ciwe, równe
3443
,
1
27
)
3
(
3
≈
=
−
e
f
.
Zadanie 45.
Wyznacz ekstrema funkcji
x
x
x
f
3
)
(
2
−
=
.
Rozwi zanie
Funkcja okre lona jest przez wzór
∈
+
−
∞
∪
−∞
∈
−
=
−
=
)
3
,
0
(
3
)
,
3
[
]
0
,
(
3
3
)
(
2
2
2
x
x
x
x
x
x
x
x
x
f
dla
dla
Jej pochodna jest równa
∈
+
−
∞
∪
−∞
∈
−
=
′
)
3
,
0
(
3
2
)
,
3
(
)
0
,
(
3
2
)
(
x
x
x
x
x
f
dla
dla
)
0
(
f ′
nie istnieje, gdy
3
)
0
(
−
=
′
−
f
,
3
)
0
(
=
′
+
f
;
)
3
(
f ′
nie istnieje, gdy
3
)
3
(
−
=
′
−
f
,
3
)
3
(
=
′
+
f
.
Poniewa wyra enie pod znakiem warto ci bezwzgl dnej przyjmuje warto ci nieujemne, wi c w punktach
0
=
x
,
3
=
x
funkcja f ma minima lokalne równe
0
)
3
(
)
0
(
=
= f
f
.
Ponadto, wobec warunków
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
86
0
)
(
=
′ x
f
⇔
2
3
=
x
∈
−
∞
∪
−∞
∈
=
′′
)
3
,
0
(
2
)
,
3
(
)
0
,
(
2
)
(
x
x
x
f
dla
dla
0
)
(
2
3
<
′′
f
wnosimy, e funkcja ma w punkcie
2
3
=
x
maksimum lokalne wła ciwe równe
4
9
2
3
)
(
=
f
.
Zadanie 46.
Liczb 36 rozło ymy na sum takich dwóch składników, aby ich iloczyn był najwi kszy.
Rozwi zanie
Rozkładamy liczb 36 na sum dwóch składników:
x
– pierwszy składnik;
0
>
x
36 − x – drugi składnik;
0
36
>
− x
.
St d mamy
)
36
,
0
(
=
Γ
∈
x
.
Tworzymy funkcj
]
324
)
18
[(
36
)
36
(
)
(
2
2
+
−
−
=
+
−
=
−
=
x
x
x
x
x
x
f
Poniewa funkcja f jest funkcj kwadratow i współczynnik stoj cy przy drugiej pot dze jest ujemny, wi c maksimum
lokalne tej funkcji wyst puje w punkcie
)
324
;
18
(
− wierzchołku paraboli b d cej wykresem funkcji.
Je li liczb 36 rozło ymy na sum dwóch takich samych składników równych 18, to ich iloczyn b dzie najwi kszy.
Zadanie 47.
Liczb 36 rozło ymy na sum takich dwóch składników, aby suma kwadratów tych składników była najmniejsza.
Rozwi zanie
Rozkładamy liczb 36 na sum dwóch składników:
x
– pierwszy składnik;
0
>
x
36 − x – drugi składnik;
0
36
>
− x
.
St d mamy
)
36
,
0
(
=
Γ
∈
x
.
Tworzymy funkcj
]
324
)
18
[(
2
1296
72
2
)
36
(
)
(
2
2
2
2
+
−
=
+
−
=
−
+
=
x
x
x
x
x
x
g
Poniewa funkcja g jest funkcj kwadratow i współczynnik stoj cy przy drugiej pot dze jest dodatni, wi c minimum
lokalne tej funkcji wyst puje w punkcie
)
324
;
18
(
− wierzchołku paraboli b d cej wykresem funkcji.
Je li liczb 36 rozło ymy na sum dwóch takich samych składników równych 18, to suma kwadratów tych składników
b dzie najmniejsza.
Zadanie 48.
Liczb 36 rozło ymy na sum takich dwóch składników, aby suma odwrotno ci tych składników była najmniejsza.
Rozwi zanie
Rozkładamy liczb 36 na sum dwóch składników:
x
– pierwszy składnik;
0
>
x
36 − x – drugi składnik;
0
36
>
− x
.
St d mamy
)
36
,
0
(
=
Γ
∈
x
.

Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
87
Tworzymy funkcj
)
36
(
36
36
1
1
)
(
x
x
x
x
x
h
−
=
−
+
=
Wyznaczamy pochodn funkcji i jej miejsca zerowe:
2
2
)
36
(
1296
72
)
('
x
x
x
x
h
−
−
=
18
0
1296
72
0
)
('
=
⇔
=
−
⇔
=
x
x
x
h
Badamy zmian znaku pochodnej w otoczeniu punktu
18
=
x
. Poniewa mianownik jest dodatni dla ka dego
Γ
∈
x
,
wi c o znaku pochodnej decyduje wyra enie w liczniku. Poniewa
18
36
0
)
('
>
>
⇔
>
x
x
h
,
18
0
0
)
('
<
<
⇔
<
x
x
h
,
w otoczeniu punktu
18
=
x
pochodna zmienia znak z „
−” na „+”, a to oznacza, e dla
18
=
x
funkcja h osi ga minimum
lokalne.
Je li liczb 36 rozło ymy na sum dwóch takich samych składników równych 18, to suma odwrotno ci tych składników
b dzie najmniejsza.
40
Warto
najwi ksza i najmniejsza funkcji
Warto najwi ksz i najmniejsz funkcji w danym przedziale [a, b] liczymy nast puj co:
a)
Obliczamy warto ci f (a) i f (b);
b)
Obliczamy warto ci funkcji w punktach, w których funkcja jest ci gła ale nie jest ró niczkowalna (nie sprawdza-
my, czy w tych punktach s ekstrema!);
c)
Rozwi zujemy równanie
0
)
(
=
′ x
f
i dla wszystkich
)
,
( b
a
x
∈
, b d cych rozwi zaniem tego równania wyznacza-
my warto ci
)
(x
f
(te nie sprawdzamy, czy w tych punktach s ekstrema!);
d)
Porównujemy otrzymane warto ci i wybieramy element najwi kszy i najmniejszy.
Zadanie 49.
Wyznaczymy warto najmniejsz i najwi ksz funkcji
)
32
(
)
(
3
x
x
x
f
+
=
w przedziale
]
1
,
3
[
−
=
Γ
.
Rozwi zanie
(1)
Obliczamy
15
)
3
(
−
=
−
f
oraz
33
)
1
(
=
f
.
(2)
Rozwi zujemy równanie
0
)
(
=
′ x
f
0
)
(
=
′ x
f
⇔
0
32
4
3
=
+
x
⇔
2
−
=
x
.
Znajdujemy
48
)
2
(
−
=
−
f
.
Budujemy zbiór
{
)}
1
(
),
2
(
),
3
(
f
f
f
A
−
−
=
}
33
,
48
,
15
{
−
−
=
Warto ci najmniejsz naszej funkcji jest najmniejszy ele-
ment zbioru A, za warto ci najwi ksz funkcji jest element najwi kszy zbioru A. St d:
48
}
33
,
15
,
48
min{
)
(
min
;
33
}
33
,
15
,
48
max{
)
(
max
]
1
,
3
[
]
1
,
3
[
−
=
−
−
=
=
−
−
=
−
∈
−
∈
x
f
x
f
x
x
Zadanie 50.
Dana jest funkcja
2
2
1
2
5
2
)
(
x
x
x
x
f
+
+
−
=
. Wyznaczymy jej warto ci ekstremalne w przedziale
]
2
,
[
2
1
−
=
Γ
.
Rozwi zanie
(1)
Obliczamy
0
)
(
2
1
=
−
f
oraz
4
)
2
(
=
f
.
(2)
Rozwi zujemy równanie
0
)
(
=
′ x
f

Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
88
0
)
(
=
′ x
f
⇔
0
)
1
(
5
5
2
2
2
=
+
−
x
x
⇔
}
1
,
1
{
−
∈
x
.
Znajdujemy
2
1
)
1
(
−
=
f
;
Γ
∉
−1
.
St d:
2
1
2
1
]
2
,
[
2
1
]
2
,
[
}
4
,
0
,
min{
)
(
min
;
4
}
4
,
0
,
max{
)
(
max
2
1
2
1
−
=
−
=
=
−
=
−
∈
−
∈
x
f
x
f
x
x
Zadanie 51.
Znajdziemy najmniejsz i najwi ksz warto funkcji
x
x
x
f
2
cos
cos
)
(
2
1
+
=
w przedziale
]
2
,
0
[
π
=
Γ
.
Rozwi zanie
(1)
Obliczamy
2
3
)
0
(
=
f
oraz
2
3
)
2
(
=
π
f
.
(2)
Rozwi zujemy równanie
0
)
(
=
′ x
f
0
)
(
=
′ x
f
⇔
0
cos
sin
2
sin
=
⋅
−
−
x
x
x
⇔
0
)
cos
2
1
(
sin
=
+
⋅
−
x
x
⇔
}
2
,
,
,
,
0
{
3
4
3
2
π
π
π
π
∈
x
.
Znajdujemy
4
3
3
2
)
(
−
=
π
f
,
2
1
)
(
−
=
π
f
,
4
3
3
4
)
(
−
=
π
f
.
St d:
4
3
2
3
2
1
4
3
]
2
,
0
[
2
3
2
3
2
1
4
3
]
2
,
0
[
}
,
,
min{
)
(
min
;
}
,
,
max{
)
(
max
−
=
−
−
=
=
−
−
=
π
∈
π
∈
x
f
x
f
x
x
Zadanie 52.
Znajdziemy najmniejsz i najwi ksz warto funkcji
1
2
)
(
3
2
+
=
x
x
f
w przedziale
]
1
,
2
[
−
=
Γ
.
Rozwi zanie
(1)
Obliczamy
3
)
2
(
=
−
f
oraz
3
2
1
)
1
(
+
=
f
.
(2)
Znajdujemy pochodn funkcji.
3
3
4
4
3
4
4
3
4
)
(
x
x
x
x
f
=
=
′
dla
0
≠
x
Znajdujemy
1
)
0
(
=
f
(w punkcie
0
=
x
nie istnieje pochodna!).
St d:
1
}
3
,
2
1
,
1
min{
)
(
min
;
3
}
3
,
2
1
,
1
max{
)
(
max
3
]
1
,
2
[
3
]
1
,
2
[
=
+
=
=
+
=
−
∈
−
∈
x
f
x
f
x
x
41
Kształt wykresu – wypukło
Definicja
Funkcja f jest
wypukła w dół
(inaczej:
wypukła
) na przedziale
)
,
( b
a
, je li ka dy odcinek ł cz cy punkty poło one na
wykresie funkcji le y ponad wykresem funkcji lub si z nim pokrywa; je li ka dy odcinek ł cz cy punkty poło one na
wykresie funkcji le y pod wykresem funkcji lub si z nim pokrywa, to funkcja jest
wypukła w gór
(inaczej:
wkl sła
) na
przedziale
)
,
( b
a
.

Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
89
Przy badaniu wypukło ci funkcji posiadaj cej drug pochodn korzystamy z faktów:
(1)
Je li dla ka dego
)
,
( b
a
x
∈
0
)
(
>
′′ x
f
, to funkcja f jest
wypukła w dół
na przedziale
)
,
( b
a
;
(2)
Je li dla ka dego
)
,
( b
a
x
∈
0
)
(
<
′′ x
f
, to funkcja f jest
wypukła w gór
na przedziale
)
,
( b
a
.
Znajdowanie punktów przegi cia polega na wyznaczeniu punktów, w których funkcja zmienia rodzaj wypukło ci i
sprawdzeniu, w których z nich istnieje f ′ .
Zadanie 53.
Dana jest funkcja
1
3
)
(
3
+
−
=
x
x
x
f
. Wyznaczymy przedziały, w których funkcja jest wypukła, a tak e przedziały, w
których jest wkl sła. Podamy punkty przegi cia wykresu tej funkcji.
Rozwi zanie
Funkcja
1
3
)
(
3
+
−
=
x
x
x
f
jest okre lona i ró niczkowalna w zbiorze R. Obliczamy pierwsz i drug pochodn tej
funkcji.
( )
3
3
2
−
=
′
x
x
f
,
( )
x
x
f
6
=
′′
.
Badamy znak drugiej pochodnej:
)
;
0
(
0
)
(
∞
∈
⇔
>
′′
x
x
f
)
0
;
(
0
)
(
−∞
∈
⇔
<
′′
x
x
f
Funkcja
1
3
)
(
3
+
−
=
x
x
x
f
jest wypukła w dół (wypukła) w przedziale
)
;
0
(
∞ , za wypukła w gór (wkl sła) w prze-
dziale
)
0
;
(
∞
−
. Punktem przegi cia jest punkt o odci tej równej zero (poniewa
)
0
(
f ′
istnieje).
Zadanie 54.
Dana jest funkcja
1
2
)
1
(
)
(
2
+
+
−
=
x
x
x
x
f
. Zbadamy jej wypukło .
Rozwi zanie:
Funkcja
1
2
)
1
(
)
(
2
+
+
−
=
x
x
x
x
f
jest okre lona i ró niczkowalna w zbiorze R. Wzór tej funkcji mo emy przekształci
nast puj co
|
1
|
)
1
(
)
1
(
)
1
(
1
2
)
1
(
)
(
2
2
+
⋅
−
=
+
−
=
+
+
−
=
x
x
x
x
x
x
x
x
f
−
<
−
−
≥
+
−
=
.
1
1
,
1
1
2
2
x
x
x
x
dla
dla
Wyznaczamy pierwsz i drug pochodn naszej funkcji:
−
<
−
>
−
=
′
.
1
2
,
1
2
)
(
x
x
x
x
x
f
dla
dla
)
1
(
−
′
f
nie istnieje, gdy
2
)
1
(
−
=
−
′
−
f
,
2
)
1
(
=
−
′
+
f
−
<
−
>
−
=
′′
.
1
2
,
1
2
)
(
x
x
x
f
dla
dla
Funkcja
1
2
)
1
(
)
(
2
+
+
−
=
x
x
x
x
f
jest wypukła w gór w przedziale
)
;
1
(
∞
−
, za wypukła w dół (wypukła) w prze-
dziale
)
1
;
(
−
∞
−
. Poniewa w punkcie
1
−
=
x
nie istnieje pierwsza pochodna, wi c funkcja nie ma punktów przegi cia.
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
90
Zadanie 55.
Funkcja okre lona jest wzorem
π
∈
=
;
0
,
2
cos
)
(
x
x
x
f
. Wyznaczymy przedziały, w których funkcja jest wypukła, a w
których jest wkl sła. Podamy punkty przegi cia wykresu tej funkcji.
Rozwi zanie:
Funkcja
x
x
f
2
cos
)
(
=
jest dwukrotnie ró niczkowalna na zbiorze
)
,
0
(
π . Obliczamy pierwsz i drug pochodn poda-
nej funkcji.
x
x
x
f
x
f
2
cos
4
)
2
sin
2
(
)
)
(
(
)
(
−
=
′
−
=
′
′
=
′′
Rozwi zujemy nierówno (przy zało eniu
π
<
< x
0
)
)
,
(
0
2
cos
0
2
cos
4
0
)
(
4
3
4
π
π
∈
⇔
<
⇔
>
−
⇔
>
′′
x
x
x
x
f
Funkcja jest wypukła w dół w przedziale
)
,
(
4
3
4
π
π
, za wypukła w gór w przedziałach
)
,
(
,
)
,
0
(
4
3
4
π
π
π
. Punktami prze-
gi cia wykresu funkcji s punkty
)
0
,
(
))
(
,
(
4
4
4
1
π
π
π
=
=
f
P
,
)
0
,
(
))
(
,
(
4
3
4
3
4
3
2
π
π
π
=
=
f
P
.
Zadanie 56.
Zbadamy wypukło funkcji
1
)
(
2
+
=
x
x
x
f
.
Rozwi zanie.
Obie pochodne funkcji:
2
2
2
)
1
(
1
)
(
+
−
=
′
x
x
x
f
,
3
2
2
)
1
(
)
3
(
2
)
(
+
−
=
′′
x
x
x
x
f
.
Mianownik drugiej pochodnej jest zawsze dodatni. Licznik jest równy zero dla
}
3
,
0
,
3
{
−
∈
x
.
Funkcja jest wypukła w dół na przedziałach
)
0
,
3
(
−
,
)
,
3
(
∞ i jest wypukła w gór na przedziałach
)
3
,
(
−
−∞
,
)
3
,
0
(
. Poniewa w ka dym z punktów zbioru
}
3
,
0
,
3
{
−
istnieje pierwsza pochodna oraz funkcja zmienia rodzaj
wypukło ci, wi c te punkty s punktami przegi cia.
Stanisław Kowalski, Wykłady z matematyki –
Pochodna funkcji jednej zmiennej
– wykład 7 i 8
91
Zadanie 57.
Zbadamy wypukło funkcji
1
)
(
+
=
x
x
x
f
.
Rozwi zanie.
Wyznaczamy dziedzin funkcji
0
)
,
0
[
≥
=
∞
=
R
D
f
. Obliczamy
2
)
1
(
2
1
)
(
+
−
=
′
x
x
x
x
f
,
3
3
2
)
1
(
4
1
6
3
)
(
+
−
−
=
′′
x
x
x
x
x
f
. Funkcja
jest wypukła w dół, gdy
0
)
(
>
′′ x
f
, tzn. na przedziale
)
,
3
1
(
3
2
∞
+
; funkcja jest wypukła w gór , gdy
0
)
(
<
′′ x
f
, tzn.
na przedziale
)
3
1
,
0
(
3
2
+
. Punkt o odci tej
3
1
3
2
+
=
x
jest punktem przegi cia.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron