Opracował i wykonał: Stanisław Zoń
Całka krzywoliniowa nieskierowana
∫
l
l
P
f
d
)
(
Zadania na ćwiczenia
1.1
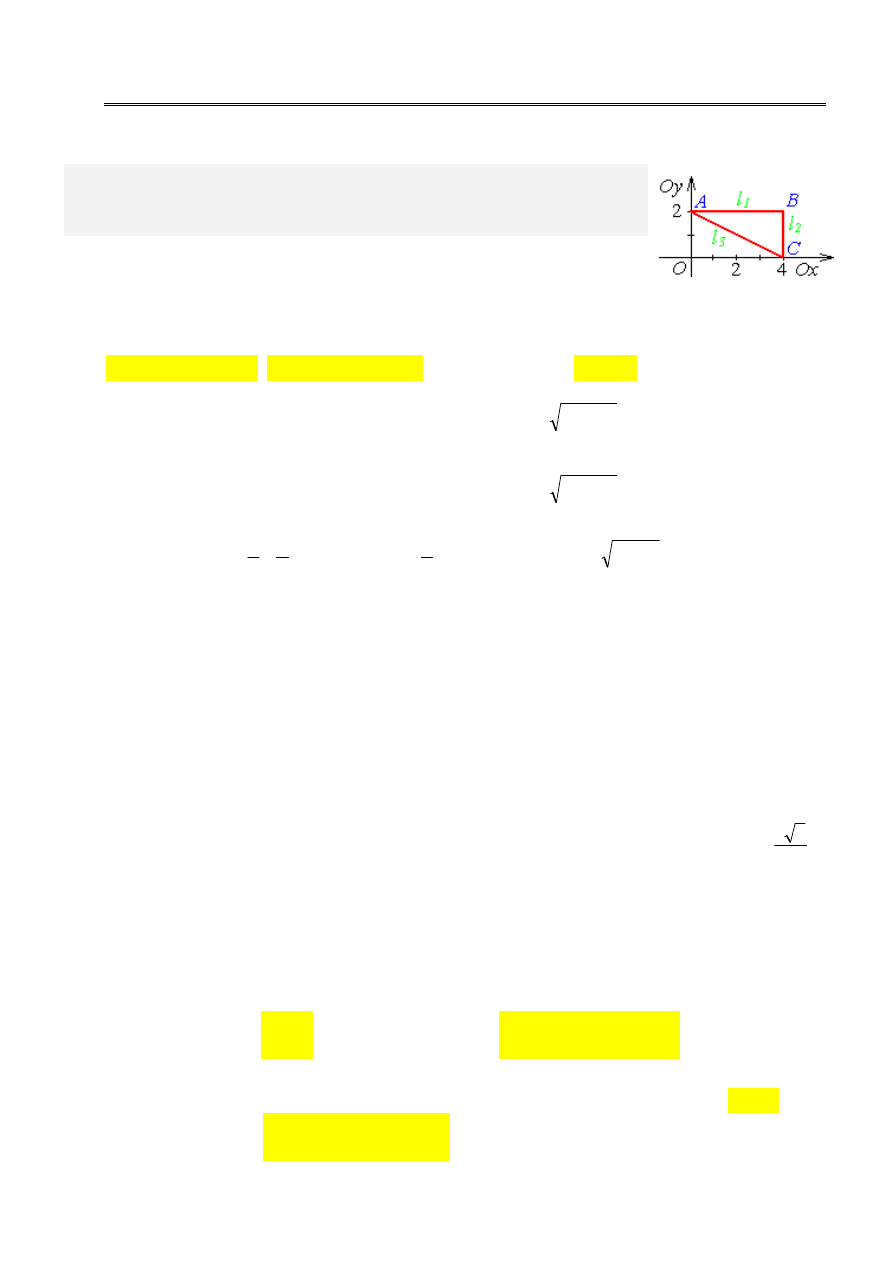
Zadanie 1.
Obliczyć całkę
∫
l
l
xy d wzdłuż krzywej
l która jest obwodem
trójkąta o wierzchołkach
)
2
,
0
(
=
A
,
)
2
,
4
(
=
B
,
)
0
,
4
(
=
C
.
Rozwiązanie.
Ponieważ krzywa
3
2
1
l
l
l
l
∪
∪
=
, zatem
3
2
1
3
2
1
l
l
l
l
l
l
l
∫
∫
∫
∫
∫
+
+
=
=
∪
∪
.
Równanie odcinka o końcach
AB wyrażają wzory:
t
x
x
x
x
A
B
A
⋅
−
+
=
)
(
,
t
y
y
y
y
A
B
A
⋅
−
+
=
)
(
, w których zmienna
]
1
,
0
[
∈
t
. Zatem:
•
na odcinku
AB,
=
=
.......
..........
.......
..........
:
1
y
x
l
,
różniczka łuku
=
+
=
t
y
x
l
d
d
2
2
&
&
………………………
•
na odcinku
BC,
=
=
.......
..........
.......
..........
:
2
y
x
l
,
różniczka łuku
=
+
=
t
y
x
l
d
d
2
2
&
&
………………………
•
na odcinku
CA,
1
2
4
:
3
=
+
y
x
l
, czyli
2
2
x
y
−
=
, różniczka łuku
=
+
=
x
y
l
d
1
d
2
'
…………………
∫
∫
=
.....
.....
.....
..........
d
1
l
l
xy
…………………………………………………………………………Odp. 16.
∫
∫
=
....
....
.....
..........
d
2
l
l
xy
………………………………………………………………………… Odp. 8.
∫
∫
=
.....
....
.....
..........
d
3
l
l
xy
…………………………………………………………………….……………
………………………………………………………………………………………..… Odp.
3
5
8
.
Ostatecznie,
∫
l
l
xy d = …………………………………………………………………………………
Zadanie to będzie miało sens fizyczny jeśli sformułujemy je np. tak:
Obliczyć ładunek elektryczny
q rozłożony na krzywej l gdy gęstość liniową
λ
ładunku elektrycz-
nego wyraża funkcja
xy
=
λ
. Wtedy bowiem ładunek
∫
∫
∫
=
=
=
l
l
l
l
xy
l
q
q
d
d
d
λ
.
lub
Obliczyć masę
m rozłożoną na krzywej l gdy gęstość liniową
γ
masy wyraża funkcja
xy
=
γ
.
Wtedy bowiem masa
∫
∫
∫
=
=
=
l
l
l
l
xy
l
m
m
d
d
d
γ
.
Opracował i wykonał: Stanisław Zoń
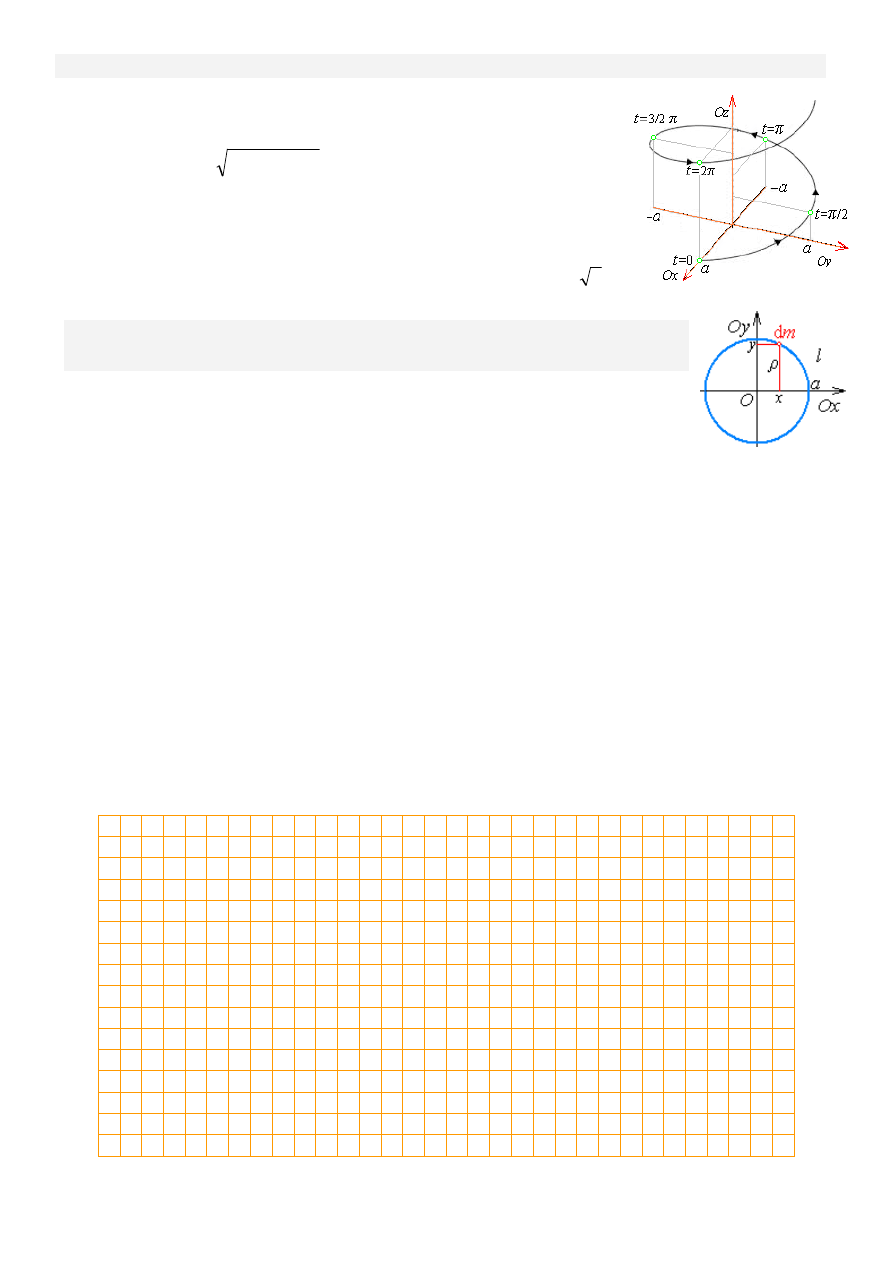
Zadanie 2.
Obliczyć długość jednego zwoju linii śrubowej
}
),
sin(
),
cos(
{
at
z
t
a
y
t
a
x
=
=
=
,
]
2
,
0
[
π
∈
t
.
Rozwiązanie. Długość łuku
∫
=
l
l
l
d , dlatego wpierw musimy wyznaczyć
różniczkę
=
+
+
=
t
y
x
l
z
d
d
2
2
2
&
&
&
……………………………………
…………………………………………………………………………
Zatem
∫
∫
=
=
....
....
....
d
l
l
l
………………………………….. Odp.
2
2 a
π
.
Zadanie 3.
Obliczyć moment bezwładności pręta w kształcie okręgu o promieniu „a”
i stałej gęstości liniowej masy
γ
, względem jego średnicy.
Odp.
3
a
πγ
.
Rozwiązanie. Umieśćmy środek okręgu w początku układu współrzędnych.
Jego równanie we współrzędnych biegunowych jest
a
r
=
)
(
ϕ
,
]
2
,
0
[
π
ϕ
∈
.
Wybierzmy oś Ox (która jest średnicą okręgu) jako oś obrotu. Wtedy,
∫
∫
=
=
l
l
x
m
y
m
I
d
d
2
2
ρ
. Ze wzorów przejścia do współrzędnych biegunowych
)
sin(
)
sin(
ϕ
ϕ
a
r
y
=
=
.
Różniczka masy
l
m
d
d
γ
=
, a więc
(
)
∫
∫
∫
∫
=
=
=
=
l
l
l
l
x
l
a
l
a
l
y
l
y
I
d
)
(
sin
d
)
sin(
d
d
2
2
2
2
2
ϕ
γ
ϕ
γ
γ
γ
.
We współrzędnych biegunowych, różniczka łuku
=
l
d
…………………………………………….
Zatem
∫
=
......
......
2
2
)
(
sin
ϕ
γ
a
I
x
………………………………………………………………………….
………………………………………………………………………………………………………
………………………………………………………………………………………………………
Opracował i wykonał: Stanisław Zoń
Operacje różniczkowe
Zadania na ćwiczenia
1.2
Zadanie 4.
Odległość dowolnego punktu P = (x,y,z) od początku układu
współrzędnych Oxyz wyraża funkcja (pole skalarne)
2
2
2
z
y
x
r
+
+
=
.
Wyznaczyć
r
grad
.
Odp
]
,
,
[
1
,
,
grad
z
y
x
r
r
z
r
y
r
x
r
=
=
.
Rozwiązanie.
∂
∂
∂
∂
∂
∂
=
z
r
y
r
x
r
r
,
,
grad
=…………………………………………..…………………………………
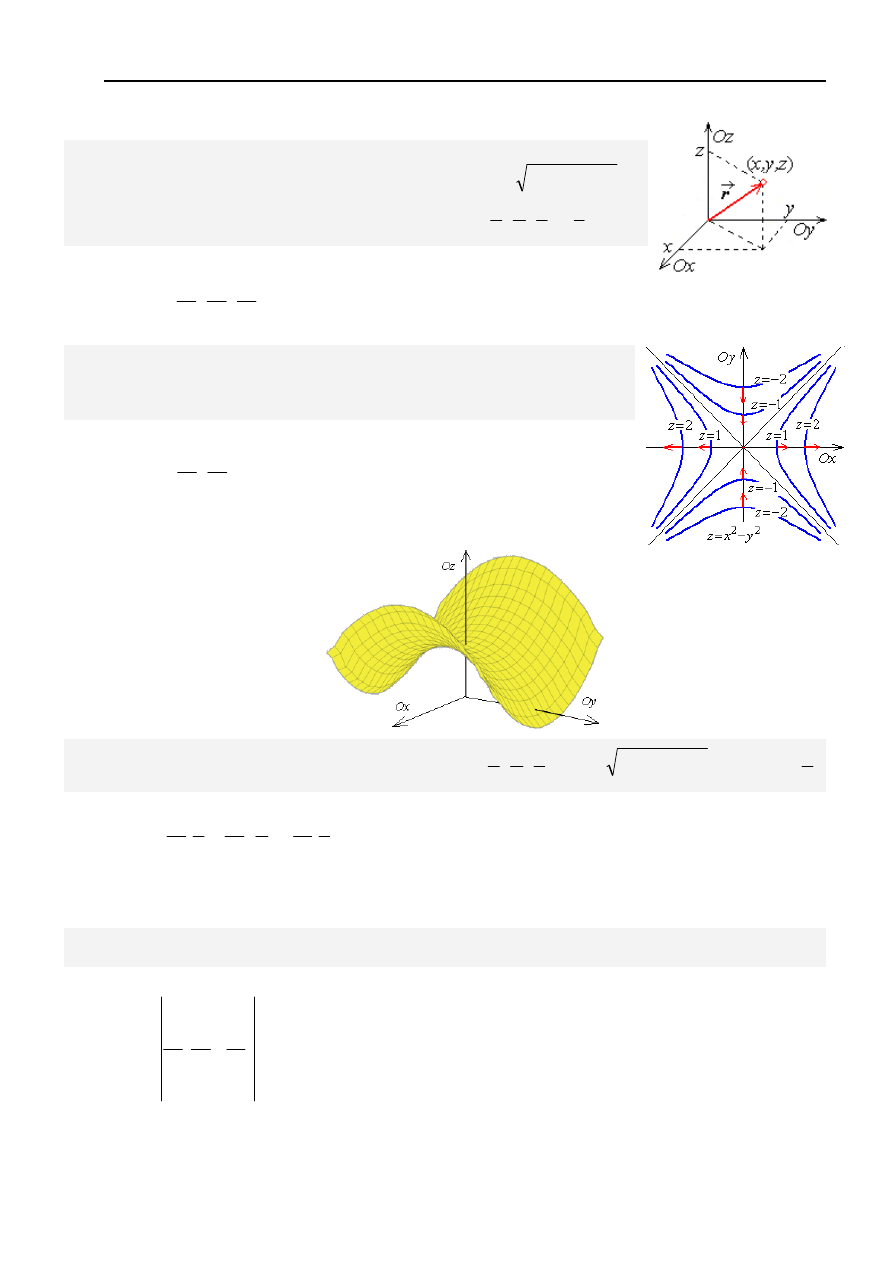
Zadanie 5.
Na rysunku obok narysowano hiperbole, które są warstwicami
funkcji
2
2
y
x
z
−
=
oraz kilka wektorów. Co wskazują te wektory?
Wyznaczyć
z
grad w kilku punktach zaczepienia tych wektorów.
∂
∂
∂
∂
=
y
z
x
z
z
,
grad
=…………………………………………………….
…………………………………………………………………………..
Zadanie 6.
Wyznaczyć
→
F
div
gdy pole wektorowe
=
→
r
z
r
y
r
x
,
,
F
, a
2
2
2
z
y
x
r
+
+
=
.
Odp.
r
2 .
( )
( )
r
z
z
r
y
y
r
x
x
∂
∂
+
∂
∂
+
∂
∂
=
→
F
div
=………………………………..…………………………………
……………………………………………………………………………………………………….
Zadanie 7.
Wyznaczyć
→
F
rot
gdy pole wektorowe
[
]
z
x
x
yz
+
=
→
,
,
2
F
.
Odp.
]
2
,
1
,
0
[
z
x
y
−
−
.
=
⋅
+
⋅
−
⋅
=
+
∂
∂
∂
∂
∂
∂
=
→
→
→
→
→
→
→
....)
(.........
....)
(.........
......)
(.........
rot
2
k
j
i
k
j
i
F
z
x
x
yz
z
y
x
……………………………
……………………………………………………………………………………………………….
Opracował i wykonał: Stanisław Zoń
Zadanie domowe 1
1.1 Całka krzywoliniowa nieskierowana
Z
ADANIE
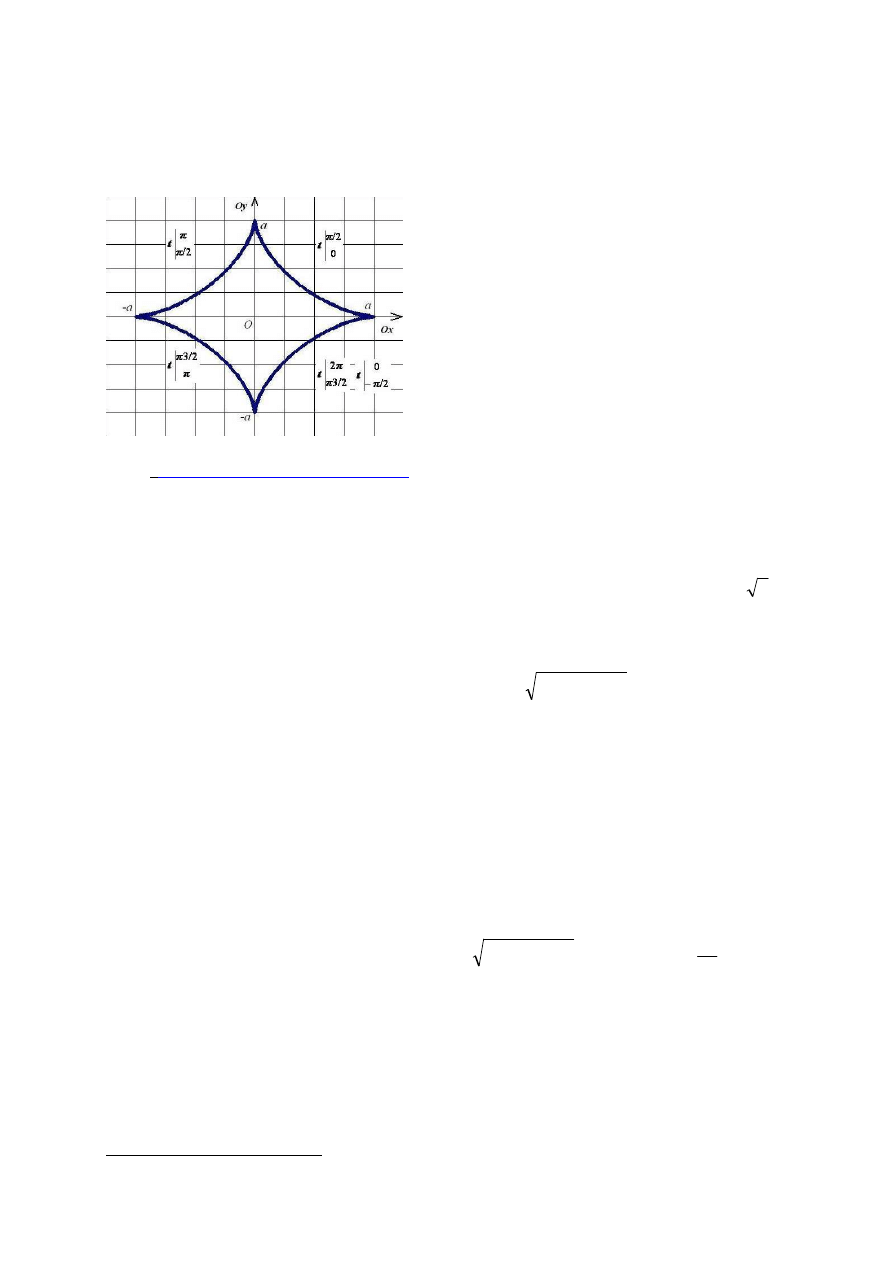
1
. Obliczyć długość jednego łuku asteroidy o równaniu:
⋅
=
⋅
=
)
(
sin
)
(
cos
3
3
t
a
y
t
a
x
, (a>0).
Odp.,
2
/
3a
l
=
.
Zobacz.
http://pl.wikipedia.org/wiki/Hipocykloida
Z
ADANIE
2. Obliczyć całkę
∫
⋅
+
L
l
y
x
d
)
(
gdy L jest obwodem trójkąta o wierzchołkach: A(0,0). B(a,0), C(0,a)
Odp.
(
)
2
1
2
+
a
.
Z
ADANIE
3
1
. Obliczyć pole S powierzchni walcowej
x
a
y
x
=
+
2
2
, zawartej między płaszczyzną
0
)
,
(
1
=
=
y
x
f
z
, a górną półsferą
2
2
2
2
)
,
(
y
x
a
y
x
f
z
−
−
=
=
Odp.
2
2a .
W
SKAZOWKA
.
(
)
l
y
x
f
y
x
f
S
L
d
)
,
(
)
,
(
1
2
⋅
−
=
∫
, gdzie krzywa L ma równanie jak powierzchnia walca.
Użyć współrzędnych biegunowych.
1.2 Operacje różniczkowe
„Zadania z matematyki wyższej” część 2, str 183
Roman Leitner, Wojciech Matuszewski, Zdzisław Rojek
Z
ADANIE
4 (22.12 b) Wyznaczyć
)
ln(
grad
r , gdy
2
2
2
z
y
x
r
+
+
=
.
Odp.
[
]
z
y
x
r
r
,
,
1
grad
2
=
.
Z
ADANIE
5 (22.16 c) Wyznaczyć
→
F
div
gdy pole wektorowe
[
]
2
2
2
,
,
xyz
z
xy
yz
x
=
→
F
.
Odp. xyz
6
.
Z
ADANIE
6 (22.16 c) Wyznaczyć
→
F
rot
gdy pole wektorowe
[
]
)
(
,
,
z
f
x
y
−
=
→
F
.
Odp.
]
2
,
0
,
0
[
.
1
Zadanie dla ambitnych
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron