
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
1
8. Zadanie transportowe
Zadanie transportowe polega na opracowaniu planu przewozów jednorodnego towaru od m dostawców do
n
odbiorców
w taki sposób, aby wykorzystać możliwości (zapasy) dostawców i zaspokoić zapotrzebowania
odbiorców
, minimalizując przy tym łączny koszt przewiezienia całego towaru. Każdy z dostawców
z każdym z odbiorców jest połączony tzw. trasą. Trasy są odrębnymi obiektami w sensie logicznym, natomiast
fizycznie mogą się częściowo pokrywać (wspólne fragmenty drogi, linii kolejowej, rurociągu itp.).
Parametrami modelu
są:
•
i
d
, i=1,...,m - możliwości dostawców - ilości towaru zgromadzone (zapasy) czy też możliwe do zmagazy-
nowania lub wyprodukowania w danym okresie czasu u poszczególnych dostawców (liczone w t, kg, m
2
,
m
3
, mb, szt. itp.);
•
j
o
, j=1,...,n - zapotrzebowania odbiorców- ilości towaru, jakie chcą dostać poszczególni odbiorcy (liczone
w tych samych jednostkach, co możliwości dostawców);
•
ij
c
, i=1,...,m. j=1,...,n - koszty przewiezienia jednej jednostki towaru od i-tego dostawcy do j-tego odbiorcy
(liczone w PLN/t, PLN/kg etc. – jednostka miary towaru musi być taka jak ta, w której liczone są
możliwości dostawców i zapotrzebowania odbiorców; waluta może być inna, byle we wszystkich kosztach
jednostkowych taka sama).,
Zmienne decyzyjne
mają następującą interpretację:
•
ij
x
, i=1,...,m, j=1,...,n - ilość towaru przewieziona na trasie od i-tego dostawcy do j-tego odbiorcy
(zmiennych jest łącznie
n
m ⋅
)
Mamy następujące możliwości:
1)
m
d
d
+
+
...
1
n
o
o
+
+
=
...
1
łączne możliwości dostawców są równe łącznemu zapotrzebowaniu odbiorców
2)
m
d
d
+
+
...
1
n
o
o
+
+
>
...
1
łączne możliwości dostawców są większe niż łączne zapotrzebowanie odbiorców
3)
m
d
d
+
+
...
1
n
o
o
+
+
<
...
1
łączne możliwości dostawców są mniejsze niż łączne zapotrzebowanie odbiorców
Przypadek 1 to tzw. zadanie zbilansowane albo zamknięte a przypadki 2 i 3 to zadania niezbilansowane albo
otwarte
.
Model matematyczny
zadania wygląda następująco:
min
...
...
...
...
2
2
1
1
2
2
22
22
21
21
1
1
12
12
11
11
→
+
+
+
+
+
+
+
+
+
+
+
+
mn
mn
m
m
m
m
n
n
n
n
x
c
x
c
x
c
x
c
x
c
x
c
x
c
x
c
x
c
łączny koszt przewiezienia całego towaru na wszystkich trasach
przy ograniczeniach
0
≥
ij
x
,
i
=1,...,
m, j
=1,...,
n
- ilości towaru nie mogą być ujemne.
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
2
Ad 1)
m
mn
m
m
n
n
d
x
x
x
d
x
x
x
d
x
x
x
=
+
+
+
=
+
+
+
=
+
+
+
...
...
...
...
2
1
2
2
22
21
1
1
12
11
warunki bilansowe
dla dostawców
(od każdego z dostaw-
ców będzie wywiezio-
ne tyle towaru, ile
może on wysłać)
n
mn
n
n
m
m
o
x
x
x
o
x
x
x
o
x
x
x
=
+
+
+
=
+
+
+
=
+
+
+
...
...
...
...
2
1
2
2
22
12
1
1
21
11
warunki bilansowe dla
odbiorców
(wszyscy odbiorcy otrzy-
mają tyle towaru, ile
wynosi ich
zapotrzebowanie)
Ad 2)
m
mn
m
m
n
n
d
x
x
x
d
x
x
x
d
x
x
x
≤
+
+
+
≤
+
+
+
≤
+
+
+
...
...
...
...
2
1
2
2
22
21
1
1
12
11
warunki bilansowe dla
dostawców
(przynajmniej od
jednego z dostawców
będzie wywiezione
mniej towaru niż może
on wysłać)
n
mn
n
n
m
m
o
x
x
x
o
x
x
x
o
x
x
x
=
+
+
+
=
+
+
+
=
+
+
+
...
...
...
...
2
1
2
2
22
12
1
1
21
11
warunki bilansowe dla
odbiorców
(wszyscy odbiorcy
otrzymają tyle towaru. ile
wynosi ich
zapotrzebowanie)
Ad 3)
m
mn
m
m
n
n
d
x
x
x
d
x
x
x
d
x
x
x
=
+
+
+
=
+
+
+
=
+
+
+
...
...
...
...
2
1
2
2
22
21
1
1
12
11
warunki bilansowe dla
dostawców
(od każdego z dostaw-
ców będzie wywiezio-
ne tyle towaru, ile
może on wysłać)
n
mn
n
n
m
m
o
x
x
x
o
x
x
x
o
x
x
x
≤
+
+
+
≤
+
+
+
≤
+
+
+
...
...
...
...
2
1
2
2
22
12
1
1
21
11
warunki bilansowe dla
odbiorców
(przynajmniej jeden z
odbiorców nie dostanie tyle
towaru, ile wynosi jego
zapotrzebowanie)
Zadanie transportowe zbilansowane z warunkami ograniczającymi zadania niezbilanso¬wa¬ne-go
Zadanie transportowe zbilansowane może być zapisane z warunkami ograniczającymi zadania niezbilansowa-
nego w dowolnej wersji (tzn. albo z „nadmiarem” u dostawców albo z „nadmiarem” u odbiorców). Wynika to
z faktu, że jeśli wartości zmiennych spełniają warunki ograniczające z równościami, to spełniają je również
z nierównościami „słabymi” czyli ≤ lub ≥.
Twierdzenie o istnieniu rozwiązań zadania transportowego
Każde zadanie transportowe w „klasycznej” postaci tzn. bez górnych limitów przepustowości tras, zarówno
zbilansowane jak i niezbilansowane, ma rozwiązanie, ponieważ dla dowolnych dodatnich wartości
i
d
oraz
j
o
warunki ograniczające nie są sprzeczne.
Dodanie choćby jednego górnego ograniczenia przepustowości tras może jednak spowodować sprzeczność wa-
runków ograniczających.
Twierdzenie o rozwiązaniach całkowitoliczbowych zadania transportowego.
Jeżeli w zadaniu transportowym (zbilansowanym lub niezbilansowanym) wszystkie parametry
i
d
(możliwości
dostawców) oraz
j
o
(zapotrzebowania odbiorców) przyjmują wartości całkowite, to wtedy istnieje rozwiązanie
całkowitoliczbowe
*
*
1
,...,
n
x
x
tego zadania.
Uwaga
„Gwarantowana” całkowitoliczbowość dotyczy jedynie rozwiązań wierzchołkowych (tzn. będących współ-
rzędnymi wierzchołków zbioru rozwiązań dopuszczalnych
D
). W przypadku istnienia rozwiązań wielokrotnych
rozwiązania niewierzchołkowe są całkowitoliczbowe jedynie sporadycznie - istnieje ich co najwyżej skończona
liczba wobec nieskończenie wielu wszystkich rozwiązań niewierzchołkowych.
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
3
Zadanie cz. 1. „Klasyczne” zadanie transportowe
Znaleźć optymalny plan przewozu kontenerów od 4 dostawców do 3 odbiorców. W tabeli dane są koszty
jednostkowe przewozu towaru na poszczególnych trasach, możliwości dostawców i zapotrzebowanie
odbiorców.
Odbiorcy
Dostawcy
Koszty jednostkowe przewozu towaru na
poszczególnych trasach (PLN/szt
)
Możliwości
dostawców(szt.)
O1
O2
O3
D1
17
15
20
28
D2
11
19
24
25
D3
16
13
9
23
D4
10
14
16
19
Zapotrzebowanie odbiorców (szt.)
17
26
24
Uwagi
1)
Przy tworzeniu modelu matematycznego należy zwrócić uwagę, czy jest to zadanie zbilansowane czy
niezbilansowane (poprzez obliczenie sum możliwości dostawców i zapotrzebowań odbiorców i porównanie
ich ze sobą).
2)
Zrzuty ekranów zostały wykonane przy ustawieniu w większości komórek czcionki Arial 8 zamiast
domyślnej Arial 10, aby pomieścić napisy, dlatego też po wpisaniu danych przy ustaleniach domyślnych
arkusz może wyglądać nieco inaczej.
3)
Ponieważ kontenery są niepodzielne tzn. liczone w sztukach, tylko rozwiązanie całkowitoliczbowe jest
poprawne. Należy zwrócić uwagę na ten fakt przy tworzeniu modelu i analizie wyników.
Model matematyczny do zadania
Zmienne decyzyjne
mają standardową interpretację:
ij
x
,
i
=1,2,3,4;
j
=1,2,3 – liczba kontenerów (w sztukach) przewieziona od
i
-tego dostawcy do
j
-tego odbiorcy
Funkcja celu
oznacza łączny koszt przewiezienia wszystkich kontenerów na wszystkich trasach:
min
16
14
10
9
13
16
24
19
11
20
15
17
43
42
41
33
32
31
23
22
21
13
12
11
→
+
+
+
+
+
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
przy ograniczeniach
0
≥
ij
x
,
i
=1,2,3,4;
j
=1,2,3 - liczba przewiezionych kontenerów nie może być ujemna
19
23
25
28
43
42
41
33
32
31
23
22
21
13
12
11
≤
+
+
≤
+
+
≤
+
+
≤
+
+
x
x
x
x
x
x
x
x
x
x
x
x
Od każdego dostawcy jest wywiezione co najwyżej tyle
kontenerów, żeby nie przekroczyć możliwości żadnego z tychże
dostawców
24
26
17
43
33
23
13
42
32
22
12
41
31
21
11
=
+
+
+
=
+
+
+
=
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
Każdy odbiorca dostanie dokładnie tyle kontenerów, ile wynosi
jego zapotrzebowanie.
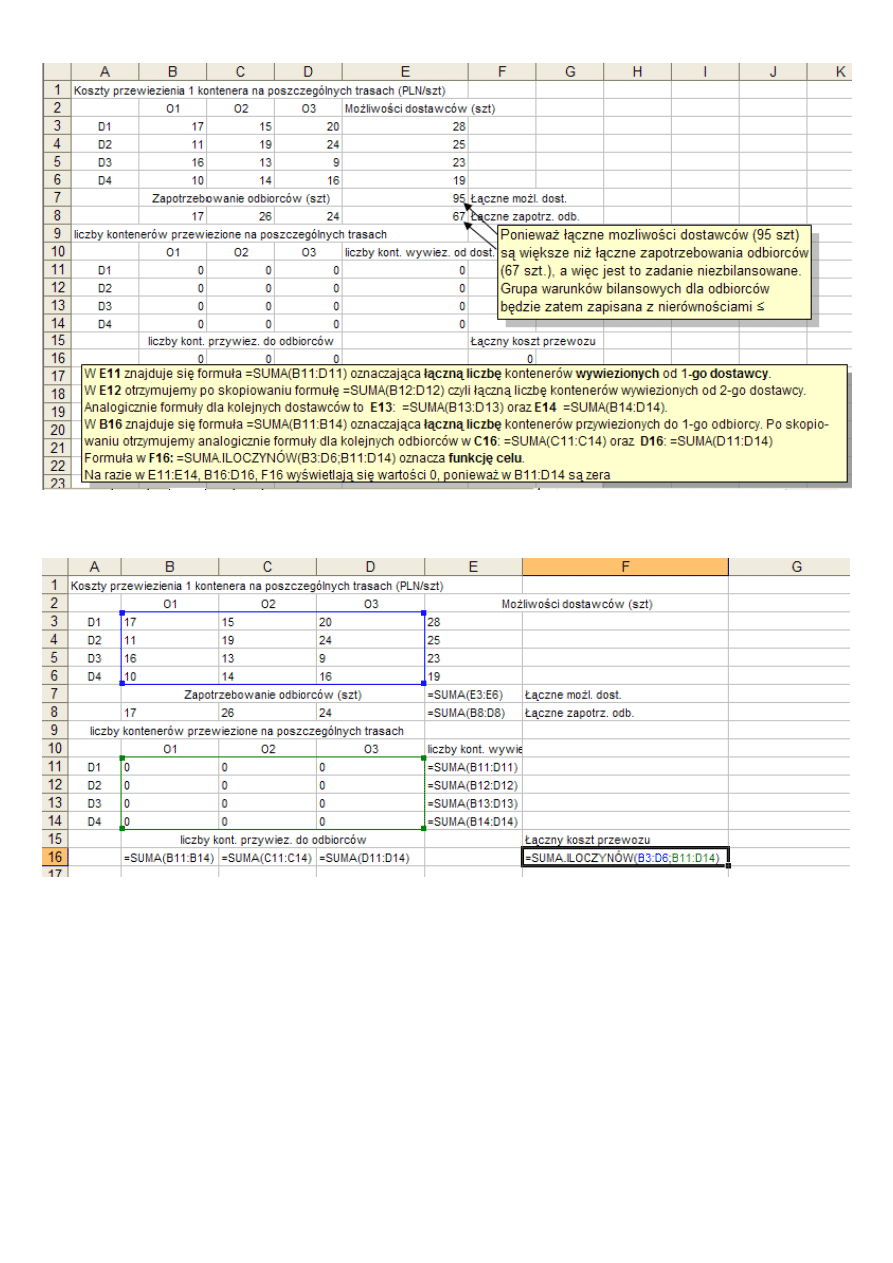
Warunki ograniczające mają postać charakterystyczną dla wariantu 2 (zadanie niezbilansowane z „nadmiarem
po stronie dostawców”). Jest tak dlatego, że łączne możliwości dostawców (28+25+23+19=95) są większe niż
łączne zapotrzebowania odbiorców (17+26+24=67).

P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
4
Funkcja celu „rozpisana” z jednostkami
szt
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
x
szt
PLN
szt
x
szt
PLN
43
42
41
33
32
31
23
22
21
13
12
11
16
14
10
9
13
16
24
19
11
20
15
17
+
+
+
+
+
+
+
+
+
+
+
Jak wida
ć
, po „skróceniu” jednostek towaru (sztuk) funkcja celu jest wyra
ż
ona w PLN.
Nie ma potrzeby „rozpisywania” warunków ograniczaj
ą
cych, poniewa
ż
lewe strony warunków - sumy
zmiennych s
ą
wyra
ż
one w sztukach (tak samo jak i prawe strony).
Wprowadzanie danych do komórek arkusza
W niniejszym zadaniu komórkami pełni
ą
cymi rol
ę
zmiennych decyzyjnych b
ę
d
ą
B11, C11, D11, B12, C12,
D12, B13, C13, D13, B14, C14, D14 czyli (w skrócie) zakres (tablica) B11:D14. Odpowiednio
ść
pomi
ę
dzy
komórkami a zmiennymi jest nast
ę
puj
ą
ca:
B11 -
11
x , C11 -
12
x , D11 -
13
x
,
B12 -
21
x , C12 -
22
x , D12 -
23
x
,
B13 -
31
x
, C13 -
32
x
, D13 -
33
x
,
B14 -
41
x , C14 -
42
x , D14 -
43
x
,
Rozmieszczenie danych liczbowych
Funkcja celu to suma iloczynów. Poniewa
ż
współczynniki tej funkcji celu znajduj
ą
si
ę
w komórkach B3, C3,
D3, B4, C4, D4, B5, C5, D5, B6, C6, D6 czyli (w skrócie) zakres (tablica) B3:D6 zatem odpowiednikiem
funkcji
43
42
41
33
32
31
23
22
21
13
12
11
16
14
10
9
13
16
24
19
11
20
15
17
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
b
ę
dzie formuła
=B3*B11+C3*C11+D3*D11+
B4*B12+C4*C12+D4*D12+
B5*B13+C5*C13+D5*D13+
B6*B14+C6*C14+D6*D14

P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
5
Zastosujemy jednak (w tym przypadku du
ż
o prostsz
ą
przy wprowadzaniu) równowa
ż
n
ą
formuł
ę
=SUMA.ILOCZYNÓW(B3:D6;B11:D14).
Rozmieszczenie formuł
Informacja na temat formuł: wprowadzanych przez użytkownika i kopiowanych (funkcja celu i warunki
ograniczające)
Zapis matematyczny
Formuły „dosłowne” tzn. takie które należałoby
wpisać przy literalnym „przełożeniu” zapisu
matematycznego na składnię Excela
K
om
ór
ka
Formuły z SUMA.ILOCZYNÓW lub SUMA
odpowiadające formułom „dosłownym”
Uwagi
43
42
41
33
32
31
23
22
21
13
12
11
16
14
10
9
13
16
24
19
11
20
15
17
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
=B3*B11+C3*C11+D3*D11+
B4*B12+C4*C12+D4*D12+
B5*B13+C5*C13+D5*D13+
B6*B14+C6*C14+D6*D1
G15
=SUMA.ILOCZYNÓW(B3:D6;B11:D14).
Wprowadzona
przez użytkownika
13
12
11
.x
x
x
+
+
= B11+C11+D11
E11
=SUMA(B11:D11)
Wprowadzona
przez użytkownika
23
22
21
x
x
x
+
+
= B12+C12+D12
E12
==SUMA(B12:D12)
Otrzymana przez
kopiowanie z E11
33
32
31
x
x
x
+
+
= B13+C13+D13
E13
=SUMA(B13:D13)
Otrzymana przez
kopiowanie z E11
43
42
41
x
x
x
+
+
= B14+C14+D14
E14
=SUMA(B14:D14)
Otrzymana przez
kopiowanie z E11
41
31
21
11
x
x
x
x
+
+
+
= B11+ B12+B13+B14
B16
=SUMA(B11:B14)
Wprowadzona
przez użytkownika
42
32
22
12
x
x
x
x
+
+
+
=C11+ C12+C13+C14
C16
=SUMA(C11:C14)
Otrzymana przez
kopiowanie z B16
43
33
23
13
x
x
x
x
+
+
+
=D11+ D12+D13+D14
D16
=SUMA(D11:D14)
Otrzymana przez
kopiowanie z B16
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
6
Widok po skopiowaniu. Zrzut ekranu powy
ż
ej
nie ilustruje żadnych czynności
, a jedynie słu
ż
y do
kontroli
poprawności
wprowadzenia danych!!!
To samo, co powy
ż
ej, ale
zamiast wyników formuł
(które to wyniki na tym etapie s
ą
, jak ju
ż
wiadomo,
zerami) s
ą
wy
ś
wietlone
same formuły
.
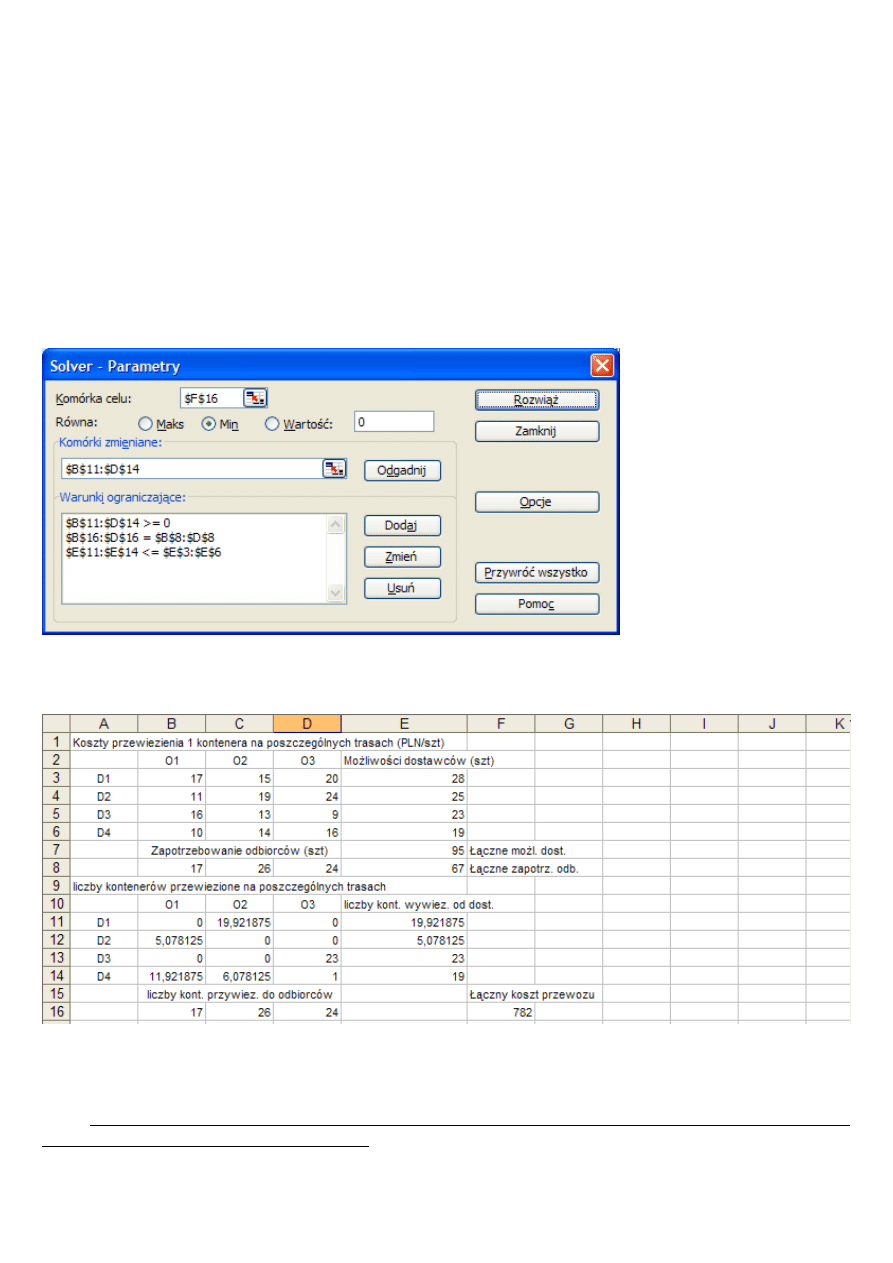
Ustawienia Solvera
Na tym etapie zako
ń
czyło si
ę
wprowadzanie danych bezpo
ś
rednio do komórek arkusza.
Mamy nast
ę
puj
ą
ce zwi
ą
zki mi
ę
dzy zapisem matematycznym a zapisem w Excelu:
B11 -
11
x
, C11-
12
x
, D11 -
13
x ,
B12 -
21
x
, C12 -
22
x
, D12 -
23
x ,
B13 -
31
x , C13 -
32
x , D13 -
33
x ,
B14 -
41
x
, C14 -
42
x
, D14 -
43
x ,
ij
x
, i=1,2,3,4, j=1,2,3– liczba kontenerów (w sztukach)
przewieziona od i-tego dostawcy do j-tego odbiorcy
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
7
F16
min
16
14
10
9
13
16
24
19
11
20
15
17
43
42
41
33
32
31
23
22
21
13
12
11
→
+
+
+
+
+
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
łączny koszt przewiezienia wszystkich kontenerów na wszystkich
trasach
przy ograniczeniach
E11
E12
E13
E14
17
23
25
28
43
42
41
33
32
31
23
22
21
13
12
11
≤
+
+
≤
+
+
≤
+
+
≤
+
+
x
x
x
x
x
x
x
x
x
x
x
x
E3
E4
E5
E6
B16
C16
D16
24
26
17
43
33
23
13
42
32
22
12
41
31
21
11
=
+
+
+
=
+
+
+
=
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
B8
C8
D8
B11:D14
0
≥
ij
x
, i=1,2,3,4, j=1,2,3
Ustawienia Solvera dla zadania transportowego niezbilansowanego z „nadmiarem” po stronie
dostawców
Rozwiązanie „klasycznego” zadania transportowego
Solver znalazł rozwi
ą
zanie niecałkowitoliczbowe zadania, cho
ć
, jak wiadomo ze stosownego twierdzenia, po-
winno istnie
ć
rozwi
ą
zanie całkowitoliczbowe. Nie jest to jednak rezultat bł
ę
du Solvera. Po prostu twierdzenie
mówi wył
ą
cznie o istnieniu całkowitoliczbowych rozwi
ą
za
ń
wierzchołkowych tzn. takich, które s
ą
współrz
ę
-
dnymi wierzchołków zbioru dopuszczalnego. Niniejsze zadanie ma rozwi
ą
zania wielokrotne, a Solver znalazł
jedno z rozwi
ą
za
ń
wielokrotnych niewierzchołkowych o warto
ś
ciach niecałkowitych. Fakt, i
ż
Solver nie
znalazł rozwi
ą
zania wierzchołkowego wynika z tego,
ż
e domy
ś
lnym jego ustawieniem jest u
ż
ycie algorytmu
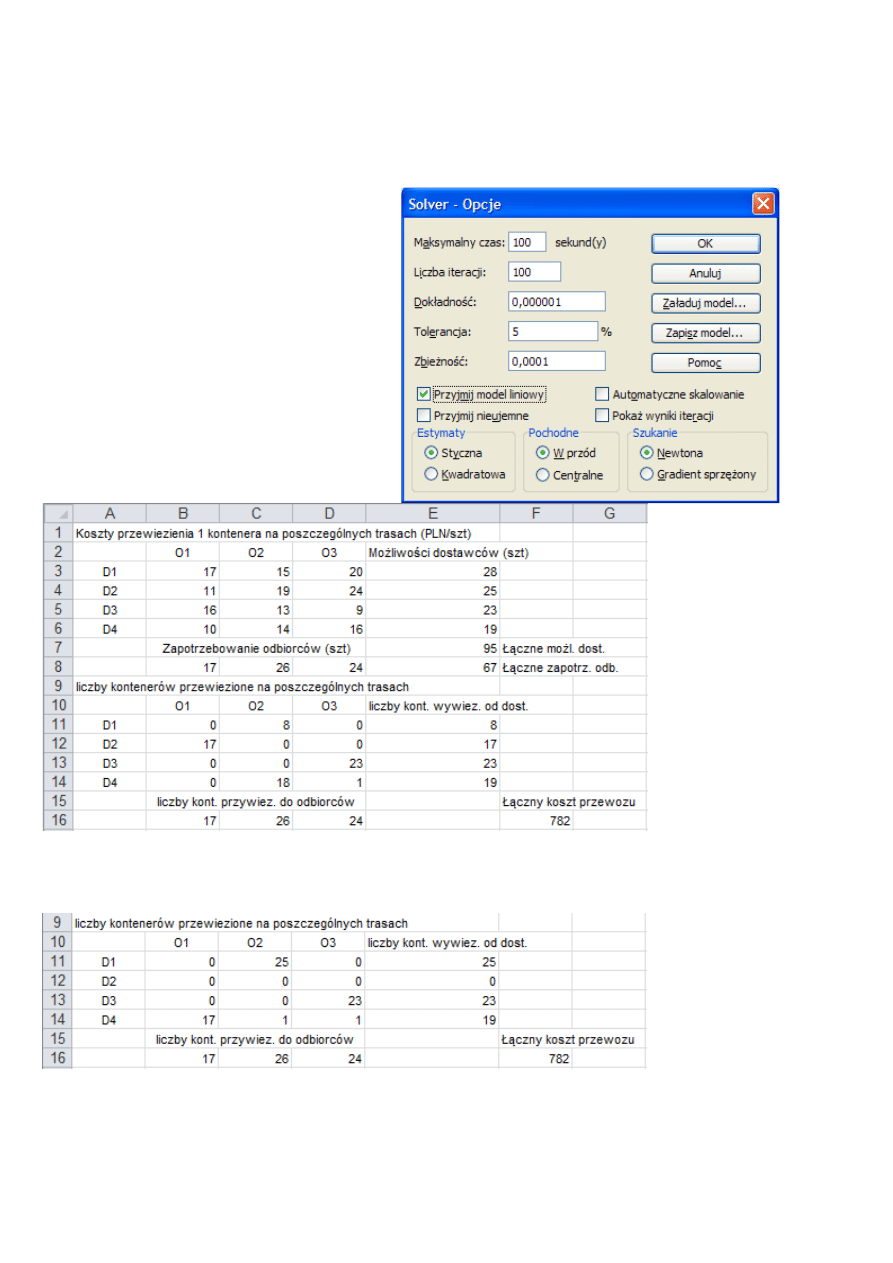
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
8
„ogólnego” tzn. stosowanego zarówno w programowaniu liniowym jak i nieliniowym. Aby mimo wszystko
znale
źć
rozwi
ą
zanie całkowitoliczbowe, w tym przypadku nie ma potrzeby dodawania warunków całkowito-
liczbowo
ś
ci zmiennych – wystarczy „wymusi
ć
” u
ż
ycie algorytmu simpleks, który znajduje wył
ą
cznie
rozwi
ą
zania wierzchołkowe.
Aby
przeł
ą
czy
ć
Solvera
z
algorytmu
„ogólnego: na algorytm simpleks (u
ż
ywany do
rozwi
ą
zywania zada
ń
programowania liniowe-
go) nale
ż
y klikn
ąć
w Opcje w głównym oknie
Solvera, a nast
ę
pnie w nowym oknie, które si
ę
otworzy zaznaczy
ć
Przyjmij model liniowy
i klikn
ąć
w OK.
.
Rozwiązanie całkowitoliczbowe
– otrzymane po zaznaczeniu opcji Przyjmij model liniowy w oknie Solver-
Opcje
i ponownym rozwi
ą
zaniu przez klikni
ę
cie Rozwi
ąż
w głównym oknie tzn. Solver-Parametry).
Mo
ż
e te
ż
pojawi
ć
si
ę
alternatywne rozwi
ą
zanie wierzchołkowe (oczywi
ś
cie równie
ż
całkowitoliczbowe
)
Nale
ż
y tu wyra
ź
nie stwierdzi
ć
,
ż
e nie istnieje prosta i wygodna metoda pozwalaj
ą
ca znajdowa
ć
przy u
ż
yciu
Solvera wszystkie alternatywne rozwi
ą
zania wierzchołkowe. Alternatywne rozwi
ą
zanie podane powy
ż
ej zosta-
ło znalezione poprzez ponowne rozwi
ą
zanie zadania z zaznaczon
ą
opcj
ą
„Przyjmij model liniowy”. Nie ma jed-
nak
ż
adnej gwarancji,
ż
e to rozwi
ą
zanie jest jedynym alternatywnym rozwi
ą
zaniem wierzchołkowym. W zale
ż
-
no
ś
ci od zadania oraz wersji Excela ponowne przeliczenie Solverem mo
ż
e da
ć
w rezultacie alternatywne roz-
wi
ą
zania – wszystkie lub tylko niektóre, ale te
ż
mo
ż
e
ż
adnego z nich nie znale
źć
(pomimo
ż
e one istniej
ą
).
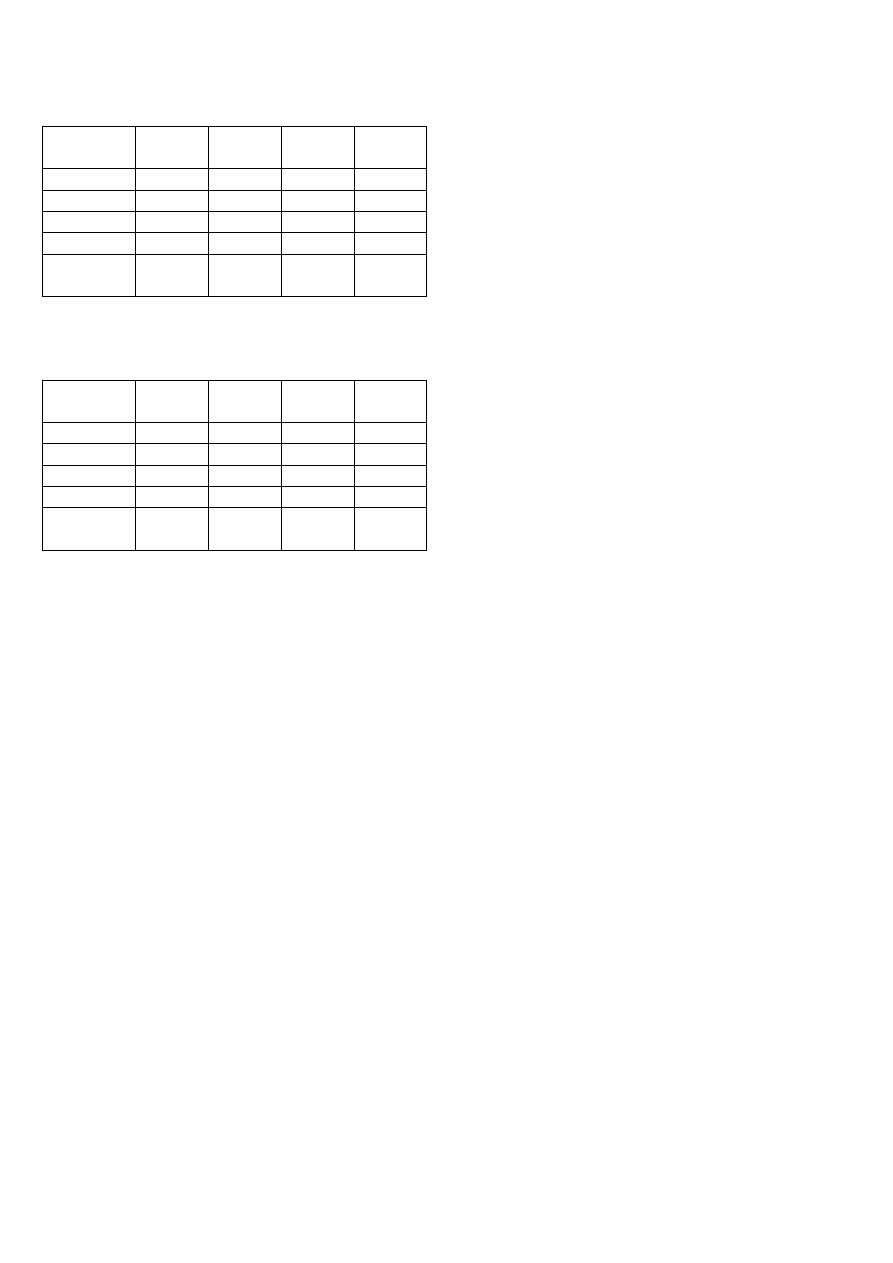
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
9
Odpowiedź „słowna”
Minimalny koszt przewiezienia kontenerów wynosi 782 PLN. Jest on osi
ą
gni
ę
ty dla nast
ę
puj
ą
cego planu
przewozów.
*
ij
x
O1
O2
O3
Razem
wysłane
D1
0
8
0
8<28
D2
17
0
0
17<25
D3
0
0
23
23
D4
0
18
1
19
Razem
otrzymane
17
26
24
Poniewa
ż
, jak ju
ż
wiadomo, istniej
ą
tak
ż
e inne rozwi
ą
zanie wierzchołkowe. Solver równie
ż
mo
ż
e je znale
źć
(cho
ć
nie oznacza to,
ż
e znajdzie). Jest to:
*
ij
x
O1
O2
O3
Razem
wysłane
D1
0
25
0
25<28
D2
0
0
0
0<25
D3
0
0
23
23
D4
17
1
1
19
Razem
otrzymane
17
26
24
Jak wida
ć
, dla obydwu rozwi
ą
za
ń
mo
ż
liwo
ś
ci dostawców D1 i D2 nie s
ą
wykorzystane w cało
ś
ci. W przypadku
drugiego rozwi
ą
zania, dostawca D2 nic nie wysyła.

P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
10
8.1 Zadanie transportowo-produkcyjne (rozszerzenie zadania transportowego)
Zadanie transportowo-produkcyjne jest pewnym uogólnieniem klasycznego zadania transportowego. Ró
ż
nica
polega na tym,
ż
e
dostawcy są również producentami przewożonego towaru
, a ponadto – co najistotniejsze -
towar
ten, niezale
ż
nie, od którego producenta-dostawcy pochodzi, jest jednakowy z punktu jego walorów
u
ż
ytkowych, natomiast
różni się kosztami wytworzenia u poszczególnych dostawców
. Zmodyfikowane
zadanie polega wi
ę
c na opracowaniu planu przewozów jednorodnego towaru od m producentów-dostawców do
n
odbiorców tak, aby wykorzysta
ć
mo
ż
liwo
ś
ci (moce produkcyjne) dostawców i zaspokoi
ć
zapotrzebowania
odbiorców,
minimalizując
przy tym
łączny koszt wyprodukowania i przewiezienia całego towaru
. Ka
ż
dy
z dostawców z ka
ż
dym z odbiorców jest poł
ą
czony tzw. tras
ą
, której znaczenie jest dokładnie takie samo jak w
przypadku klasycznego zadania transportowego.
Oznaczenia parametrów i zmiennych decyzyjnych oraz jednostki, w których s
ą
one liczone pozostaj
ą
takie
same jak w przypadku klasycznego zadania transportowego.
•
i
d
, i=1,...,m - mo
ż
liwo
ś
ci produkcyjne dostawców-producentów,
•
j
o
, j=1,...,n - zapotrzebowania odbiorców,
•
ij
c
, i=1,...,m, j=1,...,n - koszty przewiezienia jednej jednostki towaru od i-tego dostawcy do j-tego
odbiorcy,
•
ij
x
, i=1,...,m, j=1,...,n - ilo
ść
towaru przewieziona i-tego dostawcy do j-tego odbiorcy
Pojawia si
ę
jednak jeszcze jedna, nowa grupa parametrów:
•
i
b
, i=1,...,m – koszty jednostkowe produkcji towaru u dostawców-producentów (liczone w PLN/t, PLN/kg
etc. – jednostka miary towaru musi by
ć
taka jak ta, w której liczone s
ą
mo
ż
liwo
ś
ci dostawców i
zapotrzebowania odbiorców; waluta mo
ż
e by
ć
inna, byle we wszystkich kosztach jednostkowych produkcji
taka sama oraz taka sama jak w kosztach jednostkowych
ij
c
).
Jak w klasycznym zadaniu transportowym mamy 3 warianty warunków ograniczaj
ą
cych: jeden - zadania
zbilansowanego oraz dwa - zada
ń
niezbilansowanych. Jednak
ż
e, w wariantach: 1 (zadanie zbilansowane) oraz 3
(zadanie niezbilansowane z „nadmiarem” po stronie odbiorców) optymalizacja planu przewozów z uwzgl
ę
-
dnieniem kosztów produkcji jest pozorna. Dokładniej, optymalny plan przewozów b
ę
dzie dokładnie taki sam
niezale
ż
nie od tego, czy w obliczeniach zostan
ą
uwzgl
ę
dnione koszty produkcji czy te
ż
nie. Wynika to z faktu,
ż
e w obu tych przypadkach zostan
ą
wykorzystane całe mo
ż
liwo
ś
ci (moce produkcyjne) wszystkich dostawców,
a koszt produkcji niezale
ż
nie od planu przewozów (optymalnego lub nie, byle spełniaj
ą
cego ograniczenia)
b
ę
dzie stały i równy
m
m
d
b
d
b
d
b
+
+
...
2
2
1
1
. Nietrywialny jest jedynie przypadek 2, czyli nadwy
ż
ka po stronie
dostawców.
Model matematyczny wygl
ą
da nast
ę
puj
ą
co:
+
+
+
+
+
+
+
+
+
+
+
+
+
)
...
...
...
...
(
2
2
1
1
2
2
22
22
21
21
1
1
12
12
11
11
mn
mn
m
m
m
m
n
n
n
n
x
c
x
c
x
c
x
c
x
c
x
c
x
c
x
c
x
c
ł
ą
czny koszt przewiezienia całego towaru
na wszystkich trasach
min
)]
...
(
...
)
...
(
)
...
(
[
2
1
2
22
21
2
1
12
11
1
→
+
+
+
+
+
+
+
+
+
+
+
+
mn
m
m
m
n
n
x
x
x
b
x
x
x
b
x
x
x
b
)
ł
ą
czny koszt wyprodukowania całego towaru
u wszystkich producentów]
przy ograniczeniach:
0
≥
ij
x
, i=1,...,m, j=1,...,n
ilo
ś
ci towaru nie mog
ą
by
ć
ujemne.
m
mn
m
m
n
n
d
x
x
x
d
x
x
x
d
x
x
x
≤
+
+
+
≤
+
+
+
≤
+
+
+
...
...
...
...
2
1
2
2
22
21
1
1
12
11
warunki bilansowe dla
dostawców
(przynajmniej od jednego z
dostawców nie będzie
wywieziony cały towar)
n
mn
n
n
m
m
o
x
x
x
o
x
x
x
o
x
x
x
=
+
+
+
=
+
+
+
=
+
+
+
...
...
...
...
2
1
2
2
22
12
1
1
21
11
warunki bilansowe
dla odbiorców
(wszyscy odbiorcy
otrzymają tyle towaru
ile wynosi ich
zapotrzebowanie)
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
11
Zadanie cz.2. Rozszerzenie zadania
transportowego o koszty produkcji u dostawców
(zadanie transportowo-produkcyjne)
Rozszerzmy poprzednie zadanie, przyjmuj
ą
c,
ż
e dostawcy kontenerów s
ą
jednocze
ś
nie ich producentami. Teraz
nale
ż
y zminimalizowa
ć
ł
ą
czny koszt przewozu i produkcji (zakupu) kontenerów przy takich samych jak
poprzednio wymaganiach odno
ś
nie mo
ż
liwo
ś
ci dostawców i zapotrzebowa
ń
odbiorców.
Odbiorcy
Dostawcy
Koszty jednostkowe przewozu
towaru na poszczególnych trasach
(PLN/szt)
Możliwości
dostawców
(szt)
Jednostkowe koszty
produkcji(PLN/szt)
(współczynniki
i
b )
O1
O2
O3
D1
17
15
20
28
1051
D2
11
19
24
25
790
D3
16
13
9
23
865
D4
10
14
16
19
1053
Zapotrzebowanie odbiorców (szt)
17
26
24
Uwaga.
Funkcja celu musi przyj
ąć
posta
ć
odpowiadaj
ą
c
ą
postaci ogólnej dla zadania transportowo-
produkcyjnego). Warunki ograniczaj
ą
ce pozostaj
ą
bez zmian.(s
ą
to warunki dla
zadania
transportowego
z „nadmiarem” po stronie dostawców
)-.
Model matematyczny do zadania
Jedyn
ą
zmian
ą
jest „rozszerzenie” funkcji celu o koszty produkcji. Zakładamy,
ż
e dostawcy – producenci
wyprodukuj
ą
tylko tyle kontenerów, ile potem wg obliczonego planu zostanie wywiezione.
Zatem wielko
ś
ci produkcji s
ą
to sumy, które ju
ż
wyst
ę
puj
ą
w lewych stronach warunków ograniczaj
ą
cych dla
dostawców
E11
E12
E13
E14
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
Wielko
ść
produkcji u 1-go producenta-dostawcy
Wielko
ść
produkcji u 2-go producenta-dostawcy
Wielko
ść
produkcji u 3-go producenta-dostawcy
Wielko
ść
produkcji u 4-go producenta-dostawcy
Pomno
ż
enie ka
ż
dej z wielko
ś
ci produkcji (wyra
ż
onej w sztukach) przez koszt wyprodukowania 1 kontenera da
w rezultacie ł
ą
czny koszt produkcji:
)
(
1053
)
(
790
)
(
865
)
.
(
1051
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
Ł
ą
czny koszt produkcji „rozpisany” z jednostkami to:
szt
x
x
x
szt
PLN
szt
x
x
x
szt
PLN
szt
x
x
x
szt
PLN
szt
x
x
x
szt
PLN
)
(
1053
)
(
790
)
(
865
)
(
1051
43
42
41
33
32
31
23
22
21
13
12
11
+
+
+
+
+
+
+
+
+
+
+
Ostatecznie, model matematyczny wygl
ą
da nast
ę
puj
ą
co
Zmienne decyzyjne
ij
x
, i=1,2,3,4; j=1,2,3 – liczba kontenerów (w sztukach) przewieziona od i-tego dostawcy do j-tego odbiorcy
+
+
+
+
+
+
+
+
+
+
+
+
)
16
14
10
9
13
16
24
19
11
20
15
17
(
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
Nowa funkcja celu
(ł
ą
czny koszt przewiezienia całego towaru –
kontenerów - na wszystkich trasach) +

P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
12
min
)]
(
1053
)
(
790
)
(
865
)
(
1051
[
43
42
41
33
32
31
23
22
21
13
12
11
→
+
+
+
+
+
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
[ł
ą
czny koszt wyprodukowania całego towaru –
kontenerów - u wszystkich producentów]
przy ograniczeniach
0
≥
ij
x
, i=1,2,3,4; j=1,2,3 - liczba przewiezionych kontenerów nie mo
ż
e by
ć
ujemna
19
23
25
28
43
42
41
33
32
31
23
22
21
13
12
11
≤
+
+
≤
+
+
≤
+
+
≤
+
+
x
x
x
x
x
x
x
x
x
x
x
x
Od ka
ż
dego dostawcy jest wywiezione co najwy
ż
ej tyle
kontenerów,
ż
eby nie przekroczy
ć
mo
ż
liwo
ś
ci
ż
adnego z tych
ż
e
dostawców
24
26
17
43
33
23
13
42
32
22
12
41
31
21
11
=
+
+
+
=
+
+
+
=
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
Ka
ż
dy odbiorca dostanie dokładnie tyle kontenerów, ile wynosi
jego zapotrzebowanie.
Rozszerzenie poprzedniego zadania o koszty produkcji u dostawców-producentów.
Wprowadzanie danych do komórek arkusza
Dopisujemy w komórkach H3: H6 koszty jednostkowe produkcji.
H3
H4
H5
H6
1051
790
865
1053
Koszt wyprodukowania 1 kontenera u 1-go producenta-dostawcy
Koszt wyprodukowania 1 kontenera u 2-go producenta-dostawcy
Koszt wyprodukowania 1 kontenera u 3-go producenta-dostawcy
Koszt wyprodukowania 1 kontenera u 4-go producenta-dostawcy
E11
E12
E13
E14
43
42
41
33
32
31
23
22
21
13
12
11
.
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
Wielko
ść
produkcji u 1-go producenta-dostawcy
Wielko
ść
produkcji u 2-go producenta-dostawcy
Wielko
ść
produkcji u 3-go producenta-dostawcy
Wielko
ść
produkcji u 4-go producenta-dostawcy

P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
13
Ł
ą
czny koszt produkcji
)
(
1053
)
(
790
)
(
865
)
.
(
1051
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
mo
ż
na zapisa
ć
jako:
=H3*E11+H4*E12+H5*E13+H6*E14
ale wygodniej jest jako:
=SUMA.ILOCZYNÓW(H3:H6;E11:E14)
W/w formuł
ę
wpisujemy do H16 a sum
ę
=F16+H16 do G17.
Mamy zatem:
F16
43
42
41
33
32
31
23
22
21
13
12
11
16
14
10
9
13
16
24
19
11
20
15
17
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
H16
)
(
1053
)
(
790
)
(
865
)
(
1051
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
Poniewa
ż
w
G17
znajduje si
ę
formuła
=F16+H16
, a zatem
G17
staje si
ę
now
ą
komórk
ą
celu (komórk
ą
zawieraj
ą
c
ą
formuł
ę
odpowiadaj
ą
ca funkcji celu)
G17
min
)
(
1053
)
(
790
)
(
865
)
(
1051
16
14
10
9
13
16
24
19
11
20
15
17
43
42
41
33
32
31
23
22
21
13
12
11
43
42
41
33
32
31
23
22
21
13
12
11
→
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Informacja na temat formuł wprowadzanych przez użytkownika i kopiowanych (funkcja celu i warunki
ograniczające) – dotyczy formuł dodanych w 2 części zadania
Zapis matematyczny
Formuły „dosłowne” tzn. takie które należałoby
wpisać przy literalnym „przełożeniu” zapisu
matematycznego na składnię Excela
K
om
ór
ka
Formuły z SUMA.ILOCZYNÓW lub SUMA
odpowiadające formułom „dosłownym”
Uwagi
)
(
1053
)
(
790
)
(
865
)
(
1051
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
=H3*(
B11+C11+D11) +
H4*(
B12+C12+D12)+
H5*(
B13+C13+D13)+
H6*(
B14+C14+D14)
czyli
=H3*E11+H4*E12+H5*E13+H6*E14
G15
=SUMA.ILOCZYNÓW(H3:H6;E11:E14)
Wprowadzona
przez użytkownika
+
+
+
+
+
+
+
+
+
+
+
+
)
16
14
10
9
13
16
24
19
11
20
15
17
(
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
)]
(
1053
)
(
790
)
(
865
)
(
1051
[
43
42
41
33
32
31
23
22
21
13
12
11
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
+
+
+
+
+
+
+
=B3*B11+C3*C11+D3*D11+
B4*B12+C4*C12+D4*D12+
B5*B13+C5*C13+D5*D13+
B6*B14+C6*C14+D6*D14+
H3*(
B11+C11+D11) +
H4*(
B12+C12+D12)+
H5*(
B13+C13+D13)+
H6*(
B14+C14+D14)
G17
=F16+H16
Wprowadzona
przez użytkownika
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
14
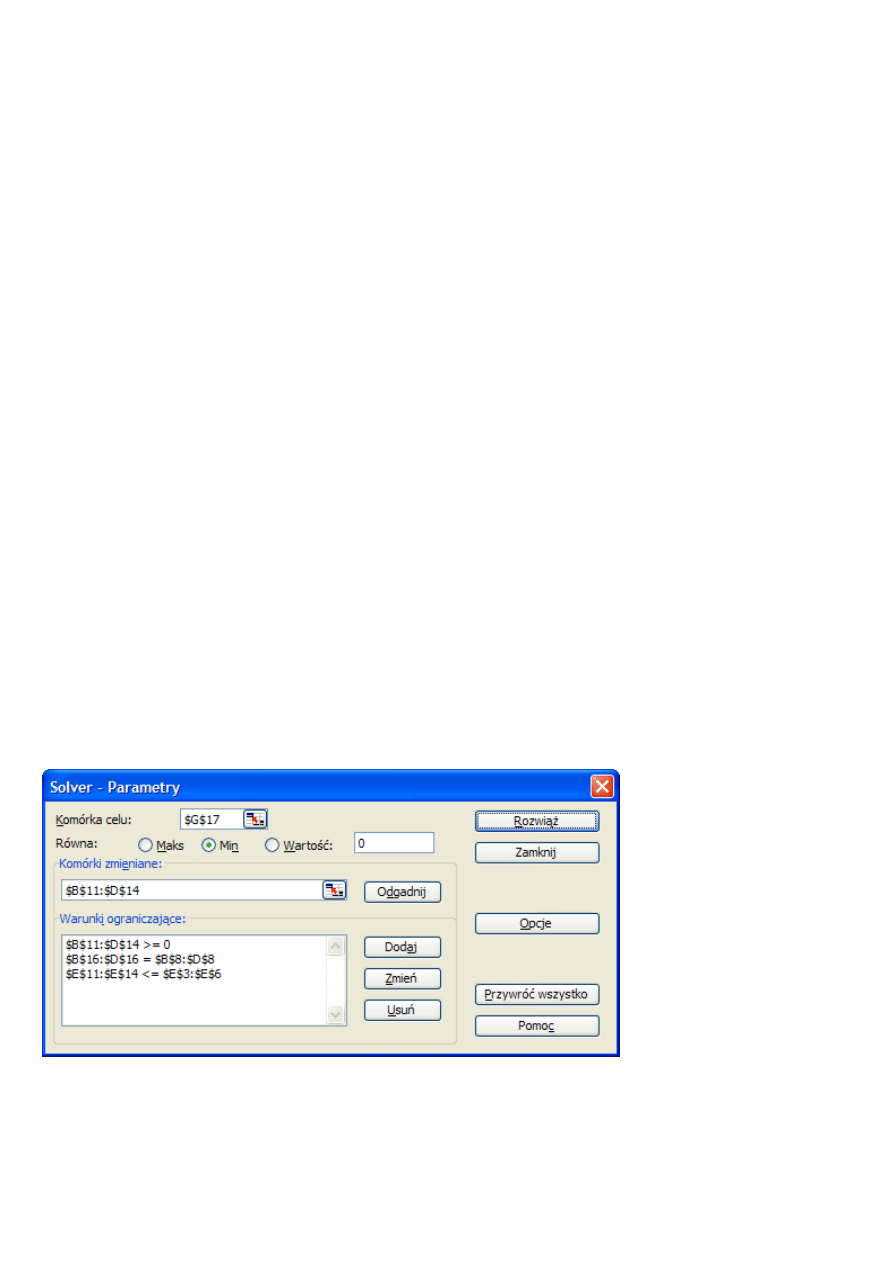
Ustawienia Solvera
Na tym etapie zako
ń
czyło si
ę
wprowadzanie danych bezpo
ś
rednio do komórek arkusza.
Mamy nast
ę
puj
ą
ce zwi
ą
zki mi
ę
dzy zapisem matematycznym a zapisem w Excelu:
B11 -
11
x
, C11-
12
x
, D11 -
13
x ,
B12 -
21
x
, C12 -
22
x
, D12 -
23
x ,
B13 -
31
x , C13 -
32
x , D13 -
33
x ,
B14 -
41
x
, C14 -
42
x
, D14 -
43
x ,
ij
x
, i=1,2,3,4, j=1,2,3– liczba kontenerów (w sztukach)
przewieziona od i-tego dostawcy do j-tego odbiorcy
F16
min
16
14
10
9
13
16
24
19
11
20
15
17
43
42
41
33
32
31
23
22
21
13
12
11
→
+
+
+
+
+
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
łączny koszt przewiezienia wszystkich kontenerów na wszystkich
trasach
H16
min
)
(
1053
)
(
790
)
(
865
)
(
1051
43
42
41
33
32
31
23
22
21
13
12
11
→
+
+
+
+
+
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
łączny koszt wyprodukowania wszystkich kontenerów u dostawców-producentów
G17 (=F16+ H16) – „kompletna” funkcja celu
przy ograniczeniach
E11
E12
E13
E14
17
23
25
28
43
42
41
33
32
31
23
22
21
13
12
11
≤
+
+
≤
+
+
≤
+
+
≤
+
+
x
x
x
x
x
x
x
x
x
x
x
x
E3
E4
E5
E6
B16
C16
D16
24
26
17
43
33
23
13
42
32
22
12
41
31
21
11
=
+
+
+
=
+
+
+
=
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
B8
C8
D8
B11:D14
0
≥
ij
x
, i=1,2,3,4, j=1,2,3
Ustawienia Solvera dla zadania transportowo-produkcyjnego.
Komórka celu zmienia się na G17
.
Pozostałe ustawienia Solvera bez zmian!!!
.
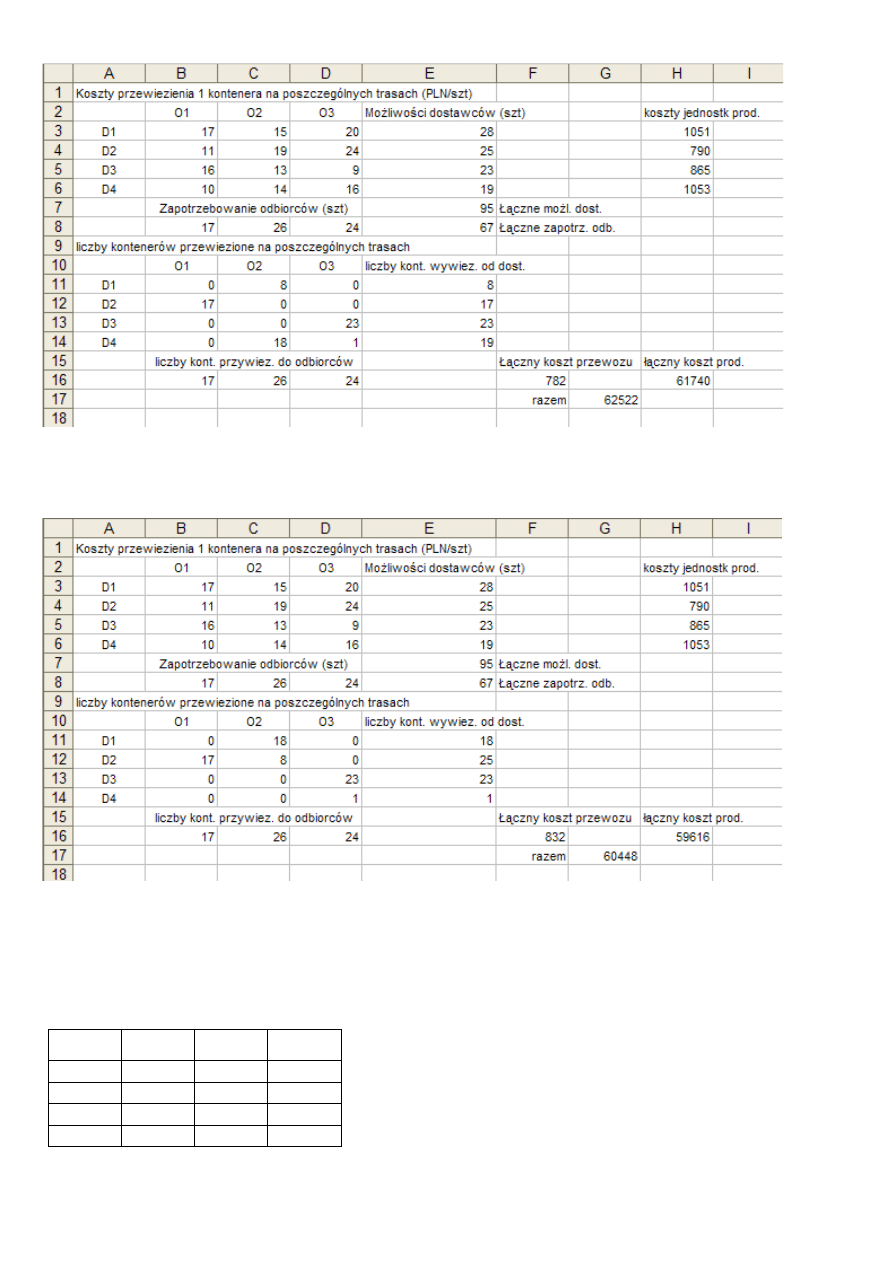
P. Kowalik, Laboratorium badań operacyjnych – zadanie transportowe i transportowo-produkcyjne
15
Zrzut ekranu wykonany po wstawieniu danych i formuł dla kosztów produkcji,
ale przed ponowną
optymalizacją
tzn.
przy pozostawieniu komórek zmienianych z takimi warto
ś
ciami, jakie zostały obliczone
przy rozwi
ą
zaniu poprzedniego wariantu zadania. Gdyby koszt produkcji oraz koszt ł
ą
czny były obliczone dla
drugiego rozwi
ą
zania wierzchołkowego, wtedy koszt produkcji wynosiłby 66177 a koszt ł
ą
czny 66959.
Rozwiązanie zadania transportowego zmodyfikowanego o koszty produkcji (zadania transportowo-
produkcyjnego).
Odpowiedź „słowna”
Minimalny koszt ł
ą
czny wyprodukowania
oraz przewiezienia kontenerów wynosi 59616
+ 832 = 60 448 PLN. Jest on osi
ą
gni
ę
ty dla
nast
ę
puj
ą
cego planu przewozów
*
ij
x
O1
O2
O3
D1
0
18
0
D2
17
8
0
D3
0
0
23
D4
0
0
1
Jak wida
ć
, optymalizacja ł
ą
cznych kosztów produkcji i prze-
wozu spowodowała podniesienie kosztów przewozu o 50
PLN (z 782 na 832). Niemniej jednak, te koszty z nawi
ą
zk
ą
zostały zrekompensowane przez redukcj
ę
kosztów produkcji
z 61740 na 59616 PLN (mniej o 2124 PLN). Ostatecznie,
oszcz
ę
dno
ść
wyniesie 62522 – 60448 = 2074 PLN. W przy-
padku drugiego rozwi
ą
zania wierzchołkowego oszcz
ę
dno
ś
ci
byłyby jeszcze wi
ę
ksze: 66959 -60448=6511 PLN.
Trzeba jednak pami
ę
ta
ć
,
ż
e nie zawsze uwzgl
ę
dnienie
kosztów produkcji musi prowadzi
ć
do lepszego wyniku (tzn.
ni
ż
szych kosztów ł
ą
cznych)!
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron