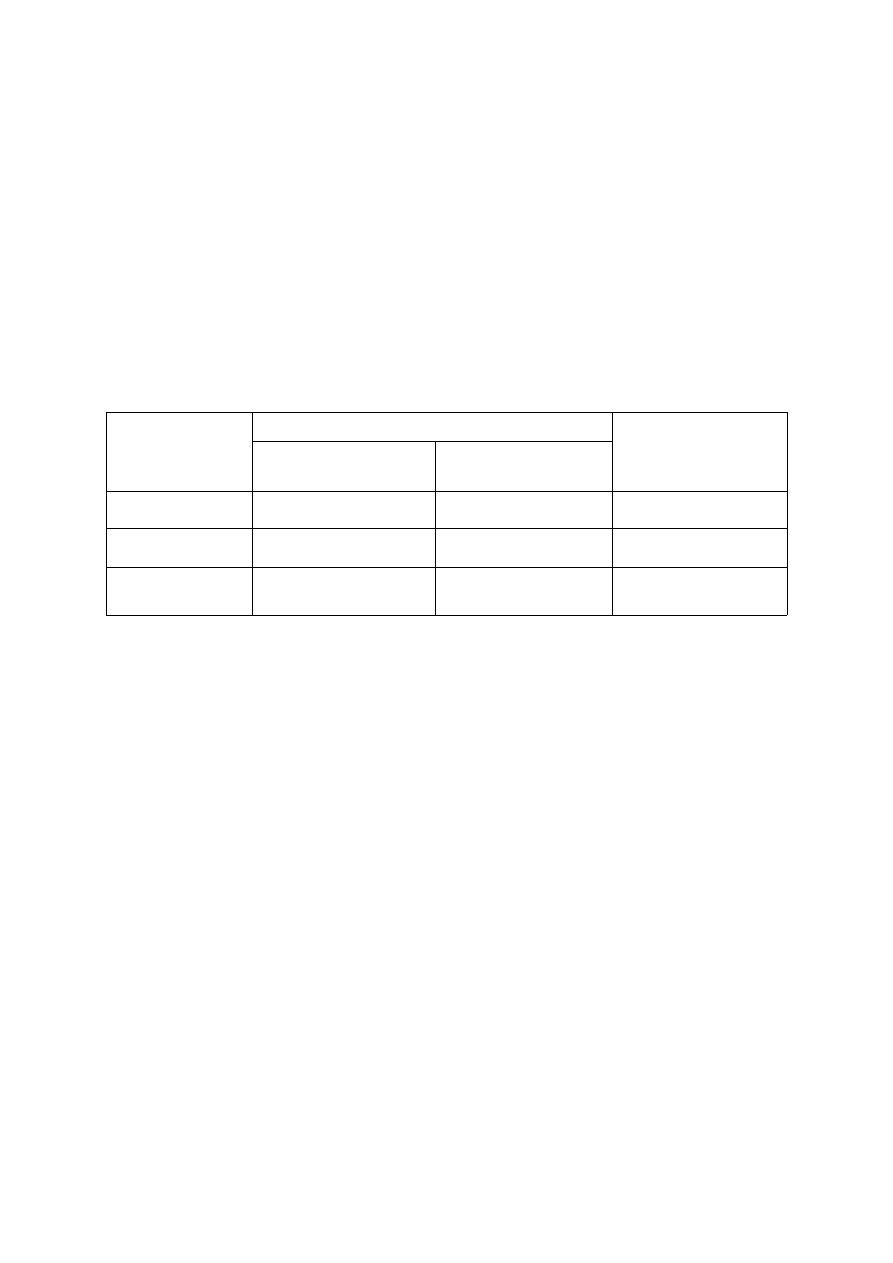
Analiza czułości, swoistości oraz krzywe ROC

   

Analiza krzywych ROC - analiza ta pozwala nam stwierdzić, czy badany parametr

laboratoryjny ma dobre własności różnicujące dla róznych punktów odcięcia. W tym

celu dla każdej interesującej nas własności punktu odcięcia (co najmniej kilku-

kilkunastu) należy zliczyć przypadki prawdziwie i fałszywie pozytywne oraz

prawdziwie i fałszywie negatywne, i na tej podstawie obliczyć czułość i swoistość

metody klasyfikacyjnej w oparciu o badany parametr. 

  WYNIK

  TESTU

   ROZPOZNANIE KLINICZNE
WYSTĘPOWANIE

    CHOROBY

  BRAK STANU

CHOROBOWEGO

 

    RAZEM

POZYTYWNY

         x

           a

        x+a

NEGATYWNY

         y

           b   

        y+b

    RAZEM

       x+y

          a+b

    x+a+y+b   

          Tab.1. Przedstawienie związku pomiędzy badanym czynnikiem, a stanem

klinicznym pacjenta.

 W terminach powyższej tabeli wzory przedstawiają się następująco:

1) Czułość – x 100%/(x+a,)

2) Swoistość – b 100/(a+b) zw. też specyficznością (ang. specificity)

3) Dokładność – x+b 100%/(x+a+y+b)

4) Dodatnia wartość predykcyjna – x 100%/(x+a)

Bardzo często metoda ta stosowany jest w analizie użyteczności testów

medycznych- porównuje się wyniki analizy ROC z własnościami tzw. testu

referencyjnego, czyli najlepszego znanego testu, zwanego także złotym testem

(ang. "gold standard test").

 Poszczególne litery zastosowane w tabeli oznaczają: x - wyniki prawdziwie

pozytywne, a - wyniki fałszywie pozytywne, y - wyniki prawdziwie negatywne, b -

wyniki fałszywie negatywne.

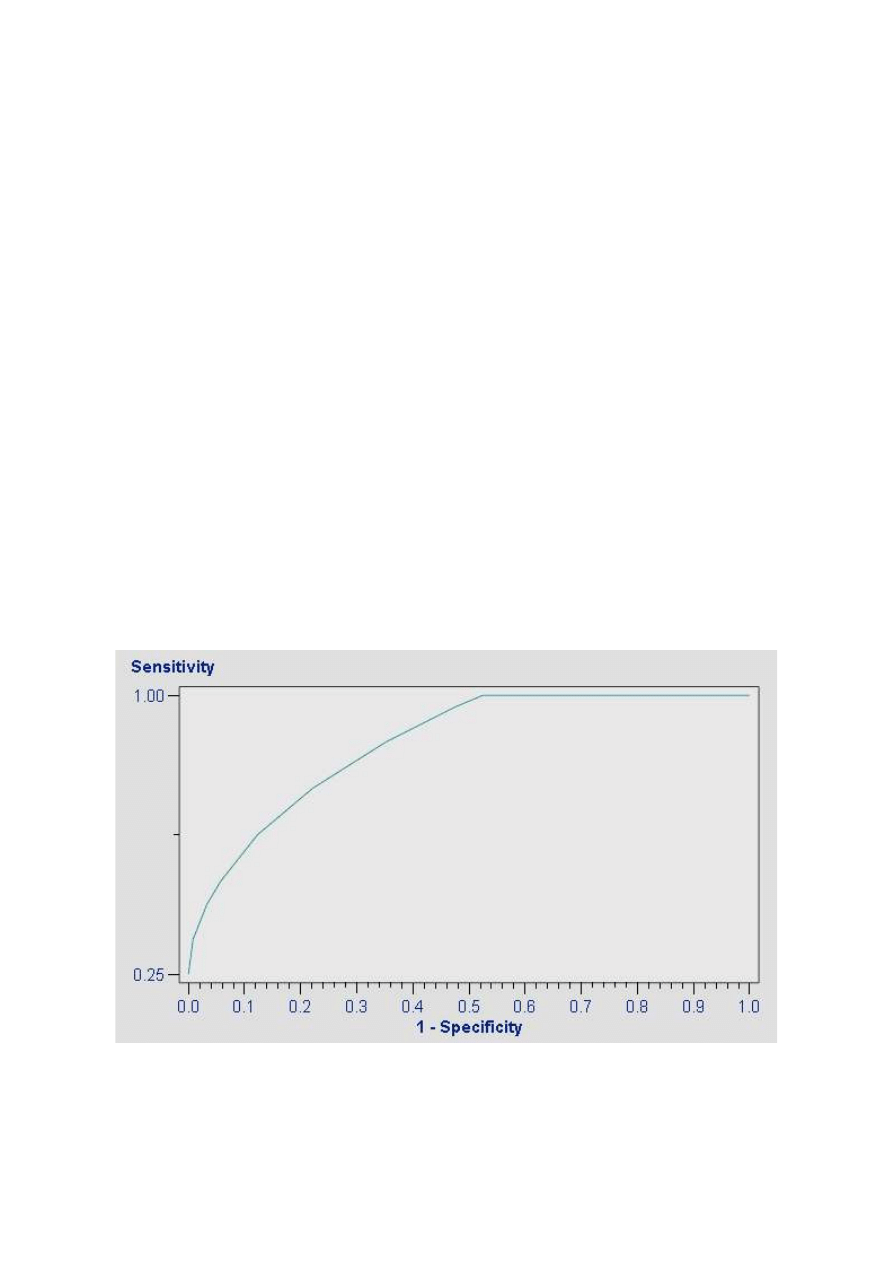
Krzywa ROC jest to wykres czułości vs (1-swoistość). Dla testów laboratoryjnych,

np. poziomu cukru na czczo, wybieranie punktów granicznych zaklasyfikowania do

choroby związane z powiększanie czułości (odp. swoistości) opłacone jest

zmniejszeniem swoistości (odp. czułości).

Dlatego też wybierając rodzaj testu chcielibyśmy, aby krzywe ROC zakreślały jak

największe pole pod nimi (AUC Area Under Curve) – wówczas osiągamy zarówno

zadowalająco duże swoistości, jak i duże czułości jednocześnie.

AUC - Area Under Curve:
>0.90

bardzo dobre własności różnicujace

0.8

0.9

dobre

0.7

0.8

średnie 

0.6

0.7

słabe

0.0

0.6

złe

Pole AUC=0.5 odpowiada losowemu wyborowi pacjentów do grupy rozpoznania-

krzywa ROC byłaby w takim przypadku prostą y=x.

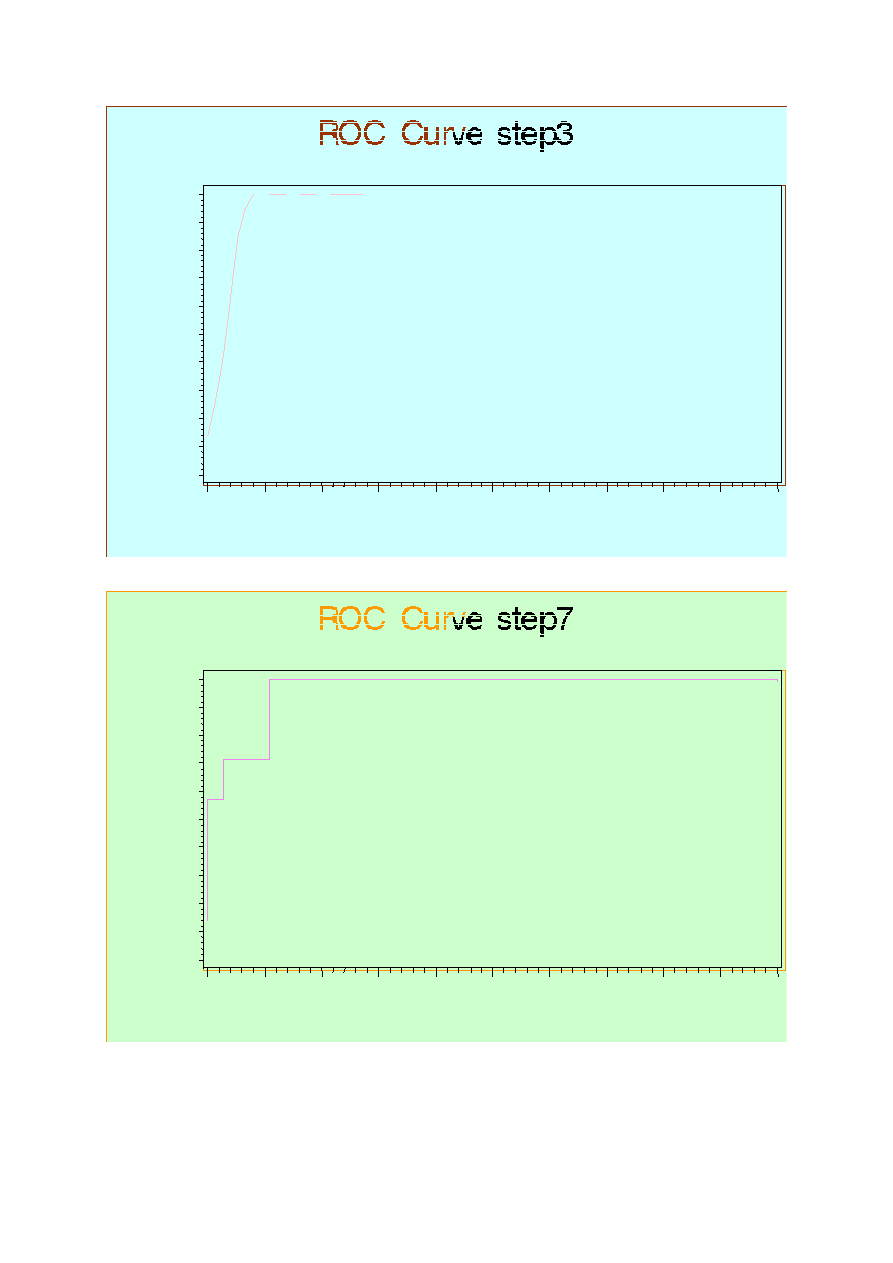
Przykład krzywej ROC (Receiver Operating Curve) o średniej własności różnicującej

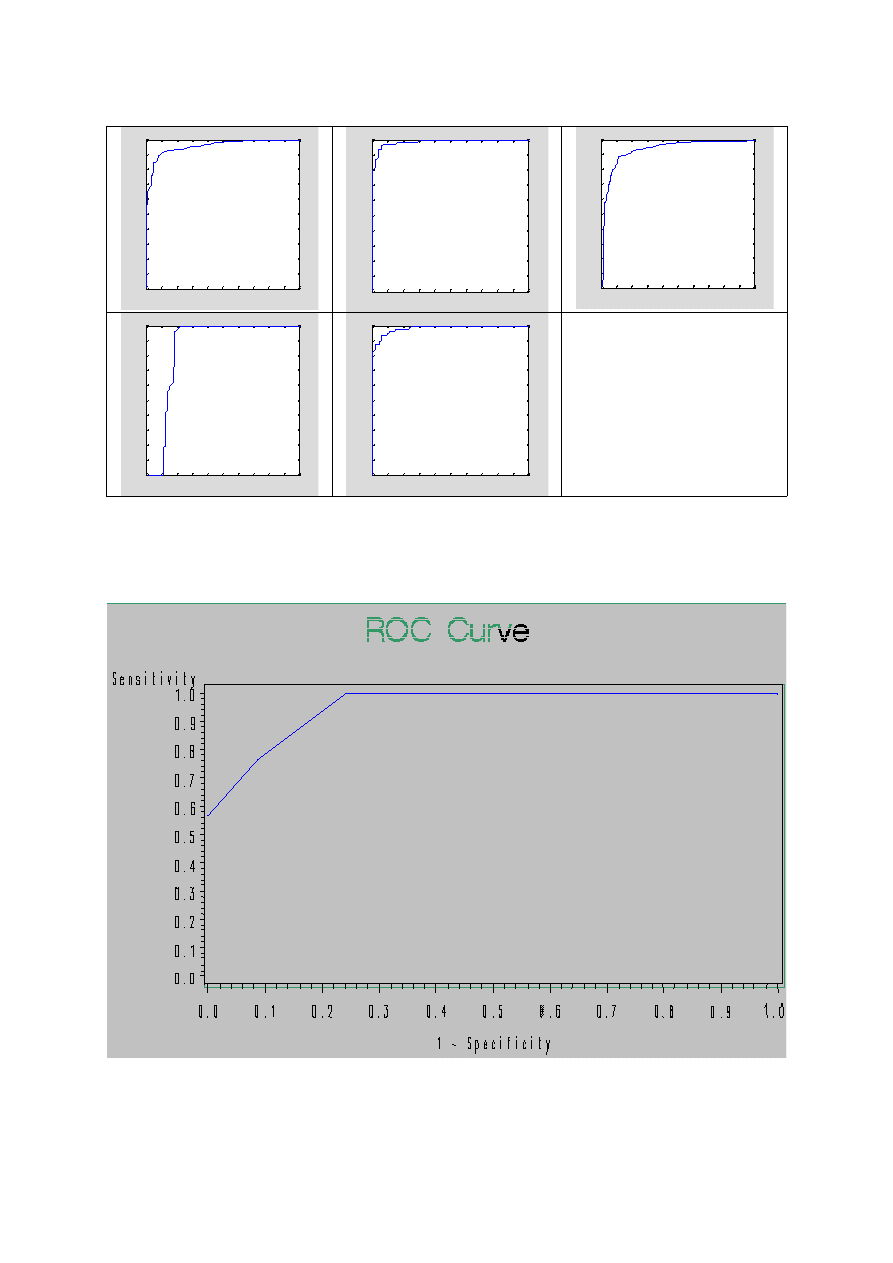
Porównaj własności dyskryminujące poniższych krzywych:

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

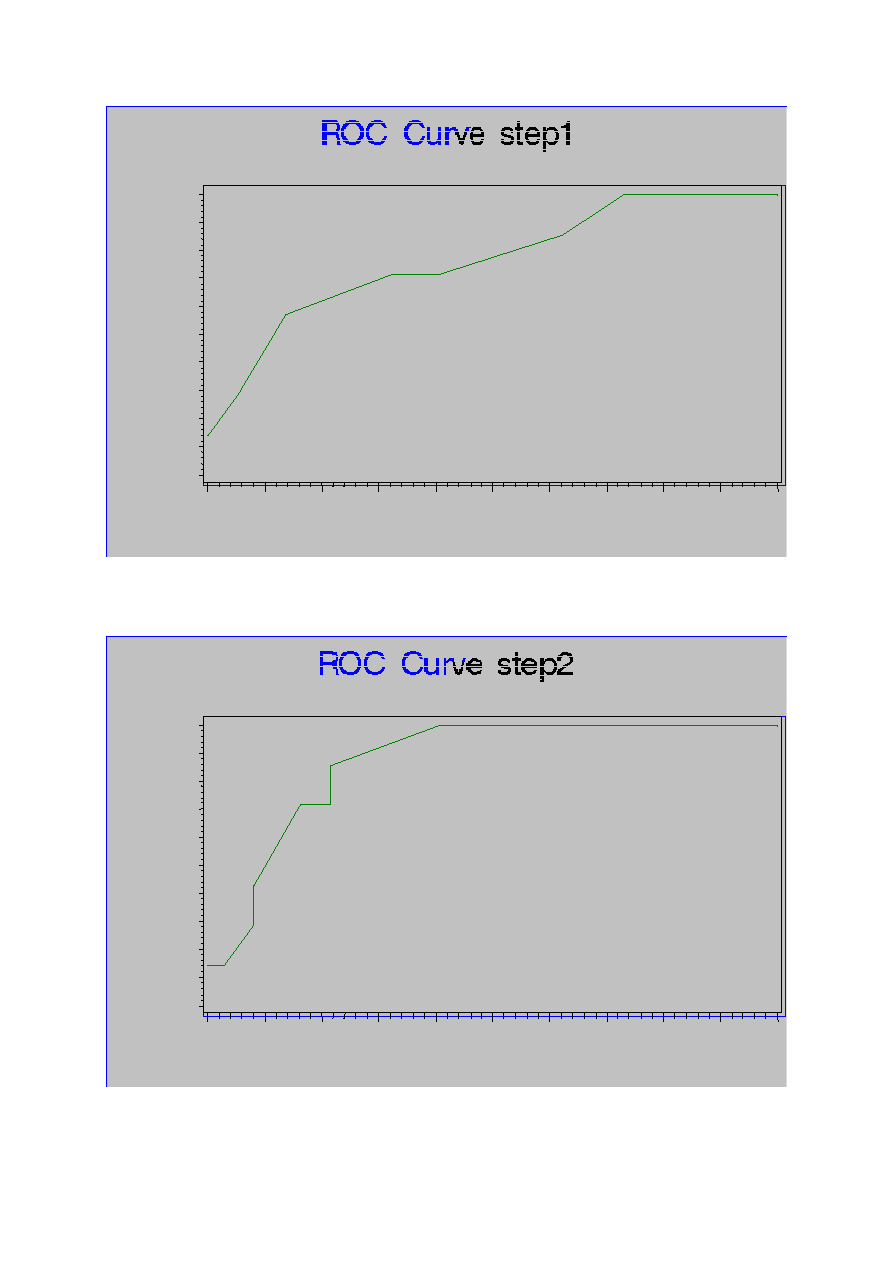
Porównaj własności dyskryminujące poniższych krzywych:

 

` 

Sensitivity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

1 - Specificity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

 

Sensitivity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

1 - Specificity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

 

Sensitivity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

1 - Specificity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

 

Sensitivity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0

 

1 - Specificity

 

0.0

 

0.1

 

0.2

 

0.3

 

0.4

 

0.5

 

0.6

 

0.7

 

0.8

 

0.9

 

1.0