Badanie bramek TTL id 76858 Nieznany (2)

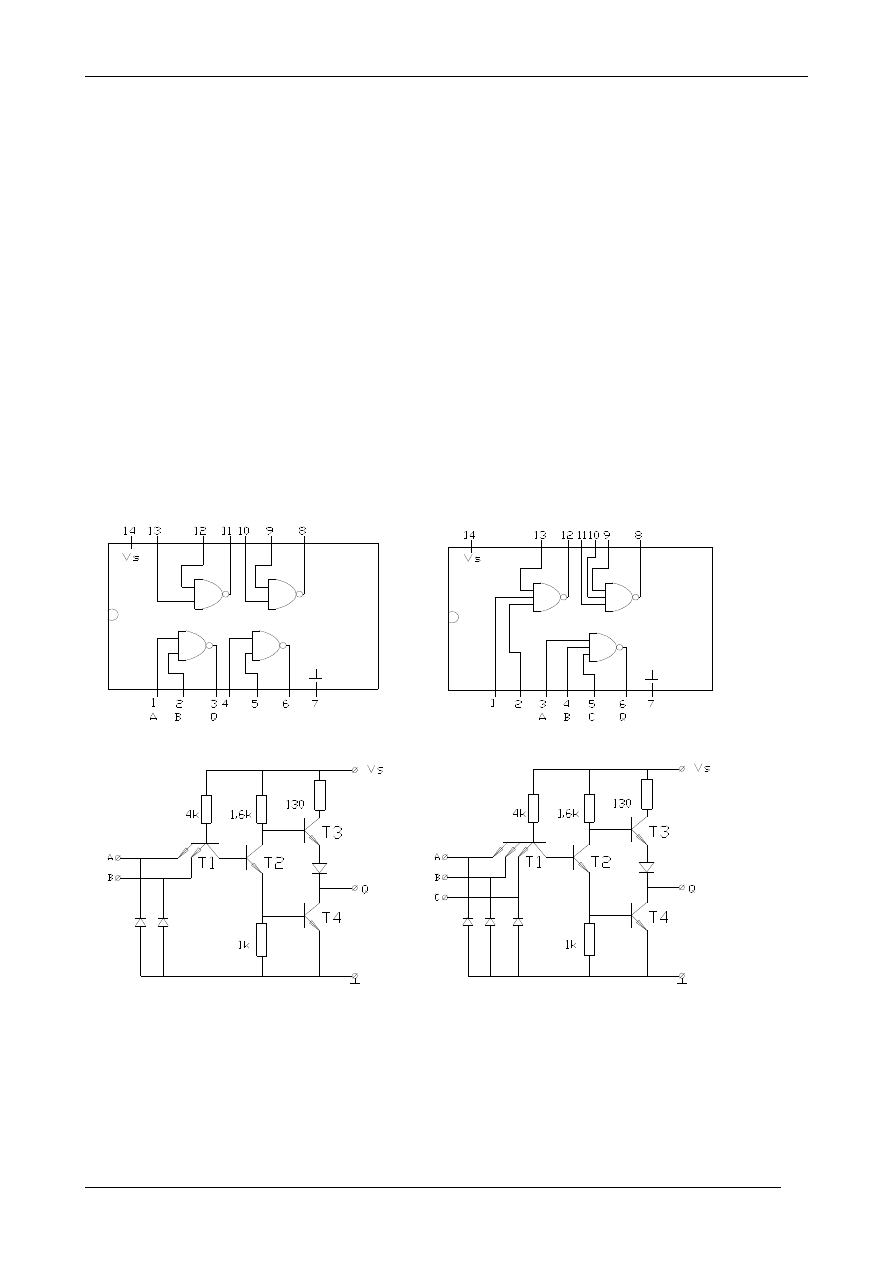
SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Ćwiczenie 3. Badanie podstawowych bramek logicznych

1. Rodzina TTL

Skrót TTL oznacza Transistor - Transistor Logic. Układy scalone realizowane w tej technice mają
następujące własności:
 duża szybkość działania,
 szeroki asortyment układów,
 niski koszt wytwarzania,
 jedno źródło zasilania,
 mała impedancja wyjściowa,
 dobra odporność na zakłócenia,
 stosunkowo niewielki pobór mocy,
 praca w szerokim zakresie temperatur.

Układy scalone serii UCY74XX stanowią podstawową, standardową serię układów scalonych

TTL.

Na rys. 1. pokazano podstawową wersję budowy wewnętrznej bramki NAND z dwoma i

trzema wejściami.

Rys. 1. Schemat połączeń wewnętrznych prostego układu TTL

Najważniejsze parametry układów TTL:
 napięcie zasilania musi być z dość dużą dokładnością stabilizowane na wartości +5V.

Dopuszczalna odchyłka napięcia nie może przekraczać 5%.

 obciążalność elementu N jest to dopuszczalna liczba standardowych wejść innych bramek,

które mogą być dołączone do wyjścia danego elementu.

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Dla standardowej serii TTL dla prądów wyjściowych:
- w stanie niskim I

= 16 mA,

- w stanie wysokim I

= 800 mA,

obciążalność wynosi w stanie niskim 10, w stanie wysokim 20 wejść innych bramek,

 Średni czas propagacji jest to średnia arytmetyczna czasów opóźnień zboczy (narastającego i

opadającego) sygnału wyjściowego względem wejściowego.

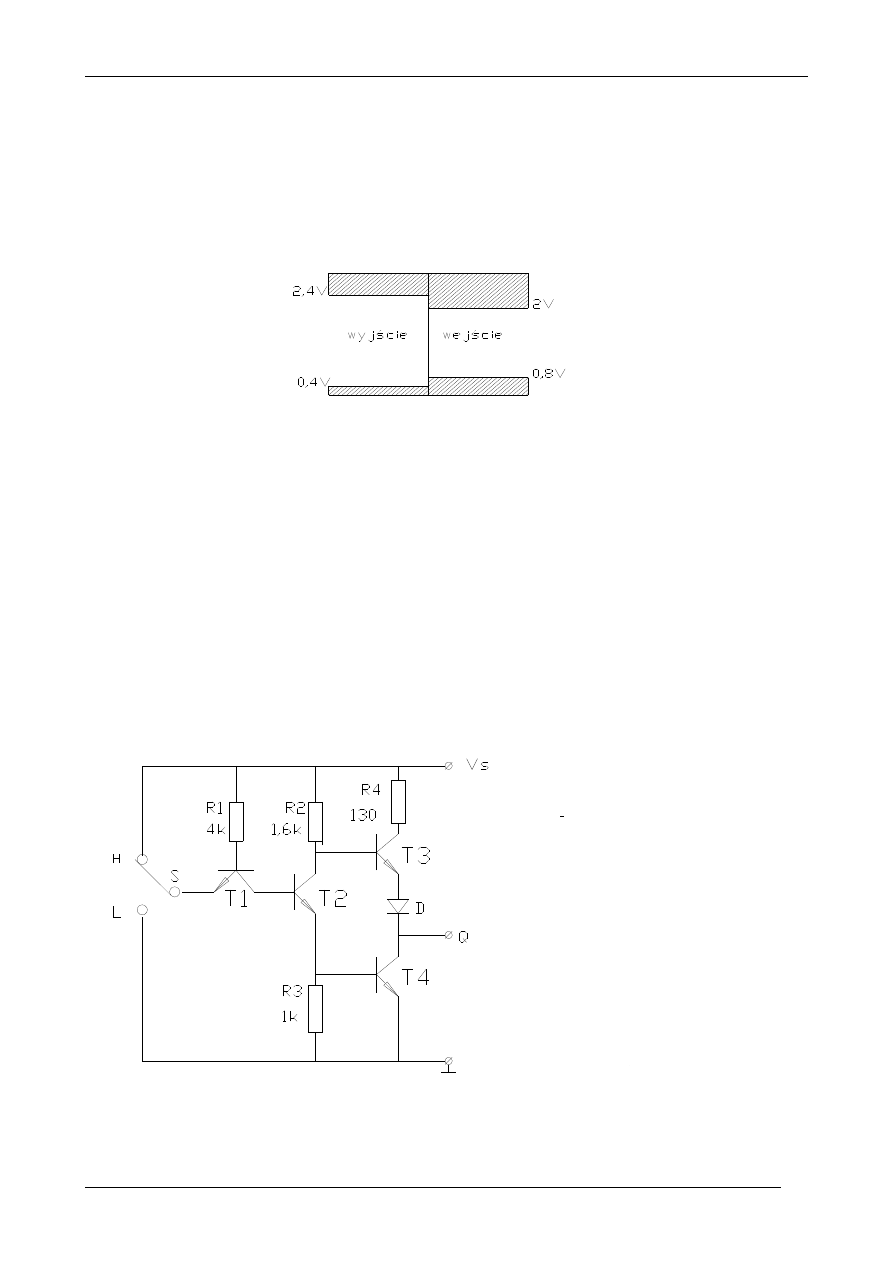
Standardowe poziomy logiczne TTL:

Do wyjaśnienia działania prostego układu inwertera posłuży schemat z rys. 2, stanowiący

uproszczoną wersję układu z rys. 1.

Oto opis stanu przy różnych poziomach napięcia wyjściowego.

 Poziom H na wejściu

Złącze emiterowe tranzystora T1 jest w stanie zaporowym. Przez R1 płynie prąd powodujący,
że T2 jest w stanie przewodzenia. Napięcie wyjściowe w punkcie Q jest bliskie 0, a tranzystor
T3 w stanie blokowania - ułatwia to dioda D, która powoduje podwyższenie potencjału
emitera o 0,6 V. Przewodzi tranzystor T4.

 Sygnał wejściowy L

Złącze emiterowe jest w stanie przewodzenia, a napięcie bazy T2 wynosi około 1 V. Oznacza
to, że tranzystor ten jest w stanie blokowania. Tranzystor T3, którego baza jest poprzez R2
dołączona do +V

, jest w stanie przewodzenia. Prąd wyjściowy ograniczony jest przez

opornik R4, a napięcie wyjściowe osiąga poziom H.

Rys. 2. Prosty układ przełączający TTL

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Modyfikacje standardowej serii TTL i inne technologie wytwarzania bramek logicznych

Oprócz standardowej serii TTL produkowane są jej modyfikacje:

 seria LTTL o zmniejszonym poborze mocy (1 mW ), ale dłuższymi czasami przełączania,

oznaczona np. 74LOO,

 seria HTTL - szybka o znacznie mniejszym ( 6 ns ) czasie przełączania, oznaczona np.

74HOO,

 seria TTL - S z diodami Schottky’ego, o bardzo krótkich czasach przełączania ( 3 ns ), ale

prawie dwukrotnie większym od standardowych układów TTL poborem mocy ( 20 mW ),

 seria TTL - LS - budowa tych układów jest identyczna ze zwykłym układem TTL - S, lecz

pobór mocy jest znacznie mniejszy. Typowa wartość to 2 mW na bramkę. Czas propagacji
bliski 8 ns i jest zbliżony do standardowych układów TTL.

Można zatem stwierdzić, że seria TTL - LS łączy zalety małego poboru mocy i krótkich

czasów przełączania. Jest to najczęściej stosowana na świecie seria układów TTL, oznaczona np.
74LSOO.

2. Rodzina MOS i CMOS

MOS - Metal Oxide Semiconductor.
CMOS - Complementary Metal Oxide Semiconductor.

Są to elementy oparte na tranzystorach unipolarnych. Dzięki tej technologii można uzyskać

bardzo dużą gęstość upakowania. Napięcie zasilania układów MOS mieści się dość szerokim
zakresie 3 - 15 V. Mają one dużą rezystancję wejściową i małą wyjściową. Oznacza to dużą
obciążalność sięgającą 50. Moc strat jest bardzo mała (w stanie statycznym 10 nW ).

Maksymalna częstotliwość przełączania układów MOS i CMOS w wykonaniu standardowym

nie przekracza 15 MHz, a w nowoczesnych osiąga 100 MHz. Margines zakłóceń w układach
CMOS nie może być jednoznacznie określony w wartościach absolutnych, gdyż zależy on od
poziomu napięcia zasilania.

I tak przy napięciu zasilania +12 V poziomom H i L odpowiadają wartości:

H - 12...8,4 V
L - 0...2,4 V

Rys. 3. Schemat elektryczny podstawowej bramki MOS

Współpraca układów TTL i CMOS

Tworząc systemy cyfrowe z układów należących do różnych rodzin układów należy osiągnąć

zgodność takich parametrów technicznych jak: napięcie zasilania, poziomy logiczne, prądy
wejściowe i wyjściowe (obciążalność wejść i wyjść). Sprzężenie pomiędzy tymi układami można
zrealizować za pomocą specjalnych układów nazywanych translatorami lub konwerterami. Dla

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

danej part rodzin układów cyfrowych mogą być potrzebne dwa rodzaje konwerterów. Jeden
umożliwiający sprzężenie wyjść rodziny I z wejściami rodziny II, drugi realizujący odwrotny
kierunek sprzężenia. Konwertery uniwersalne umożliwiają uzyskanie dowolnego kierunku
sprzężenia w zależności od stanu wejść sterujących.

Układy CMOS serii 4000B mogą być zasilane napięciem 3

 18V;

CMOS serii HC i AC 2

6V

TTL (lub CMOS serii HCT i ACT) 5V.

3. Podstawowe bramki wraz z tablicami prawdy

Do podstawowych elementów logicznych zalicza się funktory AND, OR, NOT. Tworzą one

podstawowy i funkcjonalnie pełny zestaw elementów. Oznacza to, że można przy ich pomocy
zbudować dowolnie skomplikowany układ logiczny.

Jak wiadomo wszystkie bramki logiczne można zbudować z podstawowych bramek NAND

lub NOR. Za pomocą tych funktorów można realizować także wiele złożonych funkcji. W praktyce
okazuje się, że zalety stosowania jednoelementowego zbioru do realizacji dowolnej funkcji
logicznej są bardzo duże.
a) inwerter

Q=A

b) bramka AND - funkcja logiczna I

Q=A

B

c) bramka NAND

Q=A

B

d) bramka OR - funkcja logiczna LUB

Q=A+B

e) bramka NOR

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Q= A+B

f) EX -OR - EXLUSIVE - OR - na wyjściu istnieje stan 1 wtedy i tylko wtedy, gdy wejścia mają
różne stany logiczne.

Q=A

B= AB+AB

g) EX - NOR - EXLUSIVE - NOR - na wyjściu istnieje stan 1 wtedy i tylko wtedy, gdy oba

wejścia mają jednocześnie te same stany (1 lub 0).

Q=A

B=AB+AB

Z podstawowych bramek NAND lub NOR można zbudować, wykorzystując prawo
de Morgana każdą z przedstawionych bramek.
Przypomnijmy prawa de Morgana:

B=A+B

A+B=A

B

a także zależności: a=a; a

0=0; aa=a; 0a=0

Przykłady realizacji kilku funktorów logicznych z wykorzystaniem bramki NAND:

a) Bramka OR

Badanie podstawowych bramek logicznych

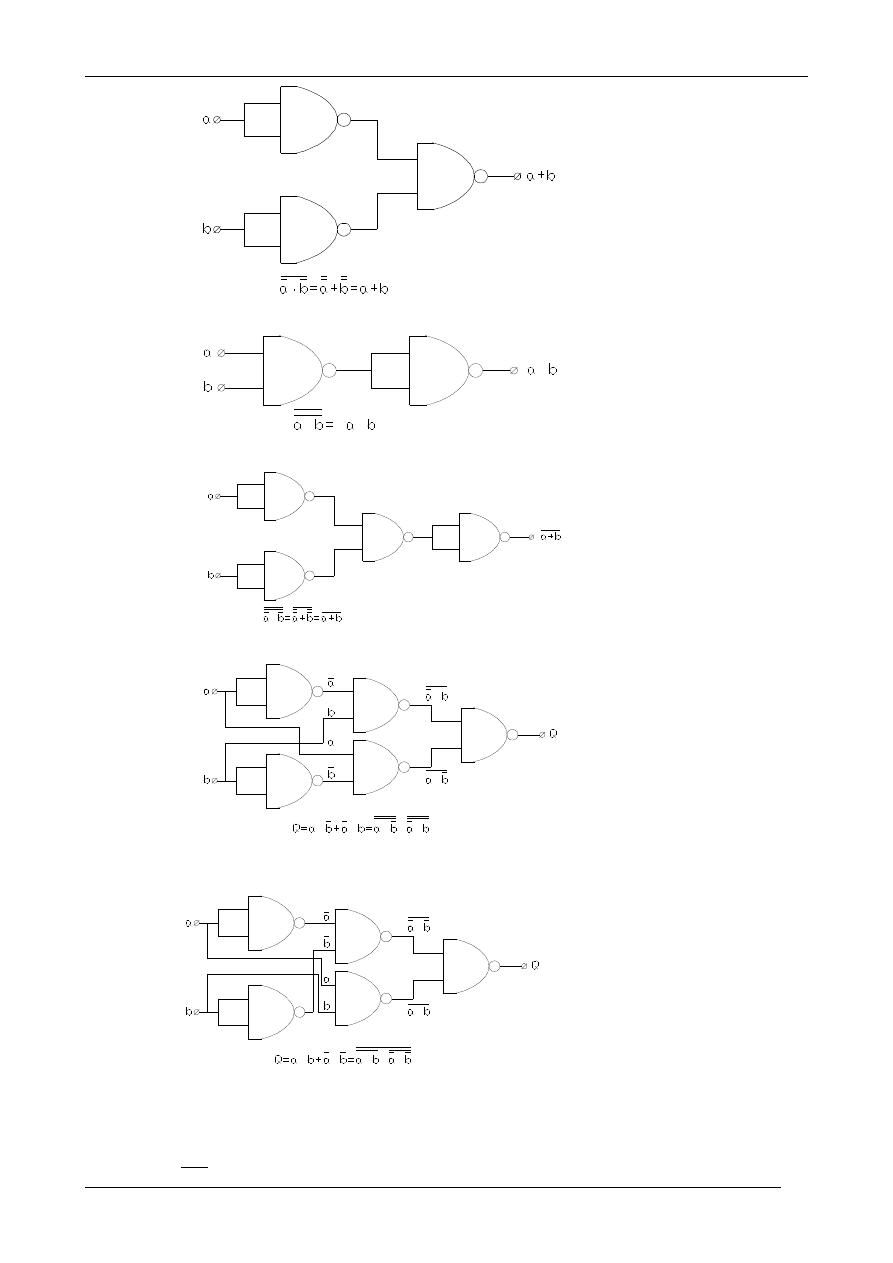
SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

b) Bramka AND

c) Bramka NOR

d) Bramka EX - OR

e) Bramka EX - NOR

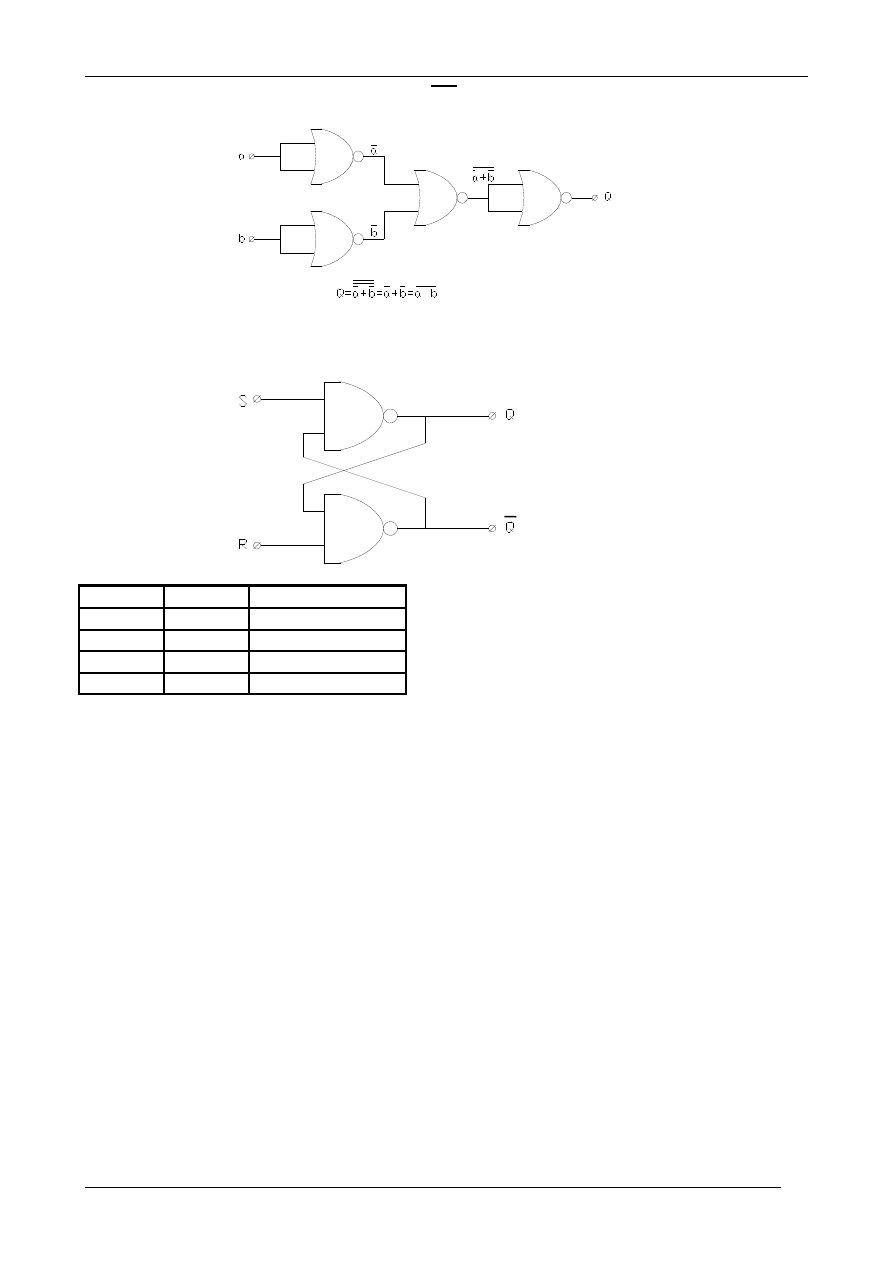
Można także otrzymać wszystkie funktory wykorzystując podstawową bramkę NOR.
Dla przykładu otrzymamy funktor NAND wykorzystując bramki NOR.

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

NOR Q=a+b; NAND Q= a

b

Realizacja najprostszego przerzutnika asynchronicznego SR zbudowanego z bramek NAND

stan niedozwolony

bez zmian

Rys. 4. Schemat logiczny i tabela przejść przerzutnika SR

Przerzutnik SR, zwany SET (ustaw) i RESET (kasuj) jest najprostszym układem przerzutnika

bistabilnego. Normalnym stanem spoczynkowym przerzutnika jest stan wejść S=1, R=1, podczas
którego stan przerzutnika nie zmienia się (pamięta on swój stan poprzedni). Dla S=1, R=0
przerzutnik zostaje wyzerowany, czyli Q=0. Przy S=0, R=1 następuje zmiana stanu przerzutnika na
Q=1. Stany jednoczesnych sygnałów 0 na obu wejściach są niedozwolone (stan wyjścia jest
wówczas nieokreślony).

4. Funkcja logiczna

Funkcją logiczną nazywamy funkcję, której argumenty (zmienne logiczne) oraz sama funkcja

może przybierać tylko dwie wartości. Zwykle są one oznaczone cyframi dwójkowymi 0 i 1.
Wartości argumentów funkcji logicznej odpowiadają stanom wejść układu cyfrowego, a wartości
samej funkcji - stanom wyjść tego układu.

Funkcja logiczna może być zadana za pomocą opisu słownego (definicji słownej), tablicy

wartości (tablicy stanów) lub wykresu czasowego, jak również graficznie w postaci schematu
logicznego lub analitycznie w postaci wyrażenia strukturalnego przypominającego wyrażenie
algebraiczne.

Wszystkie sposoby przedstawiania są całkowicie równoważne. Podstawowymi funkcjami

logicznymi są: iloczyn logiczny (koniunkcja), suma logiczna (dysjunkcja) i negacja.

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Tabela 1

zapis analityczny

nazwa skrótowa

Nazwa funkcji

algebraiczny

symboliczny

angielska

polska

iloczyn



B

AND

suma

A+B

B

LUB

negacja

-A

NOT

NIE

5. Tablica stanów

Tablica stanów, nazywana również tablicą prawdy, stanowi jedną z postaci zapisu funkcji

logicznej. Stanowi ona zestaw wszystkich możliwych wartości zmiennych niezależnych i
odpowiadających im wartości funkcji.

Liczba wierszy zależy od liczby elementów wejściowych. Przy n dwustanowych elementach

wejściowych tablica zawiera 2

wierszy.

Tablice stanów są stosowane do opisu logicznego układów cyfrowych, a także do celów syntezy.

Na podstawie tablic stanów można łatwo otrzymać postać kanoniczną wyrażenia strukturalnego.

Tabela 2. Przykład tablicy stanów funkcji logicznych trzech zmiennych.

6. Postać kanoniczna funkcji logicznej

Każdą funkcję można przedstawić w postaci rozłożonej na składniki (jedynki), z których każdy

stanowi iloczyn pełny zmiennych i ich negacji, lub czynniki (zera), z których każdy stanowi sumę
pełną zmiennych i ich negacji.

Postać uzyskana w wyniku rozkładu na czynniki (jedynki) jest nazywana kanoniczną postacią

sumy, a postać otrzymywana w wyniku rozkładu na czynniki (zera) jest nazywana kanoniczną
postacią iloczynu.

Kanoniczną postać sumy można otrzymać na podstawie tablicy stanów, biorąc pod uwagę

jedynie te wiersze, dla których F=1 i przypisując wartościom 1-zmienne nie zanegowane, a
wartościom 0 - negacje zmiennej.
Korzystając z tablicy 2, mamy więc:

F=A

BC+ ABC+ABC

Z kolei kanoniczną postać iloczynu uzyskuje się stosując odwrotną procedurę tj. Biorąc pod

uwagę tylko wiersze, dla których F=0 i przypisując wartościom 0 - zmienną, a wartościom 1 -
negację zmiennej.

Na podstawie tablicy 2 otrzymujemy:

F=(A+B+C)(A+B+C)(A+B+C)(A+B+C)(A+B+C)

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Wyrażenie strukturalne kanonicznej postaci iloczynu lub sumy, można oczywiście uprościć,

stosując podstawowe prawa algebry Boole'a. Proces upraszczania nazywa się minimalizacją funkcji
logicznej.

7. Podstawowe prawa algebry Boole’a

Spośród wielu praw algebry Boole’a podstawowe znaczenie w zastosowaniu do teorii układów

cyfrowych, mają cztery następujące prawa: przemienności, łączności, rozdzielności i de’Morgana.
Prawa te przedstawia tabela 3.

Tabela 3. Zestawienie podstawowych praw tożsamości algebry Boole’a

Nazwa przekształcenia

Wzór odniesiony do iloczynu

logicznego

Wzór odniesiony do sumy

logicznej

Prawa

przemienności

B=BA

A+B=B+A

łączności

(BC)=(AB)C

A=(B+C)=(A+B)+C

rozdzielności

(B+C)=AB+AC

A+B

C=(A+B)(A+C)

de’Morgana

B..=A+B+...

A+B+...=A

B

Tożsamości

podstawowe

0=0

A+1=1

1=A

A+0=A

A=A

A+A=A

A=0

A+A=1

dodatkowe

(A+B)=A

A+A

B=A

A+A

B=A+B

(A+B)=AB

(A+B)

(A+B)=B

B+AB=B

8. Minimalizacja funkcji logicznej

Minimalizacja funkcji logicznej, innymi słowy proces jej upraszczania, polega na takim

przekształceniu postaci kanonicznej funkcji logicznej, zgodnie z zasadami algebry Boole’a, aby
uzyskać możliwie najprostszy jej zapis. Im bardziej bowiem złożona jest postać funkcji logicznej,
tym bardziej rozbudowany system cyfrowy jest potrzebny do realizacji tej funkcji.

Zatem każde uproszczenie wyrażenia logicznego umożliwia łatwiejszą realizację układową

funkcji przy użyciu mniejszej liczby elementarnych bramek logicznych.

Metody minimalizacji funkcji logicznych można podzielić ogólnie na algebraiczne i graficzne.

Stosowanie prostych metod algebraicznych ilustrują następujące przykłady:

1. F=A

BC+ABC=AB(C+C)=AB

F=A

B+BC+AC=AB+BC(A+A)+AC=AB+ABC+ABC+AC=AB(1+C)+

C(B+1)=AB+AC

Pierwszy przykład jest bardzo prosty, w drugim dostrzeżenie rozwiązania nie jest łatwe. Prostota

końcowej postaci zależy w dużej mierze od intuicji i umiejętności projektanta. Efektywniejszą
metodą jest jedna z metod graficznych - metoda Karnaugha.

9. Tablica Karnaugha

Tablica (mapa) Karnaugha jest uporządkowaną w specyficzny sposób postacią zapisu tablicy

wartości funkcji logicznej. Tablica ma strukturę prostokątną, złożoną z elementarnych pól.

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Każde pole reprezentuje iloczyny elementów danej funkcji, czyli obejmuje wszystkie możliwe

kombinacje zmiennych wejściowych. Na marginesach tablicy wpisuje się w określonym porządku
wartości zmiennych wejściowych.

Ułożenie tablicy Karnaugha polega na takim zgrupowaniu wszystkich kombinacji zmiennych

wejściowych, aby zawsze przy przejściu z danego pola do pola sąsiedniego zmieniała swoją
wartość tylko jedna zmienna. Przedstawiamy tablicę zmiennych:

ABC

BC

Wartości zmiennych zanegowanych są opisane cyfrą 0, a zmiennych nie zanegowanych cyfrą 1.
Funkcję logiczną będącą sumą iloczynów jej argumentów (z negacją lub bez), oznacza się w

tablicy Karnaugha przypisując cyfrę 1. Jeżeli składnik analizowanej funkcji nie występuje, to polu
przypisujemy 0. Jeżeli dany składnik analizowanej funkcji jest nieistotny, to oznaczamy go kreską.

Minimalizacja funkcji logicznej przy użyciu tablicy polega na łączeniu sąsiednich pól

oznaczonych 1 w odpowiednie grupy, które wyróżnia się obwiednią. Okazuje się, że niektóre
składniki w obrębie grup mogą być eliminowane i w wyniku tego postępowania wyrażenie można
sprowadzić do prostej postaci.

Zastosujemy metodę tablic Karnaugha do minimalizacji funkcji:

F=ABCD+ABCD+ABCD+ABCD+ABCD+ABCD

ABCD

Z połączenia wyrażeń 1, 2, 3, 6 otrzymujemy:

F1=ABCD+ABCD+ABCD+ABCD

Wykorzystując prawo algebry Boole’a

(A+A=1)

otrzymujemy:

F1=AD

zmienne

B i C

zmieniały swój stan z

więc się wyeliminowały

Z połączeń wyrażeń 4, 5 otrzymujemy:

F2=ABCD+ABCD=ABD(C+C)=ABD
F=F1+F2=AD+ABD

Minimalizacja funkcji z tabeli 2 przebiega następująco:

F=ABC+ABC+ABC

Badanie podstawowych bramek logicznych

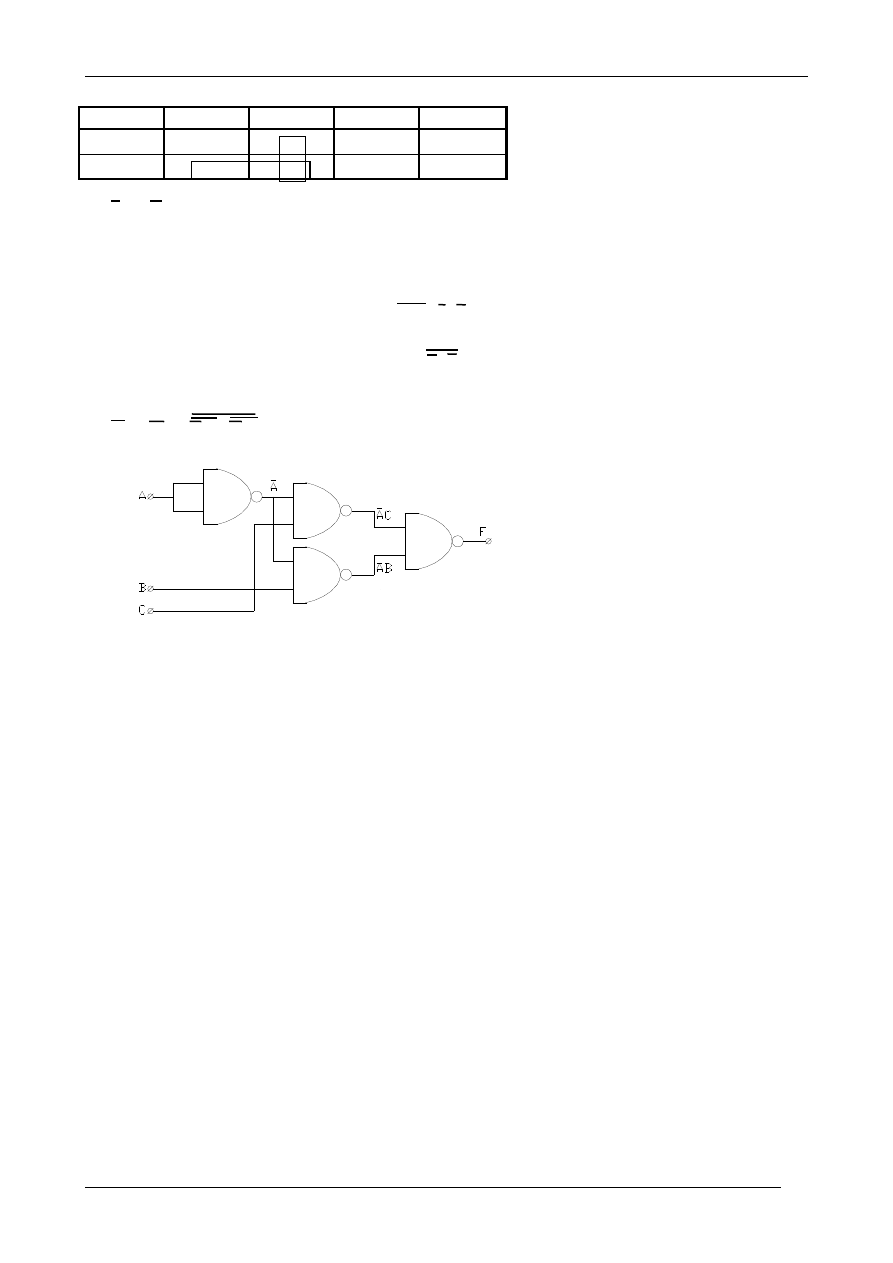
SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

ABC

F=AC+AB

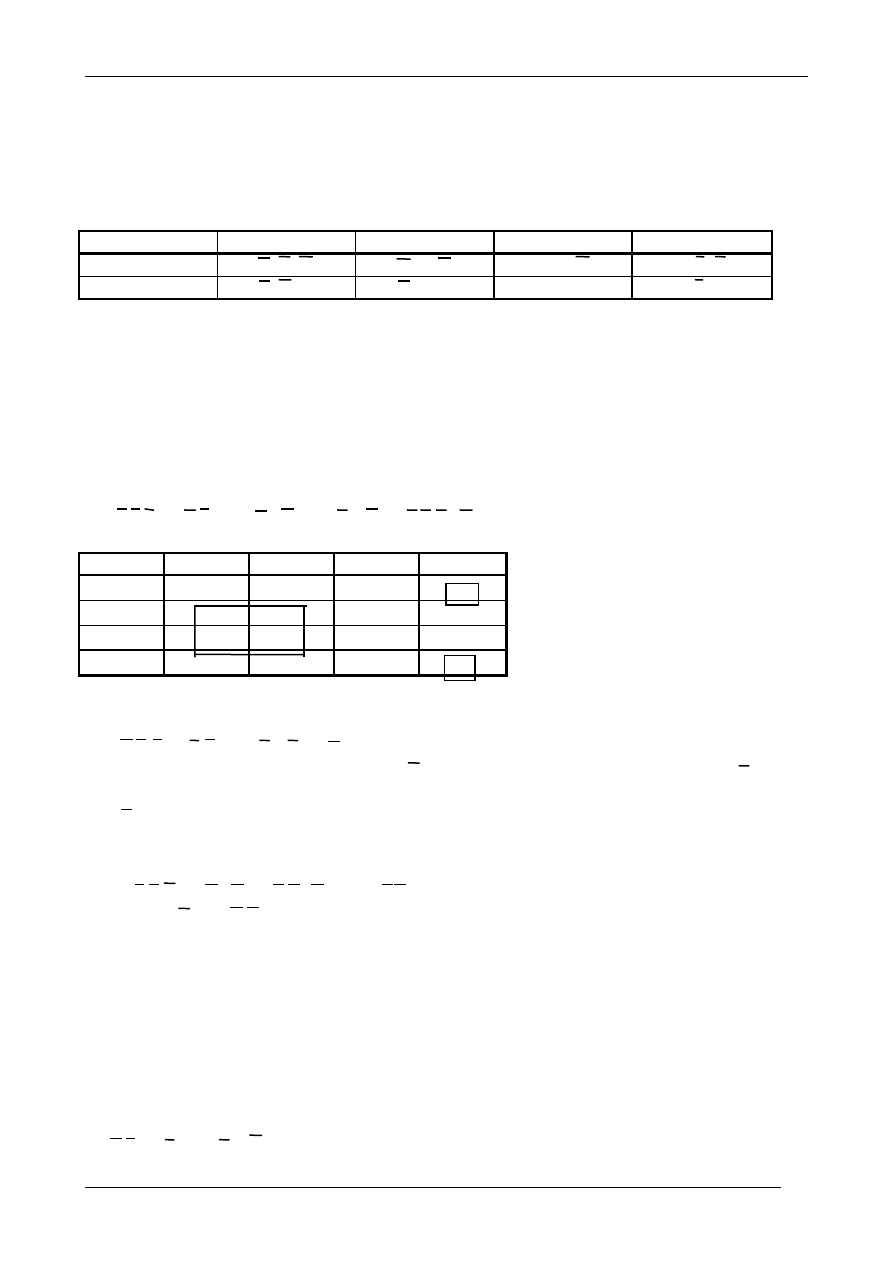
Zrealizujemy funkcję F za pomocą bramek NAND. W tym celu korzystając z praw de’Morgana

przekształcimy funkcję w postać iloczynu:

a+b=a

b

a+b=a

b

a więc:

F=AC+AB=AC

AB

II. Wykonanie ćwiczenia

Opis stanowiska laboratoryjnego

Stanowisko laboratoryjne do badania bramek TTL i CMOS składa się z następujących
bramek zgrupowanych w czterech grupach, poczynając od lewej strony:
bufory

 bramki TTL typu 74LS05 - 6 krotny negator z otwartym kolektorem
 bramki TTL typu 74LS125 -4 krotny bufor trójstanowy
 bramki CMOS typu 4050 - 6 krotny bufor konwerter

bramki Schmitta

 bramki CMOS typu 4093 - 4 krotny, 2 wejściowy iloczyn logiczny NAND
 bramki TTL typu 74LS132 - 4 krotny, 2 wejściowy iloczyn logiczny NAND

iloczyn logiczny

 bramka TTL typu 74LS30 - 8 - wejściowy iloczyn logiczny NAND
 bramki TTL typu 74LS08 - 4 krotny, 2 wejściowy iloczyn logiczny AND
 bramki TTL typu 74LS00 - 4 krotny, 2 wejściowy iloczyn logiczny NAND

suma logiczna

 bramki TTL typu 74LS86 - 4 krotna 2 - wejściowa suma logiczna EX-OR
 bramki TTL typu 74LS32 - 4 krotna 2 - wejściowa suma logiczna OR
 bramki TTL typu 74LS02 - 4 krotna 2 - wejściowa suma logiczna NOR

Każde wejście/wyjście układów logicznych posiada po dwa gniazda łączeniowe oraz

podłączone jest do układu sygnalizującego stan logiczny tego wejścia/wyjścia.

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Dwukolorowa dioda LED sygnalizuje stan niski (zero logiczne) kolorem zielonym, a stan

wysoki (jedynka logiczna) kolorem czerwonym. Stany przejściowe sygnalizowane są brakiem
świecenia lub kolorem pomarańczowym.

Każdy układ (zespół bramek) posiada czerwone gniazdo z napięciem zasilania Vcc oraz

gniazdo czarne z ujemnym biegunem zasilania Gnd.

Układy specjalne 74LS05 i 4093 mogą być łączone za pomocą dodatkowych gniazd z

elementami biernymi: rezystorami i kondensatorami.

Uwaga układy 4050 i 4093 nie są podłączone do zasilania ponieważ mogą pracować z

logiką 5 lub 10 woltową.

Dodatkowo w dolnej części stanowiska znajduje się podwójny czterobitowy zadajnik stanów

logicznych oraz źródło napięcia regulowanego 0 - 5V dla układów TTL i 0 -10V dla układów
CMOS. Zarówno zadajnik jak i źródło napięcia mogą pracować z logiką 5 lub 10 woltową.

Wybór napięcia logiki w zadajnikach polega na połączeniu gniazda Vo z gniazdem 5V lub 10V

(w źródle napięcia gniazdo Uzas z gniazdem 5V lub 10V). Logika 10 woltowa jest zawsze
sygnalizowana pulsującym czerwonym światłem.

UWAGA! podłączenie logiki 10V do układów zasilanych napięciem 5V (wszystkie bramki

TTL) może spowodować uszkodzenie układu scalonego.

Wykonanie ćwiczenia

1. Sprawdzenie funkcji logicznych bramek.

 Należy sprawdzić zgodność tabeli z rzeczywistością dla bramki NAND i NOR.
 Zbudować bramki: NOR, EX-OR z bramek NAND.
 Zbudować bramki: EX-NOR z bramek NOR.

Sprawdzić tabele prawd otrzymanych bramek.

2. Badanie przerzutnika SR.

Należy zbudować przerzutnik SR z bramek NAND i zbadać jego działanie wykorzystując tabelę
przejść.

3. Minimalizacja funkcji logicznych

Zadaniem wykonującego ćwiczenie jest zaprojektowanie układu kombinacyjnego sterującego

napełnianiem basenu. Podajemy opis słowny problemu.

Badanie podstawowych bramek logicznych

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Dopływ wody do basenu jest sterowany zaworem X, a jej odpływ zaworem Y. Podanie

wysokiego stanu logicznego do układu sterowania zaworu oznacza otwarcie zaworu, a stanu
niskiego - zamknięcie.

W basenie znajdują się trzy czujniki A, B, C, wyznaczające odpowiednio maksymalny, średni i

minimalny poziom wody. Zadziałanie czujnika następuje po zanurzeniu go w wodzie i jest
sygnalizowane pojawieniem się na jego wyjściu jedynki logicznej.

Prędkości dopływu i odpływu wody z basenu, w zależności od jej ciśnienia mogą być różne.

Lustro wody nie powinno obniżać się poniżej poziomu minimalnego.

Dodatkowo włączony jest sygnałem Z układ alarmu przy uszkodzeniu czujników A, B, C.

Jednocześnie z sygnałem alarmu następuje zamknięcie zaworu dopływu i otwarcie zaworu odpływu
wody.

Między stanami wody: maksymalnym i średnim, powinny być otwarte oba zawory w celu ciągłej

jej wymiany w basenie. Dla ułatwienia podana jest tablica wartości X, Y, Z w zależności od
argumentów A, B, C.

Należy przeprowadzić minimalizację wybranej funkcji X, Y, Z.
Przekształcić otrzymane wyrażenia do postaci iloczynu i zbudować z bramek NAND

odpowiednie układy logiczne.

Sprawdzić ich poprawne działanie wykorzystując do tego tablicę wartości funkcji. Cały proces

należy przeprowadzić zgodnie z algorytmem podanym w punktach 8 i 9.

4. Budowa generatorów z wykorzystaniem bramek Schmitta .

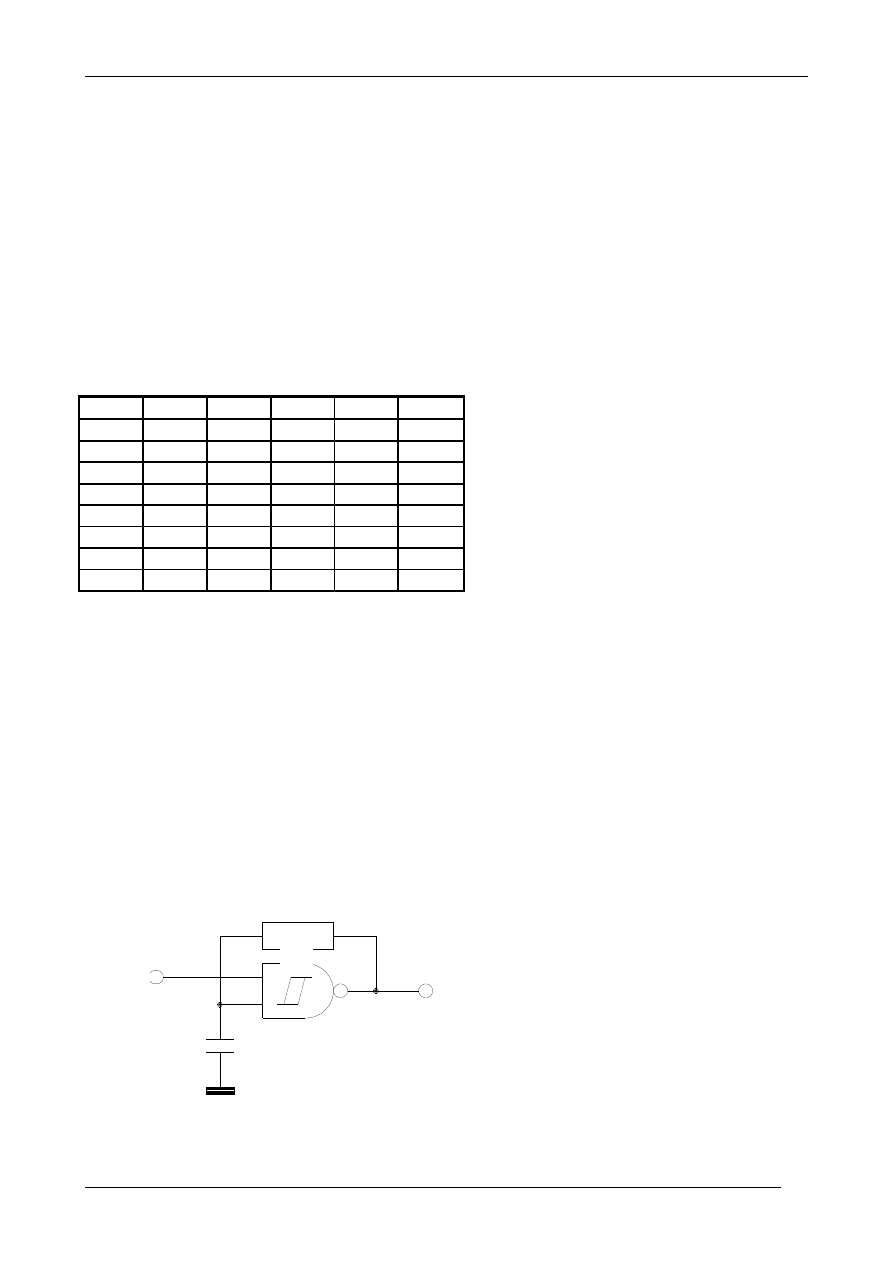
Zbudować generator lub uklad generatorów na bramkach NAND układu CMOS 4093

bazując na schemacie pokazanym na rysunku 5. Wykorzystać głośnik jako detektor
generowanych sygnałów. Zmierzyć wartości elementów pasywnych R i C.

Rys. 5. Schemat generatora na bramce
Schmitta

Badanie podstawowych bramek logicznych

GEN

Gnd

SWPW w Płocku Podstawy elektrotechniki i elektroniki - laboratorium

Wejście We

jest wejściem blokującym generator. Stan wysoki na wejściu We

uruchamia

generator, a stan niski na wejściu wymusza stan wysoki na wyjściu Wy

GEN

5. Badanie charakterystyk dynamicznych bramki NAND Schmitta 74LS132.

5.1 wyłączyć zasilanie stanowiska
5.2 ustawić źródło napięcia na zasilanie 5V łącząc gniazdo Uzas z gniazdem 5V
5.3 załączyć zasilanie stanowiska (dioda LED oznaczone etykietą 10V nie powinna świecić)
5.4 skręcić potencjometr wieloobrotowy na minimum napięcia - do oporu w lewo
5.5 połączyć wejście A wybranej bramki TTL z wyjściem źródła napięcia Ureg
5.6 połączyć wejście B bramki TTL z gniazdem Vcc
5.7 połączyć czerwony wtyk woltomierza z wejściem A a czarny z gniazdem Gnd
5.8 znaleźć położenie suwaka potencjometru, dla którego wtórnik napięciowy zasilacza

wychodzi ze stanu nasycenia (Obracać powoli potencjometr w prawo, obserwując
wskazanie woltomierza. Położenie suwaka potencjometru, przy którym napięcie zacznie
rosnąć, jest tym punktem).

5.9 po przekroczeniu nasycenia wtórnika mierzyć napięcie wejściowe i wyjściowe bramki dla

tego samego położenia suwaka, przekładając czerwony wtyk. Utrzymywać jak
najmniejsze przyrosty napięcia wejściowego. Możliwy jest skok co 1mV (0.001V).
Wyniki wpisać do tabeli.

Rosnące napięcie wejściowe

wejA

[ V ]

wyjY

[ V ]

5.10 powtórzyć pomiar zmniejszając napięcie wejściowe. Wyniki zapisać w tabeli.

Malejące napięcie wejściowe

wejA

[ V ]

wyjY

[ V ]

5.11 Na podstawie otrzymanych wyników sporządzić wykres U

wyjY

= f (U

wejA

)

Badanie podstawowych bramek logicznych

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron