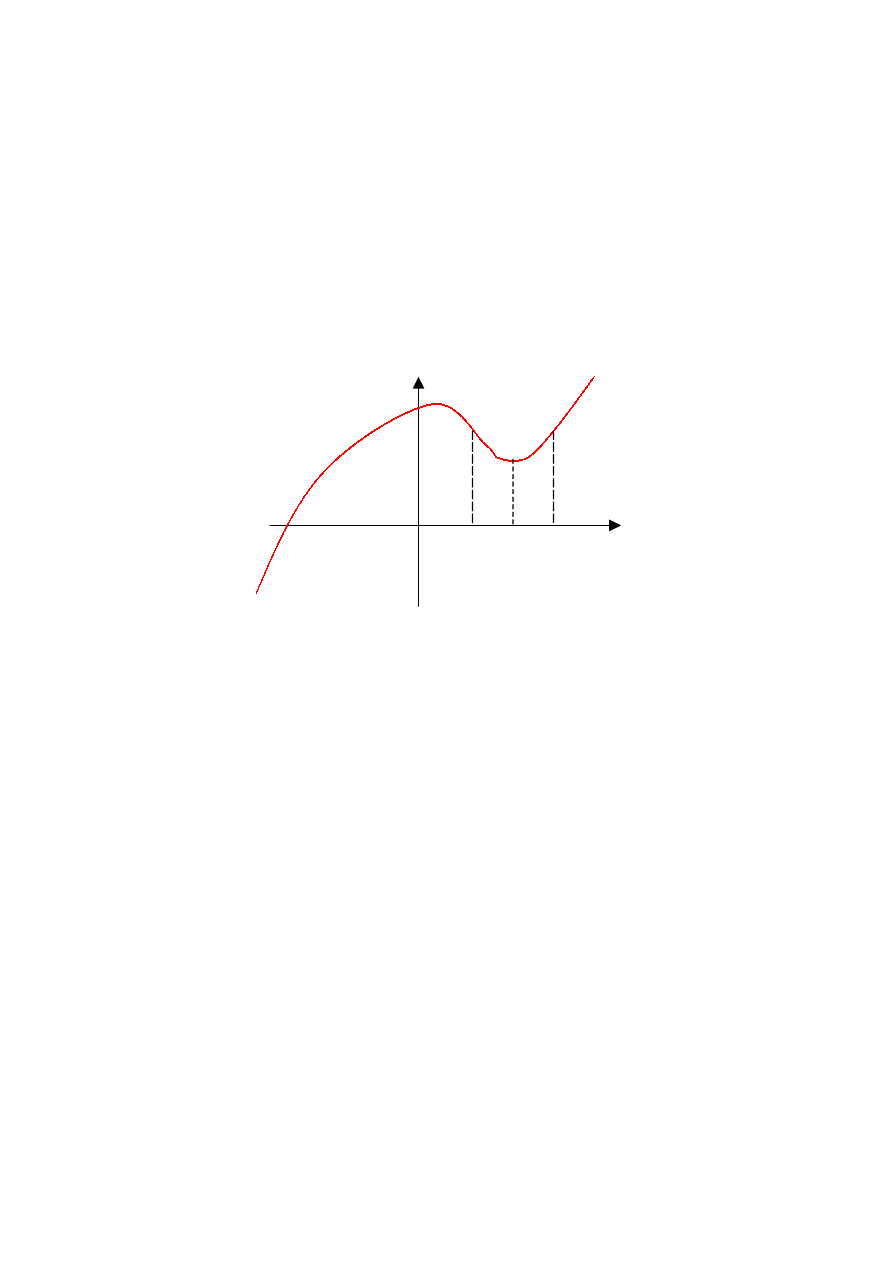
EKSTREMA LOKALNE FUNKCJI
Mówimy, że funkcja y=f(x) ma w punkcie x
0
maksimum lokalne (minimum lokalne),
jeżeli istnieje takie otoczenie punktu x
0
, że dla wszystkich punktów tego otoczenia
zachodzi nierówność
f (x) < f (x
0
) ( f (x) > f (x
0
) )
x
0
-
δ
x
0
x
0
+
δ
WARUNEK KONIECZNY ISTNIENIA EKSTREMUM
Twierdzenie. Jeżeli funkcja różniczkowalna w przedziale osiąga w pewnym punkcie
wewnętrznym x=x
0
tego przedziału ekstremum lokalne (minimum lub maksimum), to
pochodna w tym punkcie f’(x
0
) równa się zeru.
Punkt x
0
, w którym f’(x
0
)=0 nazywamy punktem stacjonarnym.
I
WARUNEK WYSTARCZAJĄCY ISTNIENIA EKSTREMUM
Jeżeli pierwsza pochodna f
‘
(x) dla x<x
0
jest ujemna (dodatnia), dla x=x
0
jest równa zeru,
a dla x>x
0
jest dodatnia (ujemna),czyli pochodna przy przejściu zmiennej x przez punkt x
0
zmienia znak z ujemnego na dodatni (z dodatniego na ujemny),to funkcja y=f(x) osiąga
ekstremum (minimum w pierwszym i maksimum w drugim przypadku).
Arkadiusz Lisak
1

II
WARUNEK WYSTARCZAJĄCY ISTNIENIA EKSTREMUM
Jeżeli dla funkcji f w punkcie stacjonarnym istnieje pochodna drugiego rzędu, która jest
różna od zera w tym punkcie, to funkcja przyjmuje w tym punkcie ekstremum. Jeśli
, to f ma w x
0
)
(
0
"
>
x
f
0
minimum lokalne, zaś jeśli
, to f ma w x
0
)
(
0
"
<
x
f
0
maksimum
lokalne.
MONOTONICZNOŚĆ FUNKCJI
Jeżeli pochodna jest w pewnym przedziale dodatnia, to funkcja jest w tym przedziale
rosnąca.
Jeżeli pochodna jest w pewnym przedziale ujemna, to funkcja jest w tym przedziale
malejąca.
Przykład:
1
2
2
−
+
=
x
x
y
(
)
1
2
2
2
'
+
=
+
=
x
x
y
(
)
0
1
2
0
'
=
+
⇔
=
x
y
,
x+1=0, x=-1
(
)
0
1
2
0
'
>
+
⇔
>
x
y
,
x+1>0, x>-1 -
funkcja rośnie
(
)
0
1
2
0
'
<
+
⇔
<
x
y
,
x+1<0, x<-1 -
funkcja maleje
Funkcja posiada minimum w punkcie x=-1,
( ) ( )
( )
2
1
1
2
2
1
1
min
−
=
−
−
⋅
+
−
=
−
f
Arkadiusz Lisak
2
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron