Podstawy konstruowania urządzeń precyzyjnych 08

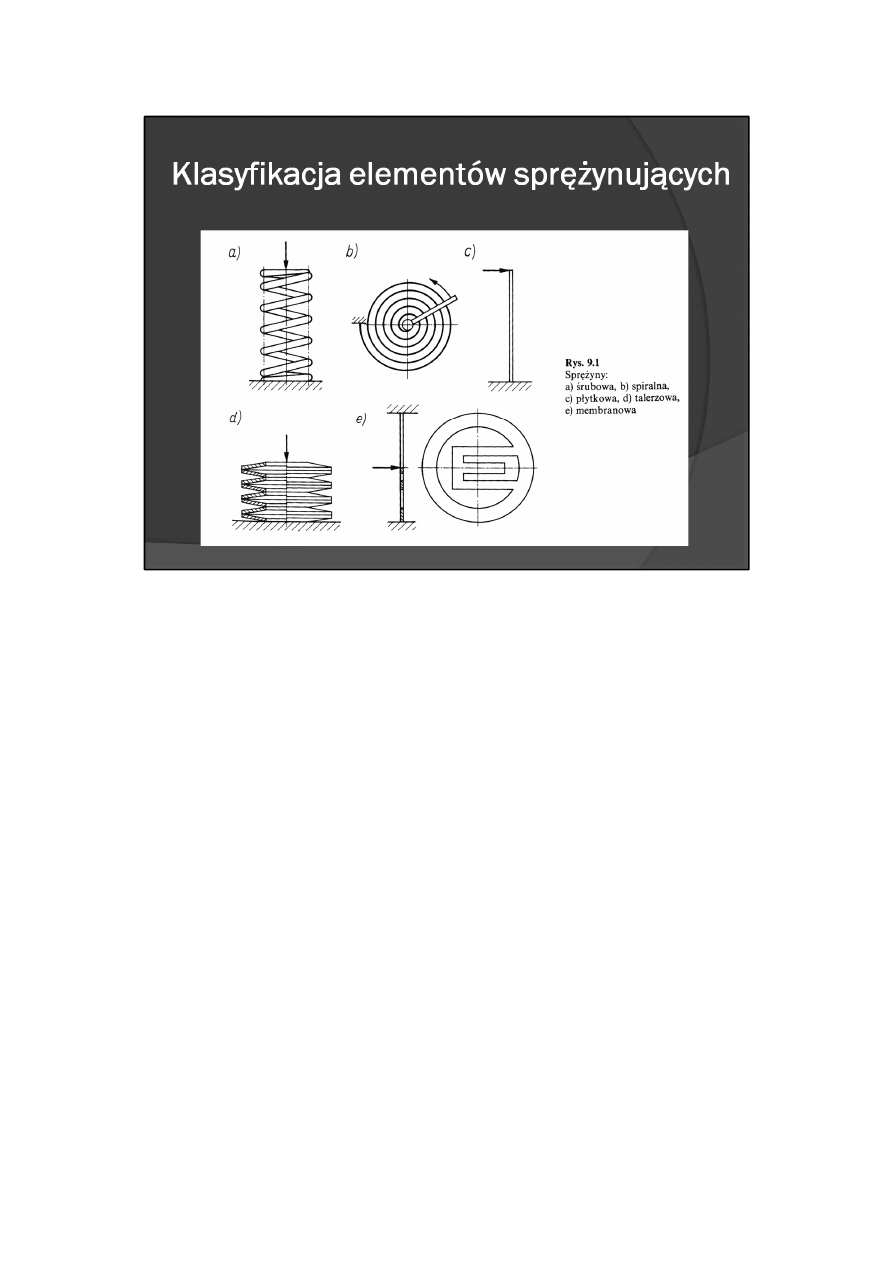
Klasyfikacja elementów sprężynujących

Elementy sprężynujące, których odkształcenie jest spowodowane siłami lub momentami zewnętrznymi,

mające za główne zadanie zmagazynowanie, a następnie oddanie energii odkształcania sprężystego,

nazywa się sprężynami. Pozostałe elementy sprężynujące, a więc odkształcające się pod wpływem zmian

ciśnienia, temperatury, czy mające za zadanie rozpraszanie, a nie magazynowanie energii, nazwano

elementami sprężynującymi o specjalnym zastosowaniu. Elementy sprężynujące mogą być metalowe

(znaczna większość) i niemetalowe (z tworzywa sztucznego lub gumy).

Najczęściej stosowane elementy sprężynujące to sprężyny. Z reguły dzieli sieje według następujących

kryteriów:

- cech konstrukcyjnych,

- rodzaju pracy sprężyny,

- trwałości sprężyny.

W zależności od cech konstrukcyjnych rozróżnia się sprężyny: śrubowe, spiralne, płytkowe, talerzowe i

inne. Przykłady takich sprężyn przedstawiono na rys. 9.1.

W zależności od rodzaju pracy rozróżnia się sprężyny: naciskowe, naciągowe, skrętowe (skrętne), zginane

(obciążone momentem gnącym).

W zależności od trwałość rozróżnia się następujące klasy sprężyn:

I __ sprężyny o trwałości praktycznie nieograniczonej, przeznaczone do pracy pod

obciążeniem dynamicznym pulsującym,

II __ sprężyny o trwałości praktycznie nieograniczonej, przeznaczone do pracy pod

obciążeniem statycznym oraz o trwałości ograniczonej, przeznaczone do pracy pod obciążeniem

dynamicznym pulsującym,

III __ sprężyny o trwałości ograniczonej, przeznaczone do pracy pod obciążeniem

dynamicznym, uderzeniowym.

Oznaczenie sprężyny powinno zawierać:

- część słowną, wynikającą z podziału wg cech konstrukcyjnych i wg rodzaju

sprężyny,

- oznaczenie klasy sprężyny (wyróżnik klasy II pomija się),

- wyróżniki wynikające z podziału wg pozostałych cech klasyfikacyjnych,

- numer normy przedmiotowej.

Energia odkształcenia zmagazynowana w elemencie sprężynującym

Energia A zakumulowana w odkształconym elemencie sprężynującym zależy od rodzaju obciążenia

(rozciąganie, ściskanie, zginanie, skręcanie), wartości obciążenia (P, M

, M

), materiału elementu

sprężynującego (E, G), objętości tego materiału (V) i kształtu jego przekroju.

Jeżeli w elemencie tym zostały wywołane naprężenia normalne σ, to wartość tej energii wyraża się

wzorem

jeżeli natomiast w elemencie zostały wywołane naprężenia styczne τ, to

Wartość współczynnika x (tabl. 9.1) zależy od rodzaju obciążenia oraz kształtu przekroju odkształconego

elementu; zawiera się ona w granicach 0,125-0,5.

Najkorzystniejszym materiałem na elementy sprężynujące, z punktu widzenia możliwości zgromadzenia

dużej energii, jest materiał o największej wartości k

,r,g/E w przypadku naprężeń normalnych i k

/G w

przypadku naprężeń stycznych (k

, k

są dopuszczalnymi naprężeniami przy ściskaniu, rozciąganiu,

zginaniu i skręcaniu).

Niedoskonałość sprężysta materiałów

Rozpatrując odkształcenia elementów sprężynujących zakłada się, że materiały tych elementów

zachowują się zgodnie z prawem Hooke'a, z którego wynika, że zmiana odkształcenia w funkcji obciążenia

ma charakter liniowy i odwracalny. Założenie to jest upraszczające, lecz w większości przypadków

dopuszczalne w praktyce przy stosowaniu sprężyn. W rzeczywistości materiały nie w pełni zachowują się

zgodnie ze wspomnianym prawem, a tę niezgodność nazywamy niedoskonałością sprężystą, która może

występować w postaci:

- opóźnienia sprężystego,

- relaksacji,

- histerezy sprężystej.

Opóźnienie sprężyste polega na tym, że element sprężynujący poddany obciążeniu uzyskuje pełne

odkształcenie nie natychmiast po przyłożeniu obciążenia, lecz dopiero po pewnym czasie jego trwania,

przy czym przyrosty tego odkształcenia w jednostce czasu maleją wraz z upływem czasu trwania

obciążenia. Jest to więc opóźnienie między przyczyną (w tym przypadku jest to obciążenie) a skutkiem

(odkształcenie).

Relaksacja jest zjawiskiem podobnym do opóźnienia sprężystego. Można ją zaobserwować wtedy, gdy

wymuszamy odkształcenie elementu i obserwujemy występujący w nim stan obciążenia. Jeżeli więc

element sprężynujący zostanie odkształcony, to pomimo, że wartość tego odkształcenia jest stała, siły

niezbędne do wywołania odkształcenia z upływem czasu maleją, przy czym ujemne przyrosty tych sił w

jednostce czasu zmniejszają się wraz z czasem trwania odkształcenia.

Histereza sprężysta polega na tym, że przebiegi odkształcania przy wzroście i zmniejszaniu obciążenia

różnią się między sobą, przy czym energia wymagana do odkształcenia elementu jest zawsze większa od

uzyskiwanej z tego elementu przy jego powrocie do stanu początkowego. Wynika to ze strat na tarcie

wewnątrz materiału zachodzące przy jego odkształcaniu.

Niedoskonałość sprężysta zależy od wielu czynników m.in. od składu chemicznego materiału, obróbki

cieplnej i mechanicznej, wartości naprężeń, sposobu obciążania, temperatury itp. Jak dotychczas, ze

względu na skomplikowany charakter zachodzących zjawisk, nie istnieją ogólne zależności analityczne

umożliwiające ilościowe obliczanie niedoskonałości sprężystej. Dokładne dane na ten temat można

uzyskać tylko na podstawie doświadczeń.

Niedoskonałość sprężysta powoduje, że teoretyczne charakterystyki elementów różnią się od

rzeczywistych nieznacznie, rzędu ułamka procentu. Z tego też względu nie rozpatruje się jej w przypadku

projektowania sprężyn. Należy jednak pamiętać o tym przy użyciu elementu sprężynującego jako

elementu pomiarowego, zwłaszcza w przyrządach pomiarowych o większej dokładności.

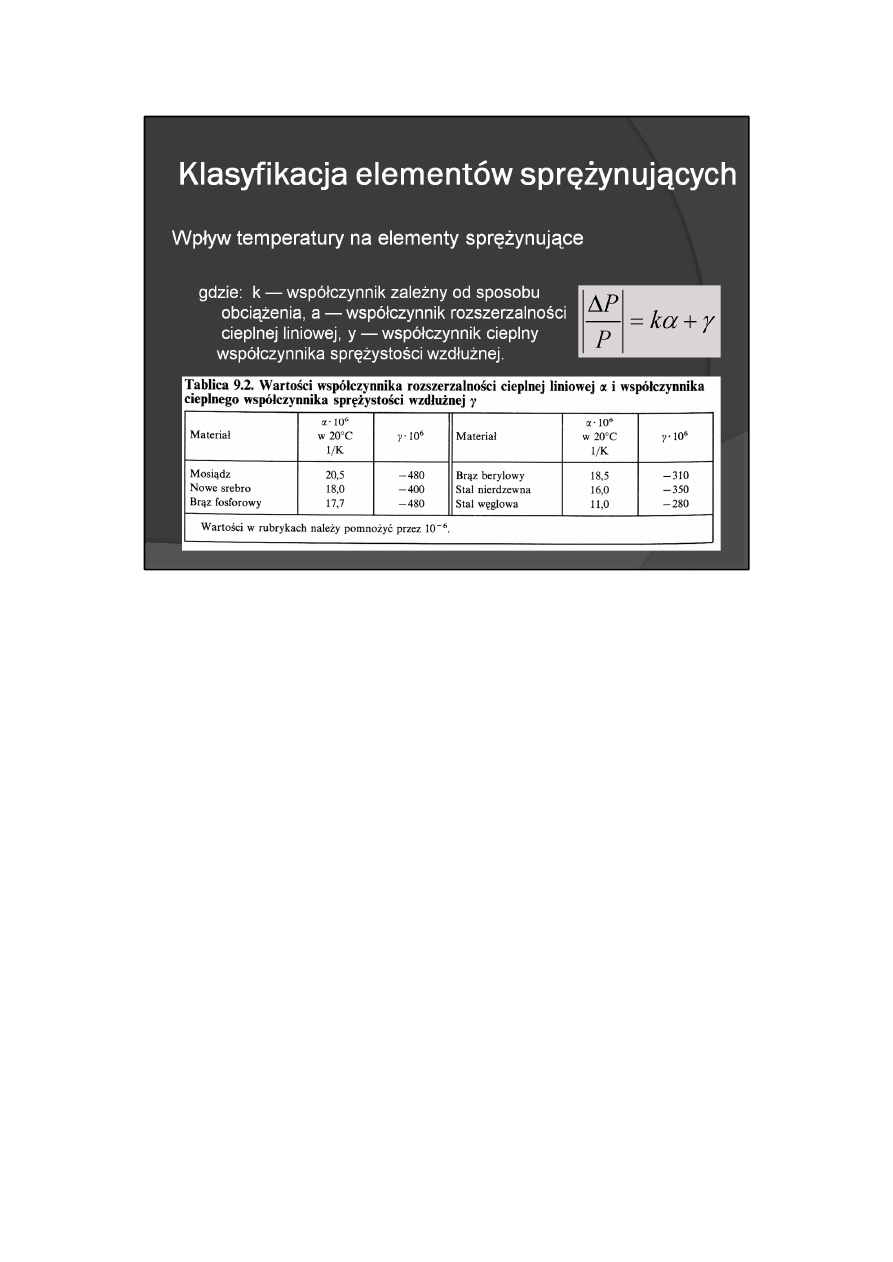
Wpływ temperatury na elementy sprężynujące

Elementy sprężynujące zmieniają swoje właściwości pod wpływem zmiany temperatury. Wynika to ze

zmiany ich wymiarów oraz zmian wartości współczynnika sprężystości wzdłużnej. W ogólnym przypadku

obciążenia elementu sprężynującego wykonanego z materiału izotropowego, względną zmianę

uogólnionego obciążenia P spowodowaną zmianą temperatury o 1 K, przy stałym względnym

odkształceniu, można obliczyć ze wzoru

gdzie: k — współczynnik zależny od sposobu obciążenia, a — współczynnik rozszerzalności cieplnej

liniowej, y — współczynnik cieplny współczynnika sprężystości wzdłużnej.

Przy rozciąganiu, ściskaniu i ścinaniu k = 2, przy zginaniu i skręcaniu k = 3. Pamiętając o tym, że

bezwzględna wartość y jest dla stali, mosiądzu, brązu około 20 razy większa niż wartość a, należy

stwierdzić, że zmiana właściwości elementów sprężynujących jest spowodowana głównie przez zmianę

współczynnika cieplnego współczynnika sprężystości wzdłużnej. Przykładowe wartości współczynników a i

y podano w tabl. 9.2.

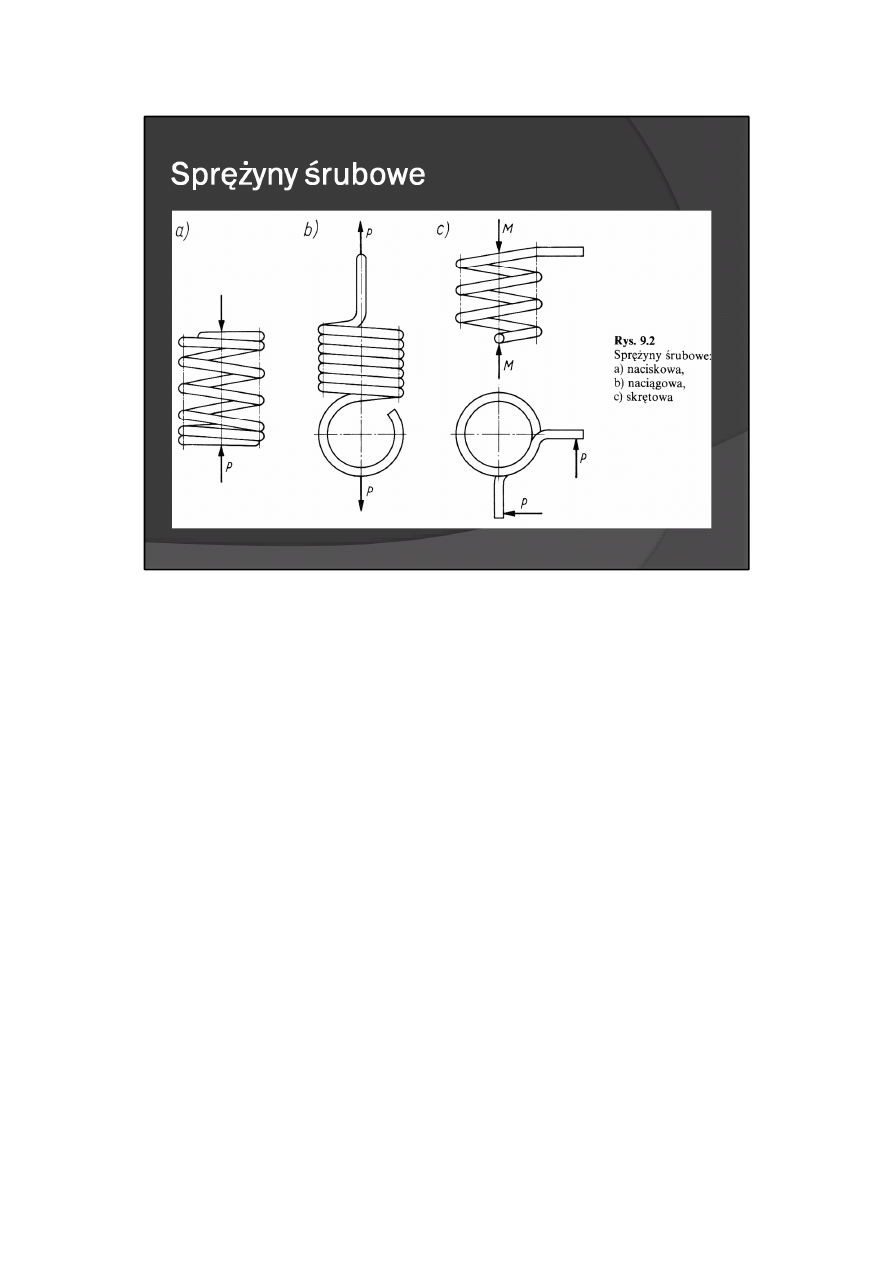
Sprężyny śrubowe

Sprężyny śrubowe najczęściej są wykonane z drutu o przekroju okrągłym, rzadziej o przekroju

prostokątnym. Ze względu na sposób obciążenia rozróżnia się sprężyny naciskowe (rys. 9.2a), ściskane siłą

osiową P, naciągowe (rys. 9.2b), rozciągane siłą osiową P i skrętowe (skrętne) (rys. 9.2c), obciążone

momentem skręcającym M (wektor momentu skierowany jest wzdłuż osi sprężyny) lub parą sił P.

Projektowanie sprężyn śrubowych

Projektowanie sprężyn polega na doborze cech geometrycznych (średnia średnica nawinięcia D, średnica

drutu d, całkowita liczba zwojów z, liczba zwojów czynnych z

, długość sprężyny w stanie nieobciążonym l

ukształtowanie zakończeń) i materiałowych (materiał drutu sprężyny i wynikające stąd wartości G lub E

oraz wytrzymałość przy rozciąganiu R

) zapewniających — przy istniejących ograniczeniach wynikających

np. z miejsca, w którym musi zmieścić się sprężyna, znormalizowanych średnic drutu itp. — spełnienie

postawionych wymagań.

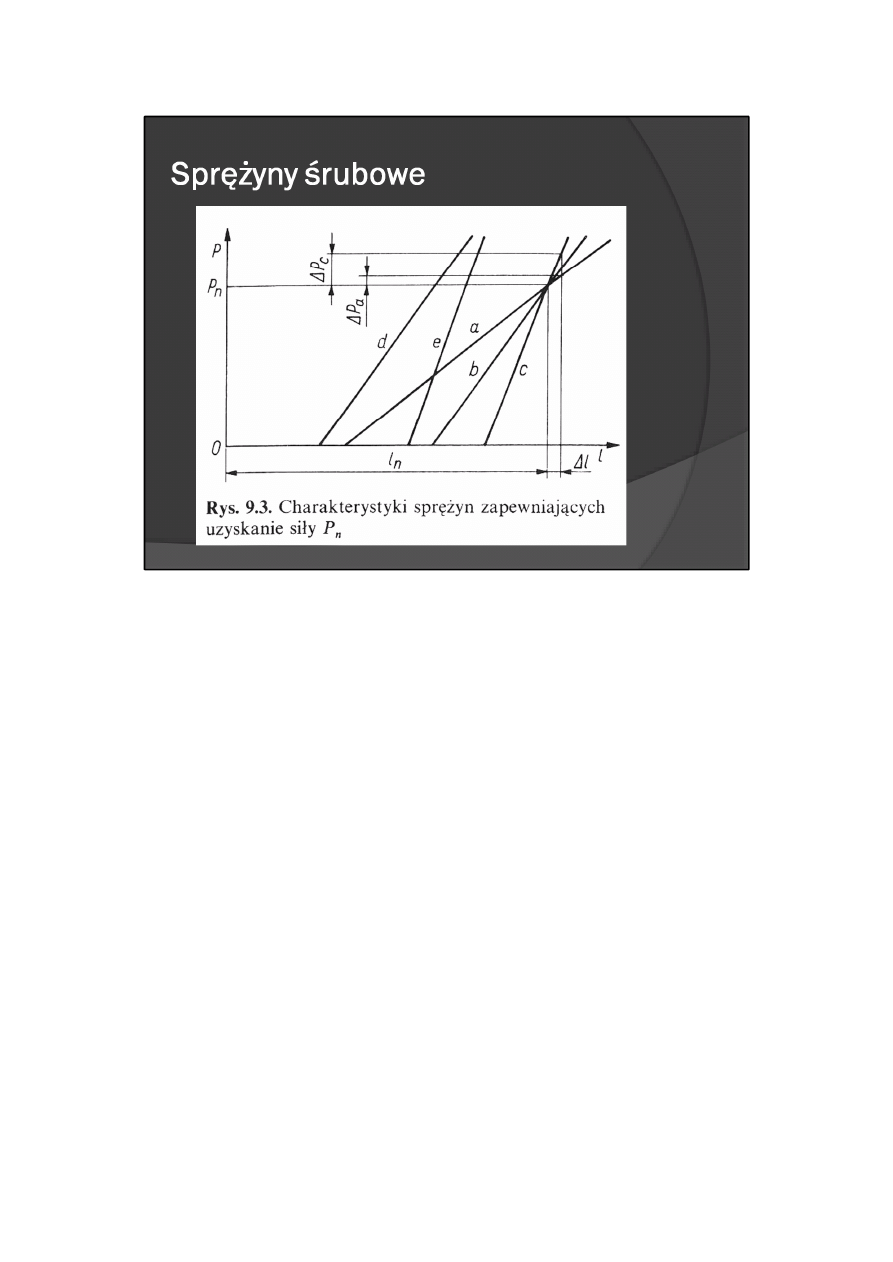
Dość często wymaga się, aby sprężyna zapewniła odpowiednią wartość siły P

(momentu M

), przy czym

konstruktor ma stosunkowo dużą swobodę w zaprojektowaniu przestrzeni, w której będzie pracowała ta

sprężyna. Występuje zatem sytuacja zilustrowana na rys. 9.3 (rozważania przeprowadzono dla sprężyny

naciągowej). Wynika z niej, że wymaganie takie spełnia wiele sprężyn, których charakterystyka przetnie

prostą określającą poziom siły P

(np. proste d i e). Jeżeli będzie postawione dodatkowe wymaganie, np.

aby długość sprężyny obciążonej siłą P

wynosiła l

, to odpowiednie okażą się sprężyny o różnych

charakterystykach (np. o charakterystykach oznaczonych a, b, c). Nie jest jednak wszystko jedno, czy

zostanie zastosowana sprężyna o większym (c) czy mniejszym (a) pochyleniem charakterystyki

(sztywności). Z reguły korzystniejsza jest sprężyna o mniejszej sztywności, gdyż w takiej sprężynie zmiana

jej wymiarów, lub wymiarów jej odkształcenia o Δl spowoduje mniejszą zmianę siły (ΔP

< ΔP

Występują też przypadki, w których sprężyny muszą zapewnić uzyskania dwóch wartości sił P

, P

oraz

pracę przy roboczym odkształceniu h. Wymagane jest wtedy zaprojektowanie sprężyny o żądanym

pochyleniu charakterystyki. Wymagania te spełnia nadal wiele sprężyn, np. wszystkie sprężyny o

charakterystykach przedstawionych na rys. 9.4.

Jeżeli będzie postawiony dodatkowy warunek np. dotyczący uzyskania długości l

przy obciążeniu P

wówczas z przedstawionej rodziny sprężyn wybierze się jedną, zaznaczoną na rysunku gwiazdką.

Jeżeli konstruktor będzie wymagał tolerowanych parametrów sprężyny (mają to być tolerancje wymiarów

geometrycznych lub charakterystyki), to koszt wykonania sprężyny wzrośnie zwłaszcza przy stolerowanej

charakterystyce. Chcąc bowiem uzyskać sprężynę o charakterystyce mieszczącej się w wymaganych

tolerancjach, należy liczyć się z koniecznością wykonania wielu sprężyn, a po zmierzeniu ich charakterystyk

uznać za dobre jedynie te, których charakterystyka zmieści się w granicach tolerancji.

Sprężyny śrubowe są elementem konstrukcyjnym często występującym w urządzeniach precyzyjnych:

Projektowanie lub dobór sprężyn jest zadaniem czasochłonnym, które konstruktor często musi

rozwiązywać. Z tego też względu już od dawna zaczęto tworzyć programy komputerowe ułatwiające

projektowanie sprężyn. Obecnie takich programów jest dużo, lecz stopień ich uniwersalności jest bardzo

różny, gdyż najprostsze z nich dotyczą tylko jednego typu sprężyny obciążonej jedną siłą, a najbardziej

złożone — np. wszystkich sprężyn śrubowych i dowolnych przypadków ich obciążenia. Należy z tych

programów korzystać, ale tylko wtedy, gdy nadają się do rozwiązania rozpatrywanego przypadku

obciążenia i odkształcenia sprężyny, nie zaś tylko przybliżonego,

i gdy skuteczność ich sprawdzono w praktyce. Stwierdzono, że zaprojektowane za ich pomocą sprężyny

poprawnie pracują w wykonanym urządzeniu.

Materiał na sprężyny śrubowe

Do wyrobu sprężyn używanych w sprzęcie precyzyjnym stosuje się z reguły drut sprężynowy ze stali

węglowej. W specjalnych zastosowaniach mogą to być stale stopowe np. nierdzewne, lecz koszt sprężyn z

takich stali jest 3^-5 razy większy niż sprężyn ze stali węglowych. Mają one jednak w warunkach

wywołujących korozję większą wytrzymałość zmęczeniową.

Sprężyny zwykle nawija się na zimno, a następnie poddaje się niskotemperaturowemu wyżarzaniu

odprężającemu w temperaturze 483-493°C. Tylko w wyjątkowych przypadkach (duża średnica drutu przy

małej średnicy nawinięcia, specjalne wymagania materiałowe) sprężyny zwija się z materiału, który

powinien być obrobiony cieplnie. Wtedy sprężyny w pełni ukształtowane poddaje się właściwej obróbce

cieplnej, zależnej od rodzaju materiału.

Stosowane są trzy rodzaje drutów sprężynowych:

- druty o zwykłej wytrzymałości — A,

- druty o zwiększonej wytrzymałości — B,

- druty o dużej wytrzymałości — C.

W zależności od tolerancji wymiarowej, wymaganej liczby skręceń drutu aż do jego uszkodzenia oraz

rozrzutu wartości wytrzymałości rozróżnia się ponadto dwie odmiany drutów sprężynowych: I i II. Drut

odmiany I ma w porównaniu z odmianą II mniejsze tolerancje, większą liczbę dopuszczalnych skręceń i

mniejszy rozrzutu wartości wytrzymałości.

Szczegółowe informacje na temat drutów sprężynowych są w PN-71/M-80057.

Średnice (d < 3 mm) produkowanych drutów sprężynowych podano w tabl. 9.3

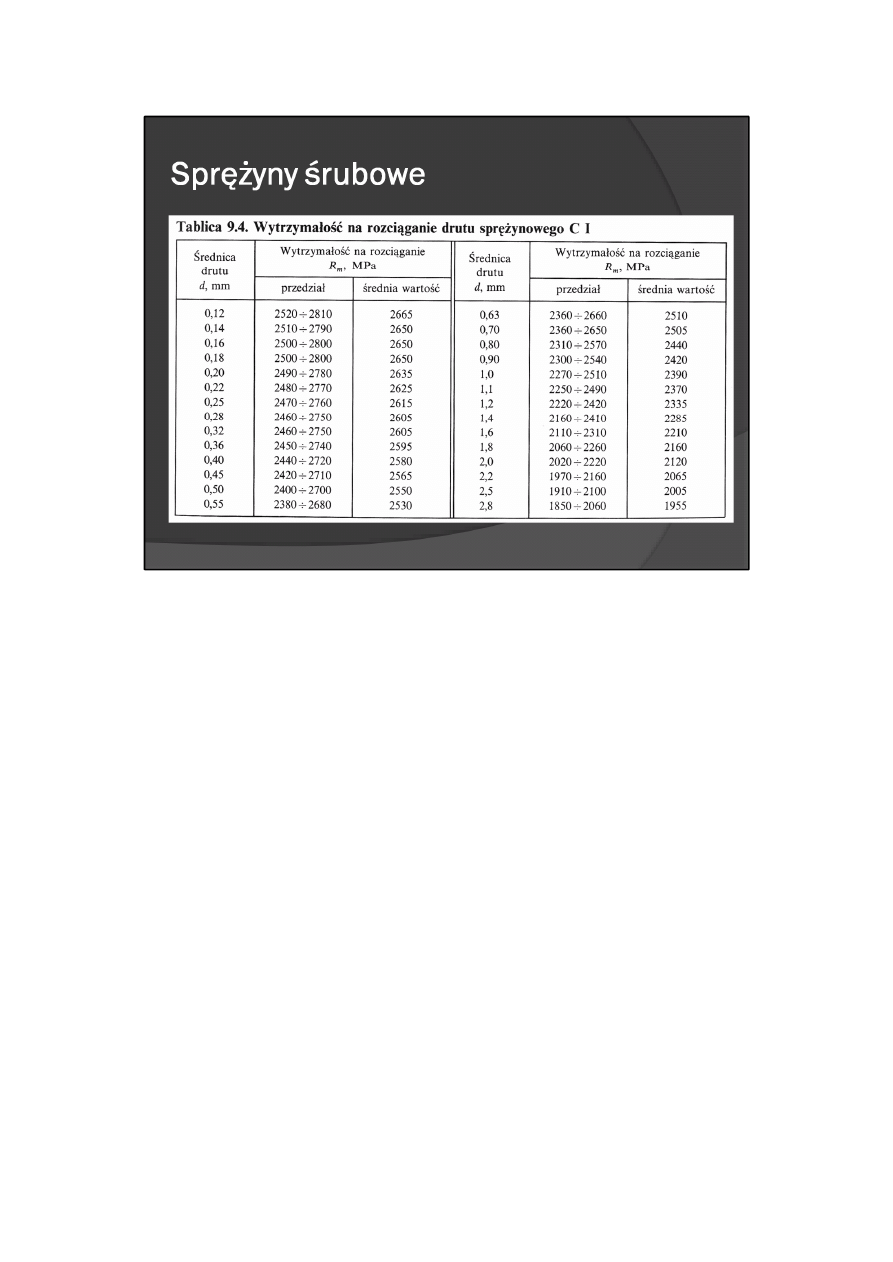
przykładowe wartości wytrzymałości na rozciąganie R

drutu sprężynowego rodzaju C i odmiany I — w

tabl. 9.4.

Orientacyjnie można przyjąć, że dopuszczalne naprężenia na skręcanie sprężyn o trwałości nie mniejszej

niż 5

cykli pracy do uszkodzenia sprężyny wynoszą k

< 0,3 R

, a sprężyn o trwałości nie mniejszej niż

cykli pracy do uszkodzenia sprężyny — k

< 0,5 R

. W przypadku sprężyn odpowiedzialnych,

pracujących pod zmiennym obciążeniem, dopuszczalne naprężenia należy dobierać korzystając z

wykresów wytrzymałości zmęczeniowej.

Wartości współczynnika sprężystości poprzecznej stali, są zawarte w przedziale G = 7,65

- 8,24

MPa. Wartość G drutu sprężynowego przyjmuje się zwykle równą 8

MPa.

Sprężyny, podobnie jak wszystkie elementy konstrukcyjne, zabezpiecza się przed korozją przez

natłuszczanie, obróbkę galwaniczną lub lakierniczą.

Przykładowe oznaczenie drutu sprężynowego przy założeniu, że sprężynę należy wykonać ze stalowego

drutu sprężynowego o dużej wytrzymałości (rodzaj C), o małych tolerancjach średnicy i małych rozrzutach

wartości wytrzymałościowych (odmiana I) oraz średnicy 0,4 mm, należy na rysunku sprężyny wpisać w

rubryce „materiał": Drut sprężynowy C I 0,40 PN-71/M-8OO57.

Sprężyny naciskowe

Projektowanie sprężyn naciskowych

Konstruktor korzystając z tych zależności powinien dobrać takie wymiary sprężyny i jej charakterystykę

(rys. 9.6) oraz takie ukształtowanie zakończenia (rys. 9.7), aby sprężyna w możliwie najlepszy sposób

spełniała określone wymagania.

Najczęściej wymagania te można sprowadzić do czterech przypadków:

- przypadek I — dane są dwa obciążenia robocze P

i ugięcie robocze h;

- przypadek II — dane są ugięcie robocze h i obciążenie P

na początku ugięcia roboczego sprężyny oraz

jest postawiony warunek, aby sprężyna na początku ugięcia roboczego była możliwie krótka;

- przypadek III — dane jest tylko jedno obciążenie P

;

- przypadek IV — dane jest jedno obciążenie P

oraz jest postawiony warunek, aby nie przekroczyć

założonej długości l

odpowiadającej temu obciążeniu.

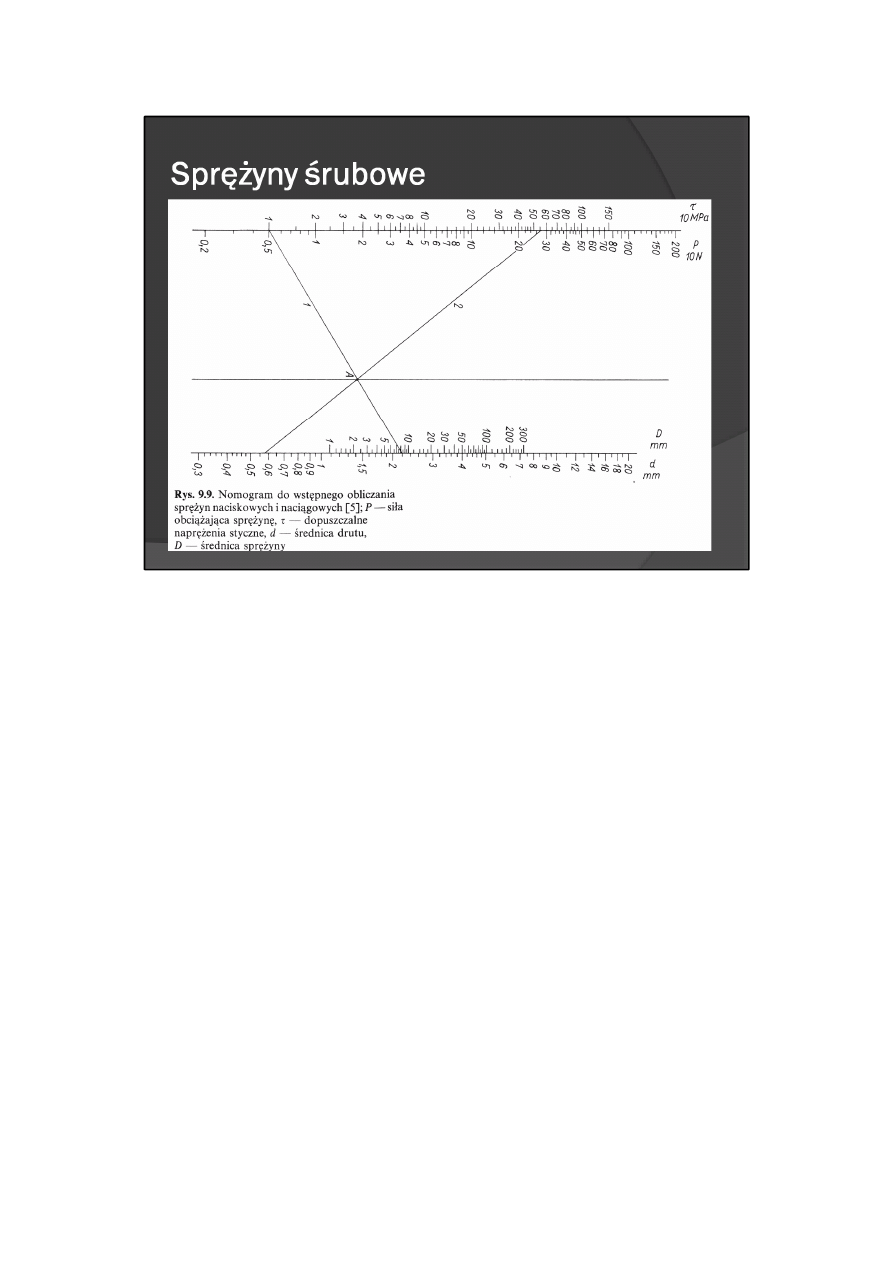
Nomogram do obliczania sprężyn naciskowych

Do wstępnego obliczania sprężyn naciskowych może być użyty nomogram przedstawiony na rys. 9.9.

Podaje on zależności między parametrami sprężyny: P, τ, d, D. Otrzymane z nomogramu wartości są

jednak przybliżone, gdyż wynikają z przyjęcia założeń upraszczających, a mianowicie, że sprężyna jest

belką prostą obciążoną jedynie momentem skręcającym M = 0,5 PD. Sposób korzystania z nomogramu

przedstawiono na przykładzie obliczenia sprężyny.

Przykład. Sprężyna naciskowa o średnicy D = 8 mm jest obciążona siłą P = 5 N. Należy wyznaczyć, jaka

powinna być średnica drutu d, z którego należy wykonać sprężynę, jeżeli dopuszczalne naprężenia styczne

dla materiału tego drutu wynoszą τ= 570 MPa?

Odpowiadając na to pytanie, należy prostą 1 połączyć punkt P = 5 N (leżący na osi P) z punktem D = 8 mm

(leżącym na osi D). Następnie przez punkt A, utworzony przez przecięcie prostej 1 z prostą pionową,

znajdującą się wewnątrz nomogramu, należy poprowadzić drugą prostą 2, przechodzącą przez punkt τ =

570 MPa leżący na osi t. Prosta 2 na osi d wskaże poszukiwaną średnicę drutu d = 0,58 mm.

Nomogram umożliwia natychmiastowe określenie wpływu zmian wartości naprężeń τ na wartość d, lub

zmianę średnicy drutu d na naprężenia styczne τ występujące w drucie sprężyny. Przez punkt A można

bowiem poprowadzić pęk prostych, których przecięcie z osiami d i τ wskaże związane ze sobą wartości

tych wielkości w sprężynie o stałych P i D.

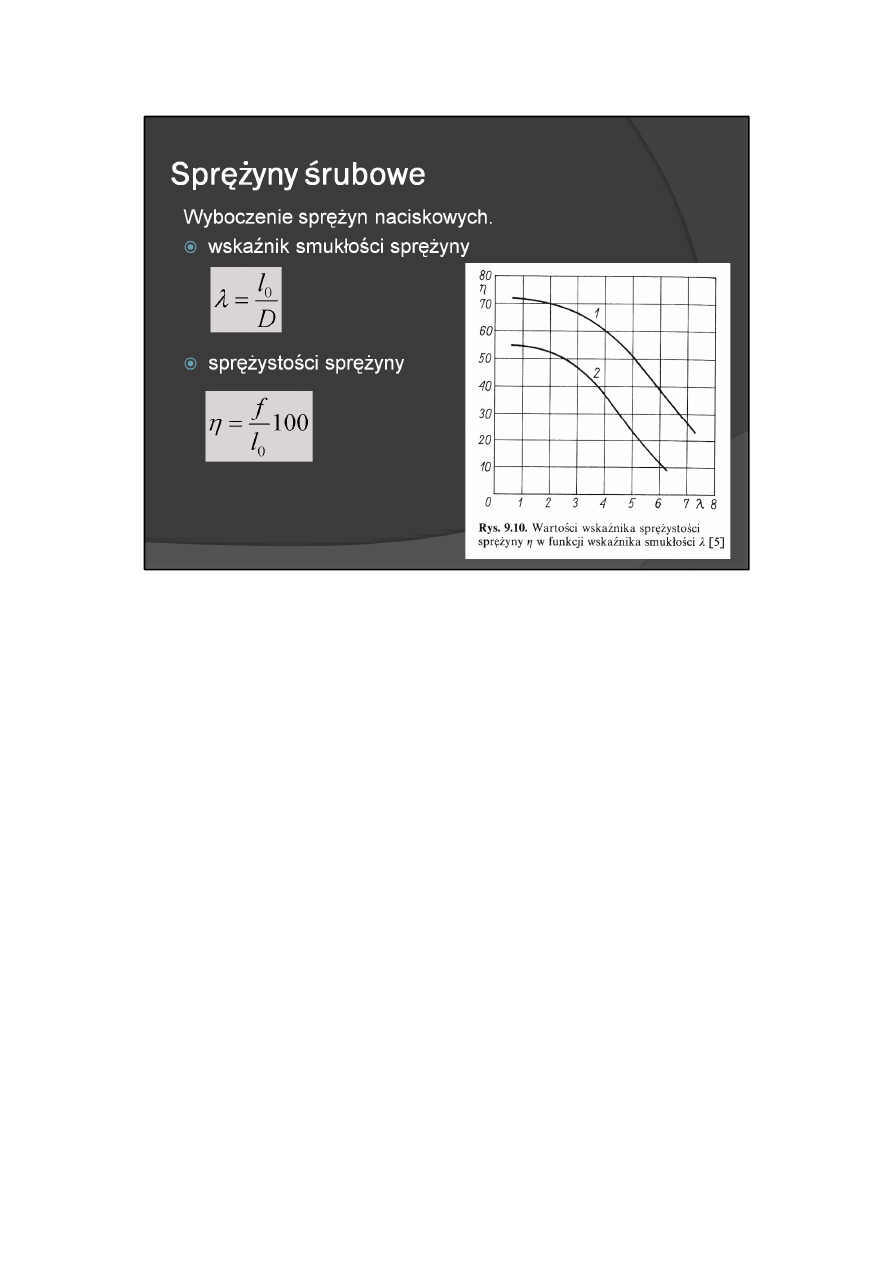
Wyboczenie sprężyn naciskowych

Sprężyny naciskowe mogą ulec wyboczeniu. Wyboczenie zależy od smukłości i obciążenia sprężyny oraz od

sposobu jej podparcia:

- wskaźnik smukłości sprężyny

- wskaźnik sprężystości sprężyny

Wykres na rys. 9.10 przedstawia graficznie zależność λ=(η) Wyboczenie sprężyny nastąpi wówczas, gdy

punkt o współrzędnych λ, η , obliczonych dla rozpatrywanej sprężyny, znajdzie się powyżej krzywych 1 lub

2. Krzywa 1 dotyczy sprężyn z równoległymi płaszczyznami podparcia i z zamocowaniem sztywnych

końców sprężyny, krzywa 2 — wszystkich pozostałych sprężyn o zmiennych warunkach podparcia.

Sprężyny, które ze względu na wymiary mogą ulec wyboczeniu, powinny mieć przewidziane prowadzenie

w gnieździe lub na trzpieniu. W celu uniknięcia występującego w takich przypadkach tarcia sprężyny o

gniazdo lub trzpień należy —jeżeli konstrukcja to umożliwia — zastąpić jedną sprężynę o określonej

długości kilkoma krótszymi sprężynami, a nie ulegającymi wyboczeniu, oddzielonymi przekładkami

oporowymi i osadzonymi w jednym gnieździe lub na jednym trzpieniu.

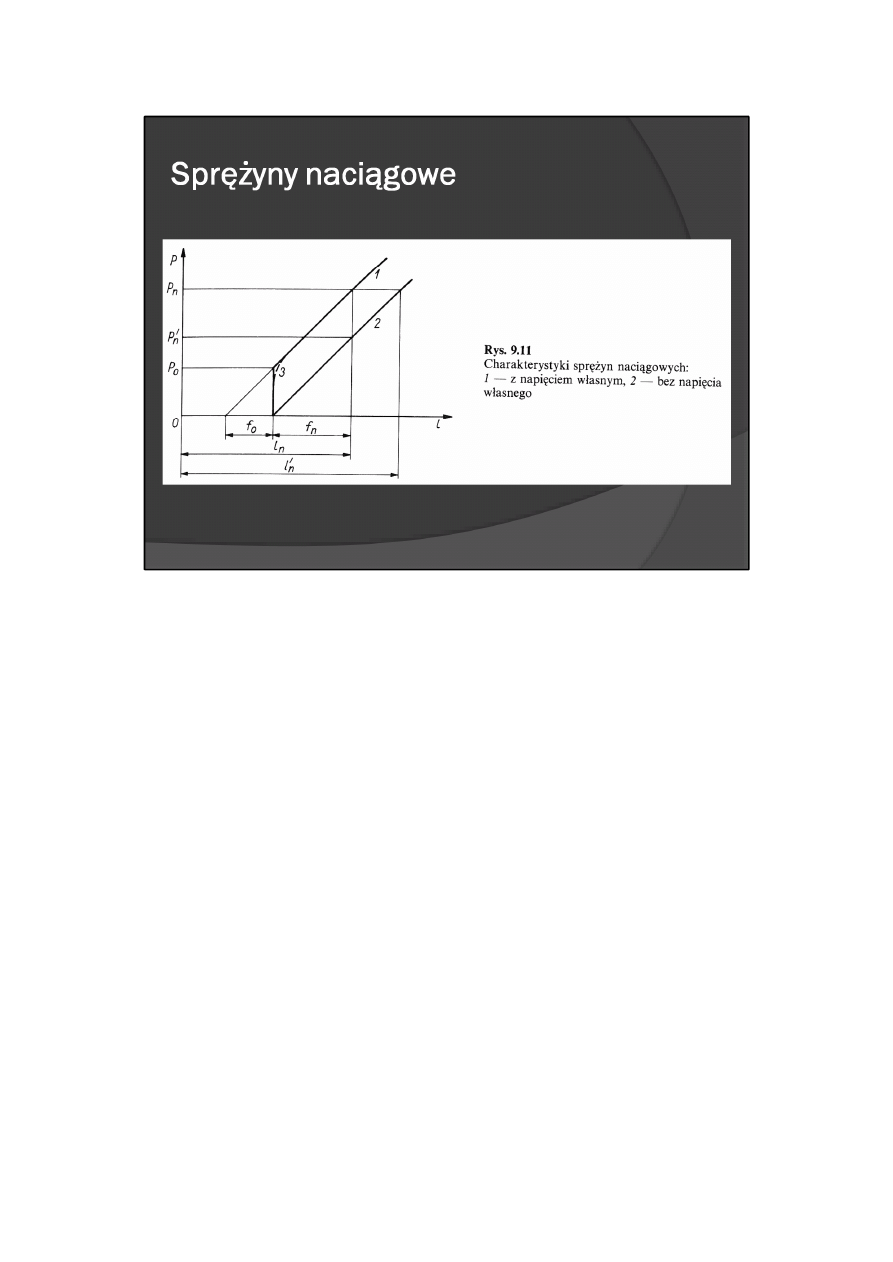
Sprężyny naciągowe

Rozróżniamy dwa rodzaje sprężyn naciągowych: z napięciem własnym i bez napięcia własnego.

Sprężyny z napięciem własnym są zwijane zwój przy zwoju i to w taki sposób, że każdy ze zwojów jest

dociskany do sąsiedniego z teoretycznie jednakową siłą P

, sprężyny te mają charakterystykę

przedstawioną na rys. 9.11 w postaci linii 1. Sprężyny bez napięcia własnego, lecz o takich samych

wymiarach i liczbie zwojów jak sprężyny z napięciem własnym, mają charakterystykę przedstawioną na

tym rysunku w postaci linii 2. W celu uzyskania przez sprężynę siły P

należy sprężynę z napięciem

własnym 1 odkształcić do długości l

, a sprężynę bez napięcia własnego 2 do długości l‘

= l

. Tak więc

przy tych samych początkowych wymiarach obu sprężyn należy dla obciążonej sprężyny bez napięcia

własnego przewidzieć więcej miejsca f

niż dla sprężyny z napięciem własnym. Z tego też względu

sprężyny z napięciem własnym są częściej stosowane zwłaszcza w przypadkach, gdy zależy na

zminiaturyzowaniu wymiarów mechanizmu i gdy siła wytwarzana przez sprężynę nie musi zmieniać się od

0, lecz od wartości większej od P

Na rys. 9.11 zaznaczono przerywaną linią odcinek rzeczywistej charakterystyki sprężyny z napięciem

własnym, różniący się od charakterystyki teoretycznej. Okazuje się bowiem, że w wykonanej sprężynie nie

wszystkie zwoje są dociskane do siebie z jednakową siłą. Dlatego też przy wzroście siły rozciągającej

sprężynę odkształceniu podlegać będą nie wszystkie zwoje w tej samej chwili, lecz najpierw te, które były

dociśnięte z najmniejszą siłą, a następnie dołączą do nich zwoje dociskane z siłą większą; stąd w

rzeczywistej charakterystyce wystąpi odcinek krzywej 3 zaznaczony linią przerywaną.

Napięcie własne może występować tylko w sprężynach zwijanych na zimno i nie poddanych

wysokotemperaturowej obróbce cieplnej po zwinięciu.

Orientacyjne wartości naprężeń wywołanych napięciem własnym wynoszą: 0,15 k

przy 4 < w < 6; 0,1 k

przy 6 < w < 10; 0,06 k

przy w > 10.

w – wskaźnik sprężyny

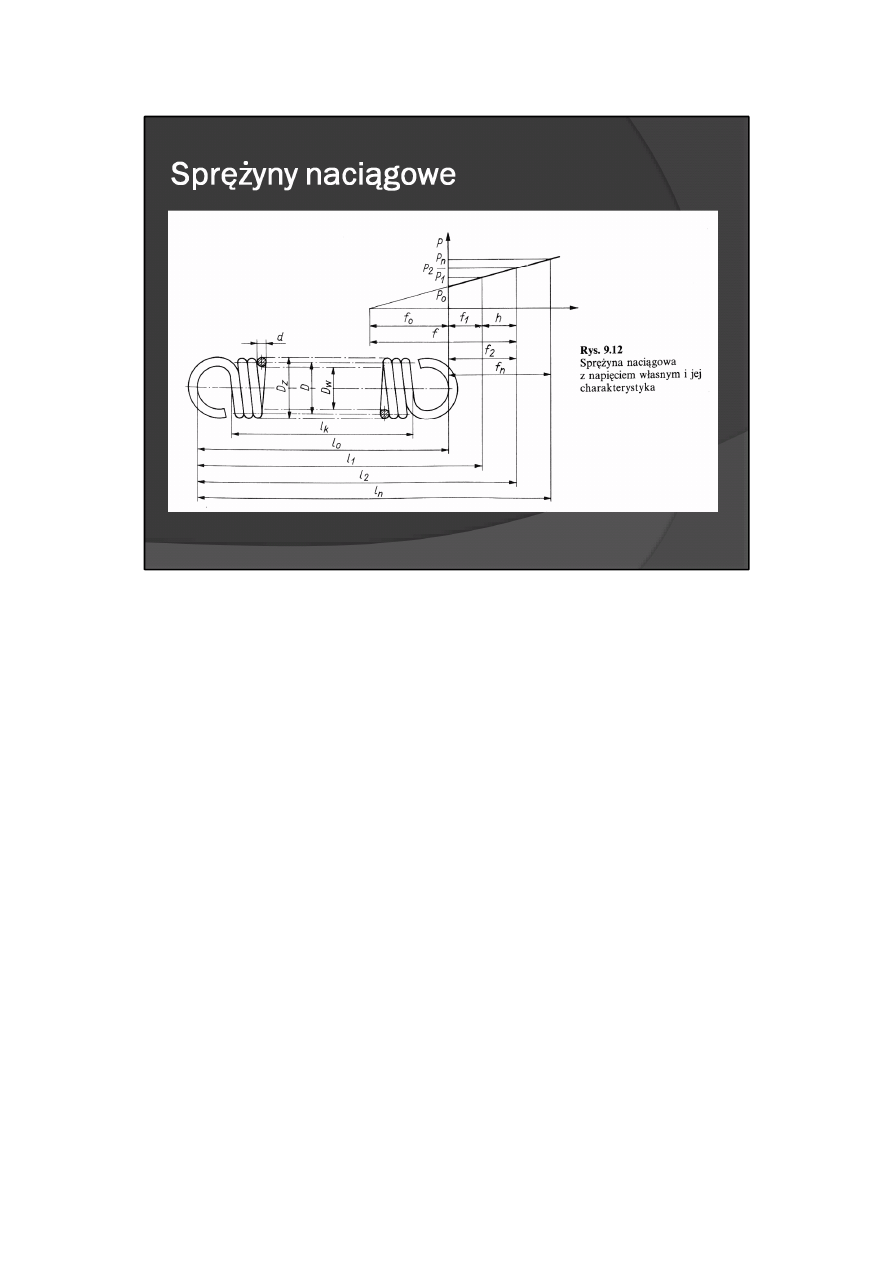
Projektowanie sprężyn naciągowych

Konstruktor, powinien tak dobrać wymiary geometryczne sprężyny i jej charakterystykę (rys. 9.12) oraz

tak ukształtować zakończenia, aby sprężyna w możliwie najlepszy sposób spełniała określone wymagania.

Wymagania te najczęściej można sprowadzić do trzech przypadków:

- przypadek I — dane są dwa obciążenia robocze P

i wydłużenie robocze h,

- przypadek II — dane jest tylko jedno obciążenie P

- przypadek III — dane jest tylko jedno obciążenie P

oraz warunek, aby nie przekroczyć założonej długości

odpowiadającej temu obciążeniu.

Regulacja siły w sprężynach naciskowych i naciągowych

Założone podczas obliczania sprężyny wartości sił mogą się okazać po wykonaniu sprężyny niewłaściwe.

Należy w takim przypadku zaprojektowaną sprężynę zastąpić inną, albo też istniejącą sprężynę

zmodyfikować, umożliwiając w ten sposób regulację siły P

. Modyfikacja sprężyny naciskowej może

polegać na:

- zmianie sztywności sprężyny na skutek skrócenia jej swobodnej długości np. przez obciążenie czy

zeszlifowanie części czynnych zwojów lub zwiększenie liczby zwojów nieczynnych; powoduje to zmianę

charakterystyki sprężyny;

- zmianie napięcia początkowego sprężyny np. przez włożenie podkładek w gniazdo, w którym znajduje

się sprężyna (zwiększenie napięcia) lub pogłębienie gniazda (zmniejszenie napięcia); powoduje to przejście

punktu pracy w inne miejsce tej samej charakterystyki sprężyny.

Modyfikacja sprężyny naciągowej również polega na zmianie sztywności (przez zmianę liczby zwojów

czynnych) i zmianie napięcia początkowego (przez zmianę ukształtowania zwojów nieczynnych czy

zmianę rozstawienia odległości zaczepów pod sprężynę).

W celu zastosowania regulacji napięcia początkowego sprężyny naciągowej nawiniętej zwój przy zwoju za

pomocą wkręcanego w nią elementu gwintowego (np. jak na rys. 9.14b) Regulacja sił jest niezbędna przy

znormalizowanych wymiarach sprężyn. Stosuje się bowiem wówczas sprężyny o wymiarach najbliższych

obliczonym.

W Polsce również opracowano (PN-71/M-80706) zalecenia dotyczące wymiarów i dopuszczalnych

obciążeń sprężyn śrubowych walcowych, naciskowych, ogólnego przeznaczenia, zwijanych na zimno z

drutów sprężynowych rodzaju A, B, C, pracujących w warunkach obciążeń stałych lub rzadko zmiennych.

Przyjęto przy tym następujące założenia ograniczające:

- wskaźnik sprężyny w = 4; 6,3; 10,

- czynna liczba zwojów zc = 3,5; 5,5; 9,5; 15,5.

Norma podaje dla każdej znormalizowanej średnicy drutu 0,2 mm < d < 8 mm średnice podziałowe D

(wynikające z przyjętych wartości w wskaźnika sprężyny), maksymalne obciążenia P

, odpowiadające mu

odkształcenie f

oraz długości nie-obciążonej sprężyny l

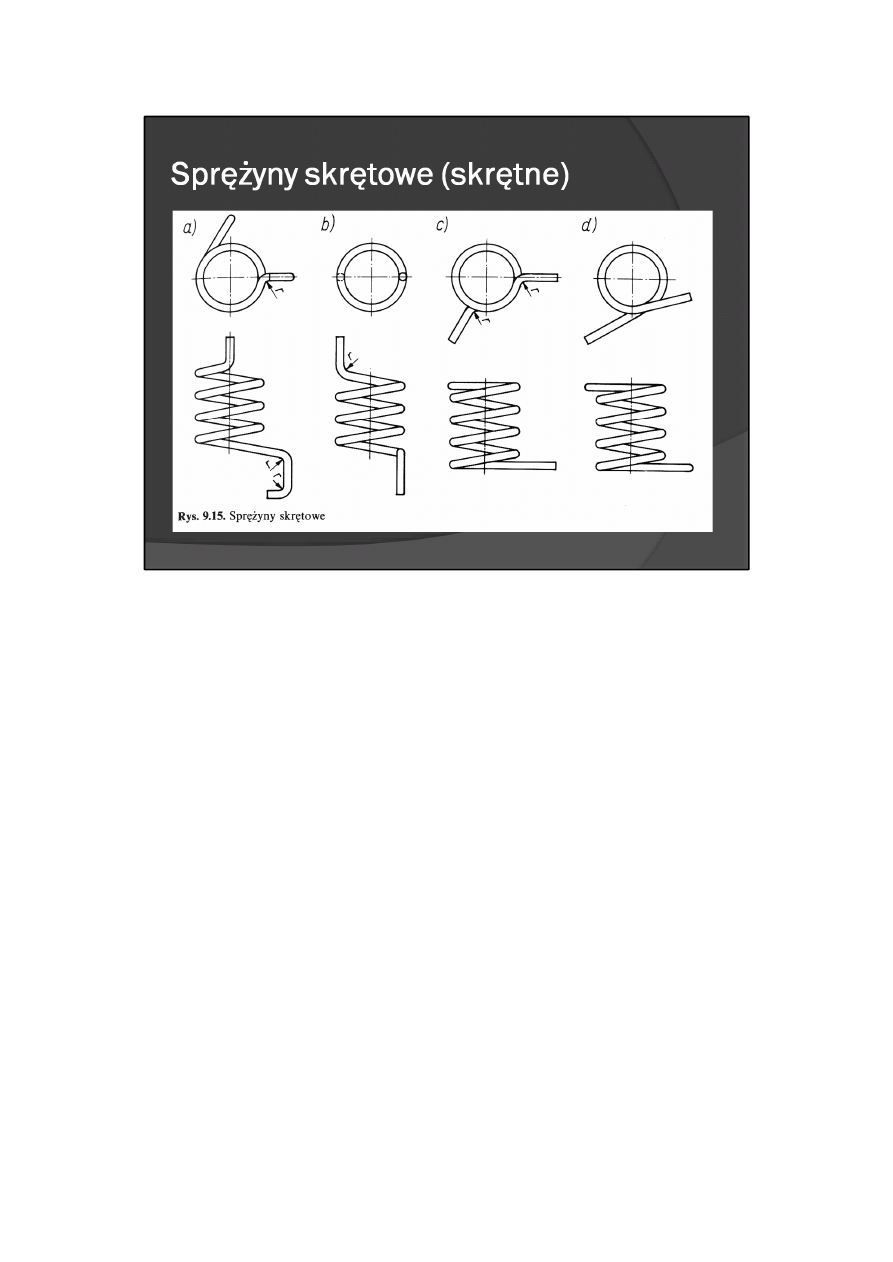
Sprężyny skrętowe (skrętne)

Najczęściej spotykane odmiany konstrukcji sprężyn śrubowych skrętowych pokazano na rys. 9.15.

Sprężyny te mogą być prawo- lub lewoskrętne.

Najmniejsze wartości promieni zagięcia zaczepów r

min

, tj. wewnętrznych promieni krzywizny przejścia od

zaczepu do części śrubowej sprężyny, są zależne od średnicy i rodzaju materiału drutu. Dla drutów

sprężynowych o średnicy d < 4 mm i rodzaju A promień zagięcia r

min

= d, dla rodzaju B — r

min

= 1,2d, dla

rodzaju C - r

min

= 1,4d.

Najmniejszy kąt początkowego odkształcenia sprężyny α

zaleca się przyjmować o wartościach α

> 60°.

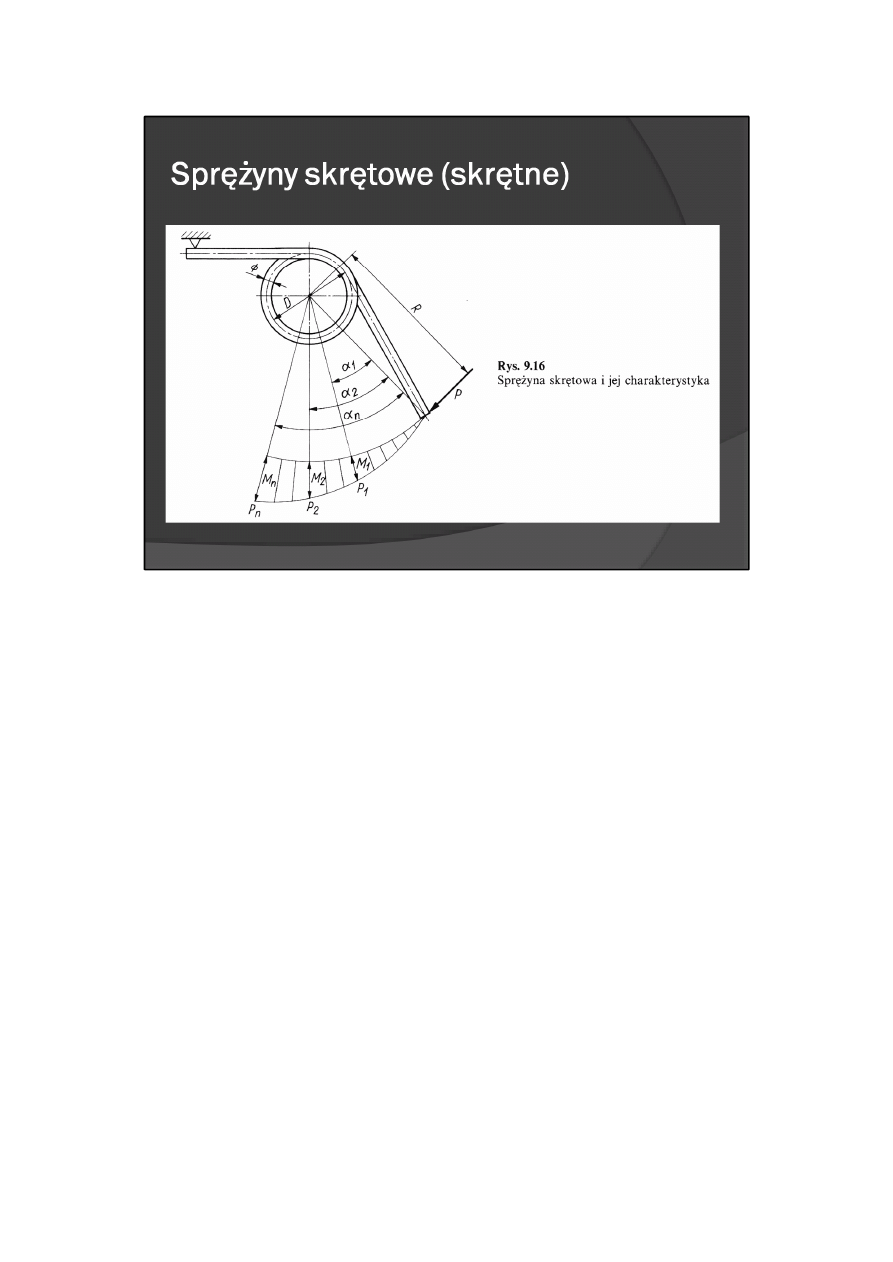
Projektowanie sprężyn skrętowych

Konstruktor powinien tak dobrać wymiary geometryczne sprężyny i jej charakterystykę (rys. 9.16) oraz tak

ukształtować jej zakończenia, aby w możliwie najlepszy sposób spełniała ona określone wymagania.

Wymagania te można zwykle sprowadzić do dwóch przypadków:

- przypadek I — są dane: moment początkowy M

( moment końcowy M

oraz roboczy kąt skręcenia

sprężyny (α

- α

- przypadek II — jest dany tylko jeden moment obciążenia M

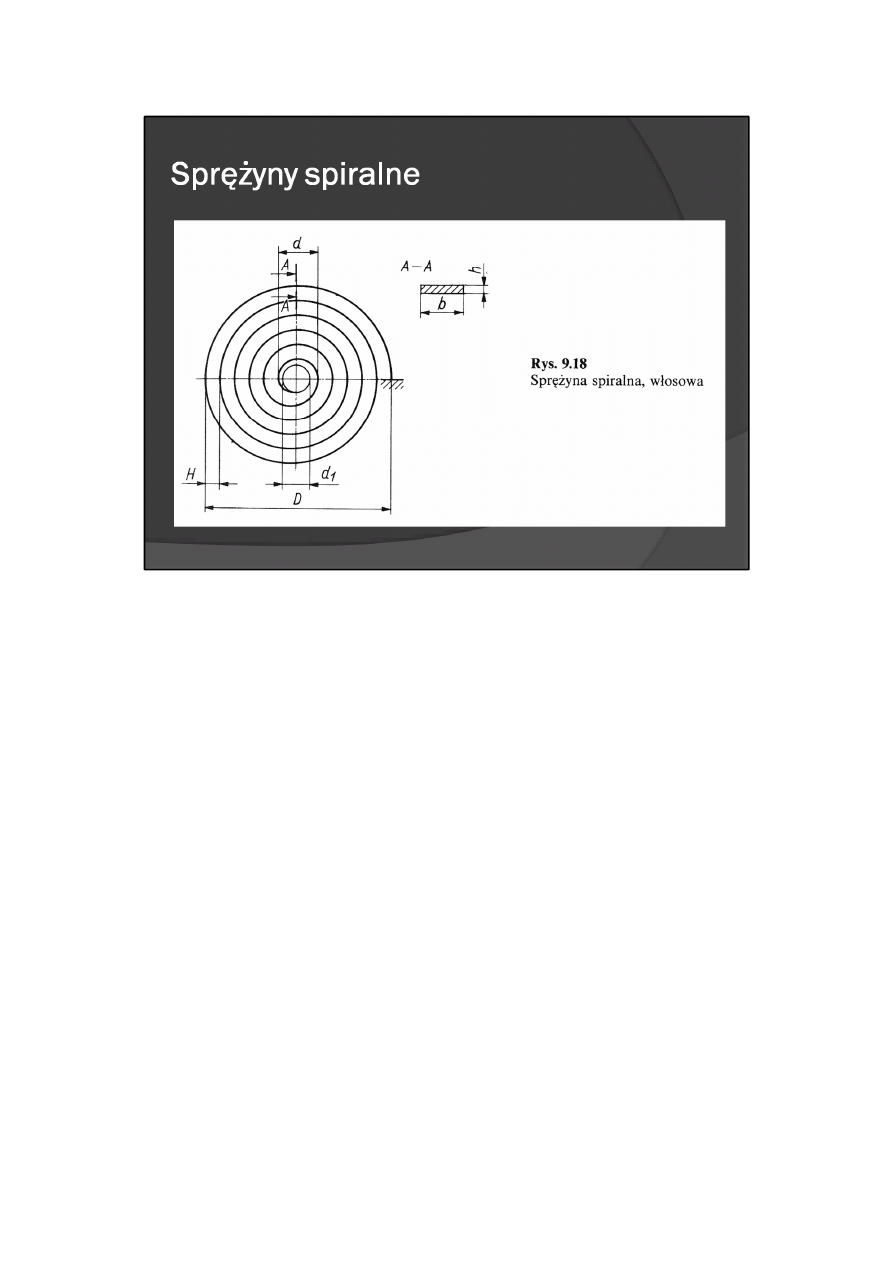
Sprężyny spiralne

Sprężyny spiralne zwykle są wykonywane z taśmy metalowej o przekroju prostokątnym. Rozróżnia się

sprężyny włosowe (stosowane w przyrządach pomiarowych jako sprężyny zwrotne miernicze, zwrotne

kasujące luz, sprężyny regulatorów balansowych, sprężyny doprowadzające prąd do części ruchomych)

oraz sprężyny napędowe (silniki sprężynowe).

Sprężyny włosowe

Sprężyny włosowe (rys. 9.18), o niewielkich wymiarach, są wykonywane z cienkiej taśmy. Oba końce

sprężyny włosowej są zamocowane sztywno, a zwoje sprężyny podczas jej pracy nie stykają się ze sobą.

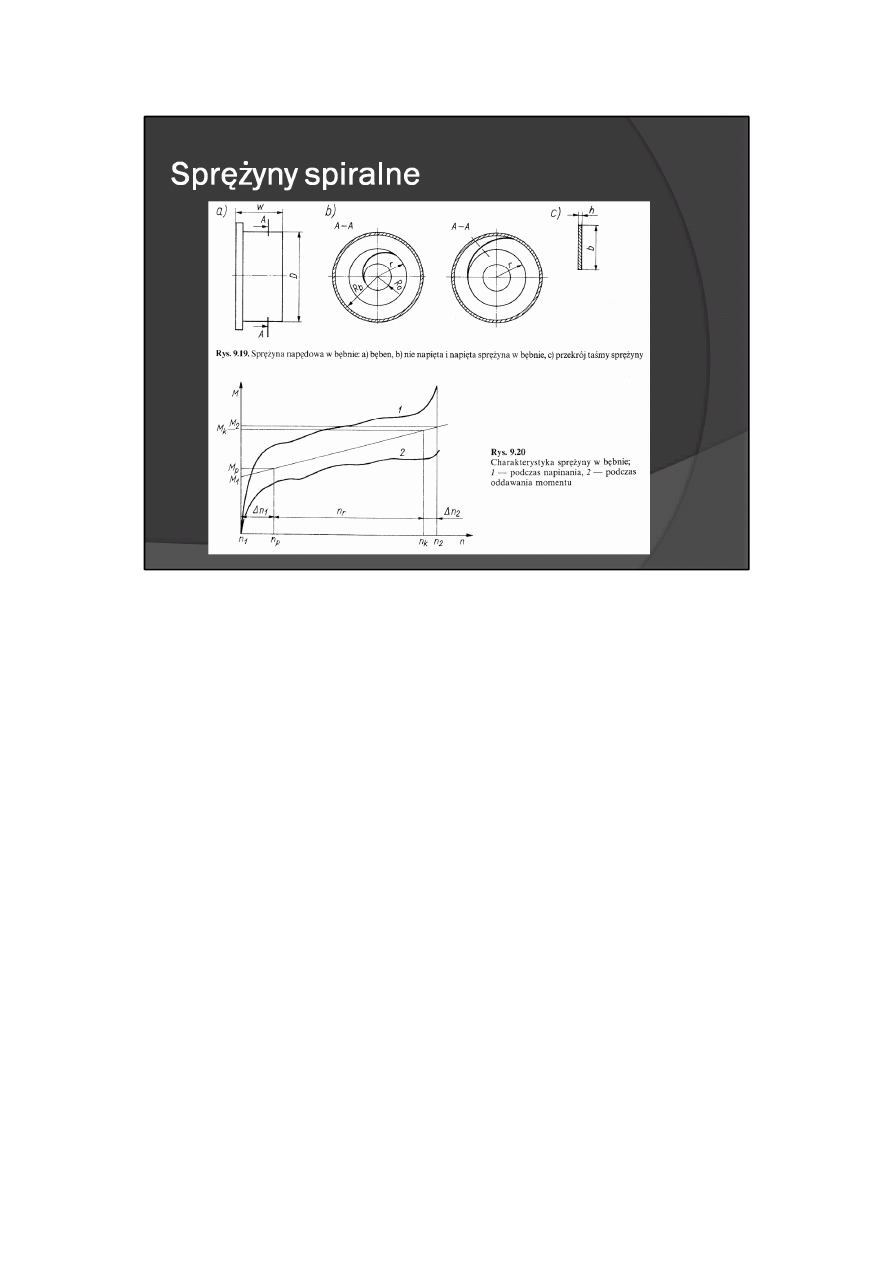
Sprężyny napędowe dzieli się na sprężyny swobodne, sprężyny w bębnie i sprężyny przewijane (negatory).

Obliczanie sprężyn napędowych w bębnie jest przybliżone i dotyczy sprężyny przedprężonej (w skrajnych

włóknach występuje naprężenie większe od dopuszczalnych) pracującej w bębnie normalnym, a więc

sprężyny o tak dobranej długości, przy której bęben wykonuje największą liczbę otworów. Jest to

najczęściej spotykany przypadek sprężyny napędowej.

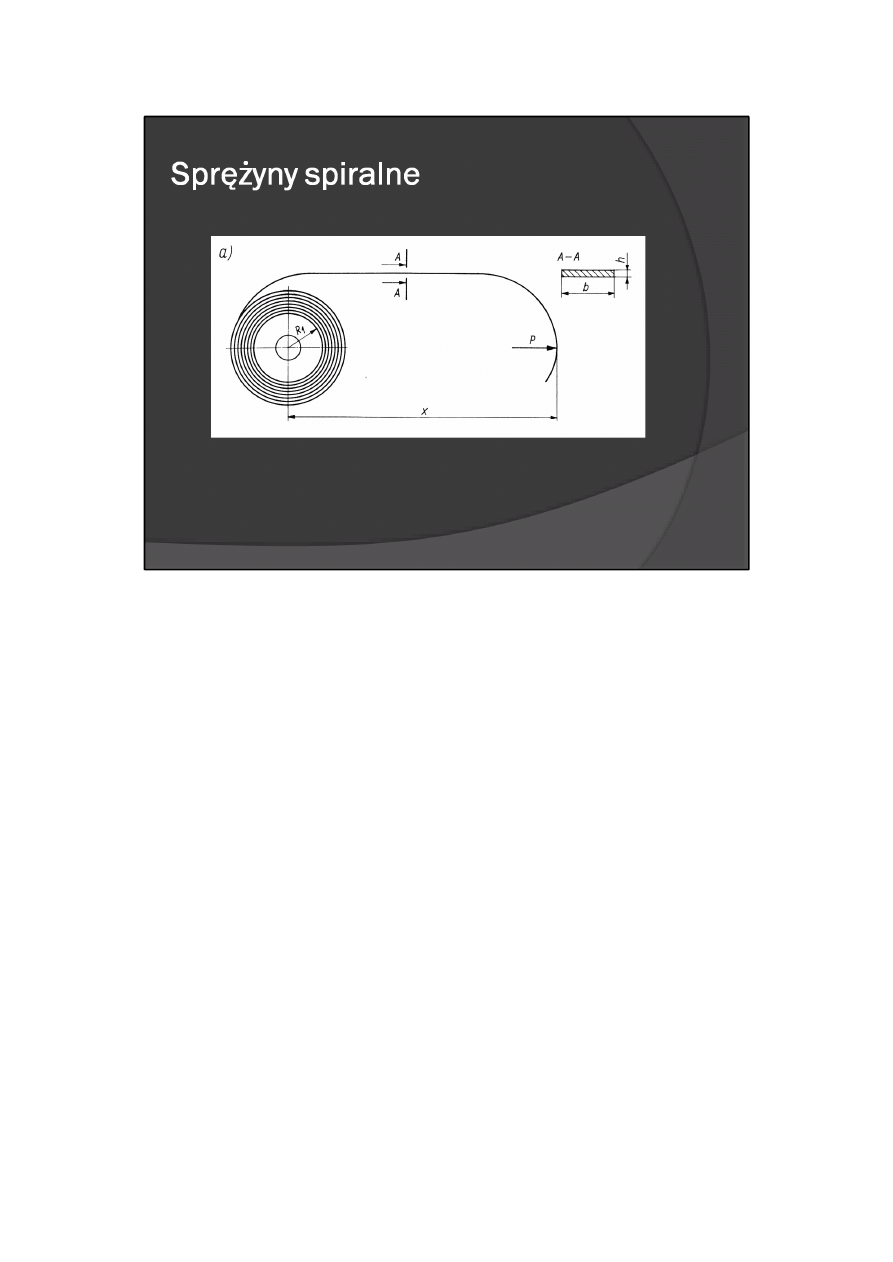
Sprężyny przewijane są wykonane z metalowej taśmy o przekroju prostokątnym i osadzone na wałku z

którym obracają się podczas pracy. Mogą zapewniać uzyskanie siły P (rys. 9.22a)

lub momentu M (rys. 9.22b, c). Sprężyny te mają bardzo płaską charakterystykę, dzięki czemu siła P

praktycznie nie zależy od wartości x, a moment M — od kąta obrotu wałków, na których osadzono

sprężynę.

Sprężyny płytkowe metalowe

Najczęściej stosowanymi sprężynami płytkowymi metalowymi są sprężyny taśmowe zginane, których

odmianami są sprężyny dociskowe, sprężyny układów stykowych, sprężyny do sprężystych łożyskowań i

prowadzeń oraz sprężyny skrętne do łożyskowań sprężystych (zawieszki skrętne).

Sprężyny dociskowe

Sprężyny dociskowe można przedstawić jako proste belki sprężyste (sprężyny proste). Sprężyny dociskowe

mogą mieć również bardziej złożone kształty.

Sprężyny układów stykowych (sprężyny stykowe)

Sprężyny układów stykowych stosuje się do zamykania, otwierania i przełączania obwodów elektrycznych

małej mocy. Schematy podstawowych układów stykowych: zamykającego (zwiernego), otwierającego

(rozwiernego) i przełączającego przedstawiono na rys. 9.23.

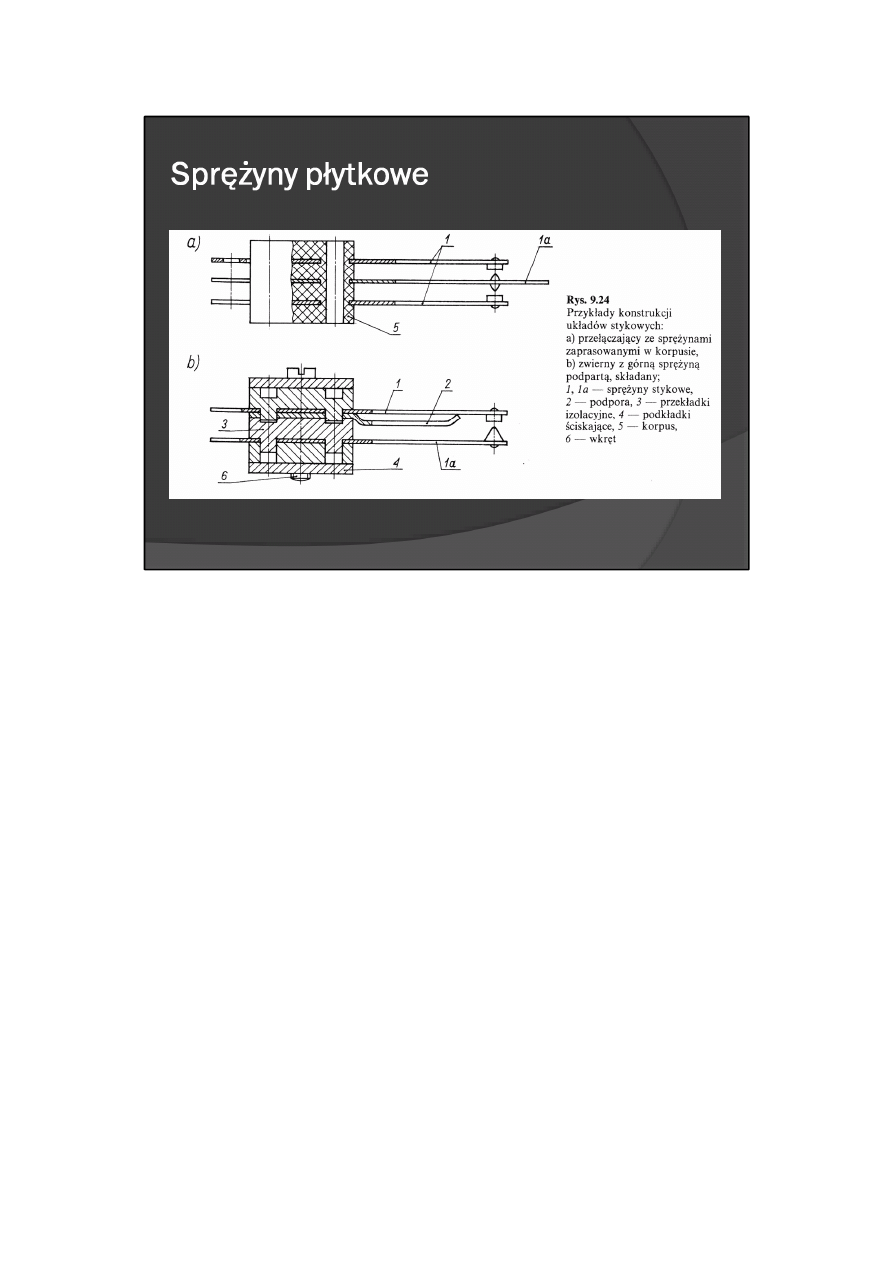
Układ stykowy składa się więc minimum z dwóch sprężyn z zamocowanymi na nich styczkami (stosuje się

również sprężyny stykowe, w których rolę styczek przejmują specjalnie ukształtowane ich zakończenia).

Sprężyny są od siebie odizolowane i służą do doprowadzenia prądu oraz wytworzenia nacisku między

styczkami. Przykłady układów stykowych przedstawiono na rys. 9.24.

Sprężyny najczęściej są wykonywane z nowego srebra, brązu (krzemowego, fosforowego, berylowego) lub

ze sprężystego mosiądzu.

Sprężyny układu stykowego przy ich zwieraniu mają tendencję do drgań. Drgania te mogą spowodować

krótkotrwałe przerwy w obwodzie elektrycznym. Przerwy te są niekorzystne, gdyż zwykle powodują

iskrzenia oraz mogą spowodować niewłaściwą reakcję urządzenia, w którym zastosowano układ stykowy

(drgania mogą być odebrane jako wysłanie nie jednego, lecz kilku impulsów).

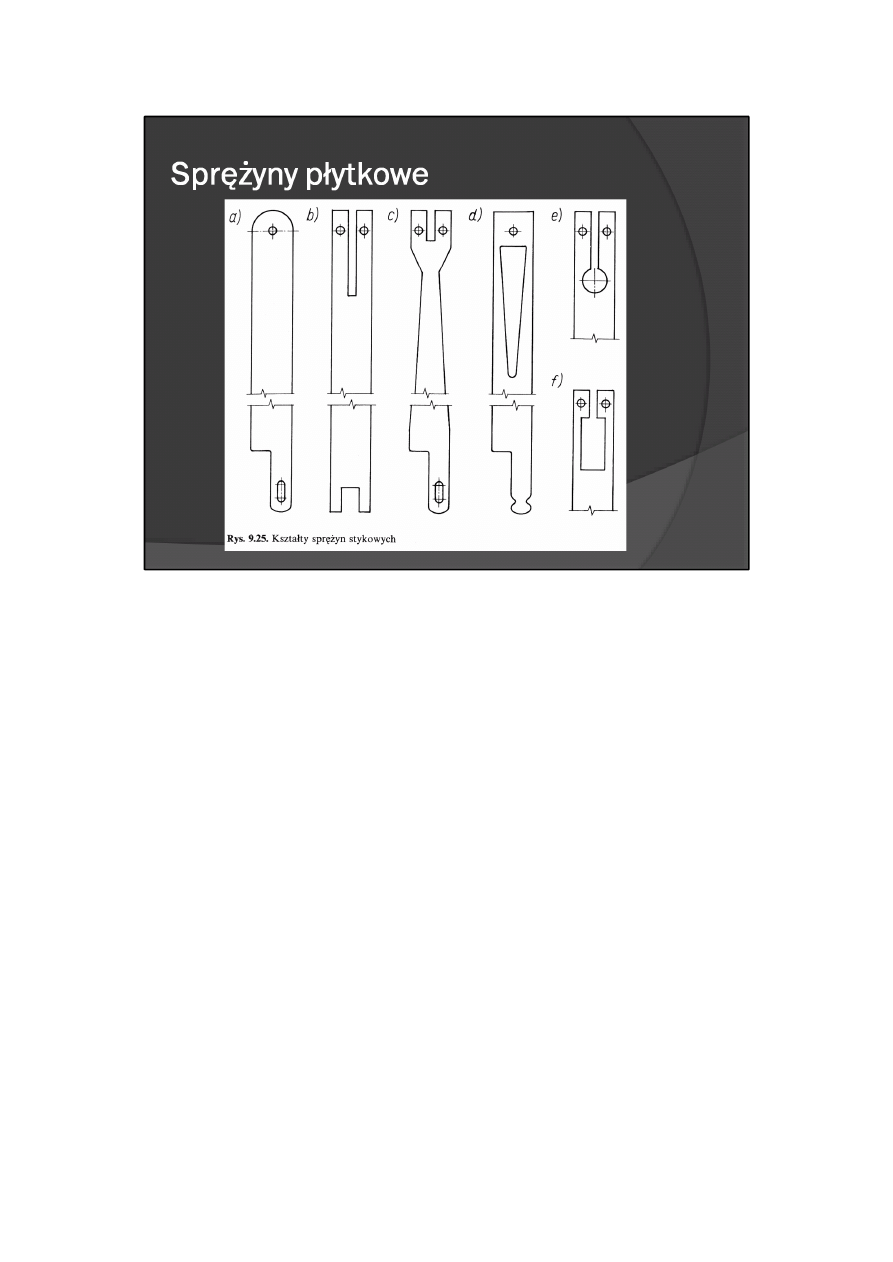
W celu zmniejszenia możliwości powstawania rozwarć w układach stykowych stosuje się:

- zróżnicowanie grubości sprężyn (różne grubości powodują różne częstotliwości drgań własnych

sprężyn);

- podparcie sprężyn (efekt podparcia powoduje podobny skutek jak zróżnicowanie grubości sprężyn);

- rozcięcie sprężyny na końcu i zamocowanie dwóch styczek (rys. 9.25b, c, e, f);

- zmniejszenie energii drgań sprężyny przez zmniejszenie jej masowego momentu bezwładności;

najskuteczniej można uzyskać to przez zmniejszenie szerokości sprężyny w pobliżu ruchomego końca

sprężyny (rys. 9.25c, d, e, i);

- stosowanie dodatkowych elementów z tworzywa sztucznego o dużej histerezie, zatapianych w

sprężynach stykowych.

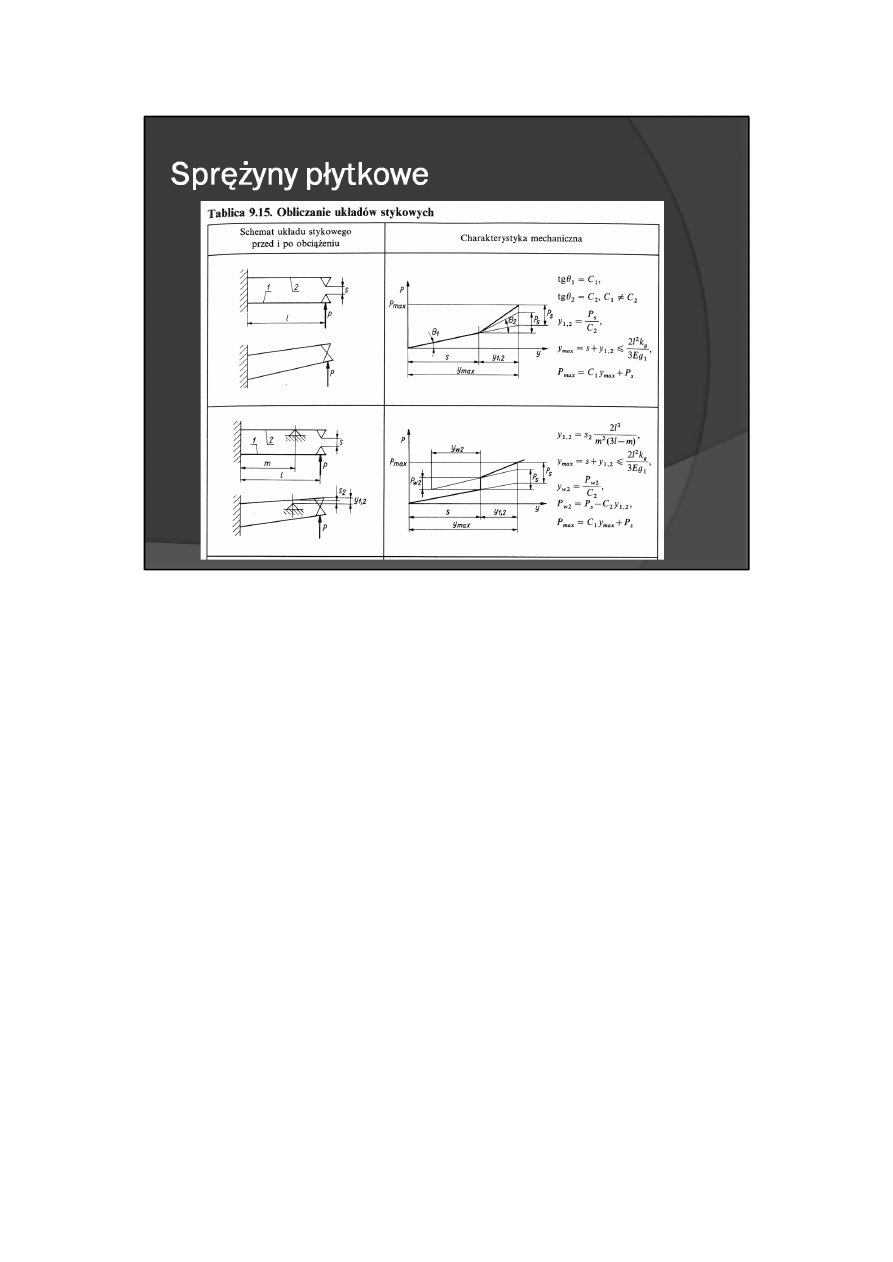
Obliczenie układu stykowego ma charakter sprawdzający i powinno umożliwić narysowanie

charakterystyki mechanicznej układu stykowego. Charakterystyka ta informuje o przemieszczeniach

styczek oraz siłach, jakie musi dostarczyć urządzenie sterujące układem stykowym, aby zapewnić żądany

nacisk stykowy. Zależności do obliczania układów stykowych oraz ich charakterystyki mechaniczne

przedstawiono w tabl. 9.15.

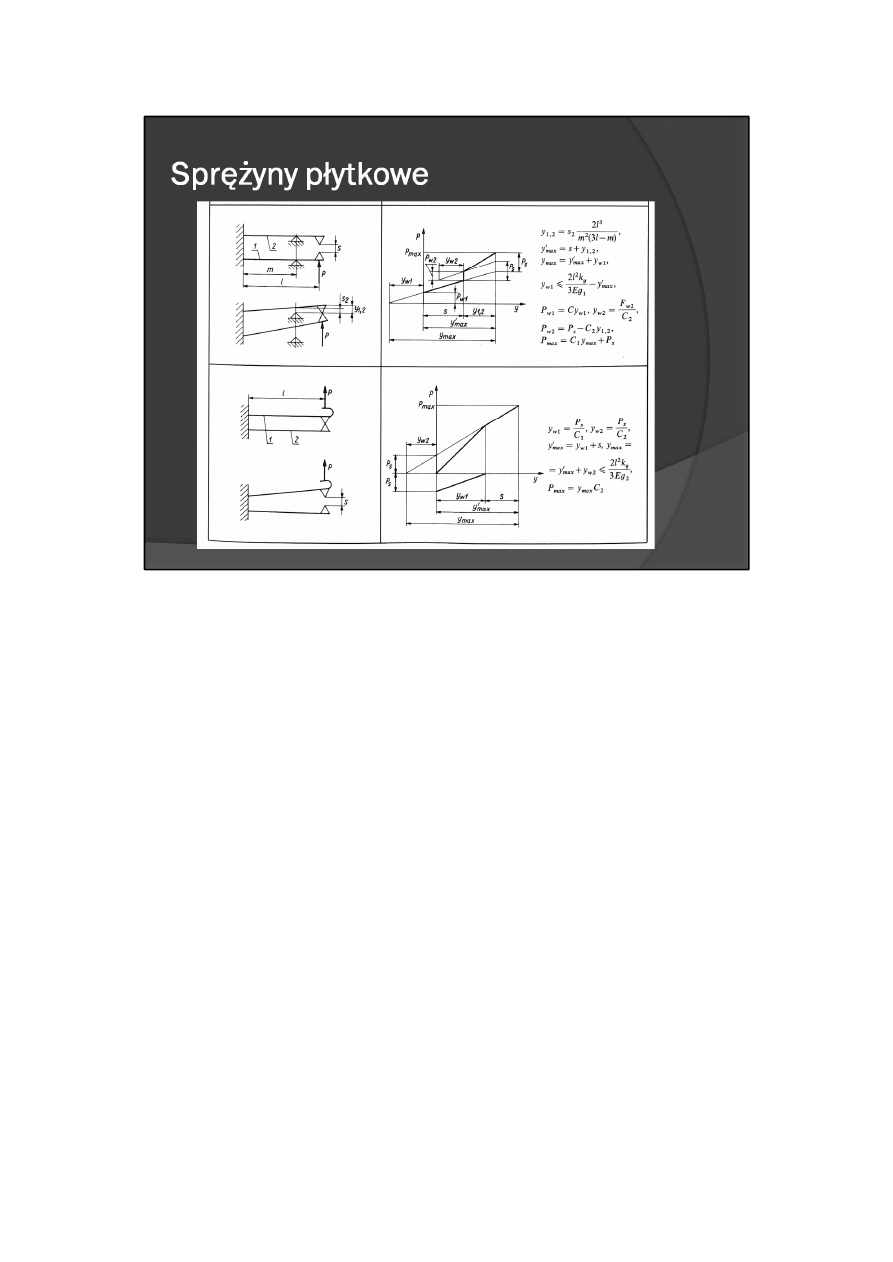
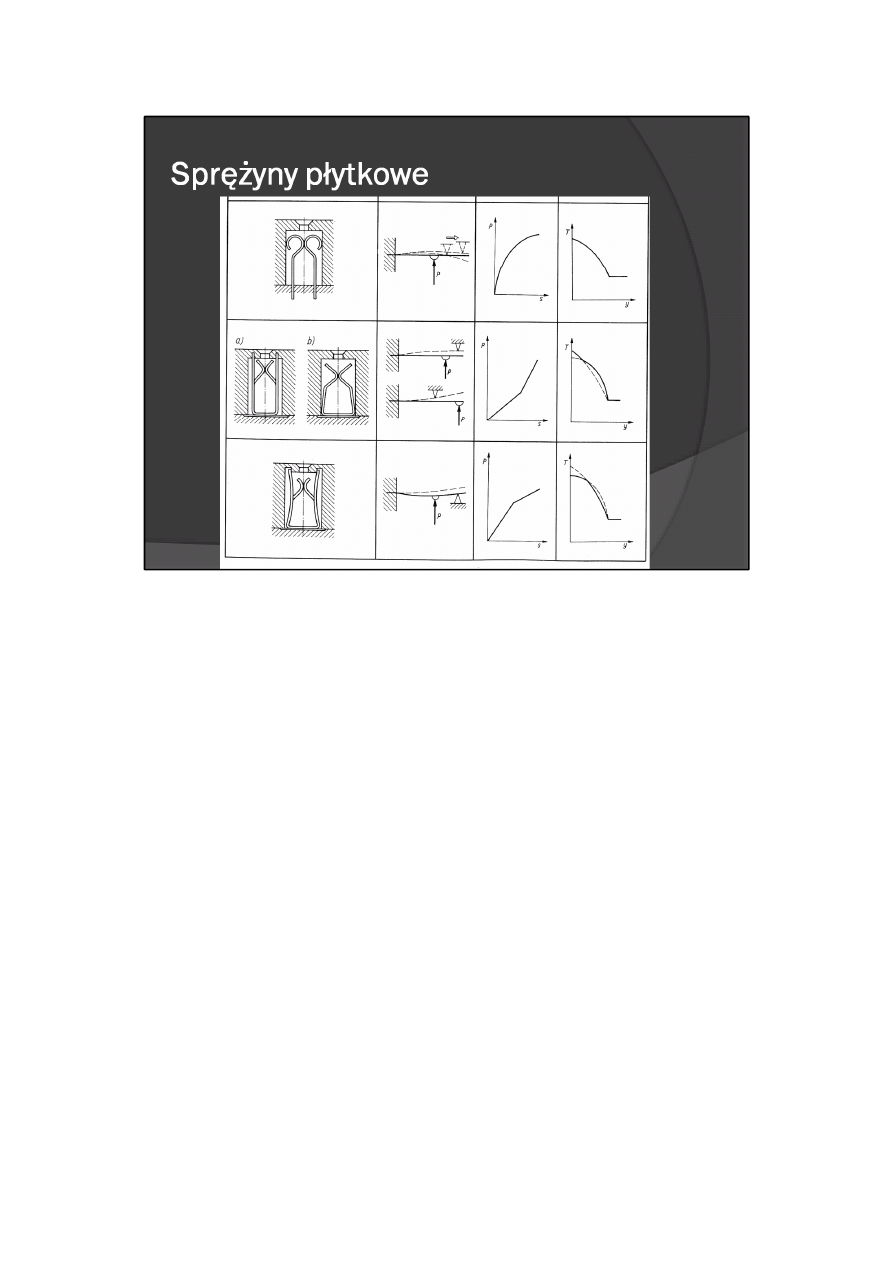
Stykowe elementy sprężynujące są również stosowane we wtykach elektrycznych. Najczęściej spotykane

kształty takich elementów z zaznaczeniem sposobu ich wbudowania w korpus wtyku, uproszczone

schematy do wyznaczania ich charakterystyk, poglądowe charakterystyki P = f(s) oraz poglądowe przebiegi

sił wtykania noża w funkcji jego przemieszczenia T= f(y) podano w tabl. 9.16 (s przemieszczenie końca

sprężyny).

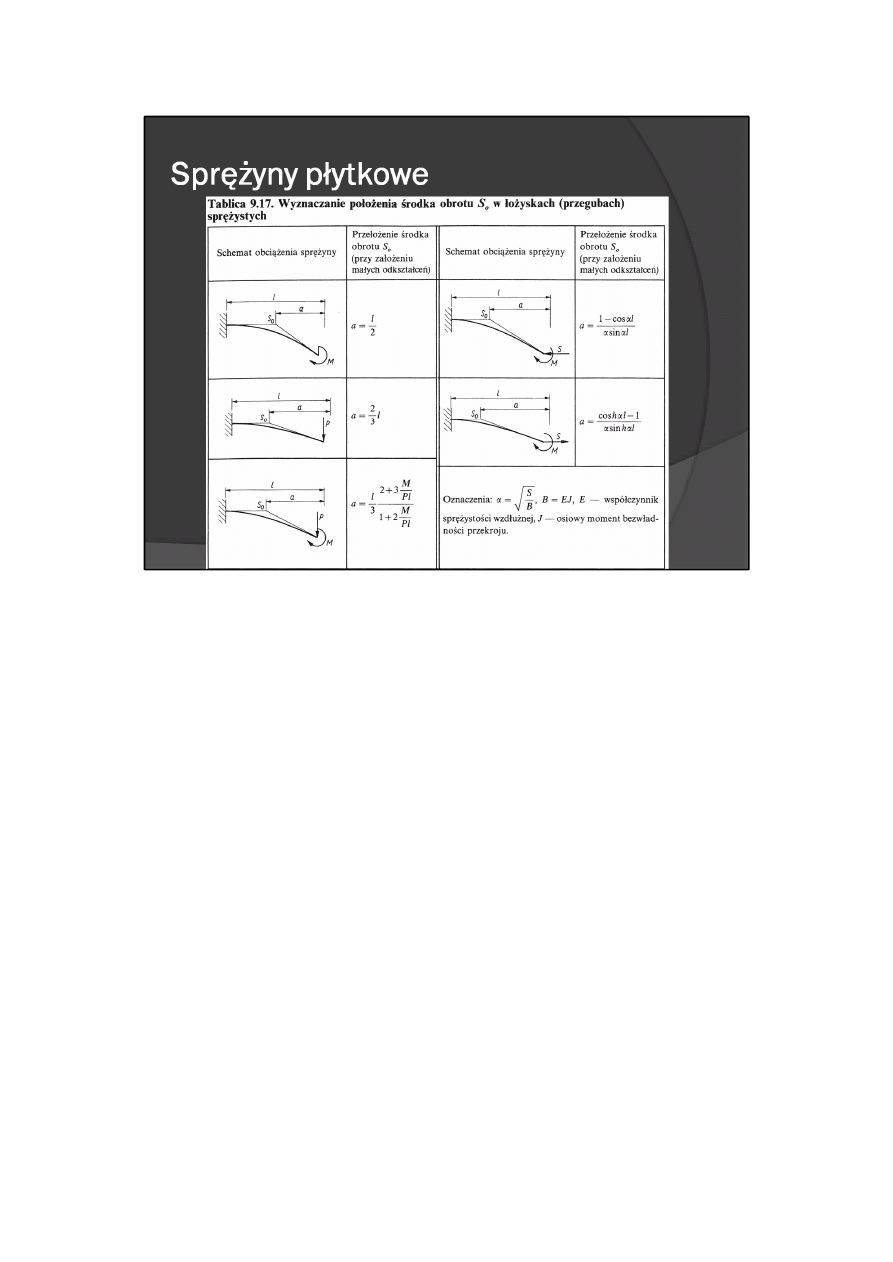
Sprężyny do sprężystych łożyskowań i prowadzeń

Zginane sprężyny, zamocowane wspornikowo, przy małych odkształceniach zachowują w przybliżeniu

stałe położenie środka obrotu S

zamocowanego na nich elementu. Dzięki tej właściwości sprężyny te

spełniają rolę łożyska sprężystego. Położenie środka obrotu sprężyn przy różnych obciążeniach podano w

tabl. 9.17.

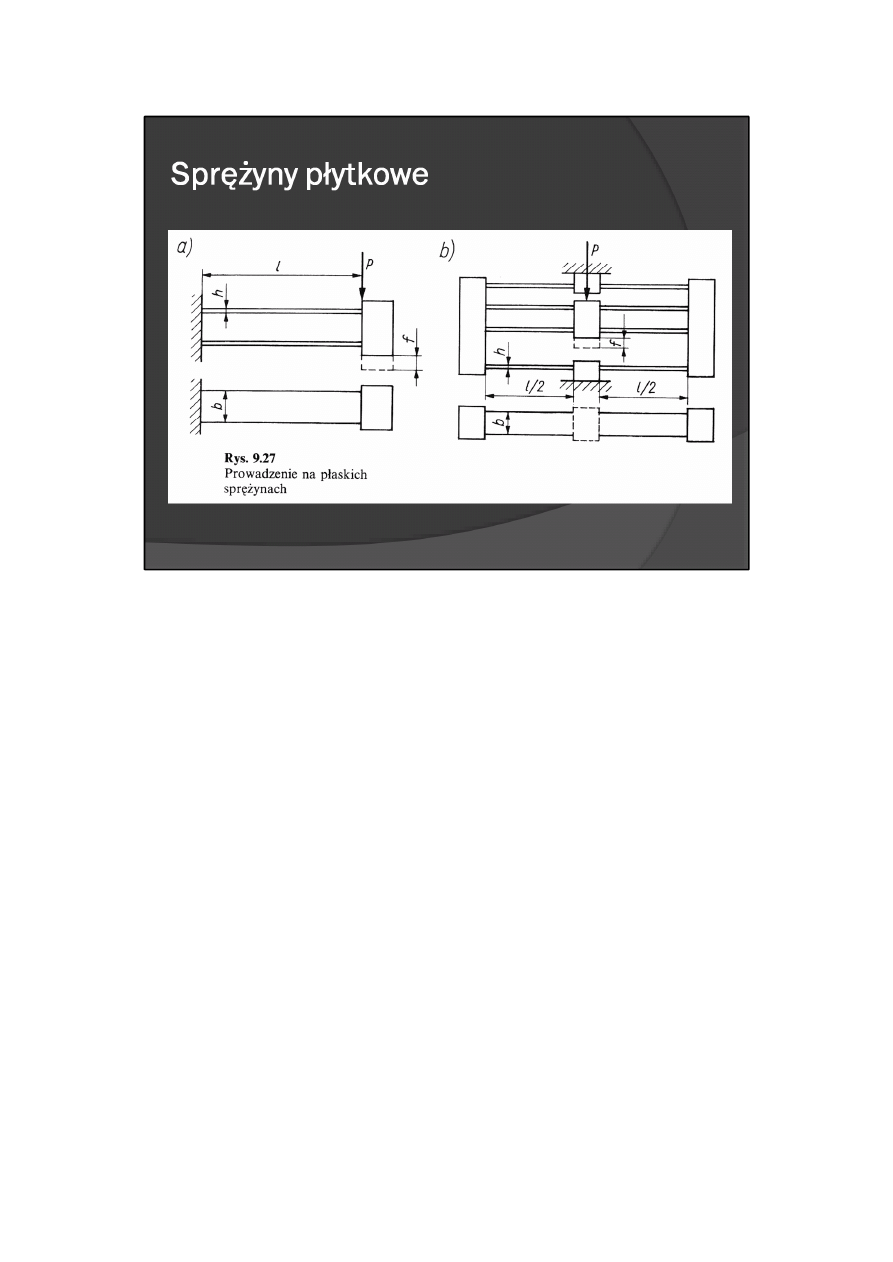
Przykład prowadzenia na sprężynach płaskich przedstawiono na rys. 9.27.

Termobimetale

Termobimetale są to elementy sprężynujące wykonywane w kształcie płytek lub taśm, składające się z

dwóch warstw metali o różnych współczynnikach rozszerzalności cieplnej, połączonych ze sobą przez ich

zgrzanie lub zlutowanie. Ogrzanie termobimetalu powoduje większe wydłużenie cieplne warstwy

wykonanej z materiału o większym współczynniku rozszerzalności cieplnej (tzw. warstwy czynnej) niż

warstwy o mniejszym współczynniku (tzw. warstwy biernej). Wskutek tego następuje wygięcie

termobimetalu w kierunku warstwy biernej.

Termobimetale stosuje się najczęściej:

- w urządzeniach do pomiaru temperatury,

- jako czujniki temperatury w urządzeniach termoregulacyjnych,

- w urządzeniach kompensujących zmiany długości, siły, przełożenia itp. powodowane zmianami

temperatury,

- w zabezpieczeniach nadmiarowo-prądowych i układach zwłocznych, w których odkształcenie

termobimetalu następuje wskutek jego bezpośredniego lub pośredniego nagrzewania płynącym prądem.

Termobimetale

Termobimetale są to elementy sprężynujące wykonywane w kształcie płytek lub taśm, składające się z

dwóch warstw metali o różnych współczynnikach rozszerzalności cieplnej, połączonych ze sobą przez ich

zgrzanie lub zlutowanie. Ogrzanie termobimetalu powoduje większe wydłużenie cieplne warstwy

wykonanej z materiału o większym współczynniku rozszerzalności cieplnej (tzw. warstwy czynnej) niż

warstwy o mniejszym współczynniku (tzw. warstwy biernej). Wskutek tego następuje wygięcie

termobimetalu w kierunku warstwy biernej.

Termobimetale stosuje się najczęściej:

- w urządzeniach do pomiaru temperatury,

- jako czujniki temperatury w urządzeniach termoregulacyjnych,

- w urządzeniach kompensujących zmiany długości, siły, przełożenia itp. powodowane zmianami

temperatury,

-w zabezpieczeniach nadmiarowo-prądowych i układach zwłocznych, w których odkształcenie

termobimetalu następuje wskutek jego bezpośredniego lub pośredniego nagrzewania płynącym prądem.

Żądane odkształcenie termobimetalu można uzyskać przez odpowiednie jego ukształtowanie.

Na skutek podgrzania termobimetalu powstają w nim naprężenia o rozkładzie pokazanym na rys. 9.29a.

W przypadku obciążenia termobimetalu zewnętrznym momentem zginającym M, rozkład naprężeń ma

przebieg przedstawiony na rys. 9.29b. W termobimetalu normalnym oś obojętna pokrywa się z miejscem

połączenia warstw. Przy jednoczesnym obciążeniu termobimetalu temperaturą i momentem

zewnętrznym naprężenia sumują się.

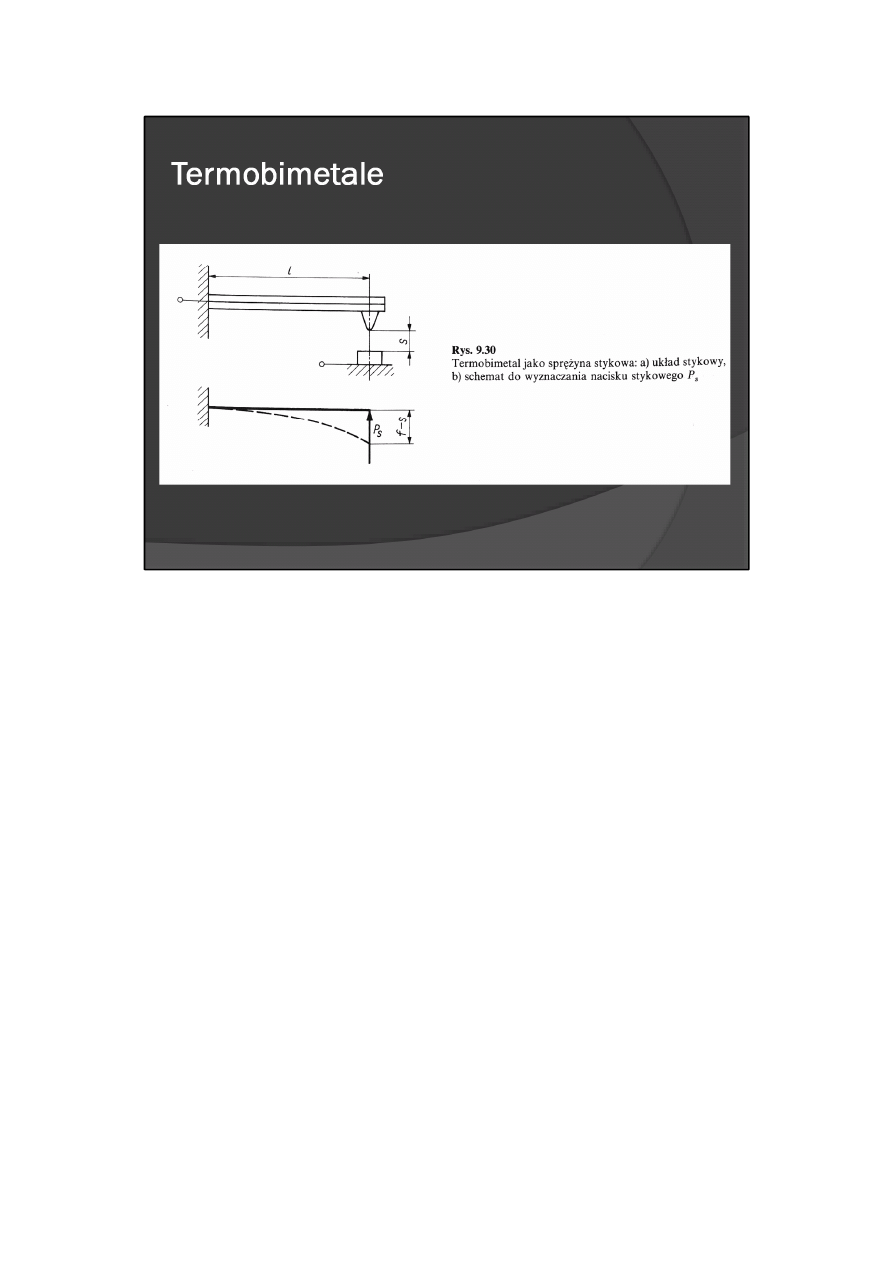
Największe naprężenia w termobimetalu występują na powierzchni łączenia warstw lub w skrajnych

włóknach. Powyższy przypadek zachodzi np. przy wykorzystaniu termobimetalu zastosowanego w

układzie stykowym do zwierania obwodu elektrycznego (rys. 9.30).

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron