05.03.2013
1
Pracownia Chemometrii Środowiska
dr hab. Tomasz Puzyn, prof. UG
Pracownia Chemometrii Środowiska
e-mail:
t.puzyn@qsar.eu.org
tel. (58) 523 54 51
Pracownia Chemometrii Środowiska
2
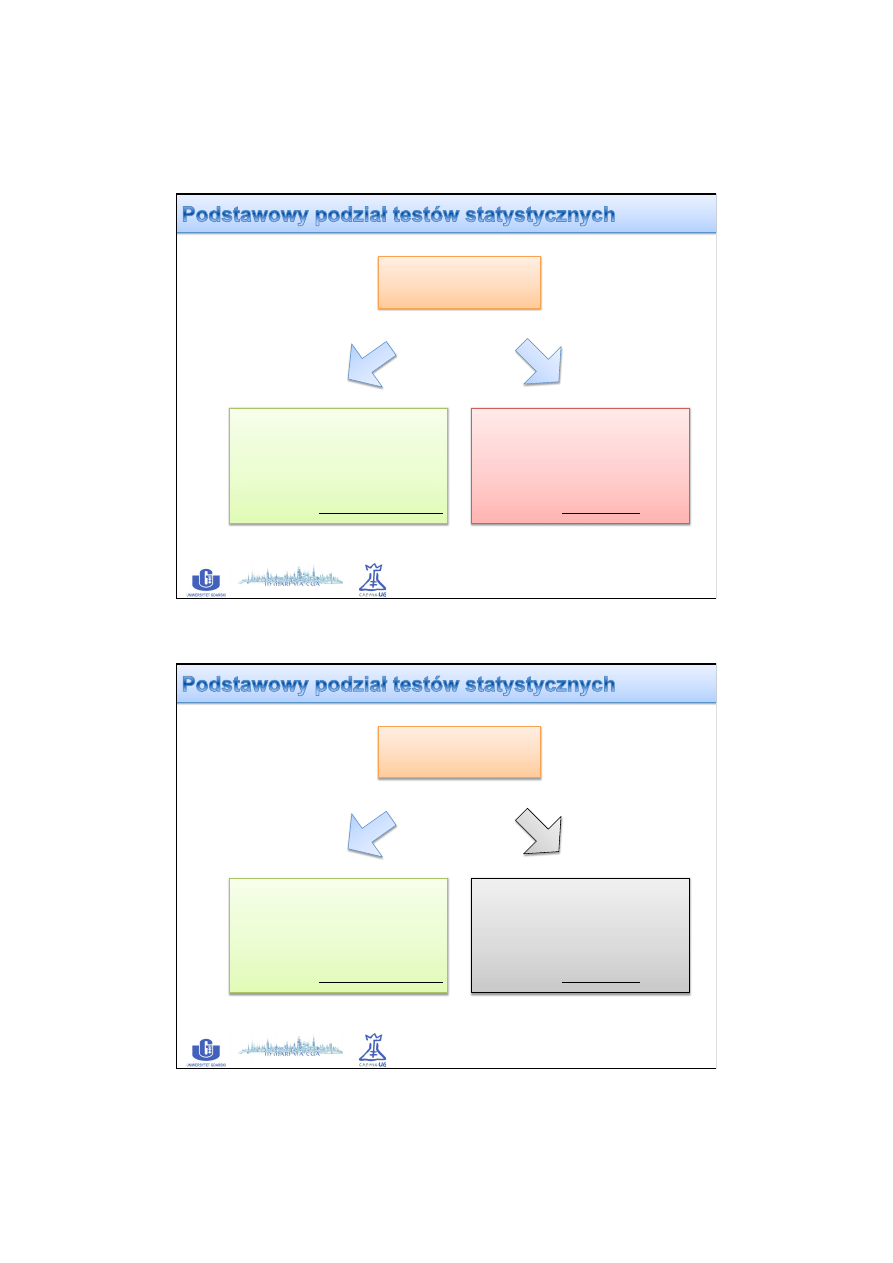
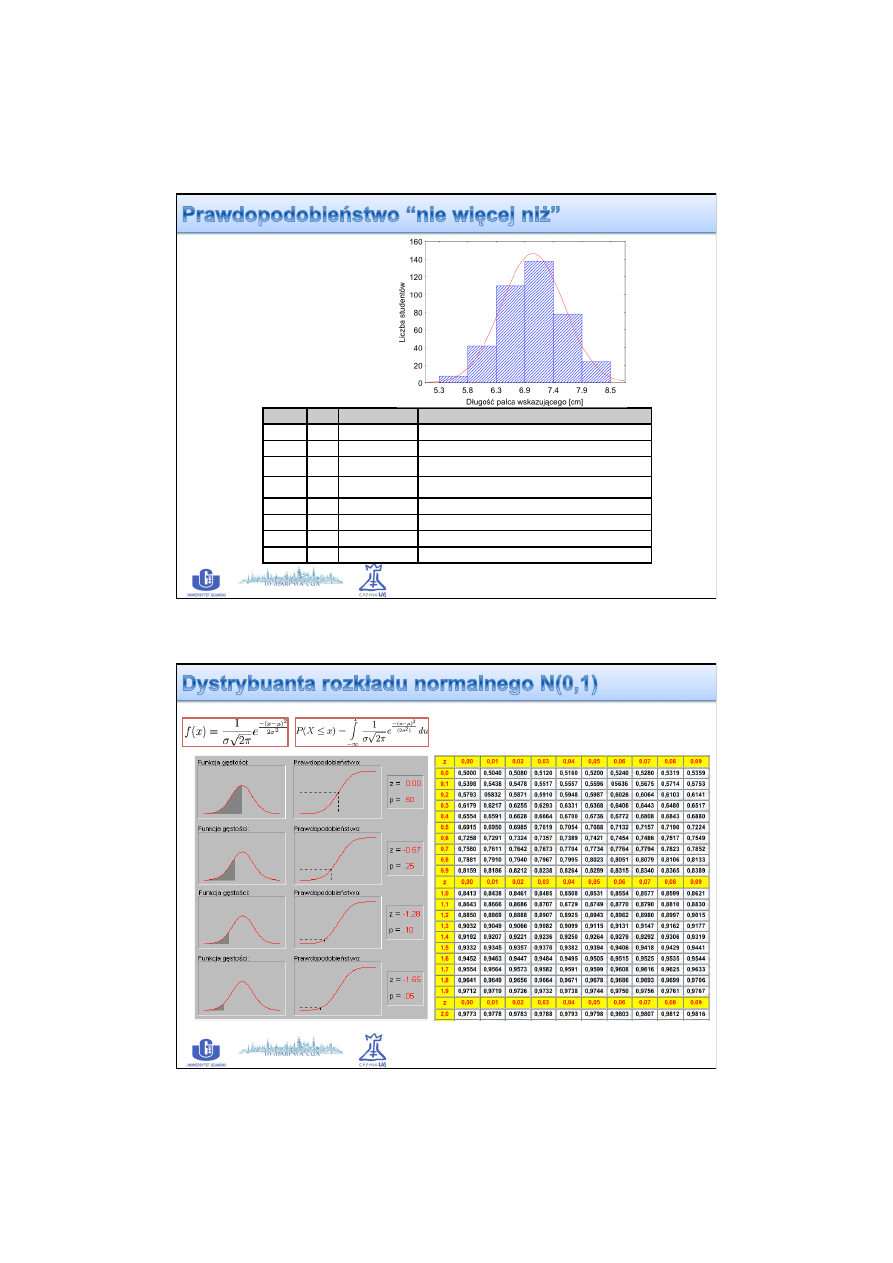
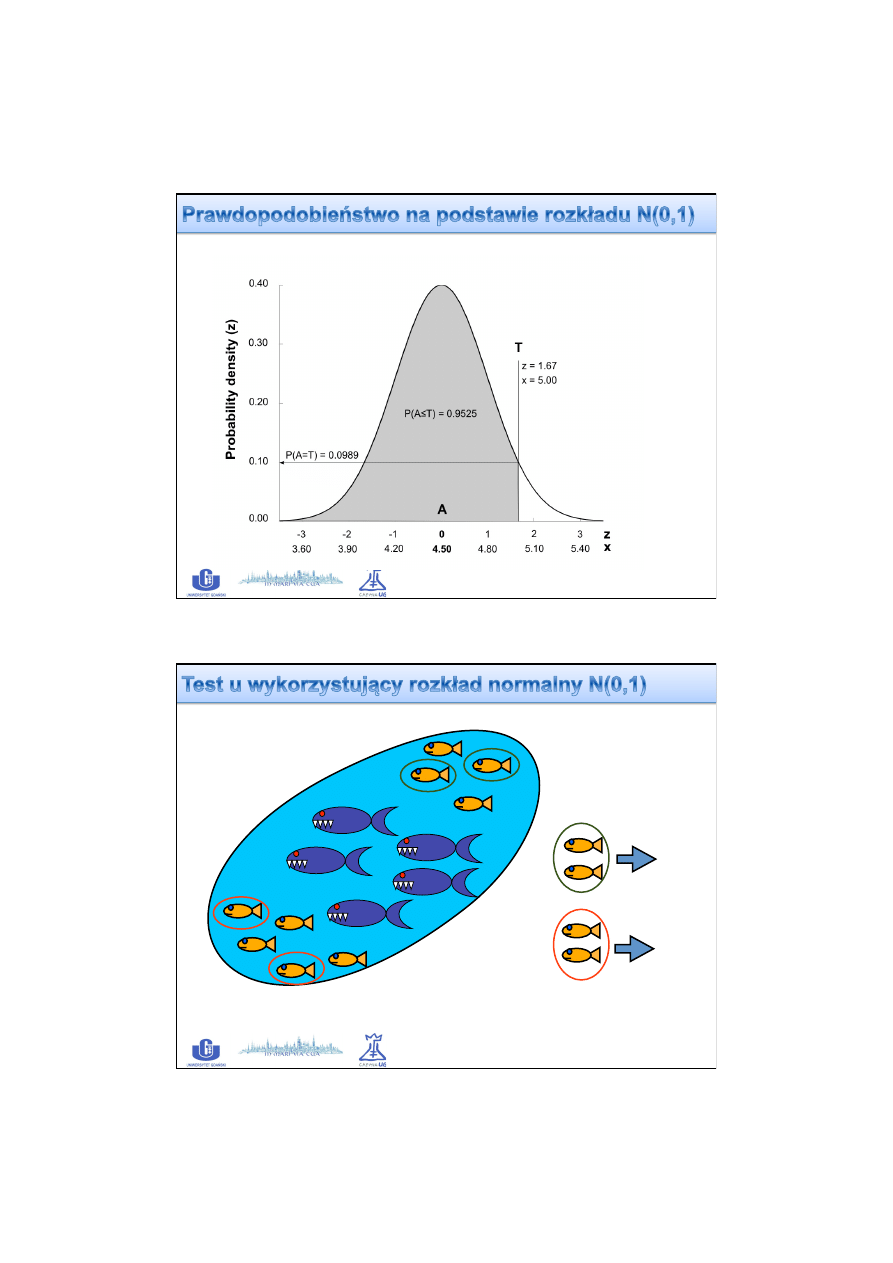
Standaryzowana wartość mierzonej cechy (x)
f(x) -‐
G
ęs
to
ść
p
raw
do
po
do
bi
eń
stw
a
σ -‐ odchylenie standardowe
μ -‐ średnia arytmetyczna
05.03.2013
2
Pracownia Chemometrii Środowiska
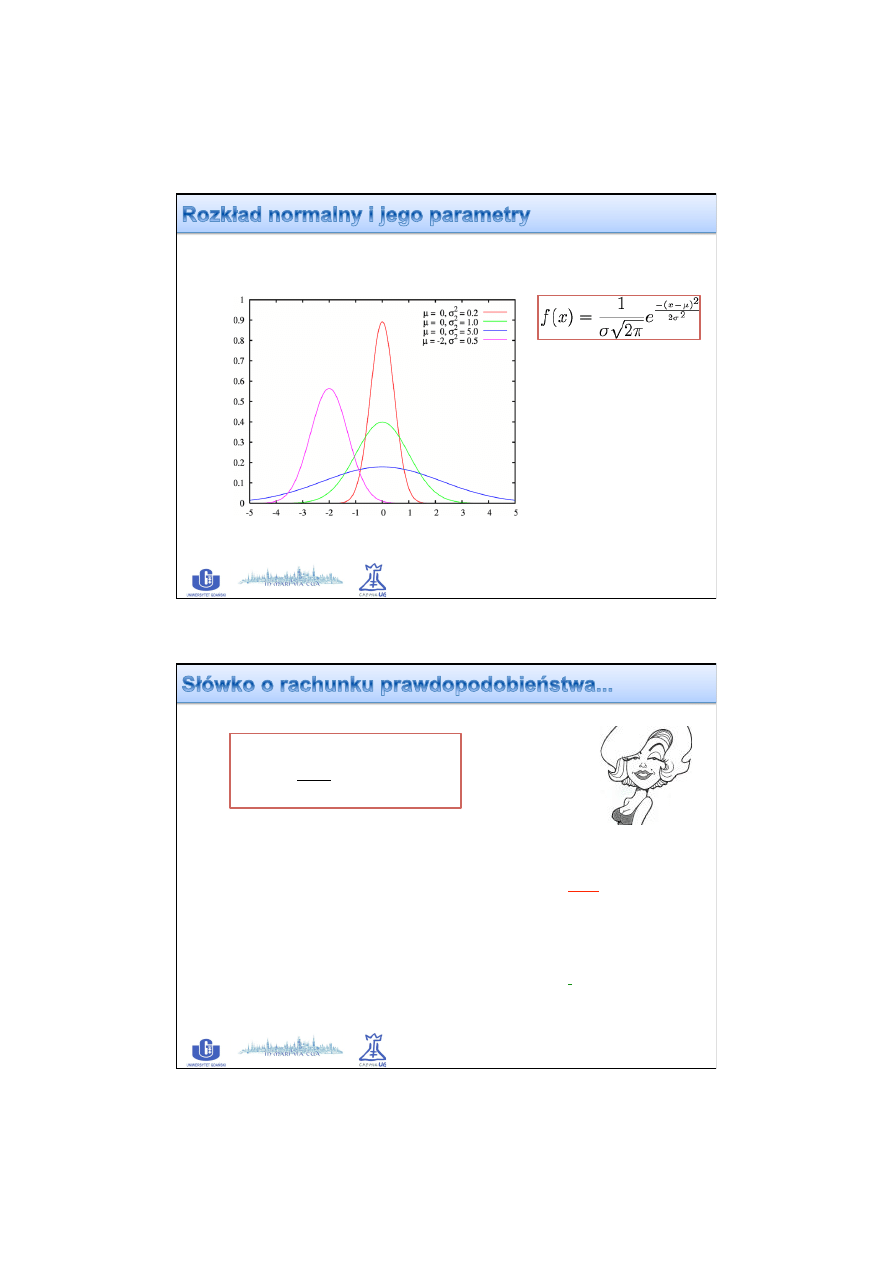
Testy statystyczne
Testy parametryczne
Zakładamy, że próby pochodzą z
populacji o rozkładzie normalnym,
porównujemy parametry rozkładów.
Testy nieparametryczne
Nie pytamy czy próby pochodzą z
populacji o rozkładzie normalnym,
porównujemy całe rozkłady.
3
Pracownia Chemometrii Środowiska
Testy statystyczne
Testy parametryczne
Zakładamy, że próby pochodzą z
populacji o rozkładzie normalnym,
porównujemy parametry rozkładów.
Testy nieparametryczne
Nie pytamy czy próby pochodzą z
populacji o rozkładzie normalnym,
porównujemy całe rozkłady.
4
05.03.2013
3
Pracownia Chemometrii Środowiska
5
Standaryzowana wartość mierzonej cechy (x)
f(x) -‐
G
ęs
to
ść
p
raw
do
po
do
bi
eń
stw
a
Pracownia Chemometrii Środowiska
P(A)
=
n(A)
n
P(A
albo
B)=P(A)
+
P(B)
P(A
i
B)=P(A)
x
P(B)
Prawdopodobieństwo
alternatywy
wykluczających się zdarzeń:
Prawdopodobieństwo
koniunkcji
zdarzeń niezależnych:
Definicja prawdopodobieństwa:
0 ≤ P(A) ≤ 1
Ma włosy blond
albo
rude.
Ma włosy blond
i
jest kobietą
.
6
05.03.2013
4
Pracownia Chemometrii Środowiska
Zakres
n
P(A)
Σ
P(A)
< 5,3
0
0/400 = 0
0/400 = 0
[5,3; 5,8)
6
6/400 = 0,02
0/400 + 6/400 = 0,2
[5,8; 6,3)
41 41/400 = 0,10
0/400 + 6/400 + 41/400 = 0,12
[6,3; 6,9) 114 114/400 = 0,28
0/400 + 6/400 + 41/400 + 114/400 =0,40
[6,9; 7,4) 139 139/400 = 0,35
...
[7,4; 7,9)
78 78/400 = 0,20
...
[7,9; 8,5)
22 22/400 = 0,06
...
8,5 ≥
0
0/400 = 0
...
n = 400
m = 7,0
s = 0,58
7
Pracownia Chemometrii Środowiska
8
Źródło: www.statsoft.pl
Wartości dystrybuanty
05.03.2013
5
Pracownia Chemometrii Środowiska
9
Pracownia Chemometrii Środowiska
m
1
s
1
n
1
m
2
s
2
n
2
µ
1
σ
2
10
µ
2
σ
2
05.03.2013
6
Pracownia Chemometrii Środowiska
11
m
1
s
1
n
1
m
2
s
2
n
2
Jeżeli z populacji o jakimkolwiek rozkładzie ze
średnią µ
i
odchyleniem standardowym σ
pobieramy
próby o dużej liczebności
, to rozkład średnich z tych prób będzie
rozkładem
normalnym
o
średniej µ
i
odchyleniu s
X
=σ/√n
Wielkość
s
X
= σ/√n
nazywana jest
błędem standardowym
i opisuje odchylenie średnich
z prób od średniej z populacji (nie mylić z odchyleniami pojedynczych pomiarów!).
Rozkład normalny
u-3Sx
u-2Sx
u-1Sx
u
u+1Sx
u+2Sx
u+3Sx
0.0
0.2
0.4
0.6
Dystrybuanta
u-3Sx
u-2Sx
u-1Sx
u
u+1Sx
u+2Sx
u+3Sx
0.0
0.2
0.4
0.6
0.8
1.0
Pracownia Chemometrii Środowiska
m
1
s
1
n
1
m
2
s
2
n
2
12
Warunek!
Próby są liczne (n
1
i n
2
>> 30
)
oraz
odchylenia
standardowe w obu populacjach generalnych
(
σ
1
i σ
2
)
są znane.
H
0
: µ
1
= µ
2
H
A
: µ
1
≠
m
2
lub µ
1
<
µ
2
lub µ
1
>
µ
2
• Jeżeli u < u
kr
=> nie ma podstaw do odrzucenia H
0
na założonym poziomie
istotności.
• Jeżeli u ≥ u
kr
=> H
0
należy odrzucić na założonym poziomie istotności i przyjąć H
A.
u
=
m
1
− m
2
σ
1
2
n
1
+ σ
2
2
n
2
05.03.2013
7
Pracownia Chemometrii Środowiska
13
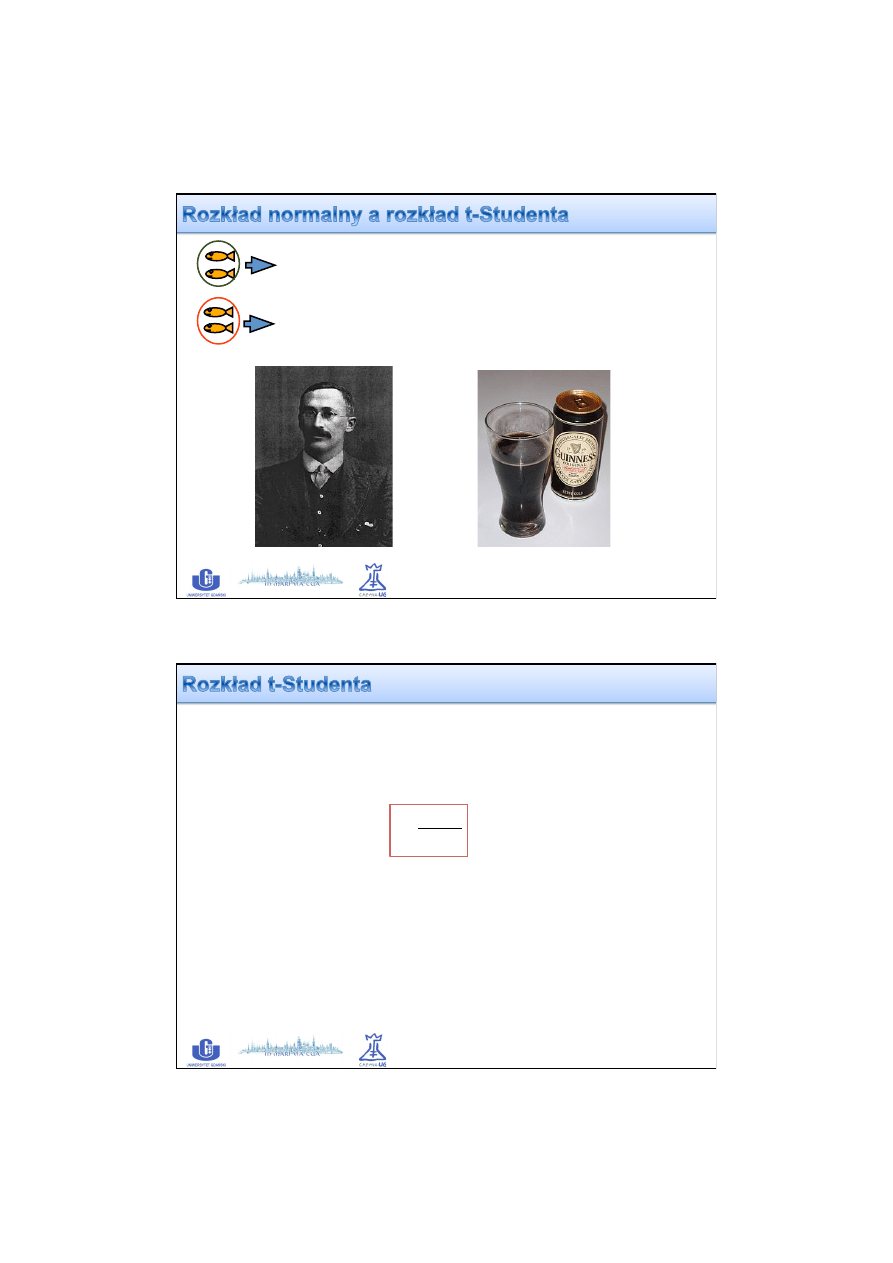
Rozkład gęstości prawdopodobieństwa N(0,1)
-3
-2
-1
0
1
2
3
0.0
0.2
0.4
0.6
1 - Dystrybuanta N(0,1)
-3.4 -2.6 -1.8 -1.0 -0.2 0.6 1.4 2.2 3.0
0.0
0.2
0.4
0.6
0.8
1.0
Obszar krytyczny
u
kr
= 1.64
u
p
α = 0.05
Pracownia Chemometrii Środowiska
14
Rozkład gęstości prawdopodobieństwa N(0,1)
-3
-2
-1
0
1
2
3
0.0
0.2
0.4
0.6
2 x [1 - Dystrybuanta N(0,1)]
-3.4 -2.6 -1.8 -1.0 -0.2 0.6 1.4 2.2 3.0
0.0
0.2
0.4
0.6
0.8
1.0
Obszar krytyczny
u
p
u
kr
= 1.96
Obszar krytyczny
α = 0.05 / 2
u
kr
= -1.96
05.03.2013
8
Pracownia Chemometrii Środowiska
Problem?
Co zrobić jeśli
próby są niewielkie
i potrafimy
obliczyć jedynie
odchylenia standardowe z prób
?
15
m
1
s
1
n
1
m
2
s
2
n
2
William S. Gosset
(1876-1937)
Pracownia Chemometrii Środowiska
16
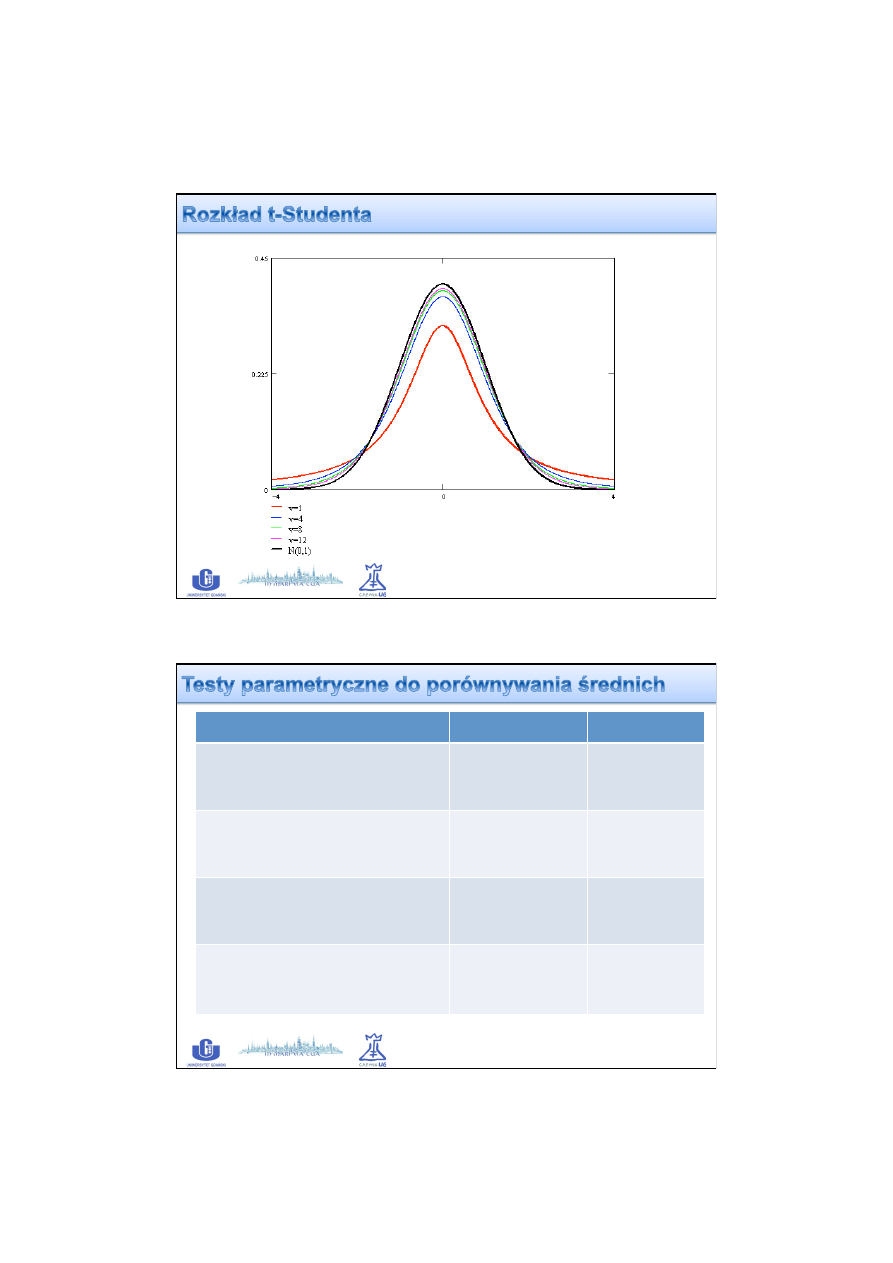
Jeżeli
z populacji generalnej o rozkładzie normalnym
pobieramy
próby
n-elementowe
, to dla każdej takiej próby można obliczyć
statystykę t
:
t
=
m
−
µ
s
X
Rozkład wartości t dla tych prób będzie zgodny z teoretycznym
rozkładem
t-Studenta
a
jedynym parametrem tego rozkładu będzie
liczba stopni swobody
v = n-1
.
Krzywa jest spłaszczona dla prób małolicznych;
ze wzrostem liczebności kształt
krzywej dąży do rozkładu normalnego
.
05.03.2013
9
Pracownia Chemometrii Środowiska
17
Pracownia Chemometrii Środowiska
Co porównujemy?
Dodatkowe warunki Nazwa testu
Porównujemy dwa wyniki badań (dwie
średnie) między sobą:
H
0
: µ
1
= µ
2
równe wariancje w
obydwu rozkładach
σ
2
1
= σ
2
2
test t-Studenta
(dla prób
niezależnych)
Porównujemy dwa wyniki badań (dwie
średnie) między sobą:
H
0
: µ
1
= µ
2
wariancje w obydwu
rozkładach różnią się
σ
2
1
≠ σ
2
2
test C-Cochrana i
Coxa
Porównujemy wynik badań (średnią) z
wartością odniesienia:
H
0
: µ = µ
0
brak
test t-Studenta
(dla średniej)
Sprawdzamy, czy różnice w parach
odpowiadających sobie wyników nie są
różne od zera:
H
0
: µ
Δ
= 0
występowanie tzw.
par wiązanych
test t-Studenta
(dla prób
zależnych lub
par wiązanych)
18

05.03.2013
10
Pracownia Chemometrii Środowiska
t
=
m
1
− m
2
(n
1
− 1)⋅ s
1
2
+ (n
2
− 1)⋅ s
2
2
⋅
n
1
⋅ n
2
(n
1
+ n
2
− 2)
n
1
+ n
2
t
=
m
1
− m
2
s
1
2
+ s
2
2
⋅ n
n
1
≠ n
2
n
1
= n
2
= n
• Jeżeli t < t
kr
=> nie ma podstaw do odrzucenia H
0
na założonym poziomie
istotności.
• Jeżeli t ≥ t
kr
=> H
0
należy odrzucić na założonym poziomie istotności i przyjąć H
A.
df
= n
1
+ n
2
− 2
19
H
0
: µ
1
= µ
2
H
A
: µ
1
≠
m
2
lub µ
1
<
µ
2
lub µ
1
>
µ
2
Pracownia Chemometrii Środowiska
Zespół Instytutu Chemii Spożywczej opracował nową metodę oznaczania stężenia
Ca
2+
(mg/dm
3
) w próbkach wody mineralnej. W celu potwierdzenia dokładności
nowej metody została ona porównana z metodą referencyjną. Uzyskane wyniki
(kilkukrotne powtórzenia pomiarów obiema metodami) zostały zestawione poniżej.
Należy sprawdzić, czy obie metody istotnie się różnią dokładnością.
Nowa:
19,8 20,1 19,9 20,0 19,8 20,1 19,8
m
N
= 19,93
s
N
= 0,14
Referencyjna:
19,9 20,2 20,0 20,3 20,1 19,8 20,1
m
R
= 20,06
s
R
= 0,17
20
05.03.2013
11
Pracownia Chemometrii Środowiska
H
0
: µ
N
= µ
R
H
A
: µ
N
≠
µ
R
0.200 0.100
0.050
6
7
8
9
10
11
12
2.179
13
14
α – poziom istotności,
test dwustronny
df
–
li
czb
a
st
op
ni
sw
ob
od
y
df
= 7 + 7 − 2 = 12
t
=
m
N
− m
R
s
N
2
+ s
R
2
⋅ n =
19, 93
− 20,06
0, 0196
+ 0,0289
⋅ 7 = 1,56
21
Pracownia Chemometrii Środowiska
22
Rozkład gęstości prawdopodobieństwa (df = 12)
-3
-2
-1
0
1
2
3
0.0
0.2
0.4
2 x [1 - Dystrybuanta (df = 12)]
-3.4 -2.6 -1.8 -1.0 -0.2 0.6 1.4 2.2 3.0
0.0
0.2
0.4
0.6
0.8
1.0
Obszar krytyczny
t = 1.56
α = 0.05 / 2
t
kr
= 2.179
t
kr
= 2.179
p = 0.15 / 2
Obszar krytyczny
α = 0.05 / 2
t = -1.56
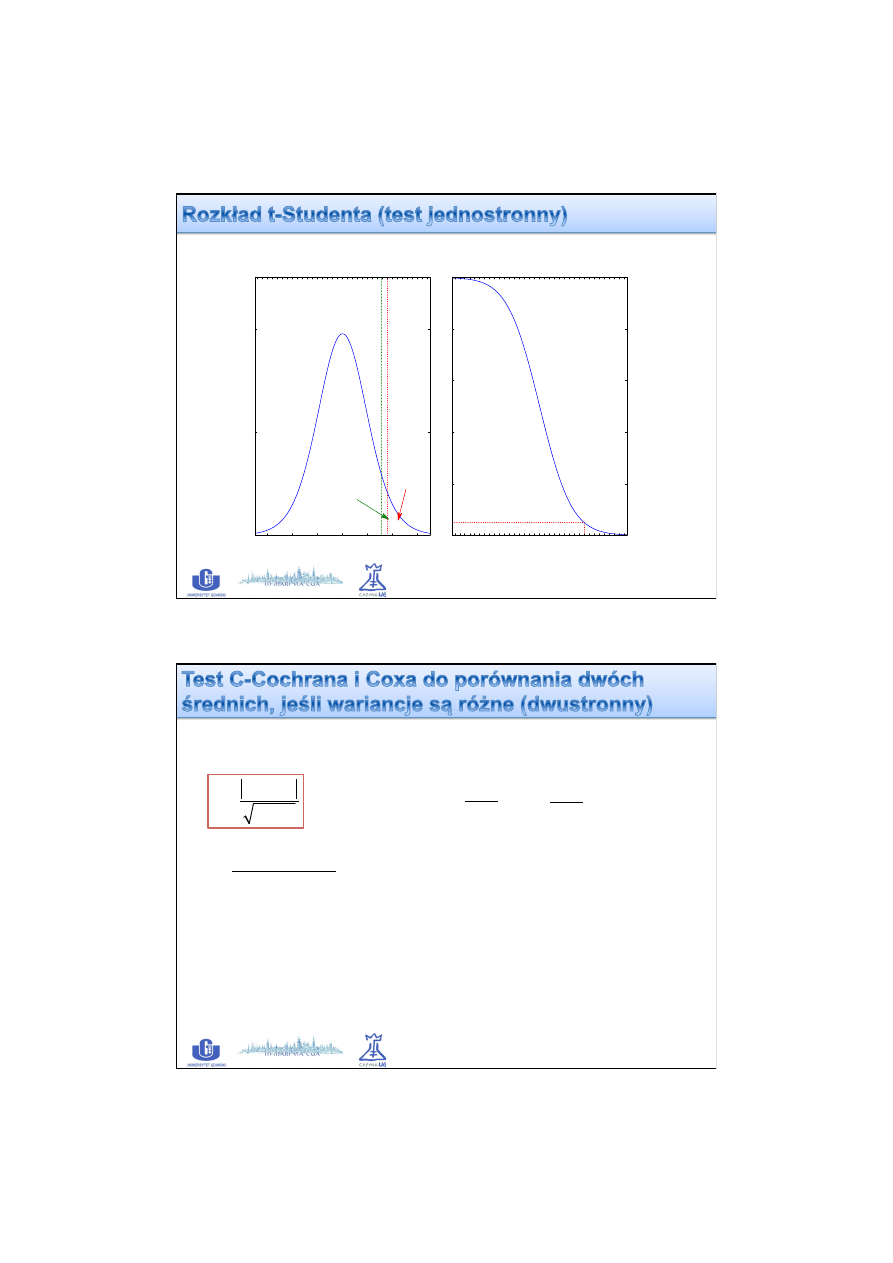
05.03.2013
12
Pracownia Chemometrii Środowiska
23
Rozkład gęstości prawdopodobieństwa (df = 12)
-3
-2
-1
0
1
2
3
0.0
0.2
0.4
1 - Dystrybuanta (df = 12)
-3.4 -2.6 -1.8 -1.0 -0.2 0.6 1.4 2.2 3.0
0.0
0.2
0.4
0.6
0.8
1.0
t
kr
= 1.782
t = 1.56
Obszar krytyczny
α = 0.05
p = 0.07
Pracownia Chemometrii Środowiska
H
0
: µ
N
= µ
R
H
A
: µ
N
≠
µ
R
C
=
m
1
− m
2
z
1
+ z
2
z
1
=
s
1
2
n
1
− 1
z
2
=
s
2
2
n
2
− 1
C
kr
z
1
⋅t
kr,1
+ z
2
⋅t
kr,2
z
1
+ z
2
• Jeżeli C < C
kr
=> nie ma podstaw do odrzucenia H
0
na założonym poziomie
istotności.
• Jeżeli C ≥ C
kr
=> H
0
należy odrzucić na założonym poziomie istotności i przyjąć H
A.
df
2
= n
2
− 1
df
1
= n
1
− 1
24
05.03.2013
13
Pracownia Chemometrii Środowiska
Sprawdzono biegłość pewnego laboranta zlecając mu analizę certyfikowanego
materiału odniesienia. Wartość certyfikowana wynosiła 20,0 mg/kg, natomiast
wartości zmierzone przez niego (osiem powtórzeń) były równe odpowiednio:
19,8 20,1 19,9 20,0 19,8 20,1 19,8 19,7. Czy na poziomie istotności α = 0,05
wynik otrzymany przez laboranta różni się od wartości certyfikowanej?
µ
0
= 20,0 mg/kg
µ = 19,9 mg/kg
s = 0,15 mg/kg
n = 8
df = n-1 = 7
s
x
= s/√n = 0,15/2,83 = 0,053
H
0
: µ = µ
0
H
A
: µ ≠ µ
0
0.200 0.100
0.050
1 3.078
6.314
12.706
2 1.886
2.920
4.303
3 1.638
2.353
3.182
4 1.533
2.132
2.776
5 1.476
2.015
2.571
6 1.440
1.943
2.447
7 1.415
1.895
2.365
8 1.397
1.860
2.306
9 1.383
1.833
2.262
α – poziom istotności,
test dwustronny
df
–
liczb
a
st
op
ni
sw
ob
od
y
Odp.: Na poziomie α = 0,05 nie różnią się.
25
t
=
m
−
µ
0
s
x
t
=
m
−
µ
0
s
x
=
0,1
0,053
= 1,89
Pracownia Chemometrii Środowiska
Zbadano czy stężenie rtęci w tkance tłuszczowej ryb pewnego gatunku przekracza
dopuszczalną normę (norma wynosi 19,8 mg/kg lipidów). Wartości zmierzone
(osiem próbek) były równe odpowiednio: 19,8 20,1 19,9 20,0 19,8 20,1 19,8
19,7. Czy na poziomie istotności α = 0,05 norma została przekroczona?
µ
0
= 19,8 mg/kg
µ = 19,9 mg/kg
s = 0,15 mg/kg
n = 8
df = n-1 = 7
s
x
= s/√n = 0,15/2,83 = 0,053
H
0
: µ = µ
0
H
A
: µ > µ
0
0.010 0.050
0.025
1 3.078 6.314
12.706
2 1.886 2.920
4.303
3 1.638 2.353
3.182
4 1.533 2.132
2.776
5 1.476 2.015
2.571
6 1.440 1.943
2.447
7 1.415
1.895
2.365
8 1.397 1.860
2.306
9 1.383 1.833
2.262
α – poziom istotności,
test jednostronny
df
–
liczb
a
st
op
ni
sw
ob
od
y
Odp.: Na poziomie α = 0,05 norma nie została przekroczona.
26
t
=
m
−
µ
0
s
x
t
=
m
−
µ
0
s
x
=
0,1
0,053
= 1,89

05.03.2013
14
Pracownia Chemometrii Środowiska
27
df = n-1
s
x
= s
Δ
/√n
H
0
: µ
Δ
= 0
H
A
: µ
Δ
≠ 0
Seria I
Seria II
Δ
1,25
1,20
0,05
2,45
2,50
-‐0,05
3,30
3,30
0,00
4,25
4,35
-‐0,10
5,50
5,45
0,05
6,00
5,90
0,10
m
d
=
0,008
Δ – różnica pomiędzy wynikami uzyskanymi dla danej próbki w obu seriach
µ
Δ
– średnia wartość Δ
t
=
µ
Δ
− 0
s
X
Pracownia Chemometrii Środowiska
Co porównujemy?
Dodatkowe warunki Nazwa testu
Porównujemy między sobą dwie
wariancje:
H
0
: σ
2
1
= σ
2
2
brak
test F-Snedecora
Porównujemy wariancję w populacji z
wariancją „wzorcową”:
H
0
: σ
2
= σ
2
0
brak
test chi-kwadrat
28

05.03.2013
15
Pracownia Chemometrii Środowiska
Zespół Instytutu Chemii Spożywczej opracował nową metodę oznaczania
stężenia Ca
2+
(mg/dm
3
) w próbkach wody mineralnej. W celu potwierdzenia
precyzji nowej metody została ona porównana z metodą referencyjną. Uzyskane
wyniki (kilkukrotne powtórzenia pomiarów obiema metodami) zostały zestawione
poniżej. Należy sprawdzić, czy obie metody istotnie się różnią precyzją.
Nowa:
19,8 20,1 19,9 20,0 19,8 20,1 19,8
m
N
= 19,93
s
N
= 0,14
Referencyjna:
19,9 20,2 20,0 20,3 20,1 19,8 20,1
m
R
= 20,06
s
R
= 0,17
29
Pracownia Chemometrii Środowiska
H
0
: σ
N
2
= σ
R
2
H
A
: σ
N
2
< σ
R
2
(F
kr
dla α)
lub σ
N
2
≠
σ
R
2
(F
kr
dla α/2)
df
N
= n
N
- 1 = 6
df
R
= n
R
- 1 = 6
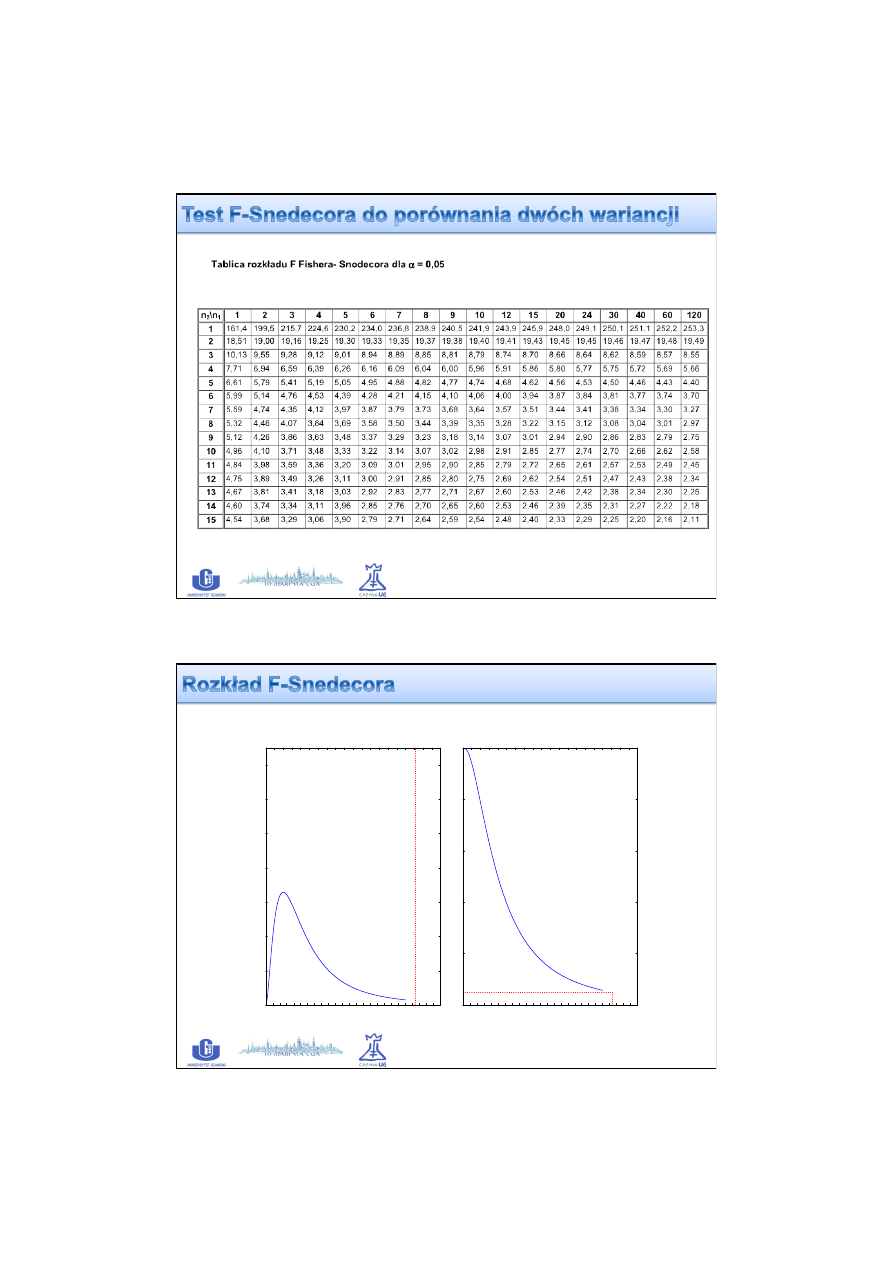
F
kr,0.05
= ?
• Jeżeli F < F
kr
=> nie ma podstaw do odrzucenia H
0
na założonym poziomie
istotności.
• Jeżeli F ≥ F
kr
=> H
0
należy odrzucić na założonym poziomie istotności i przyjąć
H
A.
F
=
s
R
2
s
M
2
=
0,17
2
0,14
2
=
0, 0289
0, 0196
= 1,47
30
F
=
s
1
2
s
2
2
s
1
2
>> s
2
2
05.03.2013
16
Pracownia Chemometrii Środowiska
df
N
= n
N
- 1 = 6
df
R
= n
R
- 1 = 6
F
0.05
= ?
31
Pracownia Chemometrii Środowiska
Rozkład F (
α = 0.05, df1 = 6, df2= 6)
0.0 0.6 1.2 1.8 2.4 3.0 3.6 4.2 4.8
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1 - Dystrybuanta
0.0 0.6 1.2 1.8 2.4 3.0 3.6 4.2 4.8
0.0
0.2
0.4
0.6
0.8
1.0
Fkr = 4.28
Obszar krytyczny
32
05.03.2013
17
Pracownia Chemometrii Środowiska
33
H
0
: σ
2
= σ
2
0
H
A
:
σ
2
> σ
2
0
(1)
lub
σ
2
< σ
2
0
(2)
lub
σ
N
2
≠
σ
R
2
(3)
χ
2
=
n
⋅s
2
σ
0
2
df = n -1
(1) χ
2
kryt
dla poziomu α
(2) χ
2
kryt
dla poziomu 1 - α
(3) χ
2
kryt1
dla poziomu 1 - α/2
χ
2
kryt2
dla poziomu α/2
(1) Odrzucamy H
0
na poziomie α jeśli χ
2
> χ
2
kryt
(2) Odrzucamy H
0
na poziomie α jeśli χ
2
< χ
2
kryt
(3) Odrzucamy H
0
na poziomie α jeśli
χ
2
kryt1
<
χ
2
lub
χ
2
<
χ
2
kryt2
Pracownia Chemometrii Środowiska
Testy statystyczne
Testy parametryczne
Zakładamy, że próby pochodzą z
populacji o rozkładzie normalnym,
porównujemy parametry rozkładów.
Testy nieparametryczne
Nie pytamy czy próby pochodzą z
populacji o rozkładzie normalnym,
porównujemy całe rozkłady.
34

05.03.2013
18
Pracownia Chemometrii Środowiska
Co porównujemy?
Dodatkowe warunki Nazwa testu
Porównujemy dwie próby między sobą
H
0
: Próba 1 = Próba 2
brak
• Test serii
(Walda-
Wolfowitza)
• Test U Manna-
Withneya
Sprawdzamy, czy różnice w parach
odpowiadających sobie wyników istotnie
różnią się od siebie
H
0
: Brak różnic w parach
występowanie tzw.
par wiązanych
Test Wilcoxona
dla par
wiązanych
35
Pracownia Chemometrii Środowiska
Pewien związek organiczny można otrzymać w drodze syntezy dwoma metodami:
A i B. W celu porównania wydajności obydwu metod kilkukrotnie przeprowadzono
syntezę metodą A i kilkukrotnie przeprowadzono syntezę metodą B. Następnie
zestawiono uzyskane wyniki (wydajność syntezy w %). Należy zweryfikować na
poziomie istotności 0,05 hipotezę zerową, że wydajności obydwu metod syntezy
się nie różnią.
Metoda A:
37 30 45 52 22 35 27 40 47 32
Metoda B:
48 57 31 53 51 64 44 61 60
36

05.03.2013
19
Pracownia Chemometrii Środowiska
Dane należy uporządkować (łącznie metody A i B), a następnie przydzielić
poszczególnym wynikom
rangi
:
37
A 22 27 30
32 35 37 40
45 47
52
1 2 3
5 6 7 8
10 11
14
B
31
44
48 51
53 57 60 61 64
4
9
12 13
15 16 17 18 19
Liczba serii r = 8 Wartość krytyczna (z tablic) dla n
1
= 10 i n
2
= 9 wynosi r
kryt
= 6
Jeżeli r < r
kryt
à
odrzucamy
hipotezę zerową (na poziomie istotności 0,05)
Jeżeli r ≥ r
kryt
à nie mamy podstaw do odrzucenia hipotezy zerowej
Pracownia Chemometrii Środowiska
Dane należy uporządkować (łącznie metody A i B), a następnie przydzielić
poszczególnym wynikom
rangi
:
38
A 1 2 3
5 6 7 8
10 11
14
B
4
9
12 13
15 16 17 18 19
U
A
= 9 + 9 + 9 + 8 + 8 + 8 + 8 + 7 + 7 + 5 = 78
U
B
= 7 + 3 + 1 + 1 + 0 + 0 + 0 + 0 + 0 = 12
U
min
= U
B
Wartość krytyczna (z tablic) dla n
1
= 10 i n
2
= 9 wynosi U
kryt
= 20
Jeżeli U
min
< U
kryt
à
odrzucamy
hipotezę zerową (na poziomie istotności 0,05)
Jeżeli U
min
≥ U
kryt
à nie mamy podstaw do odrzucenia hipotezy zerowej
rangi wiązane (te same i różne próby)

05.03.2013
20
Pracownia Chemometrii Środowiska
W celu sprawdzenia skuteczności pewnego
pestycydu wybrano 11 par poletek na łące i
przeprowadzono doświadczenie polegające na
zastosowaniu pestycydu na jednym z poletek w
każdej parze (T), pozostawiając drugie poletko w
parze jako kontrolne (N). Sprawdzano czy sucha
masa roślinności (w gramach) zebranej w każdej
parze się różni.
39
#
T
N
1.
821
810
2.
655
642
3.
915
890
4.
540
540
5.
431
439
6.
1050
1020
7.
408
388
8.
408
403
9.
724
730
10. 795
780
11. 928
920
Pracownia Chemometrii Środowiska
Obliczamy różnice w parach i różnicom przypisujemy rangi zaczynając od różnicy
najmniejszej i biorąc pod uwagę ich wartości bezwzględne:
40
#
T
N
d
Ranga
Znak
1.
821
810
11
5
+
2.
655
642
13
6
+
3.
915
890
25
9
+
4.
540
540
5.
431
439
-‐8
3,5
-‐
6. 1050 1020
30
10
+
7.
408
388
20
8
+
8.
408
403
5
1
+
9.
724
730
-‐6
2
-‐
10. 795
780
15
7
+
11. 928
920
8
3,5
+
Obliczamy sumy rang dodatnich
T
+
= 49,9 i ujemnych T
-
= 5,5
T
min
= T
-
n = 10
Jeżeli T
min
≤ T
kryt
à
odrzucamy
hipotezę zerową (na poziomie
istotności 0,05)
Jeżeli T
min
> T
kryt
à nie mamy
podstaw do odrzucenia hipotezy
zerowej
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron