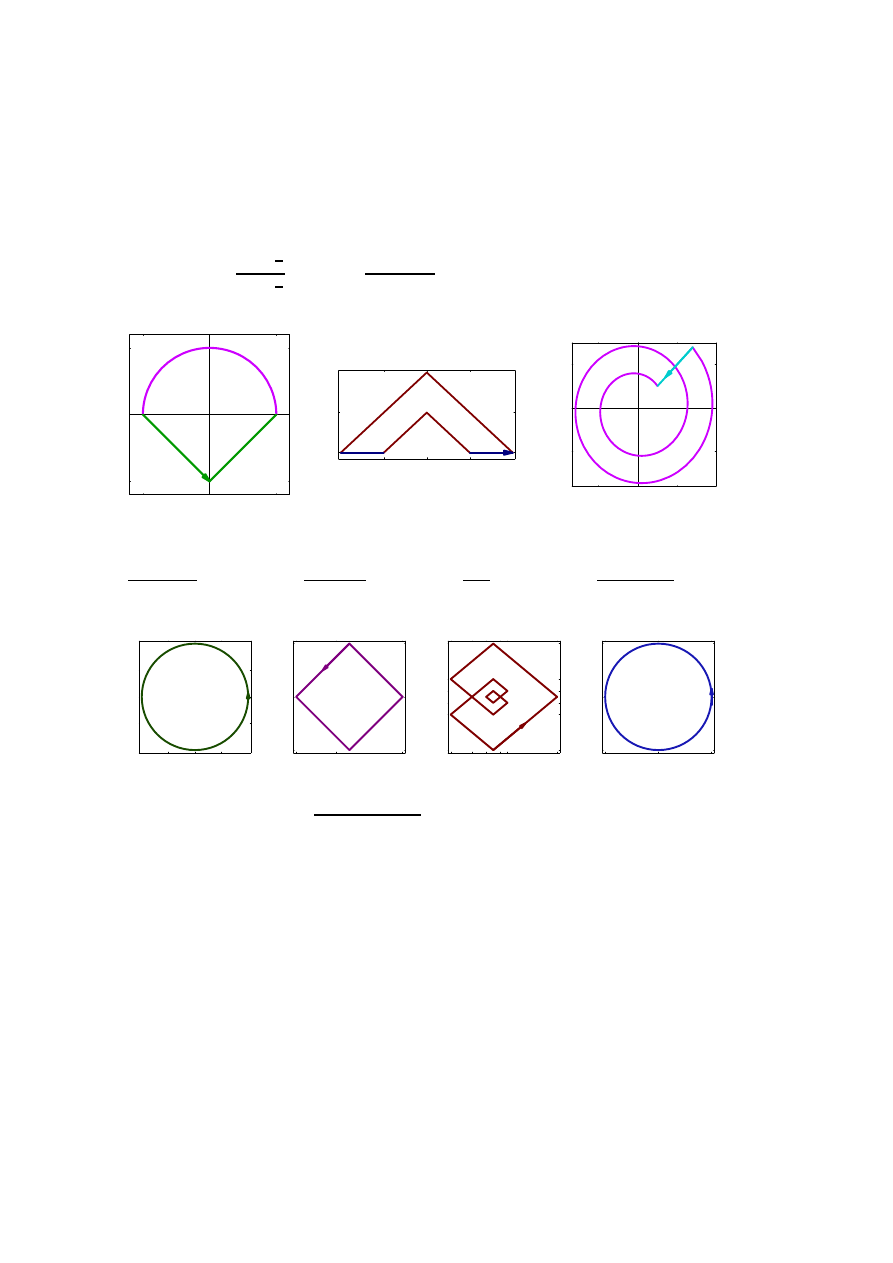
Twierdzenie Liouville’a Je˙zeli funkcja f

: C → C jest ró˙zniczkowalna w ka˙zdym punkcie

i ograniczona, to f jest stała.

Zad 1. Oblicz: a)

Z

Γ

z

2

+

1
4

z

2

−

1
4

dz, b)

Z

Γ

e

z

z

(z

2

+ 9)

dz, c)

Z

Γ

(z

2

− 1)

2

z

−1

(z

2

+ 800i)

−1

dz.

-1

0

1

-1

0

1

-1

0

1

-1

0

1

-2

0

2

0

2

-2

0

2

0

2

-10

0

10

-10

0

10

-10

0

10

-10

0

10

Zad 2. Oblicz całki zespolone:

a)

Z

Γ

z

(z

4

− 1)

2

dz,

b)

Z

Γ

cosh z

(z − 2)

n

d,

c)

Z

Γ

e

2iz

z

3

dz,

d)

Z

Γ

ze

z

(2z

3

+ 1)

2

dz.

-1

0

1

-1

0

1

-1

0

1

-1

0

1

-3

0

5

-4

0

4

-3

0

5

-4

0

4

-6 -3 -1 12

9

-9

-3

-1

1

3

9

-6 -3 -1 12

9

-9

-3

-1

1

3

9

-1

0

1

-1

0

1

-1

0

1

-1

0

1

Zad 3. Wyznacz całk˛e

Z

C

(0,R)

f

(z) dz

(z − a)(z − b)

,

|a| < R, |b| < R i badaj ˛

ac jej zachowanie

udowodnij twierdzenie Liouville’a.