Projektowanie obserwatorów stanu pełnego rz du
Układ dynamiczny opisany w przestrzeni stanu równaniami mo e by sterowany od wektora
stanu. Wektor ten, na potrzeby sterowania musi by mierzony. Jednak nie zawsze wektor
stanu jest mierzalny. Przyczyny takiego stanu s dwojakiej natury. Przede wszystkim ze
wzgl dów technicznych nie mo emy zmierzy wektora stanu lub wektor stanu mo e zawiera
elementy, które s wielko ciami niefizycznymi, a wi c równie niemierzalnymi. W
niektórych układach, z wektorem stanu fizycznym, nie wszystkie wielko ci s dost pne
bezpo rednio przez pomiar (np. w ło ysku magnetycznym bezpo rednio mierzone jest
przemieszczenie wirnika, jako jeden z elementów wektora stanu, natomiast pr dko i
przyspieszenie wirnika, pozostałe dwa elementy wektora stanu, nie s dost pne przez
pomiar).
Dlatego w systemach sterownia, wprowadza si obserwatory stanu, których zadaniem jest
odtworzenie wektora stanu obserwowanego obiektu. Obserwator do odtworzenia wektora
stanu wykorzystuje sygnały wej ciowe do obserwowanego układu oraz sygnały wyj ciowe z
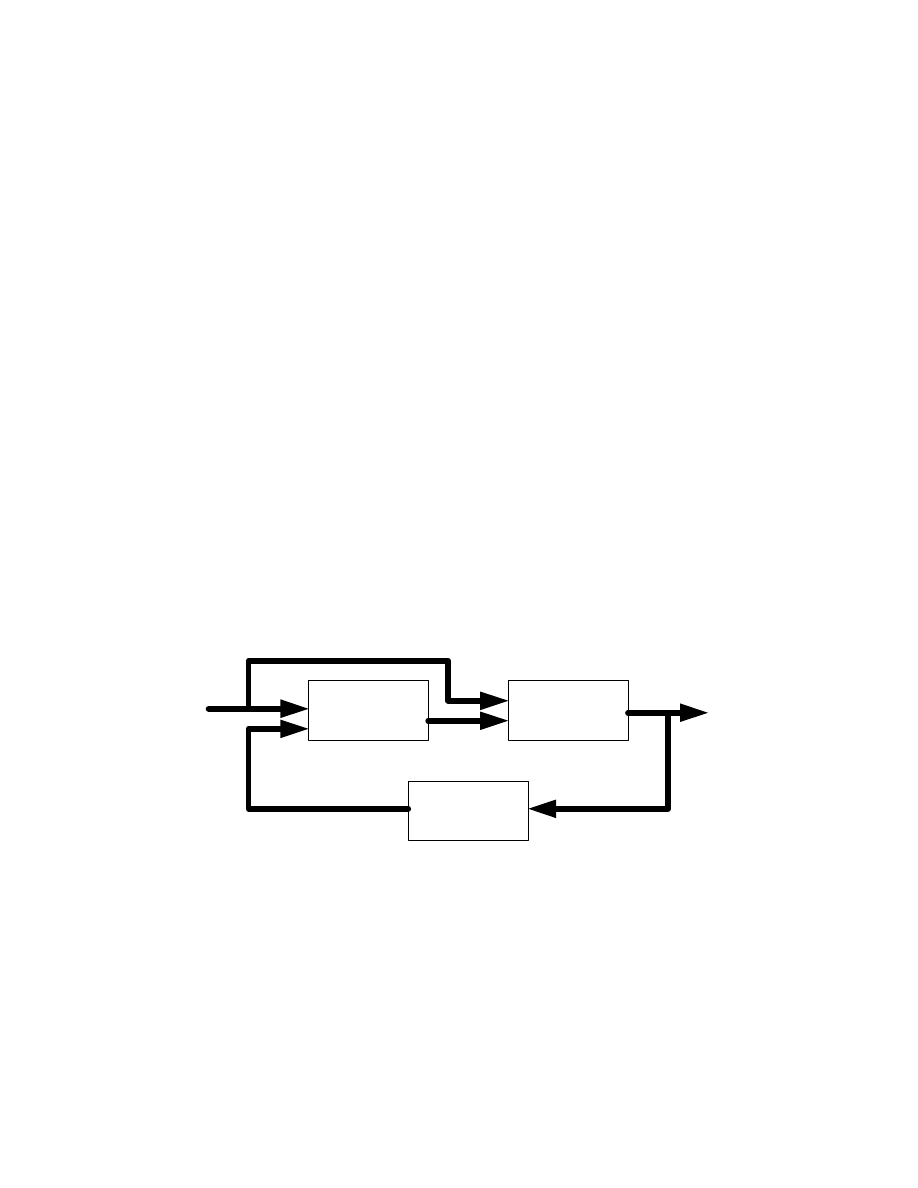
obserwowanego układu (rys. 1). Obserwator mo e by wykorzystany do wyznaczenia
pełnego wektora stanu lub tylko brakuj cych elementów wektora stanu. W pierwszym
przypadku obserwator jest obserwatorem pełnego rz du w drugim przypadku jest to
obserwator zredukowany.
Układ
Obserwator
stanu
Regulator
u(t)
u
c
(t)
y(t)
( )
ˆx t
Rys. 1. Struktura układu sterowania z obserwatorem stanu.
Układ opisany w przestrzeni stanu mo e by sterowany od wektora stanu i obserwowany
przez obserwator, je eli spełnia warunek obserwowalno ci i sterowalno ci.
Obserwator stanu
Jak zaznaczono wcze niej, nie zawsze istnieje mo liwo pomiaru wektora stanu. Jak równie
wektor stanu mo e by niefizyczny, to znaczy e nie mo emy zmierzy takiego wektora stanu
znanymi metodami.

W takim przypadku nale y zastosowa układy, które umo liwiaj oszacowanie wektora stanu
na podstawie sygnałów wyj ciowych i steruj cych układem. Układy realizuj ce powy sze
zadanie okre lane s obserwatorami stanu.
Do celów odtwarzania stanu on-line wykorzystuje si asymptotyczne obserwatory stanu
oparte o struktur obserwowanego układu. Łatwo mo na wyznaczy obserwator stanu, gdy
znane s macierze obserwowanego układu (A, B, C) i macierz stanu jest asymptotycznie
stabilna. Obserwator taki realizuje si przez symulacj modelu obserwowanego układu.
Podstawowy problem, który mo e wyst pi , dla takiego obserwatora, to nieznajomo
warunków pocz tkowych wektora stanu. Dodatkowym ograniczeniem jest wyst powanie
dynamiki bł du obserwacji, która zale y od warto własnych macierzy stanu A. Do
zagwarantowania asymptotycznej stabilno ci macierzy stanu obserwatora nale y j
zmodyfikowa przez uwzgl dnienie sygnałów wyj ciowych z obserwowanego obiektu.
Wyznaczymy obserwator stanu dla układu, który opisany jest w przestrzeni stanu
równaniami:
( )
( )
( )
( )
( )
t
t
t ,
t
t .
=
+
=
x
Ax
Bu
y
Cx
(1)
W równaniach (1) macierz transmisyjna jest macierz zerow .
Obserwator obiektu rzeczywistego (1), opisany jest równaniami w przestrzeniu stanu:
( )
( )
( )
( )
( )
ˆ
ˆ
t
t
t ,
ˆ
ˆ
t
t ,
=
+
=
x
Ax
Bu
y
Cx
(2)
gdzie:
( ) ( )
ˆ
ˆ t , t
x
x
- odtworzony wektor stanu i jego pochodna po czasie,
( )
ˆ t
y
- odtworzony
wektor wyj .
Jak zaznaczono wcze niej, macierz stanu obserwatora zostanie poddana modyfikacji, która
zapewnia asymptotyczn stabilno obserwatora oraz odpowiedni szybko obserwacji.
Wprowadzimy bł d oszacowania wektora stany
ε(t) jako:
( ) ( ) ( )
ˆ
t
t
t
=
−
x
x
.
(3)
Poniewa wektor stanu nie jest bezpo rednio dost pny, to w konstrukcji obserwatora
wykorzystamy ró nic mi dzy sygnałem wyj ciowym z obserwowanego układu i
obserwatora. Ró nica ta jest równa:
( ) ( ) ( )
ˆ
t
t
t
=
−
e
y
y
.
(4)
( )
x t
( )
ˆ t
x
( )
ˆ t
x
( )
ˆ t
y
( )
x t
( )
ˆ t
x
( )
ˆ t
x
( )
ˆ t
y
( )
x t
( )
ˆ t
x
( )
ˆ t
x
( )
ˆ t
y
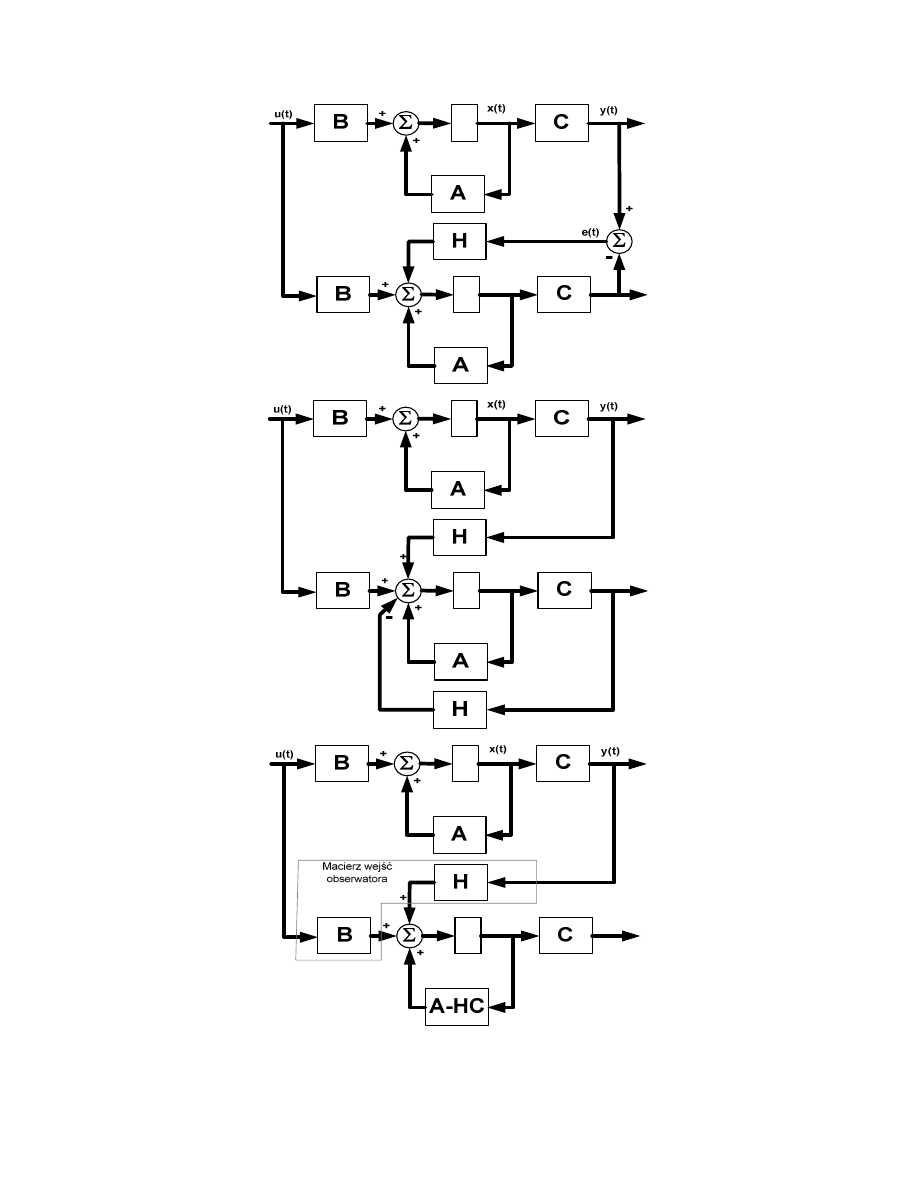
Rys. 2. Etapy wyznaczania obserwatora.

Uwzgl dniaj c na wej ciu obserwatora (2) ró nic
e(t), otrzymamy równanie stanu:
( )
( )
( )
( )
ˆ
ˆ
t
t
t
t
=
+
+
x
Ax
Bu
He
,
(5)
a po uwzgl dnieniu (4) w (5), otrzymamy:
( )
( )
( )
( ) ( )
(
)
ˆ
ˆ
ˆ
t
t
t
t
t
=
+
+
−
x
Ax
Bu
H y
y
.
(6)
Wprowadzaj c do (6) równie wyj (1), otrzymamy równanie stanu obserwatora:
( )
( )
( )
( )
( )
( )
[
]
( )
( )
( )
ˆ
ˆ
ˆ
t
t
t
x t
t ,
ˆ
ˆ
t
t
t
t .
=
+
−
+
=
−
+
+
x
Ax
Bu
HC
Hy
x
A HC x
Bu
Hy
(7)
Tym samym wyznaczony został model obserwatora stanu o zmodyfikowanej macierzy stanu
oraz macierzy wej :
( )
( )
( )
( )
ˆ
ˆ
t
t
t ,
ˆ
ˆ
C t ,
=
+
=
v
x
Fx
Vu
y
x
(8)
gdzie:
= −
F A HC - macierz obserwatora stanu,
[
]
=
v
B
B H - macierz wej ,
( )
( )
( )
t
t
t
=
v
u
u
y
- wektor steruj cy obserwatora.
Na rys. 2 przedstawiono kolejne etapy powstawania obserwatora stanu.
Jak mo na zauwa y wła ciwo ci dynamiczne obserwatora mo na zmienia przez
odpowiedni dobór macierzy
H (podobnie jak przy projektowaniu regulatora). Tym samym
mo na regulowa szybko obserwatora stanu.
Projektowanie obserwatora stanu
Obserwator stanu zaprojektujemy wykorzystuj c podobna metod , jak przy projektowaniu
regulatora wł czonego w torze sprz enia zwrotnego od wektora stanu. Przyjmiemy, e
obserwowany układ opisany jest równaniami w przestrzeni stanu:
( )
( )
( )
( )
( )
t
t
t ,
t
t .
=
+
=
x
Ax
Bu
y
Cx
(9)
Macierz stanu obserwatora stanu jest równa:
= −
F A HC .
(10)
nast pnie wyznaczymy równie charakterystyczne obserwatora stanu:
( )
[
]
o
s
det s
φ
=
−
−
I A HC
(11)
gdzie:
I – macierz jednostkowa, s- operator Laplace’a.

Zakładamy, e obserwator stanu posiada równanie charakterystyczne:
( )
(
)(
) (
)
o
o1
o2
on
s
s p
s p
s p
ϕ
= −
−
−
(12)
gdzie: p
o
– bieguny obserwatora stanu.
Jak mo na zauwa y , współczynniki równania charakterystycznego obserwatora (11) zale
od elementów macierzy
H. Porównuj c współczynniki równania charakterystycznego
obserwatora (11) z równaniem zało onym (12), otrzymamy współczynniki macierzy
H.
Przy doborze warto własnych obserwatora stanu nale y kierowa si nast puj cymi
zasadami:
1.
warto ci własne obserwatora powinny zapewnia stabiln prac obserwatora (bieguny
powinny posiada ujemne cz ci rzeczywiste),
2.
bieguny obserwatora powinny by tak dobrane, by cz ci rzeczywiste biegunów
obserwatora były du o mniejsze od cz ci rzeczywistych obserwoanego układu,
3.
obserwator mo na zaprojektowa tylko dla układu obserwowalnego i stabilnego.
Korzystaj c z powy szych zasad zaprojektujemy obserwator stanu dla układu opisanego w
przestrzeni stanu równaniami (9), który posiada macierz stanu, wej i wyj :
[
]
1
3
2
0 0 0
v
1 0 0 , = 0 , = 0 0 1
0 v
0
v
=
A
B
C
.
Przed zaprojektowaniem obserwatora nale y sprawdzi , czy układ jest obserwowalny. Je eli
spełniony jest warunek obserwowalno ci, to mo na wyznaczy macierz obserwatora.
Poniewa mierzony jest tylko jeden sygnał wyj ciowy w obserwowanym obiekcie, to mo na
przyj , e macierz
H jest nast puj ca:
1
2
3
h
h
h
=
H
,
(13)
st d macierz obserwatora (zgodnie z (10)):

[
]
1
2
3
3
1
2
3
3
1
2
3
3
0 0 0
h
1 0 0
h
0 0 1
0 v
0
h
0 0 0
0 0 h
1 0 0
0 0 h
0 v
0
0 0 h
0 0
h
1 0
h
0 v
h
=
−
=
−
−
=
−
−
F
F
F
(14)
Po wyznaczeniu macierzy stanu obserwatora, mo na wyznaczy równanie charakterystyczne
(11):
( )
[
]
1
1
o
2
2
3
3
3
3
s 0 0
0 0
h
s
0
h
s
det s
det 0 s 0
1 0
h
det 1
s
h
0 0 s
0 v
h
0
v
s h
−
φ
=
−
=
−
−
=
−
−
−
+
I F
,
( )
3
2
o
3
3 2
3 1
s
s
h s
v h s v h
φ
= +
+
+
.
(15)
Przyjmujemy trzy bieguny dla obserwatora stanu (pami taj c o podanych wcze niej
zasadach), st d równanie charakterystyczne obserwatora powinno by równe:
( ) (
)(
)(
)
( )
(
)
(
)
o
o1
o2
o2
3
2
o
o1
o2
o3
o1 o2
o1 o3
o2 o3
o1 o2 o3
s
s p
s p
s p
,
s
s
p
p
p
s
p p
p p
p p
s p p p .
ϕ
= −
−
−
ϕ
= + −
−
−
+
+
+
−
(16)
Przez porównanie współczynników równania charakterystycznego (15) i (16), wyznaczymy
współczynniki macierzy
H:
1 2 3
1
3
1 2
1 3
2 3
2
3
3
1
2
3
p p p
h
,
v
p p
p p
p p
h
,
v
h
p
p
p .
−
=
+
+
=
= − −
−
(17)
Wyznaczymy obserwator stanu dla układu niestabilnego, który opisany jest macierzami:
[
]
[ ]
0
0
0
4444
A
1
0
0 , B=
0
, C= 0 0 1 , D= 0
0
6667 0
414.5
=
−
.
Przed przyst pieniem do projektowania obserwatora nale y sprawdzi czy układ jest
sterowalny i obserwowalny. Wyznaczymy macierz obserwowalno ci dla obserwowanego
układu:

2
C
CA
CA
,
st d dla rozpatrywanego układu, otrzymamy macierz obserwowalno ci:
0
0
1
0
6667 0
6667
0
0
−
−
,
której rz d jest równy 3. Tym samym układ jest sterowalny, poniewa rz d macierzy
obserwowalno ci jest równy liczbie elementów wektora stanu. Sterowalno układu
sprawdzono w wiczeniu nr 3.
Je eli układ jest sterowalny i obserwowalny to mo na przyst pi do dalszych czynno ci
konstrukcyjnych. Jednak przed wyznaczeniem obserwatora nale y sprawdzi , czy układ jest
stabilny. Rozpatrywany układ posiada trzy bieguny o warto ci równej zero (s
1
=s
2
=s
3
=0).
Układ nie jest stabilny, st d niespełnione s podane wcze niej warunki. Przed zbudowaniem
obserwatora nale y wyznaczy regulator, który zapewnia stabiln prac układu zamknietego,
to znaczy zało ymy, e wektor stanu jest w pełni dost pny, macierz
C jest macierz
jednostkow kwadratow :
1 0 0
C
0 1 0
0 0 1
=
. Dla tak zmodyfikowanego układu zaprojektujemy
regulator
K. Czynno ci powy sze zrealizowane zostały w wiczeniu nr 3. Po umieszczeniu
regulatora
K w torze sprz enia zwrotnego od wektora stanu układ zamkni ty posiada
bieguny:
p
1
=-10+20i, p
2
=-10-20i, p
3
=-100.
Po wyznaczeniu stabilnego układu zaprojektujemy obserwator stanu, którego macierz stanu
jest równa (zgodnie z (10)):
1
2
3
0
0
h
1
0
h
0
6667
h
−
=
−
−
−
F
.
(18)
St d równanie charakterystyczne obserwatora jest nast puj ce:
( )
3
2
o
3
2
1
s
s
h s
6667 h s 6667 h
φ
= +
−
⋅
−
⋅ .
(19)
Obserwator musi odpowiednio szybko odtwarza wektor stanu. Spełnienie tego warunku jest
mo liwe przez dobranie biegunów obserwatora, tak by cz ci rzeczywiste tych biegunów były
du o mniejsze ni bieguny obserwowanego układu.
Przyjmiemy bieguny obserwatora:
p
o1
=-500+20i, p
o2
=-500-20i, p
o3
=-1000.
Równanie charakterystyczne obserwatora powinno by równe:
( )
3
2
o
s
s
2000s
1250400s 250400000
ϕ
= +
+
+
.
(20)
Porównuj c współczynniki równania charakterystycznego (20) i (19) wyznaczymy nastawy
macierzy
H:
37560
H
187.56
2000
−
= −
.
(21)
Na rys. 3 przedstawiono rozkład biegunów układu zamkni tego z obserwatorem stanu.
Pole-Zero Map
Real Axis
Im
ag
A
xi
s
-1200
-1000
-800
-600
-400
-200
0
-20
-15
-10
-5
0
5
10
15
20
1.2e+003
1e+003
800
600
400
200
1
1
1
1
0.999
0.998
0.996
0.985
1
1
1
1
0.999
0.998
0.996
0.985
System: m52
Pole: -500 + 20i
Damping: 0.999
Overshoot (%): 0
Frequency (rad/sec): 500
System: m52
Pole: -10 + 20i
Damping: 0.447
Overshoot (%): 20.8
Frequency (rad/sec): 22.4
System: m52
Pole: -100
Damping: 1
Overshoot (%): 0
Frequency (rad/sec): 100
System: m52
Pole: -10 - 20i
Damping: 0.447
Overshoot (%): 20.8
Frequency (rad/sec): 22.4
System: m52
Pole: -500 - 20i
Damping: 0.999
Overshoot (%): 0
Frequency (rad/sec): 500
System: m52
Pole: -1e+003
Damping: 1
Overshoot (%): 0
Frequency (rad/sec): 1e+003
Rys. 3. Rozkład biegunów układu zamkni tego z obserwatorem stanu.
Do rozwi zania zadania w programie Matlab mo emy wykorzysta procedury
place i acker,
z którymi zapoznali my si w wiczeniu nr 3. Do wyznaczenia obserwatorów musimy tylko
odpowiednio poda macierz stanu układu obserwowanego i macierz wyj układu

obserwowanego. Ograniczenia wynikaj ce z zastosowania procedury
acker s identyczne jak
przy projektowaniu regulatorów.
Do wyznaczenia macierzy
H obserwatora wykorzystujemy procedur place o składni:
L=place(A’,C’,p)
H=L’
lub procedur
acker o składni:
L=acker(A’,C’,p)
H=L’
gdzie:
p – zadane poło enie biegunów obserwatora. Macierz obserwatora H mo na
wyznaczy po transponowaniu wektora
L, który jest wyznaczony bezpo redni przez
procedur
place lub acker.
Pozostałe procedury niezb dne do wyznaczenia modelu zamkni tego z obserwatorem stanu
przedstawiono we wcze niejszych wiczeniach. Poni ej przedstawiony jest przykład pliku
skryptowego przeznaczonego do projektowania obserwatora stanu:
clear
% macierze układu
A=[0 0 0;1 0 0;0 -6667 0]; B=[4444;0;414.5]; C=eye(3); D=zeros(3,1);
s_o=ss(A,B,C,D); % układ otwarty
p=[-100 -10+20i -10-20i]; % bieguny docelowe
k1=place(A,B,p); % nastawy regulatora
k2=acker(A,B,p);
r1=ss([],[],[],k1); % model w przestrzeni stanu regulatora
r2=ss([],[],[],k2);
C1=[0 0 1]; %faktyczna macierz wyj
ob=rank(obsv(A,C1));
L=place(A',C1',[-500+20i -500-20i -1000]);
L1=acker(A',C1',[-500+20i -500-20i -1000]);
H=L';
A1=A;% macierze układu otwartego
B1=B;% macierze układu otwartego
C2=[0 0 0;C1];% macierze układu otwartego
D1=[1;0];% macierze układu otwartego
system_o=ss(A1,B1,C2,D1); %układ otwarty
F=A-H*C1; % macierz stanu obserwatora

V=[B H]; % macierz wej obserwatora
Co=eye(3); % macierz wyj obserwatora
Do=zeros(3,2); % macierz transmisyjna obserwatora
system_ob=ss(F,V,Co,Do); % model obserwatora
system_sz=series(system_o,system_ob); %poł czenie szeregowe układ-obserwator
system_sprz=feedback(system_sz,r1,-1)% sprz enie zwrotne z regulatorem.
damp(system_sprz)
figure(1)
pzmap(system_sprz)
sgrid
figure(2)
step(system_sprz)
grid
W pierwszej cz ci pliku skryptowego wyznaczony został regulator, dlatego zało ono e
dost pny jest przez pomiar cały wektor stanu (zadanie to zostało omówione w wiczeniu 3).
Nast pnie wyznaczono macierz
H obserwatora, dlatego wprowadzono now macierz wyj
obserwatora oznaczon C1. Jak zaznaczono wcze niej obserwator posiada dwa wej cia
pierwsze to wej cie steruj ce
u i drugie to wyj cie z układu y (rys. 4), dlatego układ otwarty
musi by odpowiednio zamodelowany (wprowadzono odpowiedni macierz wyj i
transmisyjn ). Dopiero po odpowiednim zamodelowaniu układu otwartego mo emy
szeregowo doł czy obserwator a nast pnie w sprz eniu zwrotnym umie ci regulator
K. Na
wyj ciu takiego układu dost pny jest odtworzony wektor stanu układu (rys. 4).
Rys. 4. Model układu z odtworzonym wektorem stanu na wyj ciu układu.
Poni ej przedstawiono przykład pliku skryptowego, w którym zmieniono kolejno poł cze
w układzie (prosz przeanalizowa dokładnie przykład). W tak zamodelowanym układzie
dost pny na wyj ciu jest wektor wyj z obserwowanego układu oraz wektor sterowa (efekt

wprowadzenia macierzy transmisyjnej do układu). Schemat układu przedstawiony jest na
rysunku 5.
clear
% macierze układu
A=[0 0 0;1 0 0;0 -6667 0]; B=[4444;0;414.5]; C=eye(3); D=zeros(3,1);
s_o=ss(A,B,C,D); % układ otwarty
p=[-100 -10+20i -10-20i]; % bieguny docelowe
k1=place(A,B,p); % nastawy regulatora
k2=acker(A,B,p);
r1=ss([],[],[],k1); % model w przestrzeni stanu regulatora
r2=ss([],[],[],k2);
C1=[0 0 1]; %faktyczna macierz wyj
ob=rank(obsv(A,C1));
L=place(A',C1',[-500+20i -500-20i -1000]);
L1=acker(A',C1',[-500+20i -500-20i -1000]);
H=L';
A1=A;% macierze układu otwartego
B1=B;% macierze układu otwartego
C2=[0 0 0;C1];% macierze układu otwartego
D1=[1;0];% macierze układu otwartego
system_o=ss(A1,B1,C2,D1); %układ otwarty
F=A-H*C1; % macierz stanu obserwatora
V=[B H]; % macierz wej obserwatora
Co=eye(3); % macierz wyj obserwatora
Do=zeros(3,2); % macierz transmisyjna obserwatora
system_ob=ss(F,V,Co,Do); % model obserwatora
system_sz1=series(system_ob,r1); %poł czenie szeregowe układ-obserwator
system_sprz=feedback(system_o,system_sz1,-1);% sprz enie zwrotne z regulatorem.
damp(system_sprz)
figure(1)
pzmap(system_sprz)
sgrid
figure(2)
step(system_sprz);grid
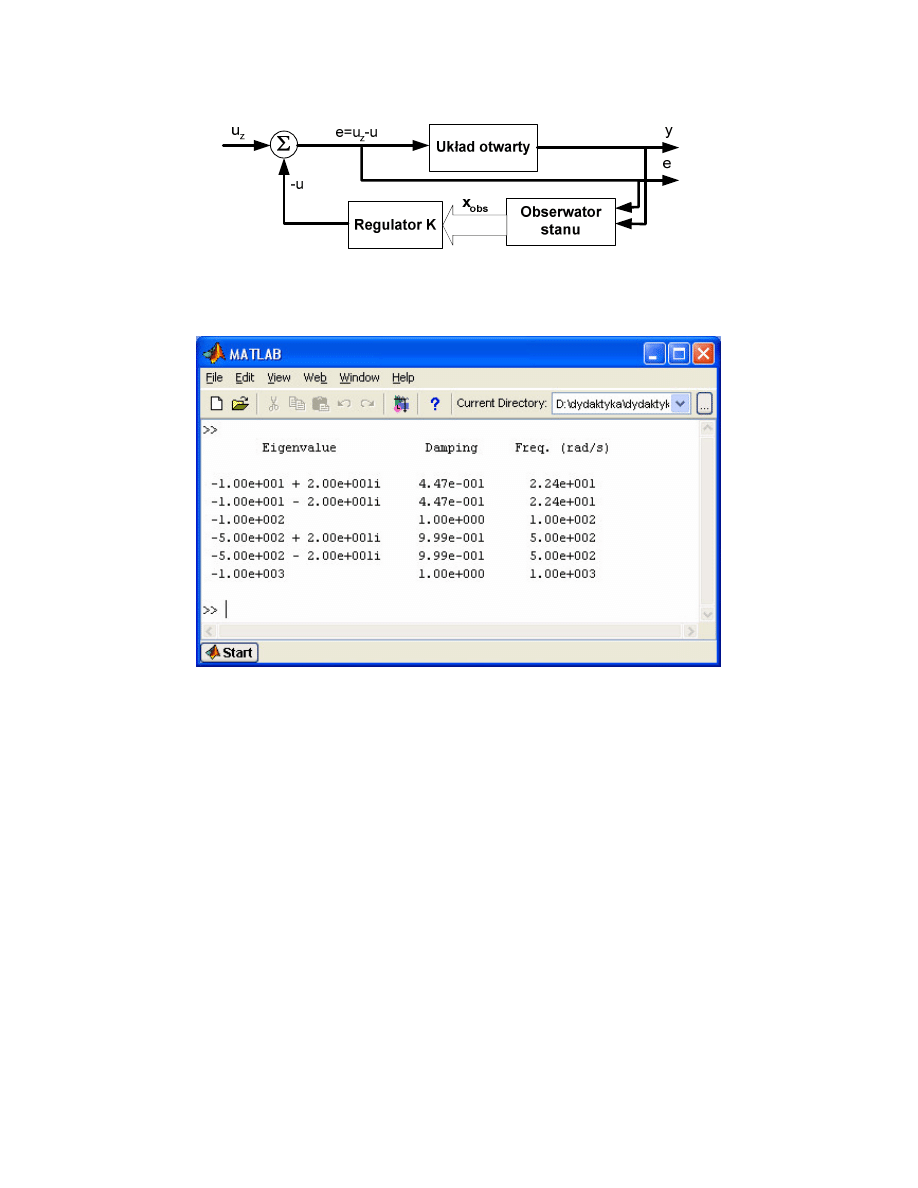
Rys. 5. Konfiguracja układu zamkni tego z wyprowadzonym na wyj ciu układu
rzeczywistym wektorem wyj ci i uchybem regulacji.
Rys. 6. Warto ci własne układu zamkni tego.
Na rysunku 6 przedstawiono wynik wykonania pliku skryptowego. Procedura
damp
wyznaczyła warto ci własne układu zamkni tego. Wyst puj ce bieguny odpowiadaj trzem
biegunom wprowadzanym przez regulator oraz trzem kolejnym wprowadzonym przez
obserwator stanu. Na rysunku 7 przedstawiony jest rozkład warto ci własnych układu
zamkni tego na płaszczy nie zespolonej.
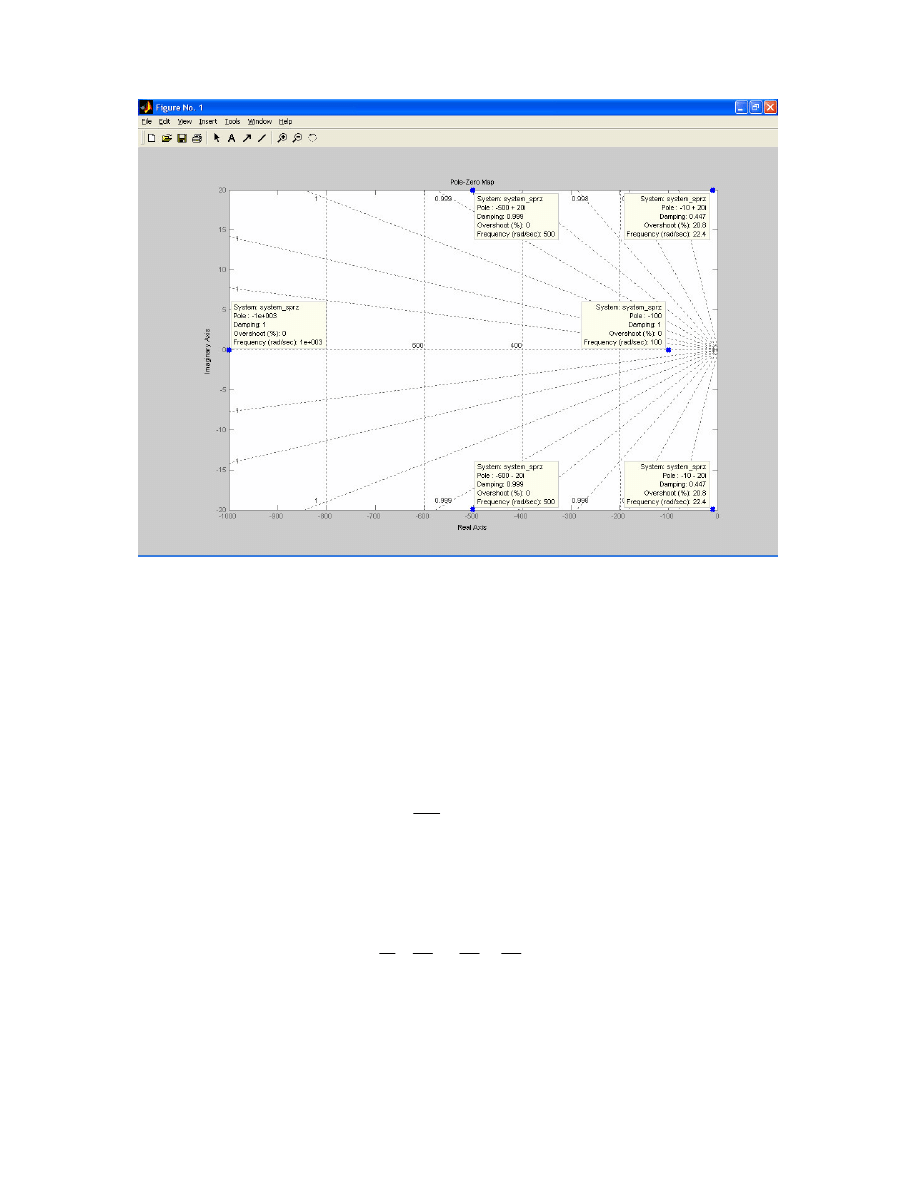
Rys. 7. Rozkład warto ci własnych układu zamkni tego na płaszczy nie zespolonej.
Zadanie
Prosz zamodelowa w przestrzeni stanu siłownik ło yska magnetycznego, a nast pnie
wyznaczy nastawy regulatora według przedstawionego powy ej przykładu. Wszystkie
obliczenia prosz wykona w programie Matlab-Simulink.
Cz
mechaniczna siłownika ło yska magnetycznego opisane jest równaniem
ró niczkowym:
2
i
x
2
d x
m
k i k x
dt
=
+
,
gdzie: m – masa ło yskowana, k
i
– sztywno pr dowa ło yska, k
x
– sztywno
przemieszczeniowa ło yska, i – pr d steruj cy, x – przemieszczenie masy z poło enia
równowagi, natomiast cz
elektryczna opisana jest zale no ci :
i
0
0
0
k
di
1
R
u
i
x
dt
L
L
L
=
−
−
,
gdzie: u – napi cie steruj ce, L
0
– indukcyjno cewki w punkcie pracy, R – rezystancja
cewki.
Parametry układu:

m= 10 [kg];
k
i
= 361,91 [N/A];
k
x
= 10857344,21 [N/m];
L
0
= 0.01 [H]
R= 0,5 [
Ω]
Model prosz wyznaczy w przestrzeni stanu z odpowiednimi macierzami. Wielko ci
wej ciow jest napi cie steruj cy
u. Wielko ci wyj ciow jest przemieszczenie masy z
poło enia równowagi x. Regulator prosz wyznaczy dla nast puj cych biegunów:
a)
p=[-10+4i -10-4i -100];
b)
p=[-10 -100+40i -100-40i];
c)
p=[-10+40i -10-40i -1000];
oraz prosz zaprojektowa układ, który charakteryzuje si :
− czasem regulacji 0,5 [s];
− bezwymiarowym współczynnikiem tłumienia 0,4.
Poniewa wektor stanu nie jest dost pny bezpo rednio przez pomiar (tylko dost pny jest
przez pomiar jeden z elementów wektora stanu – przemieszczenie x), to pozostałe elementy
wektora stanu musz by odtwarzane przez obserwator stanu. Prosz zaprojektowa
obserwator stanu, a nast pnie zamodelowa układ zamkni ty zło ony z układu otwartego,
obserwatora i regulatora. Na wyj ciu układu powinien by dost pny odtworzony wektor
stanu.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron