Grafika komputerowa
Grafika rastrowa
Rados!aw Mantiuk
Wydzia! Informatyki
Zachodniopomorski Uniwersytet Technologiczny
Grafika komputerowa
Rasteryzacja (ang. rasterization or scan-conversion)
Zamiana ci!g"ej funkcji 2D na funkcj# dyskretn!
(np. rysowanie okr#gu w rastrze na podstawie równania okr#gu).
Problem sprowadza si# do wyboru pikseli, którym trzeba nada$ kolor, aby w
efekcie otrzyma$ wymagany kszta"t geometryczny.
Problem rasteryzacji pojawi! si" w momencie upowszechnienia si" monitorów
rastrowych (Jack Bresenham).
Algorytmy grafiki rastrowej s# fundamentem grafiki komputerowej.
Grafika komputerowa
Rysowanie piksela
Nadanie odpowiedniej komórce pami"ci obrazu okre%lonej warto%ci (koloru).
(0,0)
(cols,0)
(0,rows)
(cols,rows)
(xres, yres)
Adres piksela (24 bpp):
addr(x,y) = y * cols * 3 + x * 3
x
y
Grafika komputerowa
Rysowanie linii (1)
• Linia powinna wygl#da$ w sposób ci#g!y.
• Mie$ jednakow# grubo%$ i jaskrawo%$ na ca!ej d!ugo%ci.
• Zapalane powinne by$ piksele jak najbli&ej idealnej linii.
•
Algorytm rysowania musi by$ bardzo szybki.
Zapalanie odpowiednich pikseli pomi"dzy pikselami pocz#tkowym i ko'cowym.
Courtesy of MIT (Lecture Notes 6.837)

Grafika komputerowa
Rysowanie linii (2)
Algorytm nie daje zadawalaj#cych rezultatów (nie mo&na narysowa$ linii pionowych, zaokr#glanie jest
wolne).
Courtesy of MIT (Lecture Notes 6.837)
Grafika komputerowa
Rysowanie linii:
Kod programu
Algorytm rysuje linie od 0 do
45 stopni oraz dla x1 > x0.
Grafika komputerowa
Rysowanie linii: Algorytm z punktem %rodkowym
O wyborze piksela, który b"dzie
zapalony w kolejnym kroku decyduje
po!o&enie punktu %rodkowego M
wzgl"dem obliczonego punktu Q.
Np. je&eli Q jest pomi"dzy M i NE
wybierany jest piksel NE.
y = y
p
+ 1/2
Courtesy Andries van Dam.
Modyfikacja algorytmu Bresenhama.
Grafika komputerowa
Rysowanie linii: Równanie parametryczne prostej
Równanie prostej:
Równanie parametryczne:
Obliczenie F w punkcie !rodkowym okre!la czy idealna linia znajduje si" powy#ej
czy poni#ej punktu !rodkowego
.

Grafika komputerowa
Rysowanie linii: Zmienna decyzyjna
Istotny jest znak zmiennej decyzyjnej d:
Grafika komputerowa
Rysowanie linii: Warto%$ poczatkowa zmiennej decyzyjnej
Warto%$ pocz#tkowa zmiennej decyzyjnej:
Wyeliminowanie u!amka
Grafika komputerowa
Rysowanie linii: Modyfikacja zmiennej decyzyjnej
Inkrementacyjne obliczanie d dla E:
Ró&nica pomi"dzy star# i now# warto%ci# d:
Grafika komputerowa
Rysowanie linii: Modyfikacja zmiennej decyzyjnej
Inkrementacyjne obliczanie d dla NE:
Ró&nica pomi"dzy star# i now# warto%ci# d:
Grafika komputerowa
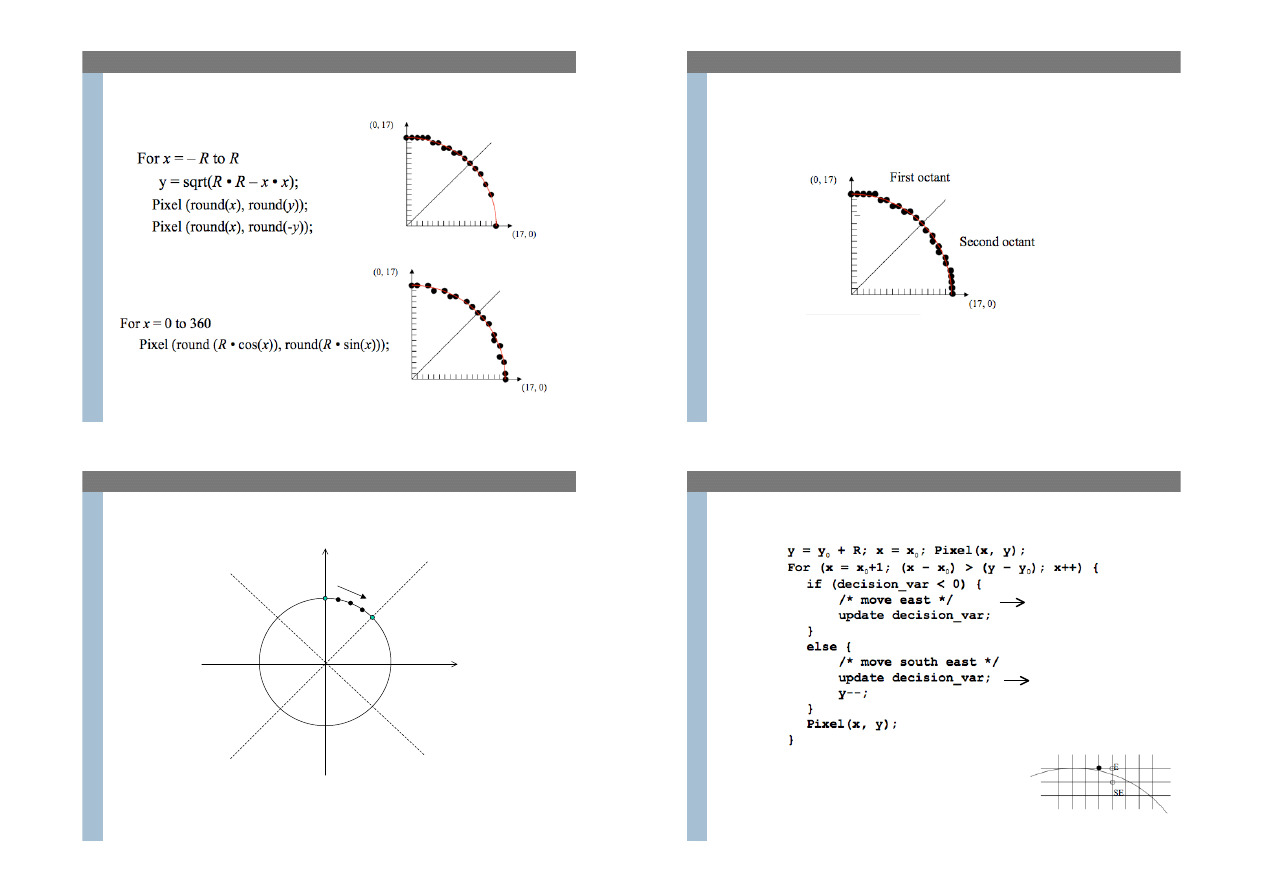
Rysowanie okr"gu (1)
Pictures courtesy of Andries van Dam.
Grafika komputerowa
Rysowanie okr"gu (2)
Algorytm rysowania okr#gu z punktem %rodkowym.
Pictures courtesy of Andries van Dam.
Grafika komputerowa
Rysowanie okr"gu (3) - Algorytm z punktem %rodkowym
x
y
(0,R)
Rysowana jest 1/8 okr"gu. Pozosta!e cze%ci uzyskuje si"
poprzez symetryczne powielenie obliczonych pikseli.
(x,y)
(y,x)
(-x,y)
(y,-x)
(-y,-x)
(-x,-y)
(x,-y)
(-y,x)
x = y
Grafika komputerowa
Rysowanie okr"gu (4) - Algorytm z punktem %rodkowym
Pictures courtesy Andries van Dam.
E
SE

Grafika komputerowa
Rysowanie okr"gu (5) - Zmienna decyzyjna
Warto%$ funkcji:
w punkcie:
E
Czy warto%$ funkcji w punkie %rodkowym jest dodatnia czy ujemna?
Pictures courtesy Andries van Dam.
Dla ujemnej warto%ci funkcji wybieramy E, poniewa& oznacza to, &e punkt M
jest wewn#trz okr"gu (odleg!o%$ punktu M od %rodka okr"gu jest mniejsza od
promienia okr"gu).
Grafika komputerowa
Rysowanie okr"gu (6) - inkrementy
Obliczanie inkrementu zmiennej decyzyjnej:
Grafika komputerowa
Rysowanie okr"gu (7)
Grafika komputerowa
Rysowanie linii ze wzorem (ang. pattern lines)
Wzór od P do Q ró&ni si" od wzoru od
Q do P.
Pictures courtesy Andries van Dam.
Wzór na!o&ony w postaci tekstury.
Niepoprawny pod wzgl"dem
geometrycznym.
Wzory geometryczne.

Grafika komputerowa
Trójk#t
Pictures courtesy of MIT (lecture 6.837)
Kszta!t geometryczny najpowszechniej wykorzystywany w
grafice komputerowej:
• bardzo prosta reprezentacja (3 wierzcho!ki i 3 brzegi),
• trójk#t zawsze jest wypuk!y (ang. convex),
• wierzcho!ki trójk#ta zawsze le&# na jednej p!aszczy(nie,
• za pomoc# siatki trójk#tów mo&na aproksymowa$ dowolny
kszta!t 3D.
Grafika komputerowa
Rasteryzacja trójk#ta - Ang. Edge walking
Pictures courtesy of MIT (lecture 6.837)
Brzegowa (ang. edge walking)
1.
Posortowanie wierzcho!ków w kierunkach x i y, wybranie kierunku wype!niania (np. z
lewej do prawej i z góry na dó!).
2.
Obliczenie pikseli brzegowych dla ka&dej poziomej linii (ang. spans).
3.
Wype!nianie liniami poziomymi od punktu p0 do p2.
• Bardzo szybki algorytm.
• Wymaga zaokr#glania warto%ci zmiennoprzecinkowych w
czasie liczenia spans.
Grafika komputerowa
Kopiowanie obszarów rastra (ang. Bit Blitting)
Pictures courtesy of MIT (lecture 6.837)
Kopiowanie warto%ci kolorów pikseli pomi"dzy obszarem (ród!owym i docelowym.
Wa&na jest kolejno%$ kopiowania
pikseli (unikamy b!"dów
wynikaj#cych z pokrywania si"
obszarów (ród!owego i
docelowego).
W czasie kopiowania mo&na wykorzystywa$ funkcje logiczne !#cz#c kopiowany obszar
z t!em w celu uzyskania okre%lonych efektów wizualnych (np. XOR kursora myszy).
Grafika komputerowa
Przezroczysto%$ - Ang. Alpha blending
Pictures courtesy of MIT (lecture 6.837)
Wykorzystanie warto%ci Alpha koloru piksela (RGBA) do uzyskania przezroczysto%ci.
== 0 -> piksel przezroczysty (ang. transparent)
== 1 -> piksel nieprzezroczysty (ang. opaque)
W bitmapie lub sprit’e zapisana informacja RGBA.
!
C = " # C
piksela
+ (1$
") # C
tla

Grafika komputerowa
Literatura
1.
Materia!y edukacyjne organizacji ACM SIGGRAPH,
http://www.siggraph.org/education/materials/HyperGraph
2.
“Lecture notes on Graphics. Lecture 6.837”, Computer Graphics Group,
Massachusetts Institute of Technology,
http://groups.csail.mit.edu/graphics/classes/6.837/F01/notes.html.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron