12/2/2012
1
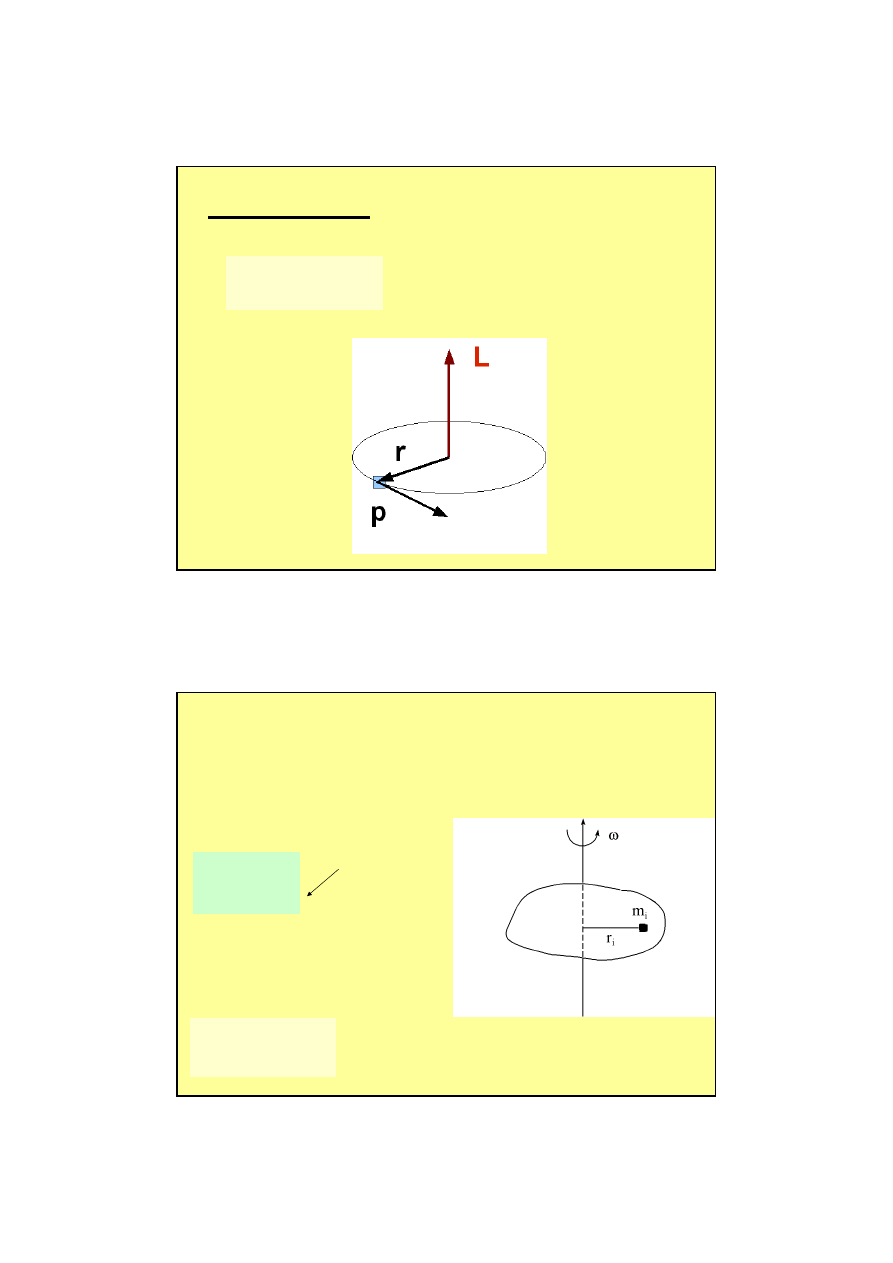
Moment pędu
p
r
L
×
=
ω
ω
ω
ω
I
=
os
L
∑
=
=
N
1
i
2
i
i
r
m
I
gdzie:
moment
bezwładności
∑
∑
=
=
=
=
N
1
i
i
i
i
N
1
i
i
i
oś
r
v
m
r
p
L
ω
=
I
L
oś
wektorowo:
Obliczmy moment pędu względem osi:
∑
=
ω
=
N
1
i
i
i
i
r
r
m
I
r
m
N
1
i
2
i
i
ω
=
ω
=
∑
=
12/2/2012
2
Ruch obrotowy ogólnie
ω
L ||
ogólnie:
=
⇔
=
z
y
x
zz
zy
zx
yz
yy
yx
xz
xy
xx
z
y
x
I
I
I
I
I
I
I
I
I
L
L
L
ω
ω
ω
ω
I
L
ˆ
ω
ω
ω
ω
L
ω
ω
ω
ω
L
0
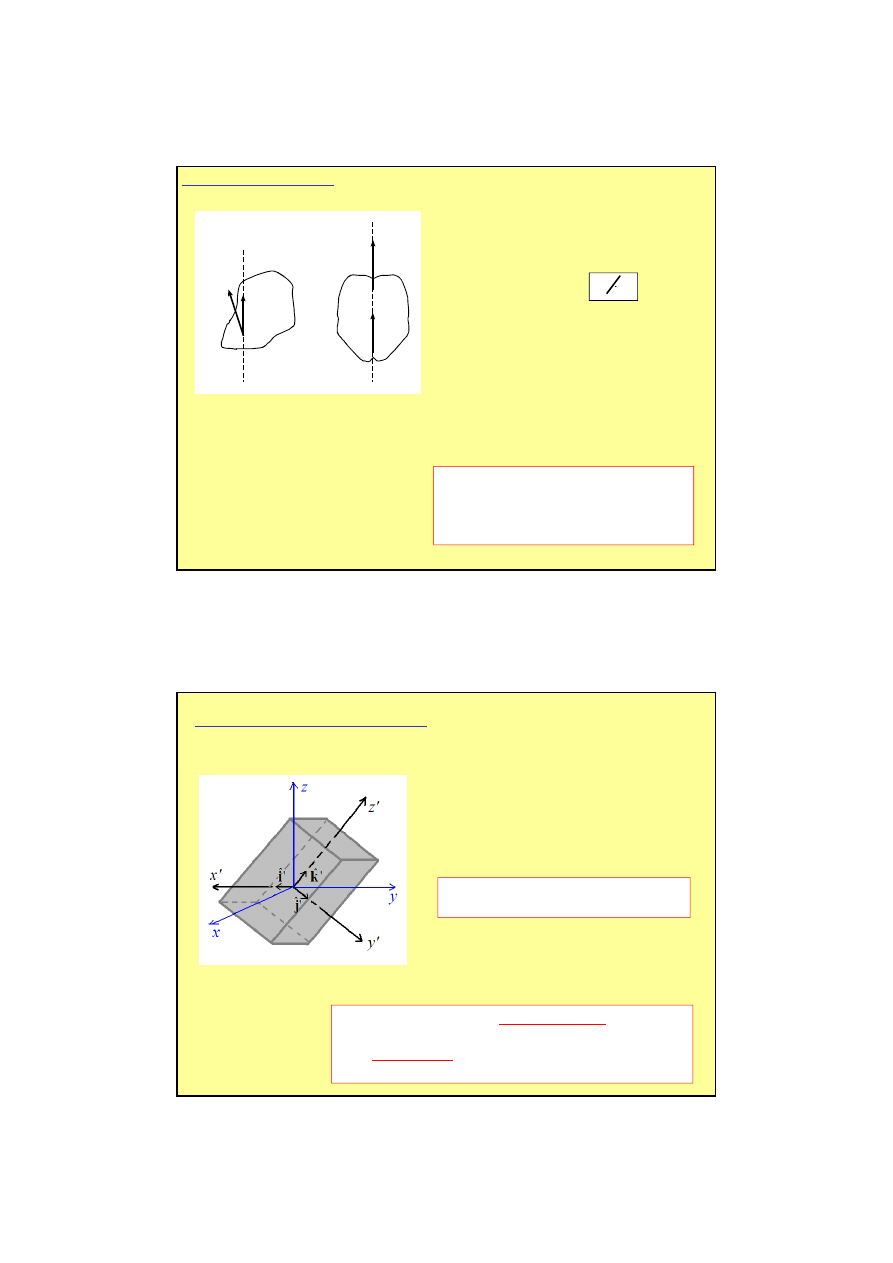
Ruch obrotowy wokół osi głównych
'
kˆ
I
'j
ˆ
I
'
iˆ
I
L
'
z
'
z
'
y
'
y
'
x
'
x
ω
+
ω
+
ω
=
1)
W ogólnym przypadku L nie jest równoległy do
ω
.
2) L jest równoległy do
ω
ω
ω
ω
wówczas, gdy osią obrotu jest jedna
z głównych osi bezwładności
12/2/2012
3
Przykład: moment bezwładności pręta
l
r
M
r
m
r
I
2
2
∆
=
∆
=
∆
∫
∫
=
=
l
0
2
V
dr
r
l
M
dl
I
0
12
Ml
I
2
=
l
dr
M
r
dm
r
dI
2
2
=
=
∑
∑
∆
=
∆
=
k
k
2
k
k
k
l
r
M
r
I
I
a ściśle:
2
/
l
2
/
l
3
3
r
l
M
−
=
12
Ml
)]
8
l
(
8
l
[(
l
3
M
2
3
3
=
−
−
=
r
l
dr
M
∆
r
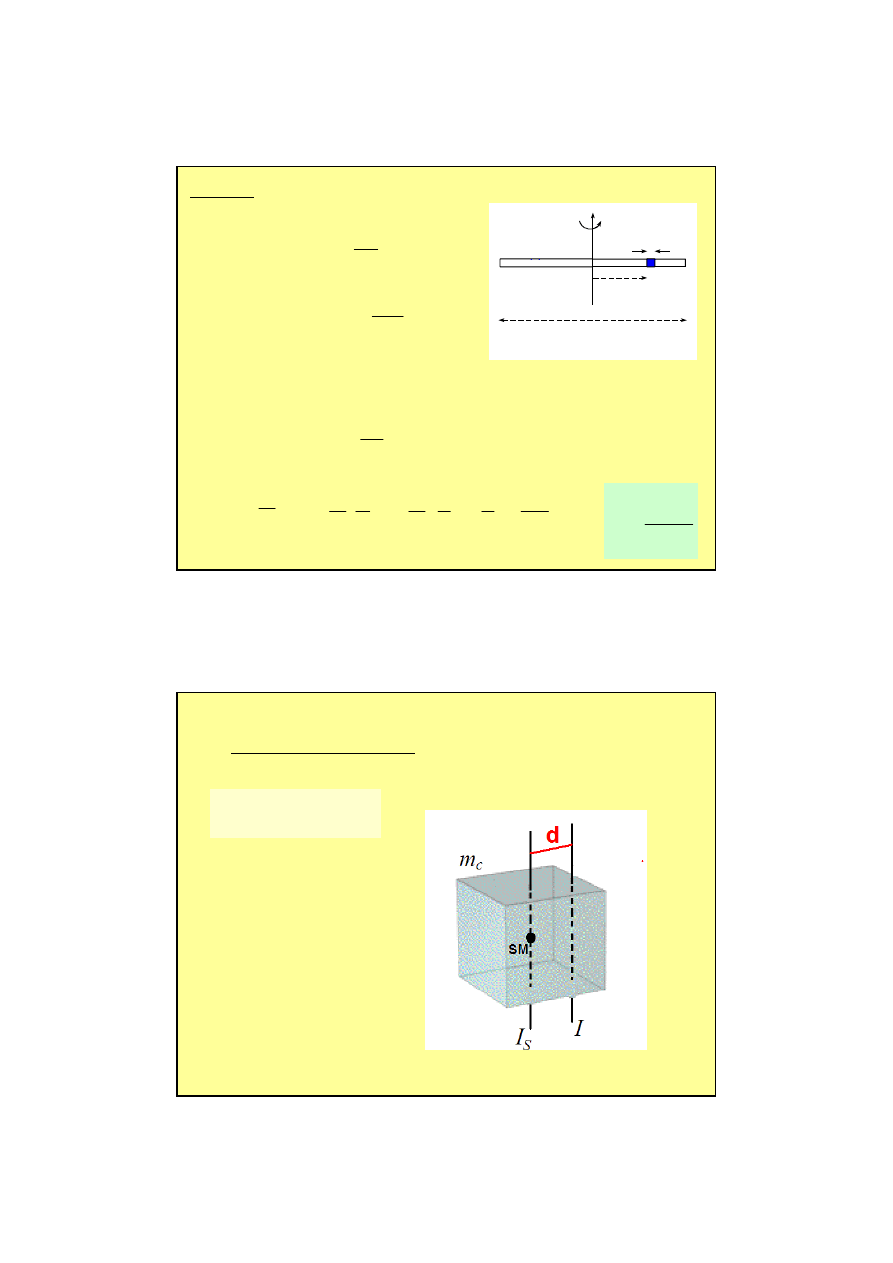
Twierdzenie Steinera:
2
d
m
Ι
Ι
c
S
+
=
12/2/2012
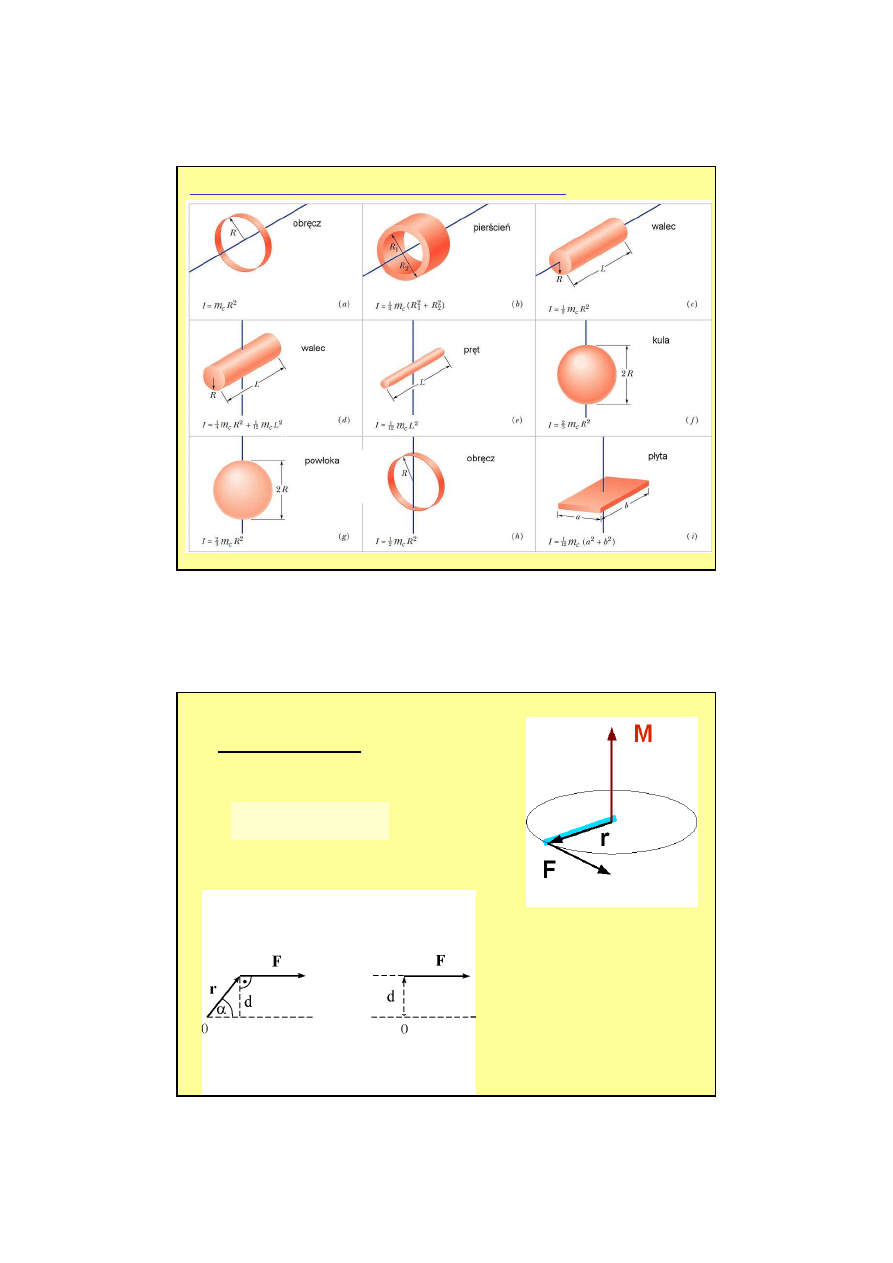
4
Przykładowe momenty bezwładno
ś
ci wokół osi głównych
Moment siły
F
r
×
=
Μ
Μ
Μ
Μ
12/2/2012
5
Zasady dynamiki ruchu obrotowego
II zasada dynamiki ruchu obrotowego
Zatem :
p
r
L
×
=
p
r
p
r
L
×
+
×
=
dt
d
dt
d
t
d
d
v
r
=
dt
d
więc:
p
v //
oraz:
0
dt
d
=
×
p
r
Zatem:
dt
d
t
d
d
p
r
L
×
=
lecz:
lecz:
εεεε
I
=
M
F
p
=
t
d
d
M
L
=
t
d
d
t
d
d L
M
=
F
r
L
×
=
t
d
d
A zatem:
ω
ω
ω
ω
I
=
L
II zasada dynamiki ruchu obrotowego :
Przypadek szczególny (obrót wokół osi symetrii ciała):
dt
d
t
d
d
p
r
L
×
=

12/2/2012
6
∑
=
i
0
i
F
∑
=
i
0
i
M
STATYKA CIAŁ
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron