
- 1 -
B
INARNE
D
RZEWA
POSZUKIWAŃ
Na podstawie: N. Wirth, „Algorytmy + struktury danych =programy”, WNT,
Eleganckim i efektywnym sposobem definiowania bardziej złożonych struktur
danych jest rekurencja. Zdefiniujmy zatem strukturę drzewiastą następująco:
Struktura drzewiasta o typie podstawowym T jest albo
1) Strukturą pustą, albo
2) Węzłem typu T ze skończoną liczbą dowiązanych rozłącznych struktur
drzewiastych o typie podstawowym T, nazywanych poddrzewami.
Przykłady drzew:
· Struktura plików systemu operacyjnego
· Książka, rozdziały, podrozdziały, sekcje, paragrafy, itd.
· Drzewo genealogiczne
· Menu telefonu komórkowego
· Drzewo opisujące wyrażenie arytmetyczne
Reprezentacja drzew
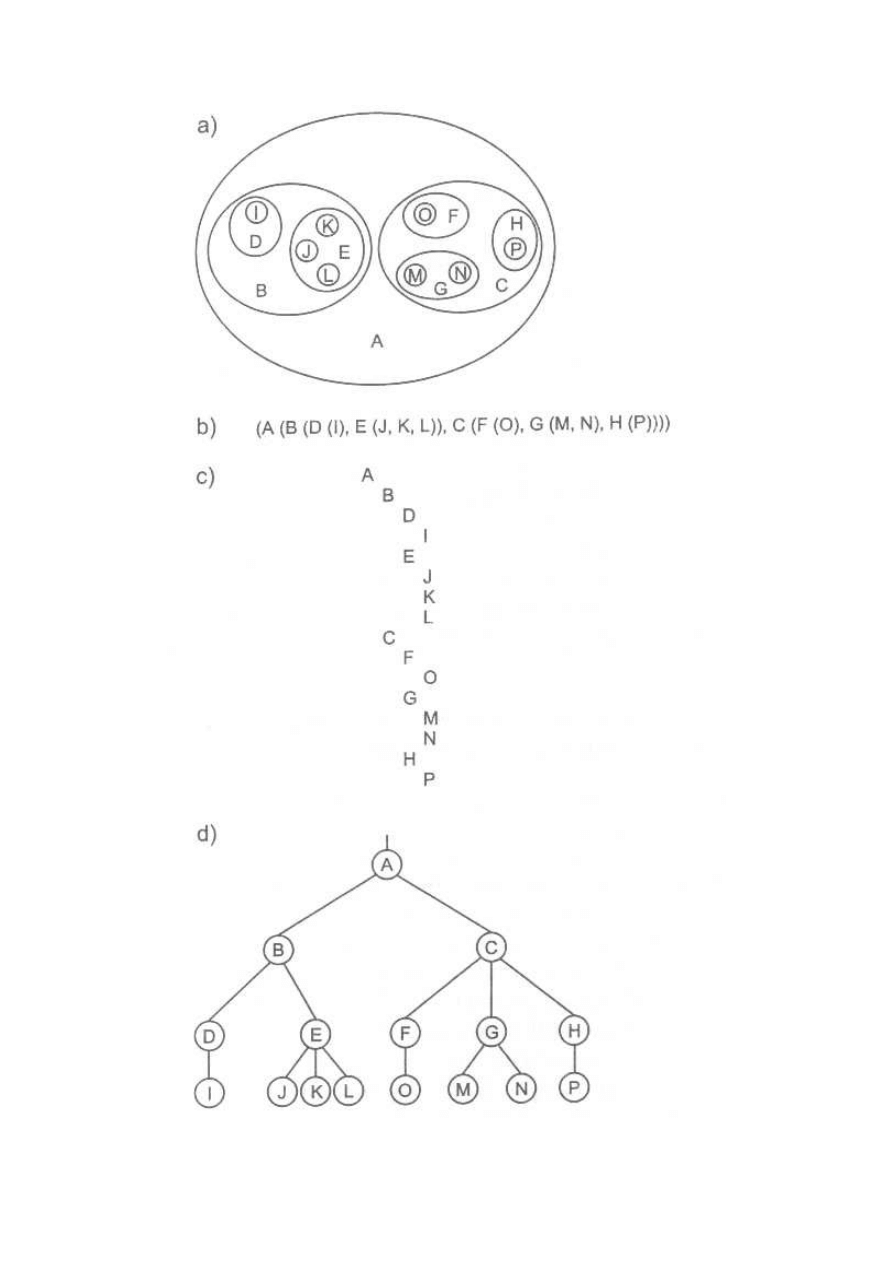
Jest wiele sposobów reprezentacji struktur drzewiastych. Na przykład niech
typ podstawowy T obejmuje litery; odpowiednia struktura jest przedstawiona
na kilka sposobów na rys. 1. Wszystkie reprezentacje mają taką samą strukturę
i dlatego są równoważne. Spośród nich graf najwyraźniej ilustruje relacje
powiązań. Charakter tych powiązań uzasadnia wybór nazwy struktury -
„drzewo". Rzecz dziwna, zwykle rysuje się drzewo odwrócone lub - wyrażając
ten fakt inaczej - uwidacznia się korzenie drzewa.
- 2 -
Rysunek 1

- 3 -
Terminologia
Korzeniem drzewa nazywamy zwykle najwyższy węzeł (A). Drzewem
uporządkowanym jest drzewo, w którym gałęzie każdego węzła są
uporządkowane. Węzeł y, który znajduje się bezpośrednio poniżej węzła x,
nazywamy (bezpośrednim) potomkiem x. Jeżeli x znajduje się na poziomie
i, to mówimy, że y znajduje się na poziomie i + 1. I odwrotnie, węzeł x
nazywany (bezpośrednim) przodkiem y. Poziom korzenia drzewa
definiujemy jako 1. Maksymalny poziom wszystkich elementów drzewa
nazywamy jego głębokością lub wysokością. Element nie mający
potomków nazywamy elementem końcowym lub liściem. Element nie
będący liściem nazywamy węzłem wewnętrznym. Liczbę (bezpośrednich)
potomków wewnętrznego węzła nazywamy jego stopniem. Maksymalny
stopień wszystkich węzłów jest stopniem drzewa. Liczbę gałęzi lub krawędzi,
przez które należy przejść od korzenia do węzła x, nazywamy długością
ścieżki (lub drogi) x. Długość ścieżki korzenia jest równa 1, jego bezpośredni
potomek ma długość ścieżki równą 2 itd. Ogólnie, długość ścieżki węzła na
poziomie i jest równa i. Długość ścieżki drzewa definiujemy jako sumę długości
ścieżek wszystkich jego składowych. Nazywamy ją także długością ścieżki
wewnętrznej. Na przykład długość ścieżki wewnętrznej drzewa z rys. 1 równa
jest 52.
Drzewo jest doskonale zrównoważone (dokładnie wyważone), jeżeli dla
każdego węzła liczby węzłów w jego lewym i prawym poddrzewie różnią się co
najwyżej o 1.
- 4 -
Drzewa binarne
Drzewa uporządkowane o stopniu 2 okazują się szczególnie ważne. Nazywane
są drzewami binarnymi. Uporządkowane drzewo binarne definiujemy jako
skończony zbiór elementów (węzłów), który jest albo pusty, albo zawiera
korzeń (węzeł) z dwoma rozłącznymi binarnymi drzewami zwanymi lewym
i prawym poddrzewem korzenia.
Każdy węzeł ma co najwyżej 2 następniki, które potocznie nazywane są
„lewym” i „prawym”. Dodatkowo, jeśli wiadomo, że dla każdego węzła t
i
wszystkie klucze z lewego poddrzewa węzła t
i
są mniejsze od klucza węzła t
i
,
a klucze z prawego poddrzewa są od niego większe, to mamy do czynienia
wtedy z drzewem poszukiwań. W drzewie takim można znaleźć określony
klucz, posuwając się wzdłuż ścieżki poszukiwania – począwszy od korzenia –
i przechodząc do lewego lub prawego poddrzewa danego węzła w zależności
tylko od wartości klucza w tym węźle.
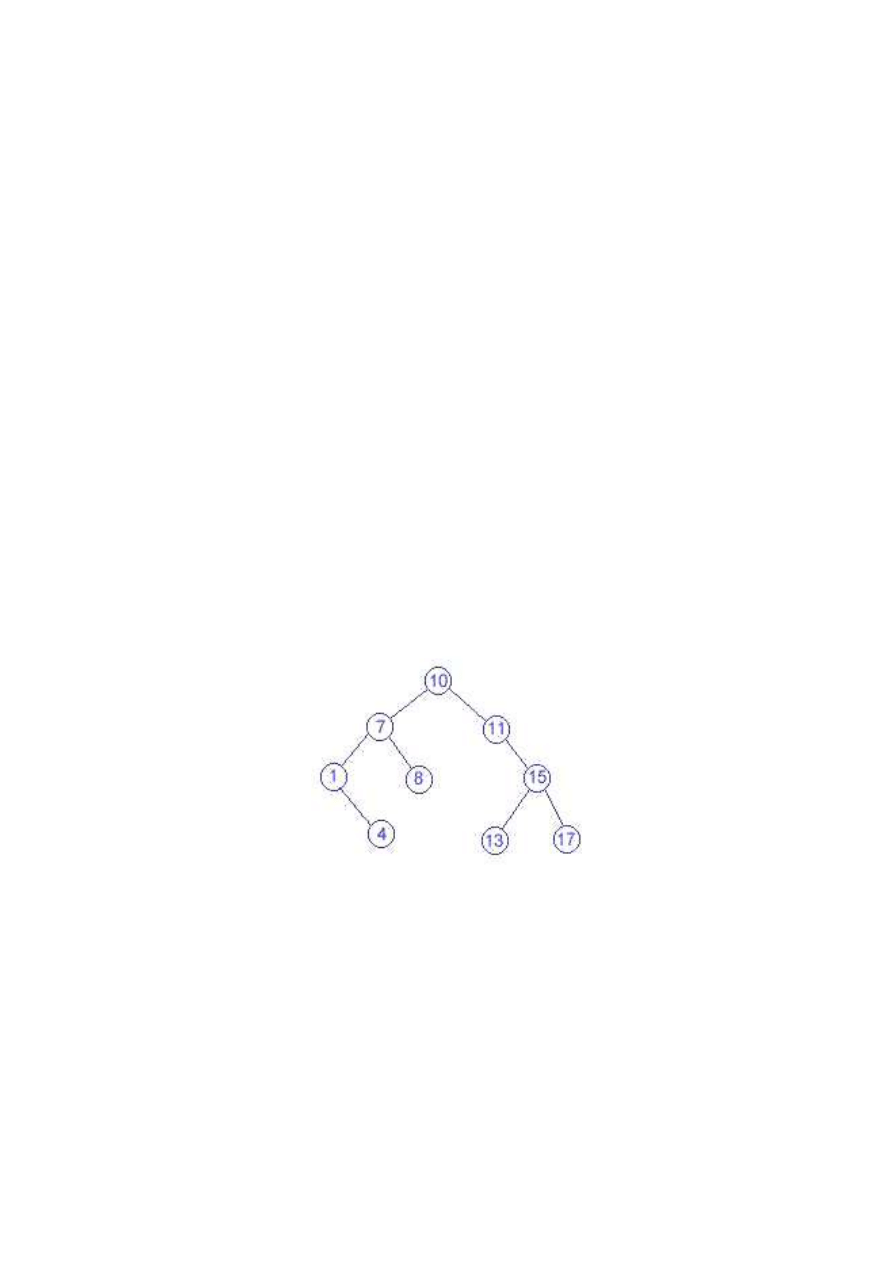
Rysunek 2
Drzewo w swym korzeniu ma wartość 10. Zauważmy, że wszystkie wartości
leżące na jego lewych gałązkach są od 10 mniejsze, a na prawych większe.
Możemy przyjrzeć się np. poddrzewu o wartości korzenia 7. Znów sytuacja się
powtarza - wszystko, co po lewej stronie jest mniejsze, a to co po prawej -
większe.
- 5 -
Przeglądanie drzewa
Czynnością powszechnie wykonywaną na strukturze drzewiastej jest
odwiedzanie wszystkich węzłów, nazywane zwykle przeglądaniem drzewa
(przechodzeniem drzewa). Jeśli rozważymy to zadanie jako proces
sekwencyjny, to odwiedzanie pojedynczych węzłów odbywa się w pewnym
porządku i można uważać, że węzły zostały ułożone wzdłuż linii.
Istnieją trzy podstawowe uporządkowania wynikające w sposób naturalny ze
struktury drzew. Podobnie jak samą strukturę drzewiastą można je zręcznie
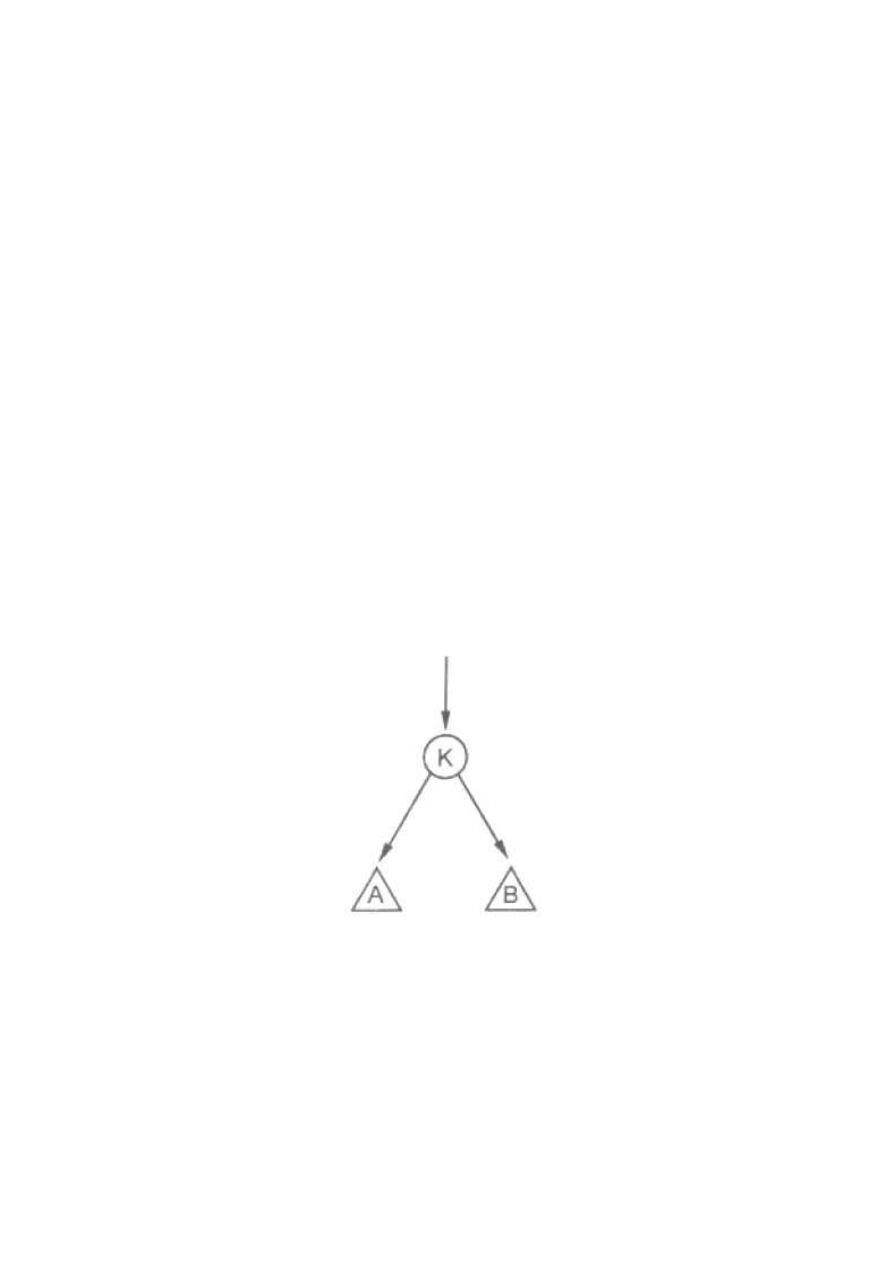
wyrazić za pomocą pojęć rekurencyjnych. Powołując się na drzewo binarne z
rys. 3, w którym K oznacza korzeń, A i B zaś – lewe i prawe poddrzewa,
wyróżniamy trzy porządki:
1) preorder (wzdłużny): K, A, B (odwiedzamy korzeń przed poddrzewami);
2) inorder (poprzeczny): A, K, B;
3) postorder (wsteczny): A, B, K (odwiedzamy korzeń po poddrzewach).
Rysunek 3

- 6 -
Implementacja
Przyjmujemy następujące definicje typów danych:
type
wsk = ^wezel;
wezel = record
klucz : integer;
licznik : integer;
lewe, prawe : wsk;
end;
Procedura Drukowanie odpowiada za wydruk powstałego drzewa na ekranie.
Zastosowano metodę inorder, dzięki czemu wydrukowane elementy są
uporządkowane rosnąco.
procedure Drukowanie (w : wsk; l : integer);
var
i : integer;
begin
if w <> nil then
with w^ do
begin
Drukowanie (lewe, l+1);
for i := 1 to l do
write (' ');
writeln (klucz);
Drukowanie (prawe, l+1);
end
end;
Procedura Szukaj_i_Wstaw szuka w drzewie elementu x, jeśli taki element
się znajduje, wtedy zwiększa licznik o 1, a jeśli nie, wtedy element jest
dodawany do drzewa.
Poczynając od pustego drzewa, szukamy w drzewie danego słowa. Po jego
znalezieniu zwiększa się licznik wystąpień. W przeciwnym razie jest ono
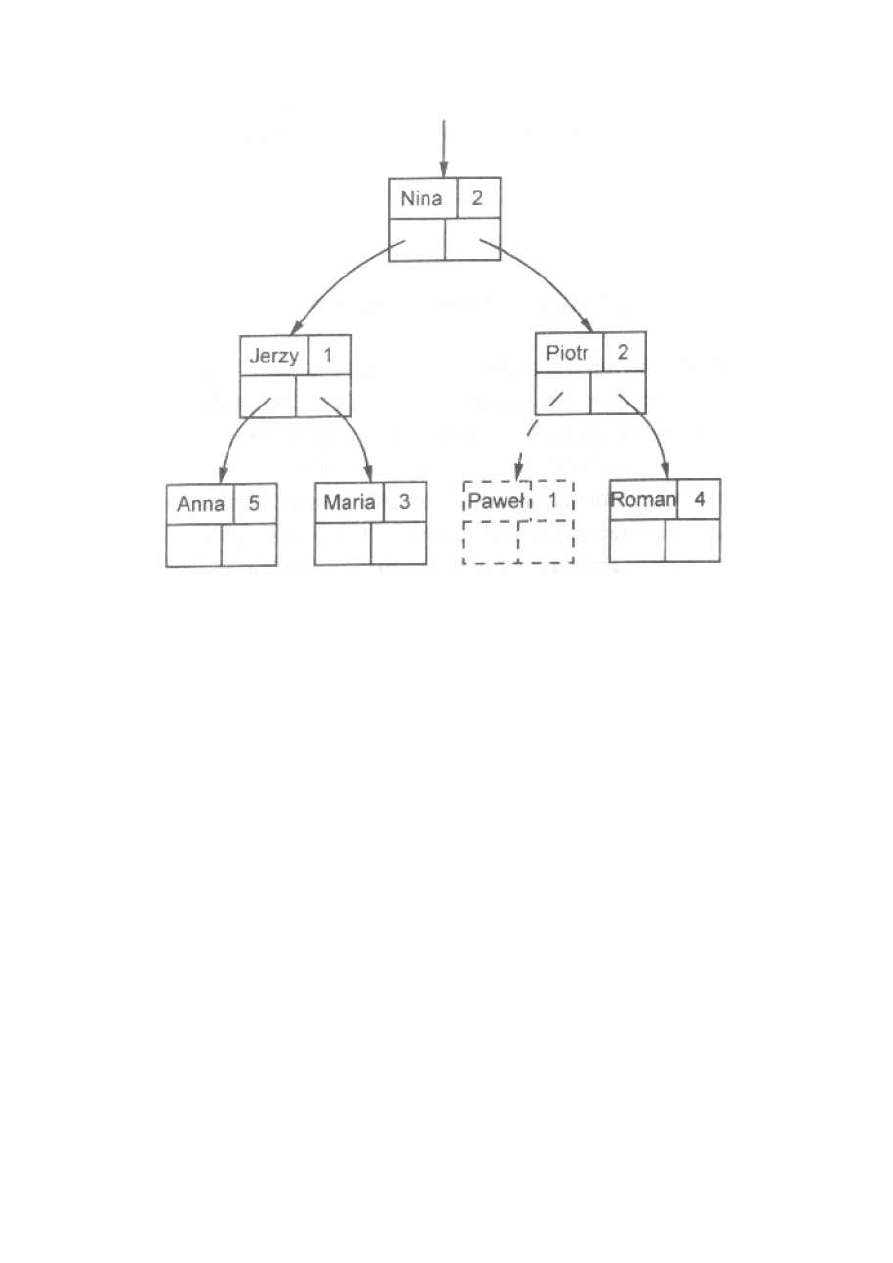
wstawiane jako nowe słowo (z licznikiem równym 1). Rozważmy na przykład
drzewo binarne z rys. 4 i wstawienie słowa „Paweł”. Wynik oznaczono liniami
przerywanymi na tym samym rysunku.
- 7 -
Rysunek 4
Proces przeszukiwania jest sformułowany w postaci procedury rekurencyjnej.
Zwróćmy uwagę, że parametr p jest przekazywany przez zmienną, a nie przez
wartość. Jest to istotne, gdyż przy wstawianiu zmiennej mającej uprzednio
wartość nil musi być przypisana nowa wartość wskaźnika.
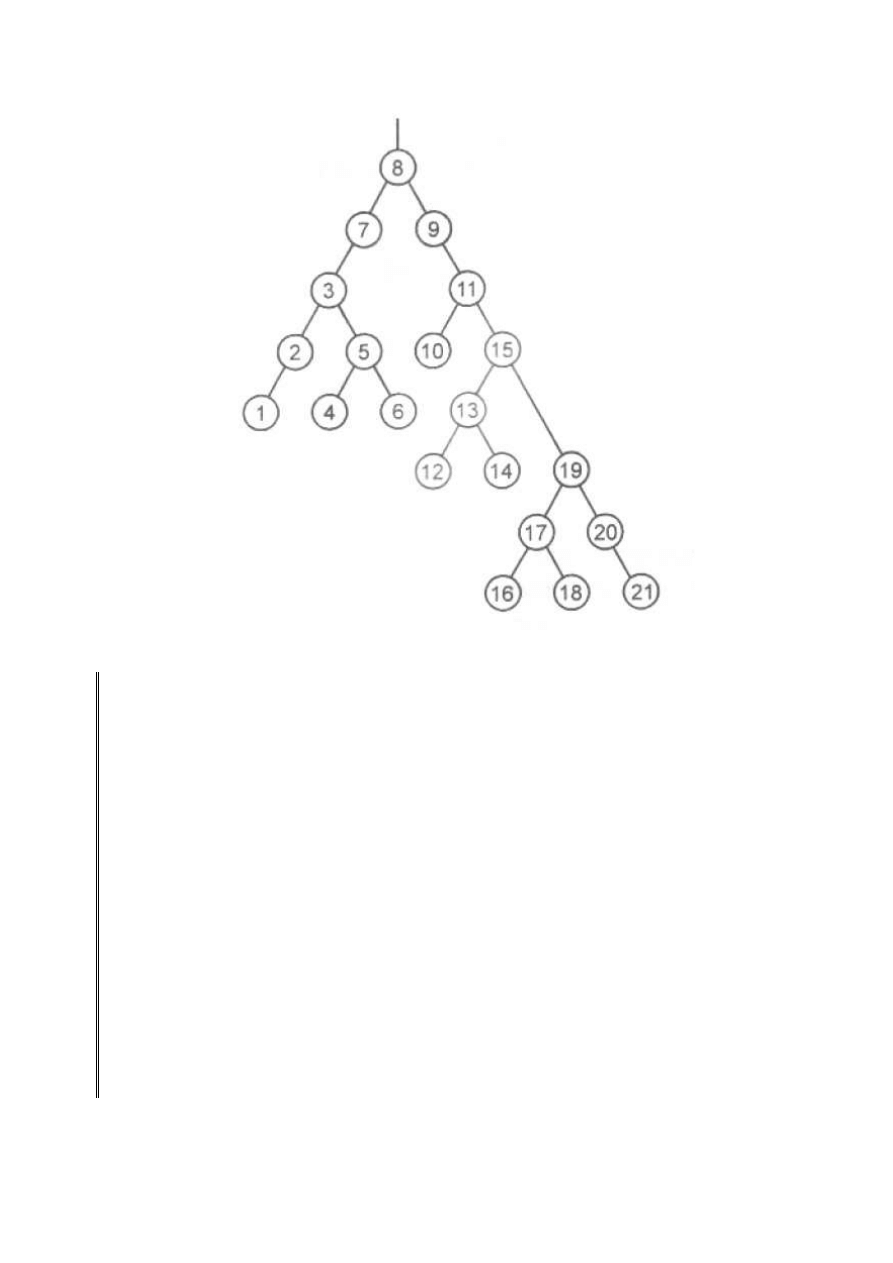
Korzystając z ciągu wejściowych 21 liczb:
8 9 11 15 19 20 21 7 3 2 1 5 6 4 13 14 10 12 17 16 18
program daje w wyniku drzewo binarne pokazane na rys. 5.
- 8 -
Rysunek 5
procedure Szukaj_i_Wstaw (x : integer; var p : wsk);
begin
if p = nil then
begin
new (p);
with p^ do
begin
klucz := x;
licznik := 1;
lewe := nil;
prawe := nil;
end;
writeln ('Elementu nie bylo w drzewie. Wstawiono nowy wezel.');
end
else
if x < p^.klucz then
Szukaj_i_Wstaw (x, p^.lewe)
else if x > p^.klucz then
Szukaj_i_Wstaw (x, p^.prawe)
else
begin
p^.licznik := p^.licznik + 1;
writeln ('Element zjadowal sie w drzewie. Zwiekszono licznik o 1.');
end;
end;

- 9 -
Przejdźmy teraz do problemu odwrotnego względem wstawiania, tj. do
usuwania. Zadaniem naszym jest zdefiniowanie algorytmu usuwania węzła o
kluczu x z drzewa z uporządkowanymi kluczami. Niestety, usunięcie elementu
nie jest na ogół takie proste jak wstawienie. Jest to łatwa operacja wtedy, gdy
usuwany element jest węzłem końcowym lub ma tylko jednego potomka.
Trudności pojawiają się przy usuwaniu elementu mającego dwóch potomków,
ponieważ jednym wskaźnikiem nie możemy wskazać dwóch kierunków. W tej
sytuacji usuwany element musi być zastąpiony przez skrajny prawy element
lewego poddrzewa lub skrajny lewy węzeł prawego poddrzewa, z których każdy
ma co najwyżej jednego potomka. Szczegóły algorytmu są zawarte w
rekurencyjnej procedurze Usuń. Rozróżnia się w niej trzy przypadki:
1) Brak składowej o kluczu równym x.
2) Składowa o kluczu x ma co najwyżej jednego potomka.
3) Składowa o kluczu x ma dwóch potomków.
Pomocnicza procedura rekurencyjna Us jest wywoływana tylko w trzecim
przypadku. „Schodzi” ona wzdłuż skrajnej prawej krawędzi lewego poddrzewa
elementu q^, który należy usunąć, a następnie wymienia związaną z q^
informację (klucz i licznik) na odpowiadające wartości skrajnie prawego
składnika r^ lewego poddrzewa, po czym r^ może być zwolniony.
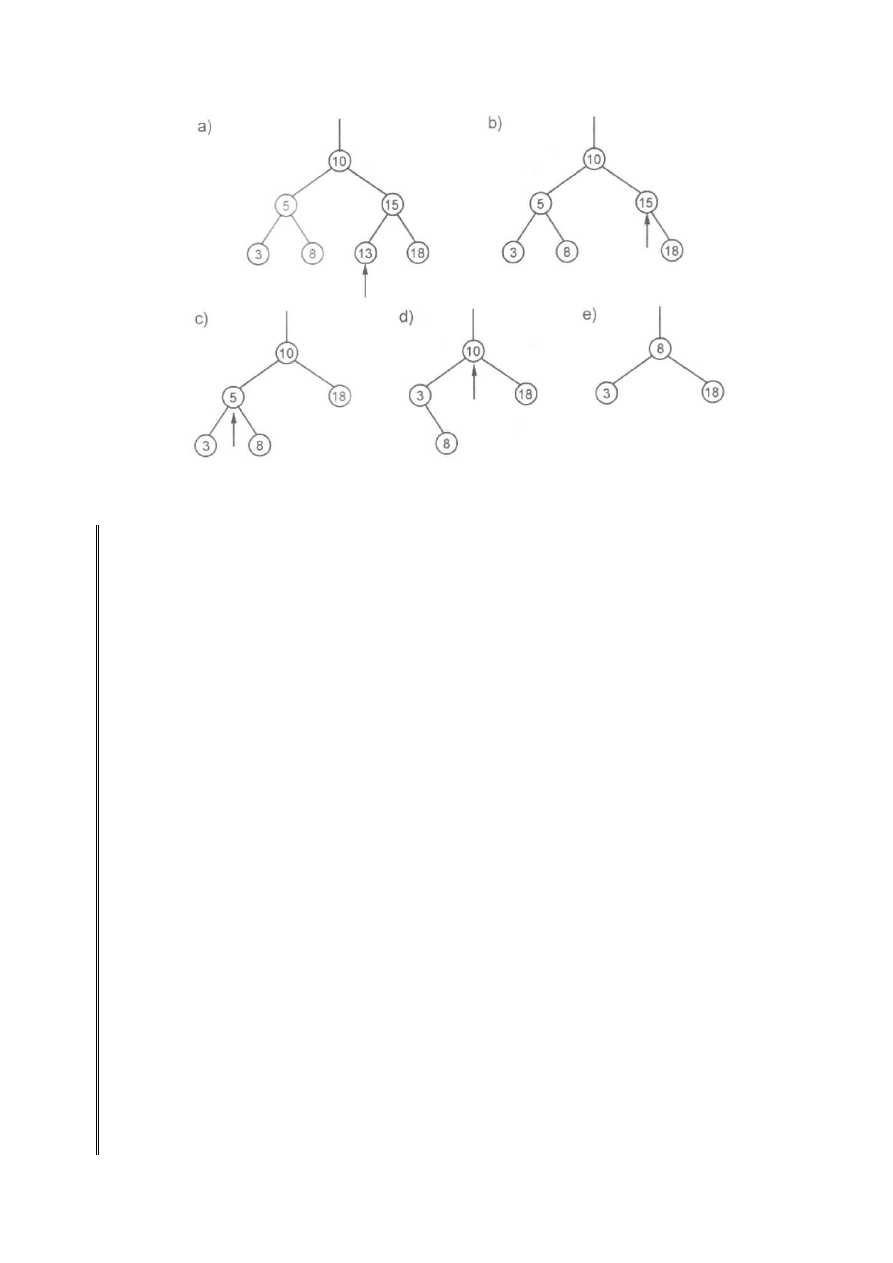
Aby zilustrować funkcjonowanie procedury, odwołamy się do rys. 6. Mamy
dane drzewo (a), następnie usuwamy kolejno węzły o kluczach 13, 15, 5, 10.
Drzewo powstałe w wyniku tej operacji pokazano na rysunku.
- 10 -
Rysunek 6
procedure Usun (x : integer; var p : wsk);
var
q : wsk;
procedure Us (var r : wsk); { Procedura pomocnicza Us }
begin
if r^.prawe <> nil then
Us (r^.prawe)
else
begin
q^.klucz := r^.klucz;
q^.licznik := r^.licznik;
q:= r;
r:= r^.lewe;
end;
end; {--- Us -}
begin
if p = nil then
writeln ('Brak slowa w drzewie.')
else
if x < p^.klucz then
Usun (x, p^.lewe)
else
if x > p^.klucz then
Usun (x, p^.prawe)
else
begin { Usun p^ }
q := p;
if q^.prawe = nil then
p := q^.lewe
else
if q^.lewe = nil then
p := q^.prawe
else Us (q^.lewe);
end
end;

- 11 -
Program drzewo.pas
program Drzewo_Binarne;
uses
Crt;
type
wsk = ^wezel;
wezel = record
klucz : integer;
licznik : integer;
lewe, prawe : wsk;
end;
var
korzen : wsk;
k : integer;
co : char;
procedure Drukowanie (w : wsk; l : integer);
var
i : integer;
begin
if w <> nil then
with w^ do
begin
Drukowanie (lewe, l+1);
for i := 1 to l do
write (' ');
writeln (klucz);
Drukowanie (prawe, l+1);
end
end; {--- Drukowanie -}
procedure Szukaj_i_Wstaw (x : integer; var p : wsk);
{ Procedura szuka w drzewie elementu x, jesli taki element sie
znajduje, }
{ wtedy zwieksza licznik o 1, a jesli nie, wtedy elemet jest dodawany
do drzewa }
begin
if p = nil then
begin
new (p);
with p^ do
begin
klucz := x;
licznik := 1;
lewe := nil;
prawe := nil;
end;
writeln ('Elementu nie bylo w drzewie. Wstawiono nowy
wezel.');
end
else
if x < p^.klucz then
Szukaj_i_Wstaw (x, p^.lewe)
else if x > p^.klucz then
Szukaj_i_Wstaw (x, p^.prawe)
else
begin
p^.licznik := p^.licznik + 1;
writeln ('Element zjadowal sie w drzewie. Zwiekszono licznik
o 1.');
end;
end; {--- Szukaj_i_Wstaw -}
procedure Usun (x : integer; var p : wsk);
var
q : wsk;
procedure Us (var r : wsk); { Procedura pomocnicza Us }
begin
if r^.prawe <> nil then
Us (r^.prawe)
else
begin
q^.klucz := r^.klucz;
q^.licznik := r^.licznik;
q:= r;
r:= r^.lewe;
end;
end; {--- Us -}
begin
if p = nil then
writeln ('Brak slowa w drzewie.')
else
if x < p^.klucz then
Usun (x, p^.lewe)
else
if x > p^.klucz then
Usun (x, p^.prawe)
else
begin { Usun p^ }
q := p;
if q^.prawe = nil then
p := q^.lewe
else
if q^.lewe = nil then
p := q^.prawe
else Us (q^.lewe);
end
end; {--- Usun -}
begin { Main }
korzen := nil; { Utworzenie pustego drzewa }
repeat
ClrScr;
writeln ('Wybierz operacje: ');
writeln ('1 - Drukowanie drzewa');
writeln ('2 - Szukaj i Wstaw');
writeln ('3 - Usun z drzewa');
writeln ('4 - Aktualizacja');
writeln;
writeln ('0 - Koniec programu');
writeln;
co := readkey;
case co of
'1' : begin
Drukowanie (korzen, 3);
write ('Nacisnij Enter, aby kontynuowac');
readln;
end;
'2' : begin
write ('Podaj wartosc k: ');
readln (k);
Szukaj_i_Wstaw (k, korzen);
write ('Nacisnij Enter,
aby kontynuowac');
readln;
end;
'3' : begin
write ('Podaj wartosc k: ');
readln (k);
Usun (k, korzen);
end;
'4' : begin
write ('Podaj stara wartosc: ');
readln (k);
Usun (k, korzen);
write ('Podaj nowa wartosc: ');
readln (k);
Szukaj_i_Wstaw (k, korzen);
end;
end;
until co = '0';
end. {--- Main -}
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron