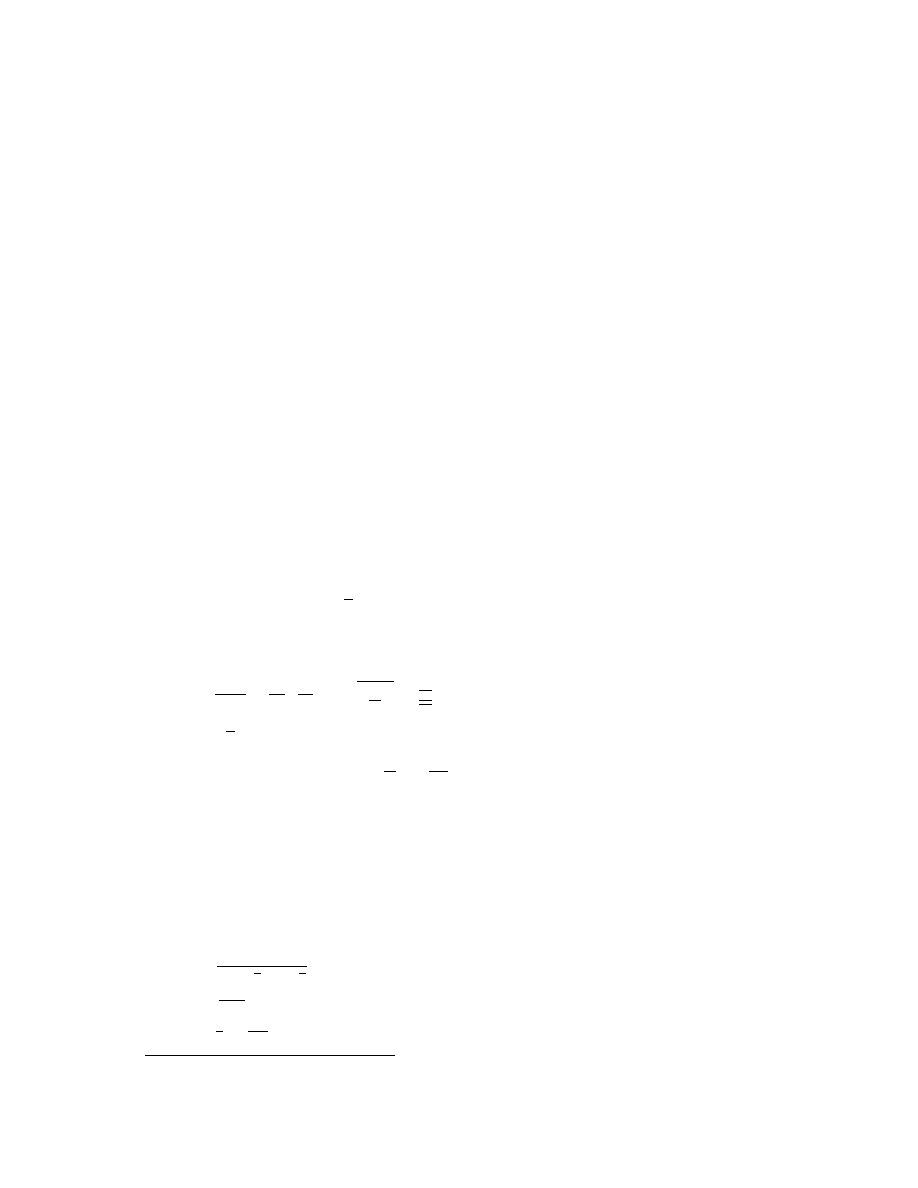
Zestaw 2.

Liczby zespolone (cz. I)

Zadanie 1.

Udowodni´c nast ¾

epuj ¾

ace w÷

asno´sci dzia÷

a´n w zbiorze liczb zespolonych:

a)

8z

1

; z

2

2 C : z

1

+ z

2

= z

2

+ z

1

;

b)

8z

1

; z

2

; z

3

2 C : (z

1

+ z

2

) + z

3

= z

1

+ (z

2

+ z

3

) ;

c)

8z 2 C : z + 0 = z; gdzie 0

df

= (0; 0) ;

d)

8z 2 C : z

z = 0;

e)

8z

1

; z

2

2 C : z

1

z

2

= z

2

z

1

;

f )

8z

1

; z

2

; z

3

2 C : (z

1

z

2

) z

3

= z

1

(z

2

z

3

) ;

g)

8z 2 C : z 1 = z, gdzie 1

df

= (1; 0) ;

h)

8z 2 Cn f0g 9!z

0

2 C : zz

0

= 1;

1

i)

8z

1

; z

2

; z

3

2 C : z

1

(z

2

+ z

3

) = z

1

z

2

+ z

1

z

3

:

Zadanie 2.

Niech z; z

1

; z

2

2 C. Poda´c interpretacj ¾

e geometryczn ¾

a nast ¾

epuj ¾

acych

liczb:

a) z; b) z; c) z

1

+ z

2

;

d) z

1

z

2

;

e) jzj ; f)* z

1

z

2

:

Zadanie 3.

Dla liczb zespolonych uzasadni´c poni·

zsze zale·

zno´sci:

a)

z

1

z

2

= z

1

z

2

oraz

z

1

z

2

=

z

1

z

2

, dla z

2

6= 0;

b)

zz =

jzj

2

;

c)

jz

1

z

2

j = jz

1

j jz

2

j oraz

z

1

z

2

=

jz

1

j

jz

2

j

;

dla z

2

6= 0,

d)

Re z

6 jzj oraz Im z 6 jzj;

e)

jz

1

+ z

2

j 6 jz

1

j + jz

2

j;

f )

jjz

1

j

jz

2

jj 6 jz

1

z

2

j.

Zadanie 4.

Sprowadzi´c do postaci algebraicznej (dwumiennej) nast ¾

epuj ¾

ace

wyra·

zenia:

a)

1

1+cos

3

+i sin

3

;

b)

1 2i
3i+2

;

c)

1

i

+

2+i
2 i

;

1

Symbol 9! oznacza „istnieje dok÷adnie jeden”.

1

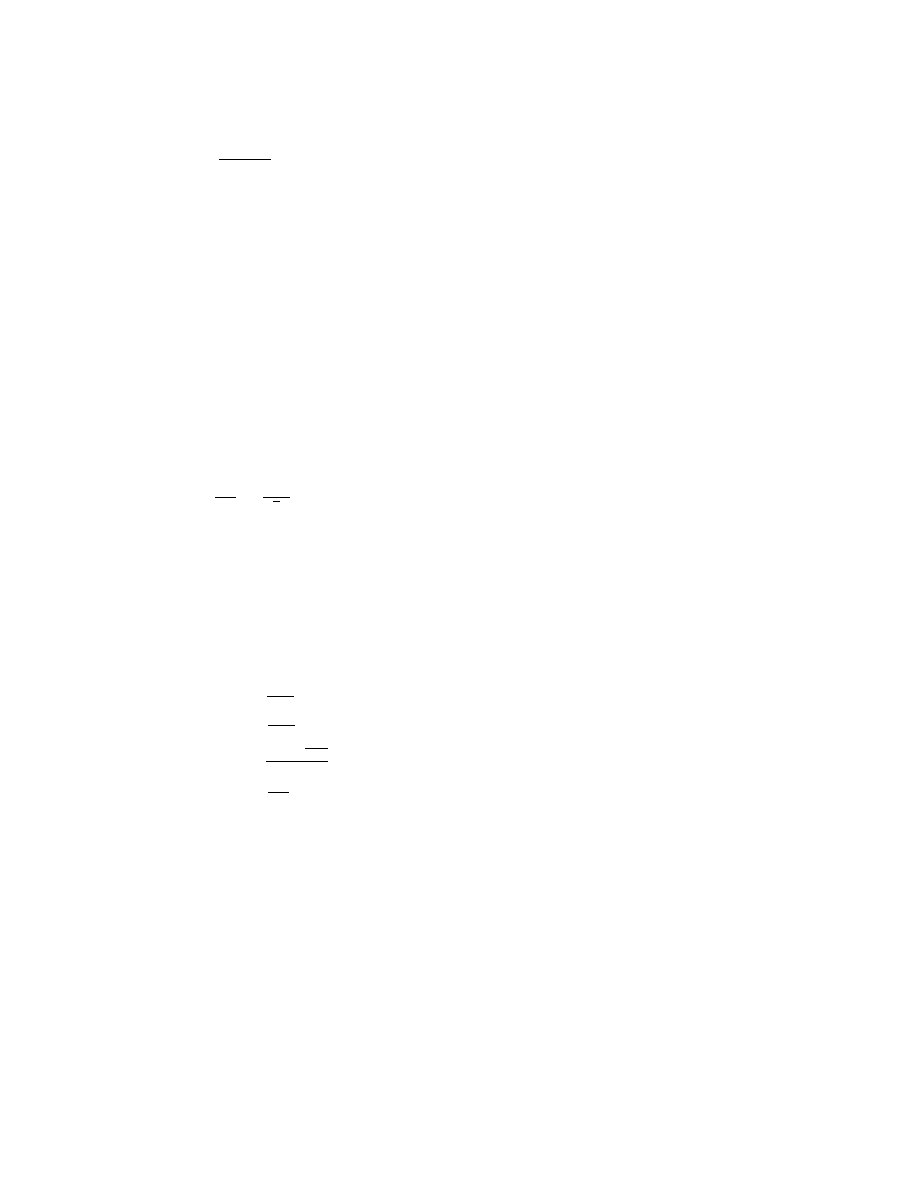
d)

(1+i)

n

(1 i)

n

2

;

dla n 2 N;

e)*

(cos

+ i sin )

n

;

dla n 2 N;

f )*

(sin

+ i cos )

n

;

dla n 2 N.

Zadanie 5.

Rozwi ¾

aza´c równania z niewiadomymi z 2 C; x; y 2 R:

a)

z

2

+ (3

2i) z + 1

3i = 0;

b)

jzj + z = 1 + i;

c)

(1 + 2i) x + (2

2i) y = 5 + 4i

(3

i) x + (4 + 2i) y = 2 + 6i

;

d)

(1

2i) x

(1

4i) y = 2

2i

( 2

i) x + (2 + 2i) y =

4

i

;

e)

(z

2)

2

+ 2 Im z + z = 1;

f )

1+i

z

=

2 3i

z

;

g)

z

4

+ 4z

2

5 = 0;

h)

z

4

+ 4z

2

+ 8 = 0;

i)

(3

i) x

2

(3 + 2i) x

(1

i) y = 13

10i;

j)

(2 + 3i) x

2

(2 + i) x + (4

4i) y = 8

17i:

Zadanie 6.

Na p÷

aszczy´znie zespolonej zaznaczy´c liczby zespolone z, dla których

a)

liczba

z+4

z 2i

jest rzeczywista,

b)

liczba

z

iz+4

jest czysto urojona,

c)

liczba

(z a)

2

z a

z a

2

jest niedodatnia,

d)

liczba

z+i
z i

nie jest ujemna.

Zadanie 7.

Na p÷

aszczy´znie zespolonej zaznaczy´c wszystkie liczby zespolone z,

których modu÷jest liczb ¾

a ca÷

kowit ¾

a oraz dla których liczba z

2

+ (1 + i) z

jest

czysto urojona.

2

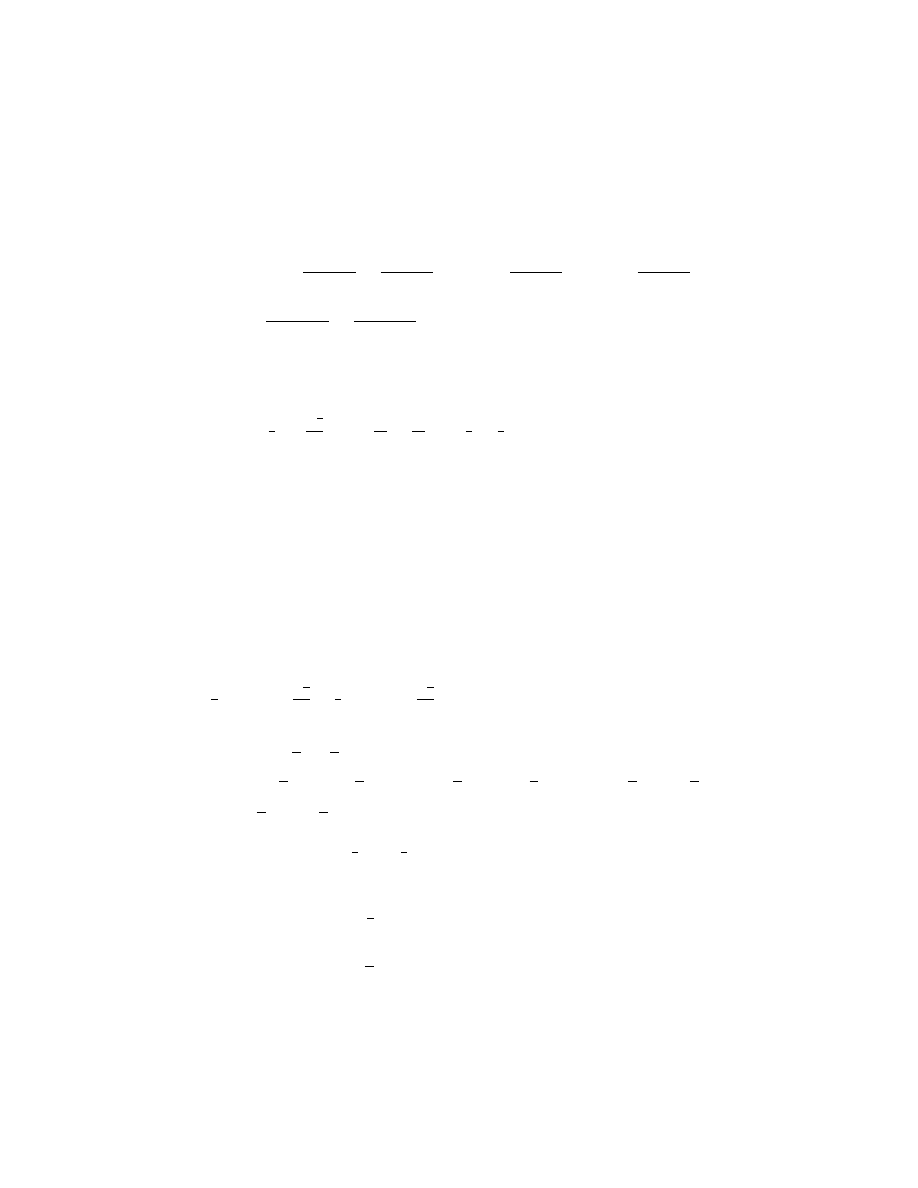
Odpowiedzi

Zadanie 3:

c) Wskazówka: wykorzysta´c w÷

asno´sci a) i b); e) Wskazówka: dla

z

1

+ z

2

6= 0 mamy:

1 = Re

z

1

z

1

+ z

2

+

z

2

z

1

+ z

2

= Re

z

1

z

1

+ z

2

+ Re

z

2

z

1

+ z

2

d)+c)

6

6

jz

1

j

jz

1

+ z

2

j

+

jz

1

j

jz

1

+ z

2

j

;

f) jz

1

j = jz

1

z

2

+ z

2

j

e)

6 jz

1

z

2

j + jz

2

j, nast¾

epnie zamieni´c rol ¾

a z

1

i z

2

.

Zadanie 4:

a)

1
2

i

p

3

6

;

b)

4

13

7

13

i;

c)

3
5

i

5

;

d) 2i

n 1

;

e) cos n + i sin n ;

f) i

n

(cos n

i sin n ) =

=

(

( 1)

n=2

cos n + i ( 1)

1+n=2

sin n

,

n = 2k

( 1)

(n 1)=2

sin n + i ( 1)

(n 1)=2

cos n

, n = 2k + 1

;

dla k 2 N:

Zadanie 5:

a)

2 + i;

1 + i;

b) i;

c) ?;
d) x = 3; y = 1;

e)

3
2

+ i 1 +

p

7

2

;

3
2

+ i 1

p

7

2

;

f) ?;
g)

1; 1;

i

p

5; i

p

5;

h)

1

p

2;

1 +

p

2 ;

1 +

p

2;

1

p

2 ;

1 +

p

2; 1 +

p

2 ;

1

p

2; 1

p

2 ;

i) (x; y) 2 f(3; 5),

1
2

;

10

3
4

g;

j) ?;

Zadanie 6:

a) (x; y) : y =

1
2

x + 2; x

6= 0 ;

b) f(x; y) : x = 0; y 6= 4g ;
c) z : 0 < jz

a

j 6

p

2 ;

d) Cn fz 2 C : Re z = 0; Im z 2 ( 1; 1]g :

3