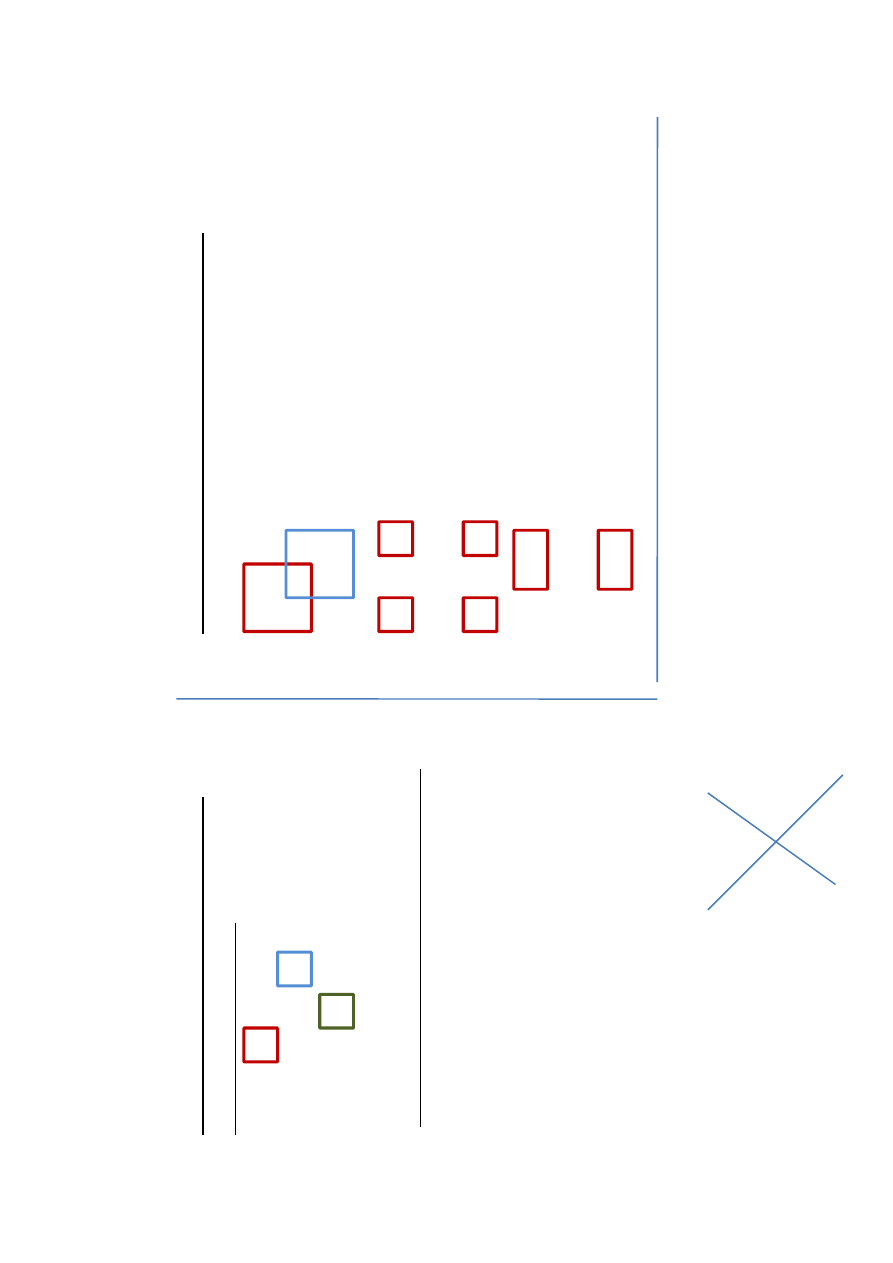
M
ac
ie
rz
e
T
w
or
ze
ni
e
m
ac
ie
rz
y
:
A
=
[
1
2
3;
5
3
2;
1
6
7]
P
ol
ec
eni
e:
1
2
3
5
3
2
1
6
7
A
=
A
(1,
1)
A
(2,
3)
A
(3,
2)
O
dw
oł
ani
e
do
pos
zc
ze
gól
ne
go
el
em
ent
u
m
ac
ie
rz
y
:
O
dw
oł
ani
e
do
da
ne
j
se
kc
ji
m
ac
ie
rz
y
:
1
2
3
5
3
2
1
6
7
A
=
P
ol
ec
eni
e:
A
(1:
2,
1:
2)
A
(2:
3,
2:
3)
1
2
3
5
3
2
A
=
P
ol
ec
eni
e:
A
([
1
3]
,[
1
3]
)
D
oł
ą
cz
ani
e
w
ie
rs
za
do
m
ac
ie
rz
y
:
1
2
3
[
]
2
2
2
u
=
5
3
2
1
6
7
A
=
1
2
3
5
3
2
1
6
7
A
=
P
ol
ec
eni
e:
A
([
1
3]
,[
2:
3]
)
1
2
3
5
3
2
1
6
7
A
=
[
]
2
2
2
u
=
P
ol
ec
eni
e:
A
=
[
A
;
u]
A
=
[
A
;
v’
]
1
2
3
5
3
2
1
6
7
2
2
2
A
=
A
=
[
A
u]
[
]
3;
3;
3
v
=
L
ic
zb
a
k
ol
u
m
n
m
ac
ie
rz
y
A
i
p
rz
y
k
ład
ow
ego
w
ek
tor
a
u
l
u
b
v
m
u
si
b
y
ć
t
ak
a
sam
a:
A
=
[
A
;
1
2
3]
M
ac
ie
rz
e
D
oł
ą
cz
ani
e
kol
um
ny
do
m
ac
ie
rz
y
:
1
2
3
5
3
2
1
6
7
A
=
[
]
2
2
2
u
=
[
]
3;
3;
3
v
=
P
ol
ec
eni
e:
A
=
[
A
u’
]
A
=
[
A
v]
A
(:
,
4)
=
[
1
;2;
3]
P
odm
ia
na
da
ne
go
w
ie
rs
za
m
ac
ie
rz
y
:
1
2
3
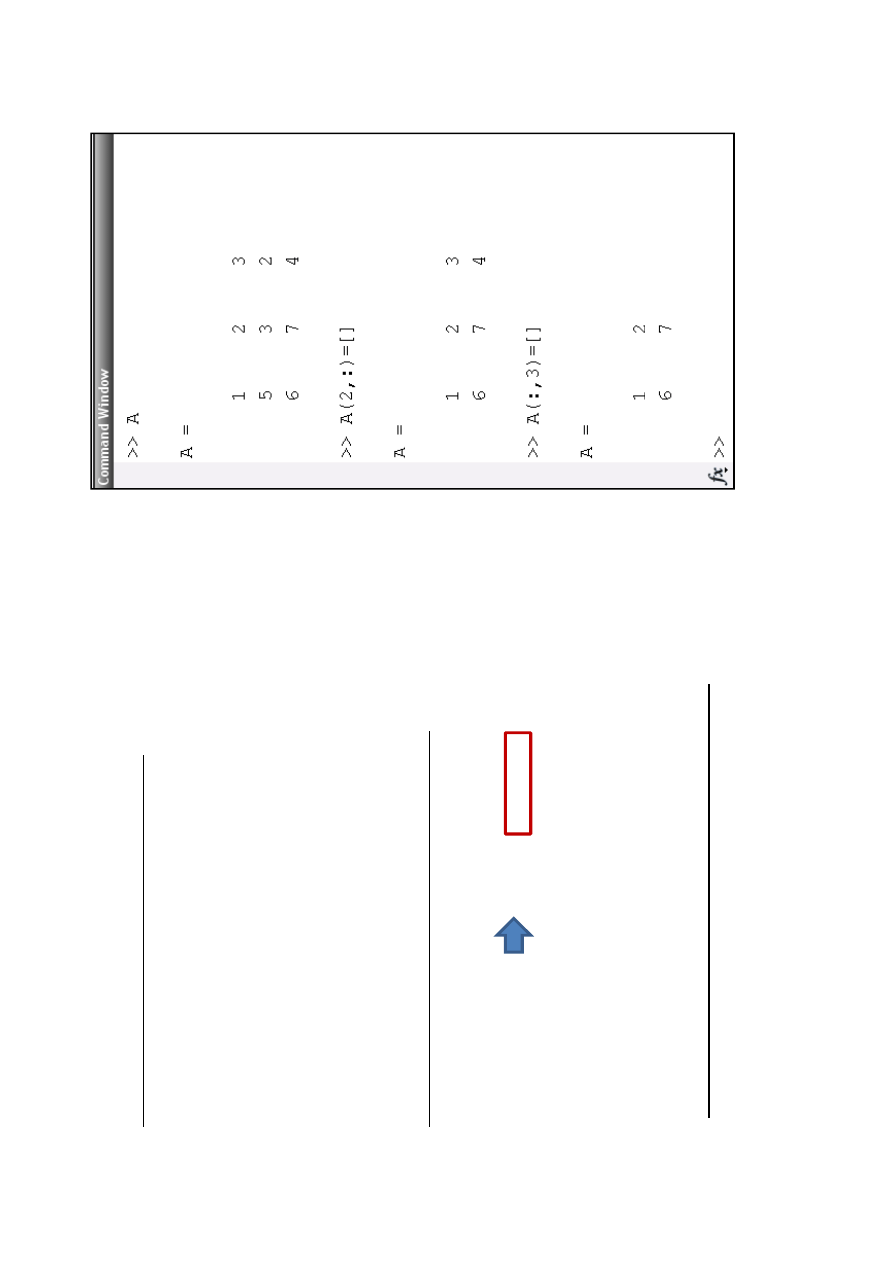
P
ol
ec
eni
e:
A
(2
,
:)
=
u
1
2
3
5
3
2
1
6
7
A
=
[
]
2
2
2
u
=
1
2
3
2
2
2
1
6
7
A
=
U
suw
ani
e
w
ie
rs
za
/
kol
um
ny
m
ac
ie
rz
y
:
P
ol
ec
eni
e:
A
(2
,
:)
=
[
]
-
us
uw
a
2
w
ie
rs
z
m
ac
ie
rz
y
A
P
ol
ec
eni
e:
A
(:
,
2)
=
[
]
-
us
uw
a
2
kol
um
n
ę
m
ac
ie
rz
y
A
P
ol
ec
eni
e:
A
(2:
3
,
:)
=
[
]
-
us
uw
a
2
i
3
w
ie
rs
z
m
ac
ie
rz
y
A
M
ac
ie
rz
e
D
oda
w
ani
e
i
ode
jm
ow
ani
e
m
ac
ie
rz
y
:
M
o
ż
n
a
d
od
aw
a
ć
i
od
ej
m
ow
a
ć
t
y
lk
o
m
ac
ie
rz
e
o
ty
ch
s
am
y
ch
r
oz
m
iar
ac
h
1
1
1
2
1
1
1
1
2
1
1
1
1
1
1
2
1
2
1
1
2
1
2
2
2
2
1
2
2
2
2
1
2
1
2
2
2
2
2
2
1
2
3
1
2
3
1
1
2
2
3
3
..
.
..
.
..
.
..
.
..
.
..
.
n
n
n
n
n
n
n
n
m
m
m
m
n
m
m
m
m
n
m
m
m
m
m
m
m
n
m
n
a
a
a
b
b
b
a
b
a
b
a
b
a
a
a
b
b
b
a
b
a
b
a
b
a
a
a
a
b
b
b
b
a
b
a
b
a
b
a
b
+
+
+
+
+
+
±
=
+
+
+
+
M
M
M
M
M
M
M
M
M
M
M
M
A
B
C
M
no
ż
eni
e
m
ac
ie
rz
y
:
M
no
ż
eni
e
m
ac
ie
rz
y
:
2
4
1
2
5
6
7
1
2
2
5
1
A
=
1
2
5
2
7
1
2
6
2
1
1
1
B
=
2
8
2
2
4
2
8
6
2
1
0
4
2
2
5
1
2
1
4
1
1
0
4
2
4
2
1
2
5
6
1
4
1
2
4
1
0
1
4
1
4
3
0
1
1
0
2
1
0
1
A
B
+
+
+
+
+
+
+
+
+
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
1
4
4
0
1
8
3
2
9
5
4
6
1
7
4
9
2
3
A
B
=
M
ac
ie
rz
e
m
o
ż
n
a
p
om
n
o
ż
y
ć
t
y
lk
o
w
te
d
y
,
gd
y
il
o
ść
k
ol
u
m
n
m
ac
ie
rz
y
p
ie
rw
sz
ej
od
p
ow
iad
a
il
o
śc
i
w
ie
rs
zy
w
d
ru
gi
ej
m
ac
ie
rz
y
M
ac
ie
rz
e
M
ac
ie
rz
t
ra
ns
ponow
ana
:
1
4
2
2
0
3
5
1
7
A
=
−
T
ij
ji
A
A
=
1
2
5
4
0
1
2
3
7
T
A
−
=
P
ol
ec
eni
e:
A
’
M
ac
ie
rz
odw
rot
na
:
1
1
d
et
D
ij
A
A
A
−
=
⋅
A
D
–
m
ac
ie
rz
doł
ą
cz
ona
D
T
A
A
=
1
3
2
6
1
2
2
9
3
7
2
2
1
8
A
−
−
−
=
−
−
−
−
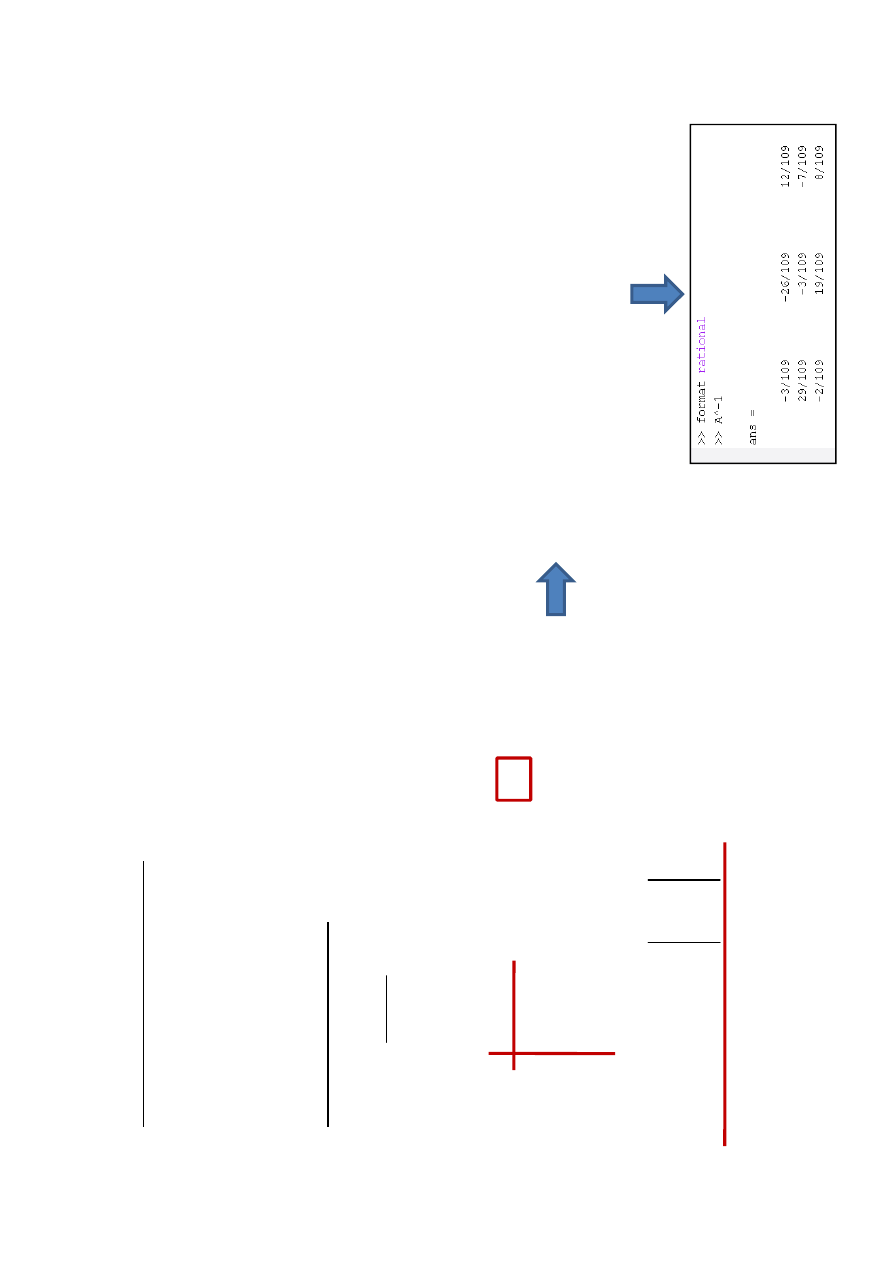
P
ol
ec
eni
e:
A
-1
A
D
–
m
ac
ie
rz
doł
ą
cz
ona
D
T
d
o
p
A
A
=
1
4
2
2
0
3
5
1
7
A
=
−
3
2
9
2
2
6
3
2
1
1
2
7
8
d
o
p
A
−
−
=
−
−
−
−
(
)
(
)
1
1
1
1
0
3
1
1
7
d
o
p
A
+
=
−
A
dop
–
m
ac
ie
rz
dope
łni
e
ń
a
lge
br
ai
cz
ny
ch
3
2
6
1
2
2
9
3
7
2
2
1
8
D
T
d
o
p
A
A
−
−
=
=
−
−
−
−

M
ac
ie
rz
e
–
op
er
at
or
y
r
el
ac
ji
2
4
1
2
5
6
7
1
2
2
5
1
A
=
P
or
ów
n
yw
a
ć
m
o
ż
n
a
ty
lk
o
m
ac
ie
rz
e
o
ty
ch
sam
y
ch
r
oz
m
iar
ac
h
2
2
5
2
3
6
1
0
4
2
6
9
B
=
P
ol
ec
eni
e:
C
=
A
>
B
W
y
ni
k:
0
1
0
0
1
0
1
1
0
0
0
0
B
=
op
er
at
or
y
l
ogi
cz
n
e
P
ol
ec
eni
e:
C
=
(
A
>
B
)
&
(A
>
4)
0
0
0
0
1
0
1
0
0
0
0
0
B
=
W
y
ni
k:
P
oz
os
ta
łe
ope
ra
tor
y
l
ogi
cz
ne
P
ol
ec
eni
e:
C
=
A
<
B
W
y
ni
k:
0
0
1
0
0
0
0
0
1
0
1
1
B
=
P
oz
os
ta
łe
ope
ra
tor
y
r
el
ac
ji
C
=
A
<
=
B
–
m
ni
ej
sz
e
b
ą
d
ź
r
ów
ne
C
=
A
>
=
B
–
w
ię
ks
ze
l
ub
rów
ne
C
=
A
=
=
B
–
rów
ne
C
=
A
~
=
B
–
ró
ż
ne
P
oz
os
ta
łe
ope
ra
tor
y
l
ogi
cz
ne
|
–
logi
cz
ne
O
R
(
al
te
rna
ty
w
a)
~
–
ne
ga
cj
a
xor
–
w
y
kl
uc
za
ją
ce
O
R
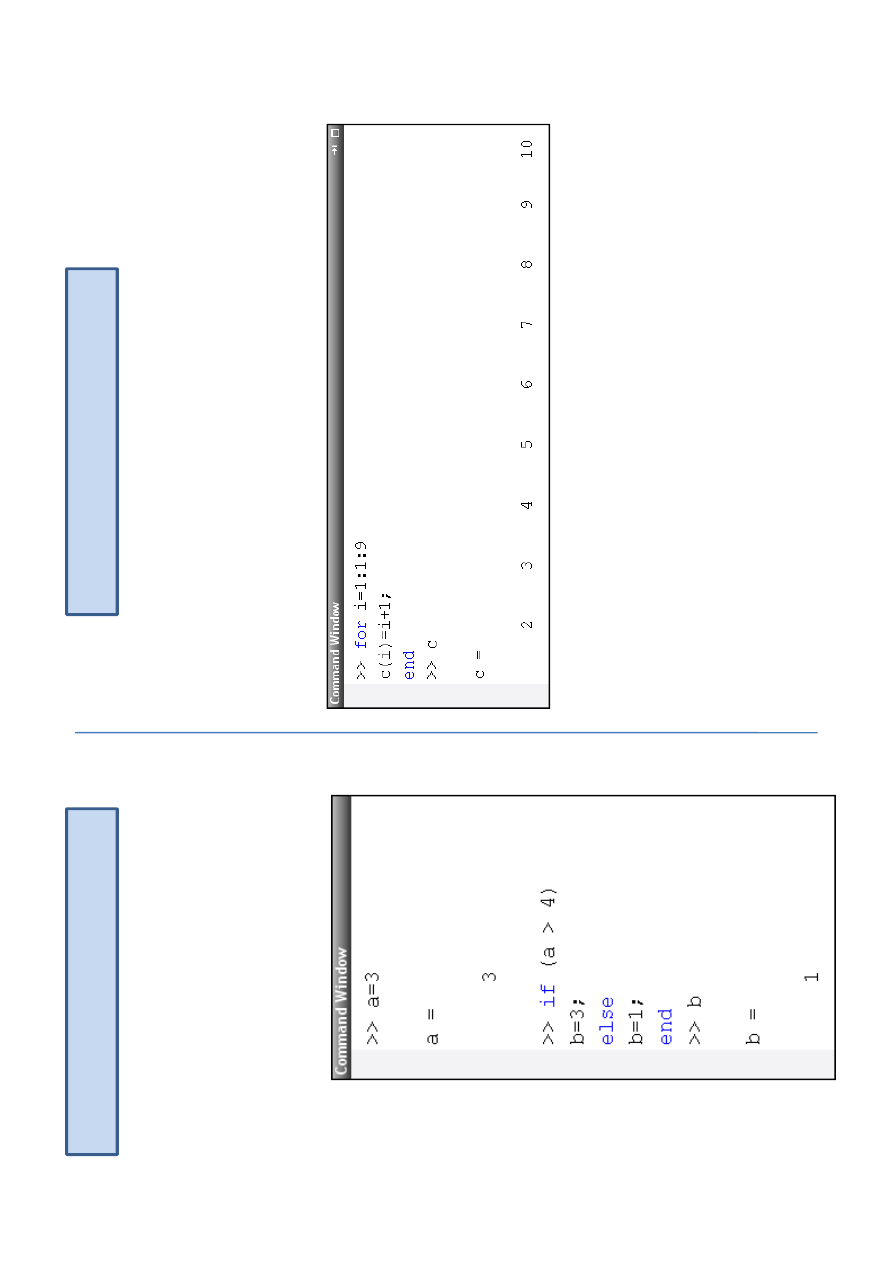
In
st
ru
k
cj
a
w
ar
u
n
k
ow
a
if
if
(w
ar
u
n
ek
)
G
ru
p
a
p
ol
ec
eń
j
eś
li
p
raw
d
a
el
se
G
ru
p
a
p
ol
ec
eń
j
eś
li
f
ał
sz
en
d
P
ę
tl
a
for
for
i
=
w
ar
to
ść
_p
oc
z
:
k
rok
:
w
ar
to
ść
k
o
ń
c
G
ru
p
a
p
ol
ec
eń
en
d

T
w
or
ze
n
ie
„m
”
p
li
k
ów
T
w
or
zon
y
p
li
k
f
u
n
k
cj
i
m
u
si
b
y
ć
z
ap
is
an
y
w
k
at
al
ogu
d
oł
ą
cz
on
y
m
d
o
zm
ie
n
n
ej
P
A
T
H
p
ak
ie
tu
M
at
lab

R
oz
w
ią
zy
w
an
ie
u
k
ład
ów
r
ów
n
a
ń
w
M
at
lab
ie
1
1
1
1
2
2
1
1
2
1
1
2
2
2
2
2
1
1
2
2
..
.
..
.
..
.
n
n
n
n
n
n
n
n
n
n
a
x
a
x
a
x
y
a
x
a
x
a
x
y
a
x
a
x
a
x
y
+
+
+
=
+
+
+
=
+
+
+
=
M
P
os
ta
ć
m
ac
ie
rz
ow
a:
A
X
=
Y
P
os
ta
ć
m
ac
ie
rz
ow
a:
1
1
1
2
1
2
1
2
2
2
..
.
..
.
n
n
a
a
a
a
a
a
A
=
1
2
x
x
X
=
1
2
y
y
Y
=
1
2
..
.
n
n
n
n
A
a
a
a
=
M
M
M
M
n
X
x
=
M
n
Y
y
=
M
R
oz
w
ią
za
ni
e
ukł
adu
w
M
at
la
bi
e:
X
=
A
^
-1
*
Y
X
=
A
\Y
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron