Egzamin dla Aktuariuszy z 17 stycznia 2005 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
Y=N-2
N – ilość rzutów do uzyskania 2 szóstek
2 miejsca przez 6 zajęte; prawdopodobieństwo sukcesu: wybór z (1,...,5)
(
)
6
4
5
4
5
1
4
2
4
−
−
=
=
=
k
k
k
N
X
P
2
6
5
6
1
)
1
(
6
1
)
(
−
−
=
=
k
k
k
N
P
(
)
∑
∞
=
−
−
−
−
=
=
=
6
2
6
4
6
5
)
1
(
36
1
5
4
5
1
4
2
4
k
k
k
LICZ
k
k
X
k
N
P
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
LICZ
−
−
=
−
−
=
−
−
−
=
−
−
−
−
−
−
−
3
2
4
1
6
1
5
6
5
5
4
24
120
6
1
6
5
)
1
(
6
1
5
4
5
1
)!
6
(
24
)!
2
(
6
2
2
6
2
2
2
6
6
4
∑
∑
∑
∞
=
∞
=
+
=
=
−
+
=
+
=
=
−
=
−
−
=
6
0
6
6
6
6
6
6
6
2
1
5
3
4
1
3
2
5
3
2
4
1
1
6
5
6
6
3
2
4
1
6
1
5
k
l
l
k
l
l
l
k
l
k
k
k
LICZ
(
)
k
k
k
X
k
N
P
−
−
=
=
=
3
2
6
1
2
1
4
6
(
)
∑
∑
∞
=
∞
=
+
=
−
+
+
=
+
=
=
−
=
−
−
=
=
6
0
6
6
6
3
2
1
6
2
1
)
6
(
6
6
3
2
6
1
2
1
4
k
l
l
k
l
l
l
l
k
l
k
k
k
k
X
N
E
18
6
3
1
3
2
6
3
3
2
2
1
6
6
6
=
+
⋅
=
(
) (
)
16
2
18
4
2
4
=
−
=
=
−
=
=
X
N
E
X
Y
E
(
)
12
4
16
4
=
−
=
=
−
X
X
Y
E
Zadanie 2
x
x
x
x
F
x
f
X
+
=
+
−
=
+
=
1
1
1
1
)
(
,
)
1
(
1
2
1
2
2
2
3
)
1
(
2
1
1
1
)
(
,
)
1
(
2
2
x
x
x
x
x
F
x
f
X
+
+
=
+
−
=
+
=
∫
∞
<
<
=
0
1
)
(
max)
(min
x
f
x
P
P
=
>
−
<
−
=
<
−
<
=
<
<
)
(min
)
(max
1
min)
(
max)
(
max)
(min
x
P
x
P
x
P
x
P
x
P
(
)
(
)
[
]
=
+
−
+
−
+
=
+
−
+
+
−
=
>
−
<
−
=
6
3
6
3
2
3
2
2
2
3
2
3
)
1
(
1
)
2
(
)
1
(
)
1
(
1
)
1
(
2
1
1
x
x
x
x
x
x
x
x
x
X
P
x
X
P
=
+
−
−
−
−
−
+
+
+
+
+
+
=
6
3
4
5
6
6
5
4
3
2
)
1
(
1
8
12
6
6
15
20
15
6
1
x
x
x
x
x
x
x
x
x
x
x
(
)
4
6
2
6
2
3
6
2
3
4
)
1
(
)
2
(
3
)
1
(
)
2
(
)
1
(
3
)
1
(
2
5
4
3
)
1
(
6
15
12
3
+
+
=
+
+
+
=
+
+
+
+
=
+
+
+
+
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
-
2x
-
2
2x
3
3
2
5
3
)
1
(
:
2
5
4
2
3
2
2
2
3
2
3
2
+
−
−
+
+
−
−
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
x
x
1
2
1
3
2
2
1
3
1
2
4
9
2
1
−
=
+
−
=
−
=
−
−
=
=
⋅
−
=
∆
x
x
∫
∫
∫
∞
∞
∞
∞
−
−
=
−
=
+
−
=
−
=
+
−
=
=
+
=
+
+
=
0
1
1
1
5
3
6
4
6
6
5
2
5
3
1
5
3
1
3
3
)
1
)(
1
(
3
1
)
1
(
)
2
(
3
t
t
t
t
t
t
t
t
x
x
x
x
P
Zadanie 3
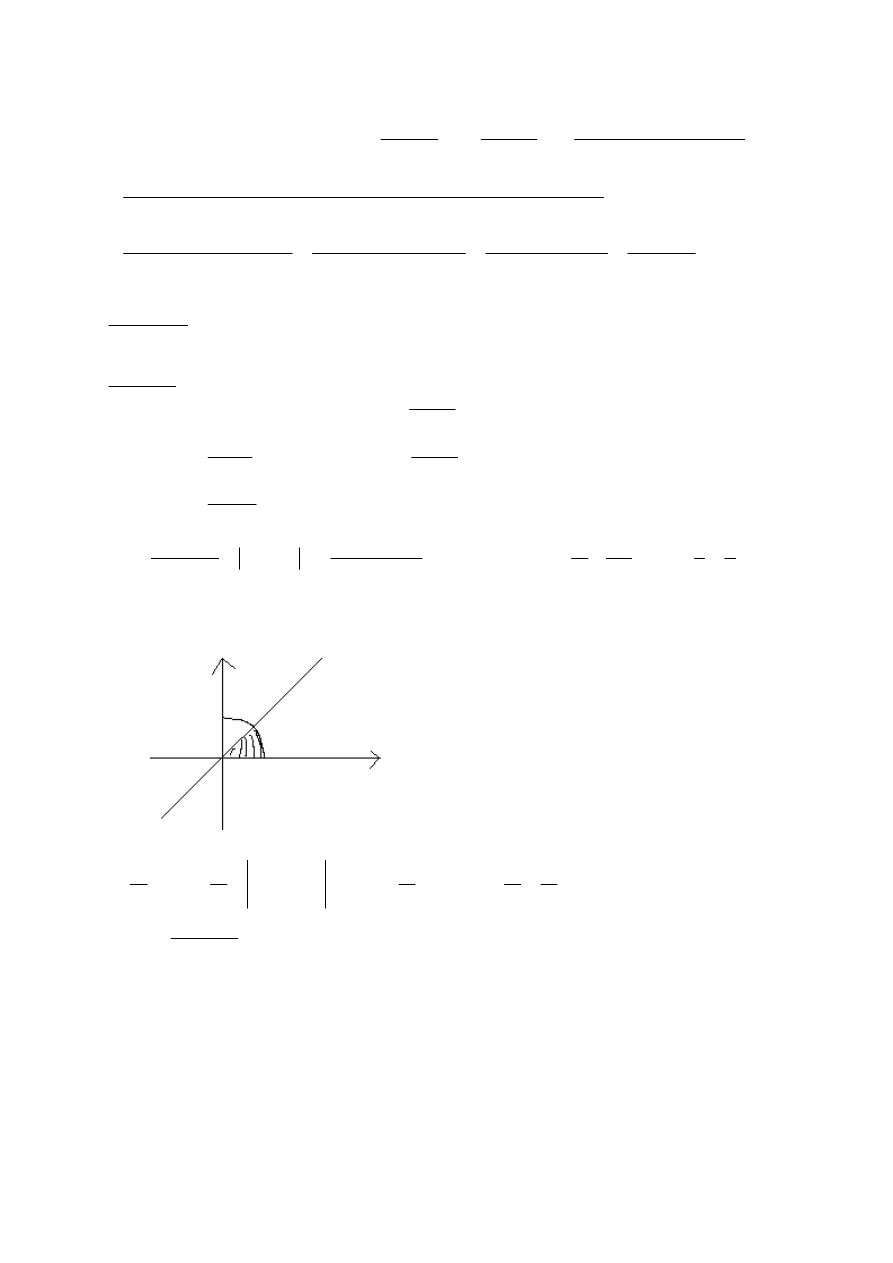
arctgt
φ
φ
tg
t
tx
y
=
=
=
,
,
∫
∫ ∫
∫
∆
Π
=
Π
=
Π
=
=
=
=
Π
=
<
arctgt
arctgt
arctgt
φ
drd
r
φ
r
y
φ
r
x
t
X
Y
P
0
1
0
0
2
2
4
sin
cos
4
(
)
)
;
0
(
,
1
2
)
(
2
∞
∈
+
Π
=
x
x
x
f
Z
Zadanie 4
)
0
(
)
1
(
1
)
2
(
=
−
=
−
=
≥
S
P
S
P
S
P
(
)
(
)
8
1
7
,...,
max
)
0
(
Y
Y
X
P
S
P
<
=
=
(
)
(
)
(
)
(
)
8
1
6
8
1
,...,
,...,
max
7
)
1
(
Y
Y
m
X
P
Y
Y
X
P
S
P
<
>
=
=

(
)
9
1
!
9
!
8
,...,
,
8
2
1
=
=
>
Y
Y
Y
X
P
2
,
0
9
8
9
1
7
9
8
1
6
7
≈
⋅
−
−
=
ODP
Zadanie 5
∫
=
=
<
t
e
t
e
x
t
X
P
0
2
2
)
(ln
∑
Γ
≅
−
)
2
,
(
ln
n
X
i
po przekształceniach:
=
−
−
<
−
+
>
∑
∑
n
n
n
X
n
n
n
X
P
i
i
5
,
0
1
1
ln
ln
lub
5
,
0
1
1
ln
ln
=
−
−
>
−
+
−
<
−
=
∑
∑
n
n
n
X
n
n
n
X
P
i
i
1
1
ln
5
,
0
ln
lub
1
1
ln
5
,
0
ln
→
−
−
>
−
−
+
−
<
−
−
=
∑
∑
n
n
n
n
X
n
n
n
n
X
P
i
i
1
1
ln
2
2
1
2
ln
lub
1
1
ln
2
2
1
2
ln
046
,
0
)
2
(
1
)
2
(
1
1
ln
2
lim
1
1
1
ln
2
lim
≈
−
Φ
−
+
Φ
=
−
−
Φ
−
+
+
−
Φ
→
−
−
n
n
n
n
Zadanie 6
Zadanie z liczby ciągów binarnych i serii (patrz: WYKŁADY Z KOMBINATORYKI)
3
,
6
3
2
2
,
9
,
6
=
=
⋅
=
⋅
=
=
=
+
=
Ω
k
k
R
m
n
n
m
n
=
−
−
−
−
=
2
8
2
5
2
1
1
1
1
2
k
m
k
n
A
143
16
!
9
!
6
!
15
28
10
2
=
⋅
⋅
=
ODP
Zadanie 7
∑
∑
=
=
−
=
−
=
∏
∏
=
10
6
5
1
2
10
6
5
5
1
5
5
2
i
i
i
i
X
θ
i
i
X
θ
i
i
e
X
θ
e
X
θ
L
∑
∑
∑
∑
=
=
=
=
−
−
+
−
−
−
=
10
6
10
6
5
1
5
1
2
ln
ln
5
ln
2
ln
5
ln
5
ln
i
i
i
i
i
i
i
i
X
θ
X
θ
X
θ
X
θ
L

∑
∑
∑
∑
=
=
=
=
+
=
→
=
−
+
−
=
∂
∂
5
1
10
6
5
1
10
6
2
10
ˆ
0
2
5
5
i
i
i
i
i
i
i
i
X
X
θ
X
θ
X
θ
θ
)
5
,...,
1
(
∈
i
(
)
∫
∫
→
=
=
=
=
=
<
−
−
2
0
0
)
(
2
1
2
t
t
w
θ
x
θ
i
θ
wykl
dw
e
θ
dw
dx
x
w
x
e
x
θ
t
X
P
)
10
,...,
6
(
∈
i
(
)
∫
∫
→
=
=
=
=
=
<
−
−
4
0
0
2
2
)
(
1
2
2
t
t
w
θ
x
θ
i
θ
wykl
e
θ
dw
x
w
x
e
x
θ
t
X
P
)
;
10
(
,
10
ˆ
θ
X
X
θ
Γ
≅
=
∫
∞
−
=
=
=
=
=
0
9
10
9
10
9
!
9
1
10
ˆ
θ
θ
β
α
e
x
θ
x
θ
E
x
θ
∫
∞
−
=
=
=
=
=
0
2
9
10
2
2
18
25
8
!
9
1
100
ˆ
θ
θ
β
α
e
x
θ
x
θ
E
x
θ
( )
2
2
2
6
1
1
9
10
2
18
25
ˆ
θ
θ
θ
θ
E
=
+
⋅
−
=
−
Zadanie 8
1
,
0
,
4
,
5
,
)
1
(
,
)
1
(
1
2
1
1
2
1
=
=
=
+
≅
+
≅
+
+
α
m
n
y
a
Y
x
a
X
a
i
a
i
(
)
(
)
∏
∏
=
+
=
+
+
+
=
4
1
1
4
2
5
1
1
5
1
2
1
1
1
i
a
i
i
a
i
y
a
x
a
L
(
)
(
)
(
)
(
)
∑
∑
=
=
+
+
−
+
+
+
−
=
5
1
4
1
2
2
1
1
1
ln
1
ln
4
1
ln
1
ln
5
ln
i
i
i
i
y
a
a
x
a
a
L
(
)
(
)
∑
∑
=
=
+
=
→
=
+
−
=
∂
∂
5
1
5
1
1
1
1
1
ln
5
0
1
ln
5
i
i
i
i
x
a
x
a
a
(
)
(
)
∑
∑
=
=
+
=
→
=
+
−
=
∂
∂
4
1
4
1
2
2
2
1
ln
4
0
1
ln
4
i
i
i
i
y
a
y
a
a
0
,
4
,
5
2
1
2
2
2
2
2
2
2
1
2
1
2
=
∂
∂
−
=
∂
∂
−
=
∂
∂
a
a
a
a
a
a
max
0
i
0
20
4
0
0
5
2
1
2
1
,
ˆ
,
ˆ
2
2
2
1
2
2
2
1
→
<
>
=
−
−
a
a
a
a
f
a
a
a
a
(
)
(
)
∑
∑
=
=
+
+
=
5
1
4
1
1
ln
4
1
ln
5
ˆ
i
i
i
i
x
y
T
(
)
(
) (
)
∫
−
+
=
=
+
=
+
=
−
<
=
<
+
=
<
+
1
0
1
2
1
)
1
(
1
1
)
1
ln(
2
t
e
a
t
t
w
x
x
a
e
y
P
e
y
P
t
y
P
( )
∫
≅
−
=
=
−
+
t
e
t
a
a
a
wykl
e
w
a
1
2
1
2
2
2
1
analogicznie:
(
)
( )
1
)
1
ln(
a
wykl
t
x
P
=
<
+
(
)
∫
∫
→
≅
=
=
=
=
<
=
<
−
−
λ
t
t
w
x
λ
wykl
e
w
x
λ
e
λ
λ
t
X
P
t
X
λ
P
2
0
0
2
2
1
2
1
2
2
2
(
)
(
)
≅
+
≅
+
→
2
1
1
ln
2
1
ln
2
1
2
wykl
x
a
y
a
i
i
Y
X
a
a
T
4
5
2
2
ˆ
1
2
=
)
10
(
2
1
,
5
),
8
(
2
1
,
4
2
2
χ
Y
χ
X
≅
Γ
≅
≅
Γ
≅
}
<
=
<
=
<
≅
c
Y
X
P
c
Y
X
P
c
a
a
T
P
F
1
10
8
1
4
5
1
)
10
,
8
(
1
2
07
,
3
1
1
10
8
1
1
2
=
→
>
=
>
d
d
Y
X
P
d
a
a
T
P
wiemy, że:
35
,
3
1
1
)
95
,
0
(
1
)
05
,
0
(
)
8
,
10
(
)
10
,
8
(
=
→
=
c
kw
kw
F
F
T
T
d
c
T
ODP
02
,
3
07
,
3
1
35
,
3
)
(
≈
−
=
−
=
Zadanie 9
(
)
(
)
2
2
2
2
2
2
2
2
2
1
4
1
4
1
2
1
)
(
)
var(
σ
µ
µ
µ
σ
ZX
E
X
Z
E
ZX
+
=
−
+
=
−
=
(
)
(
)
2
2
2
2
2
2
2
1
µ
σ
EX
EZ
X
Z
E
+
=
=
µ
ZX
E
2
1
)
(
=
(
) (
)
(
)
[
]
2
2
2
2
2
4
1
4
1
4
1
,
cov
σ
p
µ
µ
σ
p
X
Z
E
X
X
Z
Z
E
X
Z
X
Z
i
i
j
i
j
i
j
j
i
i
=
−
+
=
−
=
(
)
( )
(
)
[
]
[
]
2
2
2
4
1
,
cov
µ
σ
p
EX
EX
X
X
Z
E
X
X
Z
Z
E
j
i
j
i
i
j
i
j
i
+
=
+
=
−
+
+
=
−
+
+
=
+
+
=
)
1
(
2
1
1
2
4
4
)
1
(
2
1
4
1
4
1
2
2
2
1
4
1
2
2
2
2
2
2
2
2
n
p
σ
n
µ
n
σ
np
n
σ
n
µ
n
σ
p
n
σ
µ
n
ODP
Zadanie 10
)
4
,
2
(
Γ
≅
λ
X
EN
EX
N
S
var
)
(
var
var
2
⋅
+
⋅
=
Y
EN
EY
N
T
var
)
(
var
var
2
⋅
+
⋅
=
( )
2
1
=
=
=
λ
E
λ
N
EE
EN
( )
(
)
( )
(
)
8
5
16
2
2
1
var
var
var
var
=
+
=
+
=
+
=
λ
λ
E
λ
N
E
λ
N
E
N
8
9
2
1
8
5
var
=
+
=
S
2
9
5
,
4
4
2
1
4
8
5
var
=
=
⋅
+
⋅
=
T
)
,
cov(
2
var
var
)
var(
T
S
T
S
T
S
+
+
=
+
(
)
∑
=
+
=
+
N
i
i
i
Y
X
T
S
1
)
var(
)
(
var
)
var(
2
Y
X
EN
Y
X
E
N
T
S
+
⋅
+
+
⋅
=
+
E(X+Y)=1+2=3
var(X+Y)=1+4=5
8
65
8
20
45
2
5
8
45
5
2
1
9
8
5
)
var(
=
+
=
+
=
⋅
+
⋅
=
+
T
S
4
5
2
1
8
9
36
65
2
1
8
9
2
9
8
65
)
,
cov(
=
−
−
=
−
−
=
T
S
9
5
9
4
4
5
2
3
8
3
4
5
)
,
(
=
=
=
T
S
corr
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron