POLE MAGNETYCZNE + INDUKCJA

Zad. 1.
W dwóch bardzo długich, równolegle biegnących przewodach płyną prądy. W pierwszym
przewodzie natężenie jest dwukrotnie większe niż w drugim. Odległość między przewodami
wynosi a. Obliczyć odległość x od pierwszego przewodu, w której indukcja pola
magnetycznego B jest równa zeru, jeżeli prądy płyną:

a) w przeciwnym kierunku; b) w tym samym kierunku.

Zad. 2.

Ile wynosi natężenie pola magnetycznego na osi przewodnika kołowego, w punkcie
położonym w odległości d od jego środka, jeżeli w środku przewodnika kołowego
o promieniu R natężenie pola wynosi H

o

.

Zad. 3.

Prosty, nieskończony przewodnik posiada pętlę o promieniu R. Znaleźć natężenie prądu
w przewodniku, jeżeli wiadomo, że natężenie pola magnetycznego w środku pętli wynosi H.

Zad. 4.

Znaleźć natężenie pola magnetycznego w środku przewodnika o kształcie prostokąta
o bokach a i b, przez który płynie prąd o natężeniu I.

Zad. 5.

Po dwóch nieskończonych, równoległych przewodnikach płyną prądy o natężeniu I = 15 A
w jednym kierunku. Obliczyć natężenie pola magnetycznego w punkcie odległym o a = 0,4 m
od jednego przewodnika i b = 0,3 m od drugiego przewodnika, jeżeli odległość między
przewodnikami wynosi c = 0,5 m.

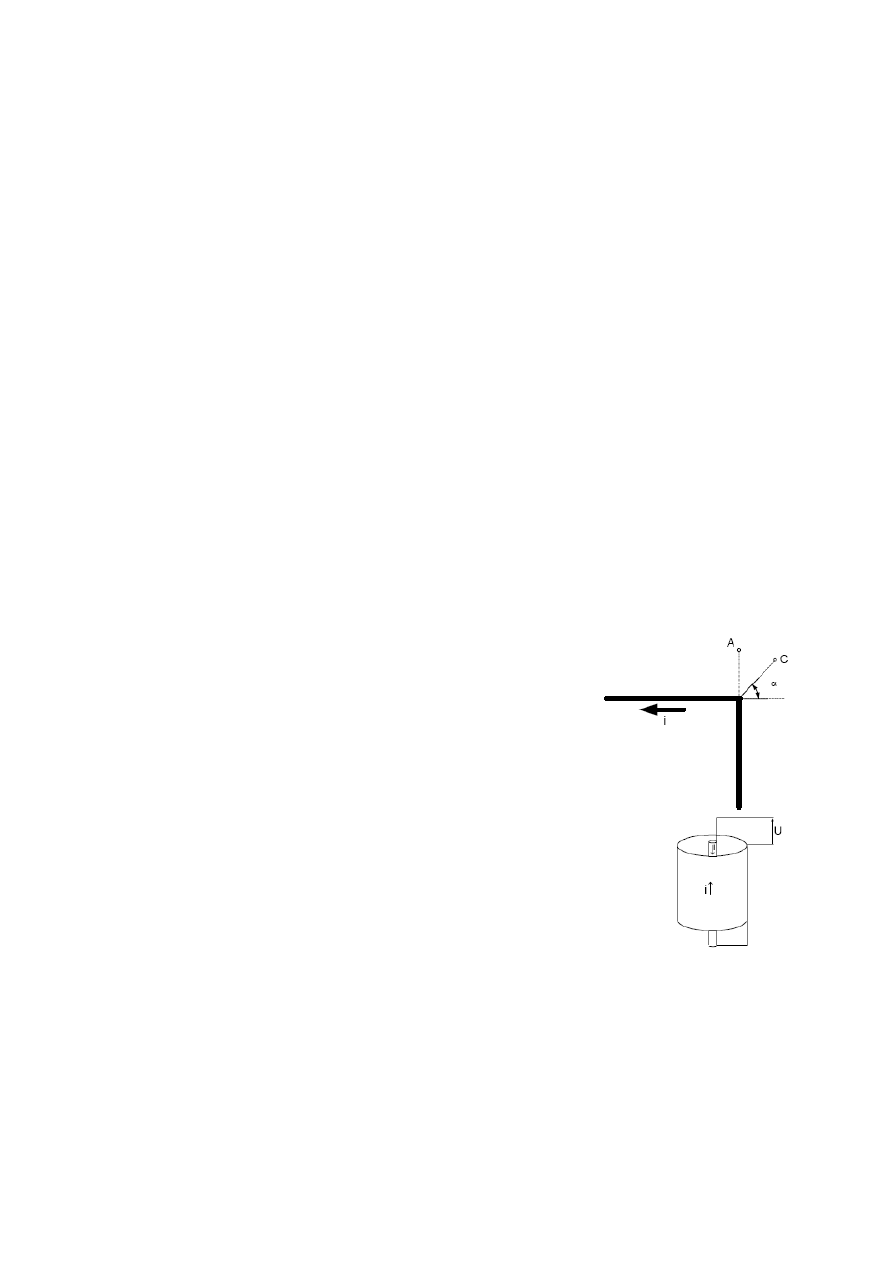
Zad. 6.

Wyznaczyć indukcję pola magnetycznego wytworzonego
przez prąd o natężeniu i, płynący przez nieskończenie długi
przewodnik zgięty pod kątem prostym:
a) W punkcie A leżącym w płaszczyźnie przewodnika
odległym od jego końca o odległość h, na przedłużeniu
jednego z ramion przewodnika.
b) W punkcie C odległym o h od osi przewodnika, leżący pod
kątem α do osi jednego z ramion przewodnika.

Zad. 7.

Wzdłuż osi cienkościennej rury biegnie prostoliniowy przewód. Prąd I
płynący w rurze wraca przewodem do źródła. Wyznaczyć wielkość indukcji
pola magnetycznego jako funkcję odległości od środka rury.

Zad. 8.

Po długim, prostoliniowym, jednorodnym drucie o promieniu R = 1 cm płynie prąd o natężeniu
I = 50 A. Wyznaczyć zależność natężenia pola magnetycznego w funkcji odległości od osi drutu.

Zad. 9.

Proton i elektron poruszają się w jednorodnym polu magnetycznym, prostopadłym do
płaszczyzn torów. Obliczyć stosunek promieni tych torów w następujących przypadkach:

a) wartość pędu elektronu jest równa wartości pędu protonu;
b) energia kinetyczna protonu jest równa energii kinetycznej elektronu.

Stosunek masy protonu do masy elektronu m

p

/m

e

= 1840. Efekty relatywistyczne pominąć.

Zad. 10.

Cząstka o masie m = 6,6∙10

-27

kg i ładunku q = 3,2∙10

-19

C porusza się po torze kołowym

o promieniu r = 0,45 m w polu magnetycznym o indukcji B = 1,2 Wb/m

2

, prostopadłym do

płaszczyzny toru. Oblicz prędkość cząstki i okres jej obiegu.

Zad. 11.

Pole magnetyczne o indukcji B = 5∙10

-4

T jest skierowane prostopadle do pola elektrycznego

o natężeniu E = 10

5

V/m. Elektron wpada z pewną prędkością v do obszaru tych pól, przy czym

jego prędkość jest prostopadła do płaszczyzny, w której leżą wektory E i B. Obliczyć:

a) prędkość elektronu, jeżeli podczas równoczesnego działania obu pól nie zostaje

odchylony;

b) promień okręgu, po którym poruszałby się elektron o takiej prędkości w przypadku

działania wyłącznie pola magnetycznego.

Zad. 12.

Naładowana cząstka o określonej energii kinetycznej porusza się w polu magnetycznym
po okręgu o promieniu R = 2 cm. Po przejściu przez płytkę ołowianą porusza się dalej po okręgu,
lecz o promieniu r = 1 cm w tym samym polu magnetycznym. Obliczyć względną zmianę energii
cząsteczki. Zmianę masy pominąć.

Zad. 13.

Indukcja jednorodnego pola magnetycznego rośnie proporcjonalnie do czasu B = αt, gdzie
α = 10 T/s. W polu tym znajduje się nieruchoma, kwadratowa ramka o boku a = 1 m zbudowana
z drutu o przekroju S = 10

-6

m

2

i oporze ρ = 1,7∙10

-8

Ωm. Płaszczyzna ramki jest prostopadła do

kierunku pola magnetycznego. Obliczyć ilość ciepła wydzielonego w ramce w czasie t = 2 s.

Zad. 14.

Miedziany pierścień o promieniu R = 10 cm wykonany jest z drutu o przekroju poprzecznym
S = 10 mm

2

. Pierścień umieszczono w zmieniającym się jednostajnie polu magnetycznym

prostopadłym do jego płaszczyzny. Z jaką prędkością zmienia się indukcja pola magnetycznego,
jeśli prąd indukowany w pierścieniu ma natężenie I = 10 A. Oporność właściwa miedzi wynosi
ρ = 1,71∙10

-8

Ωm.

Zad. 15.

W jednorodnym polu magnetycznym o indukcji B = 0,84 T obraca się jednostajnie kwadratowa
ramka o boku a = 5 cm z miedzianego drutu o przekroju S = 0,5 cm

2

. Maksymalne natężenie

prądu indukowanego w obracającej się ramce wynosi I = 1,9 A. Obliczyć częstość obrotów
ramki. Oporność właściwa miedzi ρ = 1,7∙10

-8

Ωm.

Zad. 16.

Na dwóch równoległych, poziomych szynach położono prostopadle do szyn, pręt metalowy
o skończonym oporze R i długości l. Szyny są połączone ze źródłem napięcia stałego U i znajdują
się w jednorodnym polu magnetycznym o indukcji B, prostopadłym do płaszczyzny szyn i do
pręta. Obliczyć graniczna prędkość z jaką będzie poruszać się pręt, jeżeli pominiemy tarcie.

Zad. 17.

Dany jest jednorodny pierścień o promieniu r i oporze R. W dwóch dowolnych punktach A i B
tego pierścienia przyłączono dwa długie przewody, tak by ich kierunki tworzyły przedłużenia
promieni tego pierścienia. Zasilanie ze źródła o napięciu U. Obliczyć indukcję magnetyczną
w środku pierścienia.

Zad. 18.

Przewodnik w kształcie pręta o długości l = 15 cm obraca się wykonując n = 60 obrotów/s
dookoła osi przechodzącej przez jeden z jego końców w jednorodnym polu magnetycznym
o indukcji B = 0,5 Wb/m

2

prostopadłym do płaszczyzny, w której obraca się pręt. Obliczyć

różnicę potencjałów między końcami pręta.

Zad. 19.

Dwie równoległe szyny miedziane ustawione pionowo w odległości wzajemnej l są połączone
u góry oporem R i znajdują się w jednorodnym polu magnetycznym o indukcji B prostopadłym
do płaszczyzny szyn. Po szynach zsuwa się bez tarcia przewodnik miedziany o masie m. Obliczyć
ustaloną wartość prędkości zsuwania się przewodnika. Opór szyn i przewodnika pominąć.