STAN NAPRĘŻENIA
Z
ADANIE
1
W danym punkcie stan naprężenia jest określony przez tensor
σ
T .
Wyznaczyć wektor naprężenia
( )
n
σ na płaszczyźnie określonej wektorem
jednostkowym
(
)
3
1
3
2
3
2
,
,
=
n
Z
ADANIE
2
Dany jest stan naprężenia określony tensorem
σ
T . Sprawdzić, czy w każdym
punkcie są spełnione różniczkowe równania równowagi, jeżeli współrzędne
wektora sił masowych określają funkcje
,
0
,
2
,
13
=
−
=
−
=
z
y
x
f
f
y
f
Z
ADANIE
3
Dany jest tensor naprężenia .
Wyznaczyć wartości i kierunki główne tensora.
Z
ADANIE
4
Tensor naprężenia z poprzedniego zadania rozłożyć na aksjator i dewiator.
Z
ADANIE
5
Dany jest płaski stan naprężenia określony w układzie osi x, y składowymi
σ
T .
Wyznaczyć naprężenia główne, maksymalne styczne i położenia osi naprężeń
głównych za pomocą metody analitycznej i wykreślnej (koło M
OHRA
).
Z
ADANIE
6
Dany jest płaski stan naprężenia określony w układzie osi x, y składowymi
σ
T .
Wyznaczyć:
- naprężenia główne, maksymalne naprężenia styczne i położenia głównych
osi naprężeń,
- tensor naprężenia w układzie osi obróconych o kąt
o
40
=
ϕ
Z
ADANIE
7
W płaskim stanie naprężenia danym na rysunku wyznaczyć naprężenia w układzie
obróconym o kąt
o
45
Z
ADANIE
8
W płaskim stanie naprężenia danym na rysunku wyznaczyć naprężenia w układzie
obróconym o kąt
o
15
−
Z
ADANIE
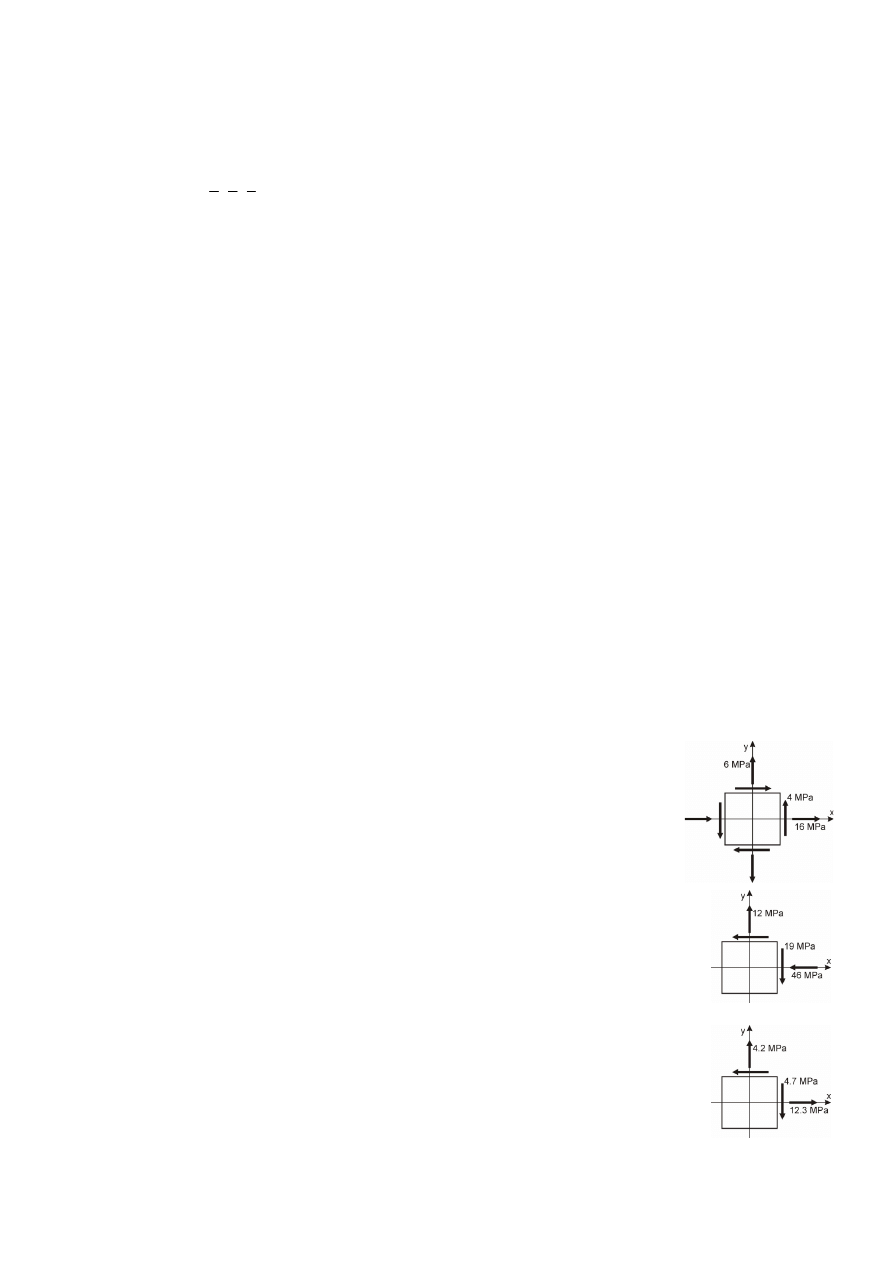
9
W płaskim stanie naprężenia podanym na rysunku wyznaczyć: kierunki główne
naprężeń i wartości naprężeń głównych, kierunki i wartości maksymalnych naprężeń
stycznych.
−
−
−
=
300
100
600
100
500
300
600
300
1000
σ
T
=
0
2
0
2
0
5
0
5
3
2
2
z
z
y
y
xy
T
σ
−
−
−
=
30
10
60
10
50
30
60
30
100
σ
T
−
−
−
=
300
100
100
200
σ
T
−
=
300
150
150
200
σ
T
Rozwiązania
Z
ADANIE
3
Obliczamy niezmienniki:
MPa
I
z
y
x
120
1
=
+
+
=
σ
σ
σ
σ
,
(
)
2
2
2
2
2
4100 MPa
I
yz
xz
xy
z
y
z
x
y
x
−
=
−
−
−
⋅
+
⋅
+
⋅
=
τ
τ
τ
σ
σ
σ
σ
σ
σ
σ
,
(
)
3
2
2
2
3
349000
2
MPa
I
xy
z
yz
x
xz
y
zx
yz
xy
z
y
x
−
=
⋅
−
⋅
−
⋅
−
⋅
⋅
⋅
+
⋅
⋅
=
τ
σ
τ
σ
τ
σ
τ
τ
τ
σ
σ
σ
σ
.
Równanie wiekowe:
0
3
2
2
1
3
=
−
+
−
σ
σ
σ
σ
σ
σ
I
I
I
.
Poszukujemy pierwiastków równania trzeciego stopnia.
Równanie postaci:
0
2
3
=
+
+
+
d
cx
bx
ax
ma trzy rozwiązania
(
)
3
,
2
,
1
3
=
−
=
i
a
b
y
x
i
i
,
przy czym charakter rozwiązania zależy od wartości wyróżnika D:
3
2
p
q
D
+
=
,
gdzie
2
2
2
3
9
3
,
2
6
3
a
b
ac
p
a
d
a
bc
a
b
q
−
=
+
−
=
.
Jeśli:
D < 0,
to równanie ma 3 pierwiastki rzeczywiste,
D > 0,
to równanie ma 1 pierwiastek rzeczywisty i 2 zespolone,
D = 0,
to równanie ma 2 pierwiastki rzeczywiste, w tym jeden podwójny.
Przy wyznaczaniu wartości głównych tensora naprężenia wyróżnik D jest zawsze mniejszy od zera.
Wówczas dalsze obliczenia przebiegają według następujących wzorów:
( )
( )
,
3
cos
,
sgn
3
r
q
p
q
r
=
=
ω
(
)
(
)
.
60
cos
2
,
60
cos
2
,
cos
2
2
2
1
ω
ω
ω
+
=
−
=
−
=
o
o
r
y
r
y
r
y
W naszym zadaniu mamy:
( )
(
)
,
2967
9
3
2
2
1
2
MPa
I
I
p
−
=
−
=
σ
σ
(
)
(
)
,
10
53
,
2
,
28500
2
6
3
6
10
3
2
3
3
2
1
3
1
MPa
p
q
D
MPa
I
I
I
I
q
⋅
−
=
+
=
−
=
−
+
−
=
σ
σ
σ
σ
( )
,
1
sgn
,
40
3
3
0
1
+
=
−
=
−
=
−
=
q
MPa
I
a
b
σ
σ
( )
,
614
,
26
176347
,
0
3
cos
,
47
,
54
2967
1
3
o
r
q
MPa
r
=
→
=
=
=
−
⋅
+
=
ω
ω

(
)
,
4
,
97
614
,
26
cos
47
,
54
2
1
MPa
y
o
−
=
⋅
⋅
−
=
(
)
,
0
,
91
614
,
26
60
cos
47
,
54
2
2
MPa
y
o
o
=
−
⋅
⋅
=
(
)
MPa
y
o
o
4
,
6
614
,
26
60
cos
47
,
54
2
3
=
+
⋅
⋅
=
Nieuporządkowane naprężenia główne wynoszą:
,
4
,
57
40
4
,
97
0
1
1
MPa
y
−
=
+
−
=
+
=
σ
σ
,
0
,
131
40
0
,
91
0
2
2
MPa
y
=
+
=
+
=
σ
σ
.
4
,
46
40
4
,
6
0
3
3
MPa
y
=
+
=
+
=
σ
σ
Po uporządkowaniu
(
)
III
II
I
σ
σ
σ
≥
≥
otrzymujemy poszukiwane
WARTOŚCI GŁÓWNE
:
,
0
,
131
2
MPa
I
=
=
σ
σ
,
4
,
46
3
MPa
II
=
=
σ
σ
.
4
,
57
1
MPa
III
−
=
=
σ
σ
KIERUNKI GŁÓWNE
możemy wyznaczyć z równań:
(
)
,
0
=
+
+
−
z
xz
y
xy
x
x
n
n
n
τ
τ
σ
σ
(
)
,
0
=
+
−
+
z
yz
y
y
x
yx
n
n
n
τ
σ
σ
τ
(
)
,
0
=
−
+
+
z
z
y
zy
x
zx
n
n
n
σ
σ
τ
τ
.
1
2
2
2
=
+
+
z
y
x
n
n
n
Do wyznaczenia któregokolwiek kierunku głównego wykorzystamy pierwsze dwa równania oraz
równanie czwarte. Wprowadzimy pomocnicze niewiadome:
.
,
3
2
x
z
x
y
n
n
n
n
=
=
λ
λ
Po podzieleniu pierwszych dwóch równań przez
x
n otrzymujemy układ dwóch równań z dwiema
niewiadomymi
2
λ i
3
λ :
( )
a
(
)
−
=
+
−
−
=
+
xy
yz
y
x
xz
xy
σ
λ
τ
λ
σ
σ
σ
σ
λ
τ
λ
τ
3
2
3
2
,
( )
b skąd
(
)
[
]
(
)
(
)
[
]
−
−
+
−
=
+
−
=
W
W
y
x
xy
xz
xy
yz
x
σ
σ
σ
σ
τ
λ
τ
τ
τ
σ
σ
λ
2
3
2
,
gdzie
(
)
y
xz
yz
xy
W
σ
σ
τ
τ
τ
−
+
=
. Z czwartego równania obliczymy
x
n :
( )
c
,
1
1
2
3
2
2
λ
λ +
+
±
=
x
n
co pozwala wyznaczyć pozostałe współrzędne
y
n i
z
n :
( )
d
.
,
3
2
x
z
x
y
n
n
n
n
λ
λ
=
=
Podstawiwszy we wzorach
( )
b kolejno
I
σ
σ =
,
II
σ
σ =
oraz
III
σ
σ =
, otrzymamy współrzędne
(
)
I
z
y
x
n
n
n
,
,
,
(
)
II
z
y
x
n
n
n
,
,
oraz
(
)
III
z
y
x
n
n
n
,
,
. Wyniki obliczeń zestawiono w tablicy:
σ
[MPa]
λ
2
λ
3
n
1
n
2
n
3
I
131,0
0,3270
-0,3524
-0,9012
-0,2947
0,3176
II
46,4
-4,5446
-1,3796
0,2060
-0,9364
-0,2842
III
-58,4
-0,5003
2,3730
0,3812
-0,1907
0,9046
Sprawdźmy ortogonalność wersorów wyznaczających kierunki główne:
( ) ( )
( ) ( )
( ) ( )
,
0
00005
,
0
≈
−
=
⋅
+
⋅
+
⋅
II
z
I
z
II
y
I
y
II
x
I
x
n
n
n
n
n
n
( ) ( )
( ) ( )
( ) ( )
,
0
00004
,
0
≈
=
⋅
+
⋅
+
⋅
III
z
I
z
III
y
I
y
III
x
I
x
n
n
n
n
n
n
( ) ( )
( ) ( )
( ) ( )
,
0
00001
,
0
≈
=
⋅
+
⋅
+
⋅
III
z
II
z
III
y
II
y
III
x
II
x
n
n
n
n
n
n
( ) ( )
( ) ( )
( ) ( )
,
1
99998
,
0
≈
=
⋅
+
⋅
+
⋅
I
z
I
z
I
y
I
y
I
x
I
x
n
n
n
n
n
n
( ) ( )
( ) ( )
( ) ( )
,
1
0000506
,
1
≈
=
⋅
+
⋅
+
⋅
II
z
II
z
II
y
II
y
II
x
II
x
n
n
n
n
n
n
( ) ( )
( ) ( )
( ) ( )
.
1
99998
,
0
≈
=
⋅
+
⋅
+
⋅
III
z
III
z
III
y
III
y
III
x
III
x
n
n
n
n
n
n
Naprężenia główne ilustruje tensor naprężenia:
.
4
,
57
0
0
0
4
,
46
0
0
0
0
,
131
−
=
σ
T
Sprawdźmy wartości niezmienników dla tensora naprężeń wyrażonego w kierunkach głównych:
MPa
I
120
4
,
57
4
,
46
0
,
131
1
=
−
+
=
σ
,
(
)
(
)
(
)
2
2
4100
4104
4
,
57
4
,
46
4
,
57
0
,
131
4
,
46
0
,
131
MPa
I
−
≈
−
=
−
⋅
+
−
⋅
+
⋅
=
σ
,
(
)
(
)
3
3
349000
348900
4
,
57
4
,
46
0
,
131
MPa
I
−
≈
=
−
⋅
⋅
=
σ
.
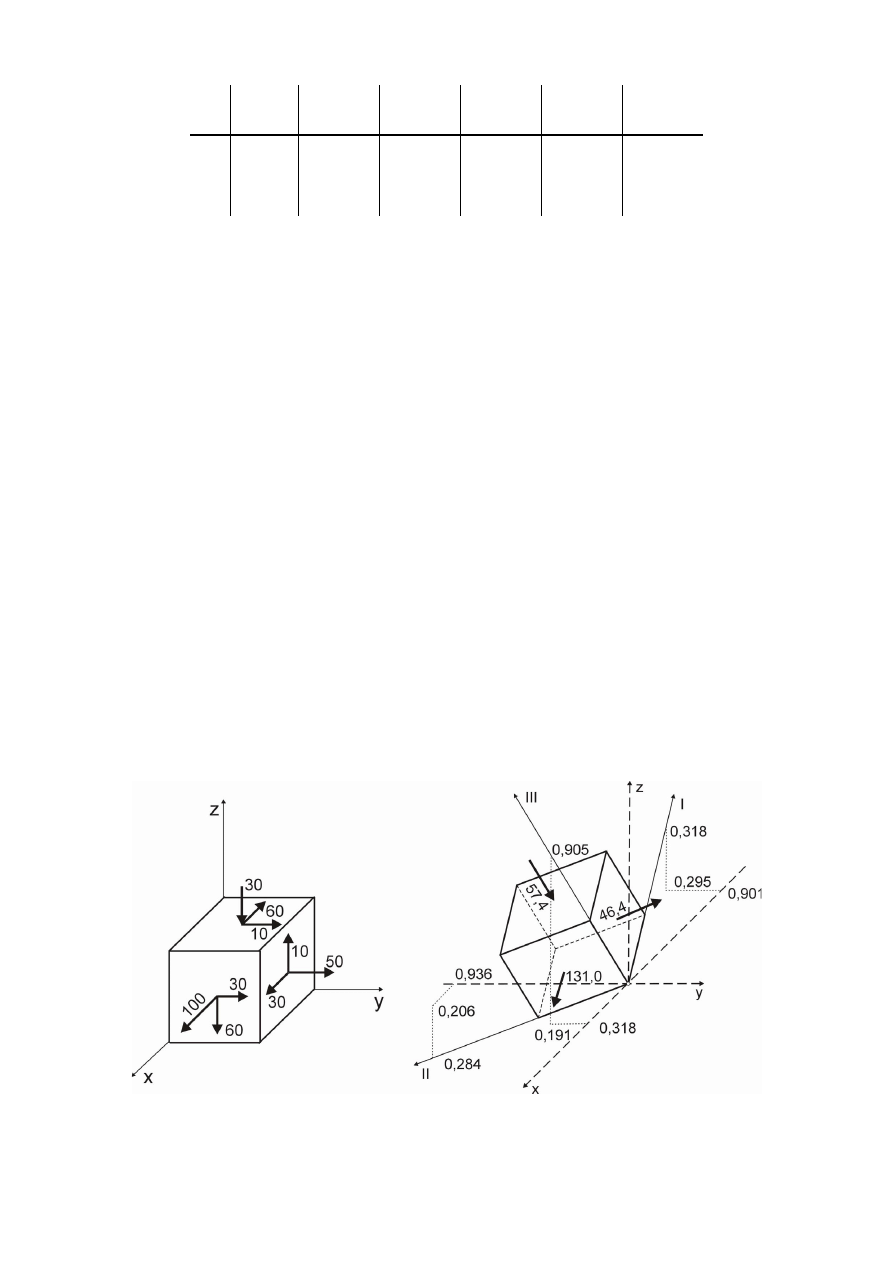
Graficzną ilustrację wyjściowego tensora naprężenia oraz usytuowanie kierunków głównych i naprężenia
główne przedstawiono na rysunku.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron