
Informatyka II
Chemia biologiczna
Wykład 3 (22.11.2010)
Egzamin ko cowy!!!
Posta graficzna wybranych miar poło enia
Miary po
ł
rednie
mediana
kwantyle
moda
arytmetyczna
harmoniczna
geometryczna
kwartyl pierwszy
kwartyl drugi
medialna
kwartyl trzeci
decyle
Miary poło enia
rednie
moda
kwantyle
mediana
arytmetyczna
harmoniczna
geometryczna
kwartyl pierwszy
kwartyl drugi
medialna
kwartyl trzeci
decyle
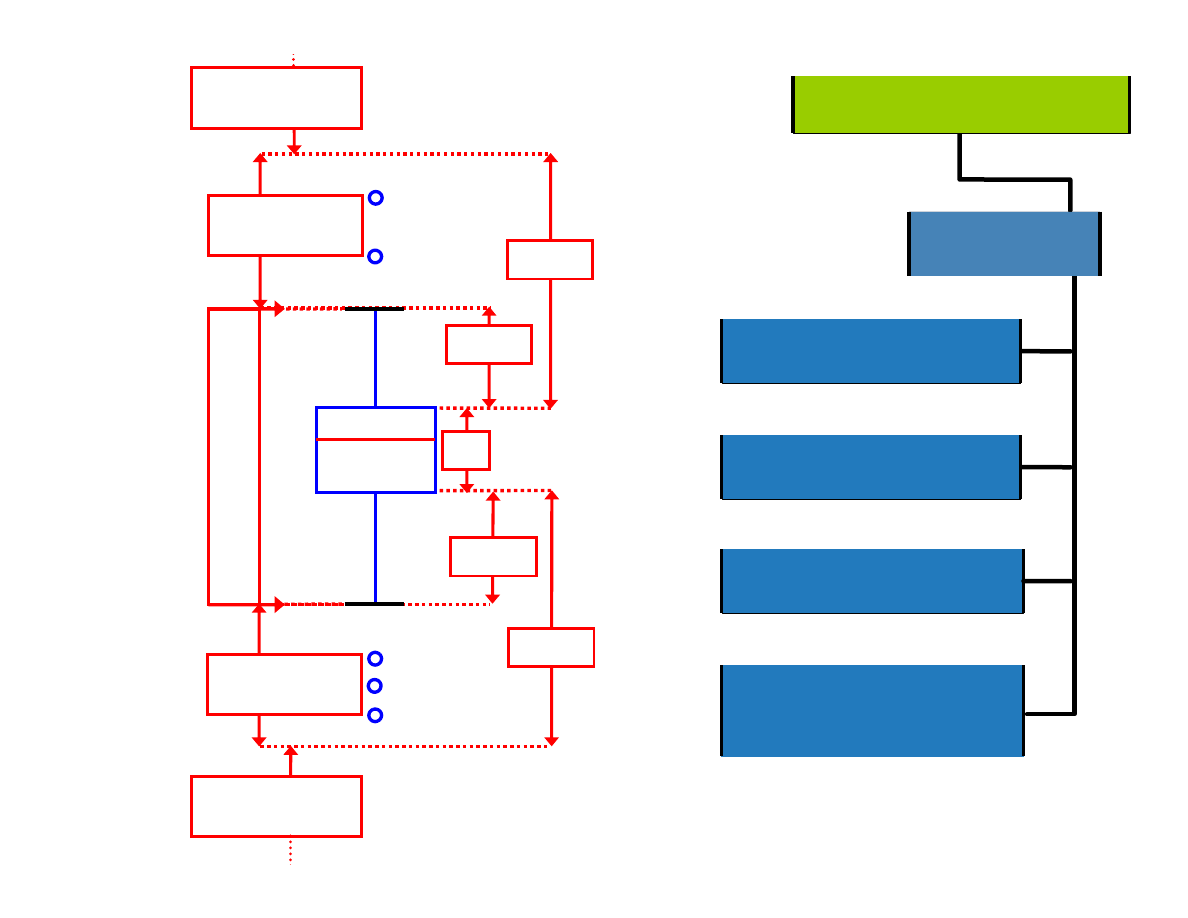
Q
3
– kwartyl trzeci
+1.5H
-1.5H
H
+3H
-3H
Warto ci
odstaj ce
Warto ci
ekstremalne
Warto ci
odstaj ce
Warto ci
ekstremalne
W
ar
to
ci
n
ie
od
st
aj
ce
kwantyle
kwartyl pierwszy
kwartyl drugi
medialna
decyle
Miary poło enia
kwantyle
Q
1
– pierwszy kwartyl
Q
2
– drugi kwartyl
medialna
H - rozst p
mi dzykwartylny
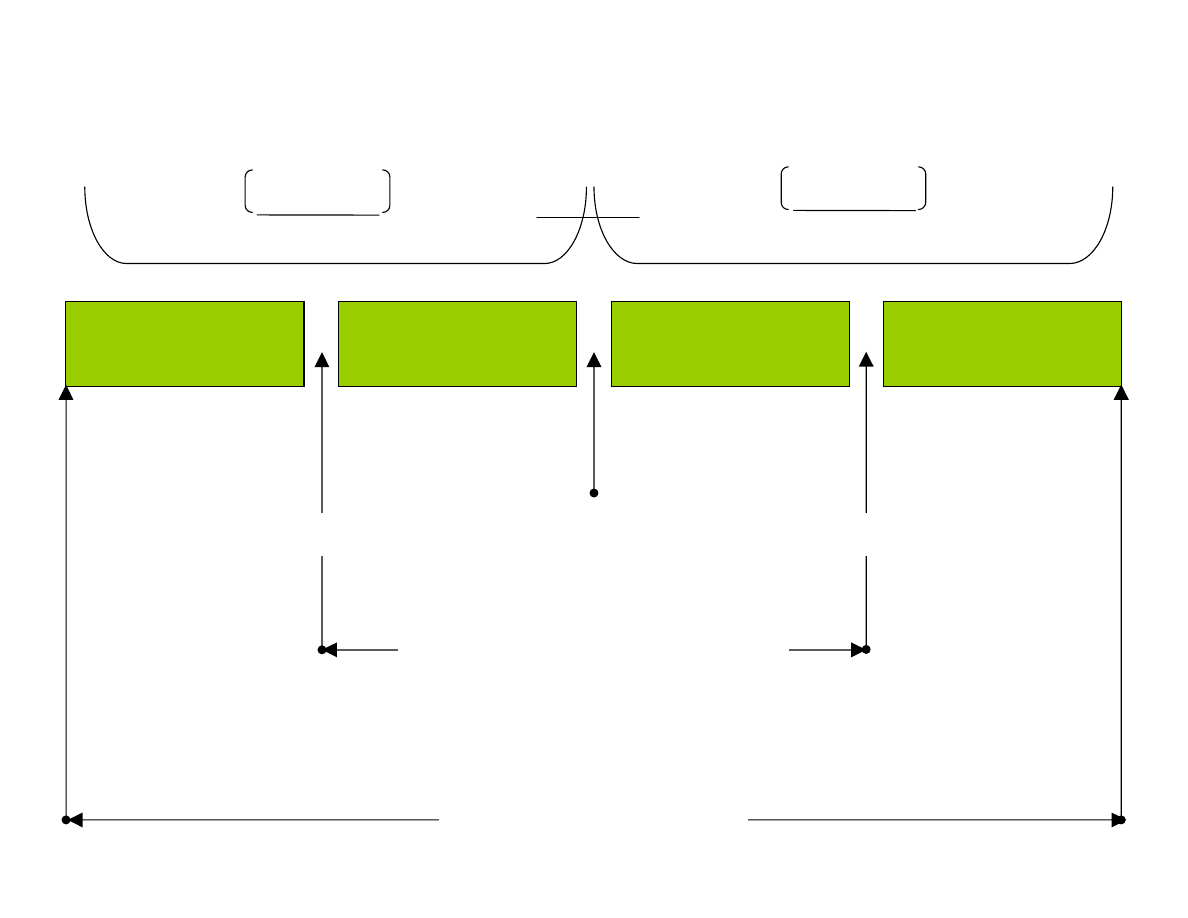
25% warto ci
zbioru próby
25% warto ci
zbioru próby
25% warto ci
zbioru próby
25% warto ci
zbioru próby
Mediana Q
2
= 35
Q
1
= 25
Q
3
= 49
Rozst p mi dzykwartylny H
H=Q
3
-Q
1
= 24
Rozst p danych R
R=x
max
-x
min
= 92-17=75
Próba X: cena szczepionki przeciw grypie A/H1N1 w wybranych 12 aptekach
23 17 32 60 22 52 29 38 42 92 27 46
Sortowanie:
17
22
23 27
23 27
29
32 38
32 38
42
46 52
46 52
60 92
2
35
2
2
25
49
Dolna granica
warto ci nieodstaj cych
Q
1
-1.5*H=25-36 = -11
Górna granica
warto ci nieodstaj cych
Q
3
+1.5*H=49+36 = 85
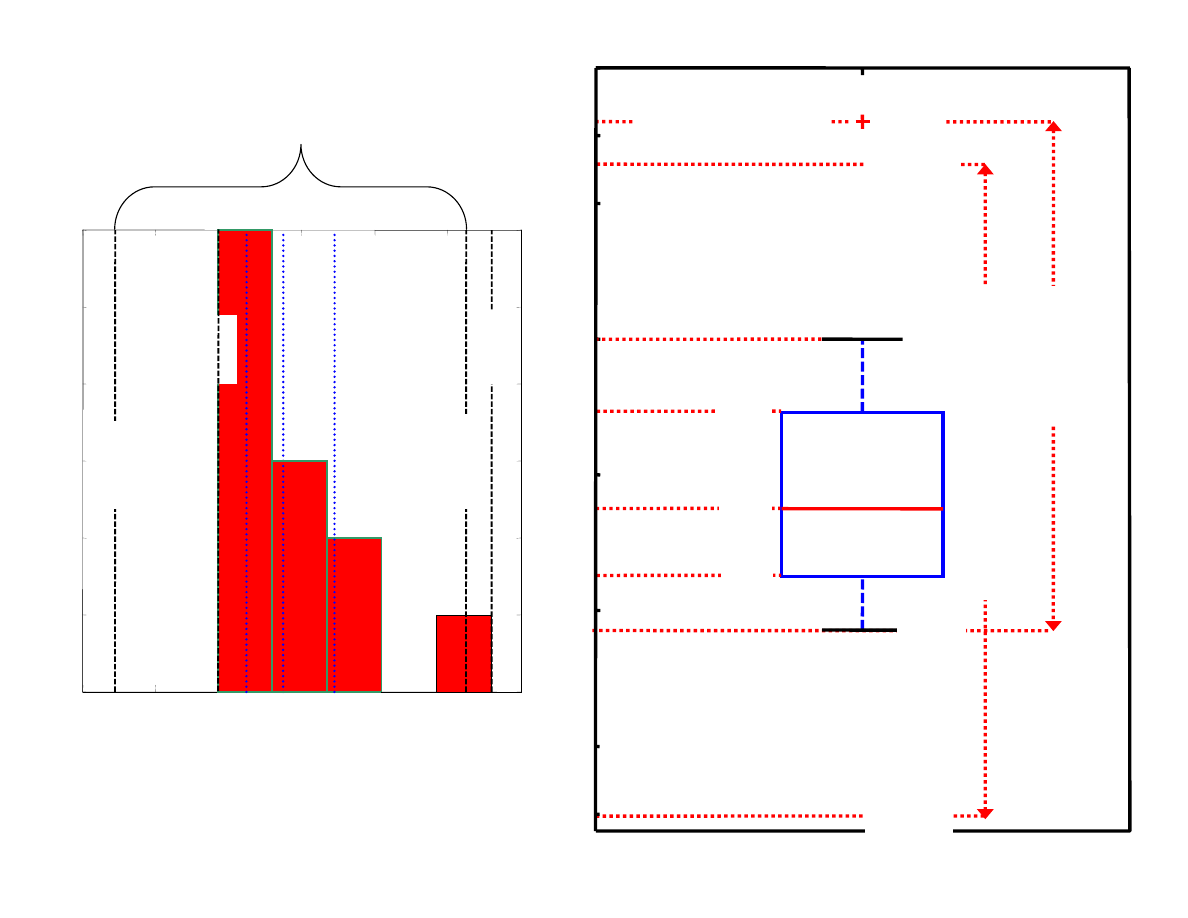
0
20
40
60
80
100
C
en
a
sz
cz
ep
io
nk
i
Próba X
Q
3
Q
2
Q
1
25
35
49
-11
17
92
92
85
85
x
min
-1.5H
+1.5H
-20
0
20
40
60
80
100
0
1
2
3
4
5
6
Q
1
Q
2
Q
3
+1
.5
H
-1
.5
H
x
m
in
x
m
ax
Zakres warto ci
nieodstaj cych
W
ar
to
od
st
aj
ca
Cena szczepionki
Li
cz
ba
a
pt
ek
Za
kre
s w
art
o
ci
nie
od
sta
j
cy
ch
Warto
odstaj ca
x
max
R
oz
st
p c
en
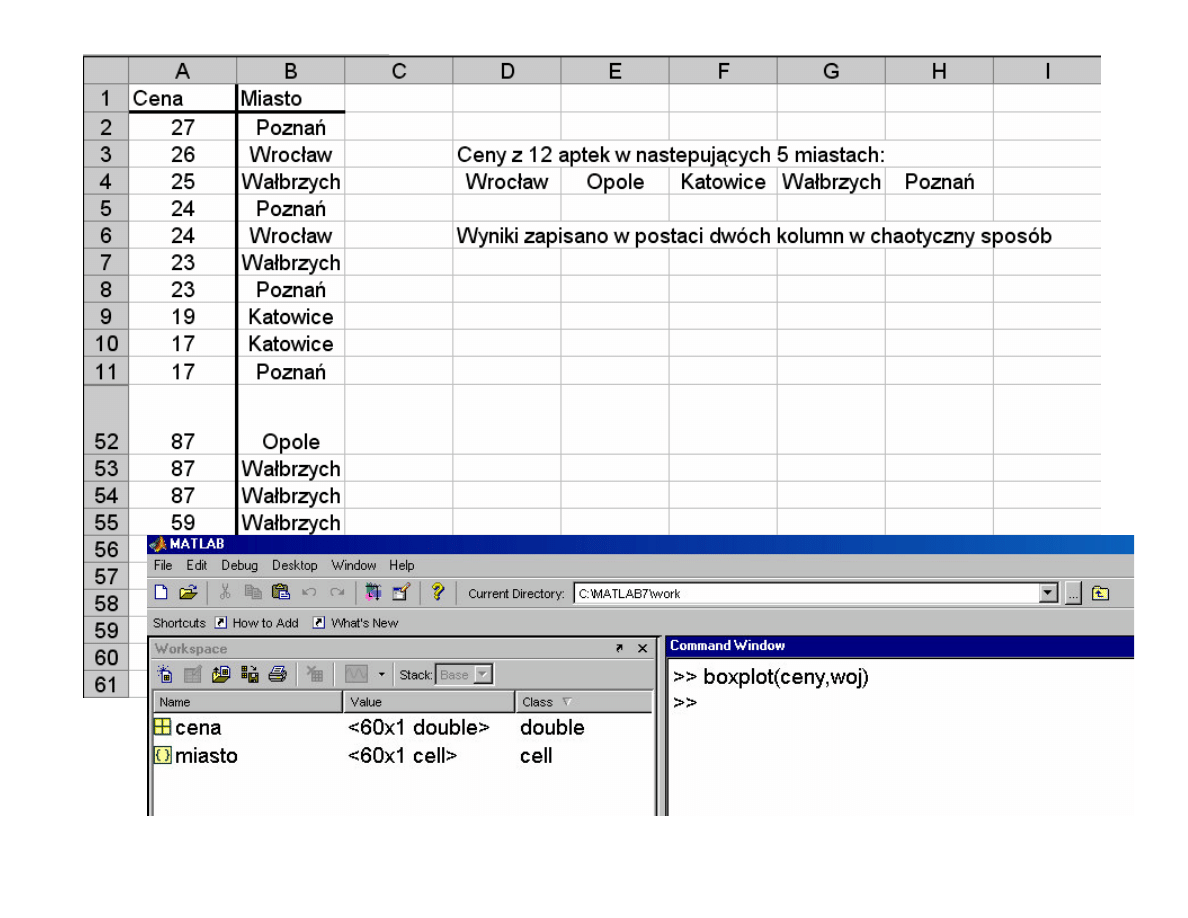
..
.
..
.
..
.
... ... ...
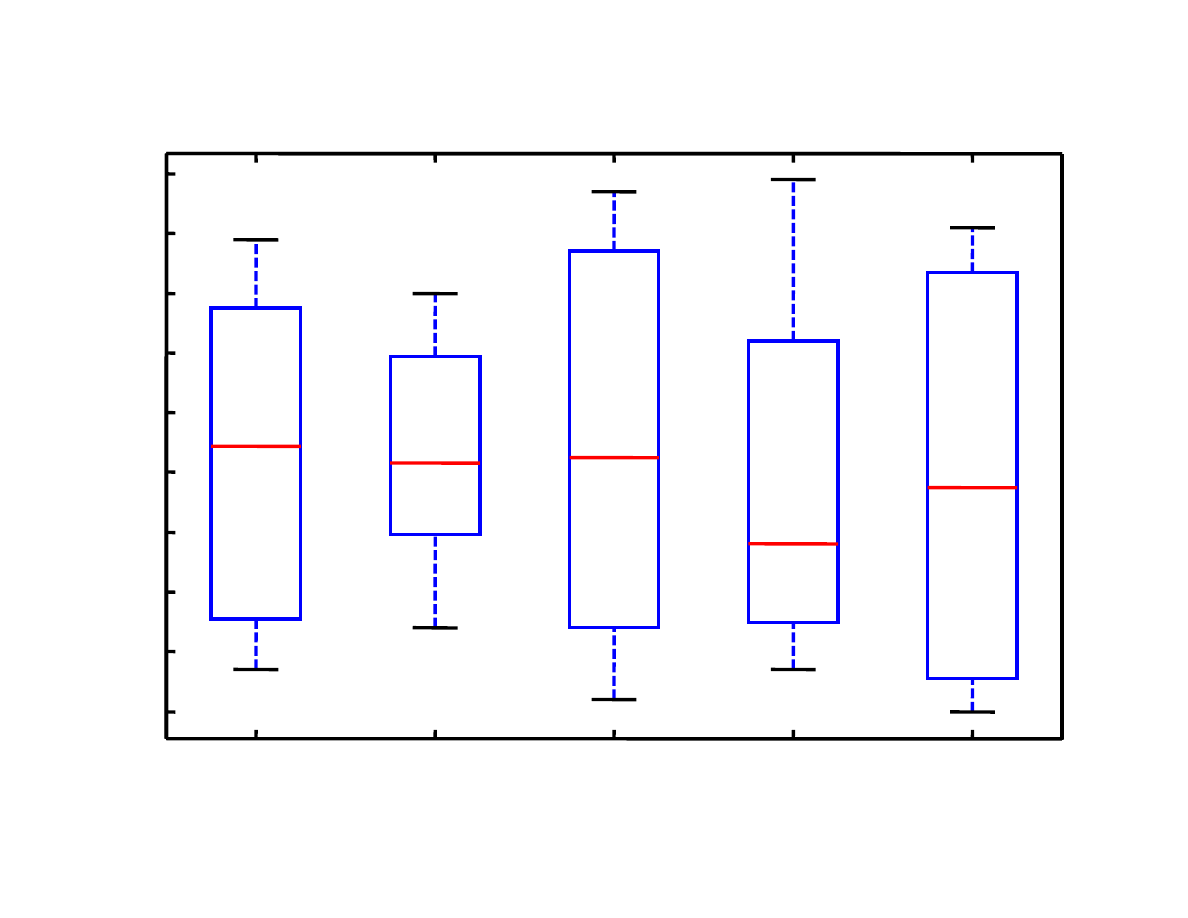
Pozna
Wrocław
Wałbrzych
Katowice
Opole
10
20
30
40
50
60
70
80
90
100
C
en
a
>> boxplot(cena,miasto)
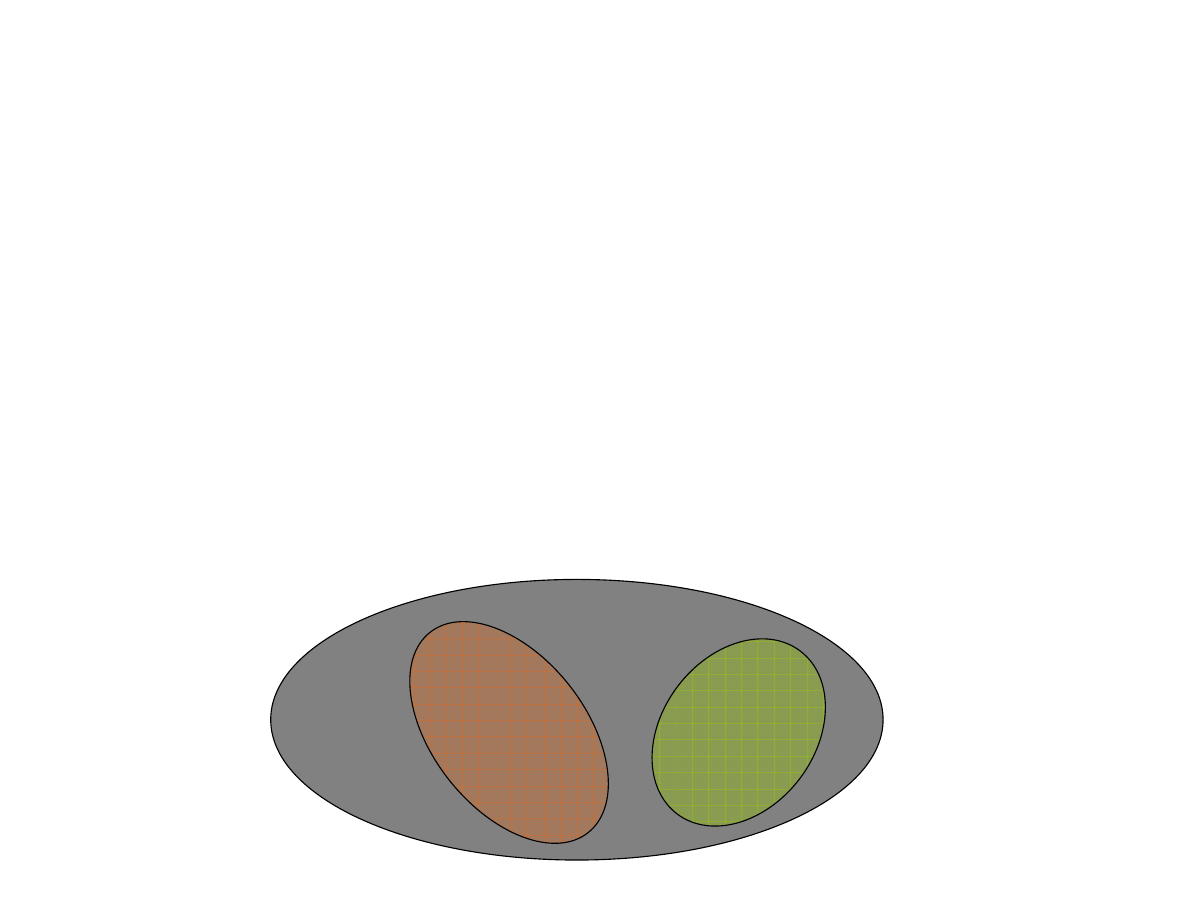
Podstawowym poj ciem rachunku prawdopodobie stwa jest
zdarzenie losowe
oraz
przestrze zdarze elementarnych
.
Do wiadczenie jest zdarzeniem losowym, je eli:
mo e by powtarzane w tych samych warunkach;
jego wynik nie mo e by przewidziany w sposób pewny;
zbiór wszystkich mo liwych wyników jest znany i mo e by opisany przed
przeprowadzeniem wiczenia.
Zbiór wszystkich mo liwych wyników zdarze losowych nosi nazw
przestrzeni zdarze elementarnych lub przestrzeni próbkow (
Ω
lub S).
Pojedynczy element przestrzeni zdarze elementarnych (pojedynczy wynik
do wiadczenia losowego) nazywany jest
zdarzeniem elementarnym
.
Dowolny podzbiór zdarze elementarnych nazywamy zdarzeniem A, B, C itd.
Ω
Ω
Ω
Ω
A
B

Przykłady:
jednokrotny rzut monet : „orzeł” (O) i „reszka” (R) to dwa zdarzenia
elementarne, które buduj cał przestrze ,
Ω
={O, R}.
rzut dwoma monetami:
Ω
={(O,O), (O,R), (R,O), (R,R)}.
wybieraj c dowolna cyfr z ksi ki telefonicznej:
Ω
={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
rozwa aj c ostatni cyfr dowolnej liczby parzystej:
Ω
={0, 2, 4, 6, 8}.
czas oczekiwania na taksówk – zdarzenia elementarne s
dowolnymi liczbami dodatnimi, a przestrze jest niesko czona.
Uwaga: Zdarzenia elementarne musza by ekskluzywne – dane
zdarzenie elementarne nie zawiera w sobie innych zdarze
elementarnych

Zmienna losowa
– dowolna funkcja o warto ciach rzeczywistych okre lona na
przestrzeni zdarze elementarnych, która ka demu zdarzeniu elementarnemu
przyporz dkowuje liczb rzeczywist z okre lonym prawdopodobie stwem.
Zmienn losow
nazywamy
dyskretn
, gdy przyjmuje warto ci ze zbioru
dyskretnego, tzn. sko czonego lub przeliczalnego. Dla ka dej warto ci mo na
wyznaczy prawdopodobie stwo jej wyst pienia (np. liczba studentów, liczba
oczek na kostce).
Je eli zmienna losowa mo e przybiera wszystkie warto ci z pewnego
przedziału liczbowego, to nazywana jest
zmienna losow ci gł
, np. ilo
wody w wiadrze, waga osobnika, temperatura za oknem).
Prawdopodobie stwo zdarzenia A
Klasyczna definicja prawdopodobie stwa: P(x)=
liczba zdarze elementarnych sprzyjaj cych zdarzeniu x
P(x)=
n liczba wszystkich zdarze elementarnych
n
x
n
Liczba wyst pie warto ci zmiennej w danej grupie
Liczba wyst pie wszystkich warto ci zmiennej
Wzgl dna cz sto
grupy
=
>> rozklad
rozklad =
18
19 20 21 22 23 24 25 26 27 28
2 6 4 5 8 3 7 3 6 3 3
50
0.04 0.12 0.08 0.1 0.16 0.06 0.14 0.06 0.12 0.06 0.06
1
4
12 8 10 16 6 14 6 12 6 6
100
Procentowa wzgl dna cz sto
grupy= Wzgl dna cz sto
grupy * 100

Wła ciwo ci rachunku prawdopodobie stwa:
Ka demu zdarzeniu losowemu A przypisujemy liczb P(A), zwana
prawdopodobie stwem tego zdarzenia, która jest nieujemna i mniejsza
b d równa jedno ci: 0 P(A) 1.
Prawdopodobie stwo zdarzenia pewnego jest równe jedno ci: P(
Ω
)=1.
Prawdopodobie stwo zdarzenia niemo liwego jest równe zeru: P(
∅
)=1.
Prawdopodobie stwo sumy zdarze losowych A oraz B:
je eli A
∩
B= 0
, jest równe sumie prawdopodobie stw tych zdarze :
P(A
∪
B) = P(A) + P(B).
je eli A
∩
B 0
, jest równe sumie prawdopodobie stw tych zdarze minus
prawdopodobie stwo ich iloczynu:
P(A
∪
B) = P(A) + P(B) – P(A
∩
B)
Prawdopodobie stwo zdarzenia przeciwnego do zdarzenia A: P( )=1-P(A)
Ω
Ω
Ω
Ω
A
B
Ω
Ω
Ω
Ω
A
B
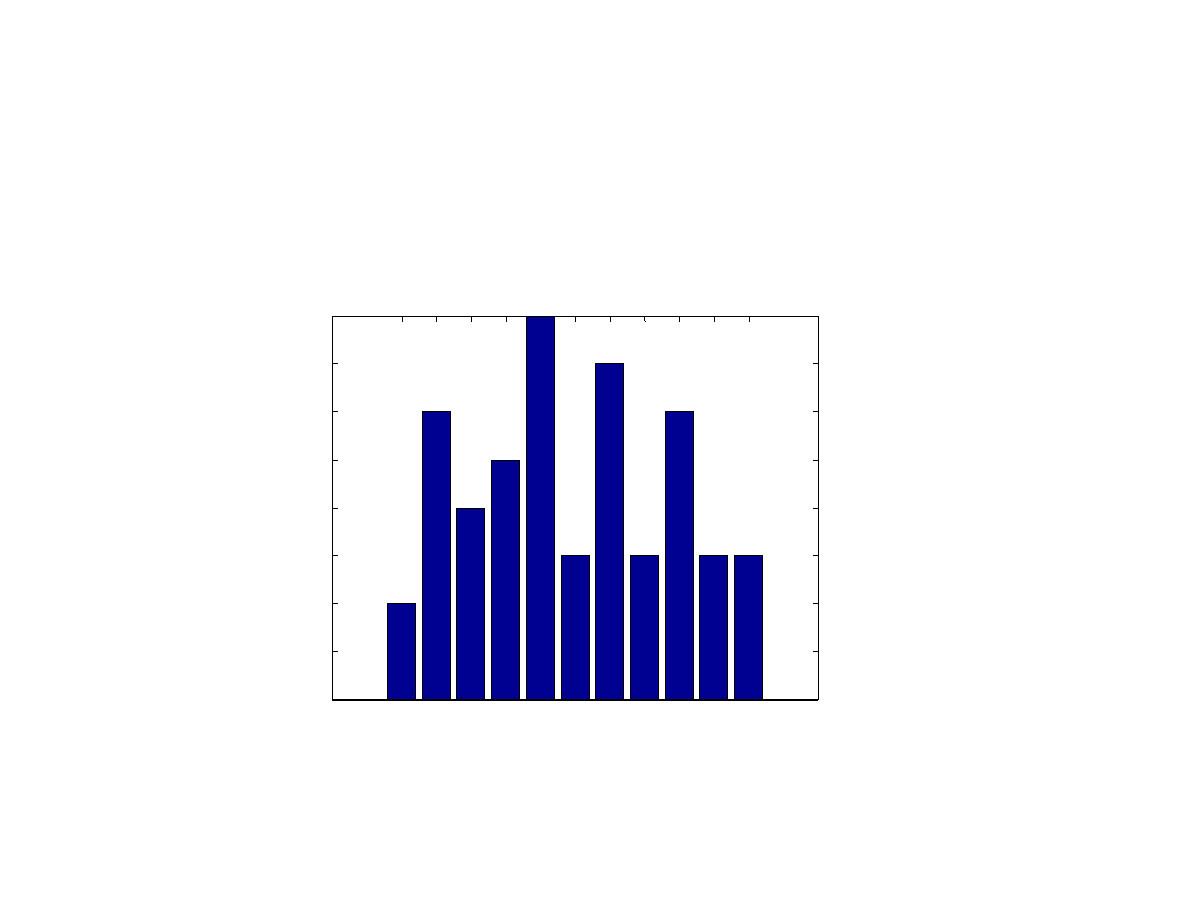
18
19
20
21
22
23
24
25
26
27
28
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
Zmienna x - grupa (wiek)
W
zg
l
dn
a
cz
st
o
gr
up
y
/ l
ic
ze
bn
o
gr
up
y
P
ra
w
do
po
do
bi
e
st
w
o
P
(x
)

Je eli X jest dowoln zmienn losow to dla tej zmiennej okre lana jest
dystrybuanta.
Dystrybuanta
- funkcja zmiennej rzeczywistej X równa prawdopodobie stwu,
e zmienna losowa przyjmie warto
nie wi ksz od x.
Jest to wi c całka oznaczona od dolnej granicy dziedziny danego rozkładu
prawdopodobie stwa zmiennej losowej (np. minus niesko czono ci lub zera)
do X, z funkcji rozkładu prawdopodobie stwa danej zmiennej losowej.
Dla dyskretnej zmiennej losowej warto
F(x
i
) mo na obliczy
przez zsumowanie (
skumulowanie
) funkcji prawdopodobie stwa dla warto ci
nie wi kszych od x
i
.
Skumulowana funkcja prawdopodobie stwa
Cumulative Distribution Function
x
i
≤
x
)= P(x
i
x
i
≤
x
F(x)=
)
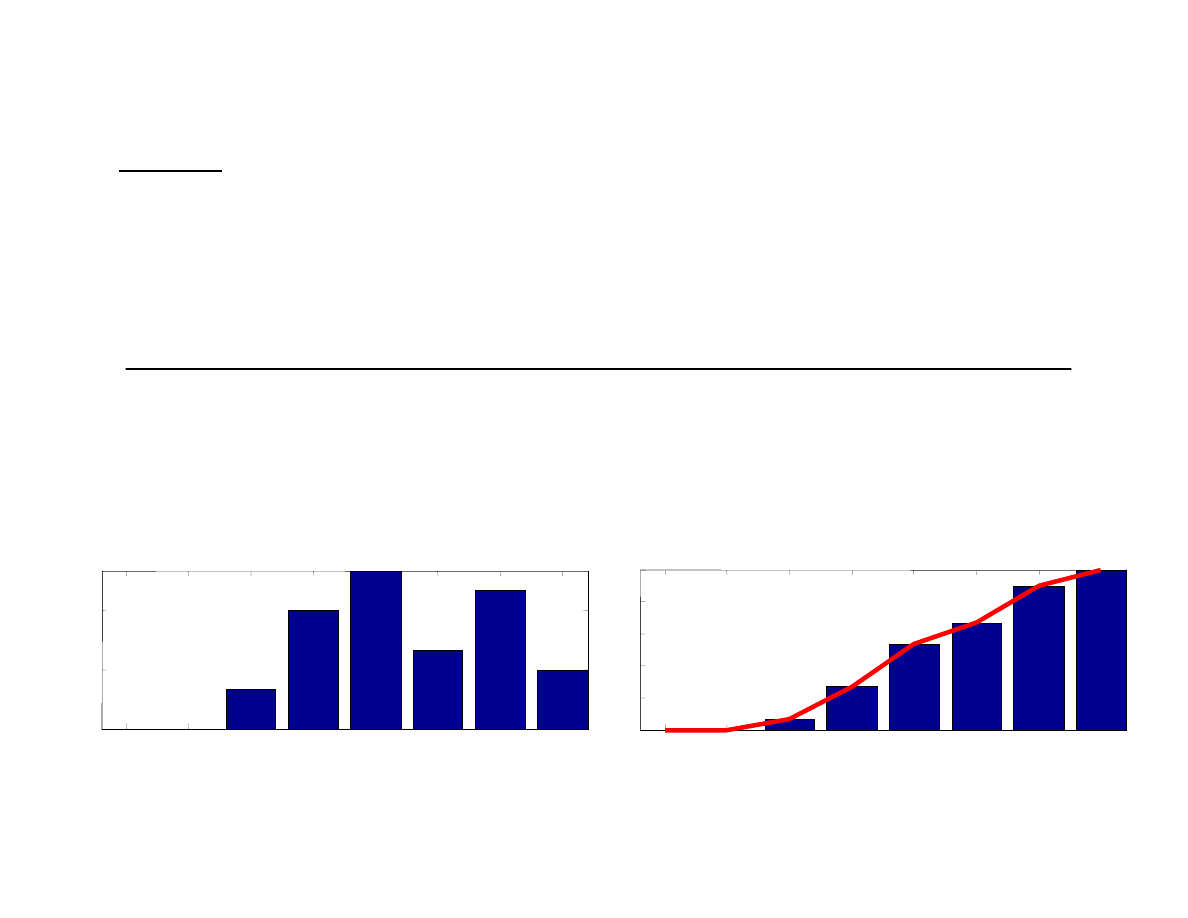
Przykład
Funkcj dystrybuanty wyznaczamy sumuj c (kumuluj c) kolejne warto ci
P(x
i
)
:
x
i
2
3
4
5
6
7
8
9
P(x
i
) 0,000 0,000
0,067 0,200 0,267 0,133 0,233 0,100
F(x
i
) 0,000 0,000
0,067 0,267 0,534 0,667 0,900 1,000
=
=
1
)
(
k
i
k
P(x
i
)
x
F
2
3
4
5
6
7
8
9
0
0.1
0.2
Zmienna X
P
(X
)
Zmienna X
2
3
4
5
6
7
8
9
0
0.2
0.4
0.6
0.8
1
F(
X
)
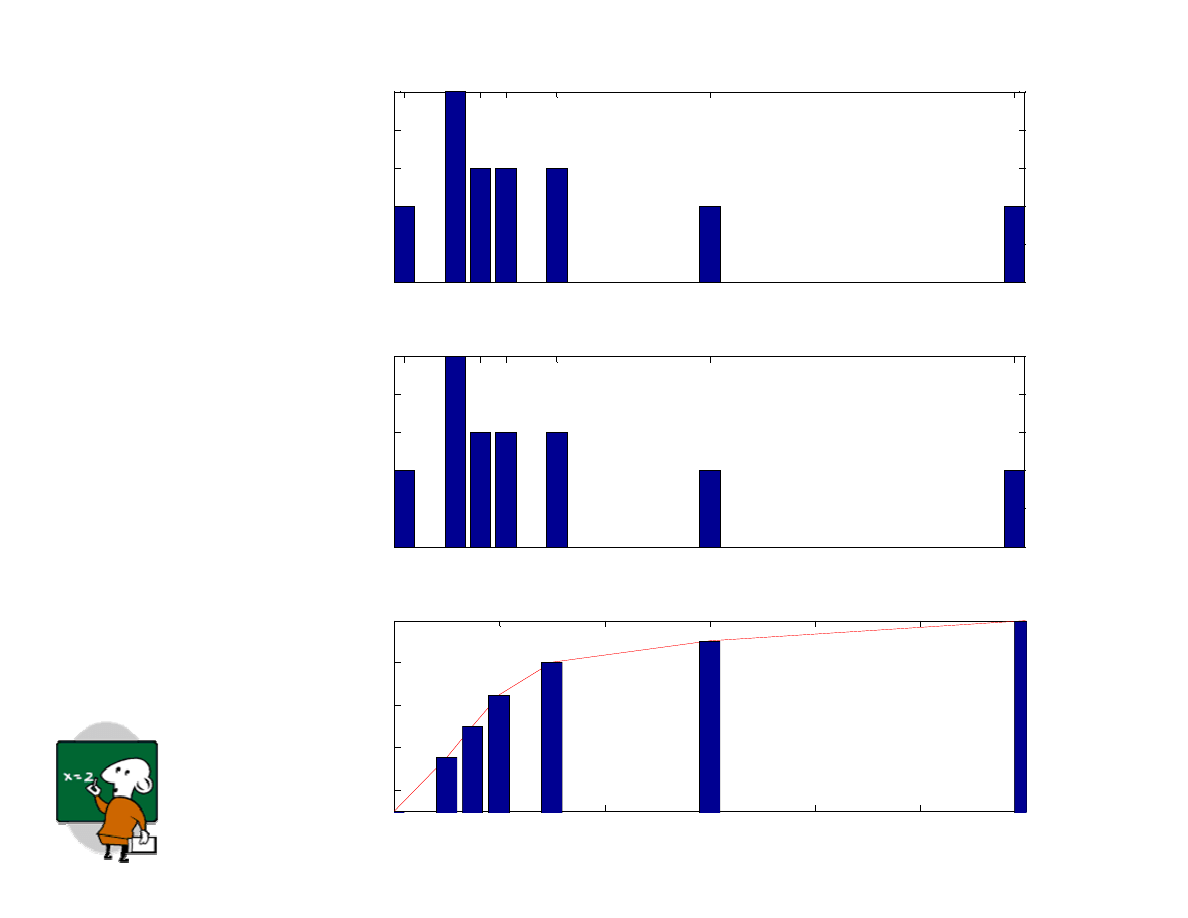
0
10 15 20
30
60
120
0
1
2
3
4
5
Czas (min)
C
ze
st
os
c
0
10 15 20
30
60
120
0
0.05
0.1
0.15
0.2
0.25
Czas (min)
P
(x
)
0
20
40
60
80
100
120
0.2
0.4
0.6
0.8
1
Czas (min)
F(
x)
Czas po wi cony
na nauk
przed egzaminem
z Informatyki II
dla próby 20 studentów:
10
20
15
0
15
30
30
20
10
15
10
60
0
10
30
20
120
60
10
120

Dla
dyskretnej zmiennej losowej
X o funkcji prawdopodobie stwa P
warto ci
redni
(oczekiwan )
nazywamy liczb
=
=
∞
∞
∞
∞
1
i
X
x
i
P(x
i
)
µµµµ
E(X)=
Wariancj dyskretnej zmiennej losowej
o funkcji prawdopodobie stwa p nazywamy
liczb
=
=
∞
∞
∞
∞
1
i
X
(x
i
-
µµµµ
X
)
2
P(x
i
)
σσσσ
2
Odchylenie standardowe
σσσσ
x
definiuje si jako
2
x
σ
V(X)=

X Cz sto
P(x)
F(x)
x*P(X)'
(x-
µ
x
)
2
*P(x)
0
2
0.1
0.1
0
91.5063
10
5
0.25
0.35
2.5
102.5156
15
3
0.15
0.5
2.25
34.8844
20
3
0.15
0.65
3
15.7594
30
3
0.15
0.8
4.5
0.0094
60
2
0.1
0.9
6
88.5063
120
2
0.1
1
12
805.5063
µµµµ
30.25
1138.6875
σσσσ
2222
33.7444
σσσσ

Funkcja g sto ci prawdopodobie stwa zmiennej losowej
typu ci głego
nazywamy funkcj f(x), okre lon na zbiorze liczb rzeczywistych
o nast puj cych własno ciach:
F(x)
≥
0
b
a
F(x)dx=P(a<X<b) dla dowolnych a<b
F(x)
g sto
zmiennej losowe X
lub
g sto
rozkładu
Warto ci
redni ci głej zmiennej losowej
o g sto ci f nazywamy wielko
+
∞
-
∞
x F(x)dx
µµµµ
=
E(X) =
Wariancj ci głej zmiennej losowej
o g sto ci f nazywamy wielko
(x-
µµµµ
)
2
F(x)
σσσσ
2
V(X)= =
+
∞
-
∞

Dystrybuanta rozkładu zmiennej losowej
X
Rozkład zmiennej losowej mo na opisa dystrybuant , czyli funkcj
zmiennej losowej
X
zdefiniowan nast puj co
F
(
x
) =
P
(
X<x
)
(probability distribution )
Dystrybuanta okre la prawdopodobie stwo, e zmienna losowa przyjmie
warto
mniejsz ni okre lone x:
Dystrybuanta jest funkcj :
niemalej c ,
z przedziału [0; 1],
o warto ciach lim F(x)=0 oraz lim F(x)=1,
x
→
-
∞
x
→∞
dla której
P
(
a x b
) =
F
(
b
)-F(a)
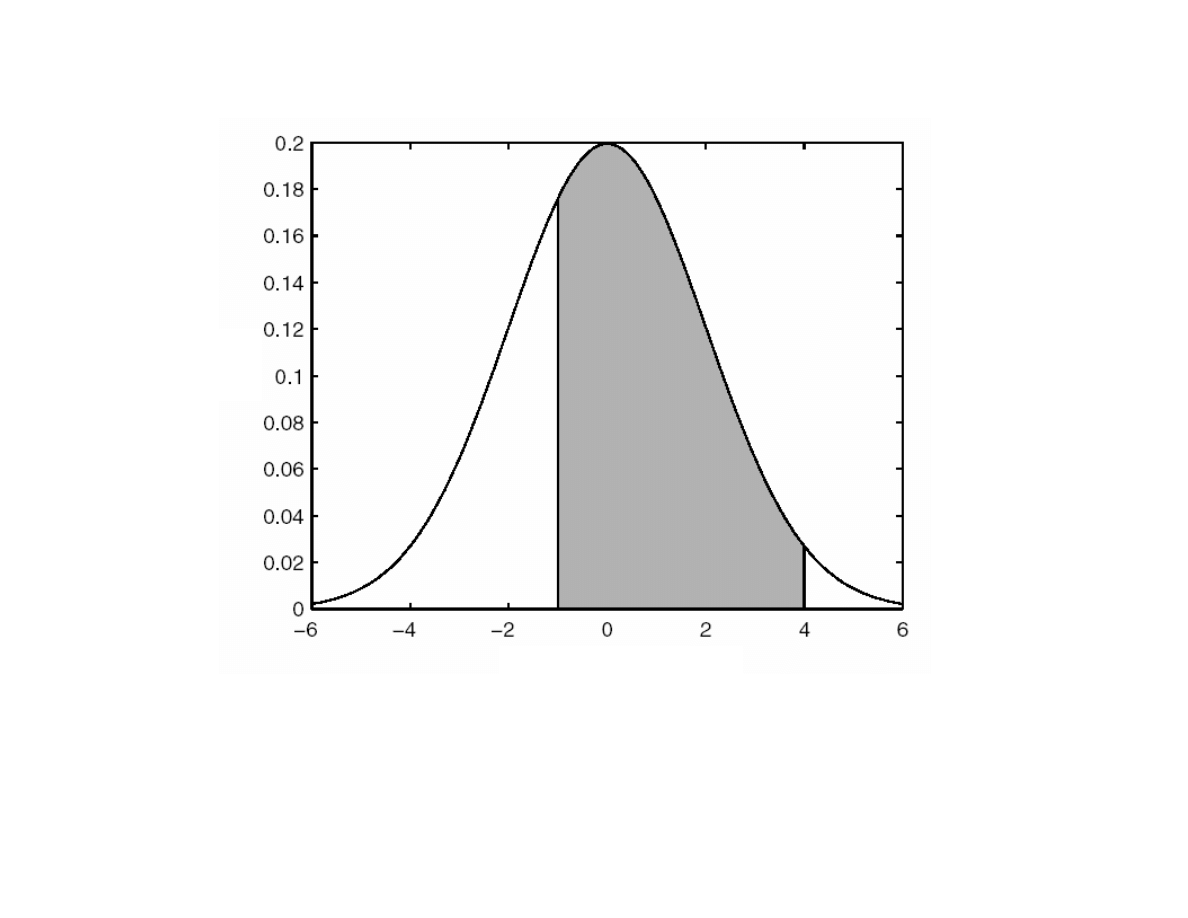
Zmienna losowa X
P
(x
)
Powierzchnia pod krzyw f(x) w przedziale [-1:4] jest prawdopodobie stwem,
e zmienna losowa, której rozkład opisuje funkcja f(x) przyjmie warto
mi dzy
warto ci -1 a 4.
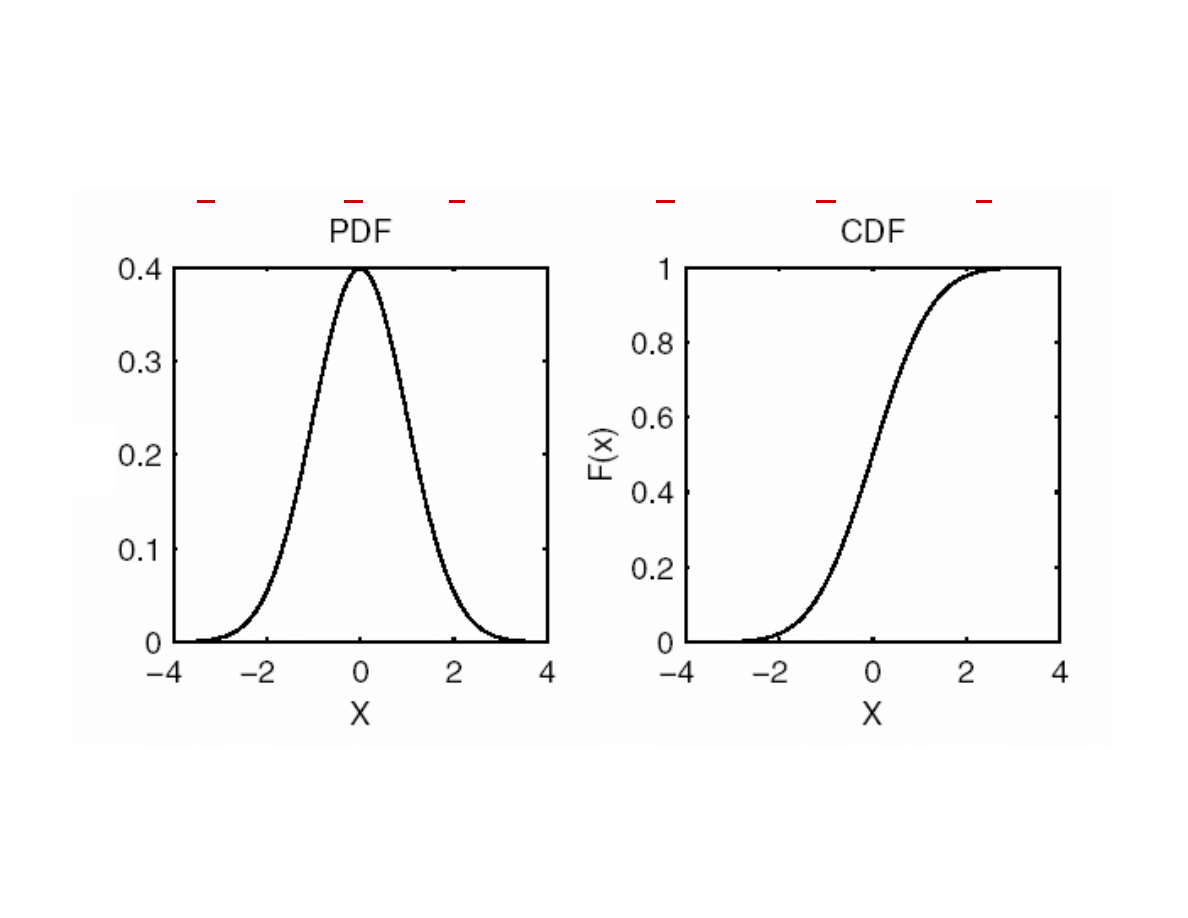
Probability Density Function
Cumulative Distribution Function
CDF
P
(x
)
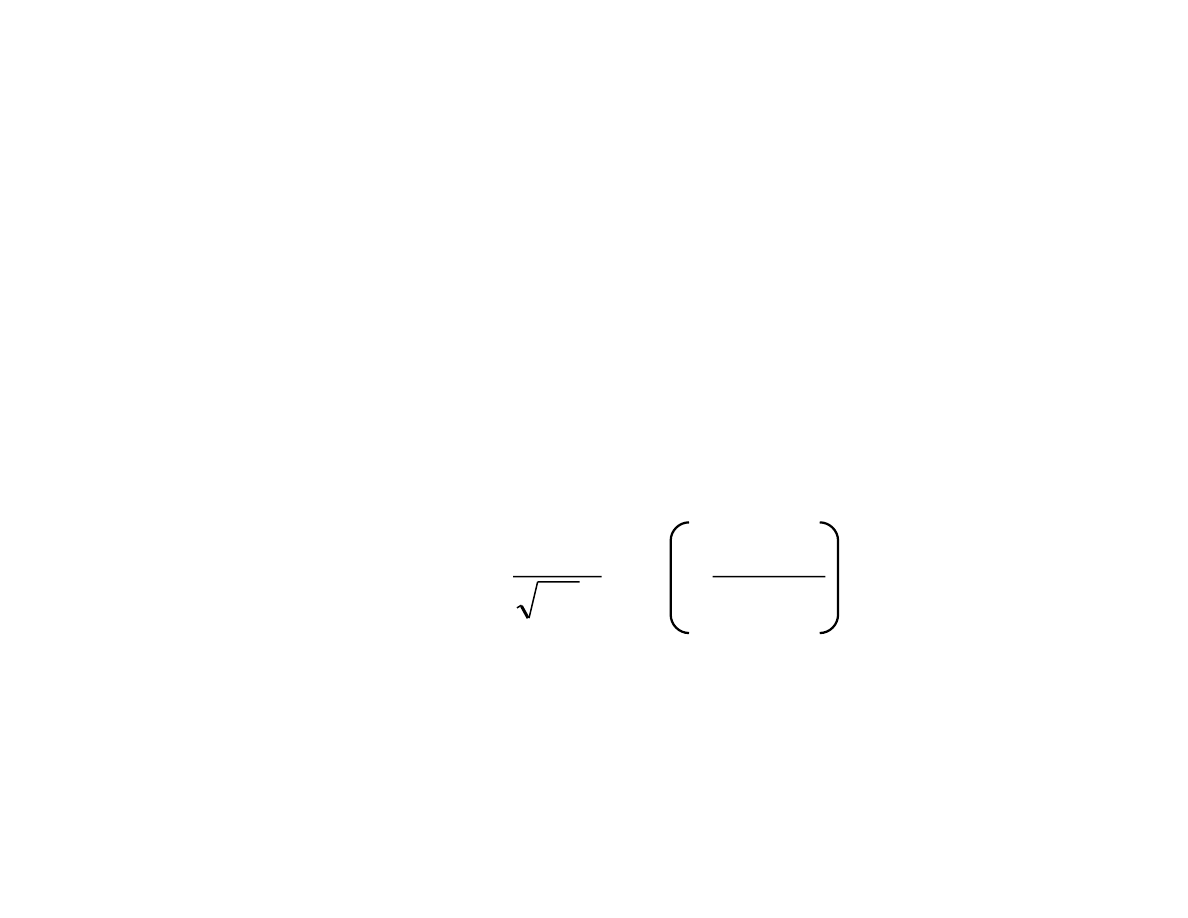
Funkcja g sto ci w rozkładzie normalnym o postaci:
okre lona dla wszystkich rzeczywistych warto ci
zmiennej X.
(
)
(
)
σσσσ
µµµµ
−
−
σσσσ
π
=
σσσσ
µµµµ
2
x
exp
2
1
,
;
x
P
2
2
Centraln rol w rachunku prawdopodobie stwa i
statystyce pełni tak zwany rozkład normalny.
Zwi zane jest z nim słynne twierdzenie nazywane
centralnym twierdzeniem granicznym. Na jego podstawie
mo na w wielu sytuacjach zakłada , e zmienna losowa,
któr jeste my wła nie zainteresowani, ma rozkład
normalny.

Rozkład normalny
Rozkład normalny (termin ten został po raz pierwszy u yty przez Galtona, 1889)
posiada funkcj g sto ci okre lon wzorem:
Dwuwymiarowy rozkład normalny.
Dwie zmienne podlegaj dwuwymiarowemu rozkładowi normalnemu,
je li dla ka dej warto ci jednej zmiennej, odpowiadaj ce warto ci drugiej zmiennej
posiadaj rozkład normalny.
Dokładny kształt rozkładu normalnego (charakterystyczna "krzywa dzwonowa")
zdefiniowany jest przez funkcj posiadaj c jedynie dwa parametry:
warto
redni i odchylenie standardowe.

Funkcja g sto ci w rozkładzie normalnym:
jest symetryczna wzgl dem prostej
x
=
µ
w punkcie
x =
µ
osi ga warto
maksymaln
ramiona funkcji maj punkty przegi cia dla x =
µ
-
oraz
x =
µ
+
rednia (
µ
) jest zarazem modaln i median ,
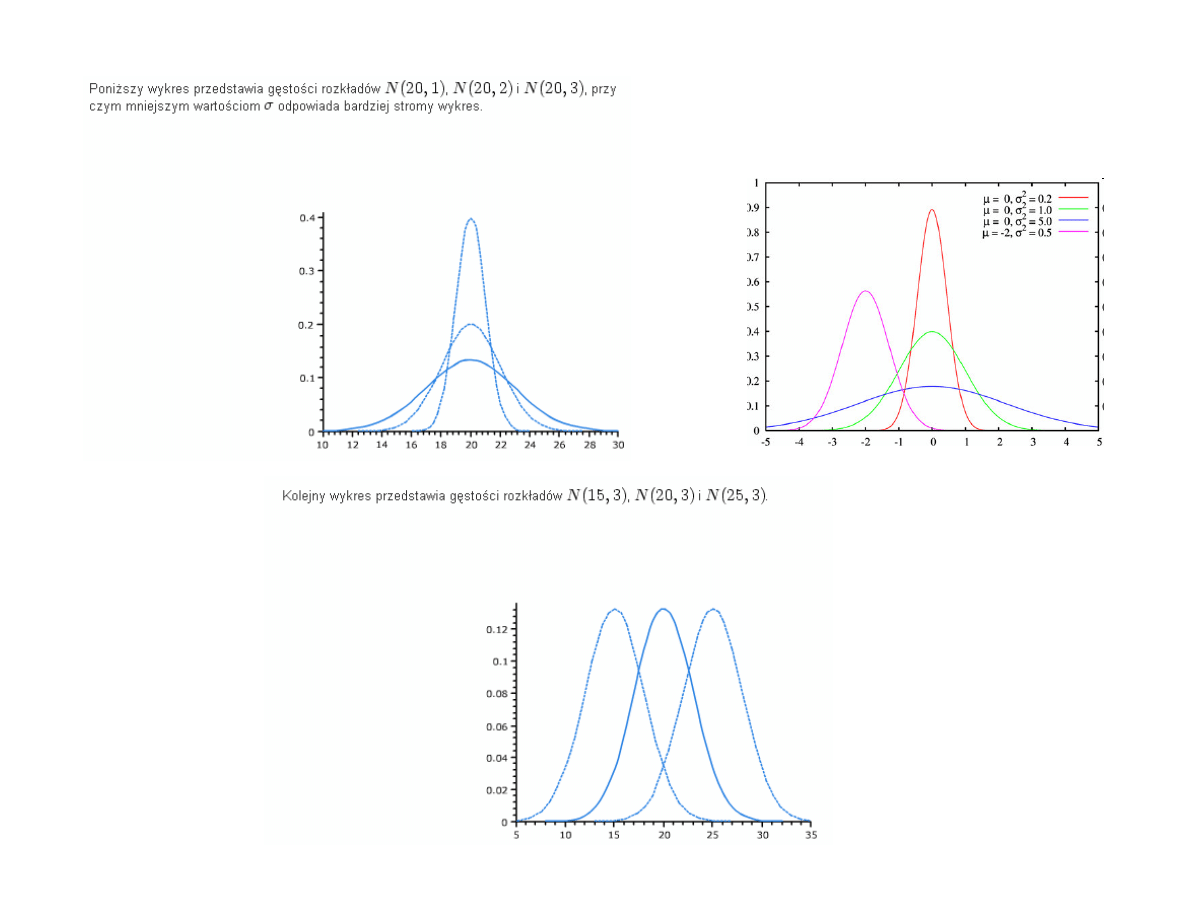
kształt funkcji g sto ci zale y od warto ci parametrów:
µ
i .
Parametr
µ
decyduje o przesuni ciu krzywej,
natomiast parametr decyduje o „smukło ci” krzywej.
Funkcja g sto ci rozkładu normalnego ma zastosowanie do
reguły
„trzech sigma”,
któr nast pnie rozwini to na
reguł „sze
sigma”
–
stosowan w kontroli jako ci
Reguła „trzech sigma” - je eli zmienna losowa ma rozkład normalny to:
- 68,3 % populacji mie ci si w przedziale (
µ
- ;
µ
+ )
- 95,5 % populacji mie ci si w przedziale (
µ
- 2 ;
µ
+ 2 )
- 99,7 % populacji mie ci si w przedziale (
µ
- 3 ;
µ
+ 3
)
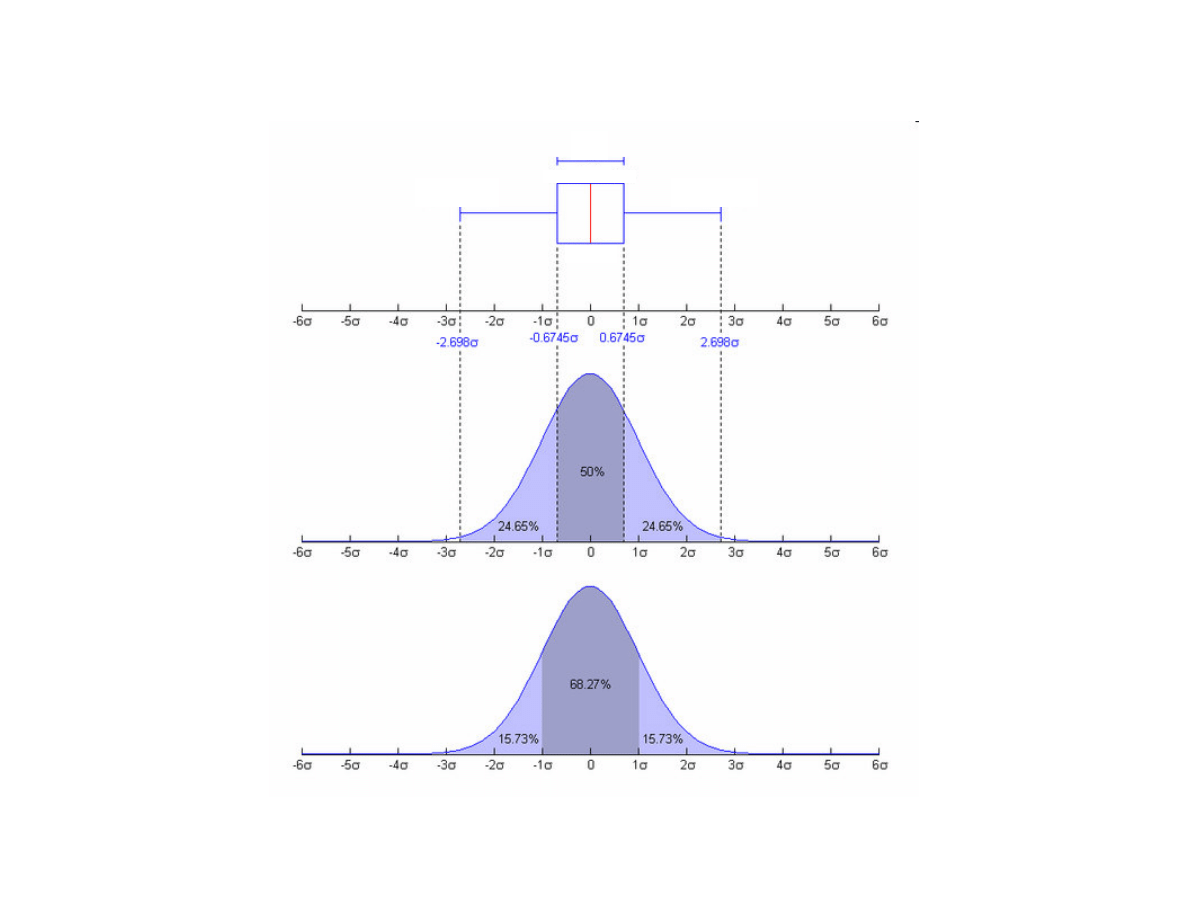
rozst p
mi dzykwartylny
Q3+1.5*H
Q1-1.5*H
H
Q3
Q1
Mediana
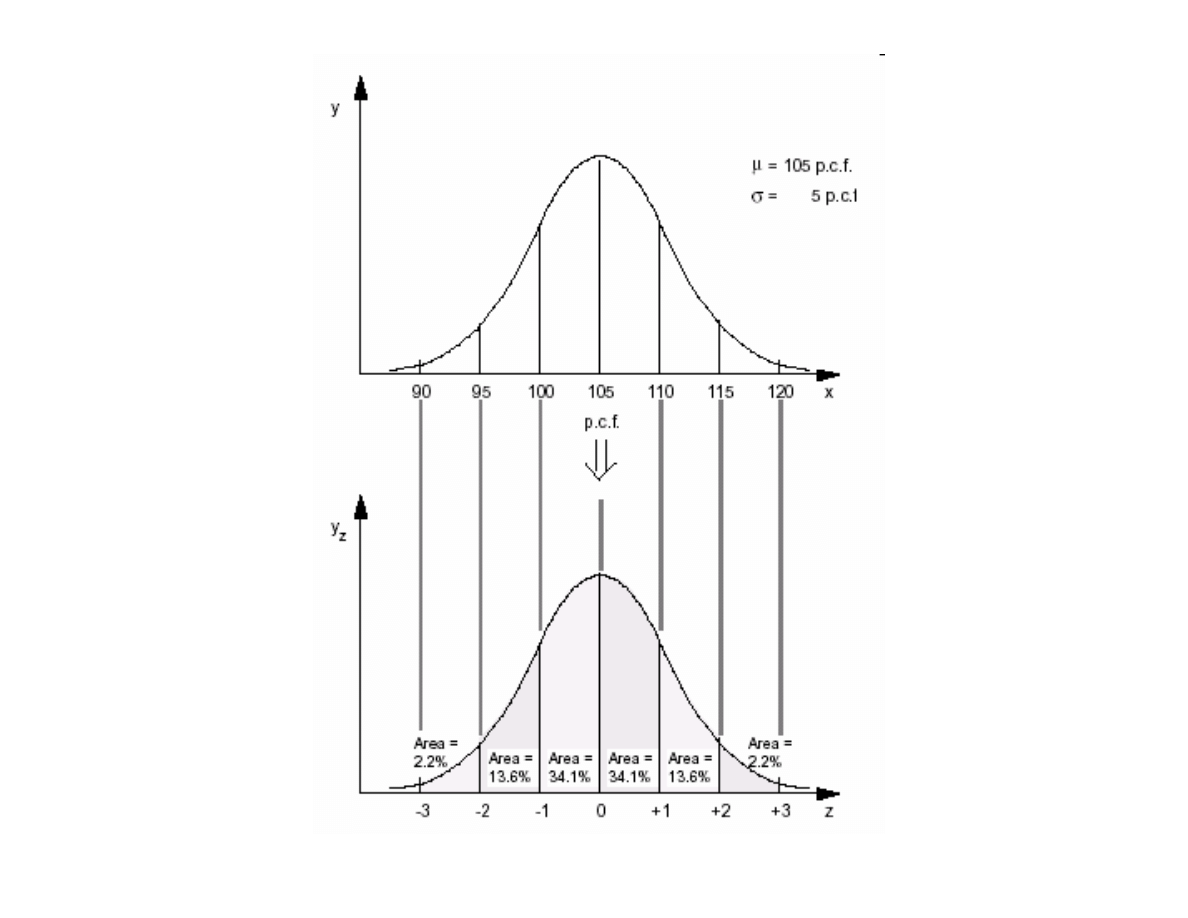

W celu obliczenia prawdopodobie stwa zmiennej X w rozkładzie
normalnym o dowolnej warto ci oczekiwanej i odchyleniu
standardowym dokonuje si
standaryzacji.
Standaryzacja polega na sprowadzeniu dowolnego rozkładu
normalnego o danych parametrach
µ
i do rozkładu
standaryzowanego (modelowego) o warto ci oczekiwanej
µ
= 0
i odchyleniu standardowym = 1.
Prawdopodobie stwo w rozkładzie normalnym wyznacza si dla
warto ci zmiennej losowej z okre lonego przedziału
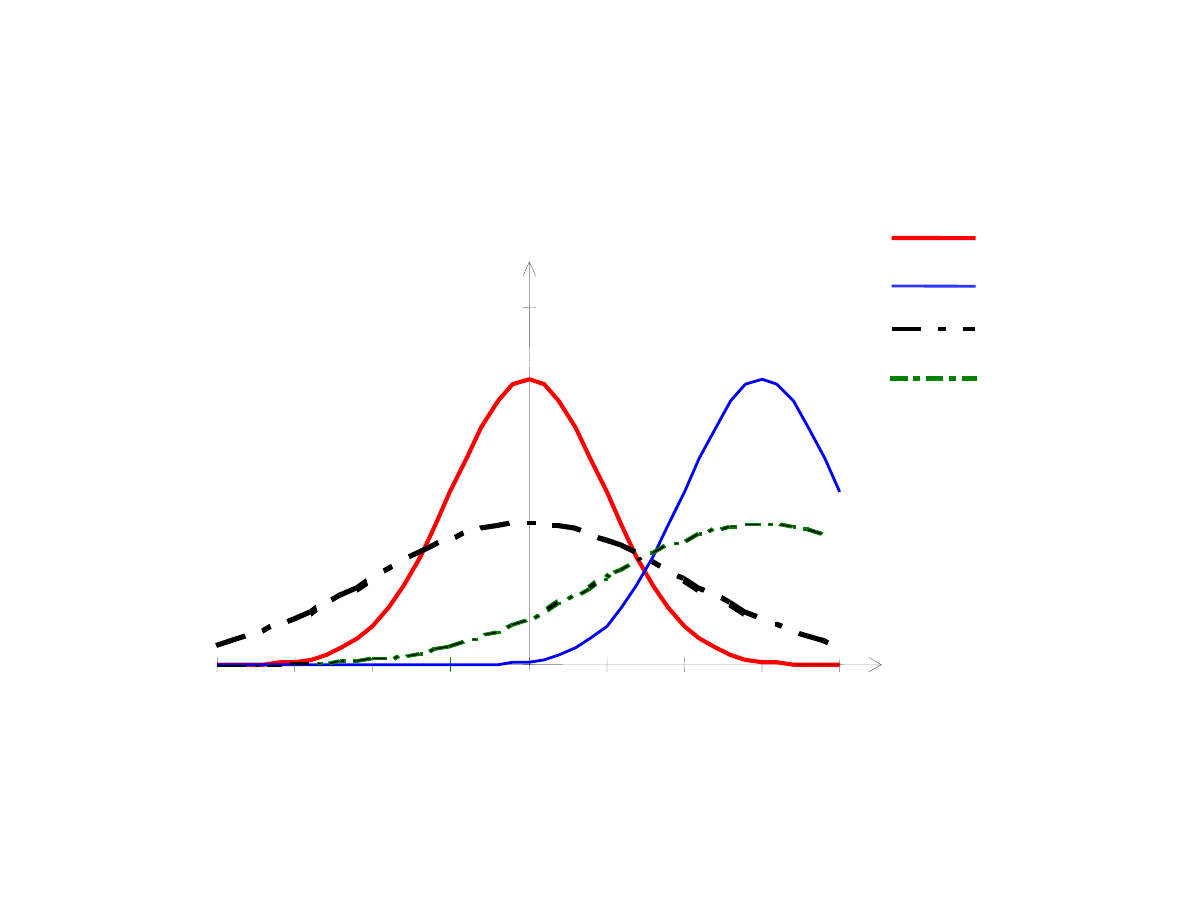
Przykładowe rozkłady funkcji g sto ci dla danych
i
0
0,5
-4
-3
-2
-1
0
1
2
3
4
N(0,1)
N(3,1)
N(0,2)
N(3,2)
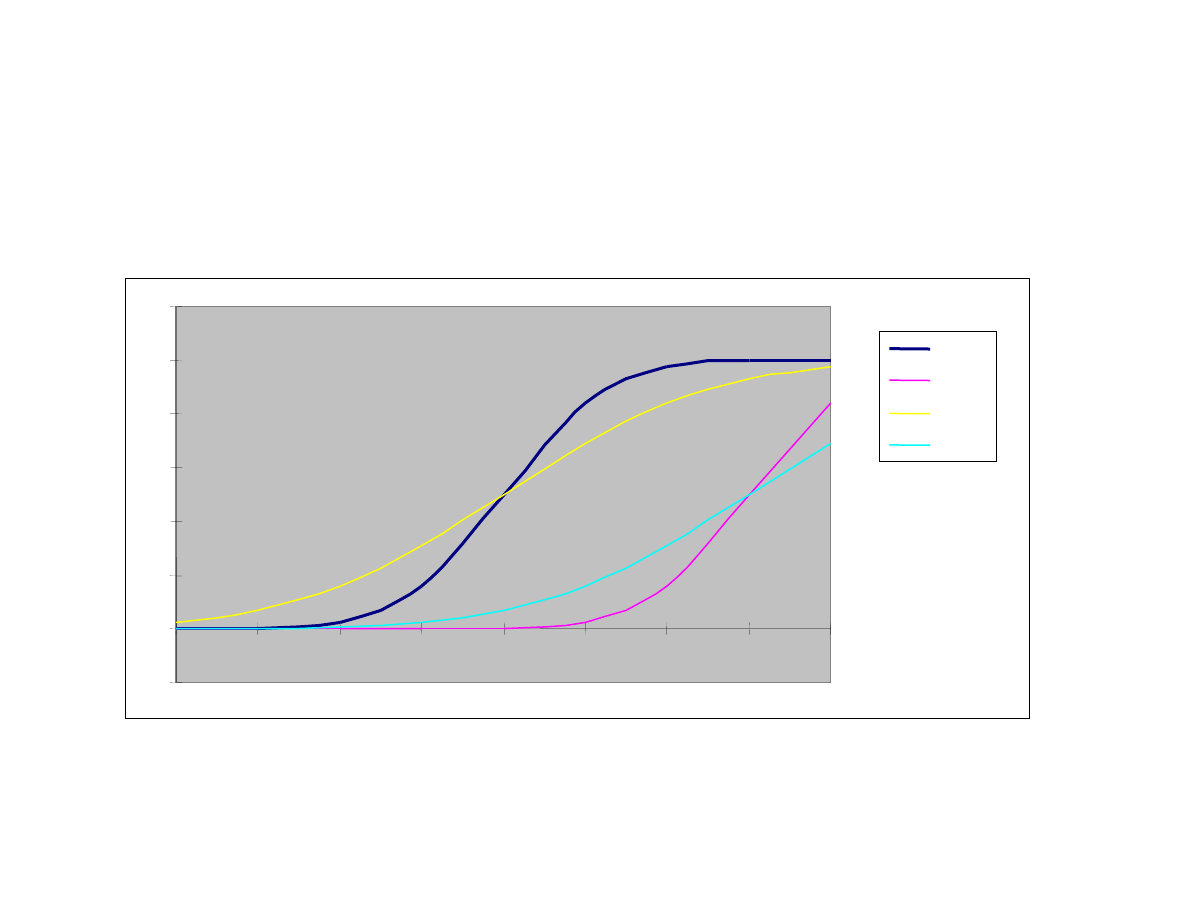
Wykres dystrybuanty rozkładu normalnego
-0,2
0
0,2
0,4
0,6
0,8
1
1,2
-4
-3
-2
-1
0
1
2
3
4
N (0,1)
N (3,1)
N (0,2)
N (3,2)
>> dist
tool
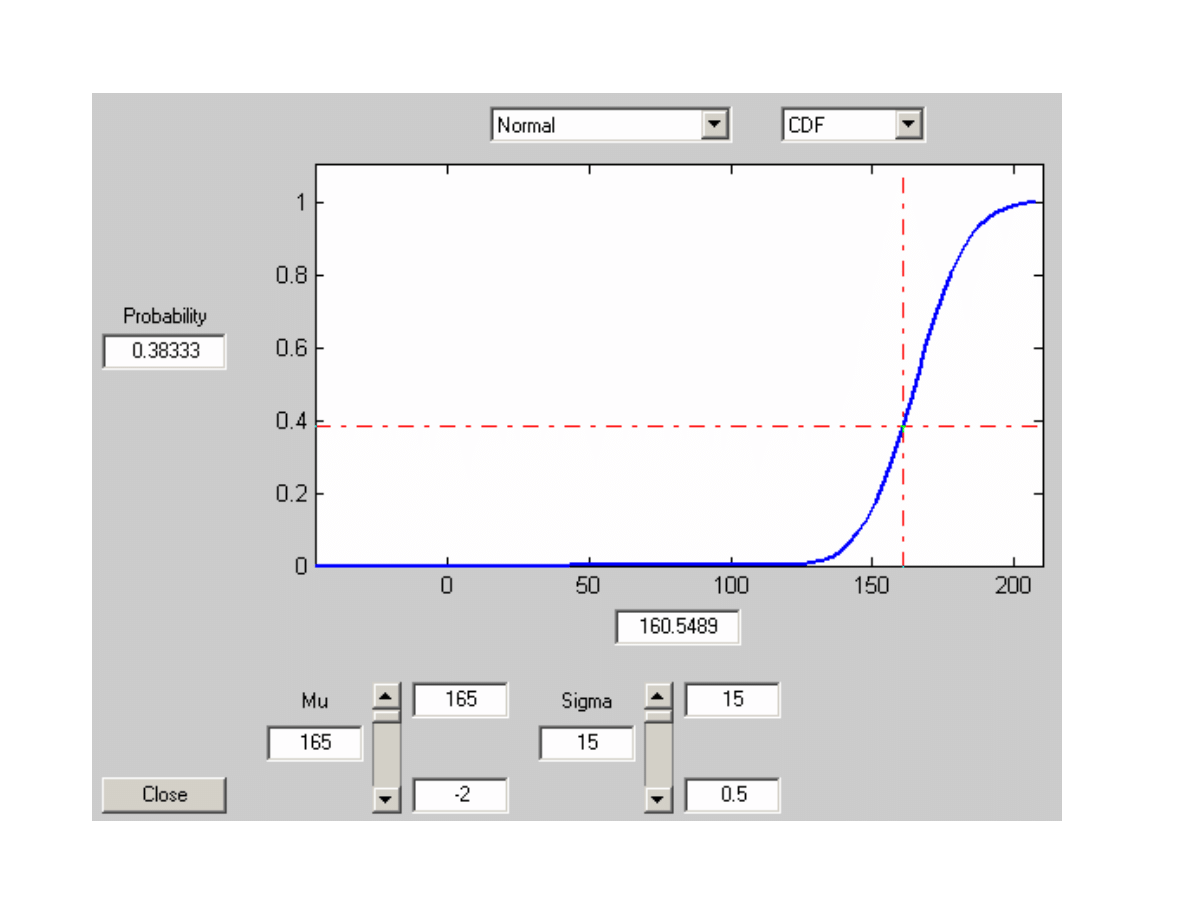
Przykład:
Wzrost kobiet w pewnej populacji ma rozk
ł
ad normalny
N(165,15). Oznacza to, i zmienna losowa jak jest wzrost
kobiet ma rozk
ł
ad normalny ze redni równa165 cm
i odchyleniem standardowym równym 15 cm.
Jaki jest udzia
ł
w populacji kobiet o wzroscie:
a)
do 160 cm,
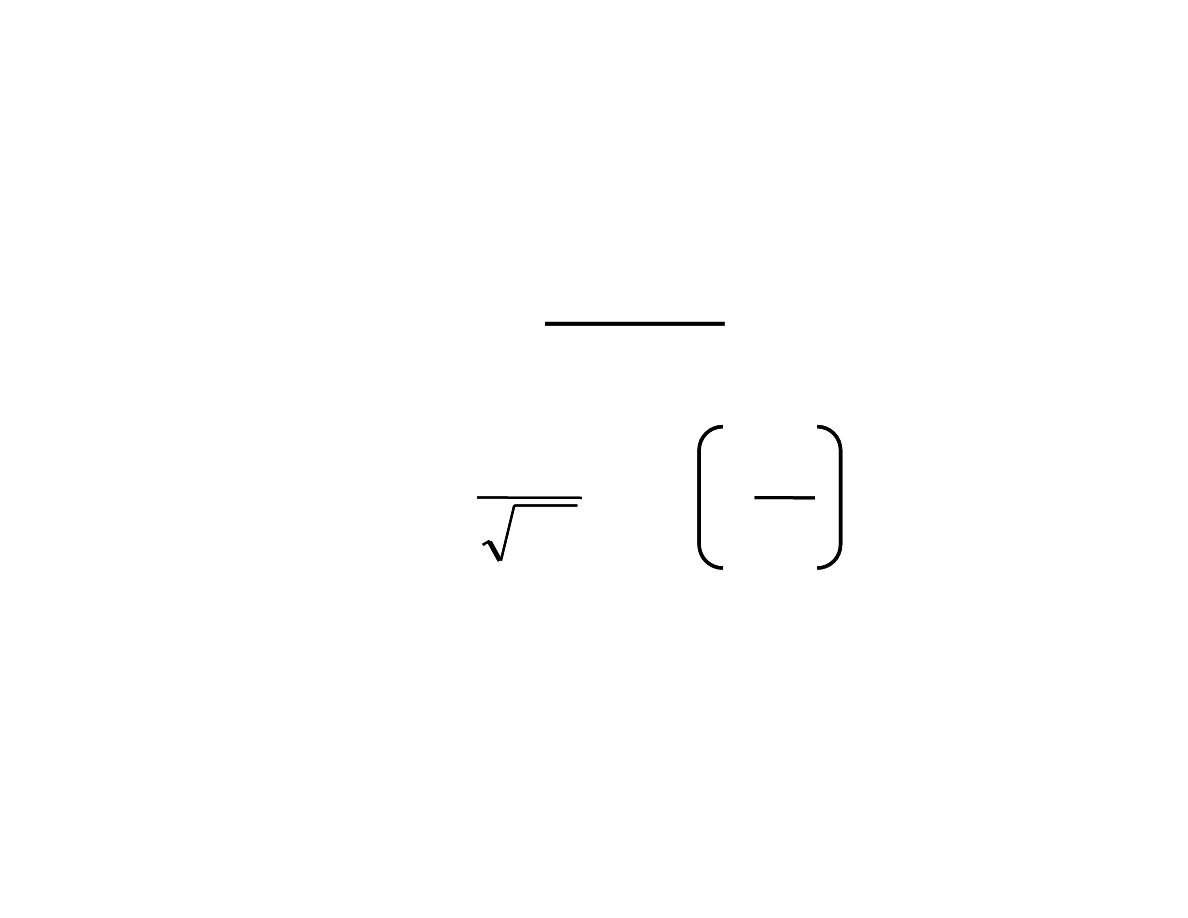
u
Zmienn losow X zast pujemy
zmienn standaryzowan u
, która ma
rozkład N(0,1)
u = zmienna standaryzowana
(
)
-
π
=
2
u
exp
2
1
1
,
0
;
f
2
σ
µ
−
= x
u
)
-
π
=
2
exp
2
1
,
;
f
2
σ
x

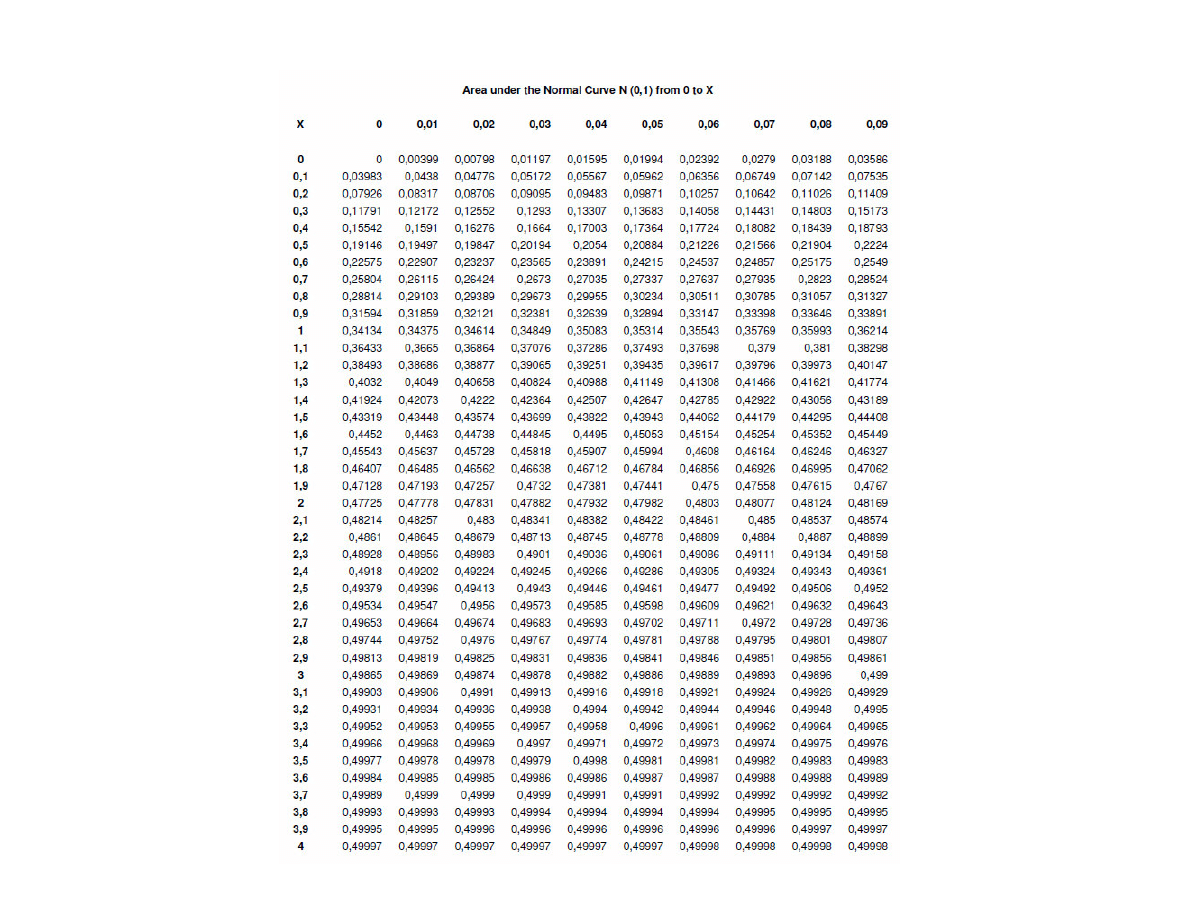
Warto ci dystrybuanty standaryzowanego rozkładu
normalnego – warto ci te zostały stablicowane
Zatem:
−
−
=
<
<
σ
µ
σ
µ
a
b
F
b
X
a
P
)
(
- F
Wzrost studentów ma rozkład
N(
175; 5). Odpowiedz, jakie jest
prawdopodobie stwo, e spotkamy studenta o wzro cie:
a. dokładnie 180 cm
b. ni szym ni 180 cm
c. wy szym ni 180 cm
d. w granicach pomi dzy 172,5 i 182,5 cm
e. w granicach pomi dzy 180 i 182,5 cm
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron