X L V I I I K O N F E R E N C J A N AU K O W A

KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN

I KOMITETU NAUKI PZITB

Opole – Krynica

2002

Jan A. KARCZEWSKI

1

Stanisław WIERZBICKI

2

Paweł KRÓ L

3

KOMPUTEROWE MODELOWANIE

WIELOŚ RUBOWEGO POŁ Ą CZENIA SPRĘ Ż ONEGO

1. Wprowadzenie

O tym czy stalowa konstrukcja budowlana została prawidłowo zaprojektowana i wykonana
decydują, w wię kszości przypadków, dwa podstawowe kryteria: nośności i odkształcalności.
Wpływ na spełnienie obu tych kryteriów ma prawidłowe przyję cie przekrojów oraz właściwe
rozwiązanie połączeń . Nośność wię kszości typowych połączeń nie budzi na ogół wię kszych
wątpliwości i może być wyznaczona według znanych metod obliczeniowych, W niektórych
przypadkach, jednakże, metody te pozostawiają w połączeniu znaczne rezerwy nośności.
Wykorzystanie czę ści tych rezerw wymaga jednak rozwinię cia metod wymiarowania
połączeń uwzglę dniających, poza nośnością, także ich odkształcalność . Przykładem może tu
być nakładkowe połączenie sprę żone, które w porównaniu z analogicznym połączeniem
ciernym charakteryzuje się wyższą nośnością przy mniejszych kosztach (wynikających z
oszczę dności na przygotowaniu powierzchni) i niewiele wię kszej odkształcalności, a w
porównaniu z połączeniem niesprę żonym jest znacznie mniej odkształcalne przy
porównywalnej nośności.

Opracowanie właściwych metod wymiarowania takich połączeń wymaga poznania

wielu zachodzących w nim zjawisk, wpływających zarówno na nośność jak i odkształ-
calność . Próby obserwacji i obliczeniowego uję cia takich zjawisk podejmowano już od wielu
lat, jednakże brak odpowiednich metod obliczeniowych i doświadczalnych uniemożliwiał
dokładniejsze rozpoznanie zagadnienia. Ponieważ istotne znaczenie mają tu zjawiska
zachodzące wewnątrz połączenia, np. na powierzchniach styku, to mało przydatne są obecnie
dostę pne metody doświadczalne.

Bardzo przydatne okazały się , intensywnie rozwijane w ostatnich latach metody

komputerowe oparte na Metodzie Elementów Skoń czonych. Pozwalają one modelowanie
i obserwację wielu zjawisk, które dotychczas nie mogły być opisywane ze wzglę du na brak
odpowiedniego aparatu. Wymienić tu należy chociażby rozkłady naprę żeń czy odkształceń ,

1

Prof. dr hab. inż., Wydział Inżynierii Lądowej Politechniki Warszawskiej

2

Dr inż., Wydział Inżynierii Lądowej Politechniki Warszawskiej

3

Mgr inż., Wydział Inżynierii Lądowej Politechniki Warszawskiej

208

które mogą być obserwowane i mierzone w dowolnym miejscu analizowanego elementu.
Dostę pne programy komputerowe oparte na MES, takie jak Abaqus czy Adina pozwalają
także w stosunkowo łatwy sposób wprowadzać zmiany w opracowanym już modelu, oraz
dają niezwykle plastyczny, przejrzysty i wygodny w analizie porównawczej z wynikami
badań doświadczalnych obraz zachowania się analizowanego elementu.

Omawiany model dwuśrubowego, nakładkowego połączenia sprę żonego oraz niesprę -

żonego stanowi kontynuację prezentowanego wcześniej modelu połączenia jednośrubowego
i jest kolejnym krokiem do uogólnienia modelu i jego opisu w sposób możliwy do zasto-
sowania w praktyce projektowej.

2. Fizyczny model połą czenia

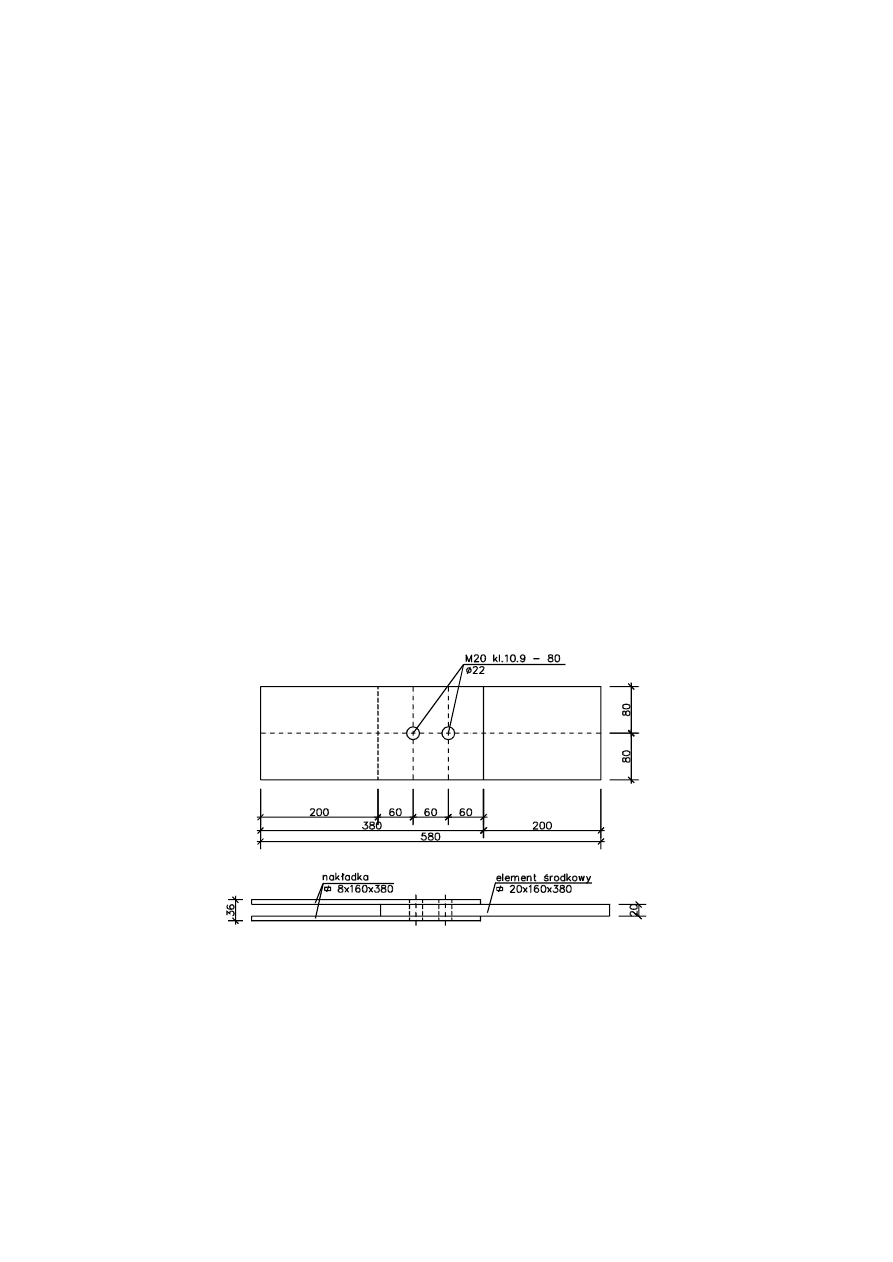
Przedmiotem analizy jest połączenie przedstawione na rys. 1. Jako materiał elementów
połączenia przyję to stal gatunku St3S. Jako łączniki zastosowano śruby M20 klasy 10.9(10).
Założono powierzchnie styku w stanie naturalnym. W celu zminimalizowania wzajemnego
oddziaływania na siebie łączników przyję to nieco wię kszy od minimalnego normowego
rozstaw śrub; nie odbiega on jednak od stosowanych w praktyce. Pominię to stosowane w
badaniach doświadczalnych otwory służące do mocowania elementu w maszynie
wytrzymałościowej oraz związane z tymi otworami wzmocnienia obszarów docisku trzpieni
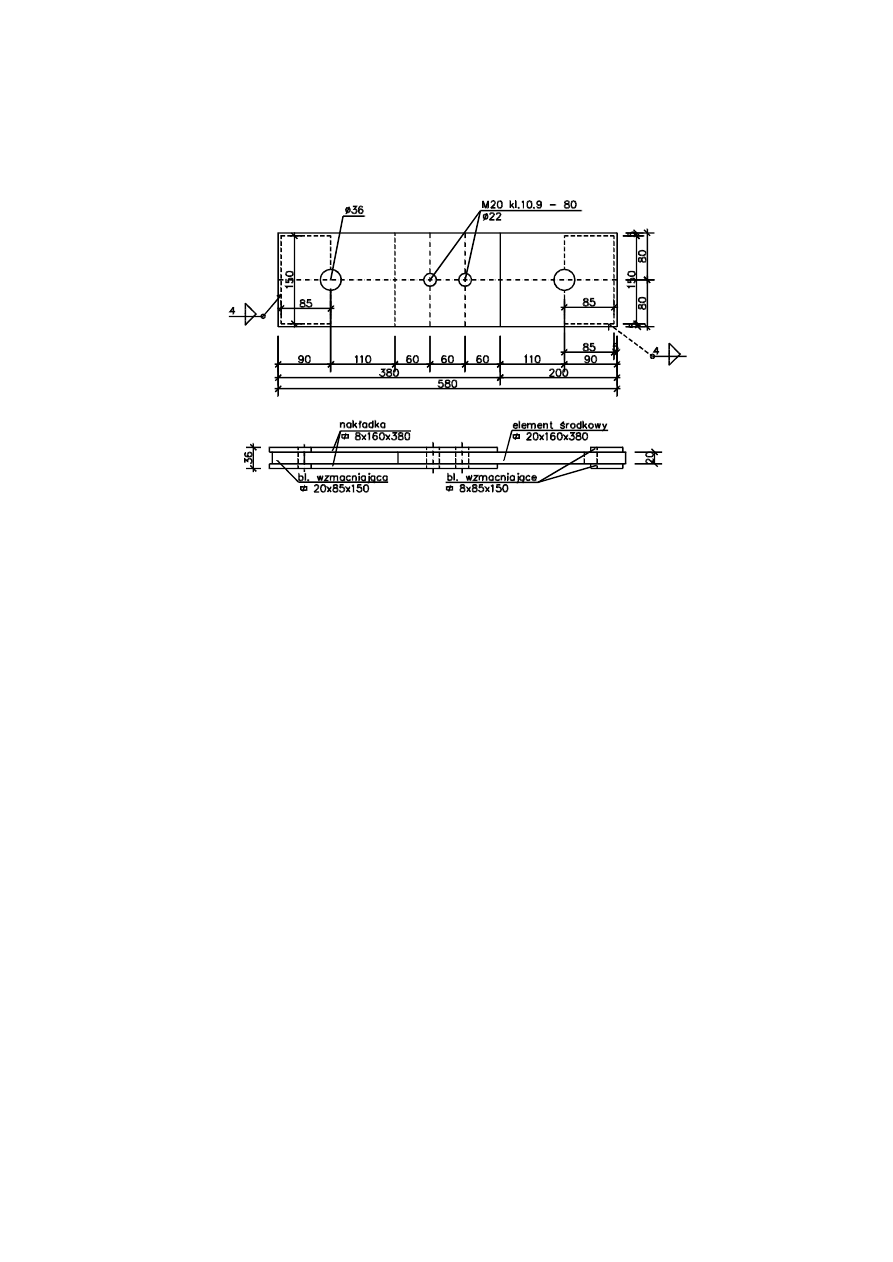
przekazujących obciążenie do ścianek otworów – rys. 2. Ponieważ odstę pstwo to dotyczy
fragmentów połączenia bę dących poza obszarem wzajemnego wpływu łączonych elementów
to nie ma ono istotnego znaczenia dla wiarygodności otrzymywanych wyników. Podstawowe
zjawiska bę dące przedmiotem analizy to odkształcalność i związana z nią zależność P-u
(siła-przemieszczenie), rozwój stref plastycznych na styku trzpienia śruby i ścianki otworu
oraz rozkład naprę żeń na elementach połączenia.

Rys. 1. Geometria analizowanego połączenia

Określono granicę plastyczności Re = 285MPa, wytrzymałość na rozciąganie R

m

=400MPa

oraz współczynnik tarcia

m

=0.2, czyli jak dla powierzchni w stanie naturalnym.

Przyję to model materiału sprę żysto-plastycznego ze wzmocnieniem izotropowym.

Związki konstytutywne dla tego rodzaju materiałów są opisane w podrę cznikach do mechaniki

209

Rys. 2. Geometria elementu doświadczalnego

konstrukcji. Teoretyczny opis zjawisk kontaktowych i sposobu ich rozwiązania w programie
Abaqus znajduje się w podrę czniku do programu [1].

Przyjmowano program obciążeń monotonicznie rosnących, przy czym docelowo

przewidywany jest program obciążeń cyklicznie zmiennych. Obciążenie realizowano
przyrostowo przyjmując zmienny krok przyrostu obciążenia dobierany automatycznie przez
program.

3. Uję cie numeryczne zagadnienia

Przestrzenny model połączenia w uję ciu MES opracowano przy pomocy programu Abaqus
[1], który umożliwia w szczególności uwzglę dnienie efektów kontaktu m.in. tarcia oraz
prowadzenie analizy sprę żysto-plastycznej w zakresie dużych odkształceń .

Prezentowany model składa się z niezależnych czę ści: nakładek, blachy środkowej,

śrub, podkładek i nakrę tek. Geometria połączenia przygotowana została przy użyciu
preprocesora programu Abaqus Cae. Model geometryczny połączenia w konwencji metody
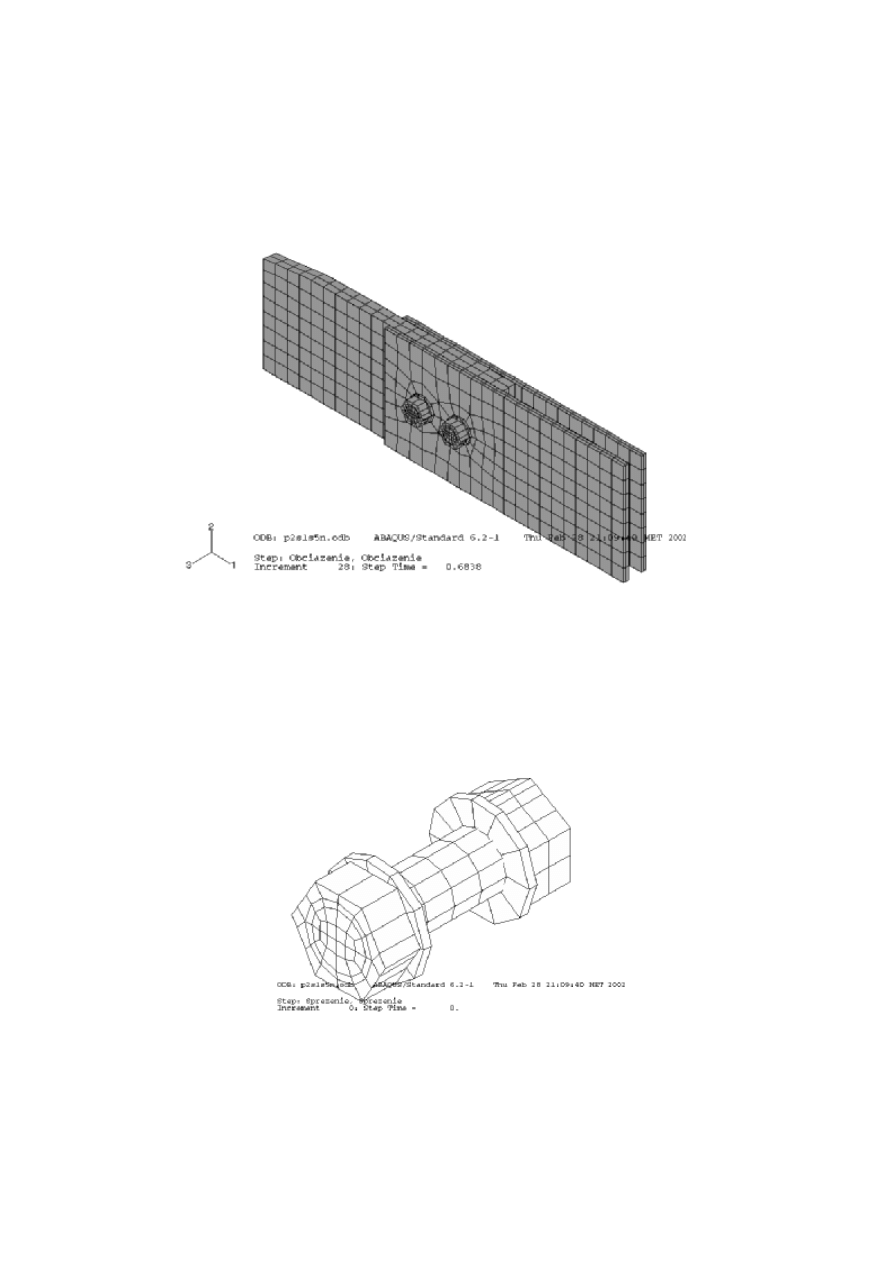
elementów skoń czonych został przedstawiony na rys. 3. Wszystkie czę ści modelu zostały
zdyskretyzowane ośmiowę złowymi trójwymiarowymi elementami izoparametrycznymi.
Model składa się z około 1500 elementów skoń czonych z 2800 wę złami. W obszarach, w
których spodziewano się najwię kszych naprę żeń zagę szczono podział na elementy. Niezbyt
duża liczba elementów i wę złów wynika z ograniczeń komputera, na którym prowadzono
obliczenia (ograniczona ilość pamię ci operacyjnej udostę pnianej poszczególnych zadaniom
obliczeniowym). Jednakże już taka dokładność modelu okazała się wystarczająca i pozwoliła
uzyskać zadowalające wyniki. Rys. 4 przedstawia geometrię śruby z nakrę tką i podkładkami
– wszystkie te elementy są w modelu oddzielnymi bryłami.

Efekty kontaktu i tarcia uwzglę dniono poprzez założenie możliwości zaistnienia

kontaktu mię dzy powierzchniami poszczególnych elementów tj. blach, podkładek i śrub.
Zastosowano algorytm kontaktu typu "master-slave". W obszarach styku powierzchni
bocznej śruby i blach połączenia założone zostały małe poślizgi. Dla powierzchni kontaktu
blach założono możliwość wystąpienia skoń czonych poślizgów.

210

Założono nastę pujące modele materiałowe: dla blach – materiał sprę żysto-plastyczny

z liniowym (izotropowym) wzmocnieniem, dla śruby – materiał liniowo-sprę żysty.

Rys. 3. Model geometryczny połączenia

Analizę numeryczną połączenia prowadzono w trzech etapach. Pierwszym etapem była

faza założenia warunków brzegowych oraz wprowadzenia kontaktu w założonych
płaszczyznach. Drugim etapem było sprę żenie. W przypadku połączenia sprę żonego
realizowano to poprzez przyłożenie siły sprę żającej 166 kN do każdej ze śrub, podczas gdy
w przypadku połączenia niesprę żonego w trzpienie śrub wprowadzono siły 30 kN, czyli
takie, które mogą być wywołane w wyniku rę cznego dokrę cenia śrub. Obciążenie to
realizowano rozciągając trzpienie śrub przy zablokowaniu możliwości przesuwu nakrę tek.

Rys. 4. Model geometryczny łącznika

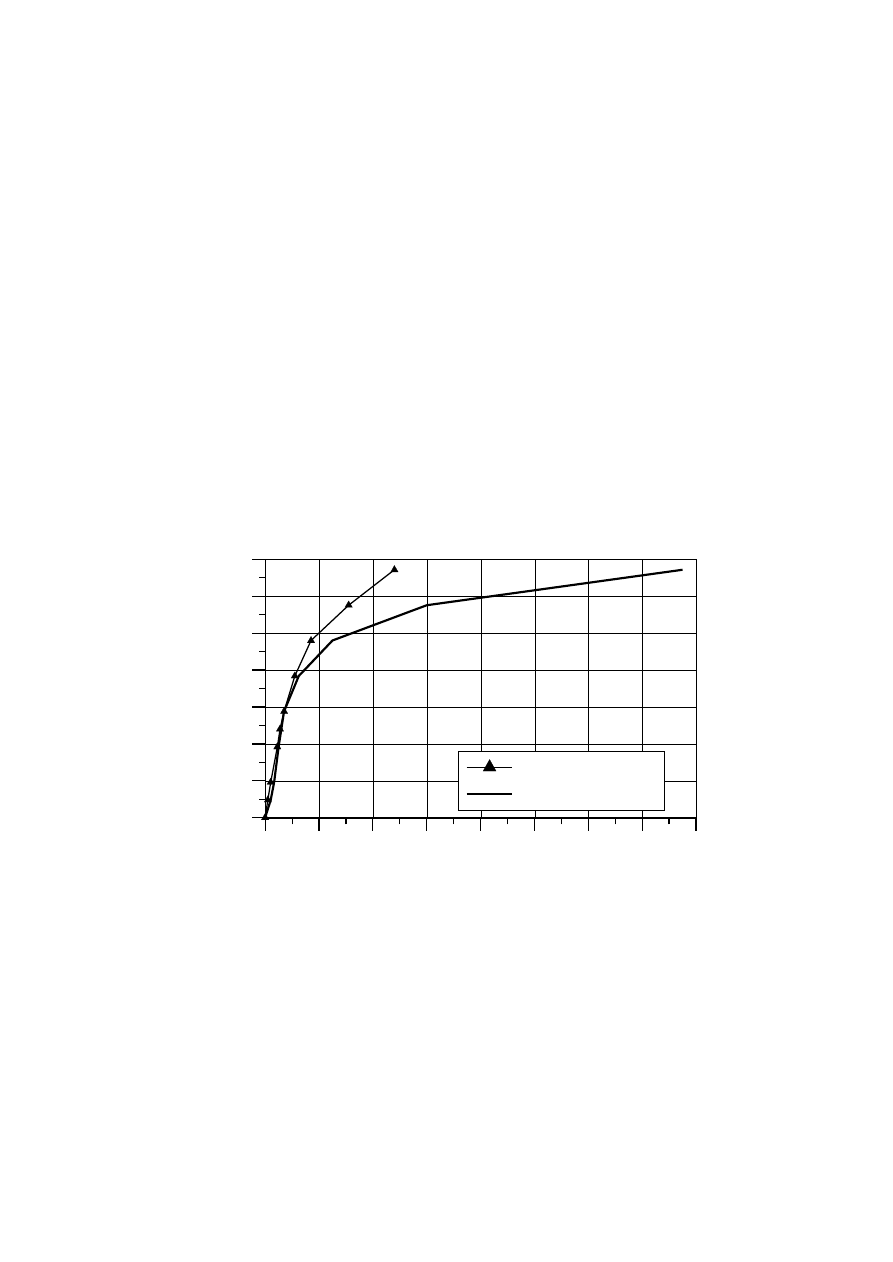
211

Trzecim etapem było wprowadzenie obciążenia głównego przykładanego do koń ca

elementu środkowego przy utwierdzeniu koń ców nakładek. Analizę prowadzono do
momentu, gdy wymagany przez program kolejny przyrost obciążenia zapewniający
prawidłowy przebieg procesu iteracji był mniejszy niż 5 kN. Etap sprę żenia i obciążenia
wykorzystywał możliwości programu w zakresie analizy geometrycznie nieliniowej.

W kolejnych etapach obciążenia uwalniano czę ść stopni swobody rezygnując z

niektórych podpór. Procedura taka wynikała z konieczności zadeklarowania we wstę pnej
fazie obliczeń takiej ilości warunków brzegowych aby żaden z 11 niezależnych początkowo
elementów nie mógł przemieszczać się w sposób niekontrolowany. Po założeniu kontaktu
pomię dzy poszczególnymi elementami czę ść ograniczeń początkowych mogła być zdję ta,
a po sprę żeniu usunię to nastę pne ograniczenia, pozostawiając tylko te, które były konieczne
do przytrzymania obciążanego elementu bę dącego już całością.

4. Wyniki analizy

Najbardziej istotna zależność opisująca zachowanie się połączenia śrubowego to funkcja
P(u) – (siła-przemieszczenie) – rys. 5. Ponieważ z założenia połączenia miały mieć
powierzchnie przylegania w stanie naturalnym, bez specjalnych zabiegów podwyższających
współczynnik tarcia, analizę prowadzono dla współczynnika tarcia o wartości

m

= 0.2.

0

2

4

6

8

10

12

14

16

Przemieszczenie - u [mm]

0

100

200

300

400

500

600

700

S

iła

-

P

[

kN

]

Polaczenie sprezone

Polaczenie niesprezone

Rys. 5. Krzywa P(u)

Odkształcenia elementów w pierwszej fazie obciążenia tzn. do momentu pierwszego
poślizgu są małe i dopiero przy obciążeniu przekraczającym 350 kN nastę puje znacznie
wię kszy przyrost odkształceń przy stosunkowo małym przyroście obciążeń . Maksymalne
obciążenie przekracza 650 kN. po czym nastę puje uplastycznienie materiału odpowiadające
jego zniszczeniu. Odkształcenie połączenia niesprę żonego przy maksymalnej sile jest ponad
trzykrotnie wię ksze niż połączenia sprę żonego.

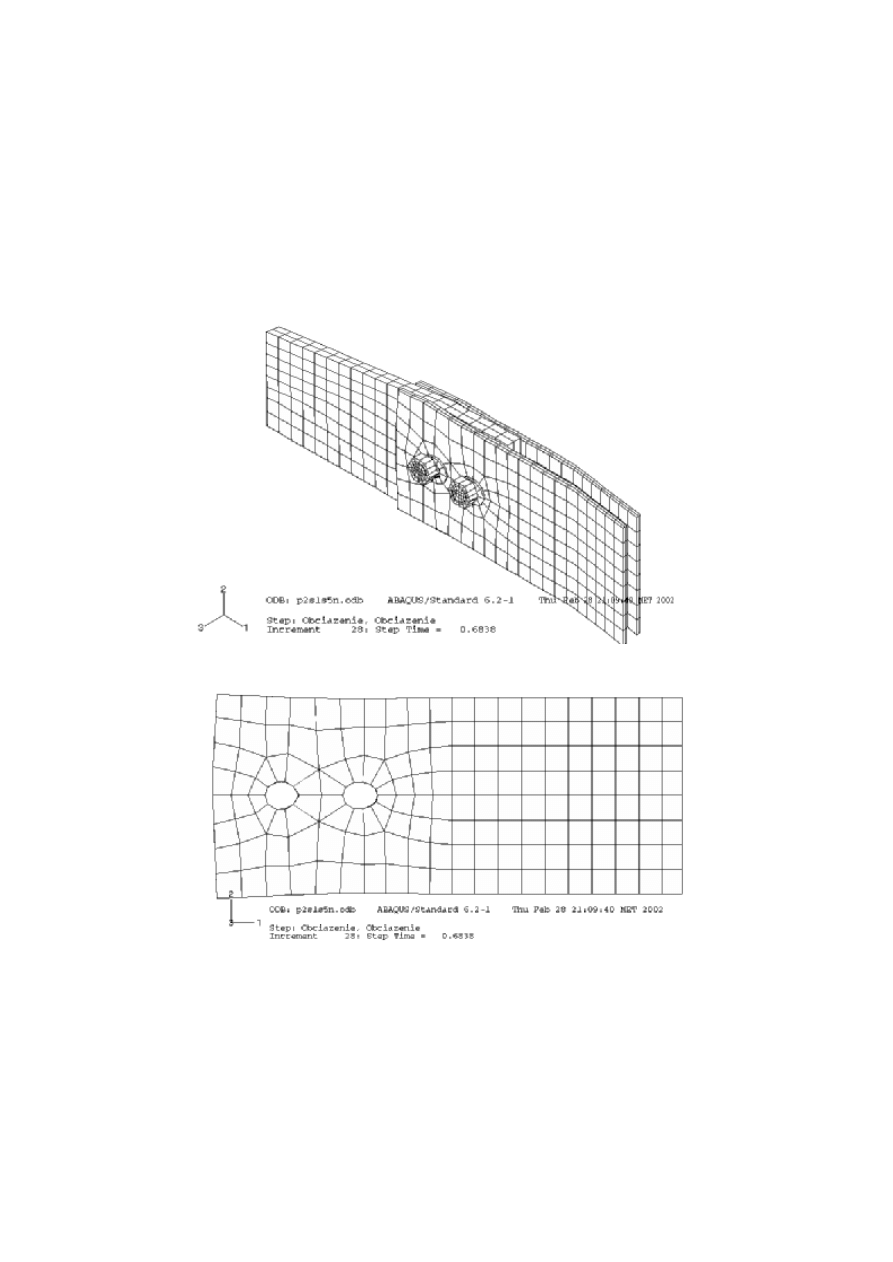
Z zależnością P(u) ściśle związane są odkształcenia połączenia. Na rys. 6 pokazano

212

połączenie niesprę żone w koń cowej fazie analizy. Odkształcenia połączenia sprę żonego są
znacznie mniejsze (analogicznie do zależności siła-przemieszczenie). Kolejny rysunek – rys. 7
przedstawia odkształcenia otworów w nakładce. Na rysunkach tych wyraźnie widać wciskanie się
trzpienia śruby zarówno w nakładkę jak i w element środkowy i wydłużanie się otworów.
Zjawisko to ma bardzo podobny charakter jak w przypadku analizowanych wcześniej połączeń
jednośrubowych i jego doświadczalne potwierdzenie świadczy o poprawności przyję tego modelu.

Rys. 6. Widok ogólny odkształconego połączenia niesprę żonego

Rys. 7. Odkształcenie otworów w nakładce połączenia niesprę żonego

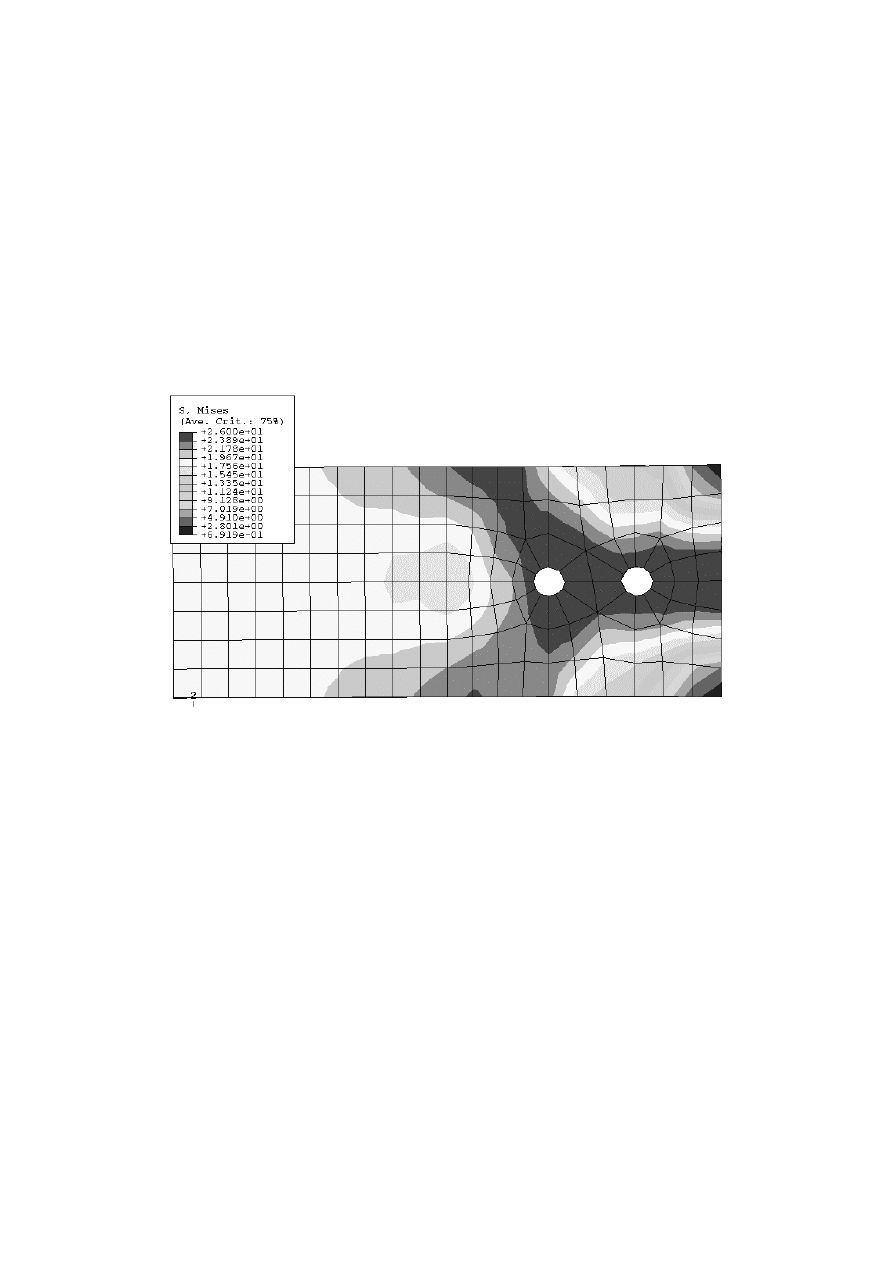
Na rys. 8 przedstawiono rozkład naprę żeń Hubera-Misesa w elemencie środkowym

połączenia sprę żonego. Brak pełnej symetrii jest spowodowany głównie niesymetrycznym
podziałem na elementy skoń czone tego elementu.

213

Przeprowadzona analiza dostarczyła znacznie wię kszej ilości informacji na temat

zachowania się połączenia, takie jak rozkłady naprę żeń , zasię gi stref plastycznych, rozkład
stref wzajemnego przemieszczania się poszczególnych elementów i wartości tych
przemieszczeń w poszczególnych punktach, jednak ze wzglę du na trudności z ich
prawidłowym przedstawieniem w postaci czarno-białej mogą one zostać zaprezentowane
dopiero w postaci kolorowych przeźroczy.

Wyniki uzyskane na podstawie opracowanego modelu sprę żonego połączenia

śrubowego bę dą porównane z wynikami badań doświadczalnych. Badania te bę dą
prowadzone dla obciążeń cyklicznie zmiennych w związku z czym także model połączenia
zostanie rozszerzony na takie obciążenia.

Rys. 8. Rozkład naprę żeń Hubera-Misesa w elemencie środkowym [kN/cm2]

5. Uwagi końcowe

Wyniki przeprowadzonych obliczeń potwierdzające rezultaty analogicznych analiz połączeń
jednośrubowych pozwalają stwierdzić , że analizowany rodzaj połączenia mógłby być szerzej
stosowany w praktycznych rozwiązaniach, zastę pując typowe połączenia niesprę żone a także
cierne. Wymaga to jednak opracowania procedury obliczeniowej takich połączeń nadającej
się do zastosowania w projektowaniu konstrukcji. Drogą do tego jest opracowanie złożonego
modelu, który pozwoliłyby na analizę zachowania się połączeń o różnych parametrach.

Duża zbieżność wyników obliczeń numerycznych z badaniami doświadczalnymi

obserwowana podczas przeprowadzonych analiz połączeń jednośrubowych, a także zgodna z
przewidywaniami a także znanymi badaniami doświadczalnymi archiwalnymi pozwala
stwierdzić , że zastosowanie MES w uję ciu komputerowym mogłoby tu być bardzo
przydatne. Opracowywane przy użyciu MES modele mogą stanowić uzupełnienie badań
doświadczalnych, które są drogie i czasochłonne, a mogą je czę ściowo zastę pować jako
tań sze, szybsze i dające czę sto wię ksze możliwości – MES zastosowana w programach
komputerowych jest narzę dziem, które umożliwia obserwację wielu zjawisk bę dących w
innych warunkach poza zasię giem możliwości ze wzglę du na ograniczenia dostę pnych

214

metod doświadczalnych. Opracowany tą metodą model może być wielokrotnie korygowany
pod kątem zmian różnych parametrów. Nie bez znaczenia jest także niezwykle czytelna
forma otrzymywanych wyników a także duża ich różnorodność .

Obliczenia numeryczne prowadzono na komputerach w COI Politechniki War-

szawskiej.

Literatura

[1] Abaqus Manual, version 6.2, Hibbit, Karlsson, Sorensen, Inc.
[2] KARCZEWSKI J. A., POSTEK E., WIERZBICKI S., Model połączenia śrubowego pod

obciążeniem cyklicznie zmiennym, XLVII Konferencja Naukowa KILiW PAN i KN
PZITB, Krynica 2001.

THE COMPUTER MODELLING OF THE MULTI-BOLT

PRESTRESSED CONNECTION

Summary

The goal of the conducted paper is to develop a 3D computational FEM model of double butt
prestressed two-bolted connections with regard to the effects of bolts, initial gaps, friction
and prestressing force. This model may be used especially for investigation of the
connections deformability, also after first slip, in the method of structures analysis. The
computational model is developed in the framework of ABAQUS general-purpose program.
The connection is discretized with 1500 3D-isoparametric brick elements. The gaps are
assumed between all of the elastic bodies and later during the loading process, non-elastic
bodies. The contact surfaces are established. The proposed model will be verified by
experiments. We expect that results obtained theoretically as well as in experiment in further
investigations, will differ insignificantly.