
Akademia Górniczo-Hutnicza
im. Stanisława Staszica
Wydział Inżynierii Mechanicznej I Robotyki
ZAKŁAD KONSTRUKCJI I EKSPLOATACJI MASZYN
PROJEKT nr 4.
Temat:
Projekt dwusłupowej prasy introligatorskiej.
(temat nr: B6.)
Wykonał:
Grzegorz Bielak
Rok
2,
Grupa 8
Rok akademicki: 2003/04
Sprawdził:
Dr
inż. Jan Łukasik
DANE OBLICZENIA
WYNIKI
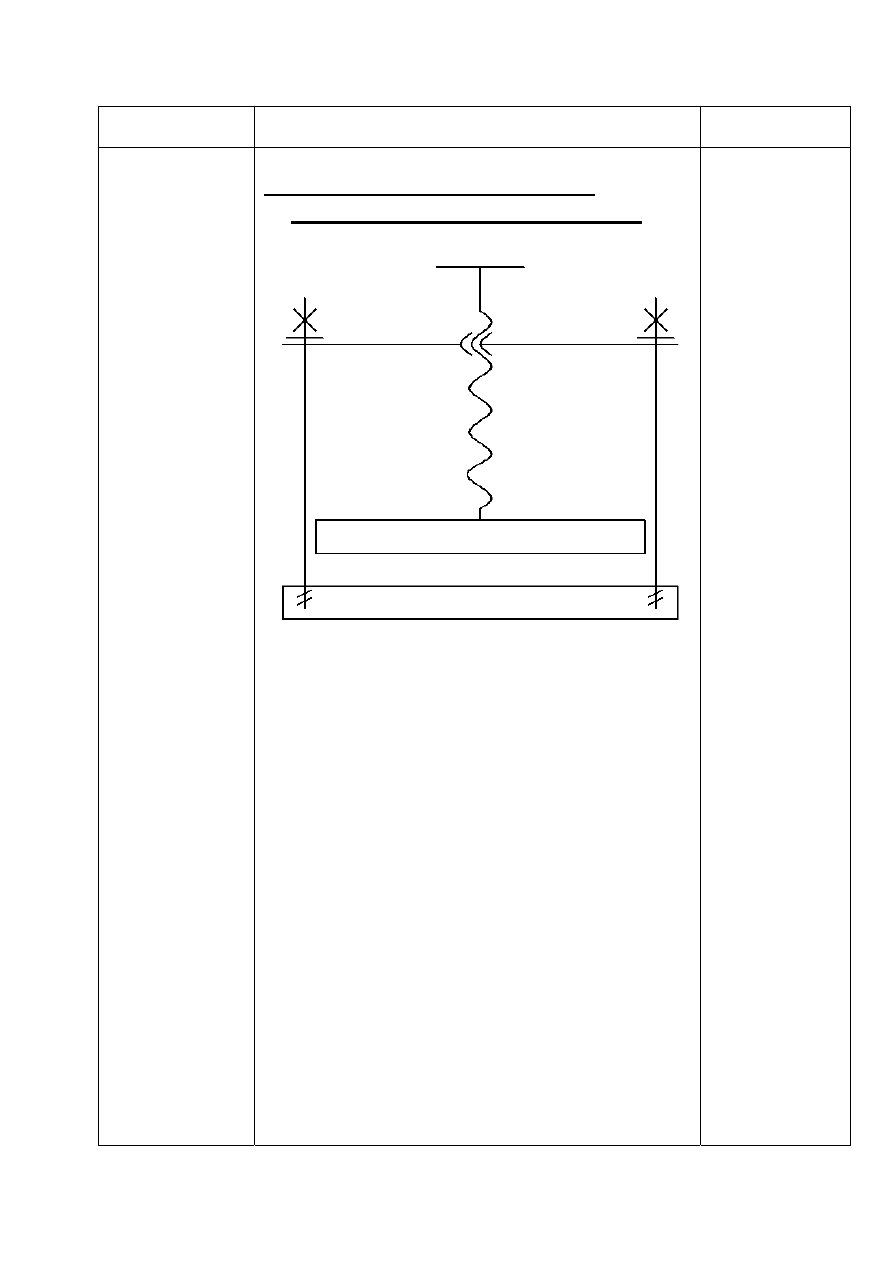
1. Schemat projektowanej prasy
introligatorskiej dwukolumnowej:
Dane konstrukcji prasy:
• siła nacisku prasy:
[ ]
23
Q
k
=
N
,
• powierzchnia płyty prasy:
[ ]
300 220
F
a b
mm
= × =
×
,
• wysokość skoku płyty:
[ ]
140
H
m
=
m
2.

DANE OBLICZENIA
WYNIKI
[
]
300
3
e
e
R
MPa
X
=
=
2. Obliczam śrubę prasy.
a) obliczam średnice śruby
1
d
z warunku na
ściskanie siłą
Q
.
Przyjmuję materiał na śrubę stal St5.
Obliczam dopuszczalne naprężenia na ściskanie :
c
k
[
]
[
]
300
100
3
e
c
e
c
R
k
X
MPa
k
M
=
=
=
Pa
Obliczam średnice rdzenia śruby :
1
d
[ ]
[
]
[ ]
2
1
1
1
4
4
4 23000
17,113
100
c
c
c
Q
k
A
d
A
Q
d
k
N
d
m
MPa
σ
π
π
π
=
≤
⋅
=
⋅
≥
⋅
⋅
≥
=
⋅
m
Dobieram gwint trapezowy niesymetryczny S26x5.
[
]
100
c
k
M
=
Pa
[ ]
[ ]
[ ]
[ ]
1
2
26
17,332
22, 250
5
d
mm
d
m
d
m
p
mm
=
=
=
=
m
m
3.
DANE OBLICZENIA
WYNIKI
0,7
α
=
[ ]
1
17,332
d
=
mm
[
]
280
H
R
MPa
=
b) sprawdzam wytrzymałość śruby na
wyboczenie:
Przyjmuje długość śruby na
[ ]
200
L
m
=
m
mm
.
Obliczam długość wyboczenia :
r
l
[ ]
[ ]
0, 7 200
140
r
r
l
L
l
mm
α
= ⋅
=
⋅
=
Obliczam promień bezwładności śruby :
i
[ ]
[ ]
min
4
1
min
2
1
1
64
4
17,332
4,333
4
4
I
i
A
d
I
d
A
mm
d
i
m
π
π
=
=
=
=
=
=
m
Obliczam smukłość śruby
λ
:
[ ]
[ ]
140
32,31
4,333
r
l
i
mm
mm
λ
λ
=
=
=
Obliczam smukłość porównawczą
p
λ
:
1675
1675
100,1
280
p
H
p
R
λ
λ
=
=
=
Wyznaczam współczynnik wyboczenia
:
w
m
32,31
0,323
100,1
p
λ
λ
=
=
⇓
1, 09
w
m
=
[ ]
200
L
m
=
m
[ ]
140
r
l
m
=
m
[ ]
4,333
i
m
=
m
32,31
λ
=
100,1
p
λ
=
1, 09
w
m
=
4.

DANE OBLICZENIA
WYNIKI
[ ]
[ ]
[
]
1
1,09
23000
17,332
280
w
H
m
Q
N
d
mm
R
MPa
=
=
=
=
[ ]
[ ]
2
5
22, 250
p
mm
d
m
=
=
m
0,1
3
µ
α
=
= °
Sprawdzam wartość naprężeń:
[ ]
[ ]
(
)
[
]
2
1
2
2
1
4
4 1,09 23000
4
106
17,332
w
H
w
H
m
Q
R
A
d
A
N
m
Q
MPa
d
mm
R
σ
π
σ
π
π
σ
⋅
=
≤
⋅
=
⋅
⋅
⋅
⋅
=
=
=
⋅
⋅
<
c) sprawdzam samohamowność gwintu:
Obliczam kąt
γ :
[ ]
[ ]
2
5
0,0715
22, 250
4,0914
p
tg
d
mm
tg
mm
γ
π
γ
π
γ
=
⋅
=
=
⋅
=
°
Obliczam pozorny kąt tarcia '
ρ
:
'
cos
0,1
'
0,1001
cos3
' 5,72
'
tg
tg
µ
ρ
α
ρ
ρ
ρ
γ
=
=
=
°
=
°
>
Gwint jest samohamowny.
[
]
106 MPa
σ
=
4,0914
γ
=
°
' 5,72
ρ
=
°
5.
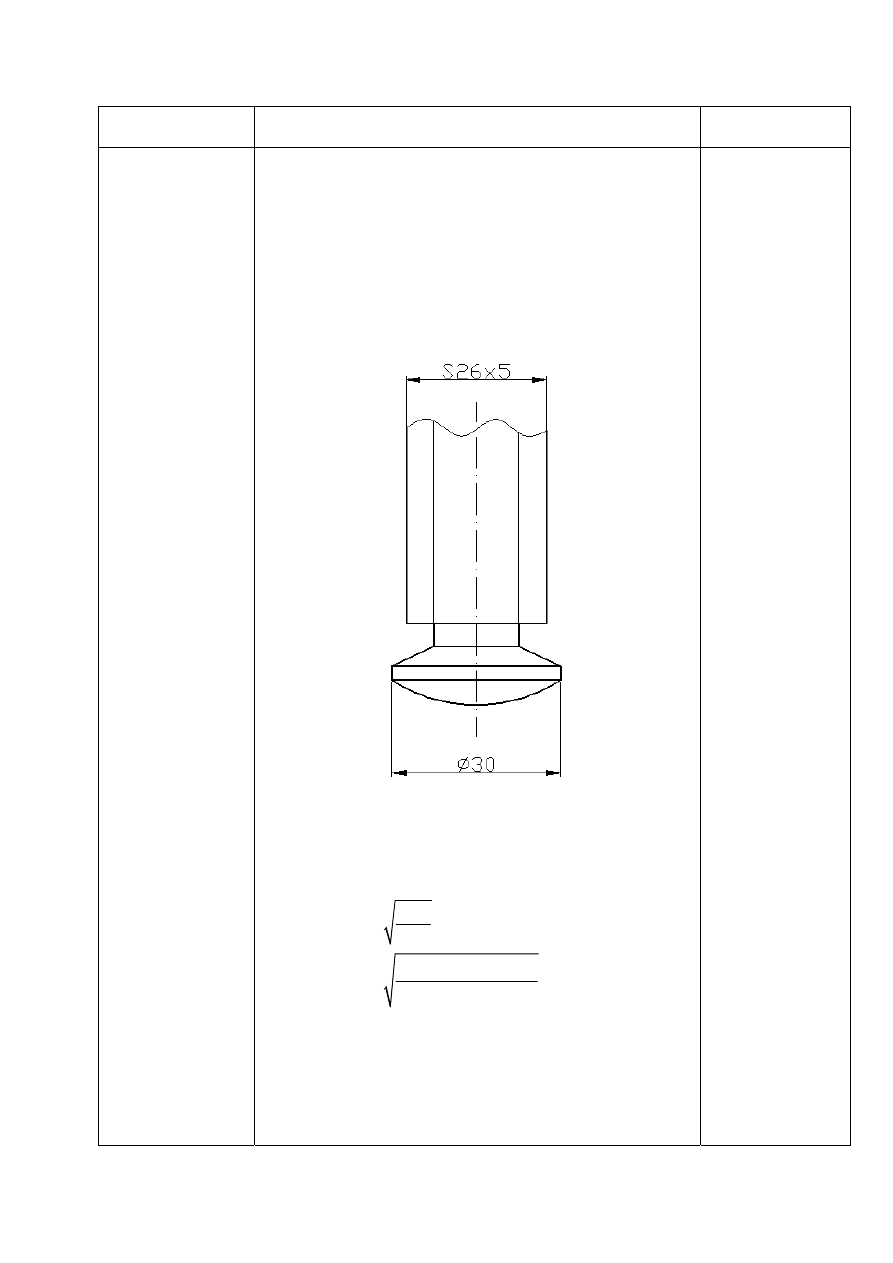
DANE OBLICZENIA
WYNIKI
[ ]
[ ]
2
23000
22, 25
4, 0914
' 5, 72
Q
N
d
m
γ
ρ
=
=
=
°
=
°
m
[ ]
[
]
5
23000
2,1 10
Q
N
E
MPa
=
=
⋅
d) Obliczam moment od sił tarcia
N
M
:
Obliczam moment skręcający na zarysie gwintu
S
M :
(
)
[ ]
[ ]
(
)
[
]
2
0,5
'
0,5 23000
22, 25
4, 0914
5, 72
44249, 7
S
S
S
M
Q d
tg
M
N
mm tg
M
Nmm
γ ρ
=
⋅ ⋅ ⋅
+
=
⋅
⋅
⋅
° +
°
=
Przyjmuje średnicę kulki
[ ]
30
d
m
=
m
Obliczam średnice powierzchni docisku
:
n
d
[ ] [ ]
[
]
[ ]
3
3
5
2, 2
2
23000
30
2, 2
2,596
2 2,1 10
n
n
Q d
d
E
N
mm
d
mm
MPa
⋅
=
⋅
⋅
⋅
=
⋅
=
⋅
⋅
[
]
44249, 7
S
M
Nmm
=
[ ]
2,596
n
d
mm
=
6.

DANE OBLICZENIA
WYNIKI
[ ]
2,596
n
d
m
=
m
[ ]
23000
0,1
Q
N
µ
=
=
[
]
44249, 7
S
M
Nmm
=
Obliczam średnicę działania siły tarcia
:
S
D
[ ]
[ ]
2
3
2
2,596
1,73
3
S
n
S
D
d
D
mm
= ⋅
= ⋅
=
mm
Obliczam moment skręcający od tarcia kuli
t
M :
[ ]
[ ]
[
]
2
1,73
23000
0,1 1989,5
2
S
t
t
D
M
Q
mm
M
N
Nmm
µ
= ⋅
⋅
=
⋅
⋅
=
Obliczam całkowity moment od sił tarcia
N
M :
[
]
[
[
]
44249,7
1989,5
46239, 2
N
S
t
N
N
M
M
M
]
M
Nmm
Nmm
M
Nmm
=
+
=
+
=
[ ]
1, 73
S
D
m
=
m
[
]
1989,5
t
M
Nmm
=
[
]
46239, 2
N
M
Nmm
=
[ ]
2
22, 250
d
m
=
m
[ ]
5
p
mm
=
3. Obliczam nakrętkę wciskaną:
a) Dobieram materiał na nakrętkę:
Wybieram brąz B10:
[
]
[
]
90
54
r
d
k
MP
k
M
=
=
a
Pa
mm
b) Obliczam wstępną wysokość nakrętki:
[ ]
[ ]
2
2
2 22, 250
44,5
H
d
H
mm
= ⋅
= ⋅
=
Przyjmuje
[ ]
45
H
m
=
m
.
c) Obliczam ilość zwojów:
[ ]
[ ]
45
9
5
H
z
p
mm
z
mm
=
=
=
[
]
[
]
90
54
r
d
k
MP
k
MP
=
=
a
a
[ ]
45
H
m
=
m
9
z
=
7.
DANE OBLICZENIA
WYNIKI
[ ]
[
]
[ ]
[ ]
1
23000
54
26
17,332
d
Q
N
k
MPa
d
mm
d
m
=
=
=
=
m
d) sprawdzam docisk śruby na
zwojach:
(
)
(
)
[ ]
[ ]
(
)
[ ]
(
)
[
]
[
]
2
2
1
2
2
2
2
1
4
4 23000
4
26
17,332
8, 663
54
d
d
d
d
d
Q
p
k
A z
d
d
A
N
Q
p
d
d
mm
mm
p
MPa
k
MPa
π
π
π
=
≤
⋅
⋅
−
=
⋅
⋅
=
=
⎡
⎤
⋅
−
⋅
−
⎣
⎦
=
<
=
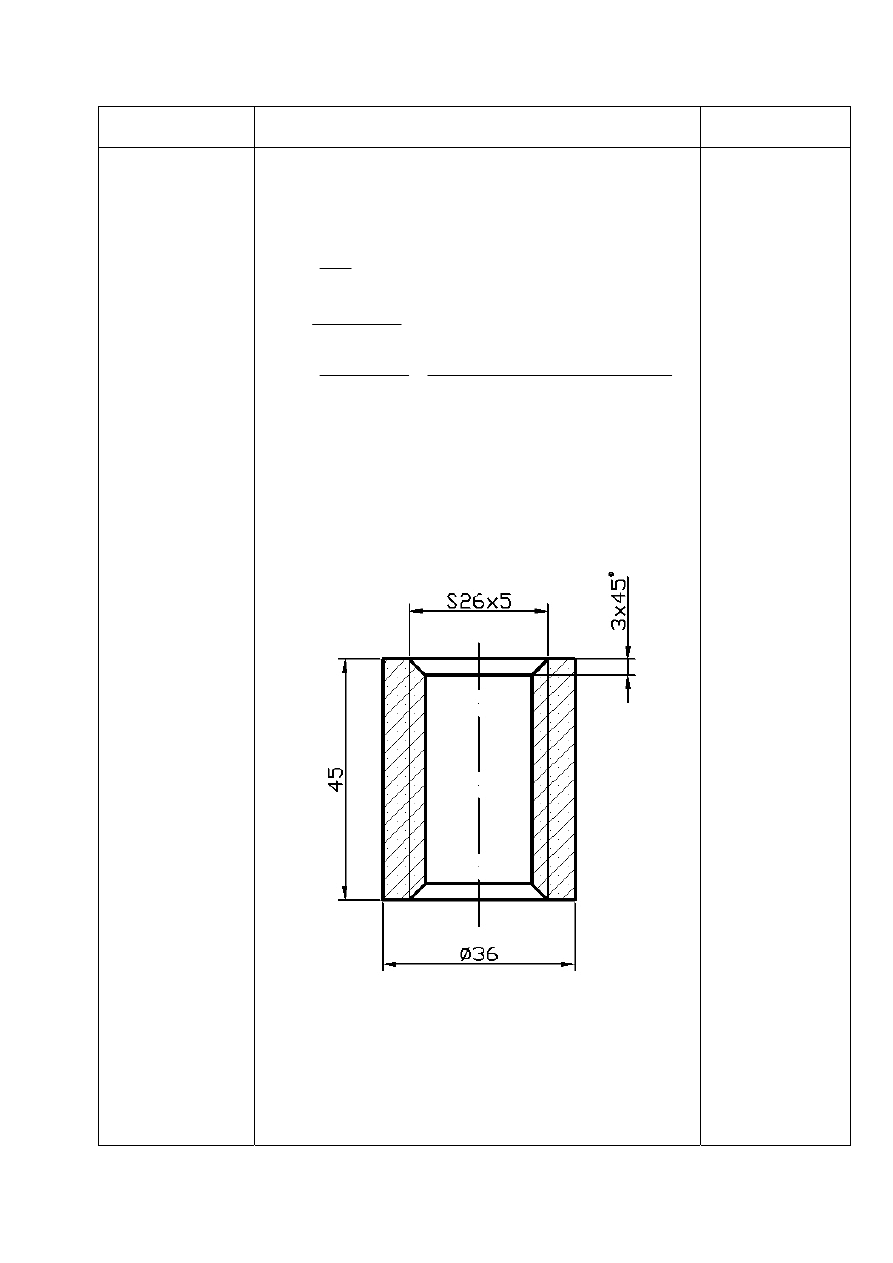
e) obieram wymiary nakrętki:
Przyjmuje średnice zewnętrzną
[ ]
36
z
d
m
=
m
:
[
]
8,663
d
p
MPa
=
8.

DANE OBLICZENIA
WYNIKI
[
]
[ ]
[ ]
46239, 2
0,1
36
45
N
M
Nmm
d
mm
H
mm
µ
=
=
=
=
[
]
[
]
5
5
0,56
0,3
2,1 10
0,63
0,35
0,85 10
st
st
st
b
b
b
E
M
E
MPa
υ
υ
∆ =
=
=
⋅
∆ =
=
=
⋅
Pa
f) obliczam pasowanie nakrętki:
Obliczam najmniejszy nacisk powierzchniowy potrzebny
do przeniesienia obciążenia:
[
]
[ ]
(
)
[ ]
[
]
2
2
2
2 46239, 2
5,047
0,1
36
45
N
d
d
M
p
d
H
Nmm
p
MPa
mm
mm
µ π
π
⋅
=
⋅ ⋅
⋅
⋅
=
=
⋅ ⋅
⋅
Obliczam współczynniki ,
st
b
c c :
2
2
2
2
2
2
2
2
1
1
1 0,56
0,3 1,61
1 0,56
1
1
1 0,63
0,35 1,02
1 0,63
st
st
st
st
st
b
b
b
b
b
c
c
c
c
υ
υ
+ ∆
=
−
− ∆
+
=
−
=
−
+ ∆
=
−
− ∆
+
=
−
=
−
Obliczam wcisk montażowy skuteczny:
[
] [ ]
[ ]
5
5
1,61
1,02
5,047
36
2,1 10
0,85 10
0,00357
st
b
d
st
b
c
c
N
p
d
E
E
N
MPa
mm
N
mm
⎛
⎞
≥
⋅ ⋅
+
⎜
⎟
⎝
⎠
⎛
⎞
≥
⋅
⋅
+
⎜
⎟
⋅
⋅
⎝
⎠
≥
Obliczam wcisk nominalny:
Przyjmuje chropowatości:
3, 2
3, 2
zst
zb
R
R
=
=
(
)
[ ]
[ ]
[ ]
(
)
[ ]
'
1, 2
' 3,573
1, 2 3, 2
3, 2
11, 25
zst
zb
N
N
R
R
N
m
m
m
m
µ
µ
µ
µ
= +
⋅
+
=
+
⋅
+
=
[
]
5, 047
d
p
M
=
Pa
1, 61
st
c
=
1,02
b
c
=
[ ]
3,573
N
m
µ
≥
[ ]
' 11, 25
N
m
µ
=
9.
DANE OBLICZENIA
WYNIKI
[ ]
' 11, 25
N
m
µ
=
3, 2
3, 2
zst
zb
R
R
=
=
Dobieram pasowanie wg stałego otworu
.
7
H
Dla otworu
36 7
H
φ
odchyłki wynoszą:
[ ]
[ ]
25
0
s
i
E
m
E
m
µ
µ
=
=
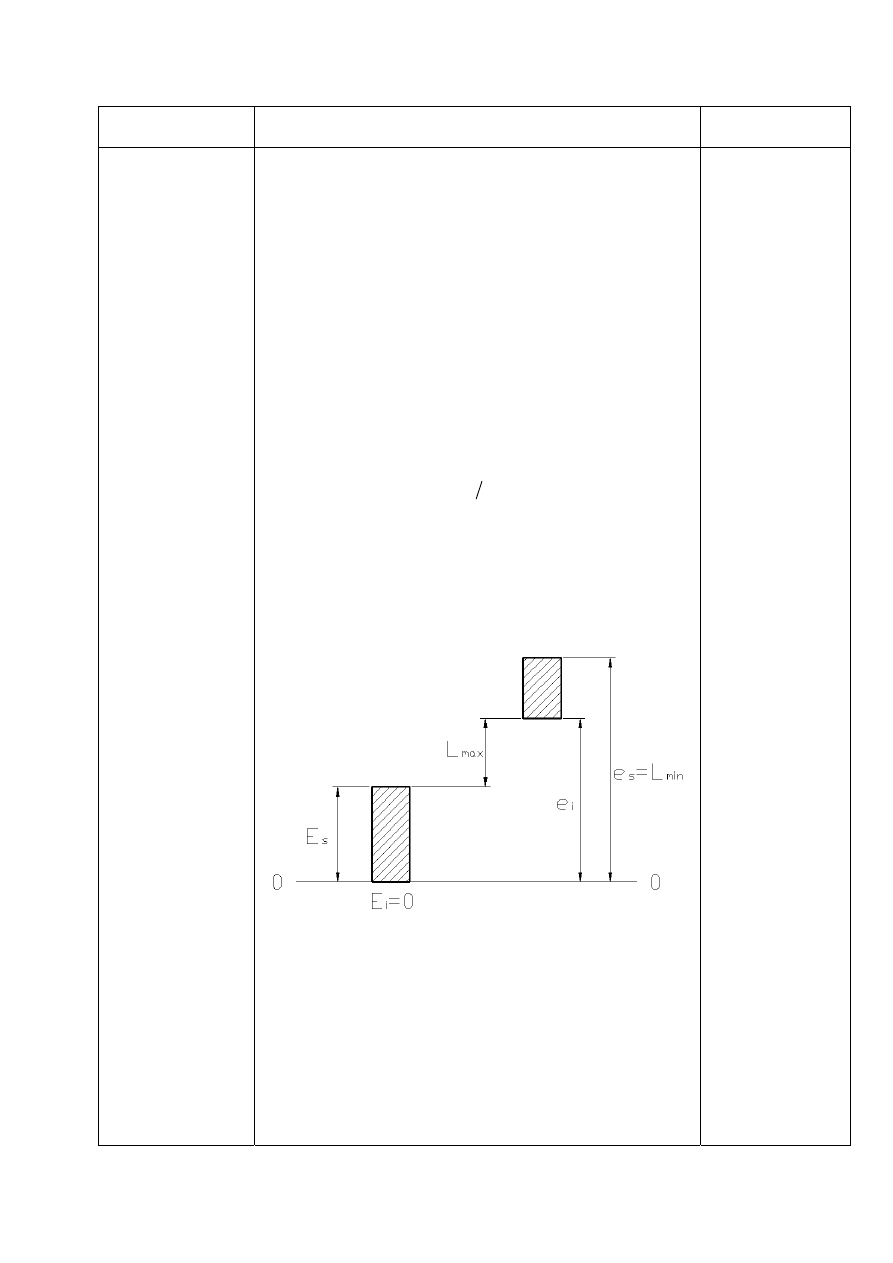
Obliczam odchyłki:
[ ]
[ ]
[ ]
[ ]
max
min
min
min
' 12
25
12
37
s
i
i
s
i
L
E
e
N
N
N
m
e
E
N
e
m
m
µ
m
µ
µ
µ
=
− = −
=
≈
=
+
=
+
=
Dobieram pasowanie
36 7 7
H
s
φ
o odchyłkach:
[ ]
[ ]
[ ]
[ ]
0
25
43
59
i
s
i
s
E
m
E
m
e
m
e
m
µ
µ
µ
µ
=
=
=
=
Obliczam największy wcisk skuteczny:
(
)
[ ]
[ ]
[ ]
(
)
[ ]
max
max
max
max
'
1, 2
'
54
1, 2 3, 2
3, 2
66,68
zst
zb
s
i
s
N
N
R
R
N
e
E
e
N
m
m
m
m
µ
µ
µ
µ
=
+
⋅
+
= +
=
=
+
⋅
+
=
[ ]
[ ]
25
0
s
i
E
m
E
m
µ
µ
=
=
[ ]
[ ]
[ ]
[ ]
0
25
43
59
i
s
i
s
E
m
E
m
e
m
e
m
µ
µ
µ
µ
=
=
=
=
[ ]
max
66,68
N
m
µ
=
10.
DANE OBLICZENIA
WYNIKI
[ ]
[ ]
max
36
66,68
d
mm
N
m
µ
=
=
[
]
[
]
5
5
2,1 10
0,85 10
st
b
E
M
E
MPa
=
⋅
=
⋅
1, 61
st
c
=
Pa
1,02
b
c
=
[
]
0,56
275
st
est
R
MPa
∆ =
=
Obliczam wartość naprężeń wywołanych wciskiem:
[ ]
[ ]
[
]
max
max
max
5
5
66,68
94,18
1,61
1,02
36
2,1 10
0,85 10
d
st
b
st
b
d
N
p
c
c
d
E
E
m
p
MPa
mm
µ
=
⎛
⎞
⋅
+
⎜
⎟
⎝
⎠
=
=
⎛
⎞
⋅
+
⎜
⎟
⋅
⋅
⎝
⎠
Obliczam wartość dopuszczalną naprężeń:
(
)
(
)
[
]
[
]
2
2
0,58 1
0,58 1 0,56
275
109,5
dop
st
est
dop
p
R
p
MPa
MPa
=
⋅ − ∆ ⋅
=
⋅ −
⋅
=
max
d
dop
p
p
<
[
]
max
94,18
d
p
MPa
=
[
]
109,5
dop
p
MPa
=
[
]
300
2,5
e
e
R
MPa
X
=
=
[ ]
23000
Q
N
=
4. Obliczam słupki prasy:
a) obliczam średnice z warunku na rozciąganie
części nagwintowanej:
Na słupki przyjmuje stal
5
St
Obliczam dopuszczalne naprężenia na rozciąganie :
r
k
[
]
[
]
300
120
2,5
e
r
e
r
R
k
X
MPa
k
M
=
=
=
Pa
Obliczam średnice gwintu:
1
d
[ ]
[
]
[ ]
2
1
1
2
4
2 23000
2
11, 046
120
r
r
r
Q
k
A
d
A
N
Q
d
mm
k
MPa
σ
π
π
π
=
≤
⋅
⋅
=
⋅
⋅
≥
=
=
⋅
⋅
[
]
120
r
k
M
=
Pa
[ ]
1
11, 046
d
mm
≥
11.
DANE OBLICZENIA
WYNIKI
[ ]
1
11, 046
d
≥
mm
[
]
[ ]
46239, 2
320
S
B
M
Nmm
L
mm
=
=
[
]
[
]
[ ]
150
120
200
g
r
k
M
k
MP
h
mm
=
=
=
Pa
a
Przyjmuje gwint metryczny
14
M
o danych:
[ ]
[ ]
[ ]
1
2
14
11,835
12, 701
d
mm
d
m
d
m
=
=
=
m
m
b) obliczam średnice słupka w części
pomiędzy podstawą a belką górną:
Obliczam siłę zginającą słupek od momentu skręcającego
S
M od śruby prasy:
[
]
[ ]
[ ]
2
2 46239, 2
289
320
S
B
M
P
L
Nmm
P
N
mm
⋅
=
⋅
=
=
Siła ta wywołuje największy moment zginający przy
podstawie prasy.
Obliczam średnice słupa z warunku na zginanie:
[ ]
[ ]
[
]
[ ]
3
3
3
32
32 289
200
32
15,77
150
g
g
g
g
g
g
g
M
k
W
M
P h
d
W
N
mm
P h
d
m
k
MPa
σ
π
π
π
=
≤
= ⋅
⋅
=
⋅
⋅
⋅ ⋅
≥
=
=
⋅
⋅
m
Przyjmuje średnicę słupka
[ ]
20
d
m
=
m
.
Sprawdzam wytrzymałość słupka na zginanie z
rozciąganiem:
[
]
[
]
2
3
2
3
2
2
32
2 23000 32 289 200
20
20
110, 2
120
g
r
g
r
M
Q
k
A
W
Q
P h
d
d
MPa
k
MPa
σ
σ
π
π
π
π
σ
=
+
≤
⋅
⋅
⋅ ⋅
⋅
⋅
⋅
=
+
=
+
⋅
⋅
⋅
⋅
=
≤
=
[ ]
[ ]
[ ]
1
2
14
11,835
12, 701
d
mm
d
m
d
m
=
=
=
m
m
[ ]
289
P
N
=
[ ]
20
d
m
=
m
12.
DANE OBLICZENIA
WYNIKI
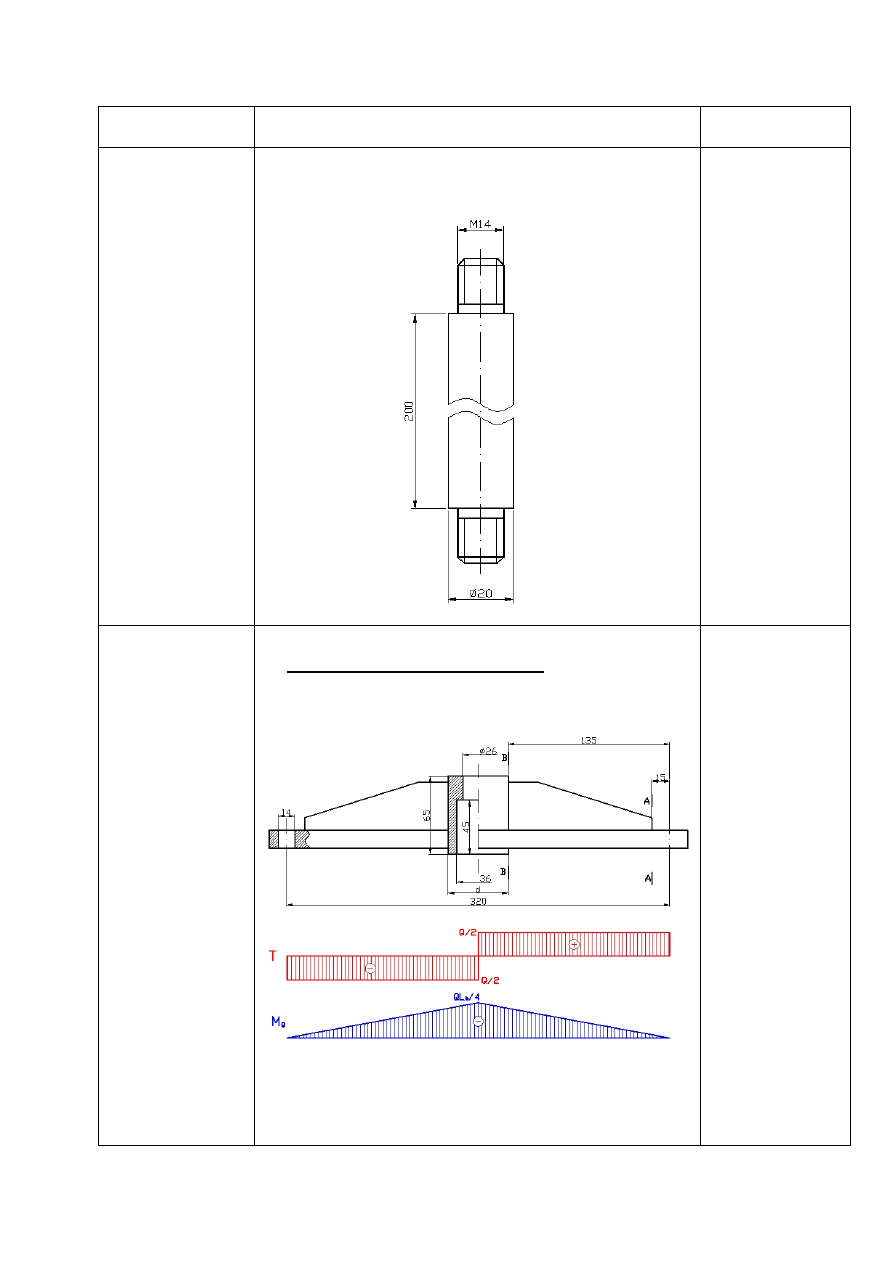
c) zestawienie wymiarów słupka:
5. Obliczam belkę górną:
13.
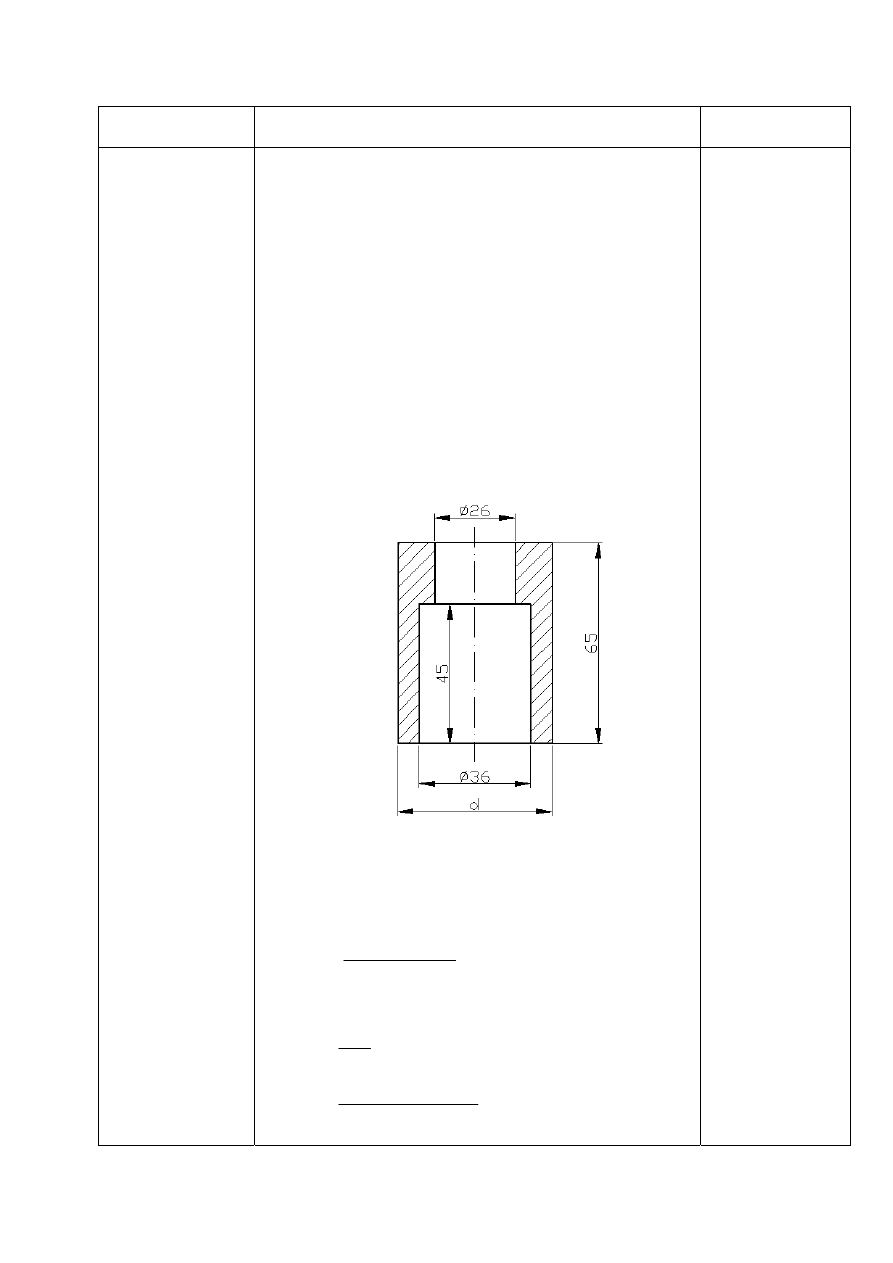
DANE OBLICZENIA
WYNIKI
a) dobieram materiał na belkę:
Przyjmuje stal
:
4
St S
[
]
[
]
[
]
[
]
275
2
137,5
165
82,5
e
e
r
g
t
R
MPa
X
k
M
k
MPa
k
MP
=
=
=
=
=
Pa
a
b) obliczam przekrój środkowej tulejki na
zginanie.
Zakładam uproszczony przekrój tulejki, taki że otwór 36
φ
jest na całej długości.
Obliczam moment bezwładności:
(
)
3
3
4
65
36 65
22885, 4
36
12
X
d
I
d
mm
⋅
−
⋅
⎡
⎤
=
=
−
⎣
⎦
Obliczam wskaźnik bezwładności:
(
)
(
)
max
3
2 22885,5
36
704,17
36
65
X
X
X
I
W
y
d
W
d
=
⋅
−
mm
⎡
⎤
=
=
−
⎣
⎦
[
]
[
]
[
]
137,5
165
82,5
r
g
t
k
M
k
MPa
k
MP
=
=
=
Pa
a
14.
DANE OBLICZENIA
WYNIKI
[ ]
[ ]
[
]
23000
320
165
g
Q
N
L
mm
k
M
=
=
=
Pa
Obliczam średnice zewnętrzną tulejki z warunku na
zginanie:
(
)
[ ]
[ ]
[
]
[ ]
[ ]
3
2
4
704,17
36
4
23000
320
36
51,8
4 704,17
165
g
g
g
X
g
X
g
X
M
k
W
Q L
M
W
d
mm
Q L
k
W
N
mm
d
m
mm
MPa
σ
=
≤
⋅
=
⎡
⎤
=
⋅
−
⎣
⎦
⋅
≤
⋅
⋅
≥
−
⎡
⎤
⋅
⋅
⎣
⎦
m
mm
=
Przyjmuje
[ ]
52
d
m
=
m
.
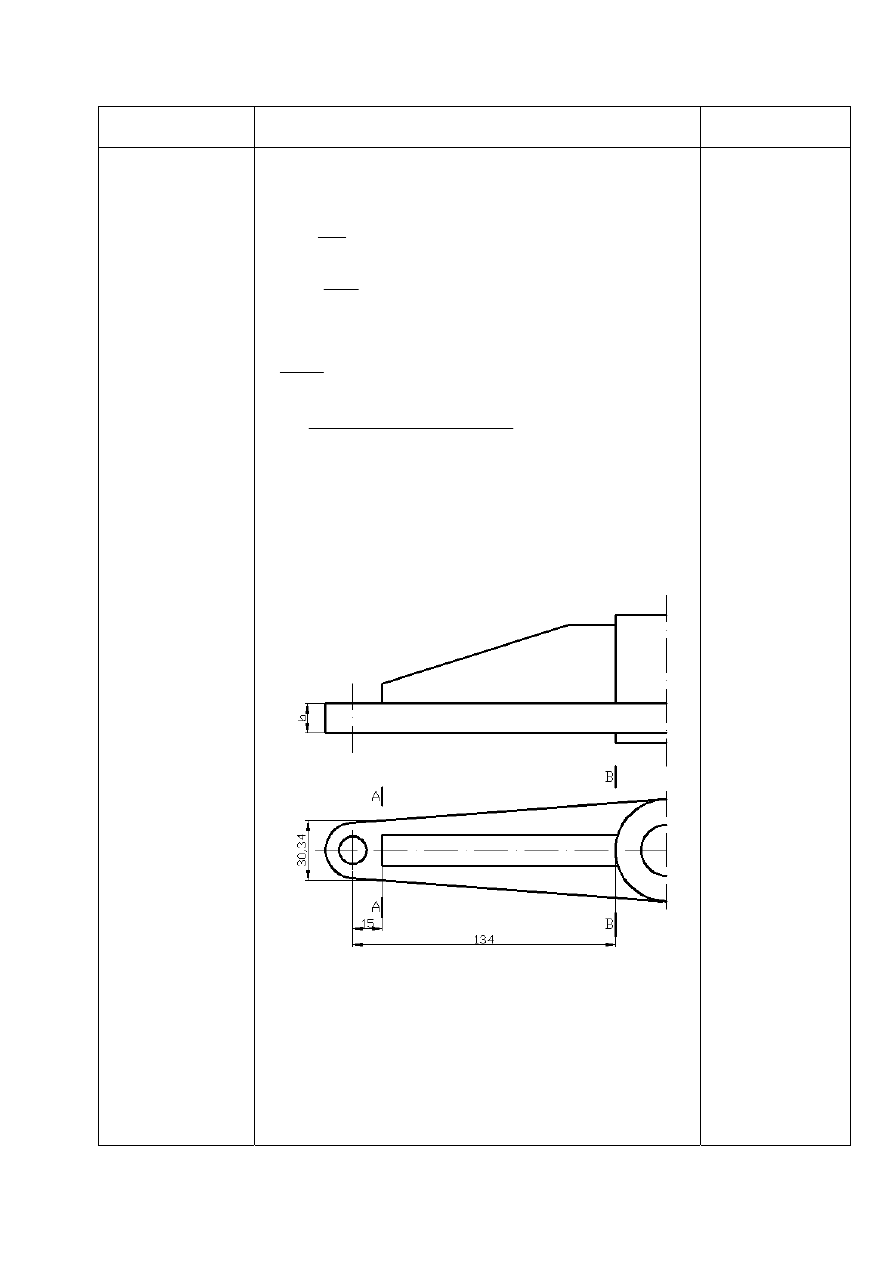
c) obliczam grubość blachy belki
b
w
przekroju
A
A
−
[ ]
52
d
m
=
m
15.

DANE OBLICZENIA
WYNIKI
[ ]
[ ]
23000
15
A A
Q
N
l
m
−
=
=
m
m
[
]
[ ]
46239, 2
'
145
s
A A
M
Nmm
l
m
−
=
=
[
]
137,5
r
k
M
=
Pa
Obliczam szerokość z warunku na zginanie belki:
[ ] [ ]
[
]
[
]
[ ]
[
]
[
]
2
23000
15
172500
2
2
30,34
6
6
172500
6
14, 4
30,34
30,34
165
g
g
g
X
A A
g
X
g
g
M
k
W
N
mm
Q l
M
N
b
W
M
Nmm
b
M
k
mm
MPa
σ
−
=
≤
⋅
⋅
=
=
=
⋅
=
⋅
⋅
≥
=
=
⋅
⋅
mm
Pa
Przyjmuje
[ ]
18
b
m
=
m
.
Sprawdzam wytrzymałość przekroju przy rzeczywistym
obciążeniem: zginaniu, skręcaniu i ścinaniu.
[
]
[
]
[
]
(
)
(
)
[
]
2
2
2
2
2
2
2
2
2
172500 6
105,6
30,34 18
2
23000
21,12
2 30,34 18
'
2
46239, 2
0, 29
145 2 30,34 18
3
105,6
3
21,12
0, 29
111,8
g
g
X
g
t
t
s
s
A A
s
z
g
t
s
r
z
z
r
M
W
MPa
Q
A
MPa
M
l
A
MPa
k
MPa
k
σ
σ
τ
τ
τ
τ
σ
σ
τ
τ
σ
σ
−
=
⋅
=
=
⋅
=
⋅
=
=
⋅
⋅
=
⋅ ⋅
=
=
⋅ ⋅
⋅
=
+ ⋅
+
≤
=
+ ⋅
+
=
<
[ ]
18
b
m
=
m
16.
DANE OBLICZENIA
WYNIKI
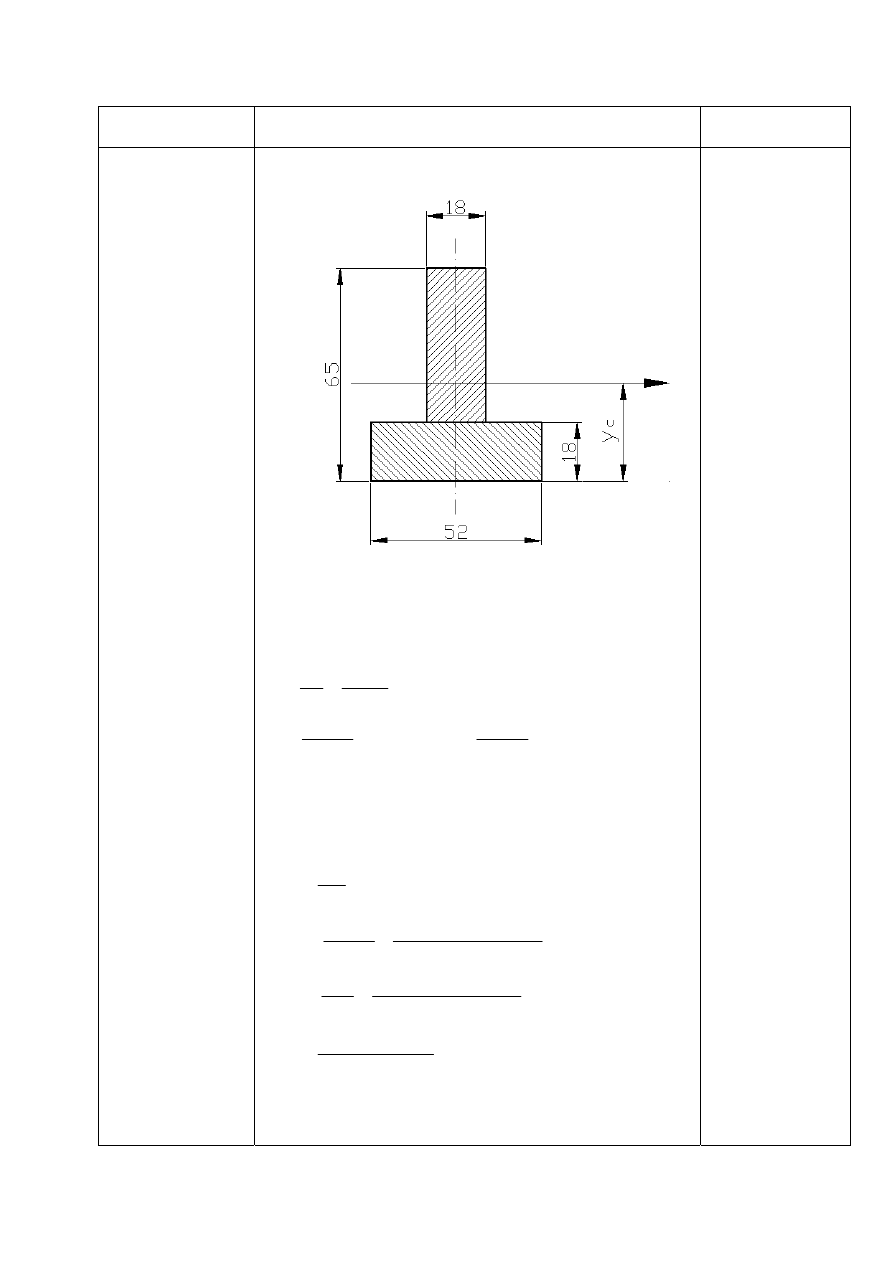
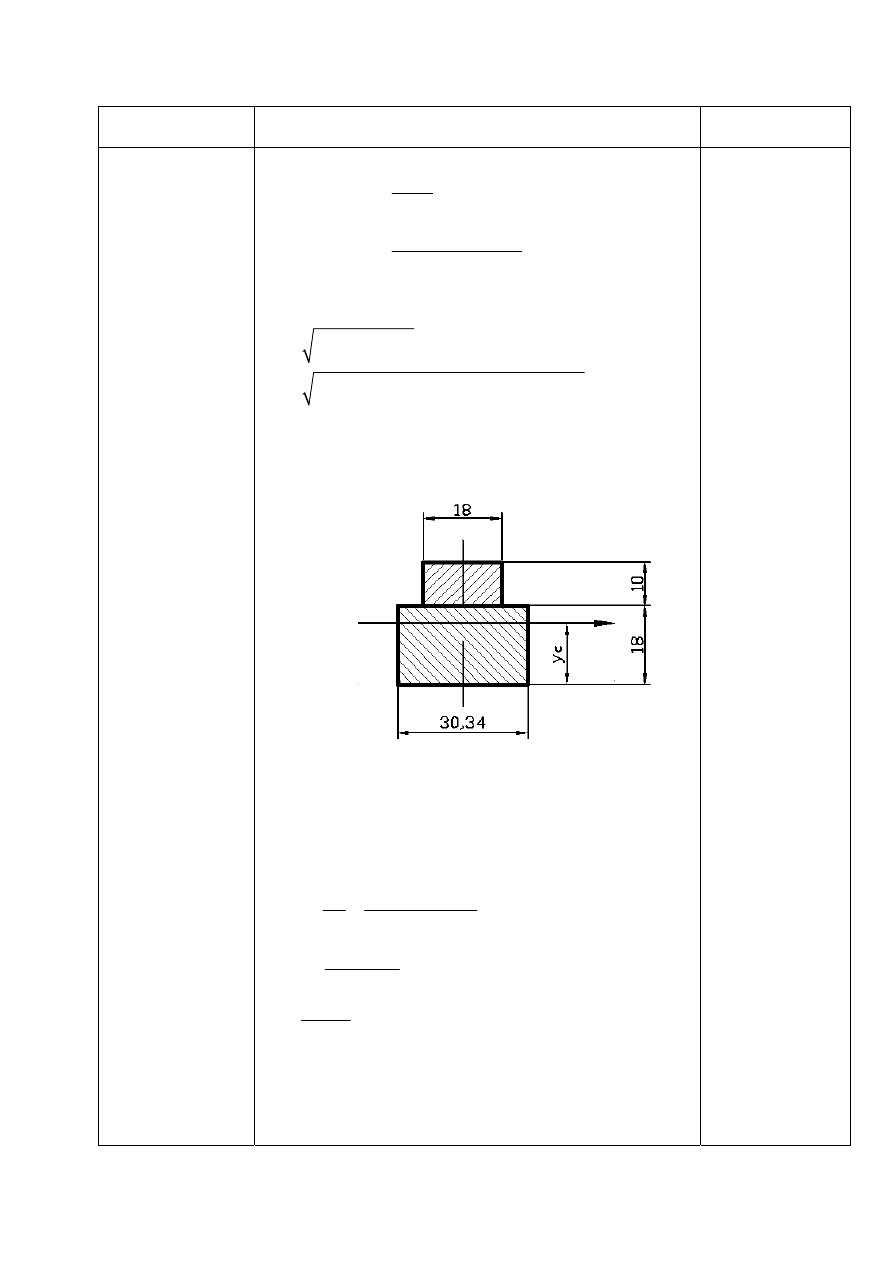
d) obliczam wytrzymałość przekroju
B
B
−
.
Obliczam moment bezwładności przekroju:
(
)
[ ]
2
3
3
3
2
2
4
18 52 42 18 1692
18 52 9 42 18 18 21
37908
37908
22, 4
1692
52 18
18 42
52 18 33, 4
42 18 16,6
12
12
1388891
X
X
c
X
X
A
mm
S
m
S
y
mm
A
I
I
mm
⎡
⎤
= ⋅
+
⋅ =
⎣
⎦
⎡
⎤
= ⋅ ⋅ +
⋅ ⋅
+
=
⎣
⎦
=
=
=
⋅
⋅
=
+
⋅ ⋅
+
+
⋅ ⋅
⎡
⎤
=
⎣
⎦
m
Sprawdzam przekrój na zginanie ze ścinaniem:
[ ]
[ ]
[
]
[ ]
[ ]
[
]
[
]
4
3
max
3
23000
134
1541000
2
2
1388891
36938,5
60
22, 4
1541000
41.72
36938,5
g
g
X
B B
g
X
X
g
M
W
N
mm
Q l
M
Nmm
mm
I
W
m
y
mm
mm
Nmm
MPa
mm
σ
σ
−
=
⋅
⋅
=
=
=
⎡
⎤
⎣
⎦
m
⎡
⎤
=
=
=
⎣
⎦
−
=
=
⎡
⎤
⎣
⎦
4
1388891
X
I
mm
=
⎡
⎤
⎣
⎦
[
]
41,72
g
MPa
σ
=
17.
DANE OBLICZENIA
WYNIKI
[ ]
2
23000
1692
Q
N
A
mm
=
⎡
⎤
=
⎣
⎦
[
]
[
]
41,72
137,5
g
r
MPa
k
M
σ
=
=
Pa
[ ]
[ ]
23000
52
Q
N
d
mm
=
=
[ ]
320
L
m
=
m
[ ]
[
]
[
]
(
)
[
]
(
)
[
2
2
2
max
2
2
2
23000
6,8
2 1692
3
41,72
3 6,8
43,35
z
g
r
z
z
r
Q
A
N
MPa
mm
k
]
MPa
MPa
MPa
k
τ
τ
σ
σ
τ
σ
σ
=
⋅
=
=
⎡
⎤
⋅
⎣
⎦
=
+ ⋅
≤
=
+ ⋅
=
<
d) Obliczam spoiny przy tulei środkowej
Przyjmuje spoinę
[ ]
8
a
mm
=
.
Obliczam naprężenia ścinające:
[ ]
[ ] [ ]
[
]
2
23000
8,8
2
52
8
t
t
Q
d a
N
MPa
mm
mm
τ
π
τ
π
=
⋅ ⋅ ⋅
=
=
⋅ ⋅
⋅
Obliczam naprężenia zginające:
[ ]
[ ]
[
]
(
)
(
)
(
)
(
)
[
]
[
]
4
4
4
4
3
3
4
23000
320
1840000
4
2
32
52 16
52
23021,6
32 52 8
1840000
69,9
23021,6
g
g
g
g
g
g
g
g
M
W
Q L
M
N
mm
M
Nmm
d
a
d
W
d
a
W
m
Nmm
MPa
mm
τ
π
π
τ
=
⋅
=
⋅
=
=
⎡
⎤
+
−
⎣
⎦
=
+
⎡
⎤
+
−
⎣
⎦
m
⎡
⎤
=
=
⎣
⎦
⋅
+
=
=
⎡
⎤
⎣
⎦
[
]
6,8 MPa
τ
=
[ ]
8
a
mm
=
[
]
8,8
t
MPa
τ
=
[
]
69,9
g
MPa
τ
=
18.
DANE OBLICZENIA
WYNIKI
[
]
3
46239, 2
23021,6
s
g
M
Nmm
W
mm
=
=
⎡
⎤
⎣
⎦
[
]
[
]
[
]
8,8
69,9
82,5
t
g
t
MPa
MPa
k
M
τ
τ
=
=
=
Pa
Obliczam naprężenia skręcające:
[
]
[
]
3
2
46239, 2
1
2 23021,6
s
s
g
s
M
W
Nmm
MPa
mm
τ
τ
=
⋅
=
=
⎡
⎤
⋅
⎣
⎦
Obliczam naprężenia zredukowane:
(
)
[
]
[
]
(
)
[
]
[
]
2
2
2
2
8,8
69,9
1
78,7
z
t
g
s
t
z
z
t
k
MPa
MPa
MPa
MPa
k
τ
τ τ
τ
τ
τ
=
+
+
≤
=
+
+
=
<
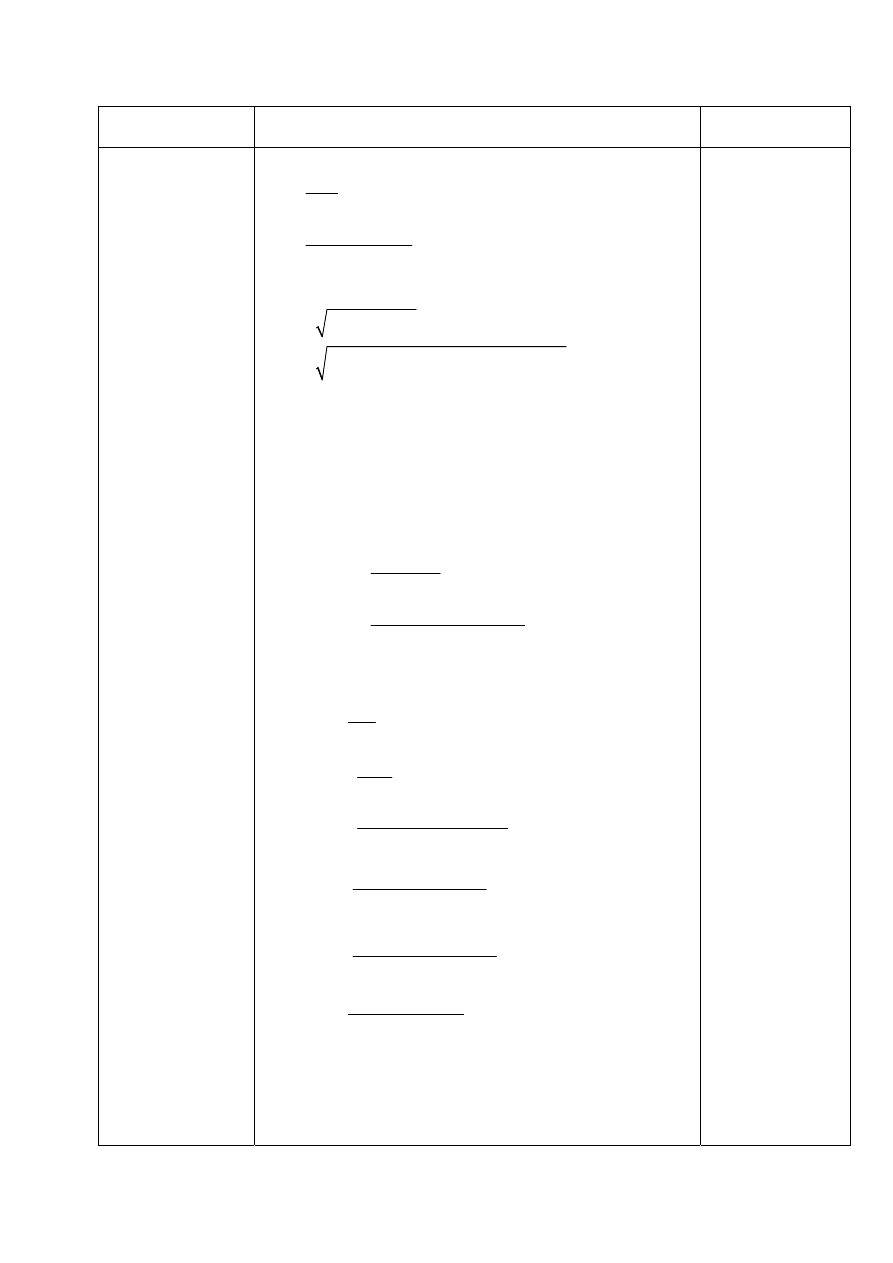
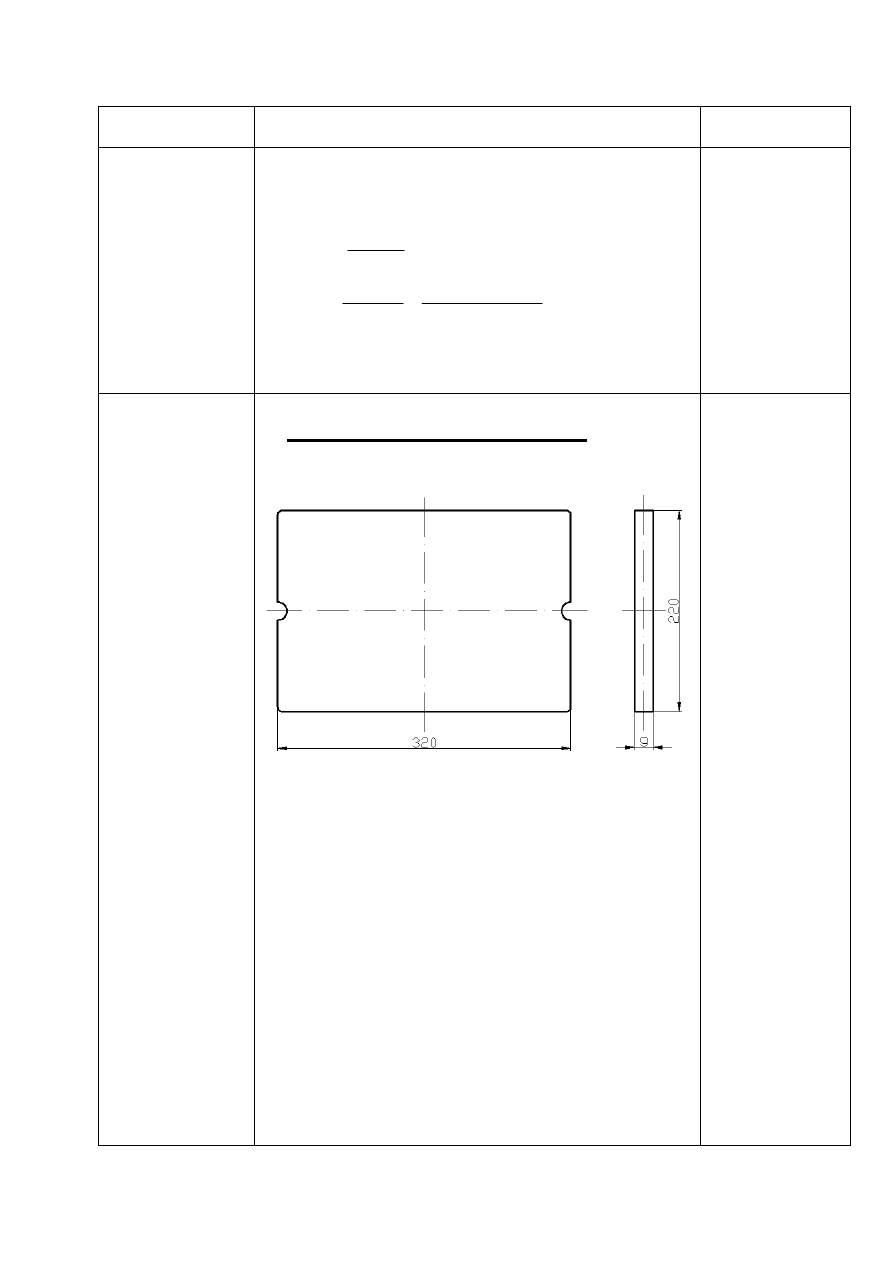
e) obliczam spoiny w przekroju
A
A
−
.
Obliczam moment bezwładności przekroju:
[ ]
(
)
(
)
2
3
3
2
3
2
3
2
4
30,34 18 10 18 726,12
30,34 18 9 10 18 23 9055,08
9055,08
12, 47
726,12
30,34 18
30,34 18 12, 47 9
12
18 10
18 10 28 5 12, 47
42779,6
18
X
X
c
X
A
mm
S
m
mm
S
y
m
A
mm
I
mm
⎡
⎤
=
⋅ + ⋅ =
⎣
⎦
⎡
⎤
=
⋅ ⋅ + ⋅ ⋅
=
⎣
⎦
⎡
⎤
⎣
⎦
=
=
=
⎡
⎤
⎣
⎦
⋅
=
+
⋅ ⋅
−
+
⋅
m
m
⎡
⎤
+
+ ⋅ ⋅
− −
=
⎣
⎦
[
]
1
s
MPa
τ
=
[
]
78,7
z
MPa
τ
=
4
42779,6
X
I
mm
=
⎡
⎤
⎣
⎦
19.
DANE OBLICZENIA
WYNIKI
[ ]
[
]
4
42779,6
23000
82,5
X
t
I
mm
Q
N
k
M
=
⎡
⎤
⎣
⎦
=
=
Pa
Obliczam szerokość spoiny :
a
(
)
[ ]
3
18 10 28 5 12, 47
1895, 4
2
23000 1895, 4
5,8
2
2 82,5 42779,6
odc
odc
s
t
X
odc
t
X
S
m
Q S
k
a I
Q S
a
m
k I
τ
m
m
⎡
⎤
= ⋅ ⋅
− −
=
⎣
⎦
⋅
=
≤
⋅ ⋅
⋅
⋅
≥
=
=
⋅ ⋅
⋅
⋅
Przyjmuje szerokość spoiny
[ ]
6
a
mm
=
.
[ ]
6
a
mm
=
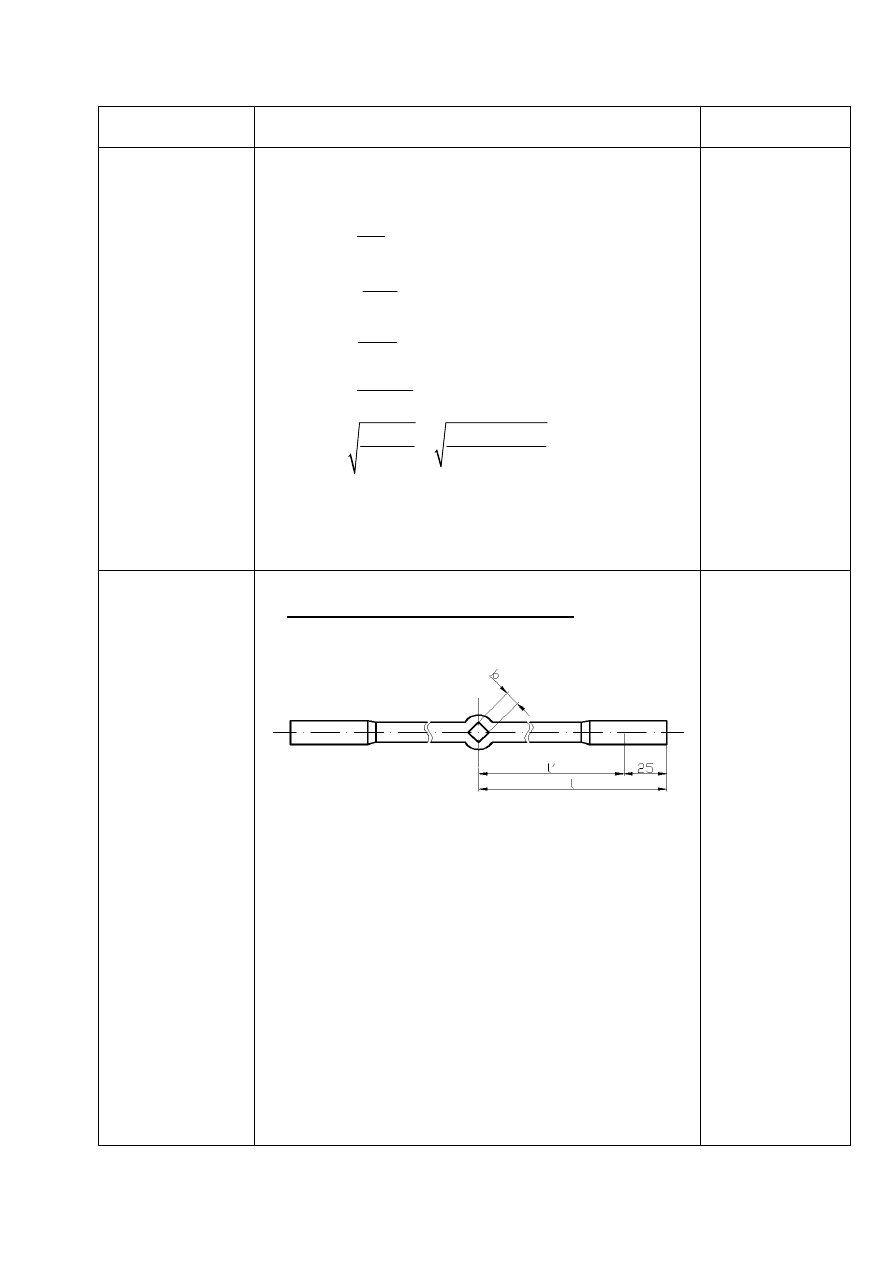
6. Obliczam płytę dociskową:
Przyjmuje wykonanie płyty z stali
.
3
St S
[
]
[
]
[
]
220
2
110
130
e
e
r
g
R
MPa
X
k
MP
k
M
=
=
=
=
a
Pa
[
]
[
]
110
130
r
g
k
MP
k
M
=
=
a
Pa
20.
DANE OBLICZENIA
WYNIKI
[ ]
[ ]
[ ]
[
]
23000
320
220
130
g
Q
N
L
mm
b
mm
k
M
=
=
=
=
Pa
Obliczam grubość płyty dociskowej z warunku zginanie:
[ ]
2
2
4
6
6
4
6
6 23000 320
19,8
4
4 220 130
g
g
g
g
g
g
g
g
g
M
k
W
Q L
M
b g
W
Q L
k
b g
Q L
g
m
b k
σ
σ
=
≤
⋅
=
⋅
=
⋅ ⋅
=
≤
⋅ ⋅
⋅ ⋅
⋅
⋅
≥
=
=
⋅ ⋅
⋅
⋅
m
Przyjmuje grubość płyty
[ ]
22
g
m
=
m
.
[ ]
22
g
m
=
m
7. Obliczam pokrętło prasy:
a) założenia wstępne:
Przyjmuje wykonanie pokrętła z stali
.
3
St
[
]
[
]
[
]
[
]
220
2
110
130
90
e
e
r
g
dop
R
MPa
X
k
MP
k
MP
a
a
p
MPa
=
=
=
=
=
Zakładam siłę potrzebna do skręcenia pokrętłem
[ ]
200
P
N
=
.
[
]
[
]
[
]
110
130
90
r
g
dop
k
MP
k
MP
a
a
p
MPa
=
=
=
21.
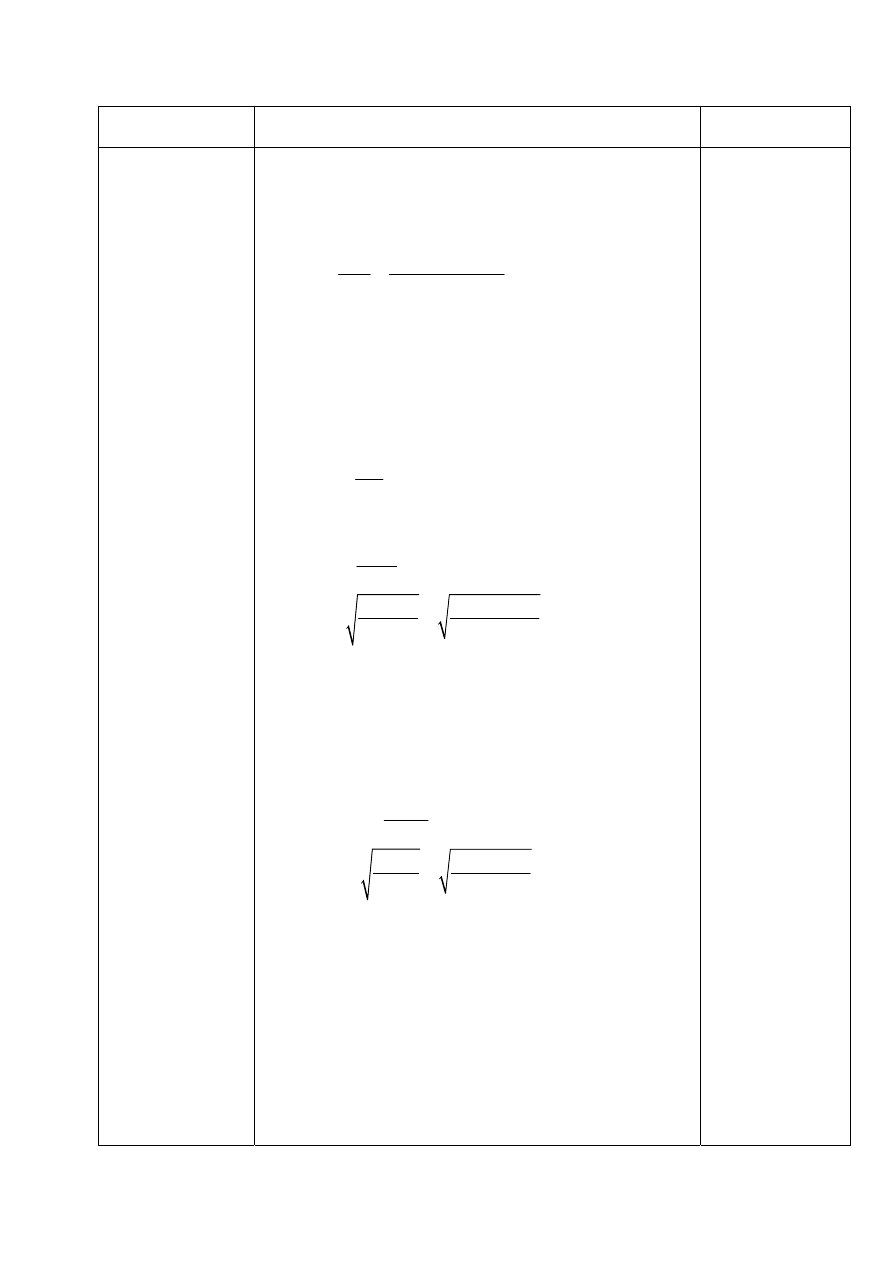
DANE OBLICZENIA
WYNIKI
[
]
[ ]
46239, 2
200
S
M
Nmm
P
N
=
=
[
]
90
dop
p
MPa
=
b) obliczam długość pokrętła:
[
]
[ ]
[ ]
[ ]
[ ]
[ ]
2
'
46239, 2
'
115,6
2
2 200
' 25 115,6
25
140,6
S
S
M
P l
Nmm
M
l
m
P
N
l
l
mm
mm
mm
= ⋅ ⋅
=
=
=
⋅
⋅
= +
=
+
=
m
Przyjmuje
[ ]
145
l
m
=
m
.
c) obliczam średnice pręta z warunku na
zginanie:
[ ]
3
3
3
'
32
32
'
32 200 115
12,17
130
g
g
g
g
g
g
g
M
k
W
M
P l
d
W
P l
d
m
k
σ
π
π
π
=
≤
= ⋅
⋅
=
⋅ ⋅
⋅
⋅
≥
=
=
⋅
⋅
m
Przyjmuje
[ ]
14
d
m
=
m
.
d) obliczam połączenie pokrętła z śrubą:
Przyjmuje długość czworoboku
[ ]
10
l
m
=
m
.
[ ]
max
2
3
3
3 46239, 2
11, 4
10 90
S
dop
S
dop
M
p
p
b l
M
b
m
l p
m
⋅
=
≤
⋅
⋅
⋅
≥
=
=
⋅
⋅
Przyjmuje
[ ]
12
b
m
=
m
.
[ ]
145
l
m
=
m
[ ]
14
d
m
=
m
[ ]
12
b
m
=
m
22.

23.
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron