
klastry obliczeniowe
34
maj 2004
Rozproszone fraktale
Marek Sawerwain
O
soby, które zajmują się
grafiką, a w szczególno-
ści techniką śledzenia
promieni, często mogą
powiedzieć, że moc obliczeniowa ich
komputerów nie jest wystarczająca.
Dotyczy to także rysowania fraktali,
szczególnie tych o skomplikowanych
wzorach. W tym artykule chciałbym
pokazać, jak rozdzielić zadanie ryso-
wania tego typu obiektów na kilka
komputerów za pomocą technologii
rozproszonych obiektów – CORBA.
Napiszemy nieskomplikowany program
tworzący coś w rodzaju klastra przezna-
czonego do rysowania fraktali.
Wbrew pozorom, proces rysowa-
nia fraktali jest bardzo pracochłonny
i tylko najbardziej popularne zbiory,
takie jak Mandelbrot, Julia czy Newton,
można narysować w czasie rzeczywi-
stym. Po wprowadzeniu kilku uprosz-
czeń, można nawet pokusić się o ich
animację. W innych przypadkach jest
to proces bardzo czasochłonny. Dość
łatwo można go przyspieszyć, gdy
sam proces rysowania podzielimy na
regiony i rozdzielimy na kilka kompu-
terów.
Kilka postanowień na
początek
Pierwsza decyzja, którą trzeba podjąć,
dotyczy języków programowania uży-
tych do napisania systemu. Serwer zosta-
nie napisany przy pomocy języka Python
i systemu CORBA OmniORB.
Dlaczego Python? Nasz system,
pomimo swoich niewielkich rozmiarów,
ma być systemem uniwersalnym i zdol-
nym do rysowania dowolnych fraktali
opartych o tzw. funkcję ucieczki. Python,
jak każdy język skryptowy, nie oferuje
wysokiej wydajności, ale posiada pewne
interesujące nas cechy, a jedną z nich
jest możliwość zdefiniowania funkcji
w czasie wykonania skryptu. Dzięki tej
własności serwer będzie odbierał od
klienta kod źródłowy funkcji i instalował
ją we własnym środowisku.
Powód, dla którego za system
CORBY po stronie serwera został
wybrany pakiet OmniORB, jest bardzo
prozaiczny. Obecnie oferuje on najlep-
szą wersję CORBY dla języka Python.
Można w nim bez zbędnych kłopotów
korzystać z usługi nazw, która ma zna-
czenie zasadnicze dla naszego klastra
rysującego fraktale.
Zastanówmy się teraz nad progra-
mem klienta. Może on być napisany
w dowolnym języku i dowolnym systemie
CORBY, zgodnym ze standardem adapte-
ra POA oraz obsługującym dynamiczne
wywołania metod (DII – Dynamic
Invocation Inteface). Takim serwerem
jest również OmniORB, ale aby pokazać
elastyczność technologii rozproszonych
obiektów, zastosujemy inny system
o nazwie MICO. Oprócz zastosowania
innego systemu CORBA, program klienta
zostanie napisany w innym języku, gdyż
będzie to C++.
Ostatni problem to: w jaki sposób
rozproszyć proces rysowania fraktala na
kilka komputerów? Zastosowany algo-
rytm rysuje fraktal linia po linii. Oznacza
to, że możemy bez problemów podzielić
cały proces rysowania na kilkanaście
komputerów rozdzielając im poszczegól-
O autorze
Autor zajmuje się tworzeniem
oprogramowania dla WIN32
i Linuksa. Zainteresowania:
teoria języków programowania
oraz dobra literatura. Kontakt
z autorem:
autorzy@linux.com.pl.
Na płycie CD/DVD
Na płycie CD/DVD znajdują
się pliki źródłowe napisanego
programu, jak również wszystkie
listingi.
35
www.linux.com.pl
klastry obliczeniowe
corba
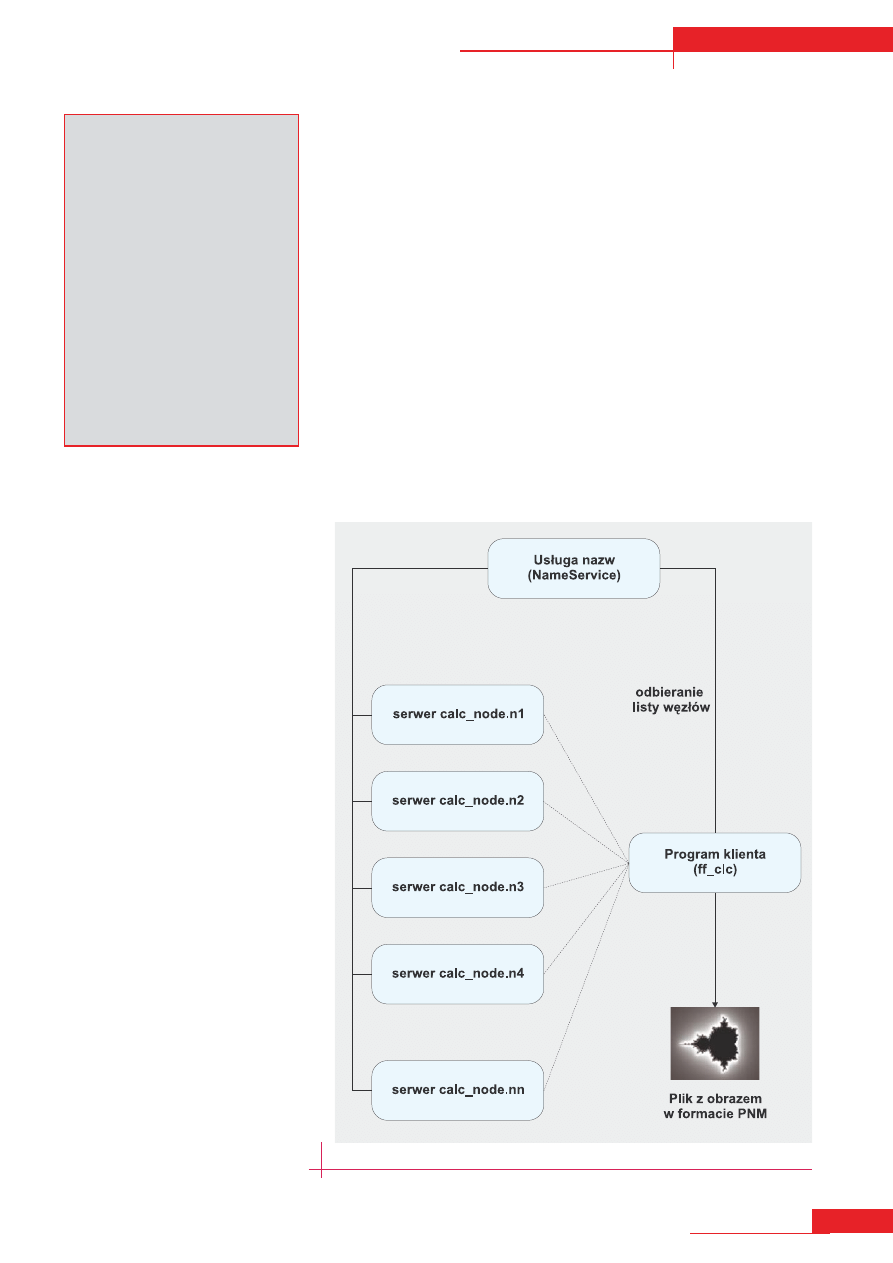
ne wiersze rysowanego obrazu. Klient
przy pomocy usługi nazw pobierze listę
zarejestrowanych węzłów i do każdego
wyśle odpowiednią ilość wierszy do
narysowania. Po otrzymaniu wyników
połączy pojedyncze wiersze w jeden
rysunek. Schematycznie zostało to przed-
stawione na Rysunku 1.
Definicja interfejsu
dfractal
Podczas pisania jakichkolwiek aplikacji
w technologii CORBA należy w pierwszej
kolejności określić interfejs obiektów roz-
proszonych. Nasz interfejs o nazwie
calc_
node
to tylko cztery metody. Jego defini-
cja znajduje się na Listingu 1. Czynności,
które wykonują poszczególne metody, są
następujące:
•
setup_iter_func
– określa postać
funkcji ucieczki;
•
setup_render_size
– określa wymia-
ry obrazu, na którym będzie rysowa-
ny fraktal (w pikselach);
•
render_one_row
– rysuje wiersz o nu-
merze
y
od pozycji
from_x
do
to_x
;
•
quit
– wywołanie tej funkcji powodu-
je zakończenie pracy węzła.
Posługiwanie się tym interfejsem jest
trywialne, np. w Pythonie, gdy chcemy
narysować cały fraktal, to w pierwszej
kolejności ustalamy wymiary oraz poda-
jemy kod funkcji ucieczki:
calc_node.setup_render_size(300,200)
calc_node.setup_iter_func(funkcja_ucieczki)
Następnie przy pomocy zwykłej pętli
while
wywołujemy metodę
render_one_
row
. Wynikiem tej metody jest jeden
wiersz obrazu. Kolory zostały zakodo-
wane w postaci trójek RGB, więc mamy
gotowe dane do bezpośredniego przenie-
sienia na ekran lub zapisu do pliku:
row=0
while row<=200:
dane=calc_node.render_one_
S
row(row,0,300)
for i in dane:
print i
row=row+1
Tworzymy serwer
Aplikacje w CORBIE są dzielone na dwie
części: serwer i klient. Prace nad naszym
systemem zaczniemy od napisania serwe-
ra, gdyż, wbrew pozorom, to mniej skom-
plikowane zadanie.
W pierwszej kolejności trzeba
poddać kompilacji plik z interfejsem,
gdyż tego wymaga odwzorowanie
OmniORB dla Pythona. Polecenie jest
następujące:
omniidl -bpython dfractal.idl
Po kompilacji pliku z interfejsem, utwo-
rzone pliki dołączamy słowem
import
.
Dołączenie wszystkich modułów konie-
cznych do poprawnej pracy serwera to
tylko trzy linie kodu:
from omniORB import CORBA, PortableServer
import CosNaming
import dfractal, dfractal__POA
W pierwszej linijce dołączamy moduły
bezpośrednio związane z danym syste-
mem CORBY, czyli w naszym przypad-
ku OmniORB. Druga linia dołącza inter-
Rysunek 1.
Schemat „klastra” rysującego fraktal
Instalacja pakietów
OmniORB oraz MICO
Autorzy obydwu pakietów przygotowali
skrypty configure, więc kompilacja prze-
biega według typowej ścieżki postępo-
wania:
./configure –prefix=/katalog/
S
gdzie/ma/zostać/zainstalowany/pakiet
make
make install
Również pakiet z wersją systemu
OmniORB dla języka Python o nazwie
omniORBpy posiada skrypt configure.
Oczywiście, warto mieć zainstalowane-
go Pythona w stosunkowo nowej wersji
2.2 albo 2.3.

36
maj 2004
klastry obliczeniowe
fejs odpowiedzialny za usługę nazw.
W trzeciej linii dołączamy nasz interfejs
oraz wygenerowany szkielet do imple-
mentacji serwera.
Kod całego serwera znajduje się na
płycie CD/DVD, ale Listing 2 zawiera
jego najważniejsze fragmenty. Jak widać,
została usunięta definicja klasy
Fractal-
Render
. Powrócimy do niej w następnym
punkcie.
Każdy, kto choć raz napisał najmniej-
szy program w technologii CORBA, od
razu pozna charakterystyczne elementy
występujące w programie serwera – pro-
gramy w CORBIE są do siebie bardzo
podobne, pomimo różnych serwerów
CORBY czy zastosowanego języka pro-
gramowania.
Centralnym elementem naszego sys-
temu renderingu jest usługa nazw. W ser-
werze oraz w kliencie musimy podać
adres symboliczny bądź numer IP, pod
którym znajduje się ta usługa. Z tego
powodu przed uzyskaniem odniesienia
do obiektu
orb
, zmiennej zawierającej
argumenty podane w linii poleceń, wpi-
sujemy adres maszyny, na której urucho-
miono usługę nazw:
sys.argv.extend([‘-ORBInitRef’,
S
‘NameService=corbaname::127.0.0.1’])
Jak widać z powyższego przykładu,
odwołujemy się do lokalnej maszyny,
więc używając tego systemu w rzeczywi-
stej sieci, trzeba zmienić tę linię kodu.
Wcześniej
wykonujemy
jeszcze
jedną istotną czynność, a mianowicie
odczytujemy podaną nazwę nasze-
go węzła. Nazwy dla poszczególnych
węzłów muszą być oczywiście inne –
w ten sposób je rozróżniamy. Proces
rejestracji naszego węzła w usłudze nazw
rozpoczynamy od uzyskania odniesie-
nia do usługi nazw. Pomimo, że serwer
jest pisany w Pythonie, to następujący
kod jest prawie identyczny z tym, który
omówię przy okazji klienta (napisanego
przy pomocy języka C++):
ns = orb.resolve_initial_references
S
(„NameService”)
root_ctx = ns._narrow
S
(CosNaming.NamingContext)
Sam proces rejestracji obiektu poprzedza-
my jego wstępnym utworzeniem:
servant = CalcNodeServant()
objref = servant._this()
Gdy w zmiennej
objref
mamy już refe-
rencję do obiektu, to wystarczy utwo-
rzyć obiekt nazwy bazujący na typie
CosNaming.NameComponent
oraz dokonać
jego rejestracji metodą
bind
obiektu
root_ctx
:
name = [CosNaming.NameComponent
S
(„calc_node”, node_name)]
root_ctx.bind(name, objref)
Ostateczna aktywacja serwera to typowy
kod dla dowolnego serwera CORBY.
Dokonujemy aktywacji adaptera POA:
poa._get_the_POAManager().activate()
oraz uruchamiamy cały serwer:
orb.run()
.
Jak widać na Listingu 2, pomiędzy tymi
poleceniami został jeszcze utworzony
obiekt typu
FractalRender
.
Dzięki zdefiniowaniu oddzielnej klasy
do rysowania samego fraktala, poszczegól-
ne metody obiektu
CalcNodeServant
są
bardzo krótkie i nie zawierają zbyt skom-
plikowanej treści. Wszystkie odwołują się
do globalnego obiektu
fractal
. I to on
wykonuje całą „robotę” związaną z obsłu-
gą procesu rysowania. Wyróżnia się tylko
metoda
quit
, kończąca działanie naszego
serwera. Dokonuje ona także zwolnienia
nazwy, pod którą konkretny serwer jest
reprezentowany w usłudze nazw.
Rysowanie fraktala
Rysowanie fraktala to zadanie klasy
FractalRender
. Znaczenie poszczególnych
metod jest następujące:
•
ResetParam(_maxx, _maxy)
– ustala
wymiary rysunku fraktala w pik-
selach, współrzędne początku oraz
wymiary przestrzeni zespolonej, na
której powstaje fraktal;
•
S e t u pIt e r F u n c ( c o d e _ o f_ f u n c)
– tworzy funkcję ucieczki (iteracji);
•
RenderOneLine(render_y,
from_x,
to_x)
– rysuje pojedynczy wiersz,
wartością wynikową jest lista z kolo-
rami w formacie RGB.
W rzeczywistości w kodzie są jeszcze
dwie dodatkowe metody:
RenderFrag-
ment
, przeznaczona do rysowania frag-
mentu fraktala, oraz
DrawFullFractal-
MandelbrotStyle
, rysującą cały fraktal.
Obydwie, identycznie jak
RenderOneLi-
ne
, dają w wyniku listę z kolorami w for-
macie RGB.
Zastosowany algorytm należy do
najprostszych technik rysowania frak-
tali, która polega na tym, że rysowanie
Listing 1.
Definicja interfejsu dfractal
module dfractal{
typedef sequence
<long> TRow;
interface calc_node{
void
setup_iter_func(
in string code
);
void
setup_render_size(
in
long width,
in
long height
);
TRow render_one_row(
in
long y,
in
long from_x,
in
long to_x
);
void
quit();
};
};
Format pliku PNM
Pliki w formacie PNM (obsługiwany
bez problemów przez GIMP-a) mają
bardzo prostą strukturę. Do naszych
potrzeb wystarczy plik PNM o typie P3.
Jest to w pełni tekstowy format. Jego
nagłówek zaczyna się w następują-
cy sposób:
P3
# CREATOR: narysowane przez dfrac-
tal
100 100
W pierwszej linii zawarty jest typ pliku.
P3 oznacza, że będzie to w plik w for-
macie wyłącznie tekstowym. Następ-
nie podajemy komentarz – można w
nim umieścić krótką informację, kto
utworzył plik. W trzeciej linii nagłówka
podajemy dwie liczby – są to wymiary
rysunku: szerokość oraz wysokość. Po
tak skonstruowanym nagłówku poda-
jemy kolejne wartości pikseli, opisa-
ne za pomocą trójek RGB. Poszcze-
gólne wartości znajdują się w oddziel-
nych liniach.

37
www.linux.com.pl
klastry obliczeniowe
corba
w przestrzeni zespolonej rozpoczynamy
od lewego górnego rogu i linia po linii
dla każdego punktu na wydzielonym
wcześniej obszarze sprawdzamy, jaką
wartość ma funkcja ucieczki.
Cały kod funkcji rysującej wskaza-
ny wiersz zawiera Listing 3. Ma ona trzy
części.
W pierwszej części ustalamy wymia-
ry rysunku w pikselach: zmienne
vWidth
i
vHeight
. Zmienne
vfromX
i
vfromY
zawierają współrzędne lewego górne-
go rogu. Początkowe wartości zawie-
rają zmienne z przedrostkiem „new”.
Ich wartość zostaje określona metodą
ResetParam
w momencie wywoła-
nia metody
setup_render_size
obiektu
calc_node
. Ostatnie dwa przypisania do
kx
i
ky
określają krok, o jaki będą zwięk-
szane współrzędne zespolone. W przy-
padku rysowania wiersza istotna jest
tylko zmienna
kx
.
W części drugiej obliczamy przesu-
nięcia względem osi
x
oraz
y
, oczywi-
ście w przestrzeni zespolonej (mimo,
że mówimy o liczbach zespolonych, to
wszystkie obliczenia bazują na warto-
ściach rzeczywistych). Obliczenia dla
zmiennej
yy
polegają na tym, że podany
numer wiersz
render_y
jest mnożo-
ny przez wartość kroku
ky
i dodawany
do zmiennej zawierającej współrzędne
lewego górnego rogu
vfromY
. Ta część
funkcji wyznacza też początek rysowa-
nia w danym wierszu (początek zawie-
ra zmienna
xx
, a miejsce zakończenia
vtoX
). Oznacza to, iż metoda
RenderOne-
Line
umożliwia także rysowanie dowol-
nego fragmentu podanej linii.
Po
wyznaczeniu
współrzędnych
danego wiersza w części trzeciej pozostaje
nam tylko przy pomocy nieskomplikowa-
nej pętli przejść wzdłuż osi
x
po poszcze-
gólnych punktach należących do danego
wiersza i dla każdego wywołać funkcję
iter,
czyli funkcję ucieczki. Dopiero
w argumencie tej funkcji pojawia się kon-
struktor
complex
, który ze współrzędnych
xx
i
yy
tworzy liczbę zespoloną.
Wynikiem funkcji
RenderOneLine
jest lista zawierająca poszczególne trójki
RGB, opisujące kolory. Lista tworzona jest
w bardzo prosty sposób. Na początek two-
rzymy listę pustą, a następnie po wyzna-
czeniu wartości kolorów dodajemy te
wartości do listy. W tym miejscu podczas
wyznaczania wartości kolorów ujawnia się
Rysunek 2.
Diagram przepływu
sterowania w programie klienta
Listing 2.
Fragmenty skryptu Pythona implementującego serwer calc_node
#! /usr/bin/python
import sys
from omniORB
import CORBA, PortableServer
import CosNaming
import dfractal, dfractal__POA
class
FractalRender:
# usunięta definicja klasy rysującej fraktal
class
CalcNodeServant(dfractal__POA.calc_node):
global
fractal
„setup_iter_func”, code
fractal.SetupIterFunc(code)
def
setup_render_size(self, width, height):
global
fractal
fractal.ResetParam(width, height)
„setup_render_size w”,width,”h”,height
def
render_one_row(self, y, from_x, to_x):
„begin render”,y,from_x, to_x
r=fractal.RenderOneLine(y,from_x, to_x)
„end render”,y,from_x, to_x
return
r
def
quit(self):
global
orb, root_ctx
root_ctx.unbind(name)
„node stop ...”
orb.shutdown(
0
)
if
len(sys.argv)>
1:
node_name=sys.argv[
1
]
else:
„proszę podać nazwę węzła”
sys.exit(
0)
sys.argv.extend([‘-ORBInitRef’, ‘NameService=corbaname::
127.0.0.1’]
)
orb = CORBA.ORB_init(sys.argv, CORBA.ORB_ID)
poa = orb.resolve_initial_references(
„RootPOA”
)
ns = orb.resolve_initial_references(
„NameService”
)
root_ctx = ns._narrow(CosNaming.NamingContext)
servant = CalcNodeServant()
objref = servant._this()
name = [CosNaming.NameComponent(
„calc_node”, node_name
)]
try:
root_ctx.bind(name, objref);
except
CosNaming.NamingContext.AlreadyBound:
root_ctx.rebind(name, objref)
„Name calc_node [„,node_name,”] already existed -- rebound”
poa._get_the_POAManager().activate()
fractal=FractalRender()
orb.run()
print
„... end work ...”

38
maj 2004
klastry obliczeniowe
pewna niedoskonałość. Sposób wyzna-
czania kolorów, który bazuje na reszcie
z dzielenia, nie daje zbyt efektownych
układów kolorystycznych, więc zadaniem
dla Czytelnika jest napisanie dodatkowej
funkcji kolorującej fraktal.
Definiowanie funkcji
ucieczki (iteracji)
Zajmijmy się teraz metodą, która pozwa-
la na ustalenie postaci funkcji ucieczki,
gdyż to ta funkcja odgrywa najważniej-
szą rolę podczas rysowania różnych frak-
tali. Treść metody
SetupIterFunc
wbrew
pozorom jest zaskakująco krótka:
def SetupIterFunc(self, code_of_func):
code_of_iter_func=compile(code_of_
S
func, „<string>”, „exec”)
eval(code_of_iter_func,globals())
W pierwszej linii dokonujemy kompi-
lacji funkcji, więc warto przed rozpo-
częciem procesu rysowania dokładnie
sprawdzić, czy funkcja iteracji została
napisana bezbłędnie. Funkcję kompilu-
jemy w tzw. trybie wykonawczym (trzeci
parametr przyjmuje wartość exec). Po
wykonania funkcji
compile
otrzymujemy
obiekt reprezentujący kod, który można
wykonać przy pomocy funkcji
eval
.
Istotne jest, aby w drugim argumencie
tej funkcji podać jako argument funkcję
globals()
. Spowoduje to, iż nasza funkcja
(o nazwie
iter
, bowiem taka nazwa
występuje w metodzie
RenderOneLine
)
zostanie zdefiniowana w podstawowej
(głównej) przestrzeni, a więc będzie
widziana w każdej klasie.
Funkcja
iter
, oprócz nazwy, przyj-
muje tylko jeden parametr, który jest
liczbą zespoloną zbudowaną w oparciu
o współrzędne punktu w układzie zespo-
lonym. Przykład takiej funkcji rysującej
zbiór Mandelbrota zawiera Listing 4.
Program klienta
Program klienta jest niewiele większy niż
kod źródłowy serwera. Mimo, że to tylko
5 kB tekstu, to również omówimy tylko
jego najciekawsze fragmenty. W analizie
programu klienta pomocny będzie rów-
nież schemat z Rysunku 2.
Pierwsze zadanie naszego klien-
ta to odczytanie z usługi nazw wszyst-
kich węzłów, które są dostępne. Milczą-
co zakładamy, że będą to tylko węzły
calc_node
– uprości to nasz program.
Po przygotowaniu listy węzłów
możemy „rozdać” poszczególne wier-
sze obrazu do narysowania. I tu pojawia
się poważny problem. Wywołania metod
CORBY zazwyczaj działają w trybie syn-
chronicznym, czyli wywołanie jakiejś
metody powoduje wstrzymanie pracy
klienta do czasu, gdy serwer odpowie na
wywołanie określonej metody. Nie jest to
dobre rozwiązanie dla naszego klienta, bo
my chcemy rozdać cały zbiór poszczegól-
nych wierszy do rysowania, a dopiero po
tej czynności poczekać na gotowe dane,
aby ostatecznie połączyć wszystkie wier-
sze w jeden obraz. CORBA oferuje odpo-
wiednie rozwiązanie i jest to technika DII,
o której wspomniałem na początku arty-
kułu. Dynamiczne wywołania pozwala-
ją wywołać zdalną metodę w tzw. trybie
o opóźnionej odpowiedzi. Praca progra-
mu klienta nie jest w takim przypadku
wstrzymywana na czas wykonania zdal-
nej metody, ale to na programie klienta
spoczywa obowiązek odbioru danych.
Klient CORBY, który stosuje DII, nie
musi korzystać z dodatkowych plików
IDL. Z tego powodu nie dokonuje-
my wstępnej kompilacji naszego inter-
fejsu. Trzeba jednak utworzyć specjalny
identyfikator, który pozwoli nam rozpo-
znać dane otrzymane od metody serwe-
ra
render_one_line
(będzie to oczywiście
wiersz z kolorami RGB). Musimy utworzyć
tzw.
TypeCode
i wygląda to następująco:
CORBA::TypeCode_ptr _my_tc_longseq;
_my_tc_longseq=CORBA::TypeCode::
S
create_sequence_tc(0, CORBA::_tc_long);
Pozostałe typy danych należą do podsta-
wowych typów CORBY, więc nie trzeba
stosować dodatkowych zabiegów, aby
z nimi współpracować. Do pracy nasze-
go klienta potrzebujemy listę wszystkich
węzłów. Najlepiej skorzystać z typu
vector
:
vector<CORBA::Object_var> nodes;
Potrzebny jest jeszcze jeden typ, gdyż
podczas procesu przydzielania wierszy do
rysowania będziemy tworzyć listę aktyw-
nych wywołań. Definicja jest następująca:
typedef struct {
CORBA::Request_var req;
CORBA::Long y,from_x,to_x;
int m;
} TRequest;
Definicja listy, a dokładniej wektora oraz
iteratora niezbędnego do przeglądania,
jest następująca:
vector<TRequest> reqs;
vector<TRequest>::iterator reqsIter;
Pierwsza z istotnych czynności to uzy-
skanie od usługi nazw listy wszystkich
węzłów. Fragment z kodu klienta przed-
stawia Listing 5. Listę węzłów odczytuje-
my wywołaniem
root_ctx->list(0, bl,
bi);
(zero oznacza, że otrzymamy wszyst-
kie wpisy w usłudze nazw), a następnie
Listing 3.
Metoda klasy
FractalRender
rysująca jeden wiersz należący do
określonego fraktala
def RenderOneLine
(
self, render_y,
S
from_x, to_x
):
# część I
self.vWidth
=
self.newvWidth
;
self.vHeight
=
self.newvHeight
;
self.vfromX
=
self.newvfromX
;
self.vfromY
=
self.newvfromY
;
self.kx
=
self.vWidth/self.maxx
;
self.ky
=
self.vHeight/self.maxy
;
# część II
xx
=
self.vfromX
+ (
from_x
*
self.kx
)
yy
=
self.vfromY
+ (
render_y
*
S
self.ky
)
self.vtoX
=
self.vfromX
+
S
(
to_x
*
self.kx
);
# część III
row
=[]
while
(
xx
<=
self.vtoX
):
tc
=
iter
(
complex
(
xx,yy
));
r
=(
tc
*
128
) %
256
;
g
=(
tc
*
32
) %
256
;
b
=(
tc
*
64
) %
256
;
row.append
(
r
)
row.append
(
g
)
row.append
(
b
)
xx
=
xx
+
self.kx
return
row
Listing 4.
Przykład funkcji iteracji
odpowiedzialnej za rysowanie zbioru
Mandelbrota
moja_funkcja
=
”””
def
iter(c):
i=
0
z=complex(
0
,
0
);
while
(i <
128
and (z.real*z.real
S
+ z.imag*z.imag) <
4
):
z=(z*z)+c
i=i+
1
return
i
”””
;

39
www.linux.com.pl
klastry obliczeniowe
corba
w pętli za pomocą
resolve
otrzymujemy
odniesienia do obiektów typu
CORBA::
Object_var
. Przy okazji w zmiennej
max_
nodes
zliczamy ilość dostępnych węzłów.
Wartość ta będzie nam potrzebna pod-
czas dystrybucji poszczególnych wierszy
do węzłów.
Z poziomu funkcji
main
wystarczą
nam już tylko dwa wywołania następu-
jących funkcji:
setup_nodes(moja_funkcja, 320, 200);
render_fractal(„rysunek.pnm”, 320, 200);
Pierwsza ustali nam niezbędne począt-
kowe parametry, takie jak wymiary oraz
postać funkcji iteracji, natomiast druga
wykona całą „czarną” robotę, czyli nary-
suje fraktal oraz zapisze go w formacie
PNM (więcej informacji o tym formacie
w ramce Format pliku PNM).
Ustalanie parametrów
początkowych
Treść funkcji
setup_nodes
to tylko pętla
„przebiegająca” po wszystkich węzłach
i ustalająca potrzebne parametry. Przed-
stawia się ona następująco:
for(int i=0;i<max_nodes;i++){
setup_iter_func(nodes[i],
S
moja_funkcja);
setup_render_size(nodes[i], w, h);
}
Ponieważ ustalanie parametrów to
proces łatwy dla poszczególnych serwe-
rów, więc nie ma potrzeby stosowania
wywołania o opóźnionej odpowiedzi
– wystarczy standardowy tryb synchro-
niczny. Treść funkcji
setup_render_size
to Listing 6. Nawet dla osób nie zna-
jących CORBY jest ona czytelna. Para-
metr
obj
reprezentuje zdalny obiekt
zapisany na liście
nodes
. W funkcji sto-
sujemy metodę
_request
z argumentem
w postaci ciągu znaków reprezentujących
nazwę metody, którą chcemy wywołać.
Następnie musimy określić parametry
metody. Mamy tylko dwa: szerokość (
w
)
oraz wysokość (
h
). Obiekt
Request
posia-
da szereg udogodnień, więc za pomocą
metody
add_in_arg
i przeciążonego
operatora
<<=
dodajemy dwa parametry.
Jak łatwo wywnioskować, metodą
set_
return_type
określamy typ wynikowy
tej metody i jest to wartość
void
. Ostatnia
istotna linia z Listingu 6 to
req->invoke()
,
czyli nakazanie wywołania zdalnej
metody. W podobny sposób postąpimy
w przypadku drugiej metody, czyli usta-
lenia treści funkcji ucieczki.
Rysujemy fraktal
Teraz omówimy ostatni element naszego
systemu – funkcję
render_fracal
, w której
następuje proces rysowania fraktala.
W pierwszej kolejności musimy „rozdać”
poszczególnym węzłom kolejne wiersze
do rysowania. Poniższa pętla jest spra-
wiedliwa (choć taka strategia nie zapew-
nia największej wydajności), ponieważ
stara się poszczególnym węzłom przy-
dzielać równą ilość wierszy (zmienna
nn
zawiera numer aktualnego węzła):
for(rows=0;rows<=h;rows++){
r.y=rows; r.from_x=0; r.to_x=w; r.m=0;
reqs.push_back(r); nn++;
if(nn>max_nodes-1) nn=0;
}
Zmienna
r
służy nam do zapamiętania
wartości obiektu wywołania (
Request
)
oraz numeru wiersza aktualnie ryso-
wanego. Zapamiętujemy także wymia-
ry poziome, czyli początek i koniec.
Zawsze są to wartości: zero oraz sze-
rokość wiersza, czyli cały wiersz. Treść
funkcji
begin_render_one_row
jest bliź-
niaczo podobna do
setup_render_size
z Listingu 6. Różni się ostatnią linią:
req->send_deferred();
oraz tym, że
w wywołaniu
set_return_type
jako
typ podajemy własnoręcznie zdefinio-
wany
TypeCode
na samym początku
funkcji
main
naszego klienta. Metoda
send_deferred
zapewnia, że klient po
jej wywołaniu nie będzie czekał, aż
zostanie ona wykonana, lecz przejdzie
do dalszych czynności.
Listing 7 zawiera ostatnią już
pętlę, sprawdzającą, czy żądania
zostały poprawnie obsłużone i czy
można odczytać dane. Pętla prze-
gląda listę żądań
reqs
i spraw-
dza, czy zmienna
m
jest ustawiona
na zero. Jeśli tak, oznacza to, że żąda-
nie zostało już poprawnie obsłużone
i nie trzeba się nim zajmować. W prze-
ciwnym przypadku funkcją
req_is_end
testujemy, czy żądanie zostało już
zakończone i jeśli tak, odbieramy dane
wiersza wywołaniem
get_data
, usta-
wiamy wartość flagi
m
i zwiększamy
zmienną
i
(zawiera ona ilość wierszy
już narysowanych). Cała pętla zakoń-
czy swoje działanie, gdy liczba wierszy
będzie większa od wysokości obrazu
pomniejszonego o jedność (pamiętajmy,
że pierwszy wiersz na numer zero).
Sam proces testowania, czy zada-
nie zostało zakończone, sprowadza się
w funkcji
req_is_end
do polecenia:
req-
>poll_response()
. Sprawdza ono, czy
żądanie zostało obsłużone. Jeśli tak się
stało, to jak wcześniej podałem,
get_data
Listing 5.
Uzyskanie listy wszystkich węzłów
root_ctx
->
list
(
0,
bl, bi
);
max_nodes
=
0
;
while
(
bi
->
next_one
(
b.out
()))
{
CORBA
::
ULong k
;
for
(
k
=
0
;
k
<
b
->
binding_name.length
();
k
++)
{
name
[
0
].
id
=
b
->
binding_name
[
k
].
id
;
name
[
0
].
kind
=
b
->
binding_name
[
k
].
kind
;
nodes.push_back
(
root_ctx
->
resolve
(
name
));
max_nodes
++;
}
}
Listing 6.
Funkcja ustalająca wymiary rysowanego fraktala na odległym obiekcie
void
setup_render_size
(
CORBA
::
Object_var obj, CORBA
::
Long
w, CORBA
::
Long
h
)
{
CORBA
::
Request_var req
=
obj
->
_request
(
„setup_render_size”
);
req
->
add_in_arg
() <<=
w
;
req
->
add_in_arg
() <<=
h
;
req
->
set_return_type
(
CORBA
::
_tc_void
);
req
->
invoke
();

40
maj 2004
klastry obliczeniowe
obiera dane. Kod odbierający dane jest
bardzo krótki:
CORBA::LongSeq row;
req->get_response();
req->return_value() >>= row;
for(int i=0;i<row.length();i++)
*(_row + i) = row[i];
Metoda
get_response
kończy proces
wywołania zdalnej metody i pozwala
„wyciągnąć” z metody
return_value()
dane
reprezentujące
nasz
wiersz.
Następnie przy pomocy prostej pętli
przepisujemy dane ze zmiennej
row
do
odpowiedniego miejsca w tablicy
img
.
Kończąc opis klienta, jeszcze słowo
o tablicy przechowującej poszczegól-
ne wiersze. Tablica
img
to jednowymia-
rowy wektor, w którym są umieszcza-
ne dane wierszy dzięki odpowiedniemu
adresowaniu. Adresowanie może wyda-
wać się „nieco dziwne”, ale pamiętajmy,
że pojedynczy piksel jest opisany trzema
bajtami, więc dlatego podczas adresowa-
nia współrzędne musimy mnożyć przez
trójkę.
Jak rysować fraktale?
Zanim zaczniemy cokolwiek rysować
w naszym rozproszonym systemie,
należy uruchomić usługę nazw. Zastosu-
jemy usługę nazw dostępną w serwerze
OmniORB:
omniNames -start -logdir /tmp
Takie polecenie oznacza, że usługa nazw
założy swój log w katalogu /tmp. Po para-
metrze -start opcjonalnie można umie-
ści numer portu, na którym działa usługa
nazw – domyślnie jest to 2809. Jeśli log
jest już założony, to wystarczy podać
tylko parametr z katalogiem, gdzie ten
log się znajduje:
omniNames -logdir /tmp
Następnym krokiem jest uruchomienie
serwerów
calc_node
, oczywiście na
jak największej ilości różnych kompu-
terów. Poszczególne serwery powin-
ny oczywiście posiadać inną nazwę:
./fc_server.py
wezel_1
. W kodzie
serwera znajduje się także adres usługi
nazw. W plikach znajdujących się na
CD/DVD adres ten odnosi się do kompu-
tera lokalnego, wiec w rzeczywistej sieci
trzeba go koniecznie zmienić.
Gdy serwery zostały juz uruchomio-
ne (do poprawnego działania aplikacji
wystarczy przynajmniej jeden), można
uruchomić klienta. W jego przypadku
także podajemy adres usługi nazw, np.:
ff_clc -ORBInitRef NameService=
S
corbaloc::127.0.0.1:2809/NameService
Klient po zakończonej pracy (miejmy
nadzieję bez kłopotów) powinien pozo-
stawić po sobie plik o nazwie rysu-
nek.pnm, w którym znajduje się rysunek
z fraktalem.
Na zakończenie
Łączny kod źródłowy systemu to zale-
dwie 10 kB. Jak widać, bardzo niskim
nakładem można dość szybko uzyskać
rozproszony system (a można go nawet
nazwać klastrem), zdolny do rysowa-
nia różnego typu fraktali. Stosując tego
rodzaju podejście można bardzo łatwo
rozdzielić każdy problem, pod warun-
kiem, że da się on podzielić na mniejsze
podproblemy, czyli w przypadku rysowa-
nia fraktali – na poszczególne wiersze.
Co jeszcze można unowocześnić
w naszym systemie? Oprócz funkcji itera-
cji, warto by było wprowadzić dodatkową
funkcję kolorującą. Można również wpro-
wadzić znacznie wygodniejszego klienta
opartego np. o biblioteki QT bądź GTK+
– serwer MICO współpracuje przecież
z tymi bibliotekami bez większych pro-
blemów. Zamiast stosowania oddzielnego
serwera CORBY, można także napisać
klienta dla systemu OmniORB – mody-
fikacji nie będzie zbyt wiele. Będą one
głownie dotyczyć definicji typu wiersza,
jaki jest zwracany przez zdalną metodę
render_one_row
.
Zachęcam do modyfikacji przedsta-
wionego systemu, szczególnie te osoby,
które interesują się technologią CORBA.
Na podstawie takiego systemu można
zdobyć wiele cennych doświadczeń.
W Internecie:
– Strona domowa języka Python:
http://www.python.org/
– Strona projektu OmniORB:
http://omniorb.sourceforge.net/
– Strona projektu MICO:
http://www.mico.org/
– Strona nieaktualizowana, ale
zawierająca wiele cennych infor-
macji o fraktalach:
http://spanky.triumf.ca/
– Więcej informacji o fraktalach:
http://www.fractalus.com/ifl/
Listing 7.
Pętla odbierająca wiersze od poszczególnych węzłów
/* cześć I -- odbieranie wyników*/
unsigned char
*
img
=
new unsigned char
[(
w
+
1
)*(
h
+
1
)*
3
];
vector
<
TRequest
>::
iterator reqsIter
;
i
=
0
;
while
(
i
< (
h
-
1
))
{
reqsIter
=
reqs.begin
();
while
(
reqsIter
!=
reqs.end
())
{
r
= *
reqsIter
;
if
(
r.m
==
0
||
req_is_end
(
r.req
)==
1
)
{
get_data
(
r.req,
(
img
+ (
r.y
*
w
*
3
)));
r.m
=
1
;
i
++;
}
reqsIter
++;
}
}
/* część II -- zapis danych do pliku*/
for
(
x
=
0
;
x
<
w
;
x
++)
{
fprintf
(
f_img,
„%d
\n
”,
*(
img
+ ((
y
*
w
*
3
) + (
x
*
3
))));
fprintf
(
f_img,
„%d
\n
”,
*(
img
+ ((
y
*
w
*
3
) + (
x
*
3
)+
1
)));
fprintf
(
f_img,
„%d
\n
”,
*(
img
+ ((
y
*
w
*
3
) + (
x
*
3
)+
2
)));
}
delete
[]
img
;
Wyszukiwarka
Podobne podstrony:
05 Normalizacja struktury bazy danych (AC)
05. Access - zadania, Bazy danych-materiały, Acces
2004 05 Sybase SQL Anywhere Studio 9 0 [Bazy Danych]
2004 09 Kexi bazy danych [Bazy Danych]
24 05 2010 B&K, Bazy Danych 10 11 12
24.05.2010 B&K Bazy Danych 10 11 12
ROZPROSZONE BAZY DANYCH - ćwiczenia, informatyka
Obiektowe bazy danych rozproszenie
05 Bazy danych
Rozproszone bazy danych
wykład 1 rozproszone bazy danych, RSZBD
2004 09 Kexi bazy danych [Bazy Danych]
1 Tworzenie bazy danychid 10005 ppt
bazy danych II
więcej podobnych podstron