FIZYKA

Magnetyzm – Zadania -

Rozwiązania

ciesiolek

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Zadanie 1

Treść:
Oblicz natężenie pola magnetycznego w środku kwadratu o boku a, utworzonego
przez cztery nieskończenie długie przewodniki z prądem.
Dane:
I - prąd płynący
przez
przewodniki
a - długość boku
danego kwadratu

Szukane:
H

c

=?

Wzory:
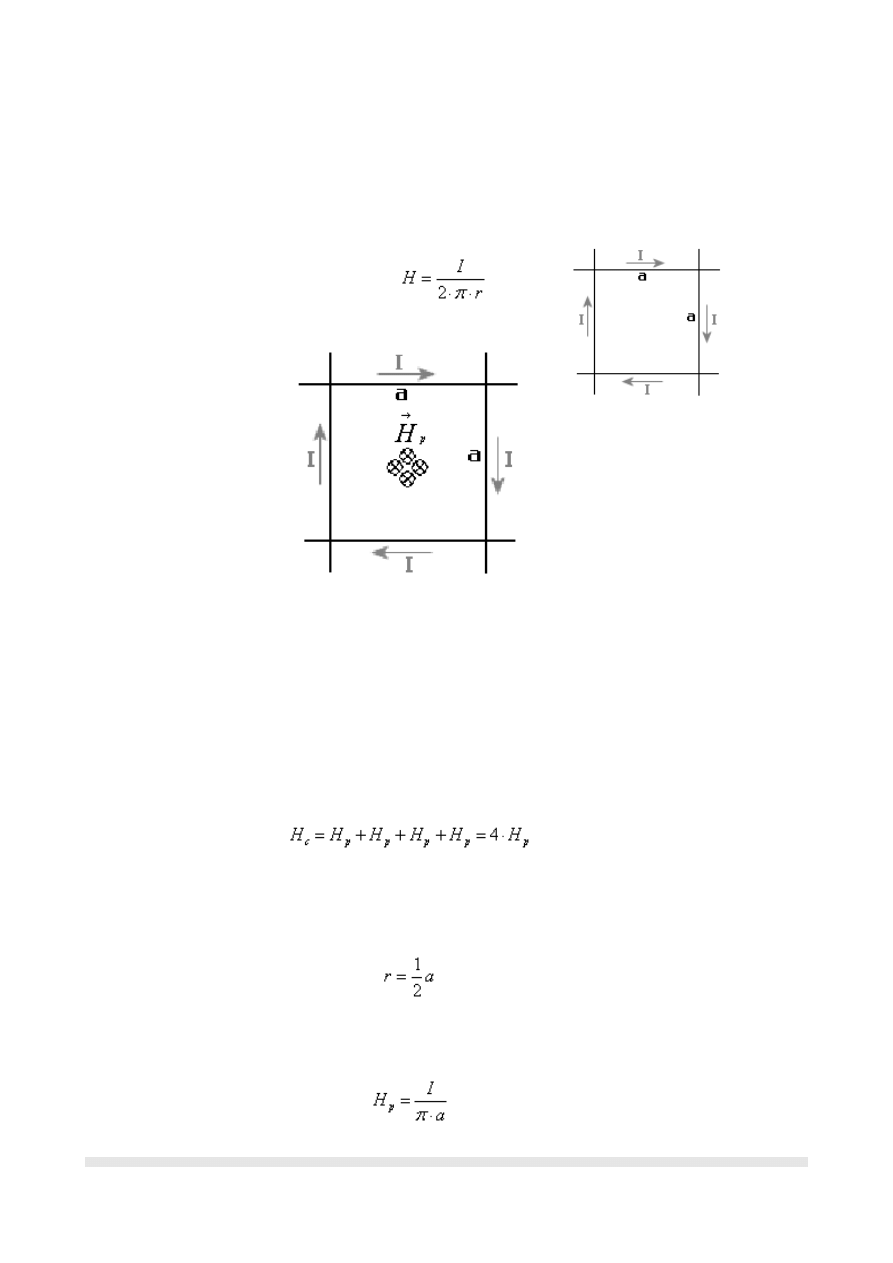
1. Natężenie pola magnetycznego w odległości r
od nieskończenie długiego przewodnika przez
który prepływa prąd o natężeniu I

Rysunek:

Rozwiązanie:
Do obliczenia natężenia pola magnetycznego należy umieścić w przestrzeni wektory H

p

pochodzące od poszczególnych przewodników.
Korzystamy przy tym zasady prawej ręki, gdzie kciuk wskazuje kierunek prądu, a
zakrzywione palce pokazują kierunek wektorów pola magnetycznego.
Powyższy rysunek przedstwia te wektory i widzimy, że są one zwrócone w jedną stron -
za rysunek. Są one idealnie pośrodku kwadratu, lecz dla wyrazistości rysunku są one
blisko siebie. Dla przejrzystości zaznaczony jest tylko jeden wektor H

p

.

Wiemy oczywiście, że wektory możemy dodawać, więc całkowite natężenie pola będzie
sumą poszczególnych wektorów H

p

:

Aby obliczyć pojedyncze pole magnetyczne H

p

skorzystajmy z podanego na początku

wzoru. W naszym przypadku odległością od przewodnika jest

Tak więc otrzymujemy:

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Ostatecznym wzorem, a zarazem odpowiedzią na zadanie będzie:

Zadanie 2

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Treść:
Cząstka α wpada w pole magnetyczne o indukcji B=0.02T prostopadle do
kierunku wektora indukcji B i zatacza krąg o promieniu r=0.2m. Oblicz energię
cząstki (w J i keV).
Dane:
B = 0,02T
r = 0,2 m
e = 1,6

.

10

-19

C

q

α

= 2e

m

α

= 6,644

.

10

-27

kg

1eV = 1,6

.

10

-19

J

Szukane:
E = ? (w J i keV)

Wzory:
Siła dośrodkowa

Siła Lorenza

Energia kinetyczna

Energia kondensatora

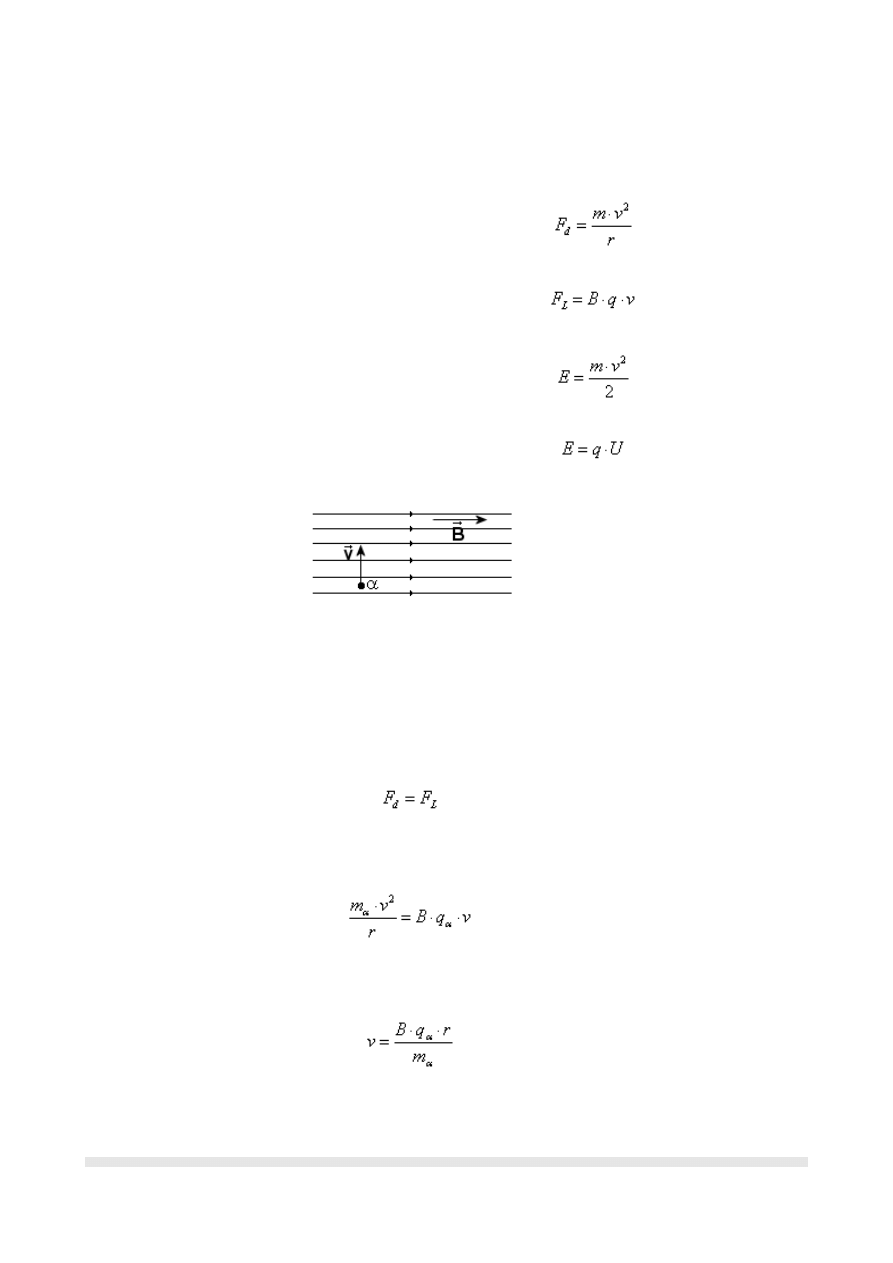
Rysunek:

Rozwiązanie:
Skąd się bierze zorza polarna? Pokrótce dlatego, że Ziemia posiada własne pole
magnetyczne (niezbędne dla życia), które naładowane cząsteczki pochodzące ze Słońca
"ściąga" na bieguny.
Tak samo zachowuje się cząstka α w naszym zadaniu, która wpada w pole magnetyczne
o idukcji B. Mając prędkość v zatacza ona krąg o promieniu r.
Siłą zakrzywiającą jest siła Lorenza. Możemy to przedstawić następująco:

czyli:

Skracamy jedno v i wyliczamy prędkość tej cząstki:

Prędkość nie jest tak duża, że trzeba używać wzorów relatywistycznych, dlatego

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

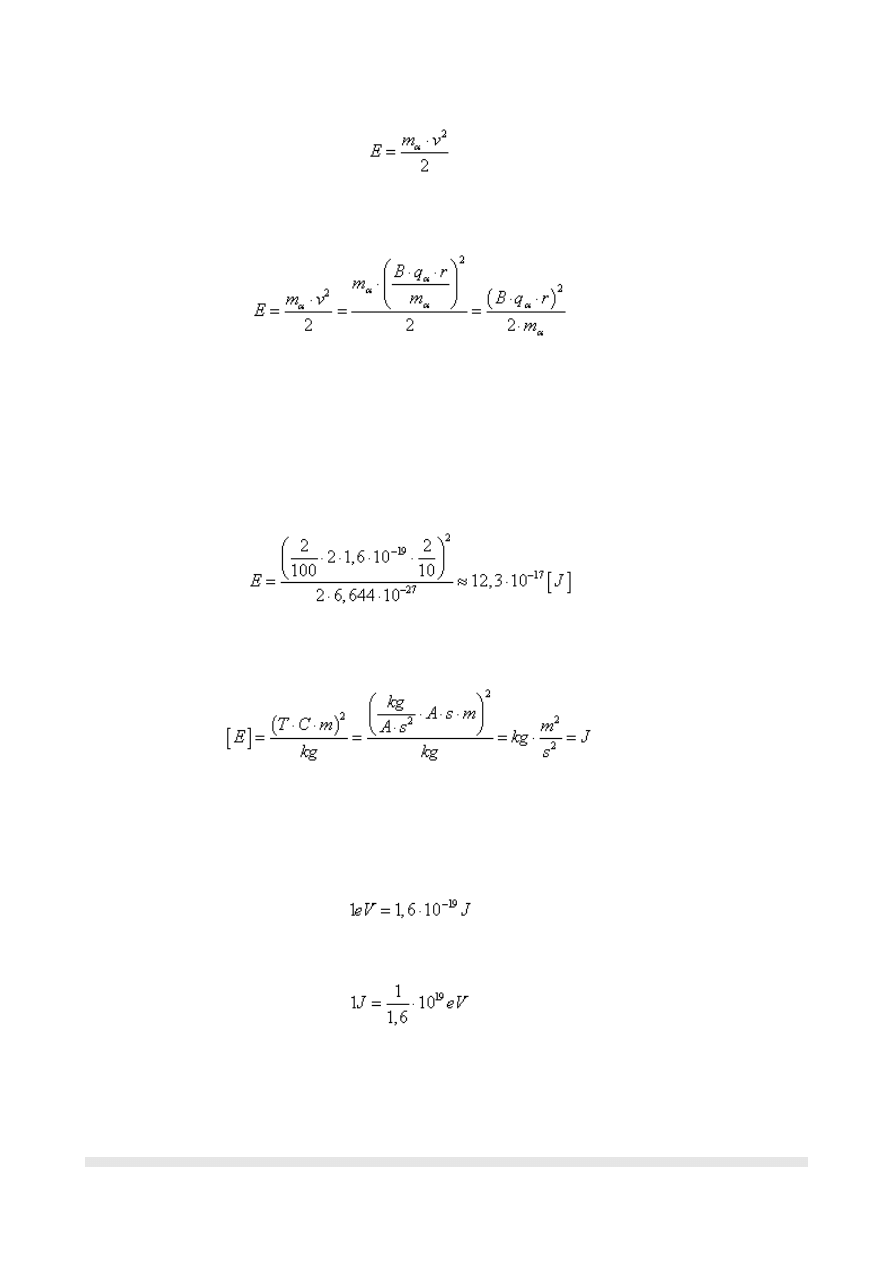
użyjemy zwykłego wzoru na energię:

Podstawiając otrzymaną prędkość dostajemy:

Tak otrzymaliśmy ostateczny wzór na energię tej cząstki. Wiemy, że cząstka α jest po
prostu jądrem atomu helu. Tak więc posiada 2 protony i 2 neutrony.
Z tego wnioskujemy, że masa jest równa w przybliżeniu 4 masom protonu (dla
dokładności obliczeń masę cząstki odczytujemy z tablic). Jeśli chodzi o ładunek to łatwo
się domyślamy, że wyniesie q=+2e.
Teraz już mamy wszystko, aby obliczyć energię. Na początku użyjmy podstawowych
jednostek układu SI (czyli ładunek będzie w C):

Sprawdźmy jeszcze jednostkę:

Aby obliczyć energię w eV musimy znaleźć związek między eV oraz J. Skorzystajmy
wpierw na wzór podany powyżej na energię przejścia ładunku q przez potencjał U.
Energia ta jest równa 1J, gdy ładunek będzie równy 1C (korzystamy tutaj z energii
kondensatora) . A więc przy przejściu tego ładunku przez potencjał 1U więc stwierdzamy,
że:

czyli:

Energia wyniesie więc:

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Energia cząstki α wynosi E=12,3

.

10

-17

J (0,77 keV).

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Zadanie 3

Treść:
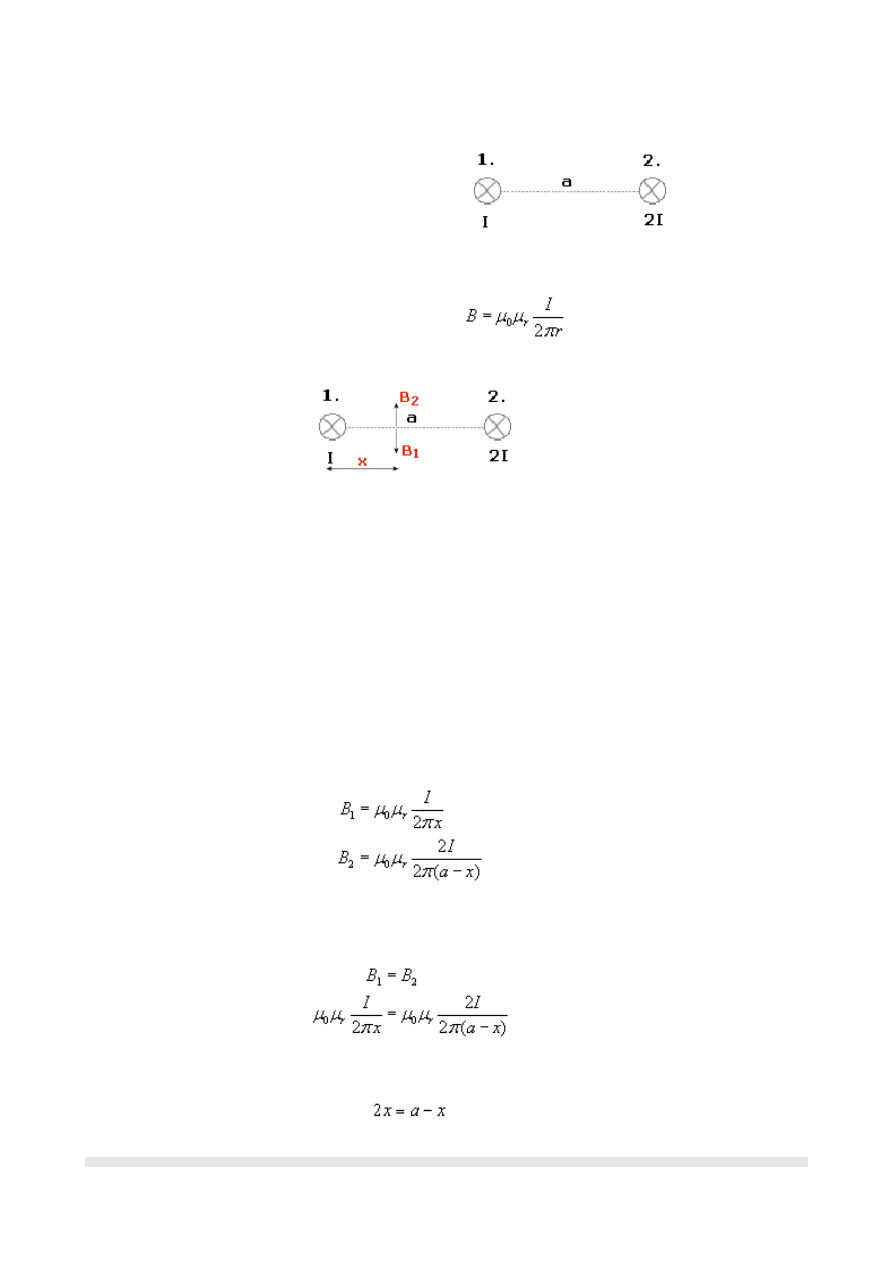
W dwóch długich, równoległych i ustawionych do
płaszczyzny rysunku przewodnikach płyną prądy
w tych samych kierunkach. W jakiej odległości od
pierwszego przewodnika indukcja magnetyczna
jest równa zero?
Dane:
a
I

1

= I

I

2

= 2I

Szukane:
x - odległość od
pierwszego
przewodnika,
gdzie indukcja
się równoważy

Wzory:
1. Indukcja w odległości r od przewodnika, w
którym płynie prąd o natężeniu I

Rysunek:

Rozwiązanie:
Rozwiązanie polega na znalezieniu miejscu, gdzie indukcja magnetyczna od pierwszego
przewodnika równoważy indukcję od drugiego przewodnika.
Rozważamy układ i stwierdzamy, że te miejsce znajduje się na przerywanej linii na
rysunku (odległość między dwoma punktami jest zawsze najmniejsza na prostej łączącej
te punkty).

Aby określić kierunek i zwrot wektora indukcji pola korzystamy z reguły prawej ręki.
Przez oba przewodniki przepływa prąd skierowany "za kartkę" (czyli monitor :)). Wyobraź
sobie ten przewodnik, złap go prawą ręką kciukiem wskazując kierunek prądu (za
monitor). Pozostałe palce wskazują teraz kierunek wektora indukcji.

Indukcja B

1

i B

2

mają postać (wykorzystujemy wzór pierwszy, podstawiając odpowiednie

dane):

Ponieważ w naszym rozpatrywanym punkcie, indukcja wypadkowa wynosi zero,
stwierdzamy więc, że:

Skracamy, co się da i mnożymy "na krzyż":

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Ostatecznie:

Szukanym miejscem jest punkt oddalony od pierwszego przewodnika na odległość x =
a/3.

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Zadanie 4

Treść:
Dwa przewodniki kołowe o promieniach r i 2r umieszczone są w
jednorodnym polu magnetycznym B prostopadłym do
płaszczyzn przewodników (rys.). Ile wynosi strumień indukcji
magnetycznej przenikający przez powierzchnię między
przewodnikami?
Dane:
r
2r
B

Szukane:
Φ = ?

Wzory:
Strumień pola
magnetycznego

Rozwiązanie:
Strumień pola magnetycznego Φ o indukcji B przez powierzchnię o polu ΔS definiujemy
jako:

gdzie α oznacza kąt, jaki tworzy wektor indukcji pola magnetycznego z prostą
prostopadłą do powierzchni ΔS.
Nasza powierzchnia ΔS to powierzchnia pierścienia. Otrzymamy ją poprzez odjęcie pola
koła S

2

o promieniu r od pola powierzchni koła S

1

o promieniu 2r.

gdzie:

W zadaniu jest napisane, że przewodniki są umieszczone w polu magnetycznym
prostopadle do wektora B. Oznacza to, że prosta prostopadła do powierzchni ΔS, jaką
tworzą te dwa przewodniki, jest nachylona do wektora indukcji B pod kątem prostym,
czyli α=90

0

. Dzięki temu:

Podstawiając po kolei wyszystko co wyżej zostało napisane do pierwotnego wzoru,
otrzymujemy:

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

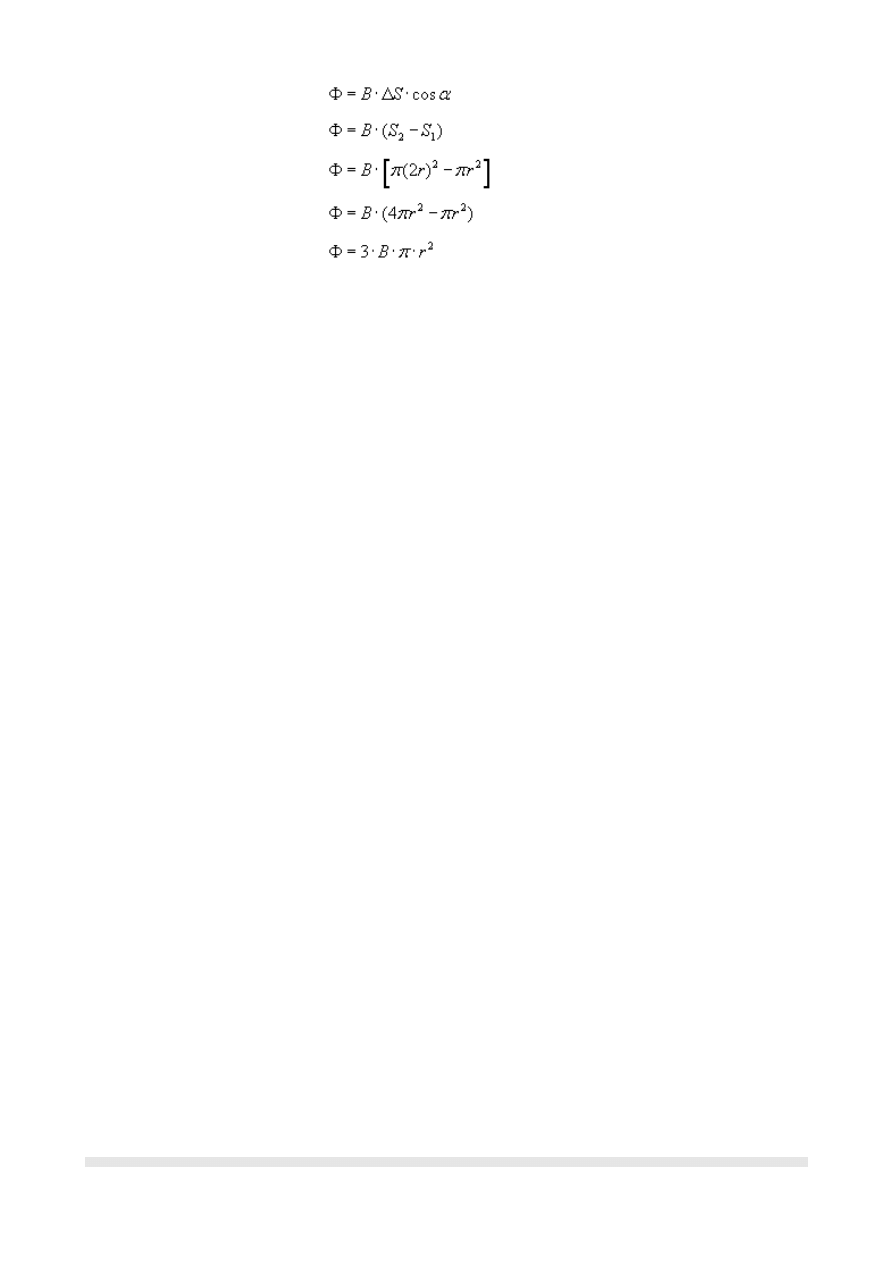
Strumień indukcji magnetycznej przenikającej przez powierzchnię między przewodnikami
(czyli pierścienia) wynosi 3Bπr

2

.

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Zadanie 5

Treść:
Ramka kwadratowa o boku a=10cm jest umieszczona prostopadle do linii sił
jednorodnego pola magnetycznego o indukcji B

1

=0.5T. Ile była równa siła

elektromotoryczna indukcji, jeżeli indukcja pola magnetycznego zmalała
jednostajnie w czasie t=0.04s do wartości B

2

=0.1T?

Dane:
a = 10 cm = 0.1 m
B

1

= 0.5 T

B

2

= 0.1 T

t = 0.04 s

Szukane:
ε = ?

Wzory:
1. Siła elektromotoryczna (prawo
Faradaya)

2. Strumień pola magnetycznego

Rozwiązanie:
Prawo Faradaya mówi nam, że siła elektromotoryczna SEM zależy od zmiany strumienia
w czasie. Potrzebujemy zatem wyznaczyć zmianę strumienia w naszym znanym czasie
t.
Strumień pola magnetycznego Φ o indukcji B przez powierzchnię o polu ΔS definiujemy
jako:

gdzie α oznacza kąt, jaki tworzy wektor indukcji pola magnetycznego z prostą
prostopadłą do powierzchni ΔS.
Zatem prawo Faradaya (czyli wzór na szukaną siłę elektromotoryczną) możemy zapisać:

W naszym przypadku powierzchnią ΔS jest powierzchnia, jaką tworzy ramka kwadratowa
o boku a:

W zadaniu jest napisane, że ramka jest umieszczona w polu magnetycznym prostopadle
do wektora B. Oznacza to, że prosta prostopadła do powierzchni ΔS jest nachylona do
wektora indukcji B pod kątem prostym, czyli α=90

0

. Dzięki temu:

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Zmiana indukcji pola magnetycznego ΔB jest różnicą pomiędzy wartością końcową pola
indukcji B

2

a wartością początkową B

1

Korzystając zatem ze wszystkich powyższych równań otrzymujemy:

Na koniec sprawdzimy poprawność jednostki:

Siła elektromotoryczna indukcji była równa 0,1 V.

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Zadanie 6

Treść:
Wartość indukcji jednorodnego pola magnetycznego wynosi B=2T. W polu tym
porusza się przewodnik o długości l=0.4m z prędkością v=50m/s. Wektory
prędkości i indukcji pola magnetycznego B są do siebie prostopadłe, a wektor
prędkości jest prostopadły do przewodnika. Oblicz wartość SEM powstałej na
końcach przewodnika.
Dane:
B = 2 T
l = 0.4 m
v = 50 m/s

Szukane:
ε = ?

Wzory:
Prawo Faradaya (siła
elektromotoryczna)

Droga przebyta ruchem
jednostajnym

Rozwiązanie:
Prawo Faradaya mówi nam, że siła elektromotoryczna SEM zależy od zmiany strumienia
w czasie.
Strumień pola magnetycznego Φ o indukcji B przez powierzchnię o polu ΔS definiujemy
jako:

gdzie α oznacza kąt, jaki tworzy wektor indukcji pola magnetycznego z prostą
prostopadłą do powierzchni ΔS.
Zatem prawo Faradaya możemy zapisać:

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

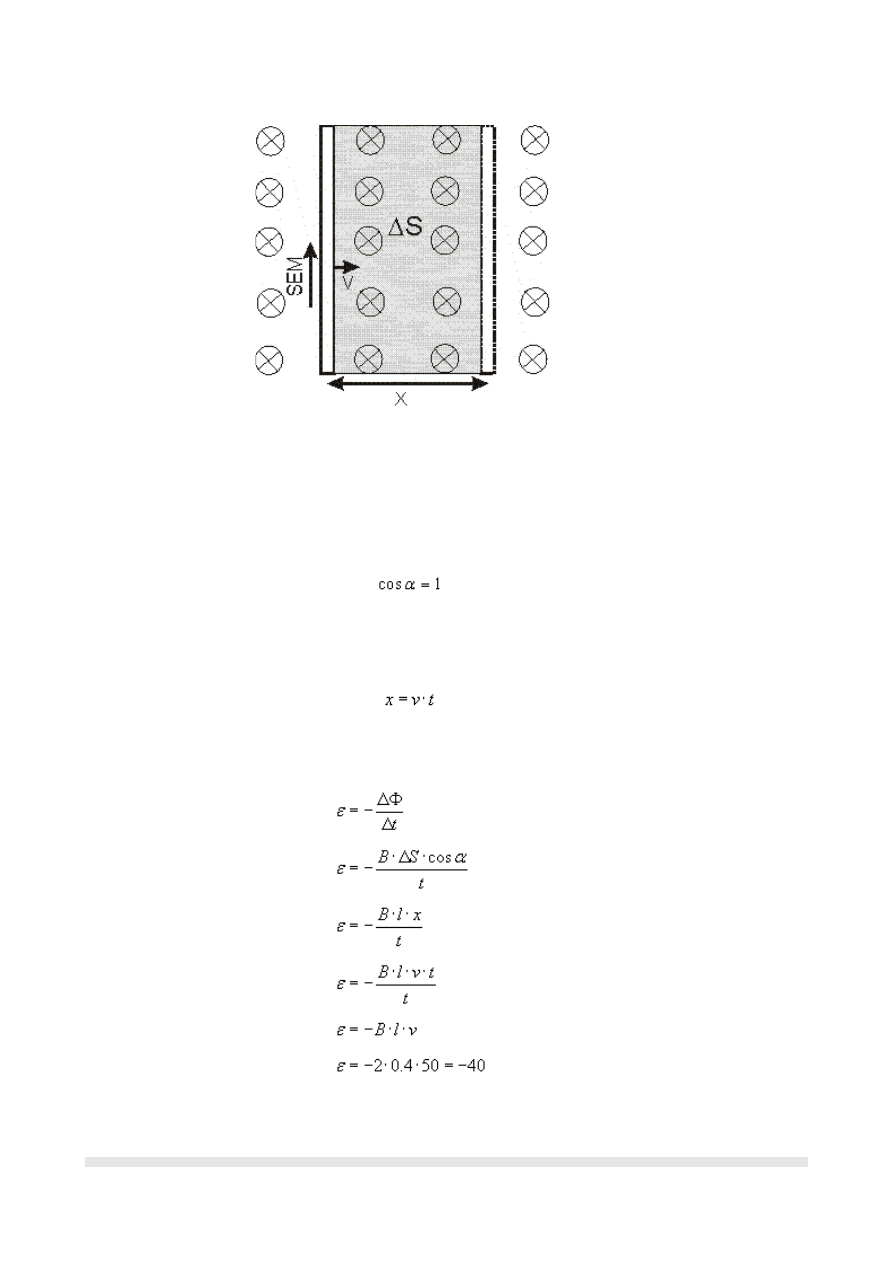
Rozpatrzmy rysunek opisujący sytuację:

Przewodnik poruszając się z prędkością v przemieszcza się o odległość x, czyli
przewodnik zakreśla pole ΔS=xt.
W zadaniu jest napisane, że przewodnik jest umieszczony w polu magnetycznym
prostopadle do wektora B. Oznacza to, że prosta prostopadła do powierzchni ΔS jest
nachylona do wektora indukcji B pod kątem prostym, czyli α=90

0

. Dzięki temu:

Pole powierzchni, które przebywa przewodnik to prostokąt o bokach l i x. Droga x jest to
droga w ruchu jednostajnym, czyli:

Podstawiając wszystko co wiemy do prawa Faradaya, otrzymujemy:

Na koniec sprawdźmy jednostkę:

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.

Na końcach przewodnika powstanie siła elektromotoryczna o wartości 40 V. Znak minus
świadczy tylko i wyłącznie o kierunku wektora siły elektromotorycznej.

Tak! Ja za to wszystko zapłaciłem! - ciesiolek, A.D. 2008.