Numeryczne Obliczenia Inżynierskie

NOI wykład 4

Materiały przygotowane dla studentów Wydziału Mechanicznego – Politechniki Opolskiej

przez: dr inż. Jacka Wydrycha

Program VBA złożony jest z instrukcji (rozkazów), które w
procesie kompilacji przetwarzane są na kod wykonywalny
zrozumiały dla procesora. Instrukcje te wykonywane są w
określonym

porządku

zdefiniowanym

przez

programistę.

Pojedynczą instrukcje możemy nazwać zdaniem języka VBA.
Zdanie takie musi być odpowiednio zbudowane i może zawierać
słowa kluczowe, wyrażenia, stałe, operatory oraz zmienne.

Pojedyncza instrukcja może np. zadeklarować zmienną, ustawić

Pojedyncza instrukcja może np. zadeklarować zmienną, ustawić
wartość lub wykonać określoną operację.

Instrukcje programu zorganizowane są w procedury, moduły
i projekty.

Procedura

jest bardzo ważną częścią programu, ponieważ

aby kod mógł być wykonany należy umieścić go w procedurze.
Jest to najmniejsza część kodu którą można uruchomić
niezależnie od innych części kodu. Procedura składa się z
przynajmniej jednej instrukcji umieszczonej między dwiema
specjalnymi instrukcjami: z których pierwsza z nich deklaruje
procedurę a ostatnia ją zamyka. Więcej informacji na temat

procedurę a ostatnia ją zamyka. Więcej informacji na temat
procedur znajdziesz na stronie Procedury.

Moduł

zawiera z jedną lub więcej procedur oraz sekcje

deklaracji w której umieszczamy instrukcje wspólne dla w
wszystkich procedur tego modułu. Możemy wyróżnić dwa
rodzaje modułów: moduł standardowy i moduł klasy.

Projekt

obejmuje wszystkie moduły, formularze, obiekty

aplikacji macierzystej dokumentu oraz sam dokument.

Programy VBA mogą być bardzo skomplikowane, mogą zawierać
wiele instrukcji i procedur rozmieszczonych w rożnych
modułach a nawet projektach. Najprostszy program składa
się z jednej procedury w której jest jedna instrukcja,
procedura ta umieszczona jest w module co daje nam już
cały projekt. Poniżej znajduje się kod takiego programu,
składa się on z jednej procedury o nazwie Powitanie, w której
umieszczona jest jedna instrukcja. Instrukcja ta wyświetla

umieszczona jest jedna instrukcja. Instrukcja ta wyświetla
okienko komunikatu i z napisem: Witam i życzę miłej zabawy.

Sub Powitanie()
MsgBox "Witam i życzę miłej zabawy"
End Sub

Procedura

- jest to najmniejsza część kodu która posiada

własną nazwę, jest to też najmniejsza część kodu którą
można uruchomić niezależnie od innych części kodu. Procedura
jest bardzo ważną częścią programu aby kod mógł działać
należy umieścić go w procedurze. Procedura składa się z
instrukcji deklarującej procedurę, linii kodu wykonywanych
wewnątrz procedury oraz instrukcji zamykającej.

wewnątrz procedury oraz instrukcji zamykającej.

Typy procedur:
Najogólniej procedury możemy podzielić na dwa typy tj.
podprogramy i funkcje.

Podprogram

- jest to podstawowy typ procedur języka

VBA. Procedurę deklarujemy za pomocą słowa kluczowego
Sub, instrukcja End Sub zamyka procedurę. Instrukcja
deklarująca procedurę kończy się parą nawiasów - można w
niej

umieszczać

parametry

podprogramu.

Jest

to

typ

procedury, który można uruchomić niezależnie od innych
procedur. Procedury tego typu wykonują akcje, lecz nie

procedur. Procedury tego typu wykonują akcje, lecz nie
zwracają wartości. Podprogram może wywołać inną procedurę.

Funkcja

-

procedura

deklarowana

za

pomocą

słowa

kluczowego

Function,

instrukcja

End

Function

kończy

procedurę. Funkcja może pobierać argumenty które są do niej
przekazywane np. przez procedurę wywołującą. Procedura
Function

jest

podobna

do

procedury

Sub,

jednak

w

przeciwieństwie do podprogramu zwraca wartość np. do
procedury która ją wywołała.

Poniżej

znajduje

się

przykład

prostego

podprogramu.

Procedura ta wykonuje tylko jedną czynność, wyświetla okienko
komunikatu z informacją aby użytkownik wprowadził wartość
numeryczną większą od Zera.

Sub BłędnaWartość()
MsgBox "Wprowadź wartość numeryczną większą od zera"
End Sub

Wywołanie podprogramu

:

Jest wiele sposobów uruchomienia podprogramu.
Podprogram można wywołać (uruchomić) z innego podprogramu.
Aby wywołać podprogram z innego podprogramu należy w
procedurze wywołującej wpisać instrukcję zawierającą jego
nazwę.
Jeżeli podprogram przez nas napisany nie posiada parametrów
możemy wywołać go tak jak uruchamia się makro. Będąc w
arkuszu Excela naciskamy kombinacje klawiszy Alt + F8, w

arkuszu Excela naciskamy kombinacje klawiszy Alt + F8, w
nowo

otwartym

oknie

wybieramy

nazwę

odpowiedniej

procedury a następnie przycisk Uruchom.
Możemy odpowiednią procedurę (bez parametrów) przypisać do
Przycisku z paska narzędzi Formularze.

Przykład funkcji:
Przykład funkcji jest również bardzo prosty. Nasza funkcja
oblicza pole kwadratu w którym długość boku kwadratu
określona jest przez parametr bok. Funkcja zwraca pewną
wartość. Aby funkcja mogła zwrócić wartość, wewnątrz funkcji
wartość ta musi zostać przypisana do nazwy tej funkcji.
W przykładzie poniżej do nazwy funkcji PoleKwadratu
przypisujemy wartość jako daje nam wynik mnożenia parametru
bok. Oczywiście wartość zwróconą przez funkcje możemy

przypisujemy wartość jako daje nam wynik mnożenia parametru
bok. Oczywiście wartość zwróconą przez funkcje możemy
wykorzystać w instrukcjach np. w procedurze wywołującej.

Function PoleKwadratu(bok)
PoleKwadratu = bok * bok
End Function

Wywołanie funkcji

:

Funkcje można wywołać (uruchomić) z podprogramu. Aby
wywołać funkcje z podprogramu w procedurze wywołującej do
zmiennej przypisujemy nazwę funkcji, oczywiście w nawiasach
podajemy też potrzebne argumenty. Funkcja zwraca wartość
dlatego poprzez przypisanie w procedurze wywołującej nazwy
funkcji do zmiennej to do tej zmiennej przypisujemy wartość
zwracaną przez podaną funkcje.
Innym sposobem wywołania funkcji jest uruchomienie jej z
poziomu arkusza Excela, poprzez wstawienie funkcji do

poziomu arkusza Excela, poprzez wstawienie funkcji do
komórki arkusza. Funkcje przez nas napisaną (umieszczoną w
module standardowym) wstawiamy do arkusza tak samo jak
każdą funkcje wbudowaną. Załóżmy ze chcemy wstawić
przedstawioną wcześniej funkcję PoleKwadratu.

Zaznaczamy dowolną komórkę Arkusza Excela np. H12.
Z Menu Wstaw wybieramy opcje Funkcja.
W nowo otwartym oknie z pola Kategoria funkcji: wybieramy
kategorie Użytkownika, następnie z pola Nazwa funkcji:
nazwę naszej funkcji PoleKwadratu i naciskamy OK (nazwy
pól w tym oknie mogą być trochę inne od podanych, zależy to
jaką wersję Excela posiadasz).
W następnym oknie wpisujemy argumenty funkcji, możesz tam

W następnym oknie wpisujemy argumenty funkcji, możesz tam
wpisać odpowiednie wartości lub nazwę komórki z której
wartości mają być pobierane np. jako argument wpisujemy B12,
naciskamy przycisk OK.
Jeżeli

jako

argument

podałeś

adres

komórki,

wpisz

przykładowe wartości do komórki B12 i przetestuj działanie
funkcji.

Parametry i argumenty

Parametr pełni role zmiennej i jest rozpoznawany wewnątrz

procedury.

Parametry

procedury

podajemy

deklarując

procedurę. Umieszczamy je w nawiasach po nazwie procedury.
Jeżeli procedura posiada kilka parametrów oddzielamy je
przecinkiem.

Argument zaś jest to wartość jaka przekazujemy do

parametru danej procedury. Argumenty podajemy np. w

Argument zaś jest to wartość jaka przekazujemy do

parametru danej procedury. Argumenty podajemy np. w
instrukcji wywołującej procedurę. W instrukcji wywołującej
procedurę

po

nazwie

procedury

podajemy

odpowiednie

argumenty

umieszczamy

je

w

nawiasach

i

oddzielając

przecinkiem

Sub ObliczPole()
Dim wartość, pole
wartość = InputBox("Podaj długość boku kwadratu do obliczenia pola
powierzchni")
If IsNumeric(wartość) = True Then
If wartość > 0 Then
pole = PoleKwadratu(wartość) ' wywołujemy funkcje PoleKwadratu.
MsgBox "Pole kwadratu wynosi " & pole

MsgBox "Pole kwadratu wynosi " & pole
Else
BłędnaWartość ' wywołujemy podprogram BłędnaWartość.
End If
Else
BłędnaWartość ' wywołujemy podprogram BłędnaWartość.
End If
End Sub

Zakres procedury

:

Zakres określa w których częściach programu procedura jest
widoczna i z jakich części programu można ją wywołać. Temat
zakresu omówię w dalszej części kursu po omówieniu tematu
Modułu. Nadmienię tylko że standardową procedura VBA
posiada zakres publiczny (z wyjątkiem procedury zdarzenia).
Zakres publiczny określa to że procedurę można wywołać

Zakres publiczny określa to że procedurę można wywołać
(uruchomić) z dowolnej części programu.

argument

- stała, zmienna lub wyrażenie przekazywane do

procedury,

komentarz

- dodany do kodu programu tekst, wyjaśniający

sposób działania kodu programu,

parametr

-

nazwa

zmiennej,

pod

którą

argument

przekazywany do pewnej procedury jest w tej procedurze
rozpoznawany. Zmienna otrzymuje przekazywany do procedury
argument, a jej zakres działania kończy się wraz z końcem
procedury.

właściwość

- opatrzony nazwą atrybut obiektu. Właściwości

właściwość

- opatrzony nazwą atrybut obiektu. Właściwości

definiują takie cechy obiektu, jak np. rozmiar, kolor i położenie
na ekranie, a także stan obiektu, na przykład to, czy jest on
aktywny czy nieaktywny. Właściwości możemy określać (zmieniać)
w oknie właściwości lub za pomącą języka Visual Basic.

zmienna

-

opatrzone

nazwą

miejsce

w

pamięci

do

przechowywania danych, które mogą ulegać modyfikacjom w
trakcie wykonywania programu. Każda zmienna zaopatrzona jest w
unikatową nazwę, która identyfikuje ją w obrębie danego zakresu.

Zasięg zmiennych

Zasięgiem zmiennej określa się moduły i procedury, w których
można ją zastosować.

Zasięg

Sposób deklarowania zmiennej w zasięgu

Pojedyncza procedura – zmienne lokalne

Zawarcie w procedurze instrukcji Dim lub Static

Pojedynczy moduł – zmienne
obowiązujące na obszarze całego modułu

Umieszczenie instrukcji Dim lub Private przed
pierwszą procedurą modułu

Wszystkie moduły – zmienne publiczne

Umieszczenie instrukcji Public przed pierwszą
procedurą modułu

Zmienna lokalna – jest zmienną deklarowaną wewnątrz
procedury. Zmienne lokalne mogą być używane wyłącznie w
procedurze, w której zostały zadeklarowane. Po zakończeniu
procedury zmienna lokalna przestaje istnieć i Excel zwalnia
zajmowaną przez nią pamięć.

Jeśli zależy na utrzymaniu przez zmienną przechowanej

wartości, należy zdeklarować ją przy użyciu słowa kluczowego
Static.

Jeśli zmienna ma być dostępna dla wszystkich procedur
modułu,

wystarczy

deklarację

zmiennej

umieścić

przed

pierwszą procedurą modułu (na zewnątrz wszystkich procedur
lub funkcji).

Dim CurrentChart As Chart

Dim Fname As String

Private Sub UserForm_Initialize()

Set CurrentChart =

ActiveSheet.ChartObjects(1).Chart
' Zapisanie wykresu w formacie GIF

' Zapisanie wykresu w formacie GIF

Fname = ThisWorkbook.Path &

Application.PathSeparator & "temp.gif"

CurrentChart.Export FileName:=Fname,

FilterName:="GIF"

ActiveSheet.ChartObjects(1).Delete

End Sub

Private Sub CloseButton_Click()

Unload Me

End Sub

Aby udostępnić zmienną wszystkim procedurom zawartym we
wszystkich modułach VBA projektu, należy na poziomie modułu
zadeklarować zmienną przy użyciu słowa kluczowego Public
zamiast instrukcji Dim.

Public CuurentRate As Long

Przesłanianie zmiennych

Przesłanianie zmiennych

Charakterystyka dobrych programów

Oto kilka cech uważanych za takie, które charakteryzują
dobry program.
• Poprawność (zgodność z wymogami użytkownika)
• Niezawodność (dobre dane wejściowe -> dobre wyniki)
• Przenośność (Łatwość instalacji na różnych komputerach)
• Łatwość konserwacji (Prosto napisany program łatwo
przystosować do różnych warunków pracy)

przystosować do różnych warunków pracy)
• Czytelność (Prostota jest jedną z najważniejszych cech
dobrych programów)
• Prawidłowe wykorzystanie zasobów (pamięci, dyski, itp),
szybkość

User-oriented aplikacja

Zadania realizowane z myślą o użytkowniku końcowym

Oto kilka ważnych kwestii związanych z projektowaniem, które
uwidaczniają się, gdy stopień funkcjonalności aplikacji staje się
coraz wyższy i nadchodzi moment pakowania i przesyłania
produktu:
• Testowanie – często zdarza się, że testowanie i usuwanie błędów
z aplikacji zajmuje taką samą ilość czasu, jak jej tworzenie,
• Zwiększanie odporności aplikacji:

• Blokowanie określonych komórek

• Blokowanie określonych komórek
• Ochrona całego skoroszytu
• Ukrywanie formuł określonych komórek
• Blokowanie obiektów arkusza
• Ukrywanie wierszy, kolumn, arkuszy i dokumentów
• Udostępnianie skoroszytu Excela w trybie tylko do

odczytu

• Przypisanie hasła
• Użycie dodatku chronionego hasłem

Zadania realizowane z myślą o użytkowniku końcowym

• Testowanie – często zdarza się, że testowanie i usuwanie
błędów z aplikacji zajmuje taką samą ilość czasu, jak jej
tworzenie,
• Tworzenie aplikacji intuicyjnej i estetycznie wyglądającej:

• Dążenie do zgodności (do okien dialogowych Excela)
• Dążenie do prostoty – błędem projektantów aplikacji

jest umieszczanie na pojedynczym ekranie lub w oknie
dialogowym zbyt wielu informacji

dialogowym zbyt wielu informacji

• Podział okien służących do wprowadzania danych
• Oszczędne używanie kolorów
• Kontrolowanie typografii i grafiki – formaty liczbowe,

zgodność kroju i rozmiaru czcionek oraz ramek

Określanie jakości walorów estetycznych jest bardzo
subiektywne. W razie wątpliwości należy zmierzać do prostoty
i przejrzystości

Zadania realizowane z myślą o użytkowniku końcowym

• Tworzenie systemu pomocy przeznaczonego dla użytkownika –
dokumentacje pomocy: papierowe i elektroniczne
• Dokumentowanie prac projektowych
• Przekazanie aplikacji użytkownikom
• Uaktualnianie aplikacji w razie konieczności

METODY CAŁKOWANIA NUMERYCZNEGO

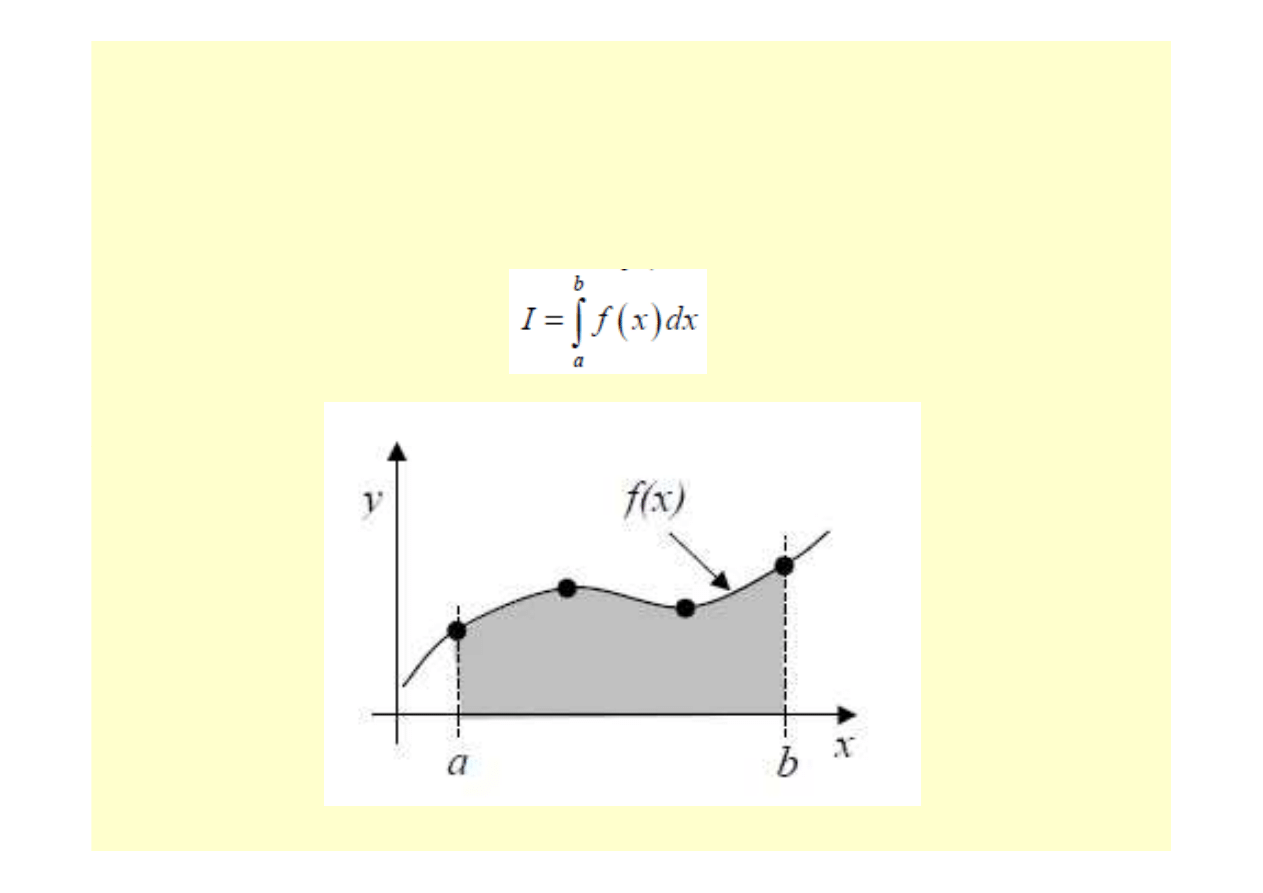
Zadanie całkowania numerycznego
Na podstawie znajomości wartości y

i

funkcji f(x) w punktach x

i

(narzuconych

lub

wybieranych)

wyznaczyć

wartość

I

całki

oznaczonej (kwadratury) z funkcji w przedziale <a,b>:

Zastosowania całek numerycznych
Wyznaczanie wielkości definiowanych całką
• Splot
• Wartość średnia, skuteczna
• Energia sygnału
• Pola powierzchni, objętości
• Prawdopodobieństwo na podstawie funkcji gęstości prawdopodobieństwa

Wartość przybliżona: odpowiadające im operacje sumacyjne na sygnałach
dyskretnych
W obliczeniach małej precyzji wystarczają proste metody prostokątów i
trapezów.

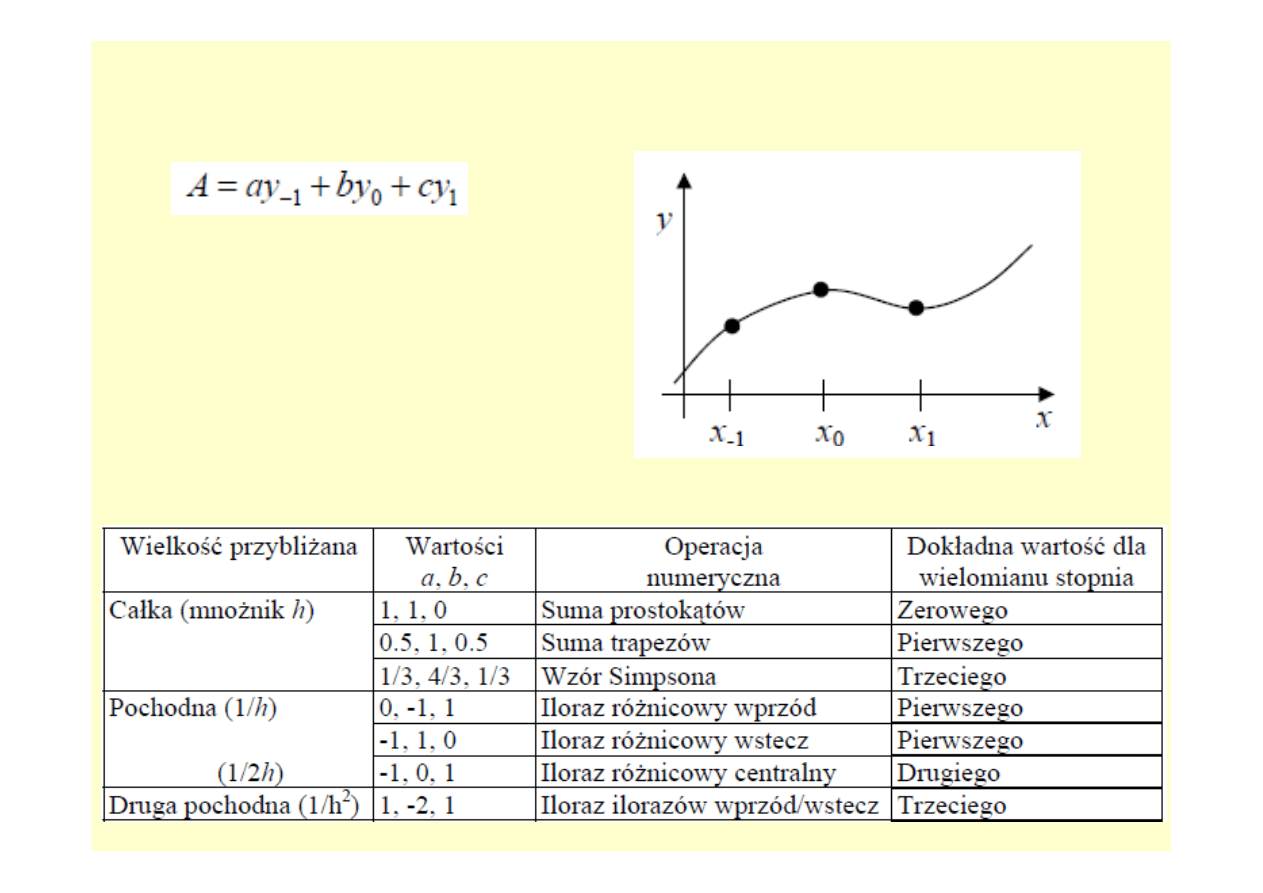
Jakie dobrać wartości współczynników ogólnego wyrażenia:

ż

eby wartość A przybliżała:

• całkę w przedziale <x

-1

, x

1

> ,

• pochodną w punkcie x

0

,

• drugą pochodną w punkcie x

0

Załóżmy punkty równoodległe z odstępem h (x

-1

=x

0

-h, x

1

=x

0

+h).

Metoda prostokątów

Metoda trapezów

Metoda parabol

(

)

∑

∑

=

−

=

+

=

n

i

i

n

i

i

h

,

x

f

h

A

1

1

1

5

0

( )

( )

( )















+

+

=

∑

∑

−

=

=

1

1

0

1

5

0

5

0

n

i

n

i

n

i

i

x

f

,

x

f

x

f

,

h

A

( )

(

)

( ) ( )















+

+

+

+

=

∑

∑

∑

−

=

−

=

=

1

0

1

1

0

1

2

5

0

4

6

1

n

i

n

n

i

i

i

n

i

i

x

f

x

f

h

,

x

f

x

f

h

A

Metoda 3/8 Simpsona

( )

(

)

(

)

( ) ( )















+

+

+

+

+

+

=

∑

∑

∑

∑

−

=

−

=

−

=

=

1

0

1

1

1

0

3

2

3

1

0

1

2

3

3

8

1

n

i

n

n

i

i

n

i

i

i

n

i

i

x

f

x

f

h

x

f

h

x

f

x

f

h

A

Zagadnienie przybliżonego obliczania całki oznaczonej

I f

( )

danej funkcji ciągłej f x

( ) w przedziale

[ , ]

a b

∫

=

b

a

x

x

f

f

I

d

)

(

)

(

(24)

często występuje w praktyce obliczeniowej, gdyż wyznaczanie funkcji pierwotnej jest bardzo trudne lub
wręcz niemożliwe, gdy funkcja

f x

( )

nie jest funkcją elementarną lub gdy funkcja

f x

( )

jest określona za

pomocą tablicy.

Zagadnienie przybliżonego obliczania całek można traktować jako aproksymację funkcjonału I innymi,
prostszymi do obliczenia funkcjonałami. W rachunku numerycznym muszą mieć one postać pozwalającą
na obliczenie ich wartości za pomocą skończonej liczby działań arytmetycznych. Wzory numeryczne
całkowania funkcji jednej zmiennej niezależnej nazywane są kwadraturami, funkcji wielu zmiennych
niezależnych - kubaturami.

niezależnych - kubaturami.

Istnieją różne rodzaje kwadratur. Najważniejsze z nich to:

- kwadratury interpolacyjne i aproksymacyjne,

- kwadratury Newtona-Cotesa,

- kwadratury Gaussa.

Mianem kwadratur interpolacyjnych lub aproksymacyjnych określamy kwadratury otrzymane przez
całkowanie wzorów interpolacyjnych lub aproksymacyjnych funkcji podcałkowej

f x

( ).

W szczególności

mogą to być wzory oparte na całkowaniu wielomianów interpolacyjnych Lagrange’a niskiego stopnia
lub też równań funkcji sklejanych.

Po scałkowaniu wielomianu interpolacyjnego Lagrange’a otrzymamy kwadraturę postaci

,

)

(

)

(

0

∑

=

=

n

i

i

i

x

f

A

f

Q

(25)

w której

x

i

są ustalonymi węzłami, a współczynniki

A

i

są określone wzorem

.

)

...,

,

1

,

0

(

)

(

n

i

x

x

A

b

n

=

ω

=

∫

d

(26)

.

)

...,

,

1

,

0

(

)

(

)

(

)

(

n

i

x

x

x

x

x

A

b

a

i

n

i

n

i

=

ω′

−

ω

=

∫

d

(26)

Dla wyznaczenia współczynników

A

i

zauważmy, że:

1) współczynniki

A

i

przy danym wyborze węzłów nie zależą od wyboru postaci funkcji

f x

( ),

2) wzór (25) jest dokładny dla wielomianu stopnia n.

Podstawiając więc

f x

x

k

n

k

( )

(

, , ..., )

=

=

0 1

we wzorze (5.25) otrzymamy układ

n

+

1

równań liniowych:























=

=

=

∑

∑

∑

=

=

=

,

..

..........

..........

,

,

0

0

1

0

0

n

i

n

i

i

n

n

i

i

i

n

i

i

x

A

Q

x

A

Q

A

Q

(27)

gdzie

,

)

...,

,

1

,

0

(

1

1

1

n

k

k

a

b

x

x

Q

k

k

b

a

k

k

=

+

−

=

=

+

+

∫

d

z którego można obliczyć współczynniki:

A

A

A

n

0

1

,

, ...,

.

Wyznacznik macierzy współczynników układu

(27) jest wyznacznikiem Vandermonda.

Prostym przykładem kwadratury interpolacyjnej tego rodzaju może być kwadratura postaci

.

6

5

2

1

6

1

2

1

0

1

0













+













+













=

∫

f

A

f

A

f

A

x

y d

(28)

Układ (27) dla

n

=

2

oraz:

∫

∫

∫

=

=

=

1

0

2

1

0

1

0

3

1

,

2

1

,

1

x

x

x

x

x

d

d

d

redukuje się do układu następującego:

+

A

A

A

0

1

2

1

+

=

,

+

A

A

A

A

A

A

A

A

A

0

1

2

0

1

2

0

1

2

1

1

6

1

2

5

6

1

2

1

36

1

4

25

36

1

3

+

=

+

+

=

+

+

=

,

,

.

Stąd:

A

A

A

0

1

2

3

8

1

4

3

8

=

=

=

,

,

i ostatecznie

.

6

5

3

2

1

2

6

1

3

8

1

)

(

1

0

























+













+













=

∫

f

f

f

x

x

f

d

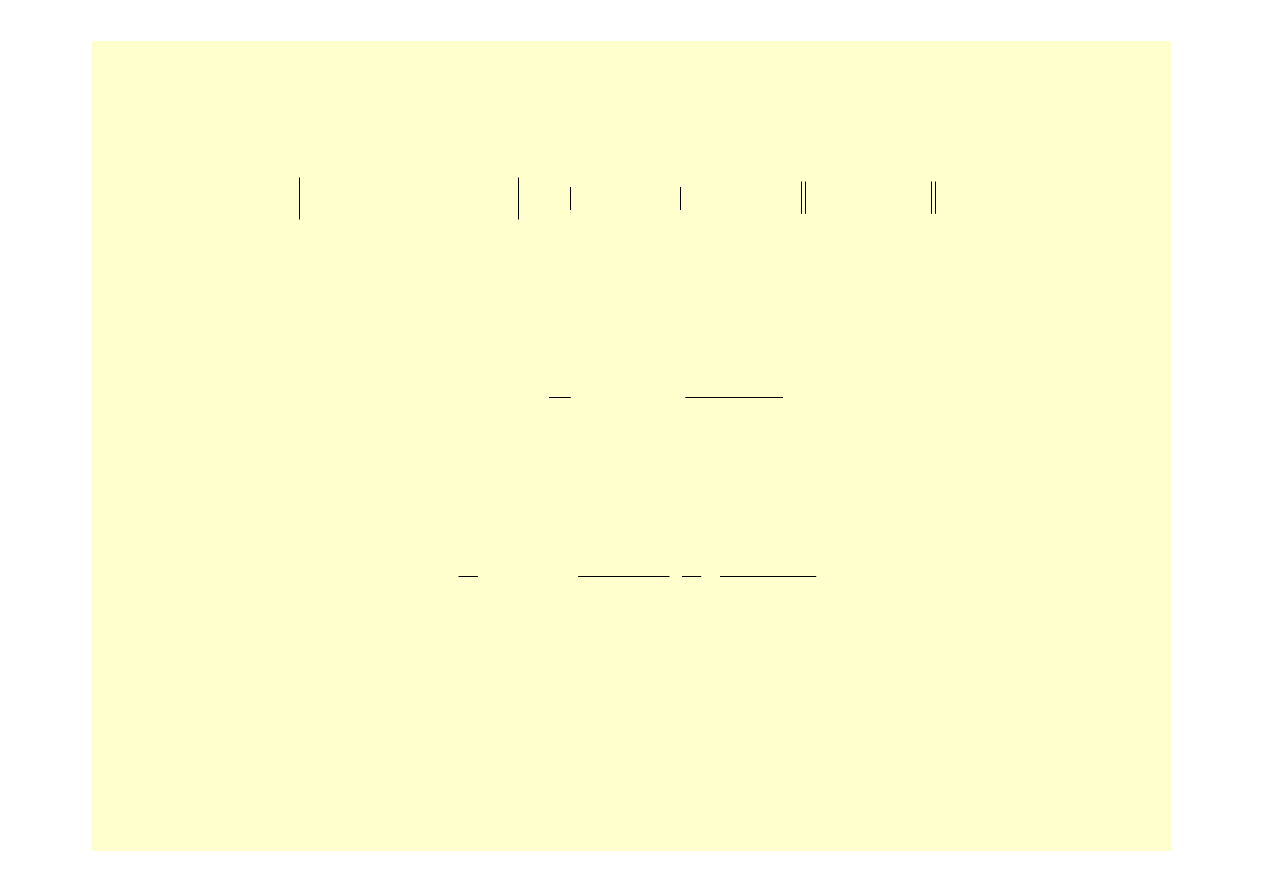
Dokładność obliczania całki (24) za pomocą kwadratur interpolacyjnych lub aproksymacyjnych zależy
od oszacowania dokładności przybliżenia funkcji

f x

( )

funkcją

F x

( )

∫

∫

∫

≤

−

≤

−

b

a

b

a

b

a

x

x

f

x

F

x

x

f

x

x

F

d

d

d

)

(

)

(

)

(

)

(

.

)

(

)

(

)

(

]

,

[ b

a

x

f

x

F

a

b

C

−

−

(29)

Wynika stąd, że w wielu przypadkach szczególnie przydatne mogą okazać się kwadratury interpolacyjne
lub aproksymacyjne oparte na całkowaniu równań funkcji sklejanych. Przy wykorzystaniu równań
wielomianowej funkcji sklejanej trzeciego stopnia otrzymujemy

.

24

)

(

2

)

(

1

3

1

1

∫

∑

=

−

−













+

−

+

=

b

a

n

i

i

i

i

i

i

i

h

M

M

y

y

h

t

t

S

d

(30)

W podobny sposób, po scałkowaniu równania hiperbolicznej funkcji sklejanej w połączeniu z układem
równań, dostajemy

.

sinh

cosh

1

2

)

(

2

)

(

1

2

1

1

∫

∑

=

σ

σ

−

−

























σ

σ

σ

−

+

σ

+

−

+

=

σ

b

a

n

i

i

i

i

i

i

i

i

i

h

h

h

M

M

y

y

h

t

t

S

d

(31)

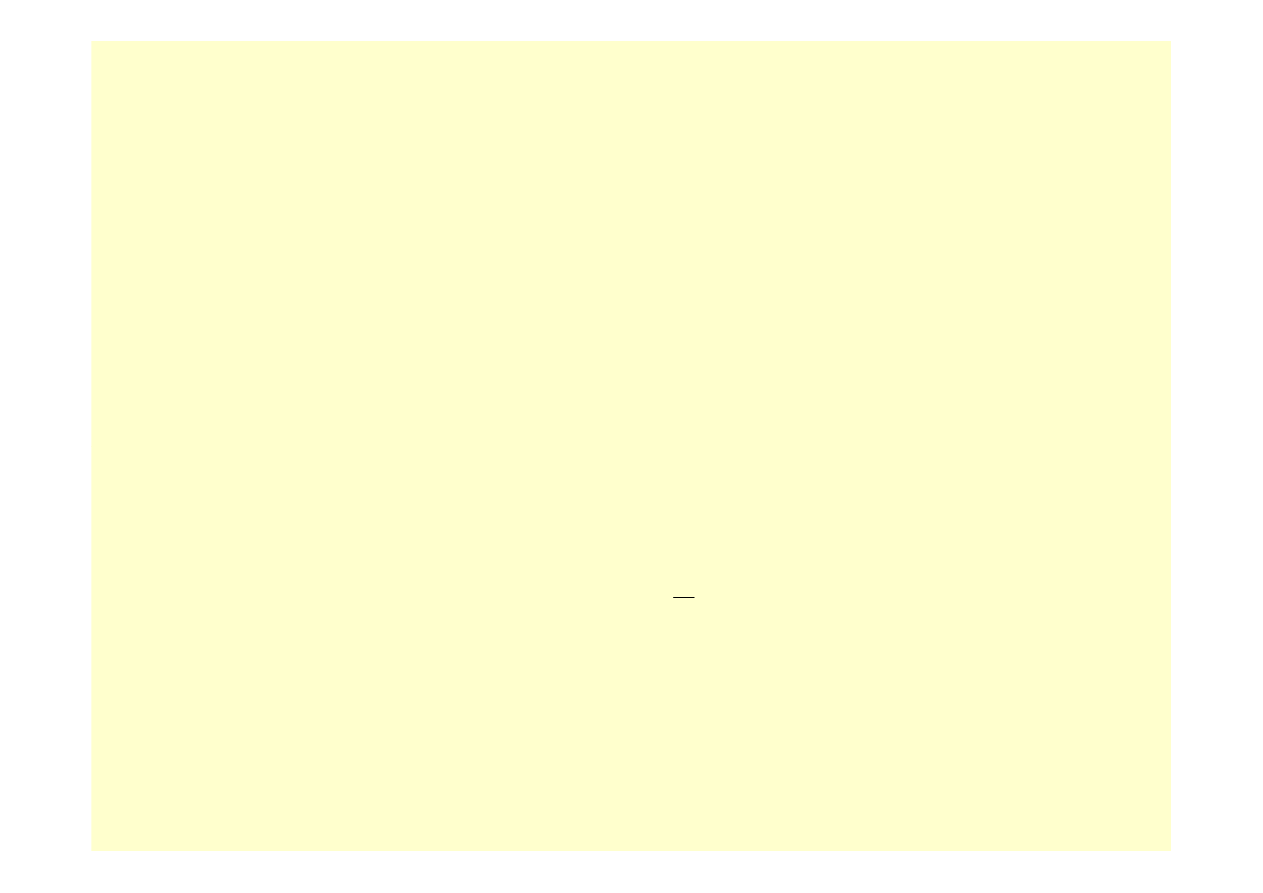
Kwadraturami Newtona-Cotesa nazywamy kwadratury postaci (25), otrzymane przez całkowanie

wielomianów interpolacyjnych opartych na równoodległych węzłach

.

,

...

,

,

1

0

b

h

n

a

x

h

a

x

a

x

n

=

+

=

+

=

=

(32)

Współczynniki kwadratur Newtona-Cotesa można wyznaczyć drogą całkowania wielomianu

interpolacyjnego Lagrange’a lub też, stosowaną w rozdziale poprzednim, metodą rozwijania funkcji

y

f x

=

( )

w szeregi Taylora względem punktu

x

0

.

Dla zastosowania drugiej z tych możliwości rozważymy zależność wynikającą ze wzorów (24)
i (25)

∫

∑

+

=

n

x

n

h

n

R

y

A

x

x

f

,

)

(

)

(

d

(33)

∫

∑

=

+

=

x

i

i

i

h

n

R

y

A

x

x

f

0

0

,

)

(

)

(

d

(33)

gdzie

)

( h

n

R

jest błędem przybliżenia. Po scałkowaniu rozwinięcia danej funkcji

f x

( )

w szereg Taylora

f x

y

y

x

x

y

x

x

( )

(

)

!

(

)

...

=

+ ′

−

+

′′

−

+

0

0

0

0

0

2

2

i podstawieniu rozwinięć

y

y

ih y

ih

y

ih

y

i

=

+

′ +

′′ +

′′′ +

0

0

2

0

3

0

2

3

( )

( )

!

( )

!

...

uzyskujemy związek

(

)

(

)

!

(

)

!

...

...

nh y

nh

y

nh

y

A y

A

y

h y

h

y

0

2

0

3

0

0

0

1

0

0

2

0

2

3

2

+

′ +

′′ +

=

+

+

′ +

′′ +











+

.

)

(

...

2

)

(

)

(

...

0

2

0

0

h

n

R

y

h

n

y

h

n

y

A

n

+













+

′′

+

′

+

+

+

(34)

Z porównania mnożników występujących przy kolejnych potęgach h, z lewej i prawej strony tego
związku, otrzymujemy równania, z których wyznaczamy nieznane współczynniki

A

i

n

i

(

, , ..., ).

=

0 1

W przypadku

n

=

1

mamy

h y

h

y

h

y

A y

A

y

h y

h

y

0

2

0

3

0

0

0

1

0

0

2

0

2

6

2

+

′ +

′′ +

=

+

+

′ +

′′ +











...

... ,

skąd wynikają równania:

A

A

h

0

1

+

=

,

A h

h

1

2

2

=

i ostatecznie po porównaniu dokładnej wartości całki

6

2

)

(

3

0

2

0

0

h

y

h

y

h

y

h

I

d

′′

+

′

+

=

z jej wartością przybliżoną

z jej wartością przybliżoną

4

2

)

(

3

0

2

0

0

h

y

h

y

h

y

h

I

p

′′

+

′

+

=

jest

.

12

)

(

2

)

(

1

0

0

3

1

0

∫

′′

−

+

=

x

x

y

h

y

y

h

x

x

f

d

(35)

Jest to znany wzór trapezów, odznaczający się nadspodziewanie małym błędem

.

)

(

3

h

O

Widzimy więc,

ż

e operacja całkowania przybliżonego jest znacznie dokładniejsza od operacji różniczkowania

numerycznego.

Zależność (34) w przypadku

n

=

2

przyjmuje postać

=

+

+

′′

′

+

′′

+

′

+

...

120

)

2

(

24

)

2

(

6

)

2

(

2

)

2

(

)

2

(

0

5

0

4

0

3

0

2

0

IV

y

h

y

h

y

h

y

h

y

h

=

+

+

′ +

′′ +

′′′ +

+











+

A y

A

y

h y

h

y

h

y

h

y

IV

0

0

1

0

0

2

0

3

0

4

0

2

6

24

...

+

+

′ +

′′ +

′′′ +

+













A

y

h y

h

y

h

y

h

y

IV

2

0

0

2

0

3

0

4

0

2

2

2

2

6

2

24

(

)

(

)

(

)

(

)

... .

Stąd otrzymujemy układ równań:

A

A

A

h

0

1

2

2

+

+

=

,

A h

A h

h

1

2

2

2

2

+

=

,

A

h

A h

h

1

2

2

2

3

2

2

4

3

+

=

,

którego rozwiązaniem są liczby:

.

3

4

,

3

1

2

0

h

A

h

A

A

=

=

=

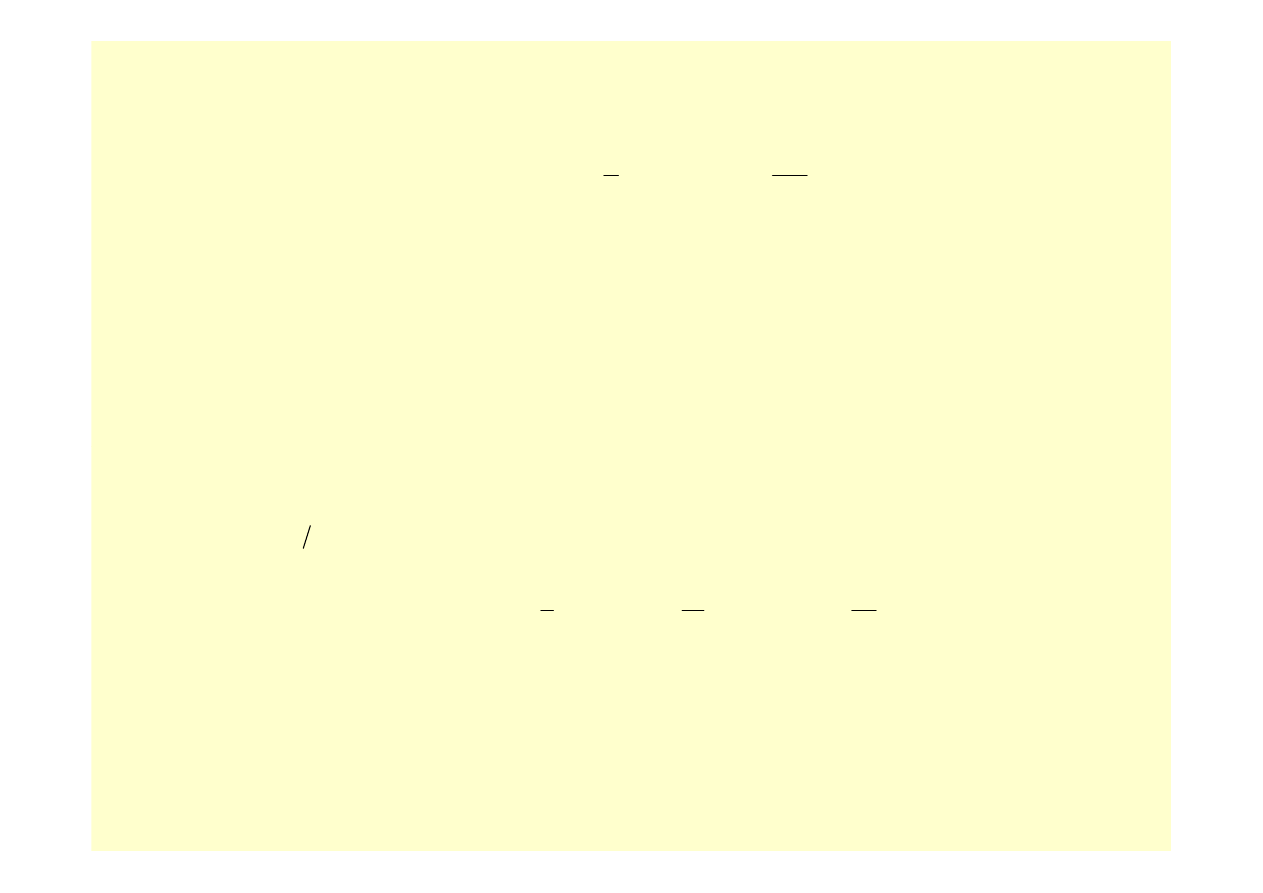
Podstawiając je do (33) uzyskujemy znany wzór parabol, zwany też wzorem Simpsona

(

)

.

90

4

3

)

(

0

5

2

1

0

2

0

IV

x

x

y

h

y

y

y

h

x

x

f

−

+

+

=

∫

d

(36)

Zwraca uwagę bardzo wysoka dokładność tego wzoru, wynikająca z tożsamościowego znikania

współczynników przy pochodnej

′′′

y

0

po podstawieniu wyznaczonych wartości A

0

,

A

1

i

A

2

.

Ze względu na trudności związane ze stosowaniem wielomianów interpolacyjnych wysokich

stopni, w praktyce raczej nie wykorzystuje się kwadratur Newtona-Cotesa wysokich rzędów. Na ogół
bardziej celowe jest podzielenie przedziału całkowania na większą liczbę podprzedziałów i stosowanie
dla nich kwadratur Newtona-Cotesa niskiego rzędu. Skonstruowane w ten sposób kwadratury, określone
na całym przedziale

[ , ]

a b

, są nazywane złożonymi kwadraturami Newtona-Cotesa.

na całym przedziale

[ , ]

a b

, są nazywane złożonymi kwadraturami Newtona-Cotesa.

Złożony wzór trapezów otrzymujemy po podzieleniu przedziału całkowania

[ , ]

a b

na m równych

części

h

b a m

= −

(

)

i zsumowaniu całek (35) dla każdego podprzedziału

Q f

h

y

y

h

y

y

y

y

i

m

i

i

m

m

( )

(

)

...

.

=

+

=

+

+ +

+











=

−

−

∑

2

2

2

1

1

0

1

1

(37)

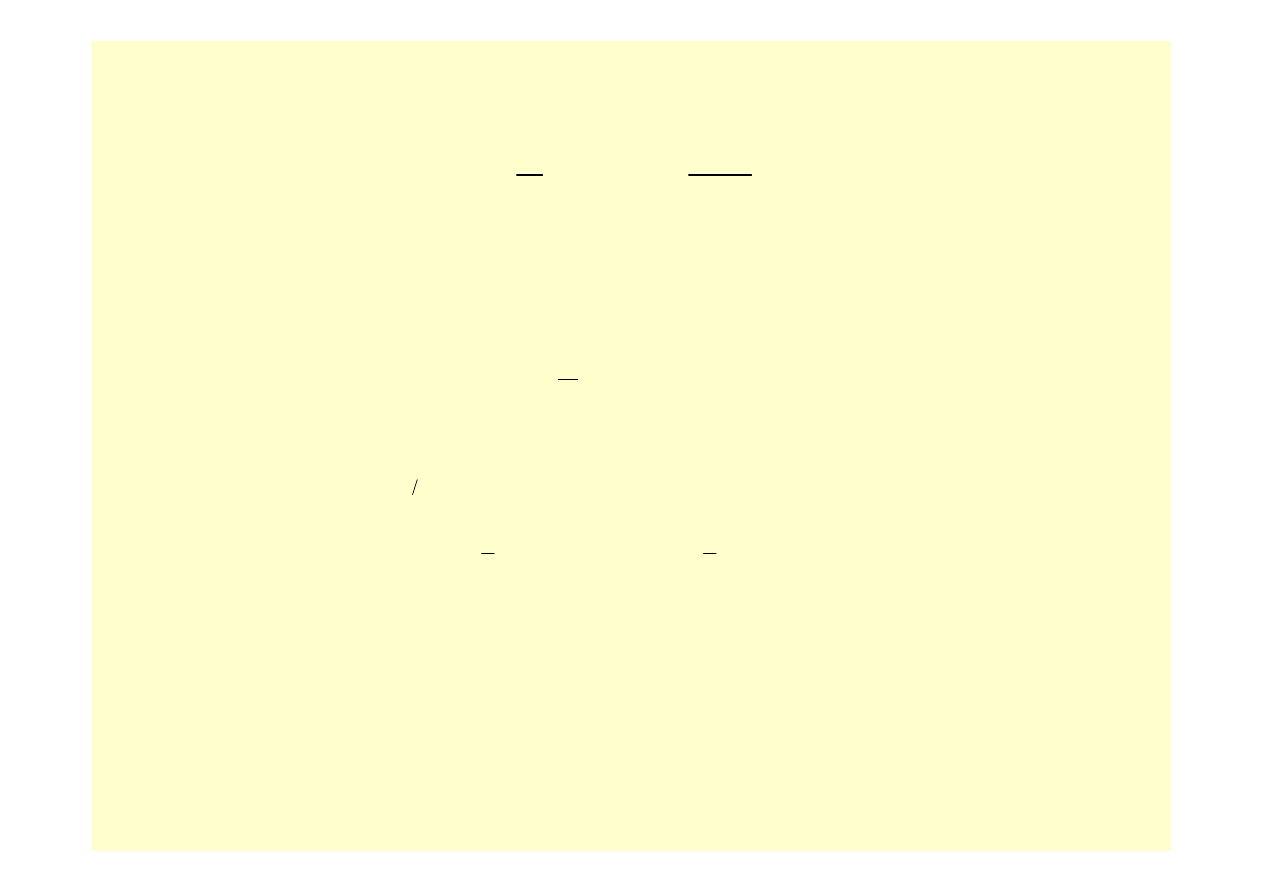
Na podstawie oszacowania (35) błąd złożonego wzoru trapezów wynosi

R

h

f

x

b

a

h f

i

i

m

1

3

1

1

2

12

12

= −

′′

= − −

′′

−

=

∑

(

)

(

)

( ),

ξ

(38)

gdzie

′′

=

′′

∈

−

=

∑

f

m

f

x

a b

i

i

m

( )

(

),

,

ξ

ξ

1

1

1

[

].

Analogicznie wyprowadza się złożony wzór parabol przy założeniu, że m jest parzyste. Po zsumowaniu

Analogicznie wyprowadza się złożony wzór parabol przy założeniu, że m jest parzyste. Po zsumowaniu
całek (5.36) dla kolejnych

m 2

podprzedziałów o długości 2 h mamy

[

]

,

2

4

)

(

3

)

4

(

3

)

(

2

1

0

2

/

1

2

1

2

2

2

σ

σ

+

+

+

=

+

+

=

∑

=

−

−

m

m

k

k

k

k

y

y

h

y

y

y

h

f

Q

(39)

gdzie:

.

...

,

...

2

4

2

2

1

3

1

1

−

−

+

+

+

=

+

+

+

=

σ

σ

m

m

y

y

y

y

y

y

Błąd złożonego wzoru parabol jest następujący:

,

)

(

180

)

(

)

(

90

2

/

1

4

2

2

5

2

∑

=

−

ξ

−

−

=

−

=

m

k

IV

k

IV

f

h

a

b

x

f

h

R

(40)

gdzie

[

]

.

,

,

)

(

2

)

(

2

/

1

2

2

b

a

x

f

m

f

m

k

k

IV

IV

=

ξ

=

ξ

∑

=

−

*

Rozważane dotąd kwadratury interpolacyjne lub aproksymacyjne, jak i kwadra-tury Newtona-Cotesa są

Rozważane dotąd kwadratury interpolacyjne lub aproksymacyjne, jak i kwadra-tury Newtona-Cotesa są
kwadraturami z ustalonymi węzłami. Kwadratury Gaussa są natomiast kwadraturami postaci (25),

w których dobierane są nie tylko współ-czynniki

A

i

n

i

(

, , ..., ),

=

0 1

ale także węzły

x i

n

i

(

, , ..., )

=

0 1

-

w taki sposób, aby kwadratura była dokładna dla możliwie najwyższego stopnia wielomianu.

Przy wyznaczaniu parametrów kwadratur Gaussa wygodnie jest w obliczanej całce (24) dokonać
liniowej zamiany zmiennej całkowania

x

b

a

b

a

t

= + + −

2

2

,

(41)

pozwalającej na transformację dowolnego przedziału

[ , ]

a b

na przedział znormalizowany

[

, ]

−

1 1

Rozważymy teraz zadanie: jak wybrać węzły:

t

t

t

n

0

1

,

, ...,

oraz współczynniki:

A

A

A

n

0

1

,

, ...,

,

żeby kwadratura

postaci

∫

∑

−

=

=

1

1

0

)

(

)

(

n

i

i

i

t

f

A

t

t

f

d

(43)

była dokładna dla wielomianu stopnia

2

1

n

+

, którego liczba współczynników jest równa liczbie

nieznanych parametrów

A

i

i

t

i

.

Oznacza to, że równość (5.43) musi być spełniona dla wielomianów:

f t

t t

t

n

( )

, ,

, ...,

,

=

+

1

2

2

1

gdyż dla

∑

+

=

=

1

2

0

)

(

n

k

k

k

t

C

t

f

mamy

∑ ∑

∑

∫

∑ ∫

∑ ∑

=

+

=

=

−

+

=

−

+

=

=

=

=

=

=

n

i

n

k

n

i

i

i

k

i

k

i

n

k

n

k

n

i

k

i

i

k

k

k

t

f

A

t

C

A

t

A

C

t

t

C

t

t

f

0

1

2

0

0

1

1

1

2

0

1

1

1

2

0

0

.

)

(

)

(

d

d

Stąd przy wykorzystaniu związków:

ego,

nieparzyst

dla

0

,

parzystego

dla

1

2

1

1











+

=

∫

−

k

k

k

t

k

t

d

otrzymujemy układ równań:





















=

=

=

=

∑

∑

∑

2

....

..........

..........

,

0

,

2

2

0

0

n

n

i

n

i

i

n

i

i

t

A

A

(44)















=

+

=

+

=

=

∑

∑

.

0

,

1

2

2

1

2

0

2

0

n

i

n

i

i

n

i

n

i

i

t

A

n

t

A

(44)

Bezpośrednie rozwiązywanie nieliniowego układu równań (44) napotyka na duże trudności
matematyczne. Dlatego też najczęściej funkcję

f t

( )

przyjmuje się w postaci

f t

t P

t

k

n

k

n

( )

( )

, , ..., ),

=

=

+

1

0 1

(

(45)

gdzie

P

t

n

+

1

( )

są wielomianami Legendre’a, zdefiniowanymi wzorami:































=

−

−

−

=

=

−

=

−

=

=

=

−

−

.

...)

,

3

,

2

(

)

(

1

)

(

1

2

)

1

(

!

2

1

)

(

..

..........

..........

..........

,

)

1

3

(

2

1

,

)

(

,

1

)

(

2

1

2

2

2

1

0

n

x

P

n

n

x

P

x

n

n

x

x

n

x

P

x

P

x

x

P

x

P

n

n

n

n

n

n

n

d

d

(46)

Wielomian Legendre’a

P x

n

( )

jest funkcją parzystą dla n = 2 m i nieparzystą dla n = = 2 m +1, dla n

≥

1

ma n różnych pierwiastków rzeczywistych, leżących w przedziale otwartym (

−

1, 1).

ma n różnych pierwiastków rzeczywistych, leżących w przedziale otwartym (

−

1, 1).

Wielomiany Legendre’a

P

t

n

+

1

( )

są ortogonalne do wszystkich wielomianów stopnia mniejszego

od n+1. Zatem mamy

1

dla

0

)

(

1

1

1

+

<

=

+

−

∫

n

k

t

t

P

t

n

k

d

i następnie po podstawieniu (45) do (43) stwierdzamy, że suma

A t P

t

k

n

i i

k

n

i

i

n

+

=

=

∑

1

0

0 1

( )

(

, , ..., )

(47)

znika dla dowolnych

A

i

,

jeśli

P

t

i

n

n

i

+

=

=

1

0

0 1

( )

(

, , ..., ).

(48)

Kwadratura (43) będzie więc dokładna dla wielomianów stopnia

2

1

n

+

,

gdy jej węzłami będą zera

wielomianu Legendre’a

P

t

n

+

1

( ).

Po obliczeniu wartości węzłów

t

i

współczynniki

A

i

(

, , ..., )

i

n

=

0 1

można

łatwo wyznaczyć z układu równań liniowych (44).

W najprostszym przypadku dla n = 0 jest

t

0

0

=

- co oznacza, że kwadratura Gaussa z jednym węzłem

jest równoważna wzorowi prostokątów

.

)

0

(

2

=

)

(

1

1

∫

−

f

t

t

f

d

1

∫

−

W przypadku

n

=

1

obliczając najpierw pierwiastki wielomianu Legendre’a drugiego stopnia

P t

t

2

2

1

2

3

1

( )

(

)

=

−

otrzymujemy:

t

t

0

1

1

3

1

3

= −

=

,

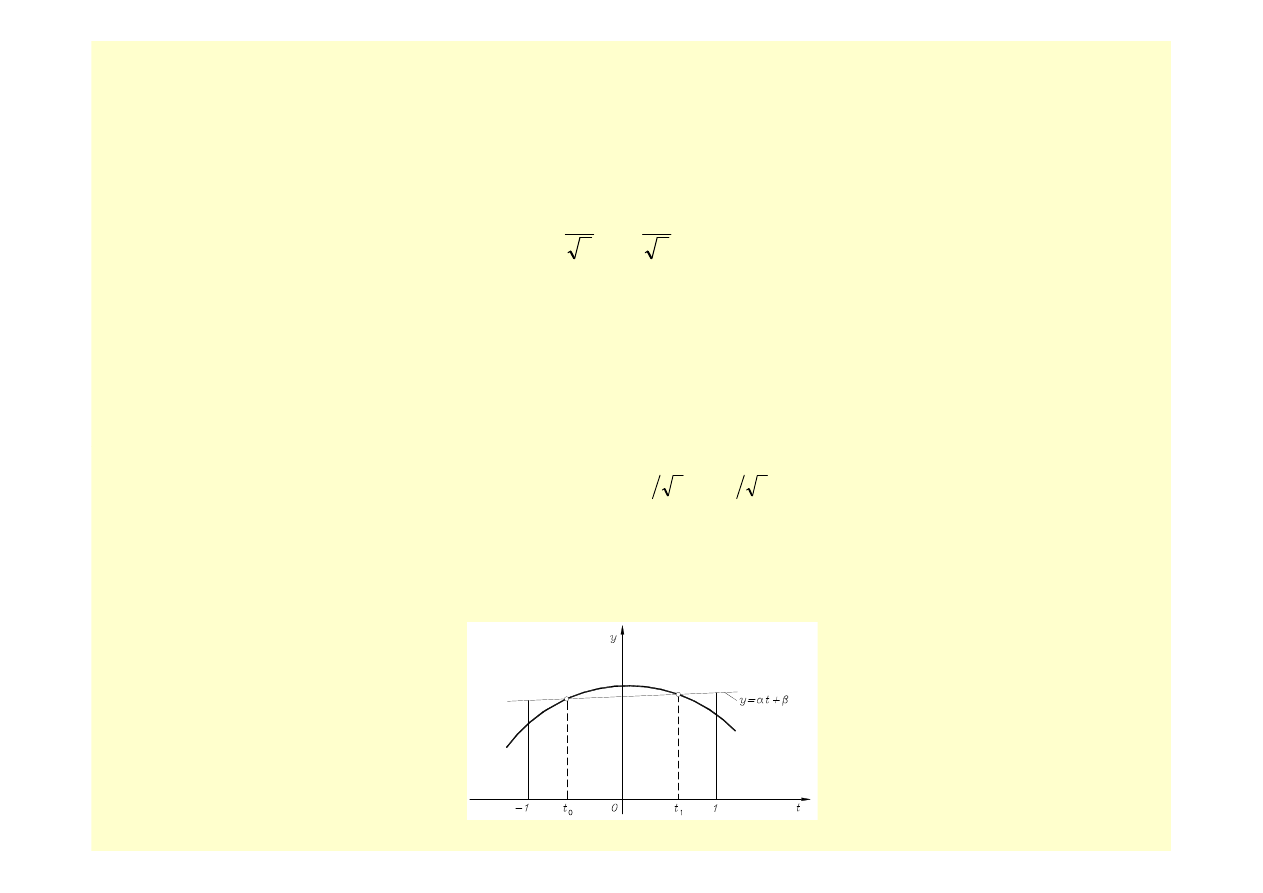
i następnie z układu równań:

A

A

0

1

2

+

=

,

−

+

=

1

3

1

3

0

0

1

A

A

,

dostajemy

A

A

0

1

1

=

=

.

Interpretacja geometryczna kwadratury Gaussa z dwoma węzłami

(

) ( )

,

3

1

3

1

)

(

1

1

f

f

t

t

f

+

−

=

∫

−

d

(49)

dokładnej dla wielomianów stopnia trzeciego, jest przedstawiona na rysunku 3. Funkcja podcałkowa

f x

( )

jest interpolowana funkcją liniową

,

β

+

α

=

t

y

przechodzącą przez punkty

f t

( )

0

i

f t

( ).

1

Rys. 3

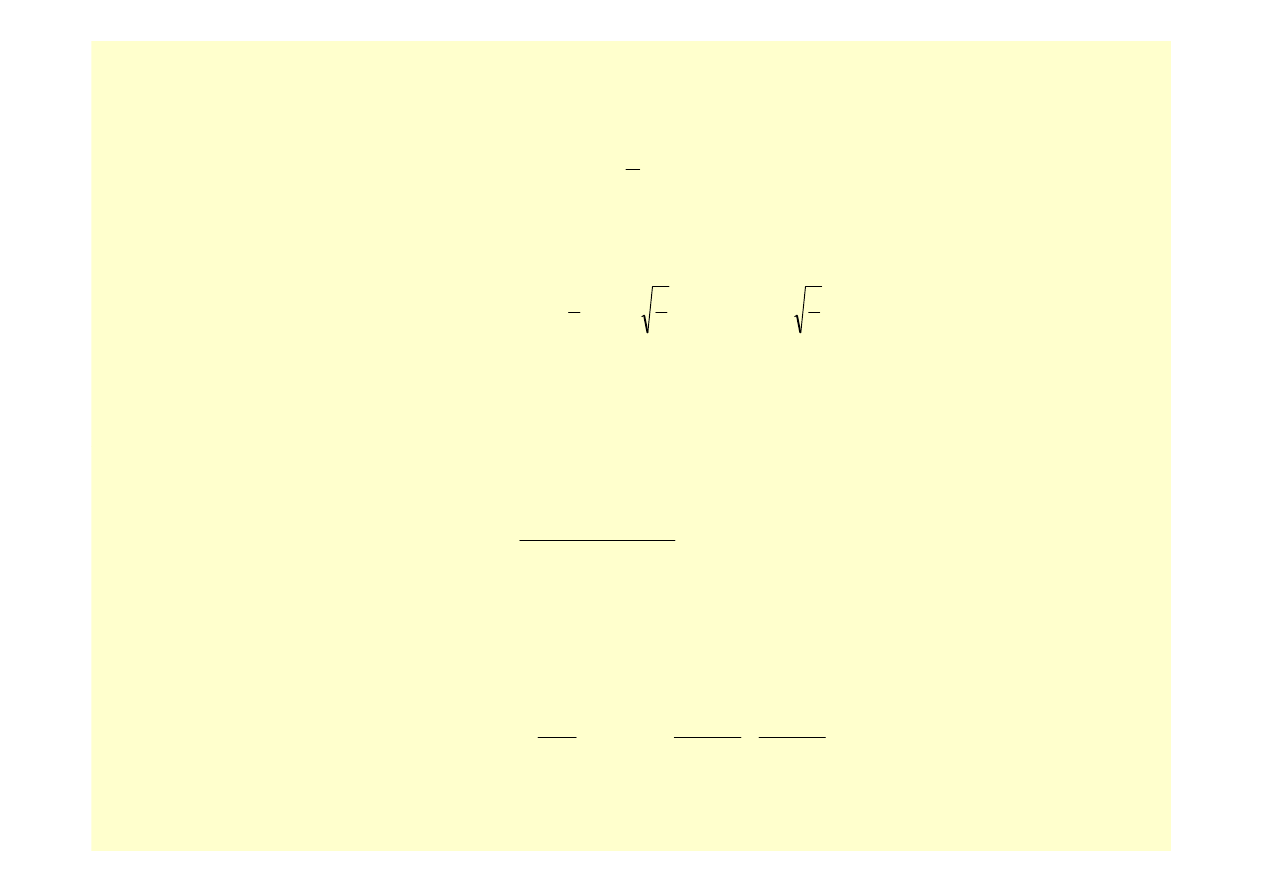
Po wyznaczeniu pierwiastków wielomianu Legendre’a trzeciego stopnia

P t

t

t

3

3

1

2

5

3

( )

(

)

=

−

można, w podobny sposób, otrzymać kwadraturę Gaussa z trzema węzłami





























+

+















−

=

∫

−

5

3

5

)

0

(

8

5

3

5

9

1

)

(

1

1

f

f

f

t

t

f

d

(50)

oraz kwadratury z większą liczbą węzłów.

Błąd popełniany przy obliczaniu całki (5.24) za pomocą kwadratur Gaussa dla dowolnej wartości

Błąd popełniany przy obliczaniu całki (5.24) za pomocą kwadratur Gaussa dla dowolnej wartości
n

wynosi

[

]

[

]

R

n

b

a

n

n

f

a b

n

n

n

=

+

−

+

+

∈

+

+

(

)! (

)

(

) (

)!

( ),

[ , ].

(

)

1

2

3

2

3

4

2

3

3

2

2

ξ

ξ

(51)

Tak samo jak w przypadku kwadratur Newtona-Cotesa można budować złożone kwadratury Gaussa
dzieląc przedział całkowania na mniejsze podprzedziały i stosując w każdym z nich kwadraturę Gaussa
ustalonego stopnia

.

2

2

2

)

(

1

0

1

1

∫

∑∑

= =

−

−













−

+

+

−

=

b

a

m

j

n

i

i

j

j

j

j

i

t

x

x

x

x

f

A

a

b

x

x

f

d

Dziękuję

Materiały przygotowane dla studentów Wydziału Mechanicznego – Politechniki Opolskiej

przez: dr inż. Jacka Wydrycha