Logika dla informatyków, Kolokwium nr 2, styczeń 2013

1/2

A) Zakres kolokwium

Zadanie 1. - przeliczalność zbiorów
Zadanie 2. - równoliczność zbiorów
Pytania pomocnicze do zadań 1-2 (patrz punkt B poniżej).

Zadanie 3. wielozbiory - działania
Zadanie 4. wielozbiory - własności działań

Zadanie 5. język formalny
Zadanie 6 - język formalny
Zadanie 7. język formalny - gramatyka
Pytanie pomocnicze do zadania 6 (patrz punkt C poniżej)

Zadanie 8. Rachunek zdań - tautologie
Zadanie 9. Rachunek zdań - tautologie
Zadanie 10. Rachunek zdań - pełność funkcjonalna zbiorów spójników
Zestaw dodatkowych spójników logicznych do zadania 10 (patrz punkt D)

B) Przyjmijmy następujące oznaczenia:
N - zbiór liczb naturalnych,
C - zbiór liczb całkowitych
E(X) - zbiór wszystkich relacji binarnych nad zbiorem X,
B(X) - zbiór wszystkich relacji równoważności nad zbiorem X,
Y*=

, gdzie

jest i-tym iloczynem kartezjańskim np.

.

B.1) Przytoczyć twierdzenia o przeliczalności podzbiorów, sum, iloczynów, itd. zbiorów
przeliczalnych.

B.2) Niech A =

df

{0, 1} i B =

df

{0, 1, 2, ..., n}. Które pary spośród zbiorów A*, B*, N* są

zbiorami równolicznymi?

B.3) Niech X={1,2} i Z={1,2,3,4}.

Czy zbiór E(X) jest równoliczny ze zbiorem B(X)?
Czy zbiór E(X)* jest równoliczny z N?
Czy zbiór (B(X)



E(X))* jest równoliczny z N?

Czy zbiór E(X)* jest równoliczny z N?
Czy zbiór

jest równoliczny z N?

B.4)
Czy zbiór

jest przeliczalny?

Czy zbiór

jest równoliczny z N?

B.5)
Czy zbiór wszystkich liczb całkowitych podzielnych jednocześnie przez 2 i 3 jest
przeliczalny?
Czy zbiór wszystkich liczb całkowitych podzielnych jednocześnie przez 2 i 3 jest
równoliczny ze zbiorem liczb naturalnych?

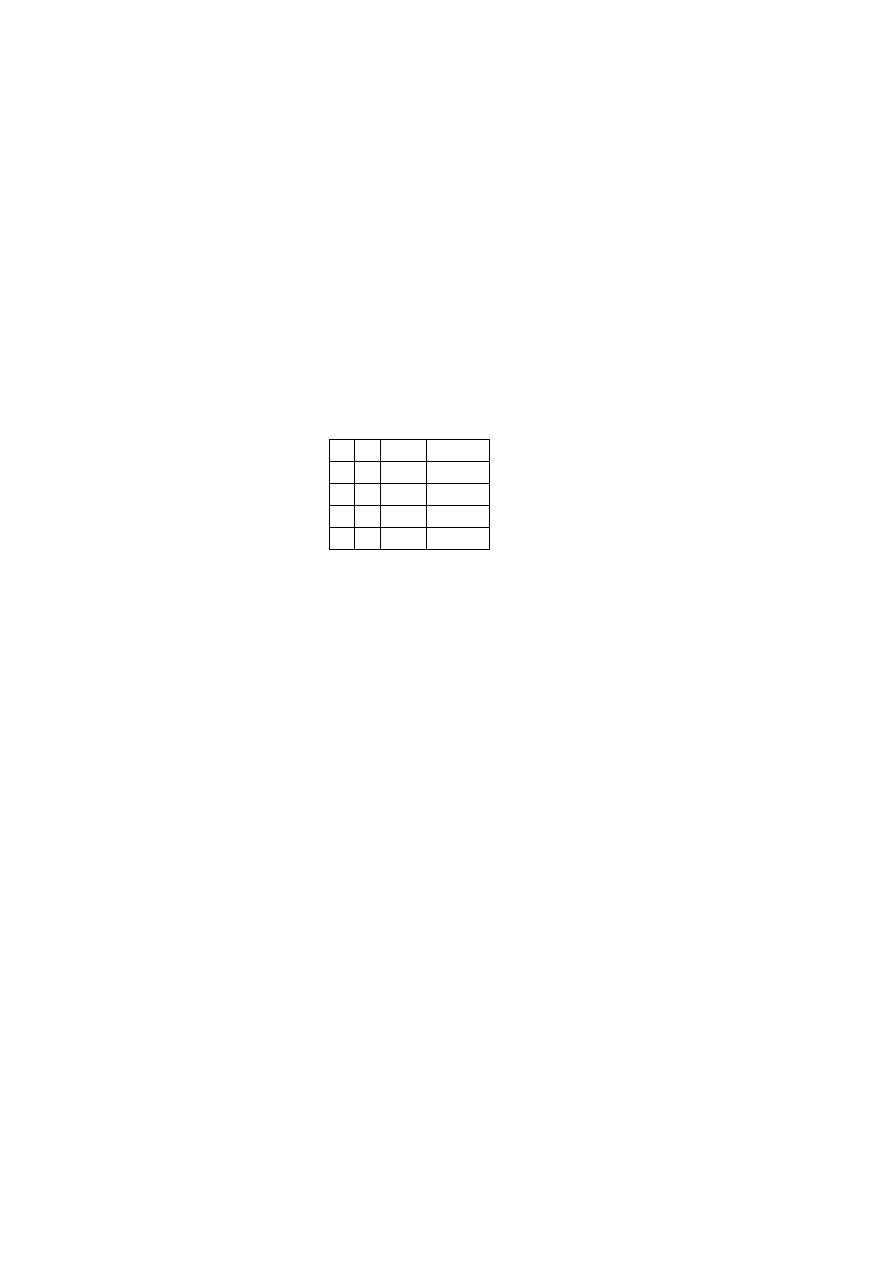
Logika dla informatyków, Kolokwium nr 2, styczeń 2013

2/2

Czy zbiór wszystkich liczb całkowitych podzielnych jednocześnie przez 2 i 3 jest
równoliczny ze zbiorem wszystkich liczb podzielnych jednocześnie przez 2, 3 i 4?

C) Niech alfabet Al języka formalnego F będzie następującym sześcioelementowym
zbiorem Al = {p,



~,



(, )}. Przyjmijmy poniższe reguły syntaktyczne definiujące język

formalny F:



Każdy symbol p, p



, p



, p



, p



, p



, .... jest poprawnym słowem języka F.



Jeżeli A jest poprawnym słowem języka F, to ciąg znaków ~(A) jest poprawnym
słowem języka F.



Jeżeli A i B są poprawnymi słowami języka F, to ciągi znaków (A), (B) i (A



B) są

poprawnymi słowami języka F.

C.1) Podać przykłady ciągów ze zbioru F

*

nie będących słowami języka F.

C.2) Podać przykłady ciągów ze zbioru F

*

będących słowami języka F.

D)

a b a



b

a



b

0 0

1

1

0 1

1

0

1 0

1

0

1 1

0

0

R.K.