Maksymalizacja zysku przez firmę doskonale konkurencyjną: 

podaż dóbr i popyt na czynniki

Maksymalizacja zysku i podaż w SR firmy doskonale 

konkurencyjnej 

Zmiany podaży w SR
Zyski i zamknięcie w SR
Popyt na jeden zmienny czynnik w krótkim okresie 
Popyt na dwa czynniki lub więcej w krótkim okresie
Przesunięcia funkcji popytu na czynnik w krótkim okresie 

Maksymalizacja zysku i podaż w SR firmy doskonale konkurencyjnej

Rozwiązaliśmy problem minTC dla każdego poziomu 

produkcji w SR i LR. Teraz stoimy przed problemem: 

Jaką wielkość produkcji będzie wytwarzać firma aby 

maxππππ

.

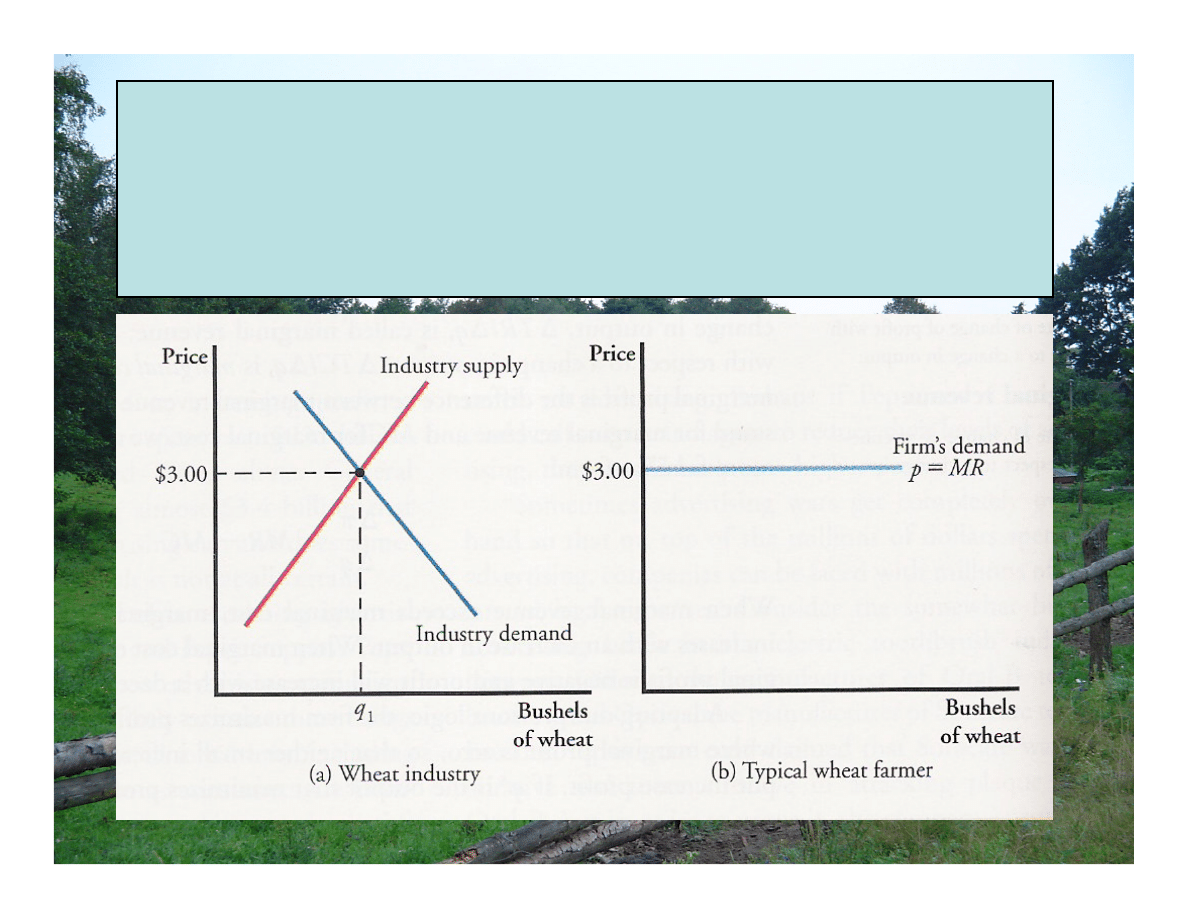
KRZYWA  POPYTU  I  PRZYCHODÓW  KRAŃCOWYCH 

DLA  FIRMY  DOSKONALE  KONKURENCYJNEJ

Cenę równowagi = $3 wyznaczoną przez rynek w (a) przyjmuje firma i napotyka poziomą,  

czyli doskonale konkurencyjną krzywą popytu w (b). 

Krzywa popytu, d, jest jednocześnie krzywą MR i AR

Maksymalizacja zysku i podaż w SR firmy doskonale konkurencyjnej

Maksymalizacja zysku

Funkcja zysku: 

π

π

π

π

(x) = TR(x) – TC(x)

Maksymalizacja zysku: 

Czyli max ππππ(x) wymaga

MR(x*) = MC(x*)

.

( )

( )

( )

( )

( )

0

*

*

*

*

=

−

=

−

=

x

MC

x

MR

x

TC

dx

d

x

TR

dx

d

x

dx

d

π

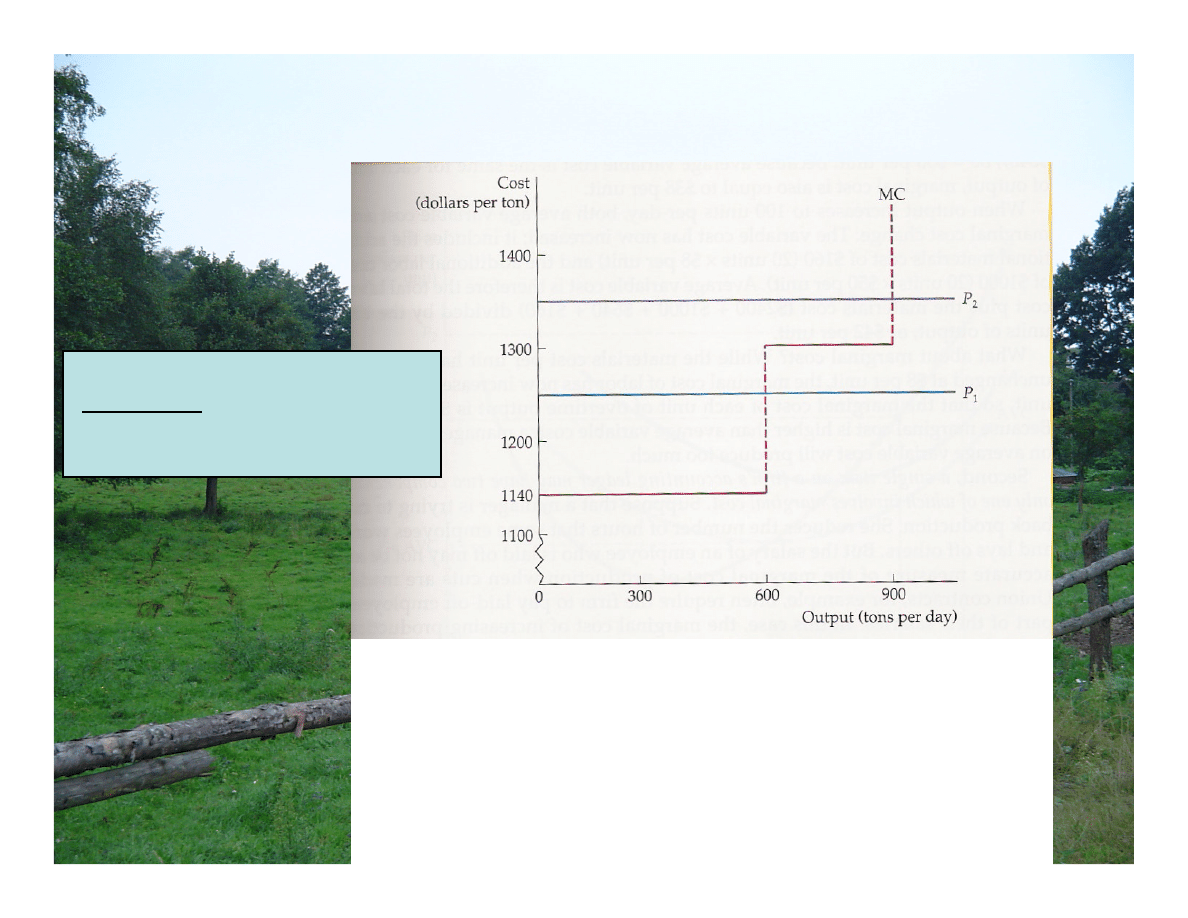
Przykład: Produkcja w SR 

huty aluminium

Produkcja huty aluminium w krótkim okresie

W krótkim okresie zakład powinien produkować 600 ton dziennie 
przy cenie wyższej od $1140 za tonę, ale niższej niż $1300 za tonę. 
Jeśli cena przekroczy $1300 za tonę, to powinien zatrudnić
dodatkową zmianę i produkować 900 ton dziennie. Jeśli cena 
spadnie poniżej $1140 za tonę, firma powinna zaprzestać produkcji, 
ale najprawdopodobniej powinna pozostać w przemyśle, gdyż
prawdopodobny jest wzrost ceny w przyszłości. 

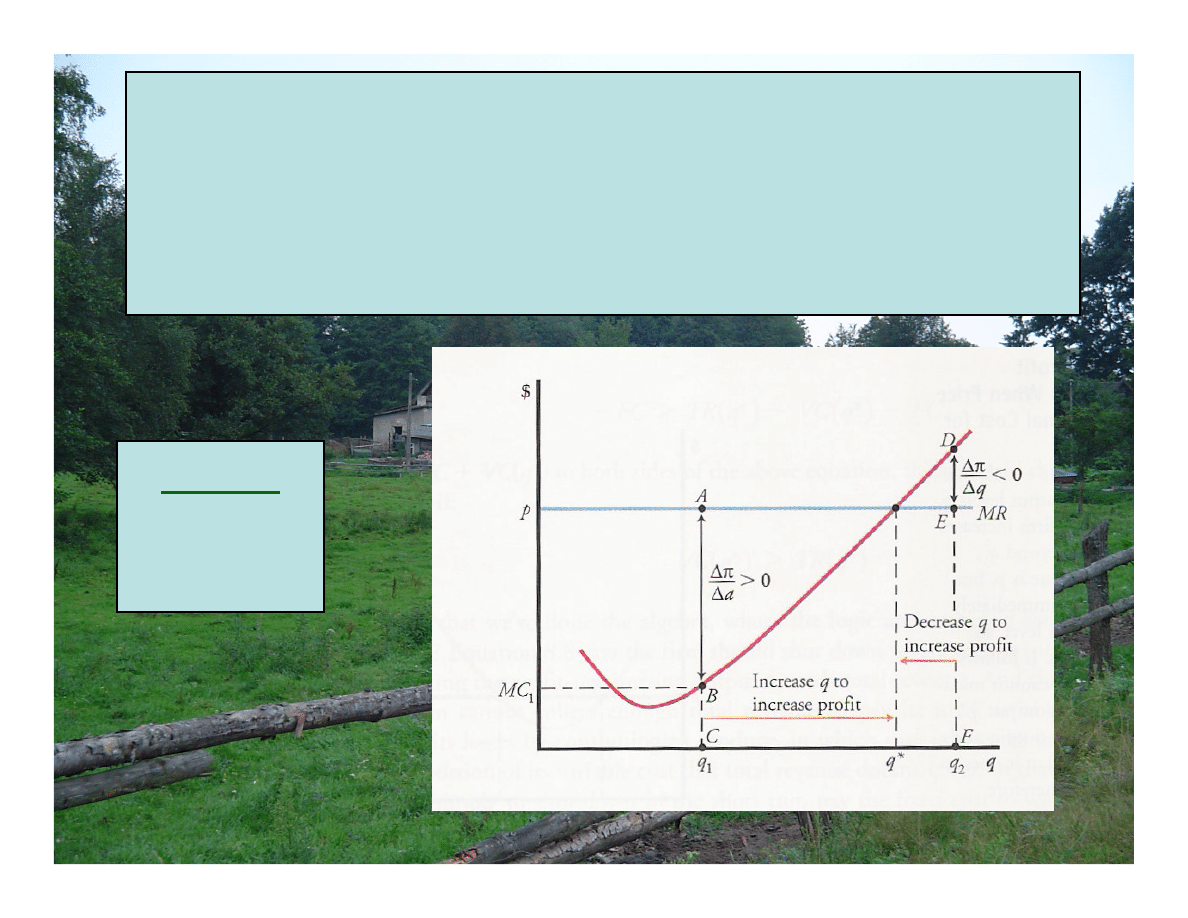
WIELKOŚĆ PRODUKCJI MAKSYMALIZUJĄCA ZYSKI

Przy cenie p jeśli firma produkuje 

q

1

, to nie max ππππ, gdyż

p>MC

, 

czyli dodatkowa produkcja więcej dodaje do przychodów niż do kosztów.

Przy cenie p jeśli firma produkuje 

q

2

, to nie max ππππ, gdyż

p<MC

, 

czyli ograniczenie produkcji więcej zabiera z kosztów niż z przychodów.

Aby max ππππ firma musi produkować

q*

, gdy 

p=MC

.

Przykład:

sprzedaż

ś

wiątecznych

choinek

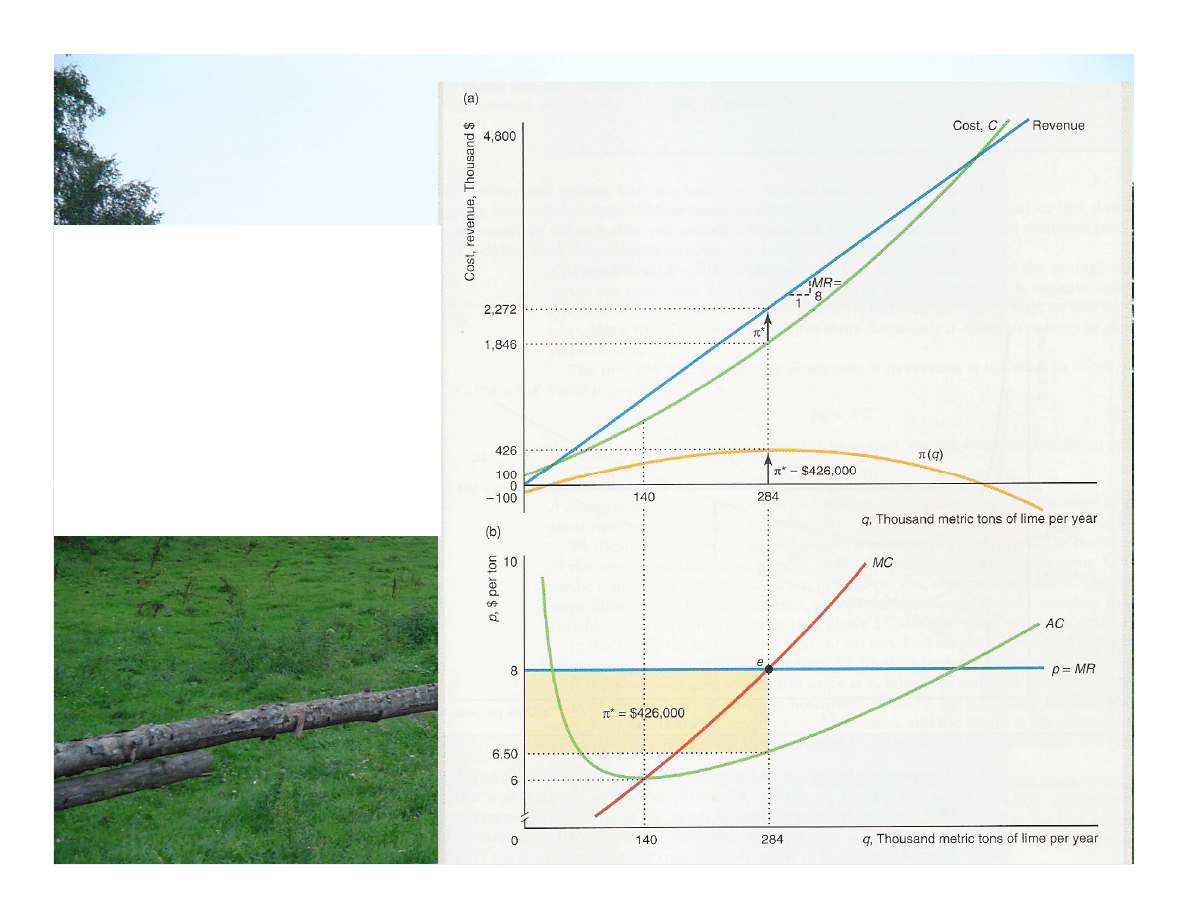
Jak firma doskonale 
konkurencyjna maksymalizuje 
zysk?

(a) Firma doskonale konkurencyjna 
produkująca 284 jednostki wapna w 
celu maksymalizacji zysku na 
poziomie $426.000.

(b) Zysk firmy osiąga maksimum, 
gdy jej MR będące ceną rynkową, 

p = $8, równają się jej MC. 

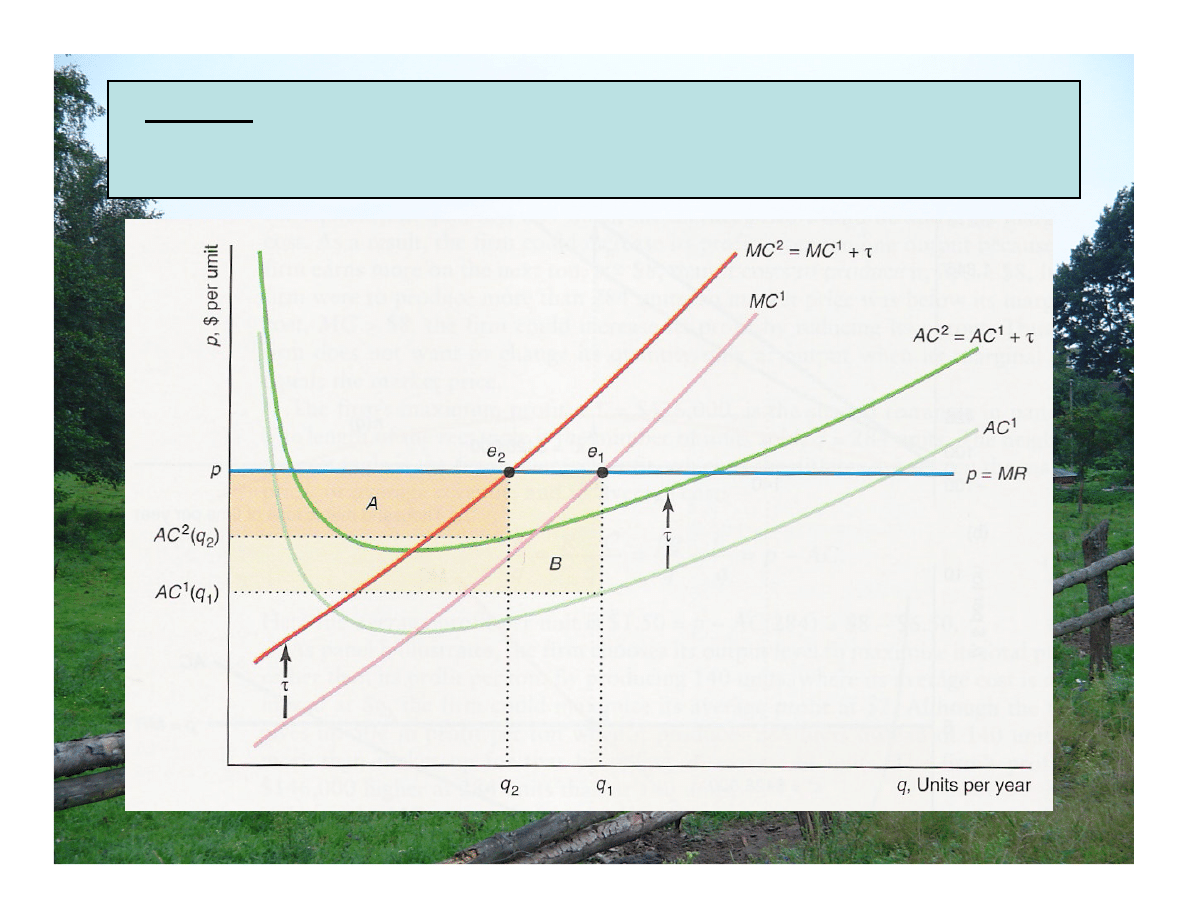
Problem: Jeżeli podatek jednostkowy zostanie nałożony od produkcji 

tylko jednej firmy na rynku doskonale konkurencyjnym, to jak ta firma 

zmieni wielkość produkcji maksymalizującą zysk i jak zmieni się ten zysk?

Maksymalizacja zysku i podaż w SR firmy doskonale konkurencyjnej

Podaż w SR

Firma jest ceno biorcą: 

TR(x) =  x

Różniczkując względem x: 

Wstawiając wartość MR(x) do warunku MC(x*) = MR(x*): 

max ππππ(x): p

x

= MC(x*)

Z powyższego równania wynika, że firma traktuje krzywą

MC jako swą krzywą podaży.

x

p

( )

( )

x

p

x

TR

dx

d

x

MR

=

=

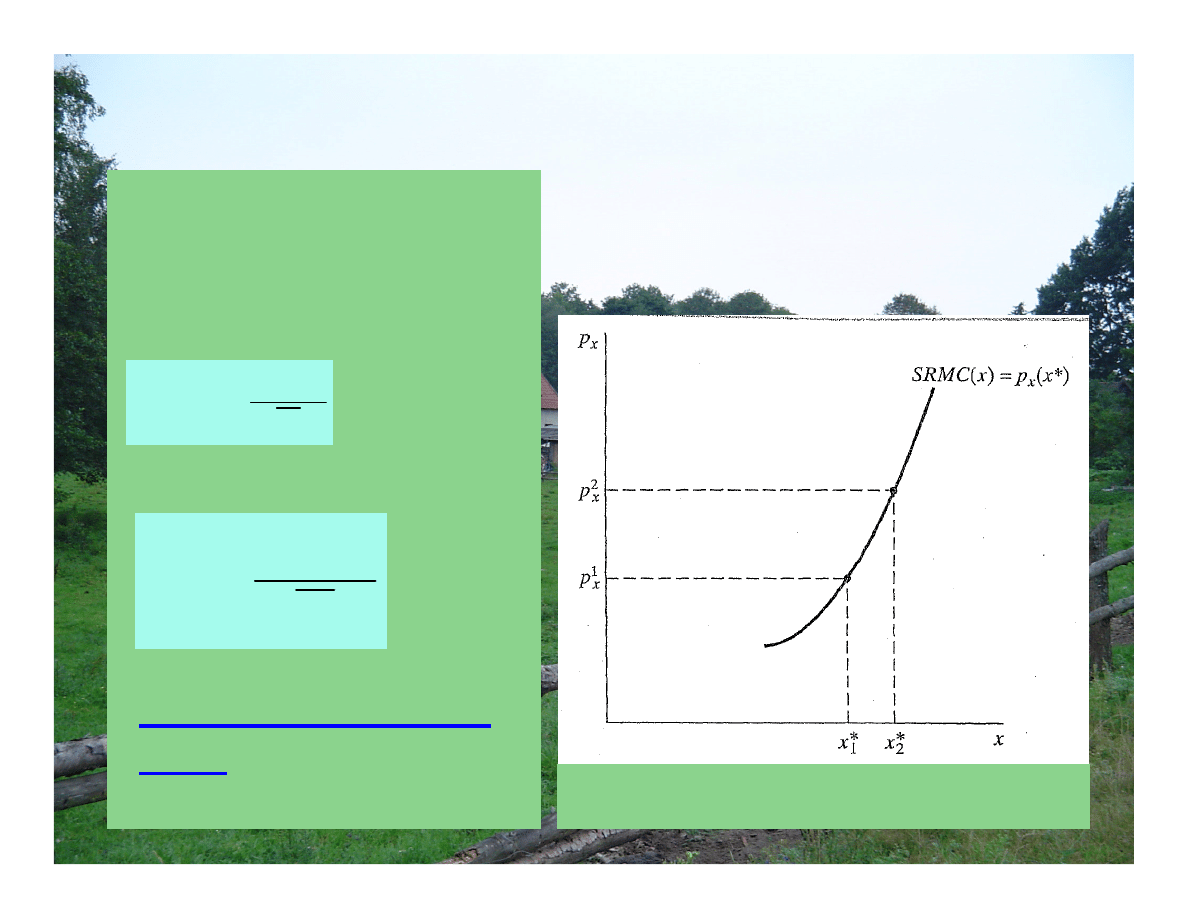
Maksymalizacja zysku i podaż w SR firmy doskonale konkurencyjnej

Przykład:

Dla funkcji produkcji

x = K

1/2

L

1/2

wyprowadziliśmy 

Zrównując p

x

z MC:  

: 

krzywa podaży firmy 
w SR

K

wx

SRMC

*

2

=

K

wx

p

x

*

2

=

Krzywa podaży firmy w SR

Zyski i zamknięcie w SR

Tak długo, jak cena jest większa lub równa SRAVC, to sytuacja 

firmy jest co najmniej tak dobra, jak byłaby gdyby firma 
zaprzestała produkcji. 

Ponieważ cena zawsze równa się MC i ponieważ SRMC równają

się AVC w ich minimum, to firma prowadzi działalność tak 
długo, jak cena jest większa od minimum AVC. 

Wielkość produkcji, dla której cena równa się minimum AVC 

nazywana jest 

punktem zamknięcia

: 

p

x

= min(SRAVC). 

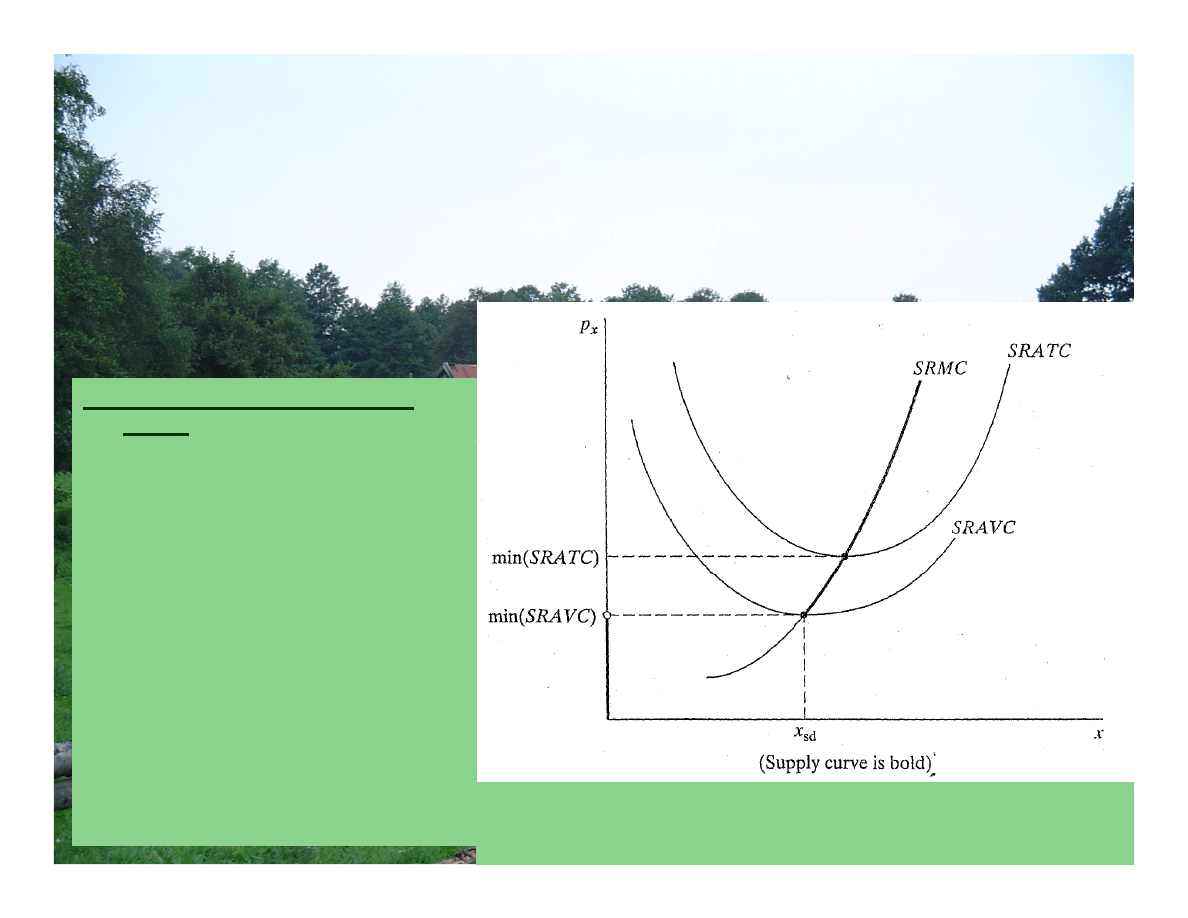
Zyski i zamknięcie w SR

Efektywna krzywa podaży 

firmy

Ponieważ firma nie produkuje, 

gdy: 

p

x

< min(SRAVC)

, 

to krzywa SRS jest 

ograniczona do części 

SRMC dla wielkości 

produkcji większej lub 

równej tej, jaka odpowiada 

min(SRAVC).

Jest ona nieciągła. 

Punkt zamknięcia firmy w SR i efektywna krzywa 

podaży (SRS)

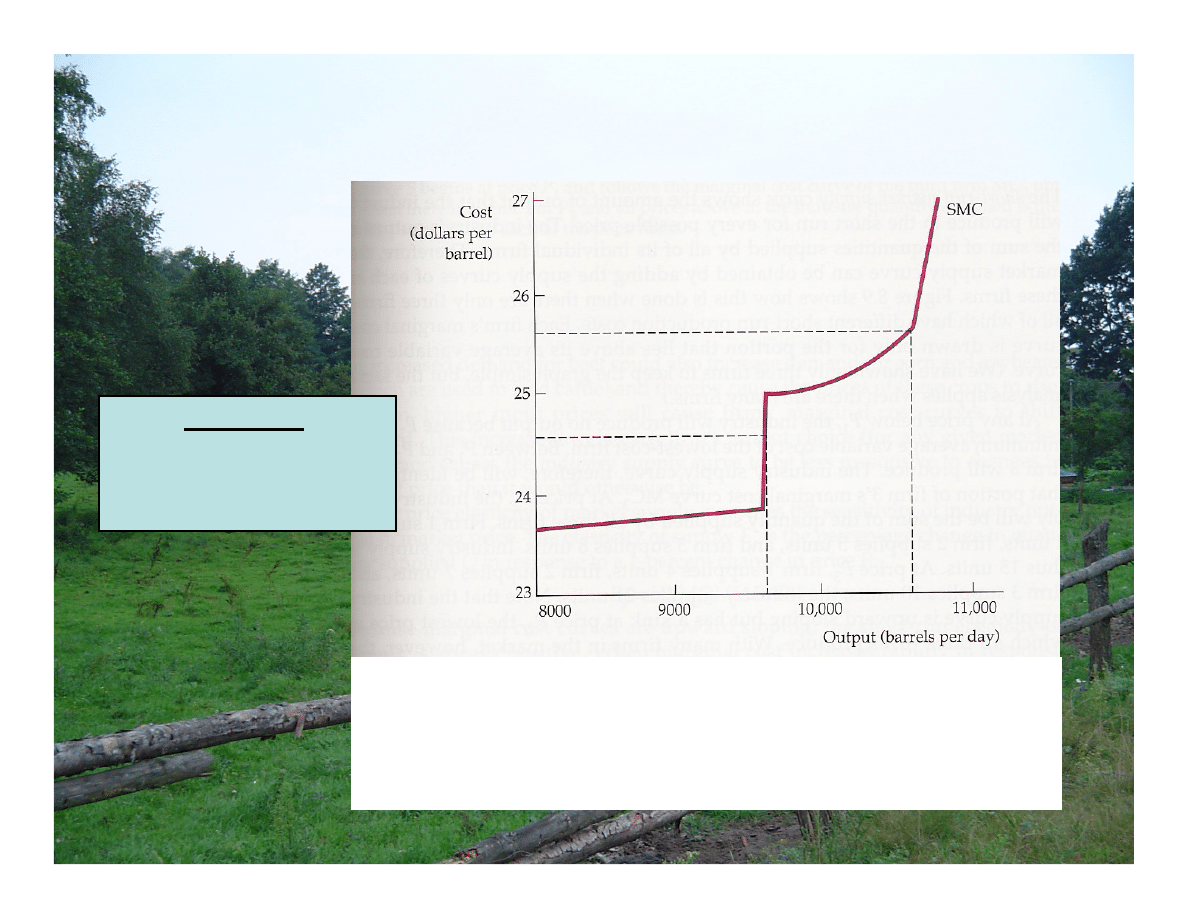
Przykład:

Produkcja  rafinerii

w SR

Produkcja wyrobów z ropy naftowej w krótkim okresie

Jeśli rafineria przejdzie od jednej jednostki wytwórczej do innej, to 
MC wytwarzania produktów z ropy naftowej rośnie gwałtownie . 
Oznacza to, że wielkość produkcji może być niewrażliwa względem 
pewnych zmian cen, ale bardzo wrażliwa względem innych. 

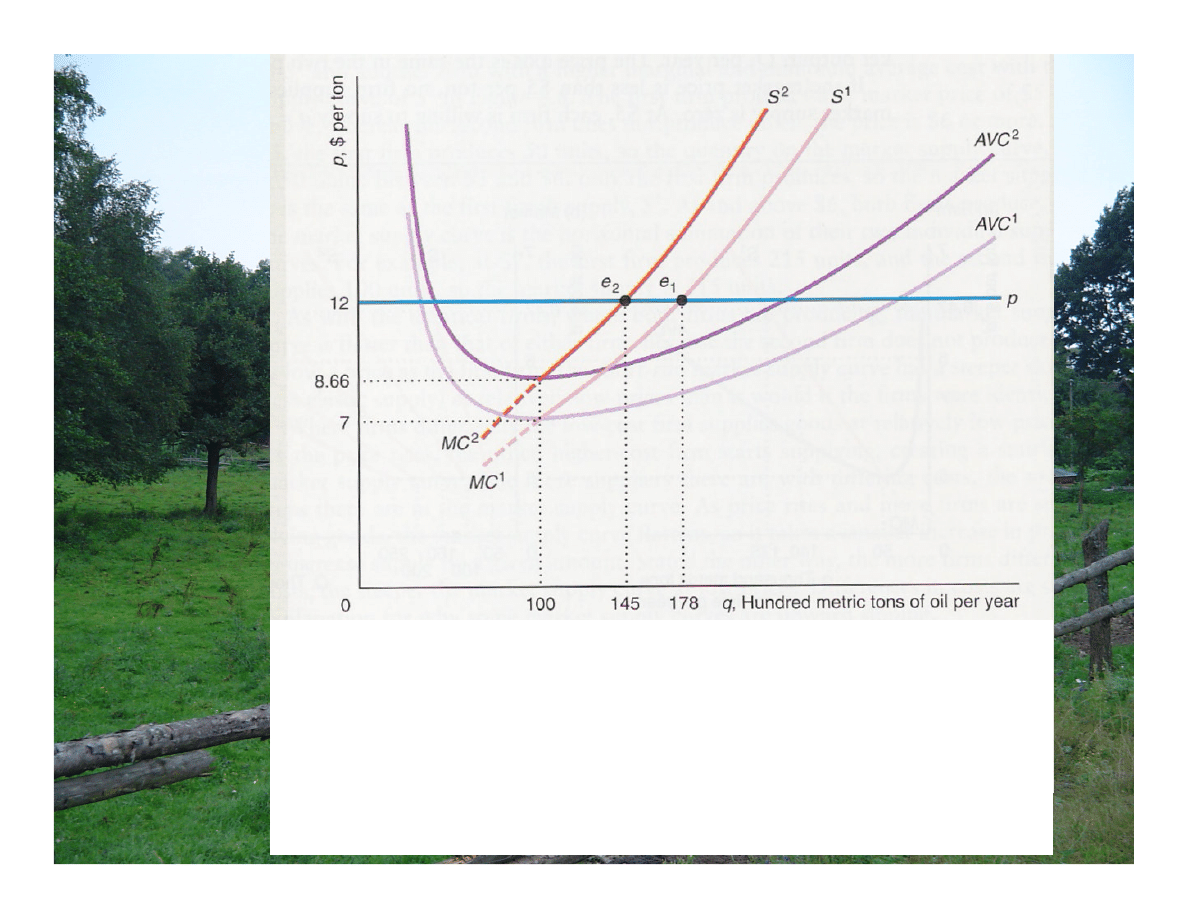
Wpływ wzrostu kosztów surowców na krzywą podaży oleju 
roślinnego

Surowce stanowią 95% kosztów zmiennych. Jeśli więc cena 
surowców rośnie o 25%, to koszty zmienne rosną o 23,75% (95% z 
25%). Krzywa podaży oleju roślinnego producenta przesuwa się
więc do góry z S

1

do S

2

. Jeśli cena wynosi $12, to wielkość podaży 

spada ze 178 jednostek do 145 jednostek. 

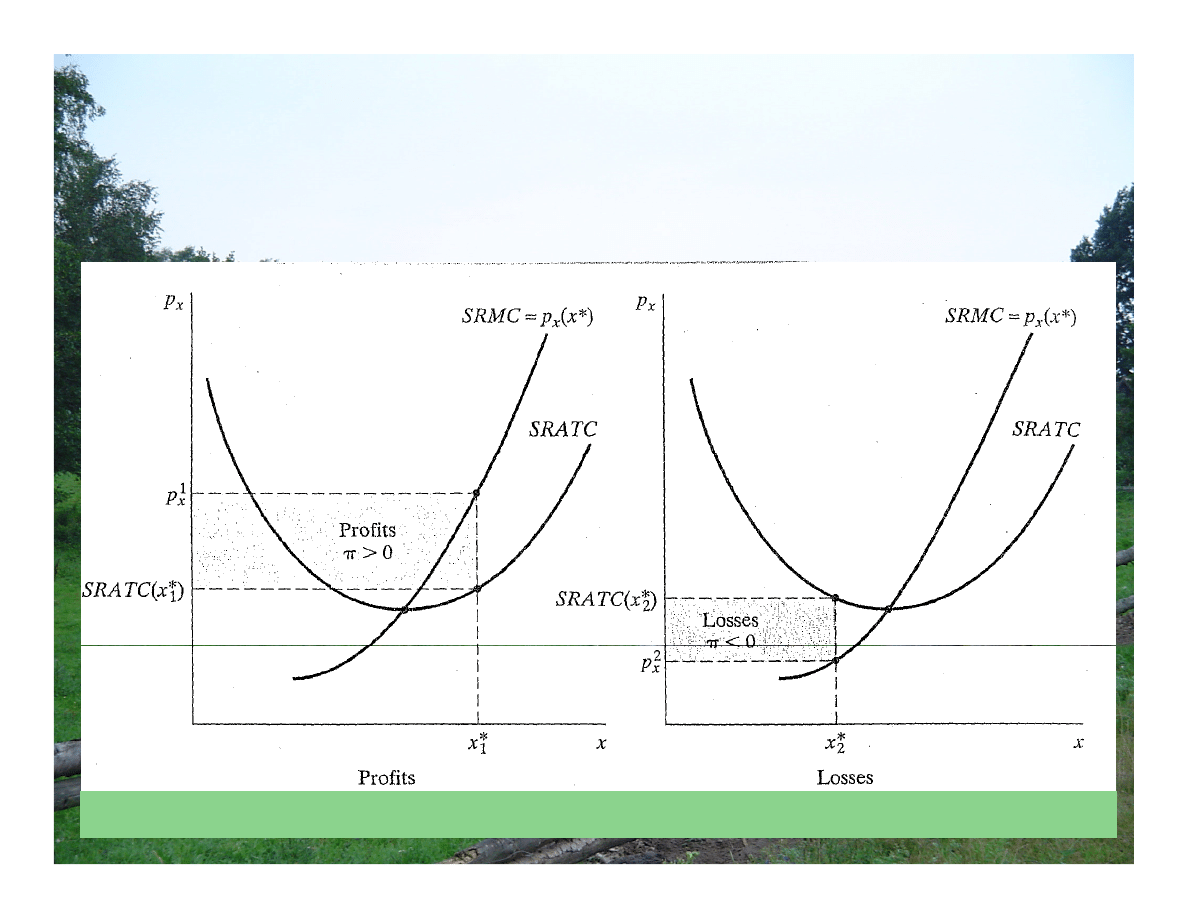
Zyski i zamknięcie w SR

Zyski i straty (

p

x

= SRMC)

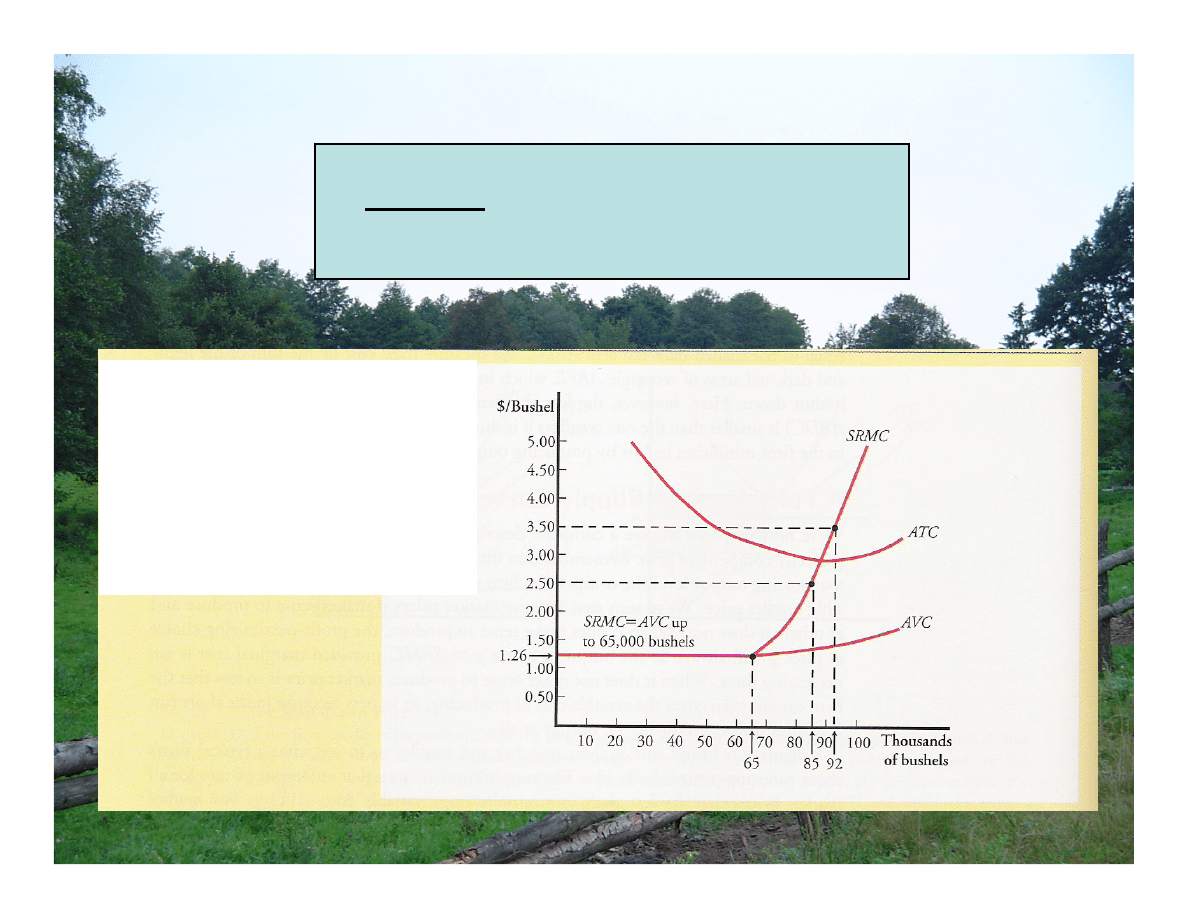
Przykład: Koszty produkcji kukurydzy 

i jej optymalna wielkość produkcji w USA

Krzywe kosztów dla 
produkcji kukurydzy

Do wielkości produkcji równej 
65.000 buszli, SRMC = AVC = 
$1,26 za jeden buszel. Powyżej 
65.000 buszli SRMC 
gwałtownie rośnie

Popyt na jeden zmienny czynnik w krótkim okresie

Popyt pochodny

Wybór wielkości produkcji maksymalizującej zysk oznacza popyt 

na czynniki umożliwiający wytworzenie takiej produkcji –

dlatego popyt na czynniki nazywamy popytem pochodnym. 

Popyt na jeden zmienny czynnik w krótkim okresie

Aby scharakteryzować ten popyt zaczniemy od sformułowania 

funkcji zysku w oparciu o czynniki:

Aby wyznaczyć popyt na czynniki maksymalizujący zysk przy 

stałym zatrudnieniu kapitału, zapisujemy pierwszą pochodną

względem pracy i przyrównujemy ją do zera: 

Po rozwiązaniu:

w = p

x

MP

L

rK

wL

K

L

x

p

K

L

x

−

−

=

)

,

(

)

,

(

π

.

0

=

−

∂

∂

=

∂

∂

w

L

x

p

L

x

π

.

Analogicznie dla kapitału: 
Czyli: r = p

x

MP

K

.

0

=

−

∂

∂

=

∂

∂

r

K

x

p

K

x

π

Popyt na jeden zmienny czynnik w krótkim okresie

Z równania 

w = p

x

MP

L

wiemy, że jeżeli praca jest 

jedynym czynnikiem, to popyt na pracę w SR na 

rynku doskonale konkurencyjnym jest 

proporcjonalny do jego produktu krańcowego. 

Praca zatrudniana jest do momentu aż jej koszt 

krańcowy (w) zrówna się z krańcowym wkładem do 

przychodów całkowitych firmy, czyli iloczynem ceny 

dobra, p

x

i MP

L

. 

Popyt na jeden zmienny czynnik w krótkim okresie

Wyprowadzenie funkcji popytu na pracę w SR dla funkcji 

produkcji: 

x = K

1/2

L

1/2

. 

Różniczkujemy funkcję produkcji względem L: 

Wstawiamy powyższy wzór do 

w = p

x

MP

L

: 

Otrzymane równanie rozwiązujemy dla L otrzymując 

funkcję

popytu na L

w SR dla danego zatrudnienia kapitału:

2

/

1

2

/

1

2

1

L

K

MP

L

=

.

2

/

1

2

/

1

2

/

1

2

/

1

2

2

1

L

K

p

L

K

p

w

x

x

=













=

.

( )

2

2

2

/

1

2

/

1

4

)

;

(

*

2

w

K

p

K

w

L

w

K

p

L

x

x

=

⇒

=

,