ZAD1
Dla podanego niżej układu wyznacz kompletny test kontrolny wszystkich niezdatności typu XXX na liniach
wejściowych (X0,X1,X2) linii 4 oraz linii wyjściowej (Y5). Wykorzystaj funkcjonalny model niezawodnościowy
układu.

S­A­C

S­A­C

Kolumny z tabeli:
n0 ­ wynik na Y5 jak wszystko dobrze (nie ma błędów);
n0(0) ­ wynik na Y5 gdyby na X0 podać zawsze 0;
n1(0) ­ wynik na Y5 gdyby na X1 podać zawsze 0;
n2(0) ­ wynik na Y5 gdyby na X2 podać zawsze 0;
n4(0) ­ wynik na Y5 gdyby na linię 4 podać zawsze 0;

ZAD2
Wyznacz sekwencję rozróżniającą automatu zdefiniowanego następująco
­zb symboli wejściowych X = {x,y}
­zb symboli wyjściowych Y = {0,1}
­zb stanów automatu S = {p,q,r}
­tabela przejść i wyjść

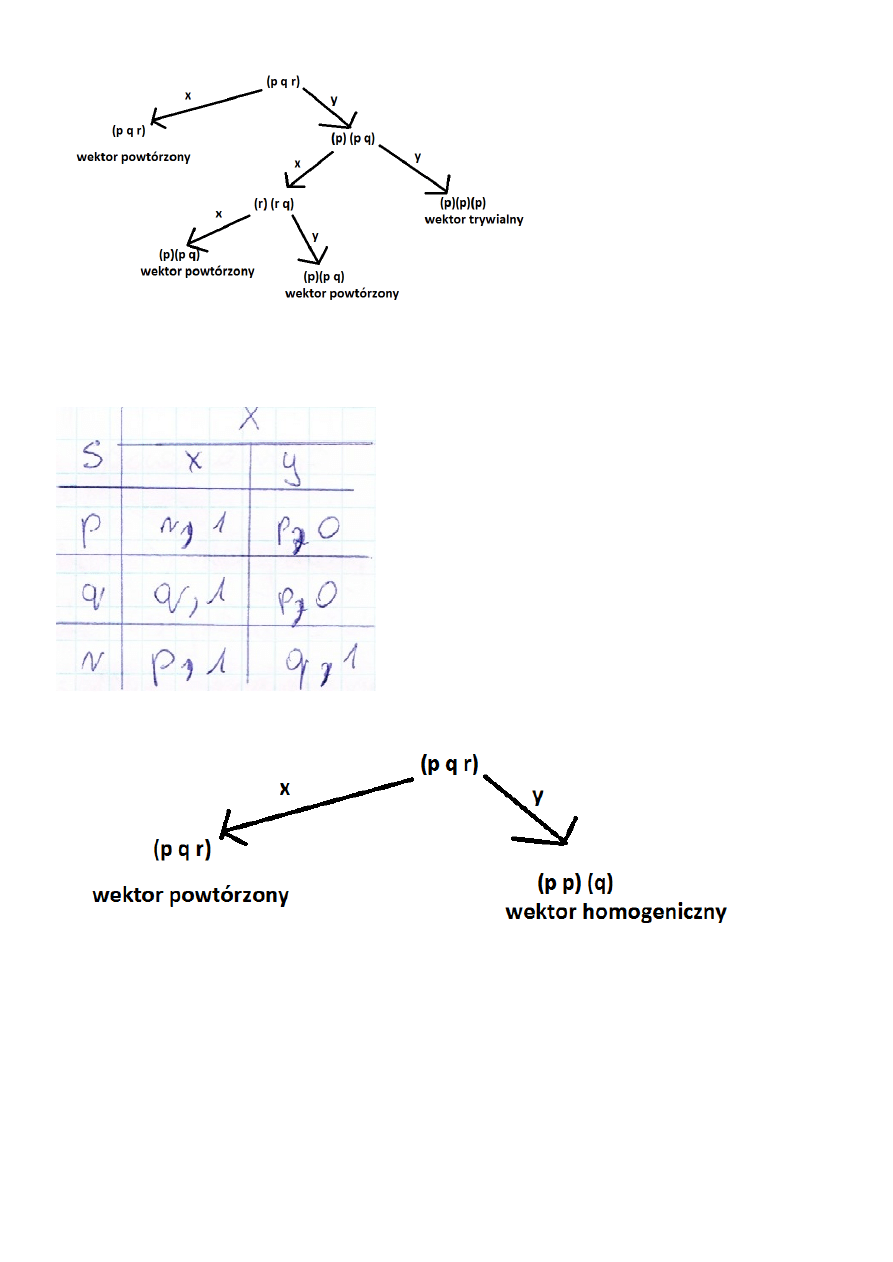
Sekwencja rozróżniająca Xd = {(yy)}.

II

Dla x nie ma sekwencji rozróżniającej, dla y uzyskujemy wektor homogeniczny. Nie istnieje sekwencja
rozrózniająca.
Xd = zbiór pusty.

ZAD 3

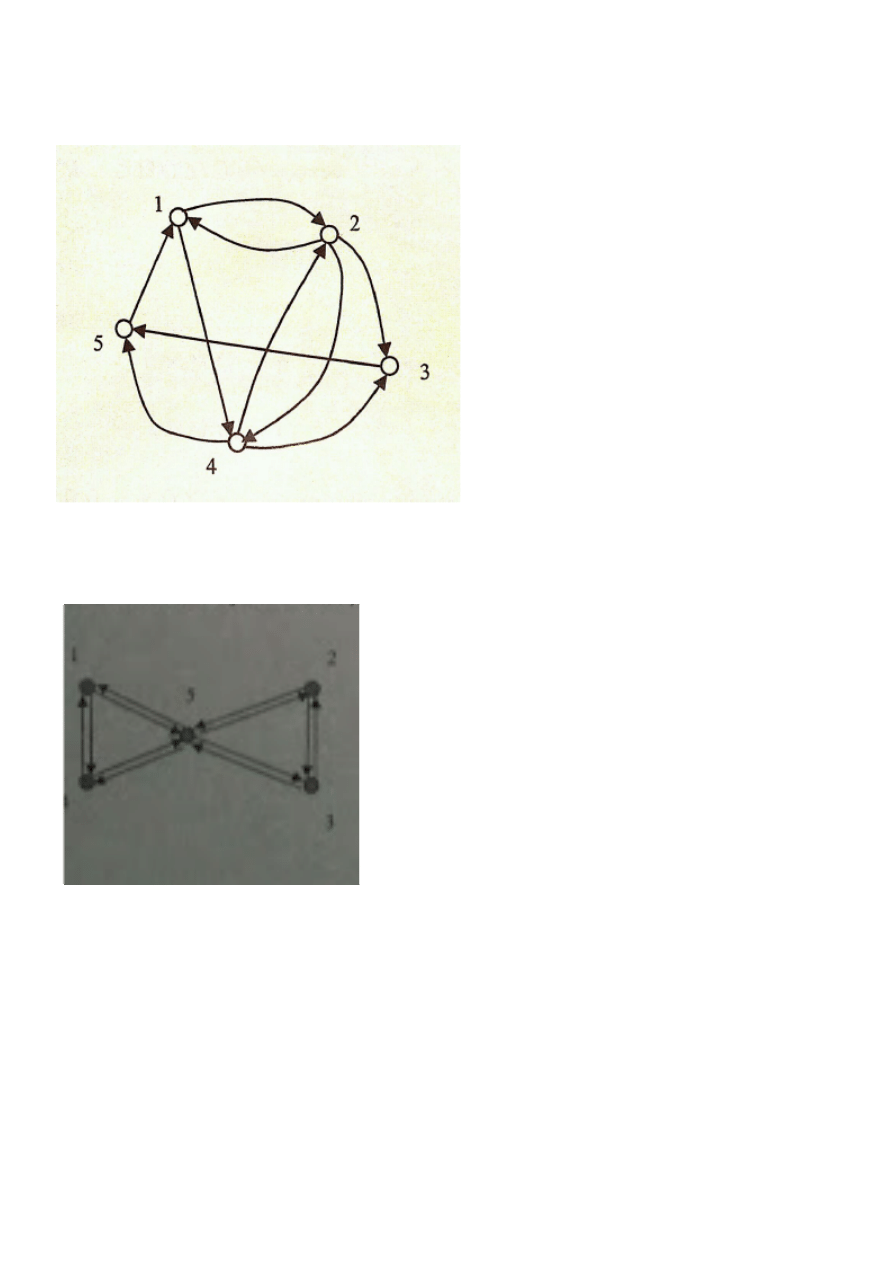
Określ własności diagnostyczne struktury opiniowania diagnostycznego podanej na poniższym rysunku wg
modeli PMC i BGM oraz strategii jednokrokowej:

wersja A:

Dla strategii jednokrokowej wg modelu PMC system jest:.......................................... (ilo diagnozowalny)
Dla strategii jednokrokowej wg modelu BGM system jest:...........................................(ilo diagnozowalny)

wersja B:

Dla strategii jednokrokowej wg modelu PMC system jest:.......................................... (ilo diagnozowalny)
Dla strategii jednokrokowej wg modelu BGM system jest:...........................................(ilo diagnozowalny)

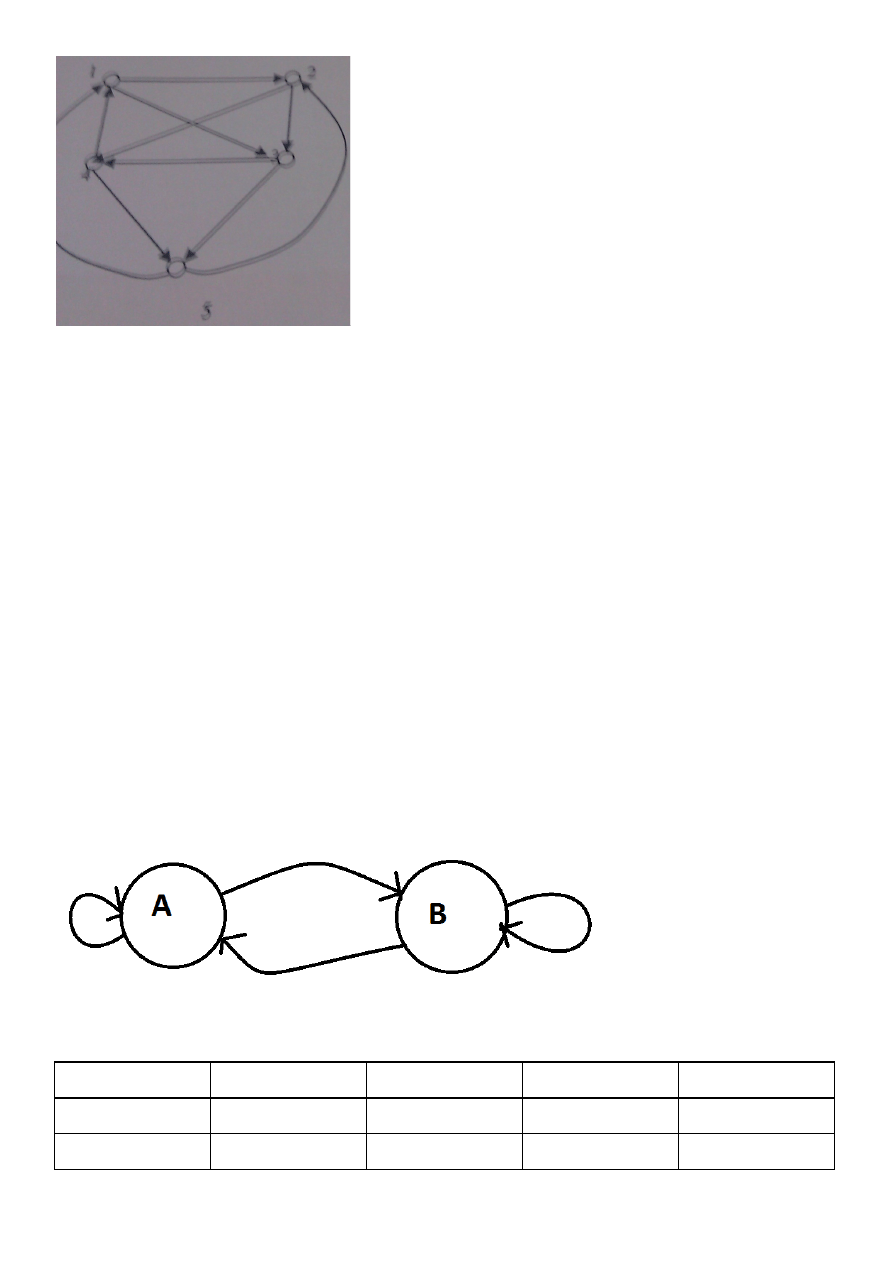
Dla strategii jednokrokowej wg modelu PMC system jest:.......................................... (ilo diagnozowalny)
Dla strategii jednokrokowej wg modelu BGM system jest:...........................................(ilo diagnozowalny)

ZAD 4.
Podaj wady i zalety monitorowania i diagnozowania sieci komputerowej z wykorzystaniem SNMP i RMON.

ZAD 5.
Wykaż (udowodnij), że w m­diagnozowalnym systemie komputerowym typu PMC wg strategii
jednokrokowej liczba niezdatnych jednostek systemu musi spełniać zależność: m<(|E|/2) [2. wariant |E| >=
2m+1] , gdzie |E| ­ jest liczbą wszystkich jednostek systemu.

Przypadek m<(|E|/2) sprowadzamy do przypadku |E|>= 2m+1:
m<(|E|/2) => 2m < |E|, a ponieważ m i |E| jest całkowitoliczbowe 2m +1 <= |E|.

Utwórzmy dwa zbiory, A i B, gdzie E = A suma B, oraz zbiory A i B nie mają części wspólnej, a także
uzyskujemy syndromy przedstawione w tabelce poniżej. Wiemy wtedy, że zbiór A zawiera elementy
poprawne, lub zbiór B. Zagregowane zbiory:

uszkodzony zbiór

dAA

dAB

dBA

dBB

A

X

X

1

0

B

0

1

X

X

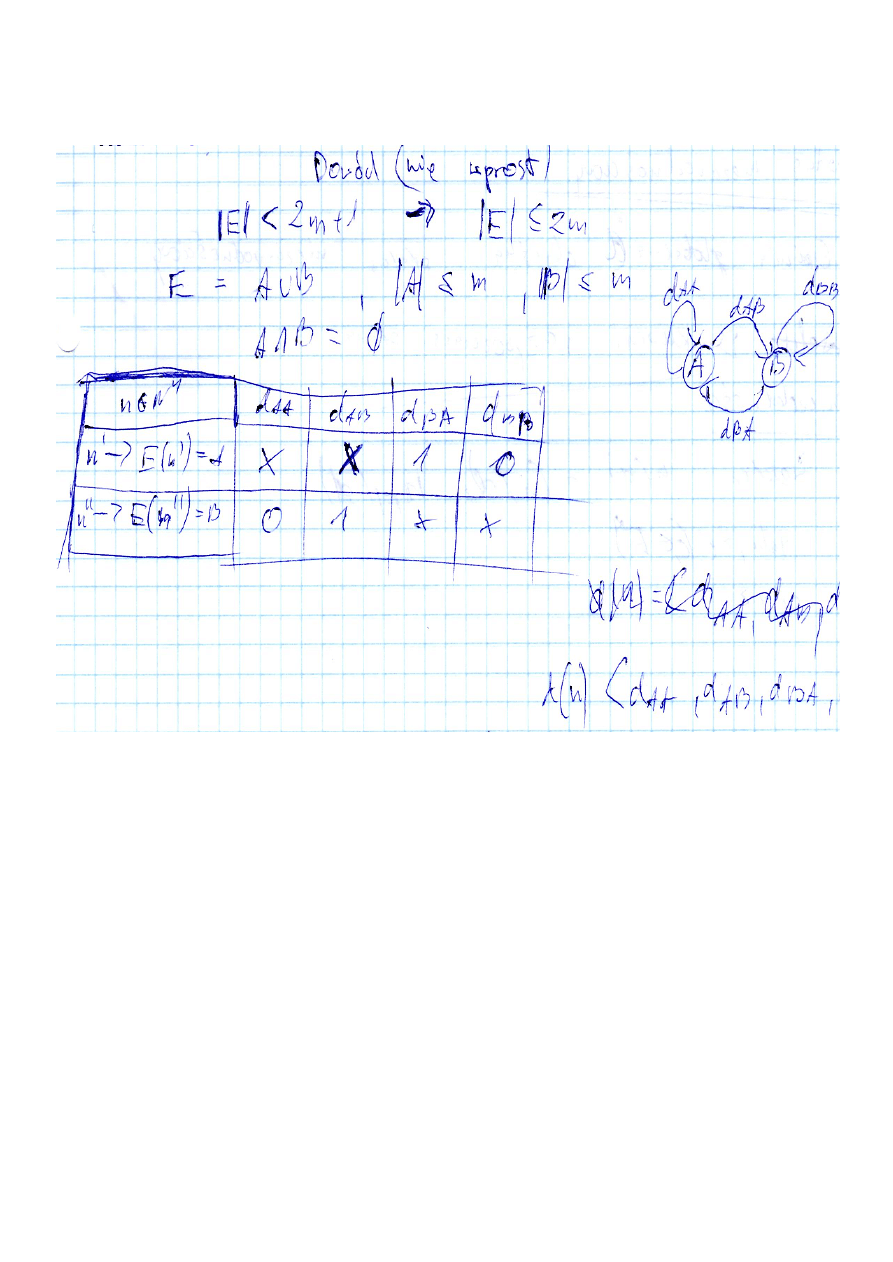
Ponieważ syndromy sie pokrywają, nie ma możliwości określenia, który ze zbiorów zawiera elementy
uszkodzone, a który sprawne.
Dopiero po nadaniu ograniczenia m<|E|/2 (m ­ liczba błędów) możemy wyznaczyć zbiór elementów
uszkodzonych, bo wtedy |A|<=m lub |B|<=m, i odpowiednio |A| lub |B| zawiera same uszkodzone elementy.

ZAD 6. Dana jest sieć procesów o topologii jak na rys a). Zakładając, że procesy moga testować tylko węzły
przyległe, sprawdź, czy istnieje dla tej sieci 2­diagnozowalna struktura opiniowania diagnostycznego typu
PMC. Jeżeli struktura istnieje, przedstaw ją w postaci grafu na rys. b). Przedstaw na odwrocie
uzasadnienie.