2014

Wykład 13B

1

Holografia,

albo iluzja trzeciego wymiaru

LITERATURA:

J. Petykiewicz - Optyka falowa – PWN Warszawa 1986
A.N. Matveev – Optika – Vysšaja Škoła Moskva 1985
E. Hecht - Optyka - PWN Warszaw 2013
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html

Hologram -

fotograficzny

zapis na nośniku przynajmniej dwufalowego

obrazu interferencyjnego

, który w odczycie daje dwa niezależne

od siebie obrazy przestrzenne

3D

(trójwymiarowe).

Holography is "lensless photography"
in which an image is captured not
as an image focused on film,

but as an interference pattern at the film.

2014

Wykład 13B

2

Nieco historii

D. Gabor, fizyk pochodzenia węgierskiego, pracował od 1933 r. w Wielkiej Brytanii. W roku 1971
otrzymał Nagrodę Nobla za wynalazek holografii (1948) i rozwój metod holograficznych zapisu obrazu.

Także Polak, M. Wolfke (1883 -1947) w 1920 r. przedstawił ideę holografii.
Jednakże uległa ona zapomnieniu.

J.N. Denisiuk (ZSRR) w 1962 przedstawił metodę

tzw. grubowarstwowej holografii.

Yuri N. Denisiuk

1927-2006

Denis Gabor 1900- 1979

2014

Wykład 13B

3

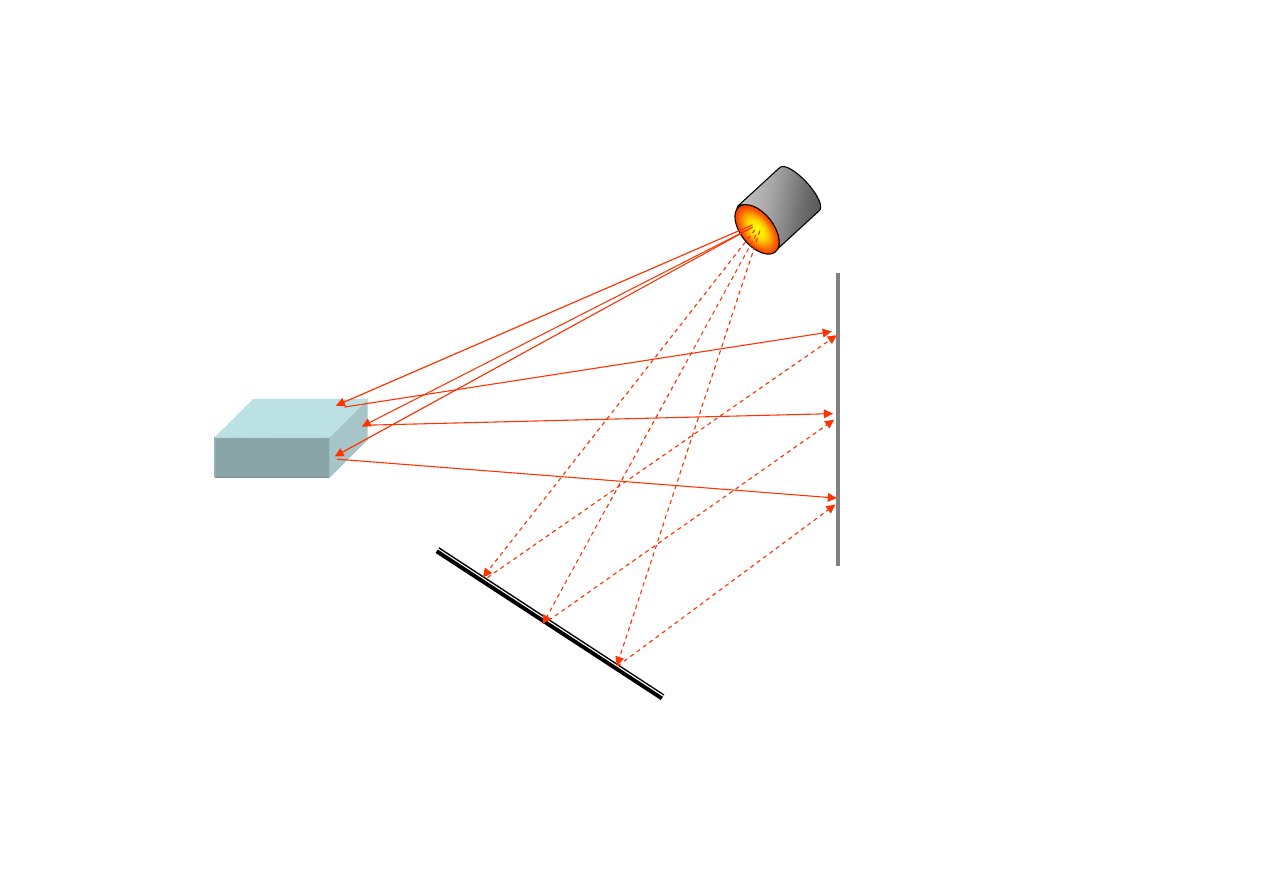
Jak powstaje hologram?

Zw

ierc

iad

ło

Przedmiot

Źródło światła

koherentnego

Zapis

- płyta holograficzna

Str

um

ień

prz

edm

ioto

wy

S

tr

um

ie

ń

re

fe

re

nc

yj

ny

Metoda E. Leitha and Yu. Upatnieksa zapisu hologramów (1962).

2014

Wykład 13B

4

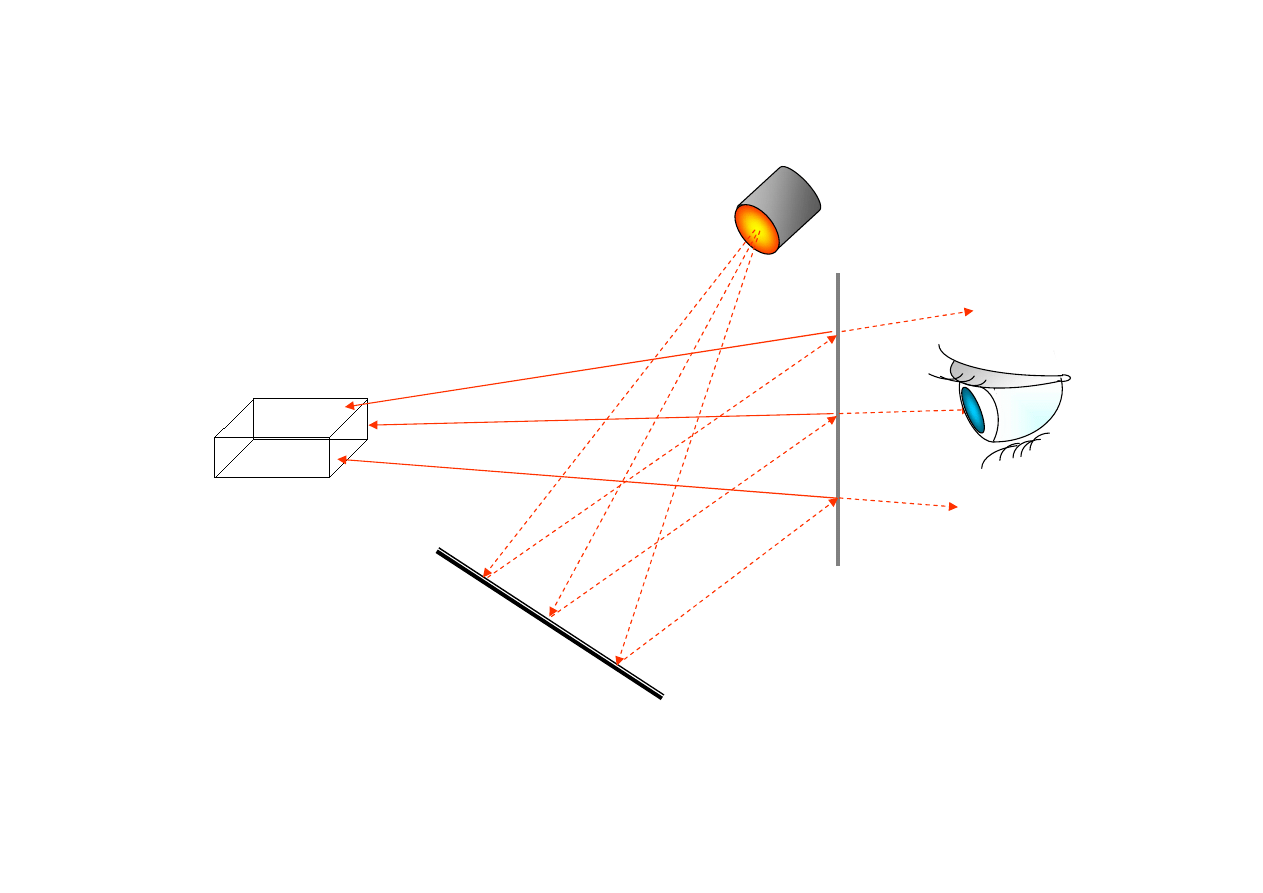
Odczyt hologramu

Zw

ierc

iad

ło

Źródło światła

koherentnego

Wirtualny

przedmiot
(rzeczywisty)

Wirtualny

przedmiot
(pozorny)

S

tru

m

ie

ń

re

ko

ns

tru

kc

yj

ny

Płyta holograficzna

2014

Wykład 13B

5

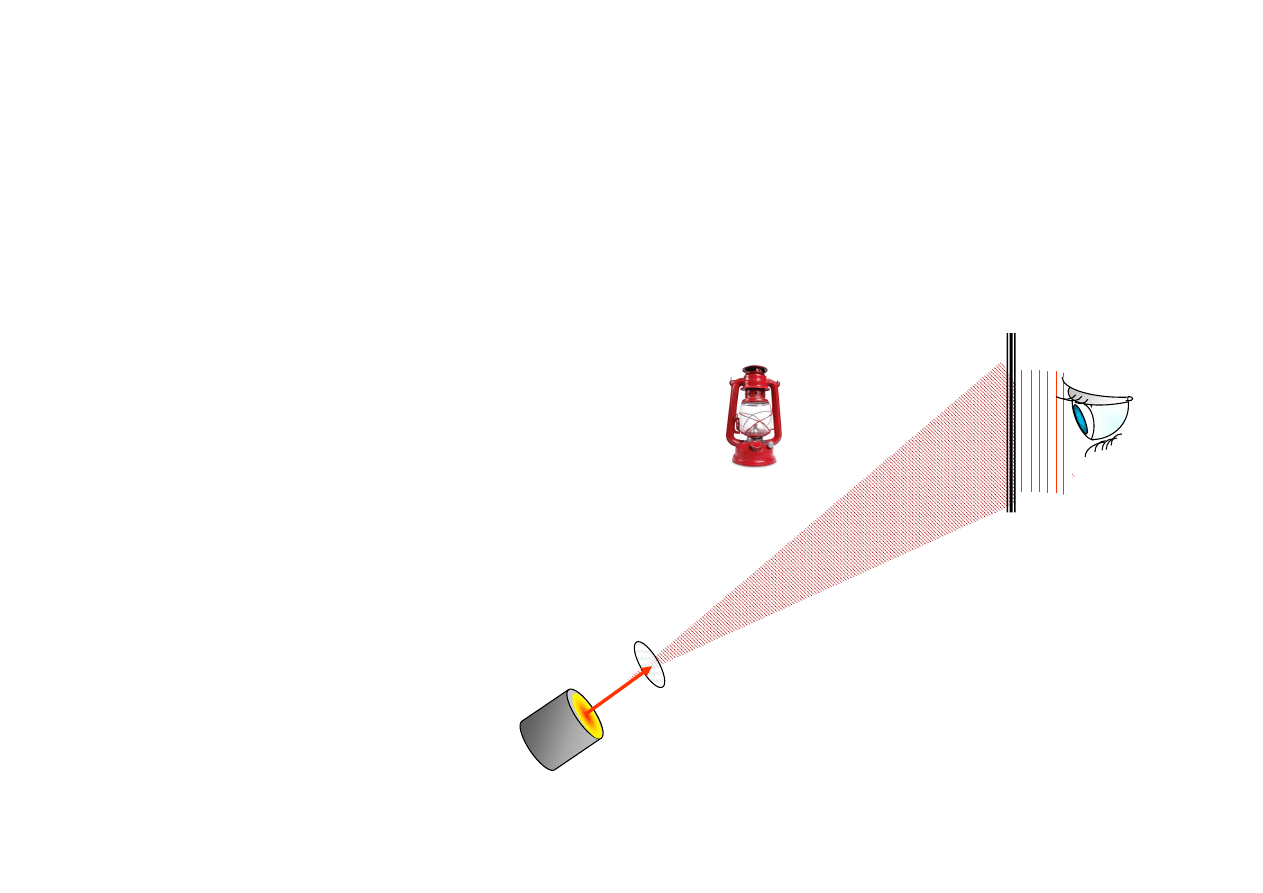
Oglądając hologram transmisyjny

Holografia jest fotografią bez obiektywu - bez soczewek. Obraz jest uchwycony na płytce fotograficznej jako
odwzorowanie interferencyjne (hologram) i może być odtworzony po oświetleniu hologramu przez koherentne
światło laserowe. Patrząc z drugiej strony na taką płytkę widzimy obraz zawieszony w przestrzeni.
Jest to charakterystyczne dla obrazów holograficznych.

Hologram

Tylko w koherentnym świetle

lasera obraz z hologramu

będzie wystarczająco ostry.
Można także użyć światła
przefiltrowanego,
ale obraz już nie będzie
tak wyraźny.

Przemiatający strumień laserowy powinien być
umieszczony i zorientowany względem płytki fotograficznej

w ten sam sposób jak strumień referencyjny użyty podczas

naświetlania płytki. Wtedy obraz będzie widoczny w tej samej pozycji

w jakiej był oryginalny przedmiot względem płytki.

To wygląda tak jakby światło odbite od przedmiotu
zostało zamrożone i teraz znowu zaczyna płynąć
do Twojego oka, odtworzone za pomocą
światła laserowego.

2014

Wykład 13B

6

Podstawowe konfiguracje do

wykonywania hologramów

Ze względu na wzajemne usytuowanie źródła wiązki odniesienia R,
obiektu O i ośrodka światłoczułego H mamy trzy typy układów
holograficznych:

• HG — układ współosiowy (hologram

Gabora

), ukł. gaborowskie, gdy

płyta holograficzna, obiekt i źródło wiązki odniesienia umieszczone są
wzdłuż jednej prostej, a więc wiązka przedmiotowa i wiązka odniesienia
biegną współosiowo;
• HL-U — układ z boczną wiązką odniesienia (hologram

Leitha-

Upatnieksa

), gdy kierunki propagacji fali przedmiotowej i fali odniesienia

tworzą ze sobą pewien kąt, lecz do płyty holograficznej dochodzą z tej
samej strony;
• HD — układ z wiązkami przeciwsobnymi (hologram

Denisiuka

), gdy

wiązki przedmiotowa i odniesienia docierają do ośrodka rejestrującego z
przeciwnych stron.

2014

Wykład 13B

7

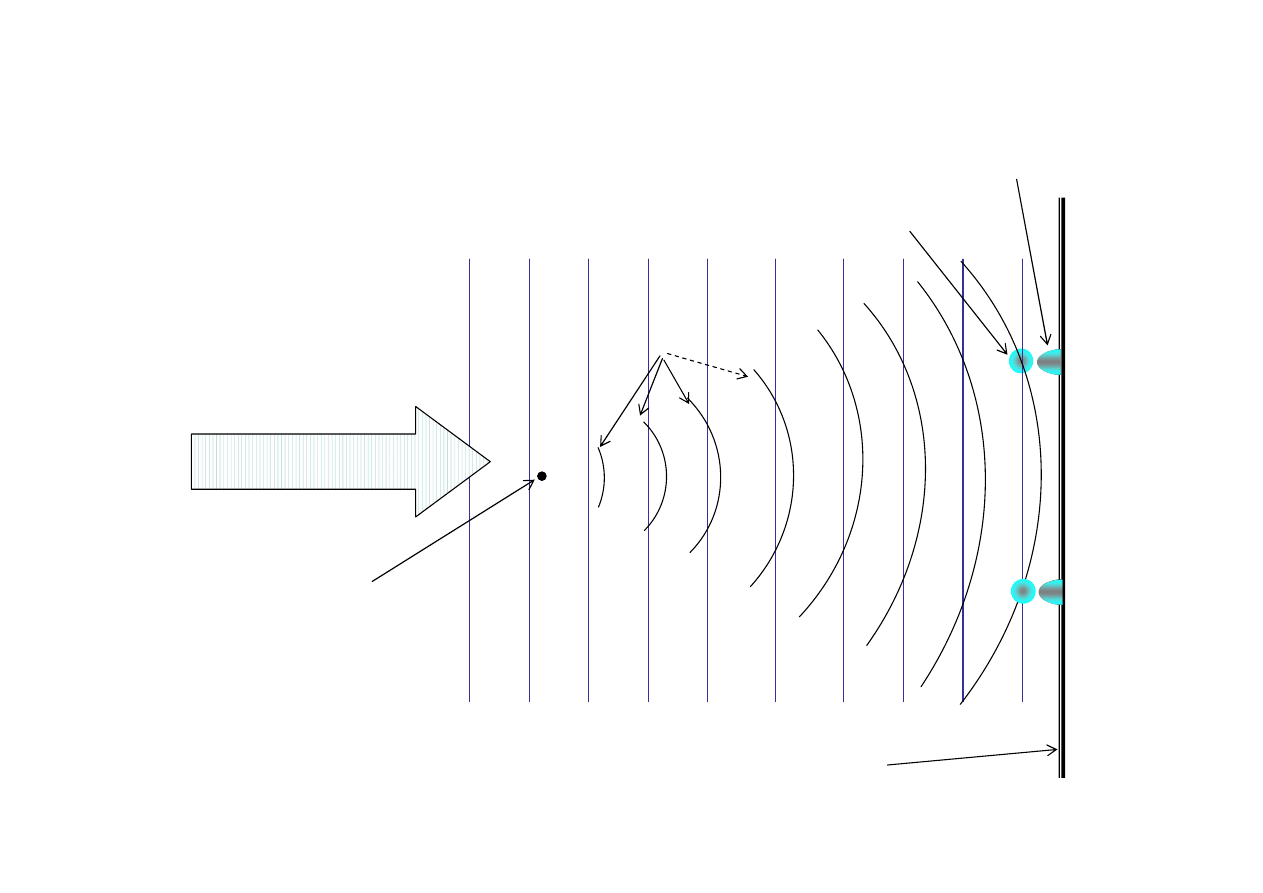
Hologram punktu

Koherentne

fale płaskie z lasera

P

Obiekt

punktowy

Płytka holograficzna

Fale rozpraszane

przez obiekt w punkcie P

Interferencja fali
płaskiej i załamanej

Obraz interferencyjny

rejestrowany na filmie

2014

Wykład 13B

8

2014

Wykład 13B

9

2014

Wykład 13B

10

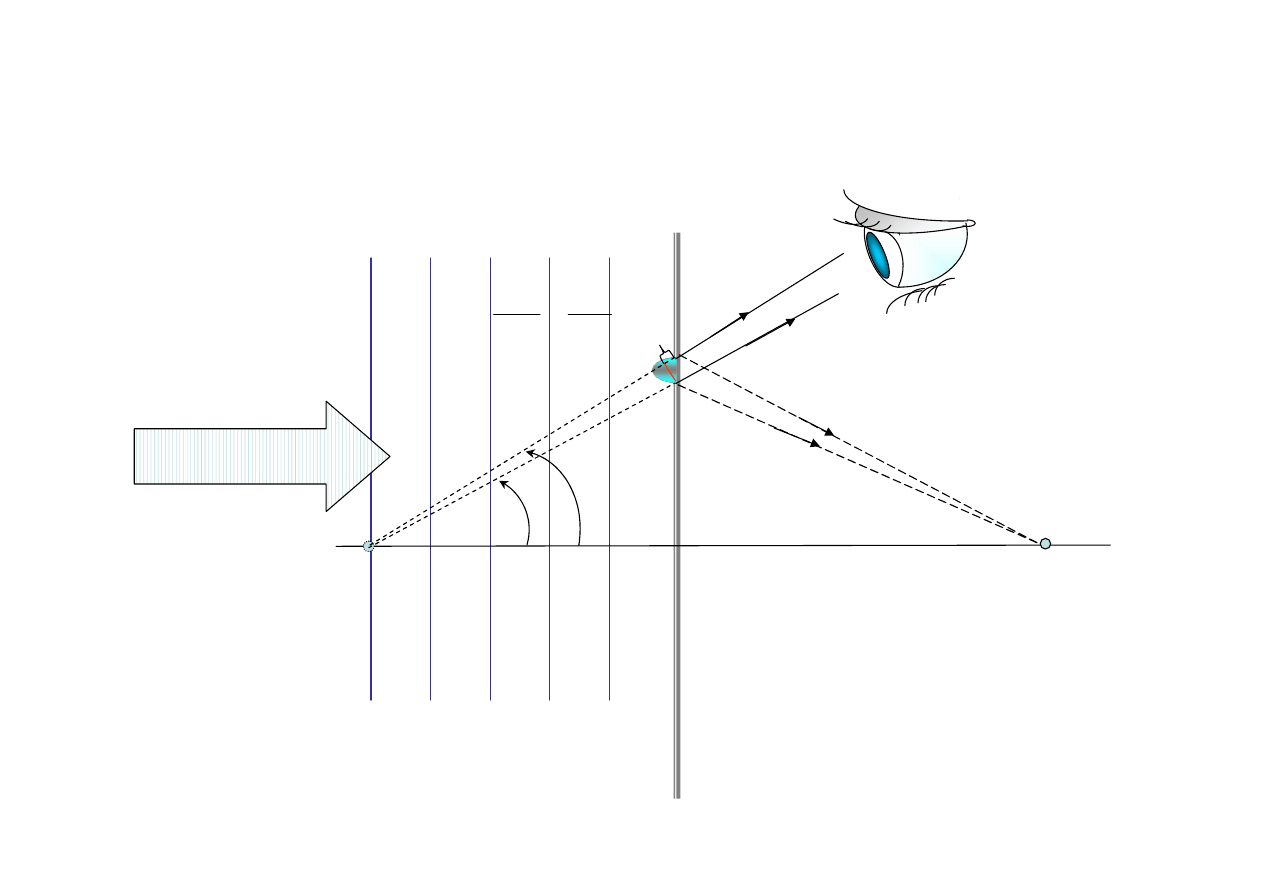
Strefa Gabora

Koherentne

fale płaskie z lasera

Obraz

wirtualny

Film

Interferencja fali
płaskiej i załamanej

Obraz

realny

P

P’

S

1

S

2



1



2

Płytka

ze strefą Gabora

2

1

PS

PS







Fale rozpraszane przez
płytkę ze strefą Gabora
interferują konstruktywnie,
dając rzeczywisty obraz
w punkcie P i wirtualny
w punkcie P’.

2014

Wykład 13B

11

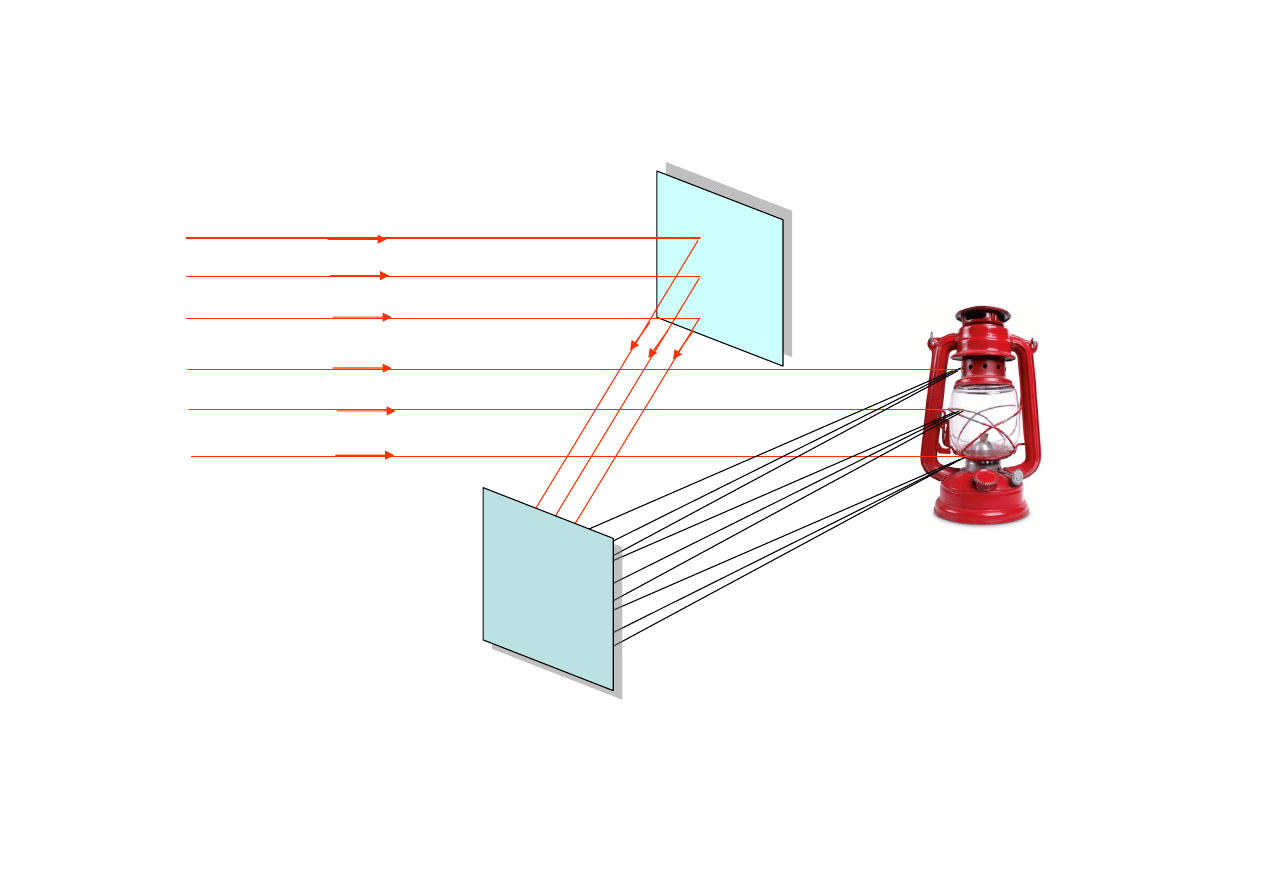
Powstawanie hologramu

Strumień z lasera

Lustro

Film

Hologram

Strumień z lasera

F

a

la

o

dn

ie

si

e

n

ia

Obiekt

Fa

la p

rze

dm

iot

ow

a

Aby otrzymać hologram
fala odniesienia musi być
koherentna ze światłem
rozproszonym przez powierzchnię
obiektu holografowanego.
Zatem dla dużych obiektów
źródło światła musi mieć duży
stopień koherencji przestrzennej.

Długość koherencji lasera powinna być większa od maksymalnej różnicy dróg przebytych przez falę
odniesienia i falę przedmiotową.

2014

Wykład 13B

12

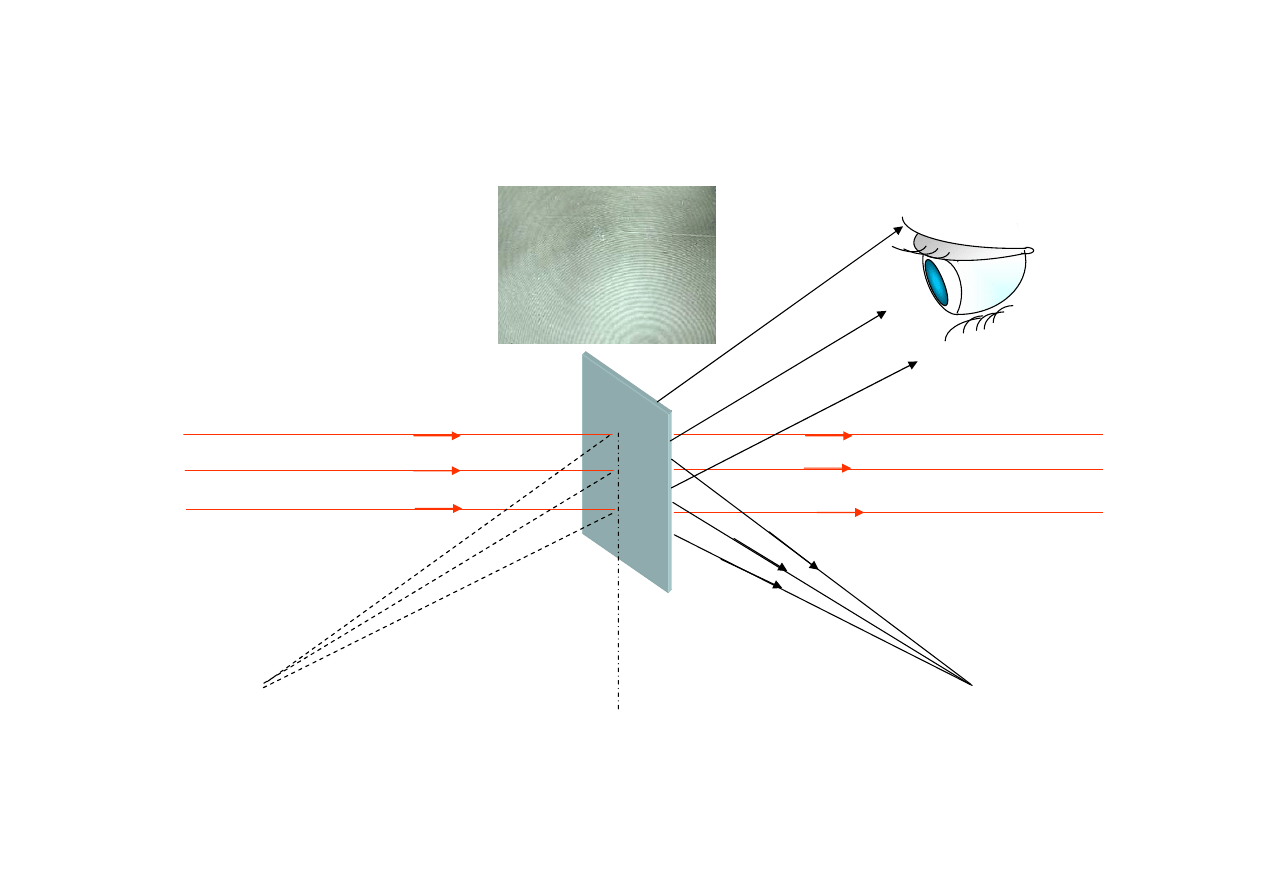
Rekonstrukcja frontów fali przez hologram

Strumień z lasera

Fala zerowego rzędu

Fala I rzędu,

prześwietlająca

Fala I rzędu

Obraz wirtualny

Obraz realny

Hologram

2014

13

Hologram fali płaskiej





j

0

e

t kz

s

s

E

E













j

0

e

z

x

t k z k z

n

n

E

E











-z dokładnością to stałej fazy, czyli
z założenia E

0s

i E

0n

- rzeczywiste

k

k

n



z

x



dla 0

Fala nośna (odniesienia):

Biorąc pod uwagę, że

sin oraz

cos

x

z

k

k

k

k

k











to z dokładnością do wielkości II rzędu względem kąta



~ 0, mamy









j

j

s

0

in

0

e

e

t kz

kx

n

s

n

s

E

E

E

E

E



















Zatem intensywność prążków na kliszy będzie funkcją

 





0

0

2

1
2

0

2

0

1

2

2

2

cos

sin

s

s

n

n

I x

E

kx

E

E

E

E



















- czyli na filmie zostanie zapisana także różnica faz pomiędzy falą sygnałową
a falą nośną (przyjmując, że faza tej drugiej jest dana).

Fala sygnałowa (przedmiotowa):

2014

Wykład 13B

14

Płytka fotograficzna hologramu

Po naświetleniu i wywołaniu emulsji srebrowej zaczernienie na kliszy wynosi

2

lg

Q

E





gdzie



– współczynnik kontrastu w teorii fotografii.

Po wywołaniu, współczynnik przepuszczania światła przez kliszę ma postać

 

2

2

E









Uwzględniając wyrażenie na E, mamy zatem





2

0

0

2

2

0

0

2

cos

sin

s

s

n

n

E

E

E E

kx























Jednakże zazwyczaj , więc powyższe wyrażenie można uprościć
następująco:

0

0

s

n

E

E



















0

0

0

0

0

0

0

0

2

2

0

2

2

2

0

1

2

cos

sin

=

2

2

2

cos

sin

s

n

s

n

n

s

n

s

n

n

E

E

E

E

E

kx

E

E

E

E E

kx





















 





























2014

Wykład 13B

15

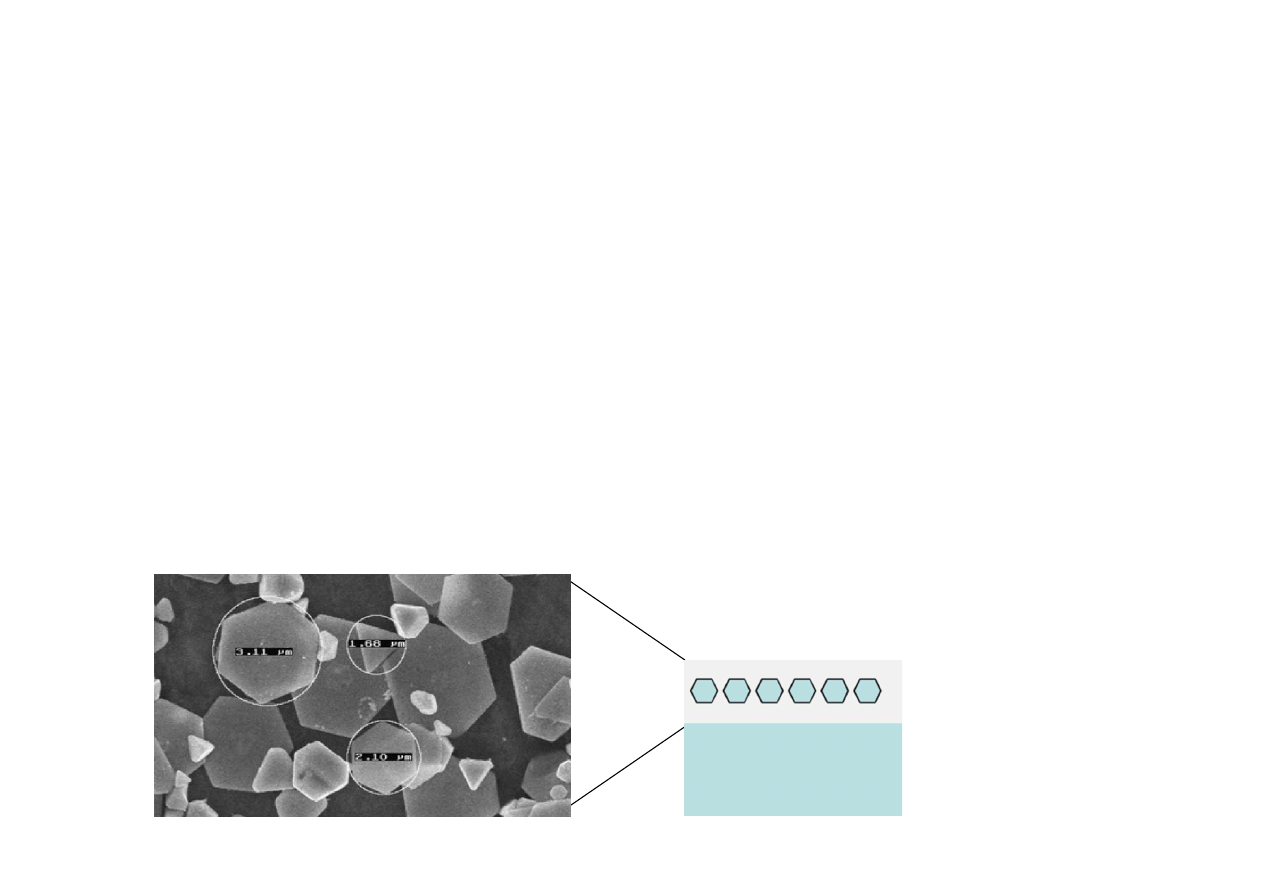
Film z emulsją z halogenkiem srebra

1. Ekspozycja: Jest to zazwyczaj bromek srebra, w którego kryształki uderzają fotony.

Jon Br

-

uwalnia elektron, który z kolei jest przechwytywany przez jon Ag

+

, tworząc neutralny

atom srebra. Atomy srebra łączą się ze sobą w małe koagulaty powodując zaczernienie filmu

w miejscach dobrze naświetlonych. W ten sposób powstaje obraz utajony.

2. Wywoływanie: Składnik wywoływacza dostarcza elektrony do ziarn, przekształcając je

w metaliczne srebro. Naświetlone ziarna przekształcają się bardzo szybko. Metaliczne srebro
jest nieprzeźroczysty, a obszary naświetlone stają się ciemne, tworząc obraz negatywowy.

3. Przerywacz: Rozpuszcza i wymywa składnik wywołujący, który mógłby dalej

przekształcać wszystkie ziarna.

4. Utrwalanie: Nie naświetlone kryształki bromku srebra są rozpuszczane, pozostawiając

przekształcone (wywołane) ziarna srebra. Do tego momentu film jest wciąż czuły na światło.

5. Płukanie: Woda usuwa pozostałe składniki chemiczne z emulsji.
6. Suszenie: Odparowanie wody

.

Kodak TMAX400. Professional B&W
negative film. Average grain size: 2-3um

2014

Wykład 13B

16

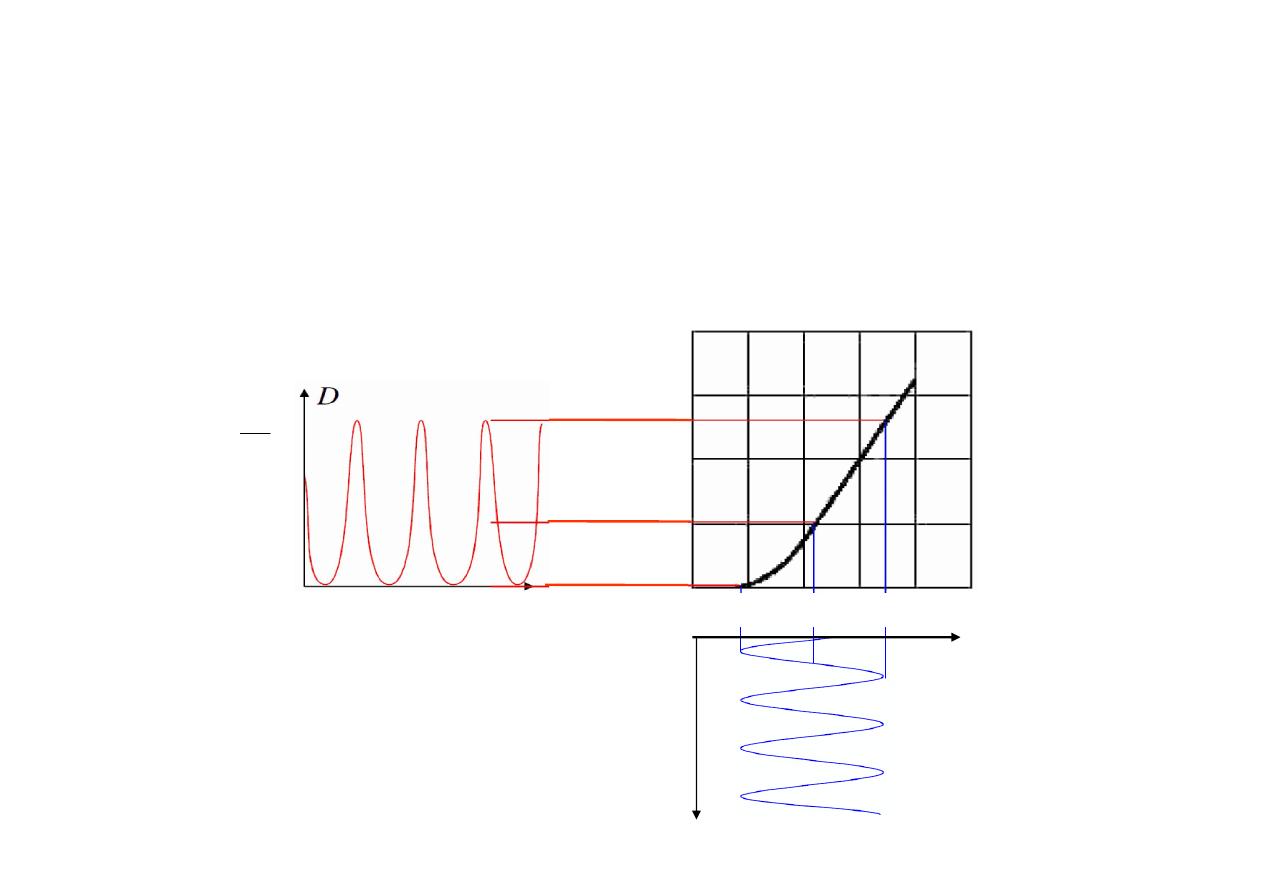
Krzywa Hurtera-Driffielda

Na podstawie ostatniego slajdu można oczekiwać, że film stanie się
bardziej nieprzeźroczysty, jeżeli jest wystawiony na więcej energii.
Jest to przedstawione jako krzywa HD zależności gęstości optycznej od
strumienia energii podczas ekspozycji.

Zatem dla D=1 mamy 10% transmisji, D=2 to 1%, itd.
- nieraz skrótowo opisane jako OD

4

3

2

1

0

0,5 1,0 1,5 2,0 2,5 [mJ/cm

2

] energii

G

ę

st

o

ść

op

ty

czna

Ekspozycja:
E

.

t= I [mJ/cm

2

][s]

x

• Zbyt mała ekspozycja = blady film
• Za duża = nieprzeźroczysty
• Potrzeba, aby



było proporcjonalne do

Ekspozycji
• Nieliniowości = składowe harmoniczne
• Pełne wykorzystanie dynamiki i zapis
liniowy są generalnie przeciwnościami w
dążeniu do wysokiej jakości hologramu

2

1

lg

D

















Gęstość

http://www.slavich.com/pfg03m.htm

2014

Wykład 13B

17

Avec ULTIMATE-08, l'Holographie est

enfin facile !

• Les plaques sont prêtes à l’emploi (pas de pré-bain avant usage)
• grains ultrafins (8nm) pour une résolution inégalée
• contraste extrèmement élevé donnant de fortes efficacité de diffracti
même à ratio objet/référence faible (1/10) comme en holographie d
Denisiuk.
• 4 versions de sensibilisation de base selon votre laser
DR= Rouge profond R=rouge, BG= bleu-vert, B= Blue
• Enregistrement d’hologrammes en transmission ou réflexion
• Meilleure efficacité de diffraction du marché (jusqu’à 95%, selon
shéma d'enregistrement)
• Meilleure rapport sensibilité/résolution du marché
• Substrats :verre de 3mm d’épaisseur ou film triacétate de 190µm
• transparence totale de la plaque après développement (aucun bruit)
• Stockage: au réfrigérateur à 4°C, durée de vie supérieure à 2 ans. Au
moins 6 mois à l'ambiant (nouveau stabilisateur).
• ET SURTOUT une autre innovation mondiale:
Un développement en 2 bains Prêts à l’Usage et Non
Toxiques (Ils se conservent au moins un an à l'ambiant)

2014

Wykład 13B

18

Simple Holography

"Making holograms has become so easy that college
and even grade-school students can
learn holography first-hand."
Read more:

http://www.integraf.com/holography_kit_1.htm#ixzz2omAROSGd

The Easiest Way to Make Holograms

2. THE LASER
The figure below shows a Class IIIa diode laser with an output
of 3 to 4 mW when operated by 3.0 v dc. If the power is supplied

by batteries, its red light of wavelength 650 nm achieves

a coherence length exceeding 1 m after a warm-up period of a few minutes.

The traditional helium-neon laser, on the other hand, operates

on dangerously high voltages, is prone to breakage, has a shorter shelf life,
and a coherence length of approximately 30 cm.

3. STABLE SUPPORT FOR LASER
An excellent support for such a small laser is a wooden clothespin, as shown below.
For mechanical stability and maneuverability, the clothespin holding the laser
is stuck into a cup of sand, salt, or sugar (not pepper!). On the other hand,
for schools with available laboratory hardware, the clothespin can be glued
to a rod and mounted on a lab stand with a right-angle clamp.

2014

19

Czytanie hologramu

0

0

0

0

0

0

2

2

j

sin

-j

sin

=2

e

e

n

s

n

s

n

s

kx

kx

E

E

E E

E E



















Następnie odrzucając niepotrzebny do dalszych rozważań mnożnik
Ostatnie wyrażenie można zapisać w wygodniejszej postaci





2

0

/ 2

n

E



 

Teraz skierujemy na taki hologram z kierunku fali sygnałowej falę płaską





j

0

e

t kz

c

c

E

E









Na wyjściu hologramu, po jego drugiej stronie pojawi się pole świetlne:

















0

0

0

0

0

0

-j

-j

sin

2

2

0

0

-j

sin

0

=

2

e

e

e

n

s

n

s

n

s

t kz

t kz kx

wy

c

c

c

t kz kx

c

E

E

E

E

E

E E E

E E E





































- które składa się z

trzech pół świetlnych.

Pierwszy człon tego wyrażenia opisuje falę płaską 1
zmierzającą w kierunku osi 0z, i prostopadle na hologram.
Drugi człon opisuje falę 2. przemieszczającą się pod kątem



względem osi 0z w kierunku dodatnich wartości x
Trzeci człon opisuje falę przemieszczającą się w dół
względem osi 0z.
To pole świetlne jest obrazem dyfrakcji fali płaskiej padającej
na hologram – i jest to dyfrakcja I rzędu, bowiem współczynnik
przepuszczania zmienia się tylko harmonicznie.

k

3

k

n

k

1

z

x

2014

Wykład 13B

20

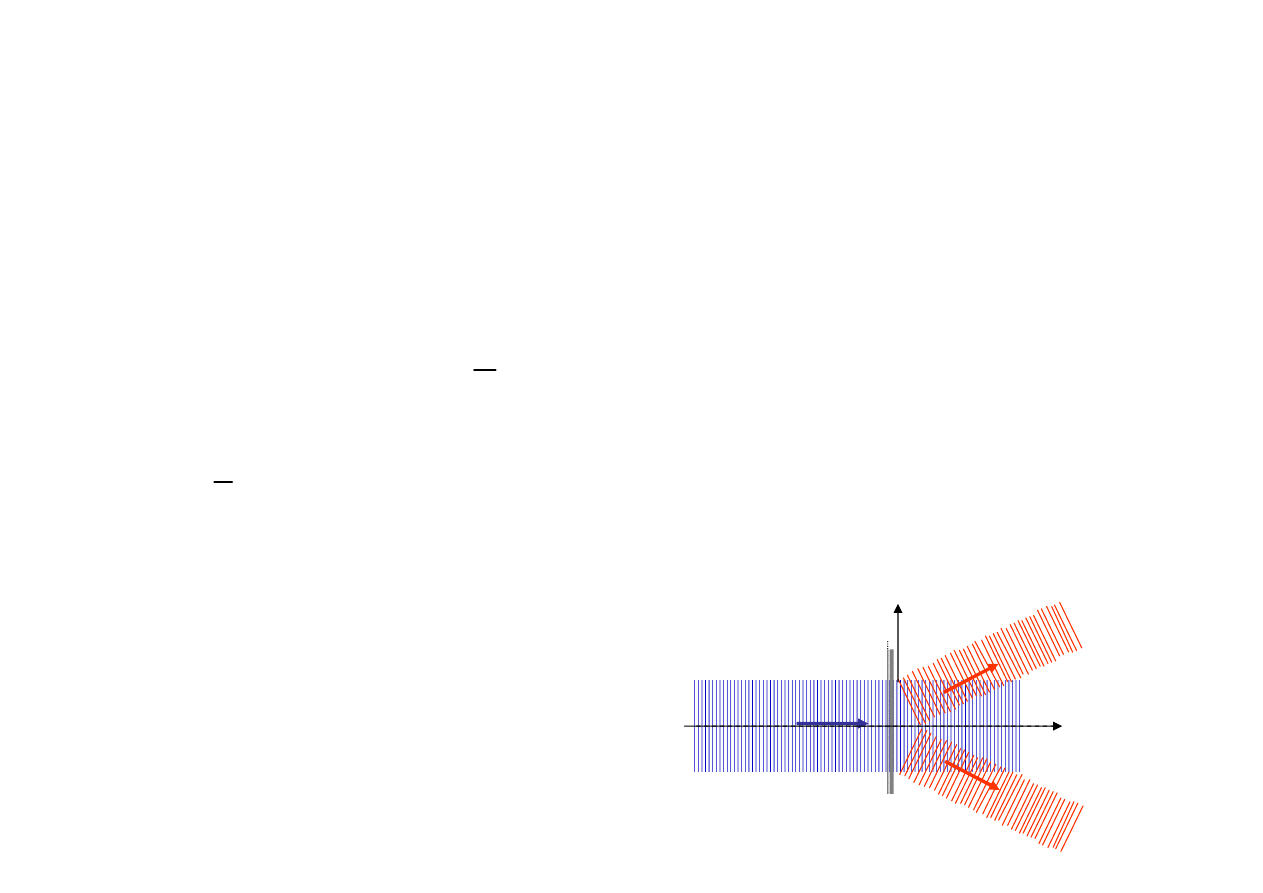
Zapis obiektu 1D na hologramie





2

0

j

2

0

e

t kz kx

z

s

s

E

E



















k

k

n

z

x

Od obiektu 1D rozchodzi się sferyczna fala,
którą na powierzchni kliszy fotograficznej
zapiszemy jako falę sygnałową

z

0

- bez uwzględnienia zmian amplitudy fali
przy oddalaniu się od obiektu 1D.

Całkowite natężenie pola na ekranie (kliszy):
tutaj przyjmuje postać

n

s

E

E

E















2

0

j

2

j

j

sin

0

0

e

e

e

kx

z

t kz

kx

n

s

E

E

E





















skąd

















2

2

0

0

2

j

sin

2

-j

sin

2

2

2

0

0

0

0

2

2

2

0

0

0

0

0

e

e

2

cos

sin

2

kx

kx

z

kx

kx

z

n

s

n

s

n

s

n

s

E

E

E

E E

E

E

E E

kx

kx

z





















































Widać zatem, że relacje fazowe między falami są uwzględnione w tym zapisie.

2014

21

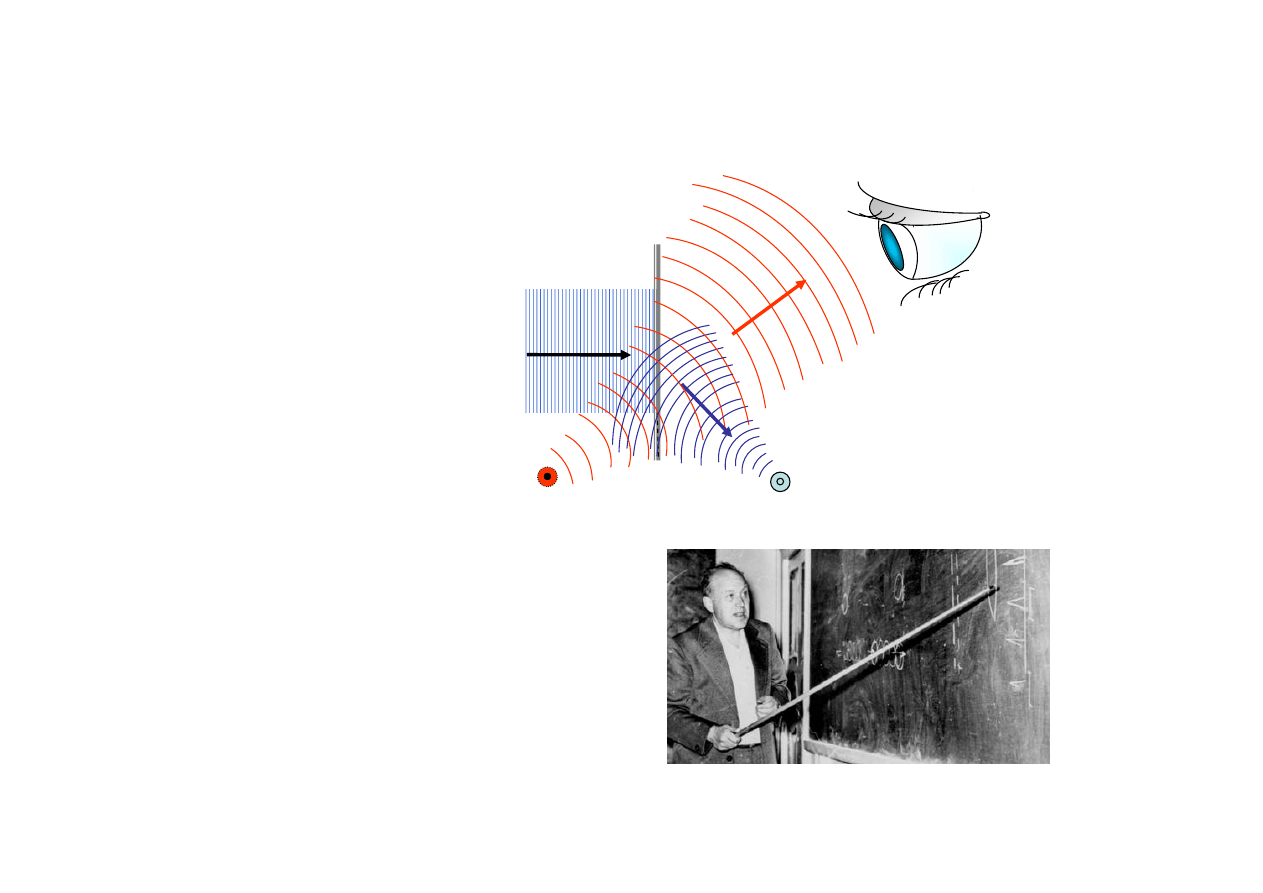
Hologram obiektu 1D









2

2

0

0

0

0

0

0

0

0

j

sin

2

-j

sin

2

2

2

=2

e

e

n

s

n

s

n

s

kx

kx

z

kx

kx

z

E

E

E E

E E











































j

0

e

t kz

c

c

E

E









Współczynnik przepuszczania światła przez taki hologram wynosi zatem

I dlatego po jego oświetleniu falą płaską
na jego wyjściu będziemy obserwować pole świetlne

























2

0

0

0

0

0

2

0

0

0

-j

sin

2

-j

2

2

0

0

-j

sin

2

0

=

2

e

e

e

n

s

n

s

n

s

t kz kx

kx

z

t kz

wy

c

c

c

t kz kx

kx

z

c

E

E

E

E

E

E E E

E E E











































Pierwszy człon tego wyrażenia opisuje falę płaską 1.
zmierzającą w kierunku osi 0z, i prostopadle padającą na hologram.
Drugi człon opisuje falę 2. przemieszczającą się pod kątem -



względem osi 0z w kierunku ujemnych wartości x,
bo w eksponencie tego wyrażenia jest jkxsinJest to zapis fali
sferycznej ugiętej w kierunku rozprzestrzeniania się fali
(bo w eksponencie jest także -jkx

2

/(2z

0

) ).

Trzeci człon opisuje falę przemieszczającą się w górę
względem osi 0z, bo w eksponencie jest -jkxsin Ta fala sferyczna
Jej czoła są ugięte są przeciwnie do kierunku przemieszczania
(bo w eksponencie jest jkx

2

/(2z

0

) ).Jest ona całkowicie identyczna

z falą sferyczną, która wychodzi od obiektu 1D podczas zapisu
hologramu i daje pozorne wrażenie tego obiektu znajdującego się

w tym samym miejscu, w którym był obiekt rzeczywisty podczas zapisu.

k

1

x

k

2

z

k

3

2014

Wykład 13B

22

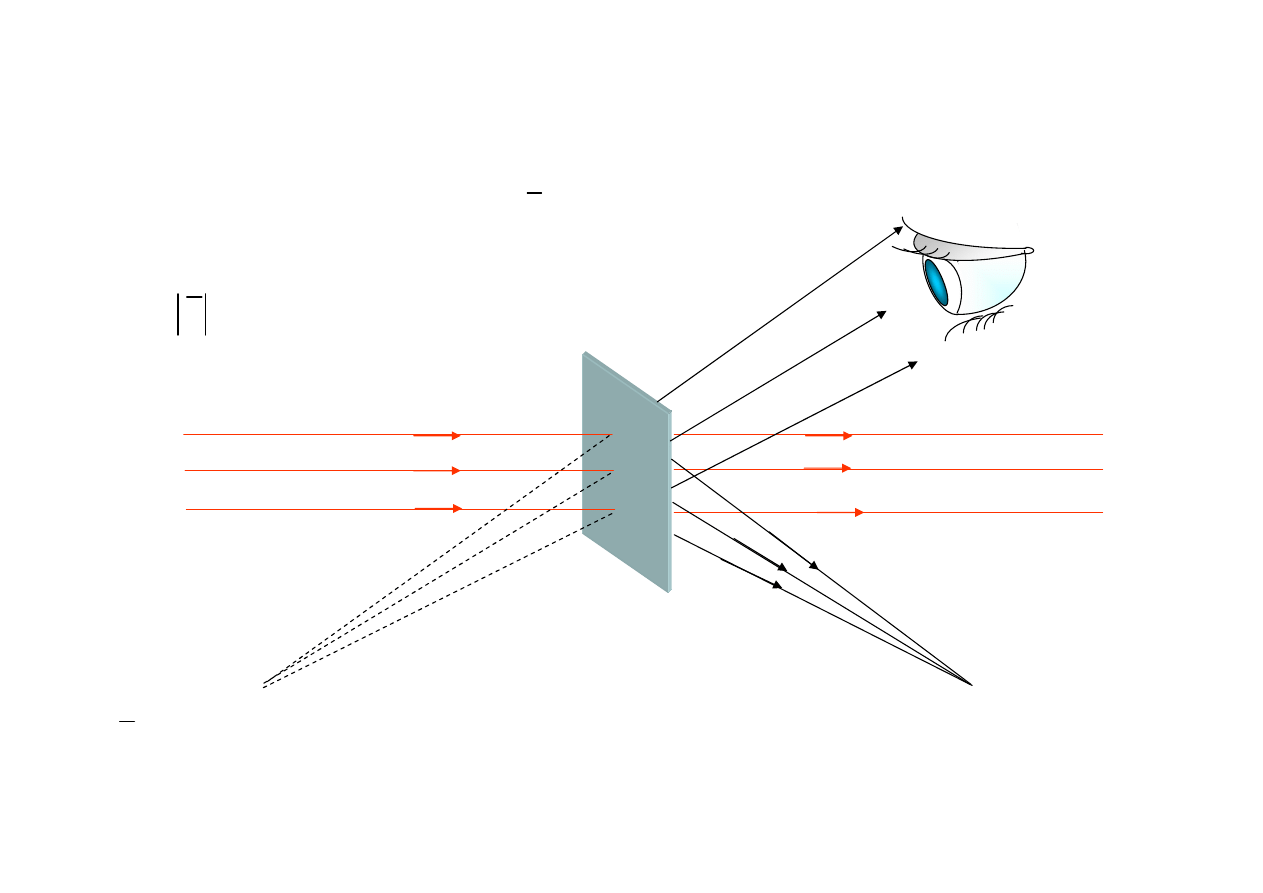
Obraz rzeczywisty i pozorny punktu

z hologramu 1D

Punkt wirtualny

Punkt realny

Denisiuk à l'Institut d'Optique d'Etat S.I. Vavilov à Leningrad

2014

Wykład 13B

23

Hologram dowolnego obiektu













j

,

0

,

,

e

t kz

x y

s

s

E

x y

E

x y

































2

j

sin

-j

sin

2

2

0

0

0

0

e

e

kx

kx

n

s

n

s

E

E

E

E E

 

 













Strumień z lasera

Fala zerowego rzędu

Fala I rzędu

Fala I rzędu

Obraz wirtualny

Obraz realny

Ho

log

ram

Fala skierowana na hologram:

Zapis na hologramie:

















0

0

0

0

0

0

-j

-j

sin

-j

sin

2

2

0

0

0

=

2

e

e

e

n

s

n

s

n

s

t kz

t kz kx

t kz kx

wy

c

c

c

c

E

E

E

E

E

E E E

E E E





 



 











 



 











Fala wygenerowana z hologramu:

2014

Wykład 13B

24

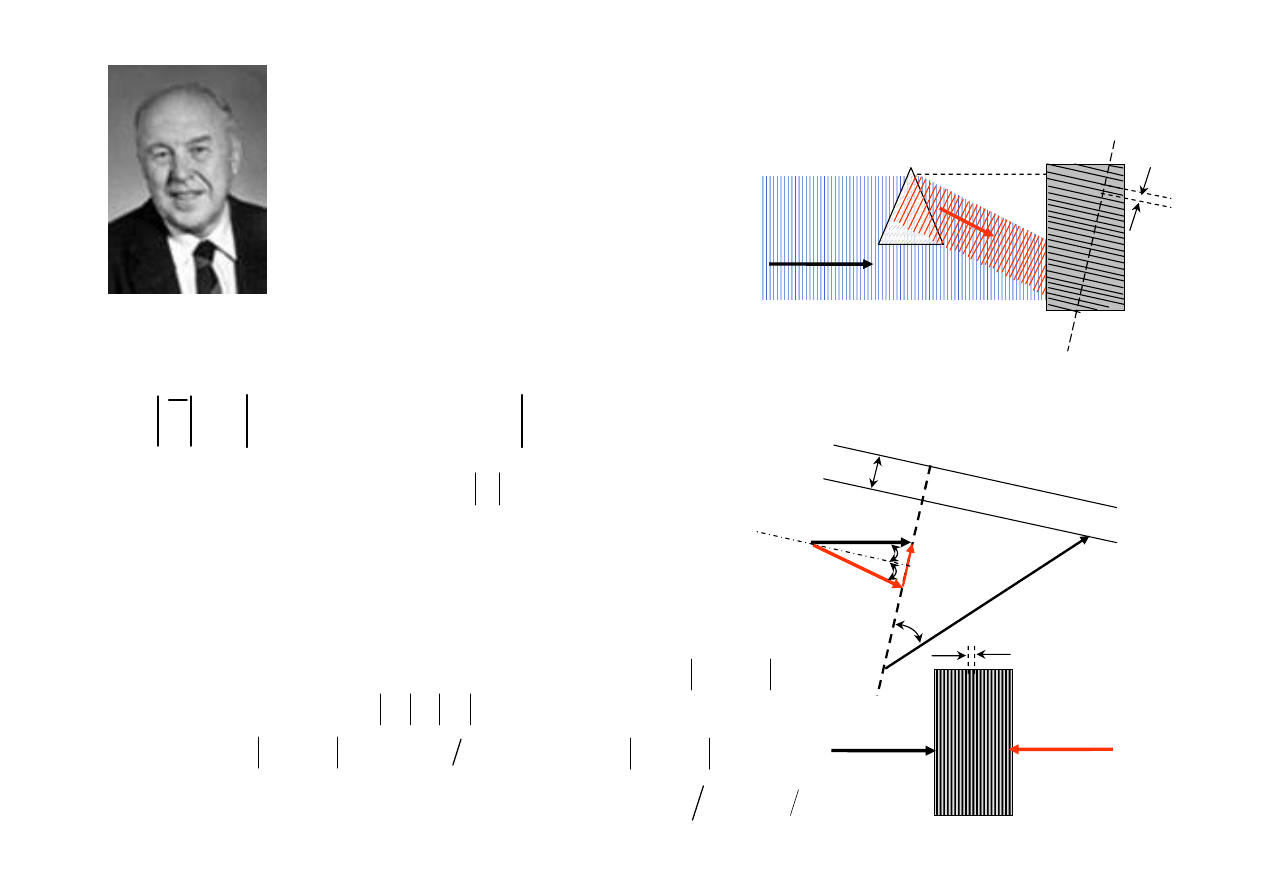
Wymagania wobec emulsji fotograficznej

W hologramie fali płaskiej

maksimum intensywności pojawia się, gdy

a odległość x między nimi określona jest warunkiem ,

czyli wynosi

 





0

0

2

2

2

1

1

0

0

2

2

2

cos

sin

s

s

n

n

I x

E

E

E

E E

kx























cos

sin

1

kx





sin

2π

k x







sin

x





 

Na przykład, niech



=15

o

, czyli sin



=0,26, wówczas ,

czyli emulsja powinna pozwolić rozróżnić linie (prążki interferencyjne) odległe
o 2 m. Zwykle hologramy są naświetlane na filmach o rozdzielczości 500 linii/mm
i pozwalają oglądać (wyświetlać) przedmioty w 3D.

4

2 m

x





 



2014

25

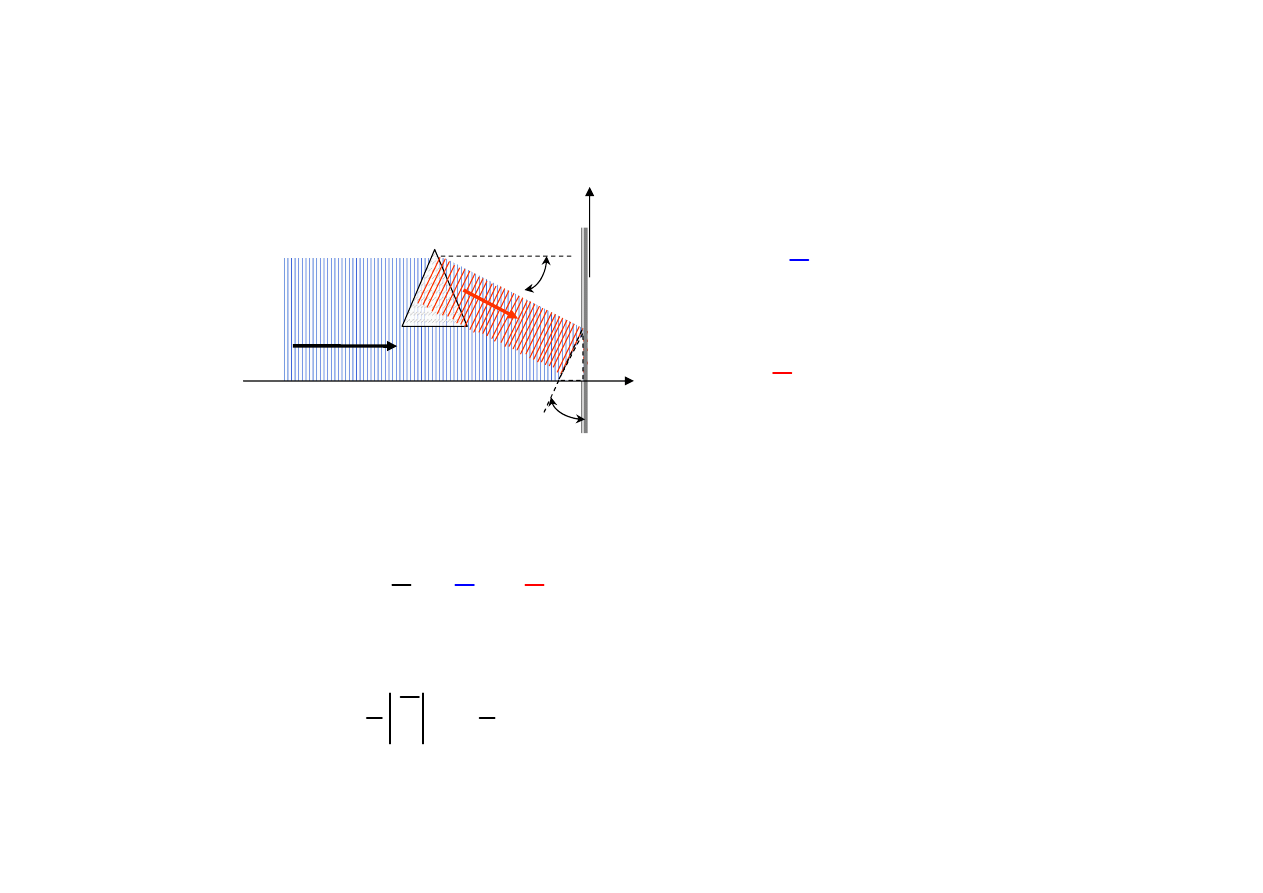
Metoda hologramów 3D Denisiuka





2

2

j

j

2

2

0

0

0

0

0

0

e

e

2

cos

n

s

n

s

n

s

n

s

n

s

E

E

E

E

E

E E

























k r

k r

k

k

r



- w wystarczająco grubej
emulsji fotograficznej
obraz interferencyjny jest 3D.

Niech k

s

i k

n

– wektory falowe fali sygnałowej i fali nośnej; wtedy zapis natężenia

pola elektrycznego w emulsji można przedstawić w postaci

Wartości maksymalne przyjmuje dla

2

E









2π

0, 1,

2, ...

s

n

m

m











k

k

r



Równanie to przedstawia system płaszczyzn
prostopadłych do wektora k

s

-k

n

(rys).

Odległość między nimi wynosi

Jeżeli przyjąć, że , to otrzymujemy

2π

s

n

d





k

k

s

n



k

k





2 sin

2

s

n

k







k

k

mamy

2π

s

n

d





k

k

, a wtedy z





2 sin

2

d















d

m+1

m

r

k

s

k

n

k

s

-k

n



k

s

k

n



d









k

s

k

n







d=



/2

2014

Wykład 13B

26

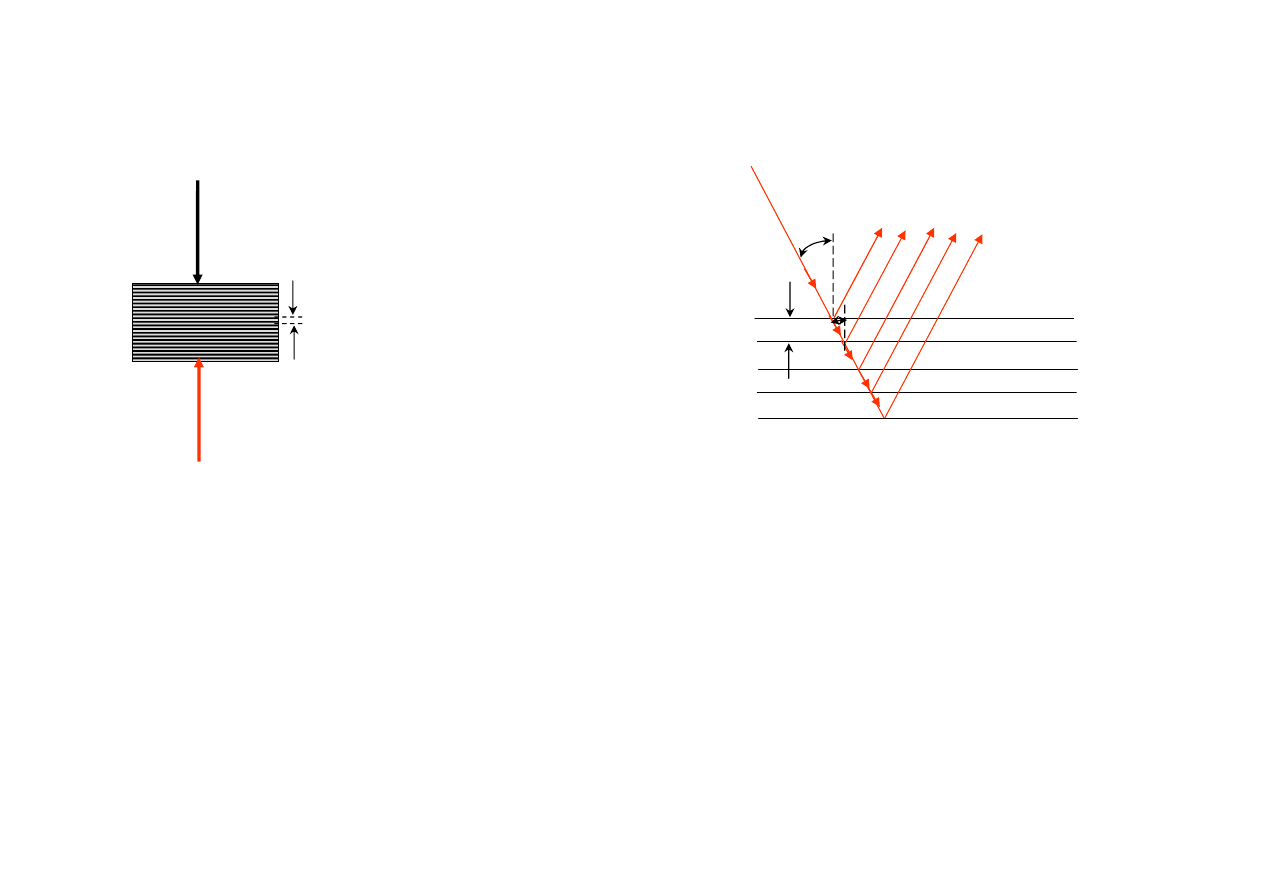
Hologram Denisiuka

Powyżej mamy pokaz z dwóch hologramów Denisiuka. Składają się one z grubej warstwy emulsji

nałożonej na odbijające światło podłoże. Na pierwszy rzut oka wyglądają one jak czarny, błyszczący kawałek
filmu. Jednakże oświetlone źródłem światła, które jest umieszczone za nami, pozwolą określić przestrzennie
pozycję przedmiotów na tym obrazie.

Optymalne warunki do oglądania obrazu z hologramu są przy świetle błyskającym
z tyłu z maksymalne dalekiej odległości. Zdjęcie po lewej stronie zostało zrobione
właśnie w takich warunkach. Głębokość pola widzenia obrazu zależy oddalenia źródła
światła.

2014

27

Warunek Wulffa-Bragga

d





2 cos

d

m







k

s

k

n








d

Odbicie fali płaskiej od takiego
hologramu nastąpi tylko wtedy,
gdy odbicia od poszczególnych
płaszczyzn wzmacniają się, czyli
przy warunku Wulffa-Bragga:

gdzie kąt załamania



t

jest równy kątowi padania



,

a współczynnik załamania materiału pomiędzy warstwami jest równy 1.

Denisiuk
Dans les années 50, Denisiuk cherche à produire des photographies d’objets en 3D qui apporteraient
l'illusion de la réalité. Mais comment enregistrer et restituer optiquement le front d'onde rayonné par
ceux-ci ? Le défi réside dans la méthode d’enregistrement et de reproduction de la distribution
de phase de ce front d’onde. Au Vavilov State Optical Institute de Léningrad, Denisiuk imagine
alors une solution sur un principe d’ondes stationnaires dans lequel une onde de référence
se propage dans une direction opposée à celle de l’onde rayonnée par un objet. Il s’inspire
des travaux de Lippmann sur la photographie interférentielle qui exploite un principe
d’enregistrement, en volume, dans l’épaisseur d’une émulsion photosensible. Denisiuk postule que
ce type d’enregistrement doit pouvoir contenir autre chose que de l’information spectrale moyennant

une technique dérivée et en effet, il parviendra à mettre en œuvre sa propre méthode. Celle-ci s’avère

tout à fait propice à l’enregistrement des informations de phase & d’amplitude. Ignorant les travaux
de Gabor et le terme « hologramme », Denisiuk propose le terme « photographie d’onde » pour qualifier
son procédé. Les enregistrements débutent en 1958 sur la base d’objets simples et spéculaires
(miroirs convexes). En 1959 et 1960, le principe d'une holographie dite Lippmann est validé.

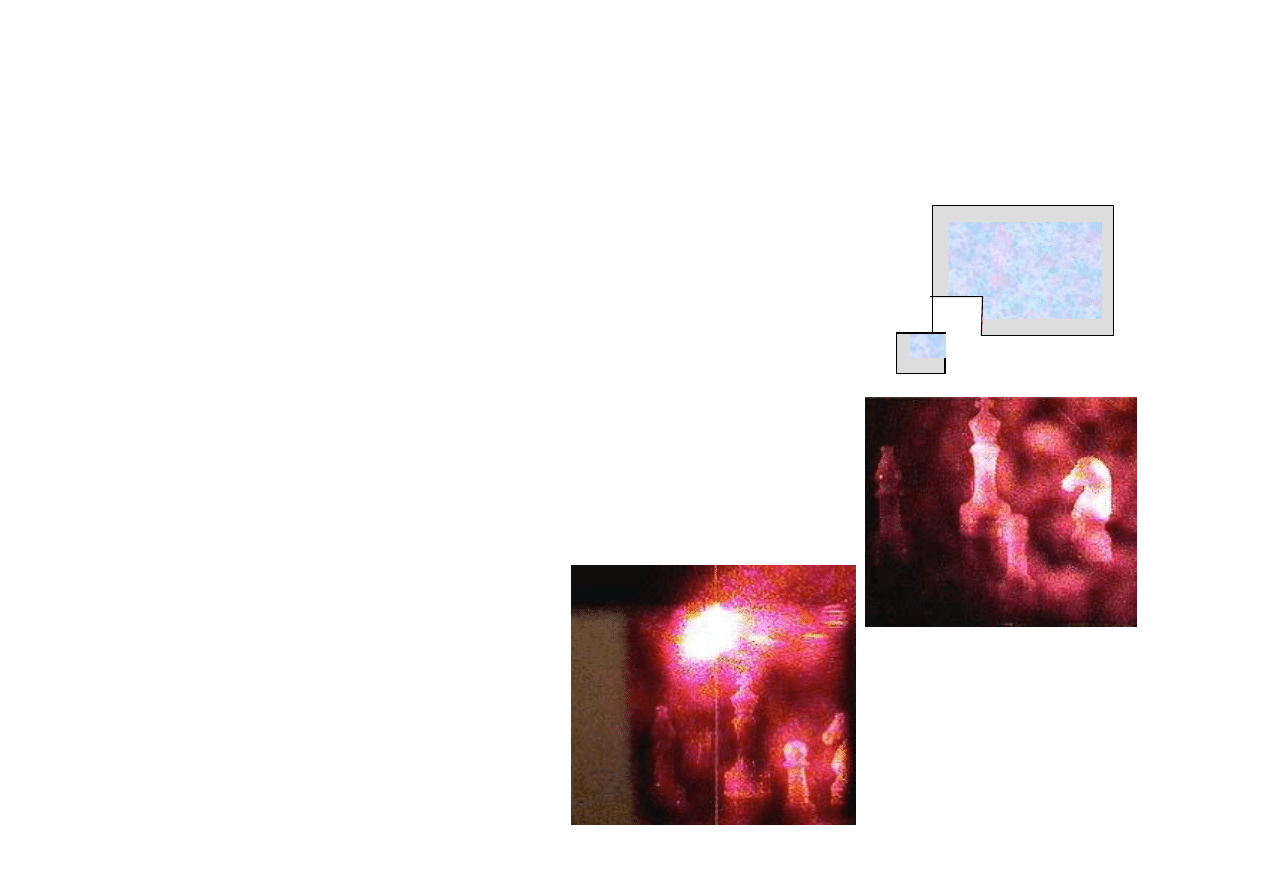
2014

Wykład 13B

28

Gdy fragment jest całością

Każda część hologramu zawiera obraz całego obiektu. Można więc odciąć
jego rożek i zobaczyć w nim cały obraz.
Dla każdego kąta patrzenia widzimy obraz w innej perspektywie, tak jakby był
to realny przedmiot. Każdy kawałek hologramu zawiera szczególną
perspektywę obrazu, ale widać na nim cały obiekt.

Na górnym zdjęciu jest obraz widziany przez większy kawałek hologramu,
zaś na dolnym jest obraz uzyskany z niewielkiego naroża odciętego od tego
hologramu.
Chociaż obraz z małego naroża jest obrazem z określonego punktu widzenia,
to zawiera on jednak cały obiekt.

2014

Wykład 13B

29

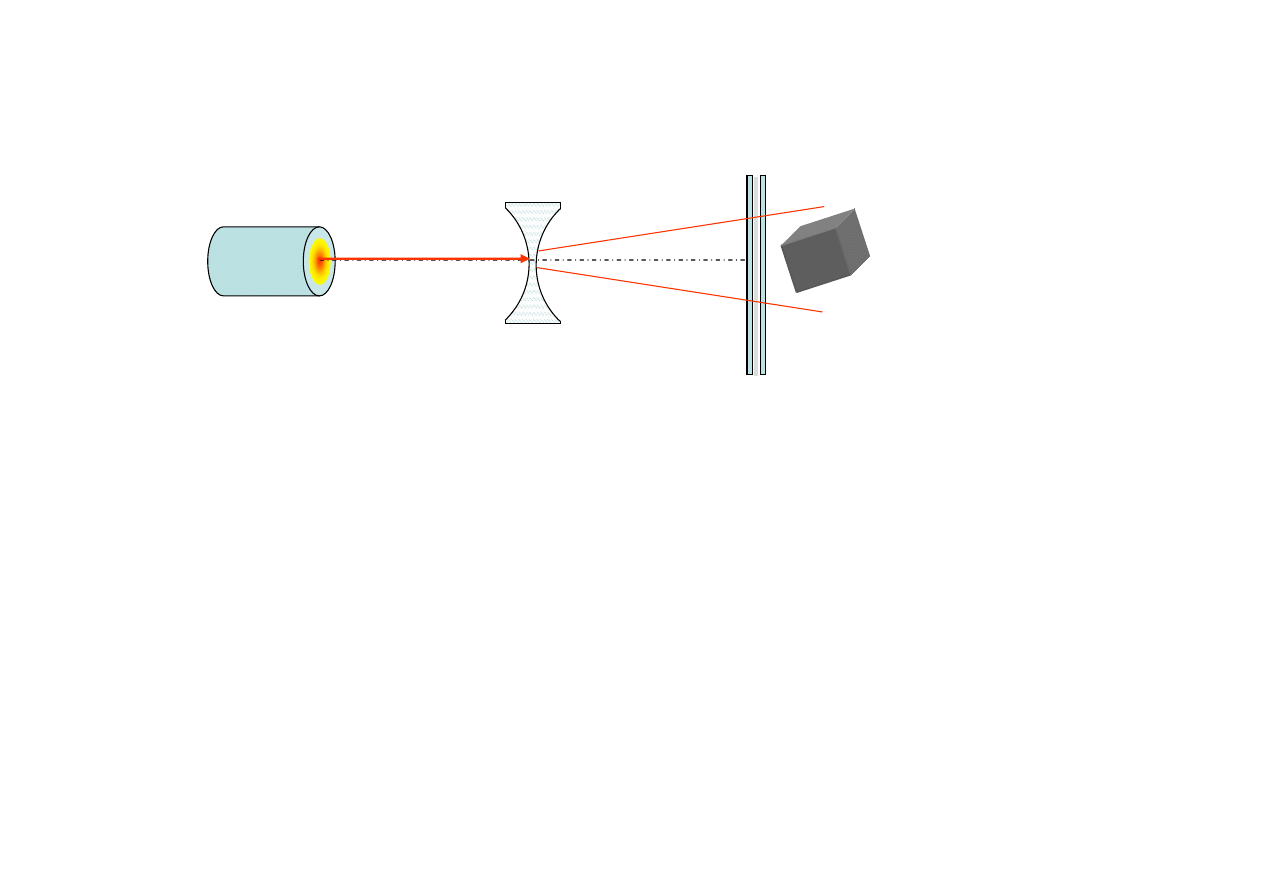
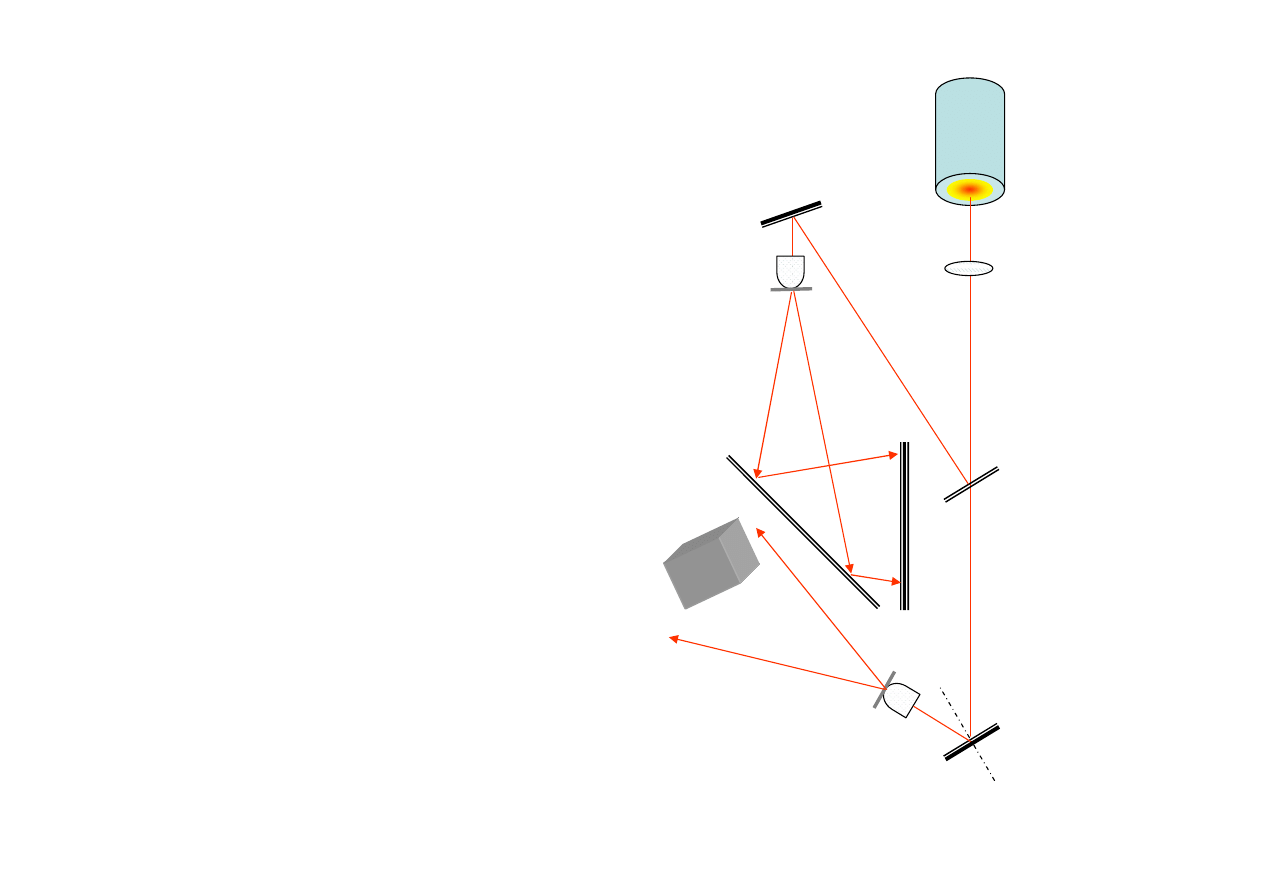
Hologramy refleksyjne

W hologramach refleksyjnych obraz jest zapisany w grubej emulsji
światłoczułej i może być przeglądany w świetle białym.
Najprościej taki hologram przeglądać w bezpośrednim strumieniu światła odbitego.
W tym przypadku bezpośredni strumień przechodzący przez film
służy także jako strumień referencyjny.

Laser

Soczewka

rozpraszająca

Klisza pomiędzy dwiema

płytami szklanymi

Obiekt

2014

Wykład 13B

30

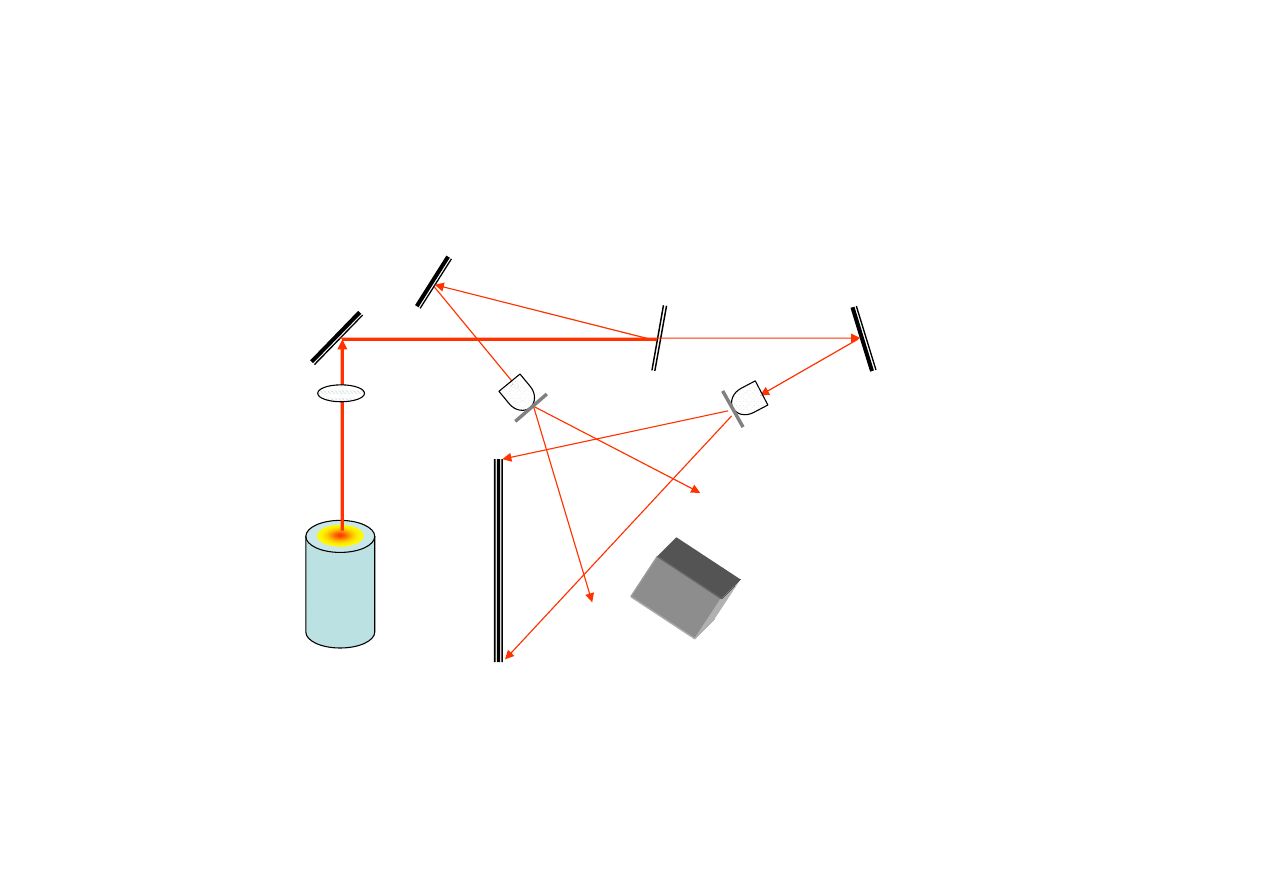
Hologramy Gabora

La
ser

Obiekt

3D

Holo

gra

m

S

M

M

FS

S

O

Filtr

przestrzenny

Filtr

przestrzenny FS

2014

Wykład 13B

31

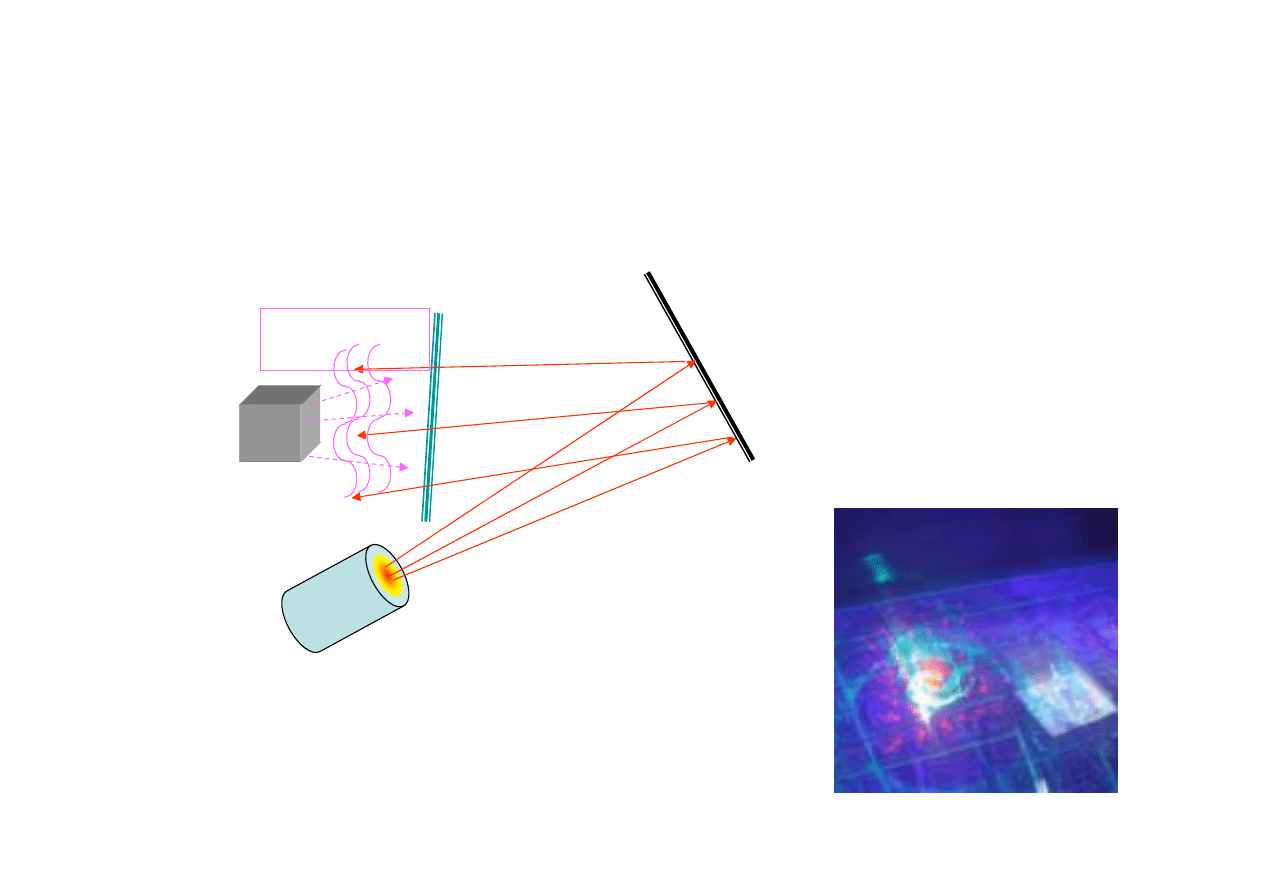
Holografia Leitha i Upatnieksa

La
ser

M

M

S

H

Obiekt

3D

FS

FS

M

O

2014

Wykład 13B

32

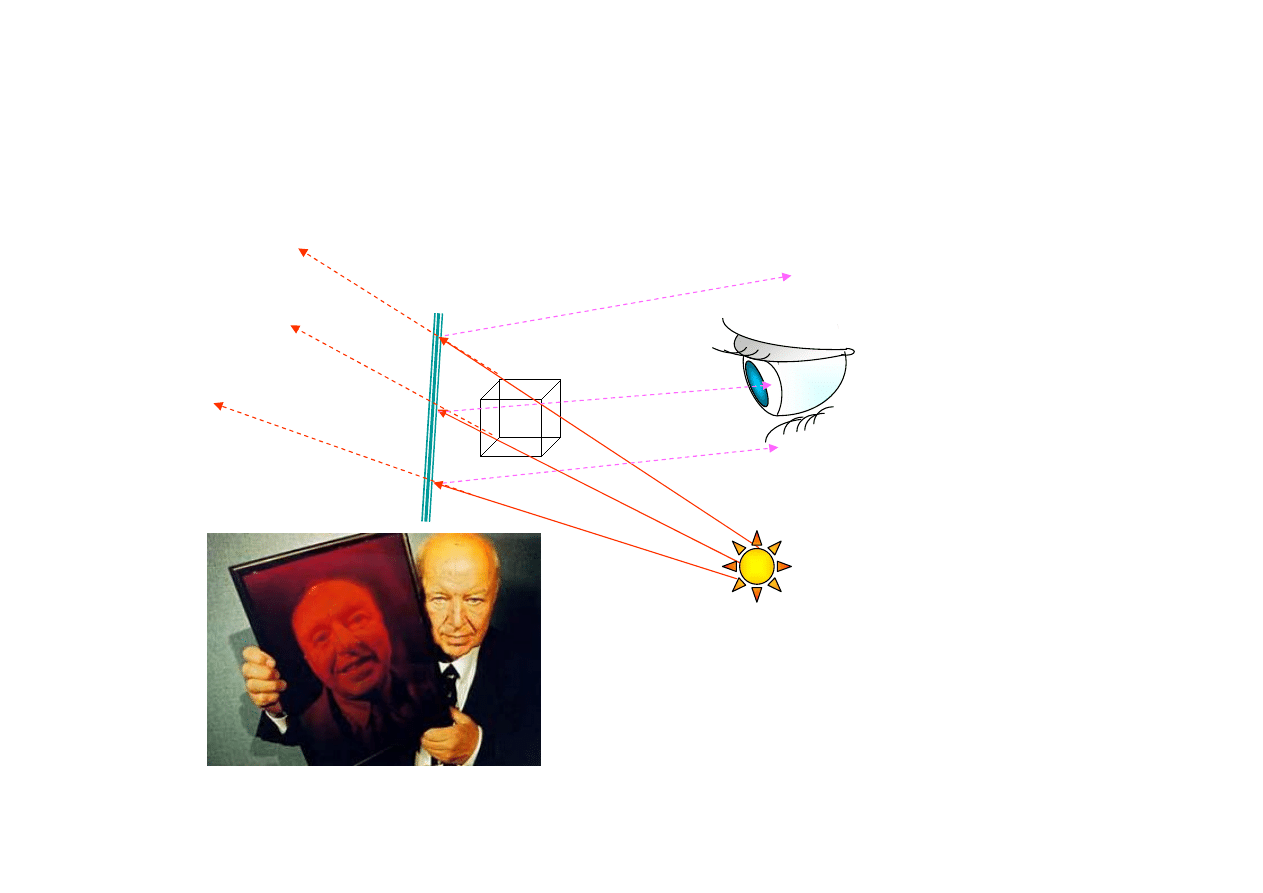
Holografia Denisiuka

La

se

r

Stru

mie

ń

refe

ren

cyjn

y

Gruba płyta

fotograficzna

Obiekt

3D

Z

w

ie

rc

ia

d

ło

Strumień odbity

od obiektu

2014

Wykład 13B

33

Odczyt hologramu Denisiuka

Białe

światło

Hologram

Wirtualny

obiekt

2014

Wykład 13B

34

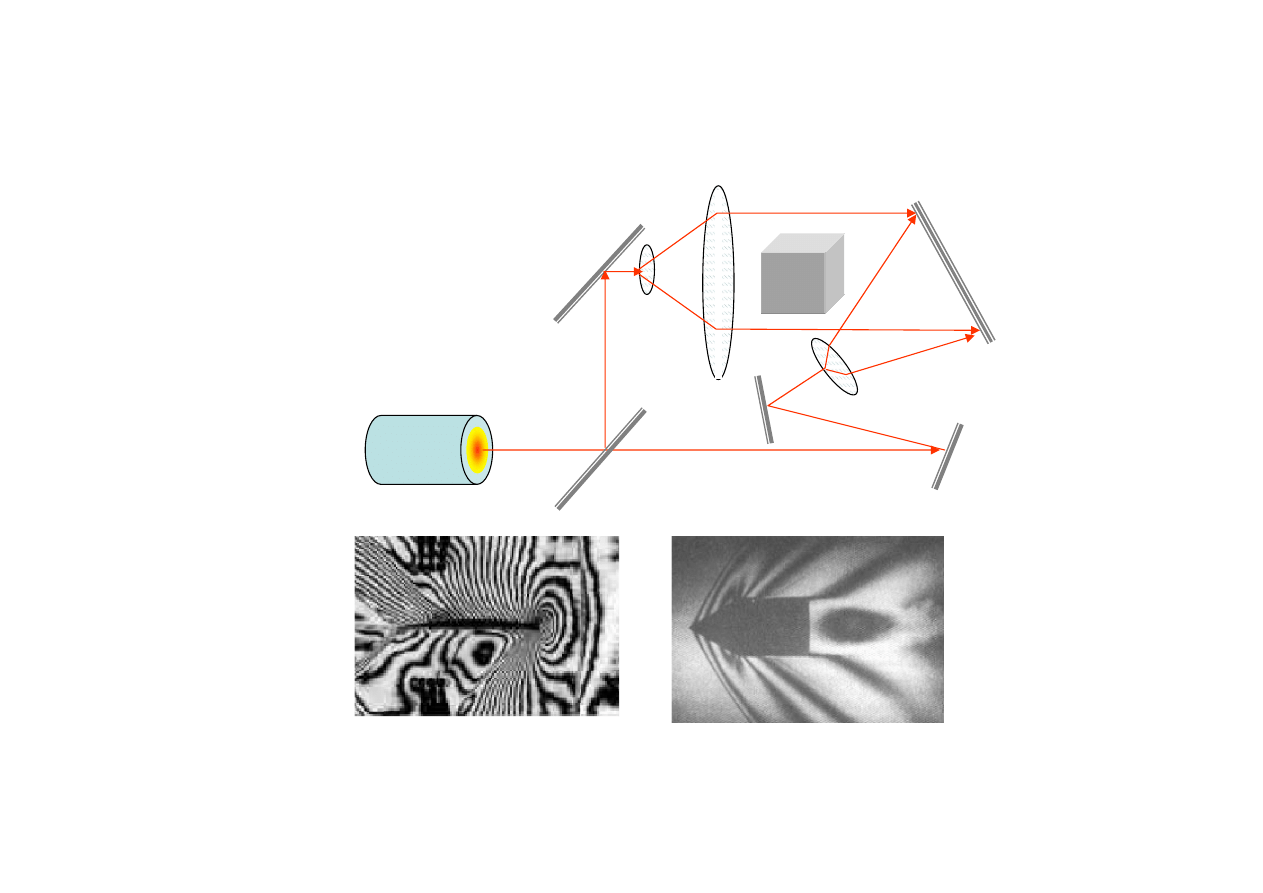
Interferometria holograficzna

Fala naddźwiękowa

w powietrzu

Pocisk w locie

Laser

Obiekt

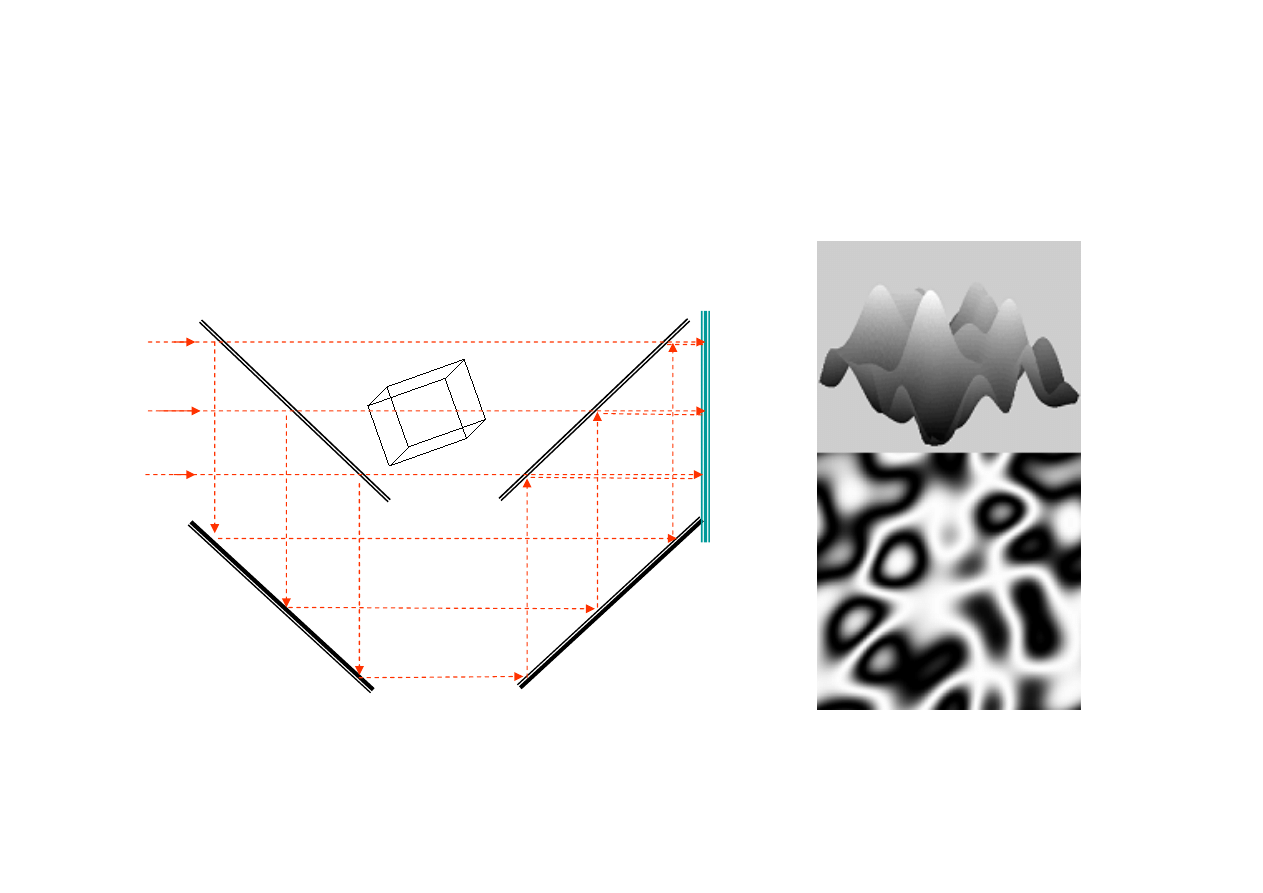
2014

Wykład 13B

35

Interferometria optyczna

Zw

ier

cia

dło

Zw

ie

rc

ia

dł

o

Strumień światła

koherentnego

Przeźroczysty

obiekt

P

ły

tka fo

togra

ficzn

a

-

sens

or

ś

w

iat

ła

S

S

2014

Wykład 13B

36

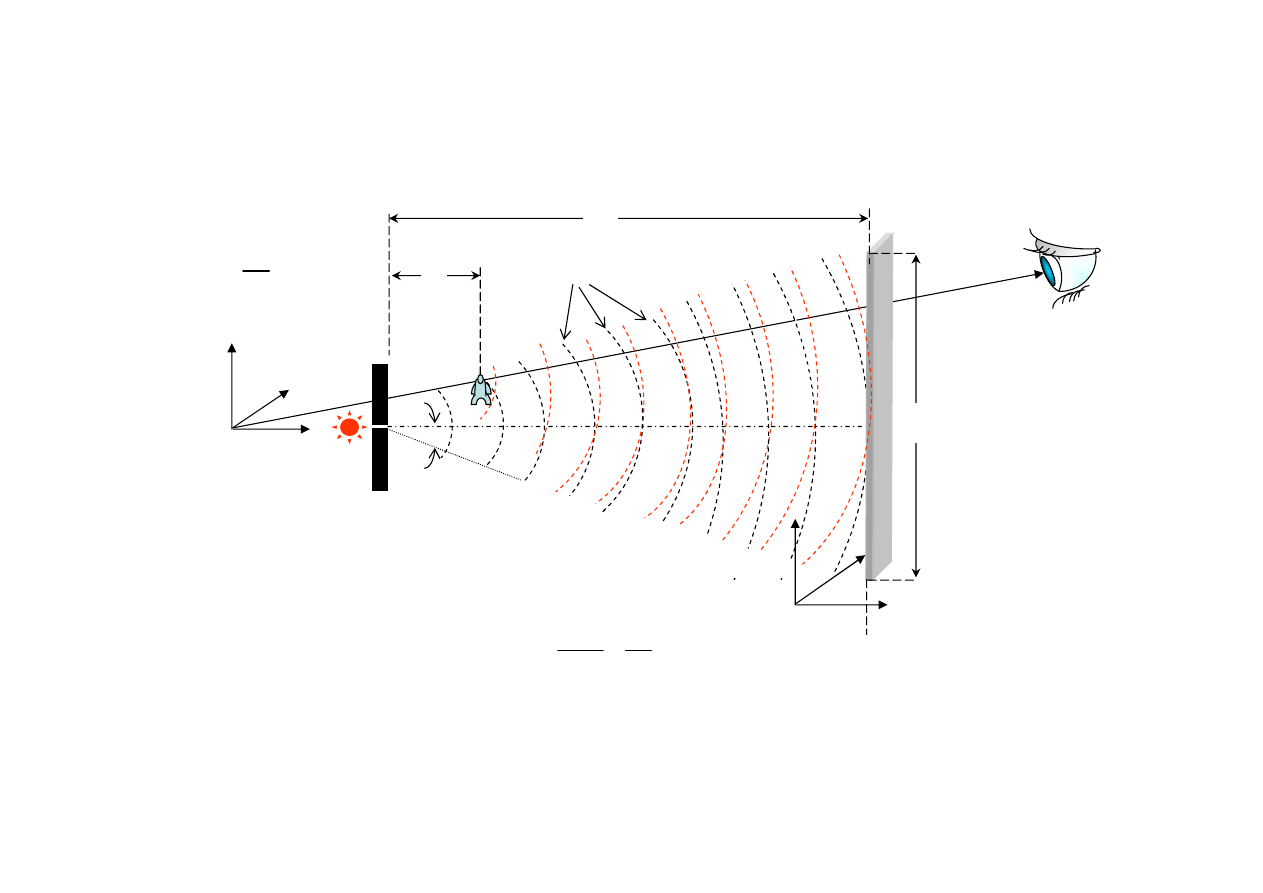
Holografia punktowa in-line

L

l

D



Powiększenie

L

M

l





L



y

z

x

r

S

Zapis na płycie jest całką Fresnela-Kirchhoffa:

 

 

2π

exp

j

S

K

I

d

 





















ξ

r

ξ

ξ

gdzie - intensywność odwzorowania holograficznego na płycie fotograficznej,

- współrzędne na powierzchni płyty odległej o L od źródła punktowego

 

I ξ





, , L

 



ξ

Sferyczne fale referencyjne

Kąt
połówkowy
strumienia

Źródło

punktowe

Detektor,
czyli płyta holograficzna
lub mozaika CCD
- całkowicie oświetlone!

2014

Wykład 13B

37

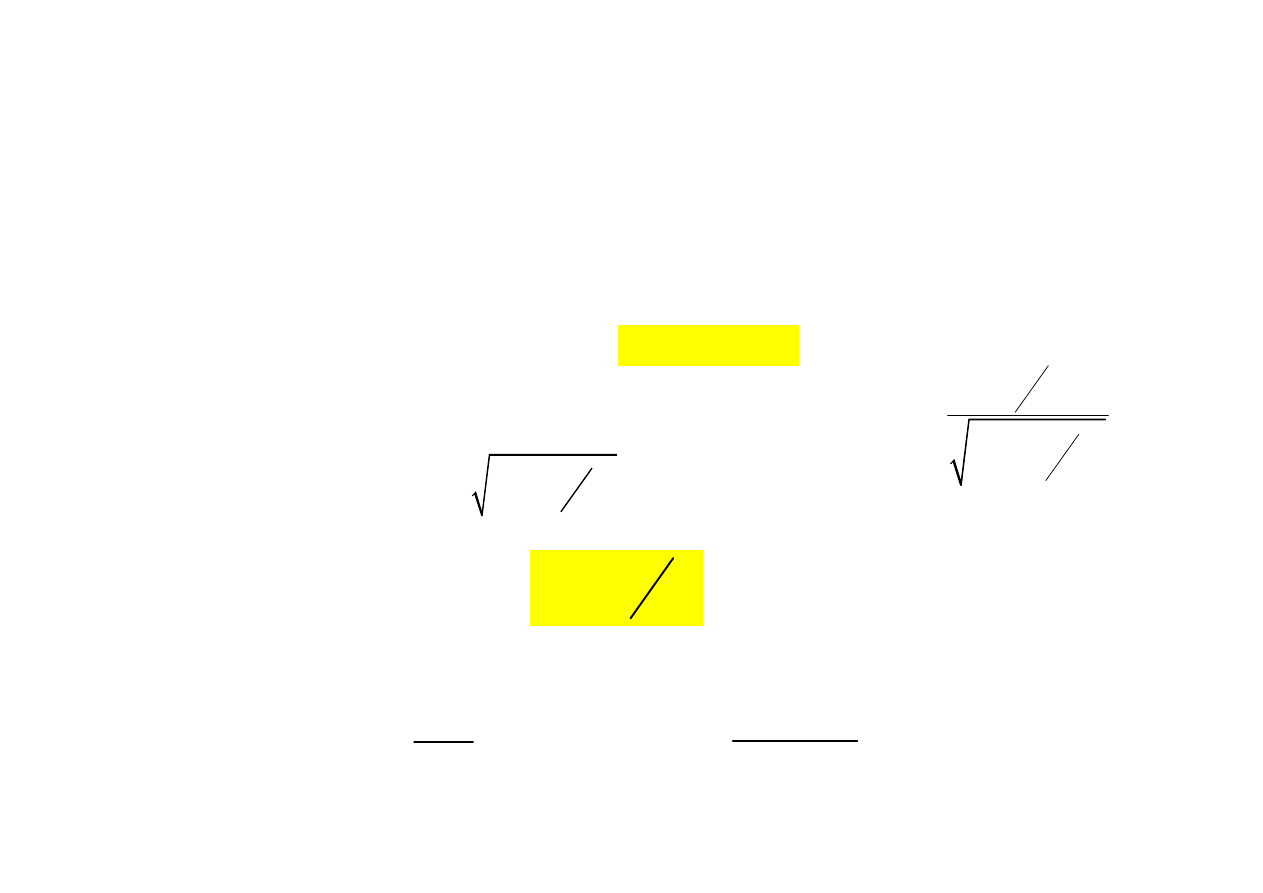
Rozdzielczość cyfrowej holografii

– in line (DIH)

- Jest określona aperturą numeryczną (NA) oraz długością fali



.

Apertura numeryczna wg definicji:

Przy całkowitym oświetleniu detektora o wymiarze D;
a ponieważ
to można przyjąć, że

A zatem NA w DIH wynosi

NA

sin

n





 

2

2

2

NA=

2

D

D

L 

L

D



 

2

2

2

D

L

L





NA=

2

D

L

Teoretyczne rozdzielczości: boczna



b

i dla głębi



g

obrazu holograficznego wynoszą,

odpowiednio

NA

b











2

2 NA

g







oraz

2014

38

Holografia cyfrowa

Rekonstrukcja numeryczna cyfrowo zapisanych hologramów

Na przełomie lat 60-tych i 70-tych zasugerowano (A. Lohmann, J. Goodman, T. Huang)
użycie techniki komputerowej do rekonstrukcji i syntezy hologramów.
Holografia cyfrowa odzwierciedla w najbardziej czysty sposób informacyjną zawartość
holografii, którą podkreślali jej wynalazcy D. Gabor i Yu.N. Denisiuk.

La

ser

Sensor

holograficzny

- kamera CCD

Obiekt

Mikroskop

Kolimator

Komputer

FS

Filtr przestrzenny

Numeryczna

rekonstrukcja

elektronicznie

zapisanego

hologramu

Strumień

obiektowy

Dane

2014

39

http://www.mt.com.pl/holografia

W praktyce holograficznej najczęściej stosuje się

światło

lasera, niemniej

jednak istnieją specjalne techniki umożliwiające uzyskiwanie hologramów w świetle białym.
Zastosowanie w procesie rejestracji i odczytu laserów o różnych długościach fal prowadzi
do uzyskania powiększonego (lub pomniejszonego) obrazu przedmiotu

(tzw. mikroskopia holograficzna). Bardzo zaawansowane są także prace

nad wykorzystaniem holografii do zapisywania nawet terabajtów (tysięcy gigabajtów) danych
na krążkach o wielkości porównywalnej z dzisiejszymi DVD.
Pierwszy napęd holograficzny już jest dostępny w handlu.
12-centymetrowe płytki holograficzne zawierają nawet 300 GB danych.
Oprócz pojemności bardzo istotna jest też prędkość zapisu i odczytu danych.
Z nośników stosowanych do tej pory

dane

odczytywane są sekwencyjnie, bit po bicie.

Hologram umożliwia jednoczesne i natychmiastowe zapisanie i odczytanie wszystkich

informacji o danym obiekcie. Bardzo interesującą cechą hologramów jest także
ich nielokalność. Oznacza to, że podczas odczytu, nawet w przypadku oświetlenia
tylko fragmentu hologramu, odtworzy się pełną informację na temat całego obiektu.

Ponadto gdy uszkodzeniu ulegnie nawet znaczna część hologramu odczytane informacje
nadal będą całkowicie prawidłowe. W przypadku pocięcia hologramu na kawałki można

nadal z pojedynczego kawałka odczytać całą informację. Dzieje się tak dlatego,

iż każdy punkt na ekranie odebrał światło ze wszystkich części fotografowanego obiektu.
Im mniejszy będzie ów pojedynczy skrawek, tym mniej szczegółowe informacje uzyskamy
o całym sfotografowanym obiekcie. W przypadku zapisywania danych w postaci
zero-jedynkowej można sobie jednak pozwolić na bardzo duży stopień miniaturyzacji.

2014

40

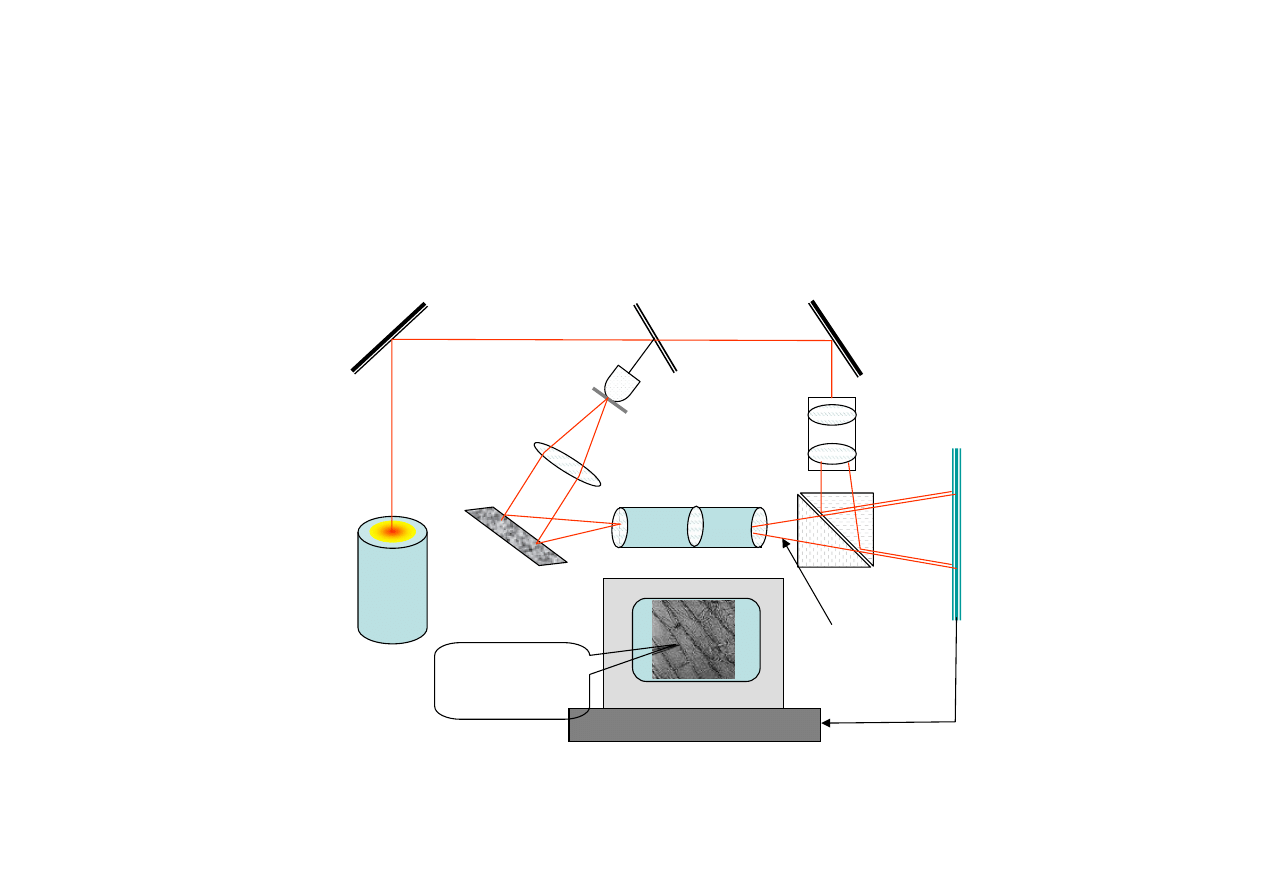
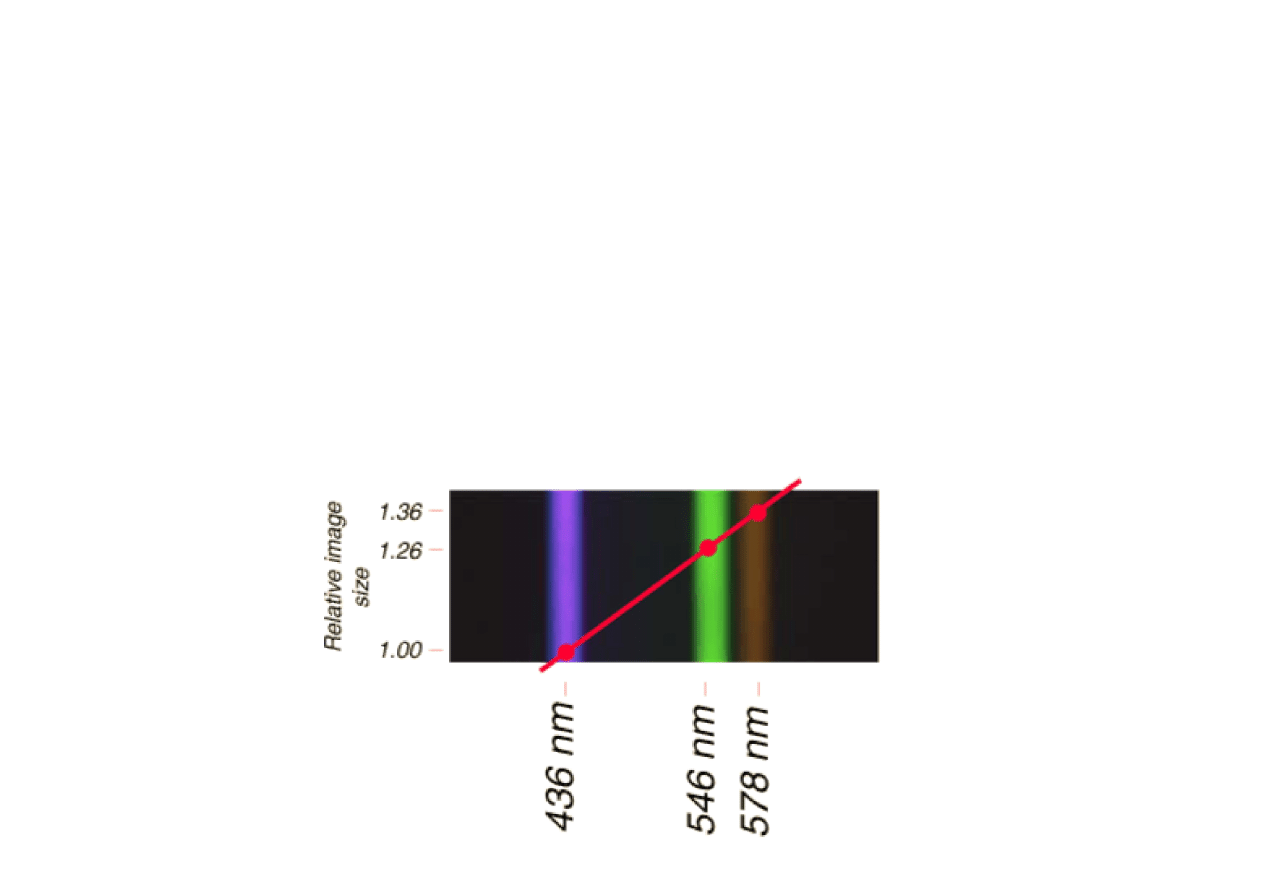
Skalowanie obrazów holograficznych

Obraz holograficzny jest skalowany długością fali.
Wywołało to początkowo wielki zachwyt ponieważ można sobie wyobrazić
wykonywanie obrazów holograficznych za pomocą promieni X, a potem
przeglądać je w świetle widzialnym, uzyskując np. trzywymiarowy obraz
w skali cząsteczki.
Jednakże hologramy rentgenowskie jeszcze nie są wykonywane i są praktyczne
trudności ze skalowaniem, ale są nadzieje, że takie hologramy będą wielkim sukcesem.

2014

Wykład 13B

41

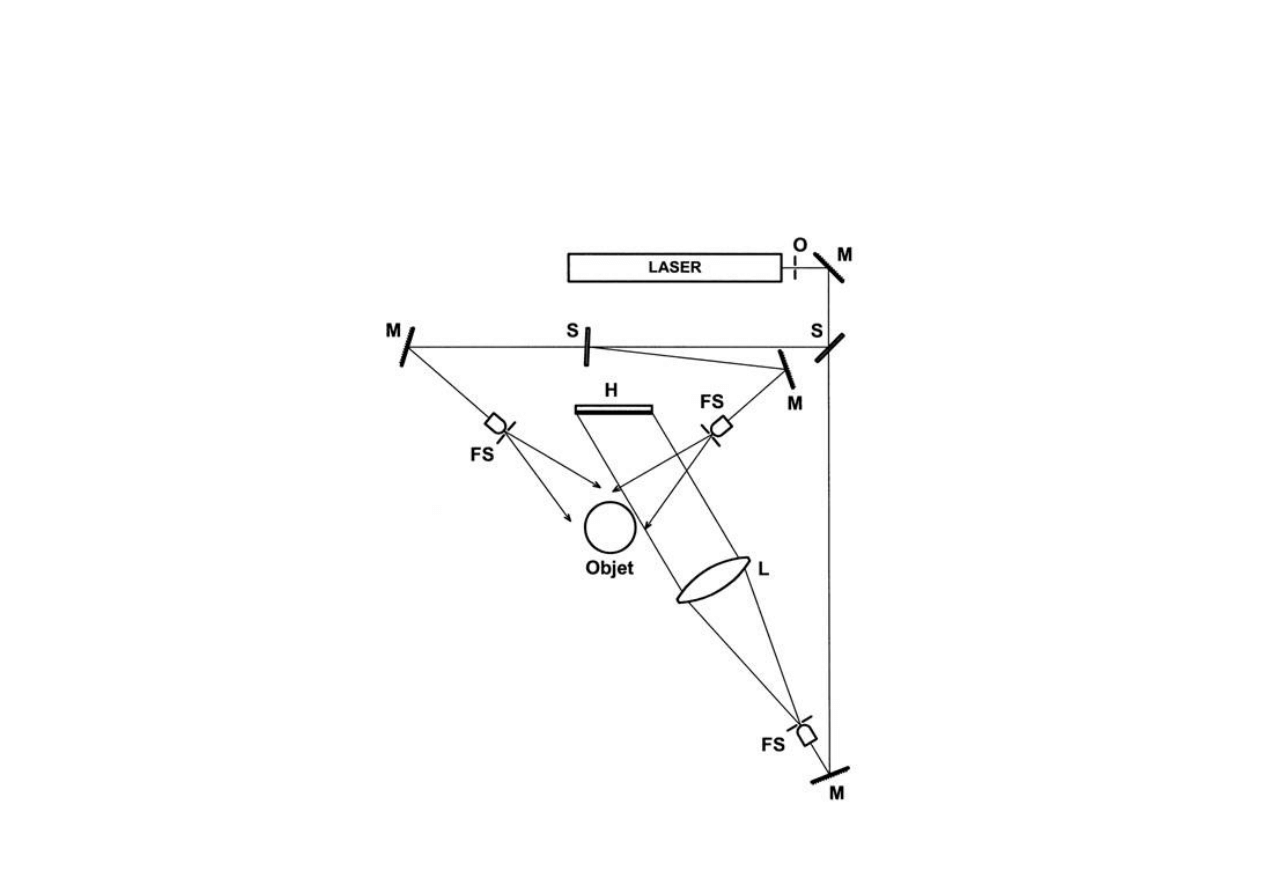
Holografia transmisyjna za pomocą

referencyjnej wiązki równoległej i podwójnego

oświetlenia przedmiotu

2014

Wykład 13B

42

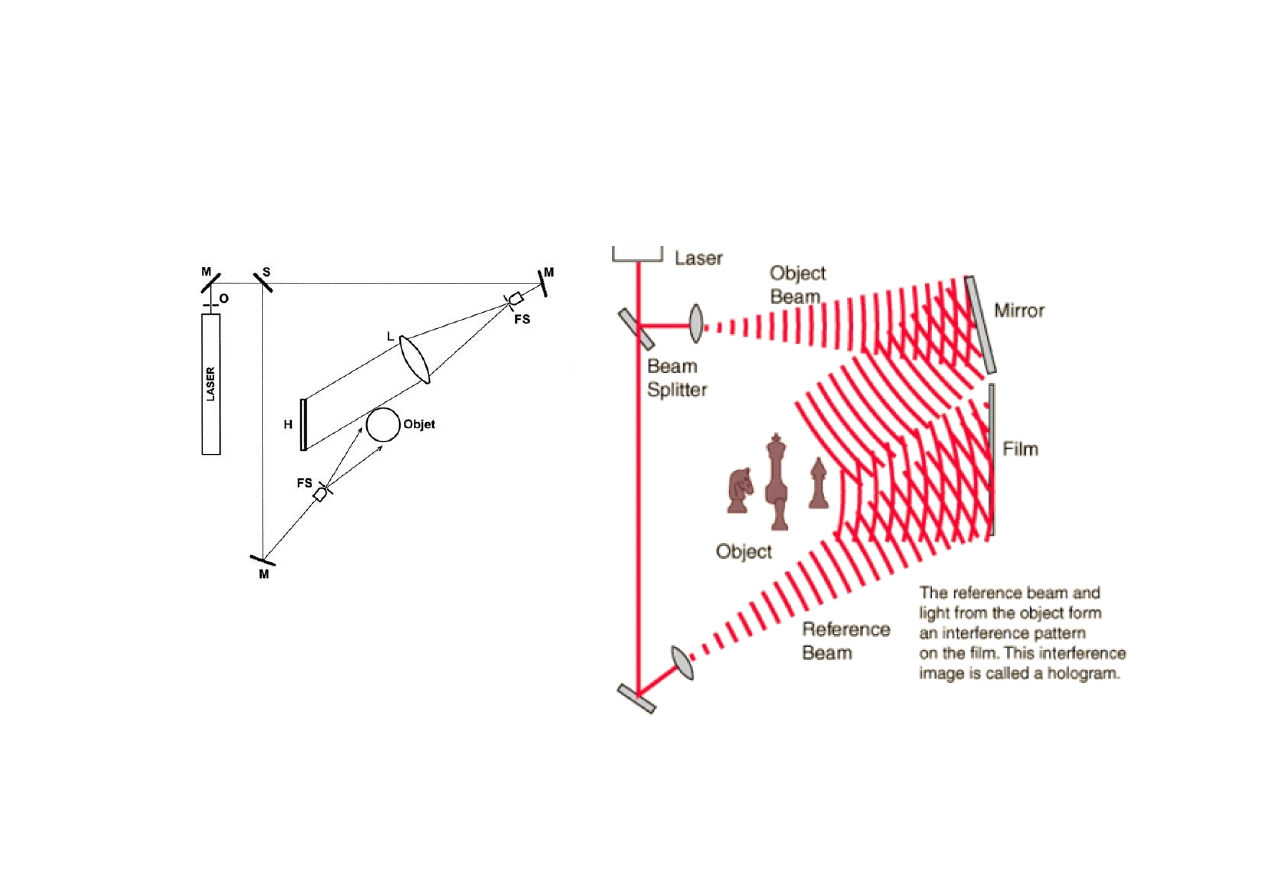
Holografia transmisyjna za pomocą

równoległej wiązki referencyjnej

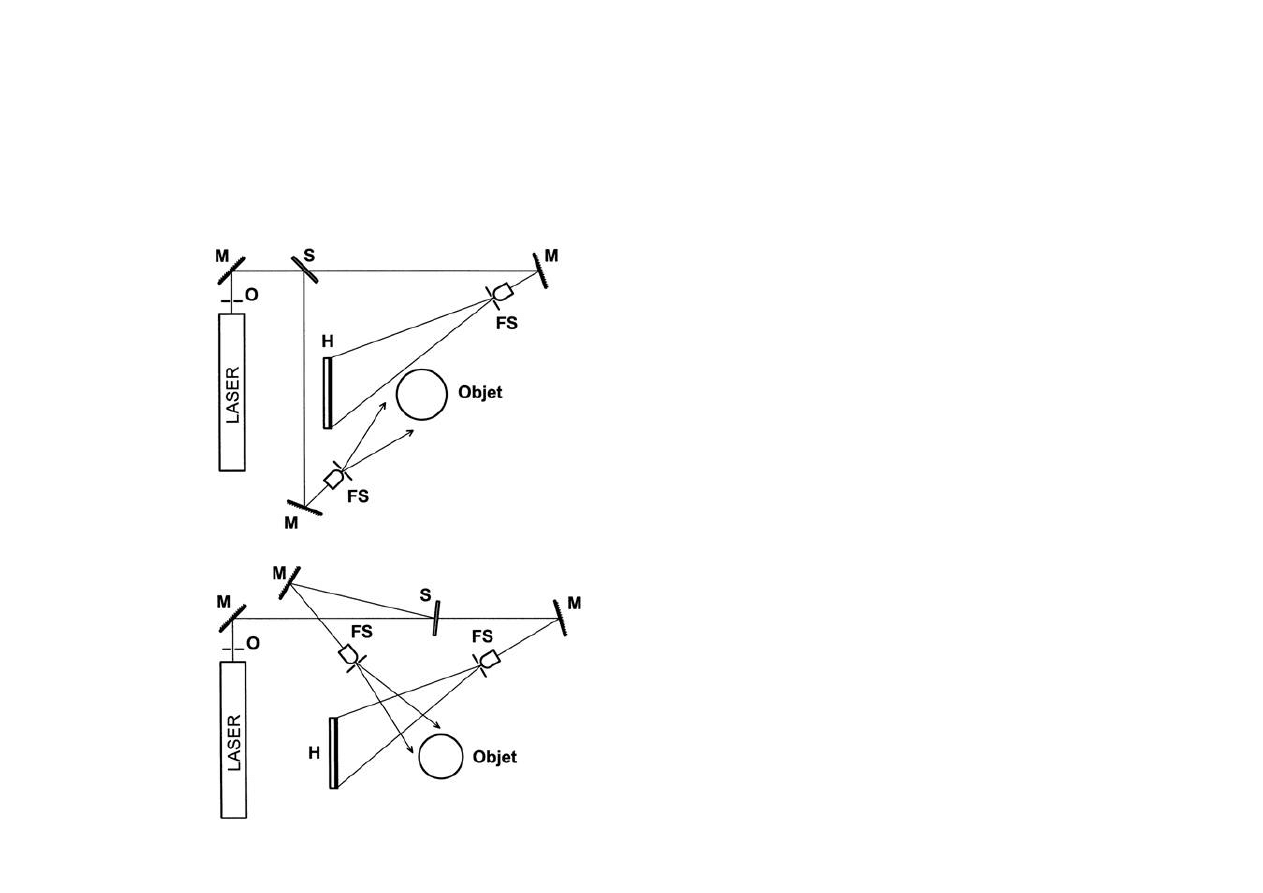
2014

Wykład 13B

43

Przykłady stanowisk do holografii

transmisyjnej