Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

1

Curiosita

Nienasycona ciekawość życia

i nieugaszone pragnienie ciągłej nauki.

Leonardo da Vinci

Podstawy konstrukcji żelbetowych

Materiały pomocnicze do zajęć z „Konstrukcji betonowych 1” i „Konstrukcji żelbetowych”

dla studentów studiów stacjonarnych (dziennych) i niestacjonarnych (zaocznych)

Drogi Czytelniku,

Przekazuję w Twoje ręce materiały pomocnicze obejmujące swoim zakresem podstawowe wiadomości na temat:
- właściwości mechanicznych betonu i stali, oraz ich współpracy,
- teorii żelbetu,
- projektowania zginanych, ściskanych i rozciąganych przekrojów żelbetowych,
- projektowania stref przypodporowych belek żelbetowych,
- stanów granicznych użytkowalności.
Oprócz podstawowych wiadomości teoretycznych zamieściłam w nich także przykłady obliczeniowe, które mam nadzieję
pomogą Ci wdrożyć się w trudną sztukę projektowania bezpiecznych konstrukcji żelbetowych. Materiały dostosowane
są do postanowień aktualnej normy

2008

:

1

1

1992







EN

PN

.

Pomimo moich starań na pewno znajdziesz Czytelniku w nich niejasności, niedopatrzenia, błędy czy braki potrzebnego
materiału do zrozumienia pracy przekroju żelbetowego. Pragnę z góry Cię przeprosić za te usterki i będę wdzięczna za
wszystkie uwagi na ten temat przesłane na adres

[e-mail]

. Pozwoli mi to w przyszłości ulepszyć materiały.

Z wdzięcznością przyjmę także wszelkie sugestie co Twoim zdaniem byłoby pomocne w nauce projektowania konstrukcji
żelbetowych.

Maria Włodarczyk

Podstawy konstrukcji żelbetowych

Materiały pomocnicze do zajęć z „Konstrukcji betonowych 1” i „Konstrukcji żelbetowych”

dla studentów studiów stacjonarnych (dziennych) i niestacjonarnych (zaocznych)

WYMIAROWANIE NA ŚCINANIE WEDŁUG PN-EN 1992-1-1:2008 (Eurokod 2)

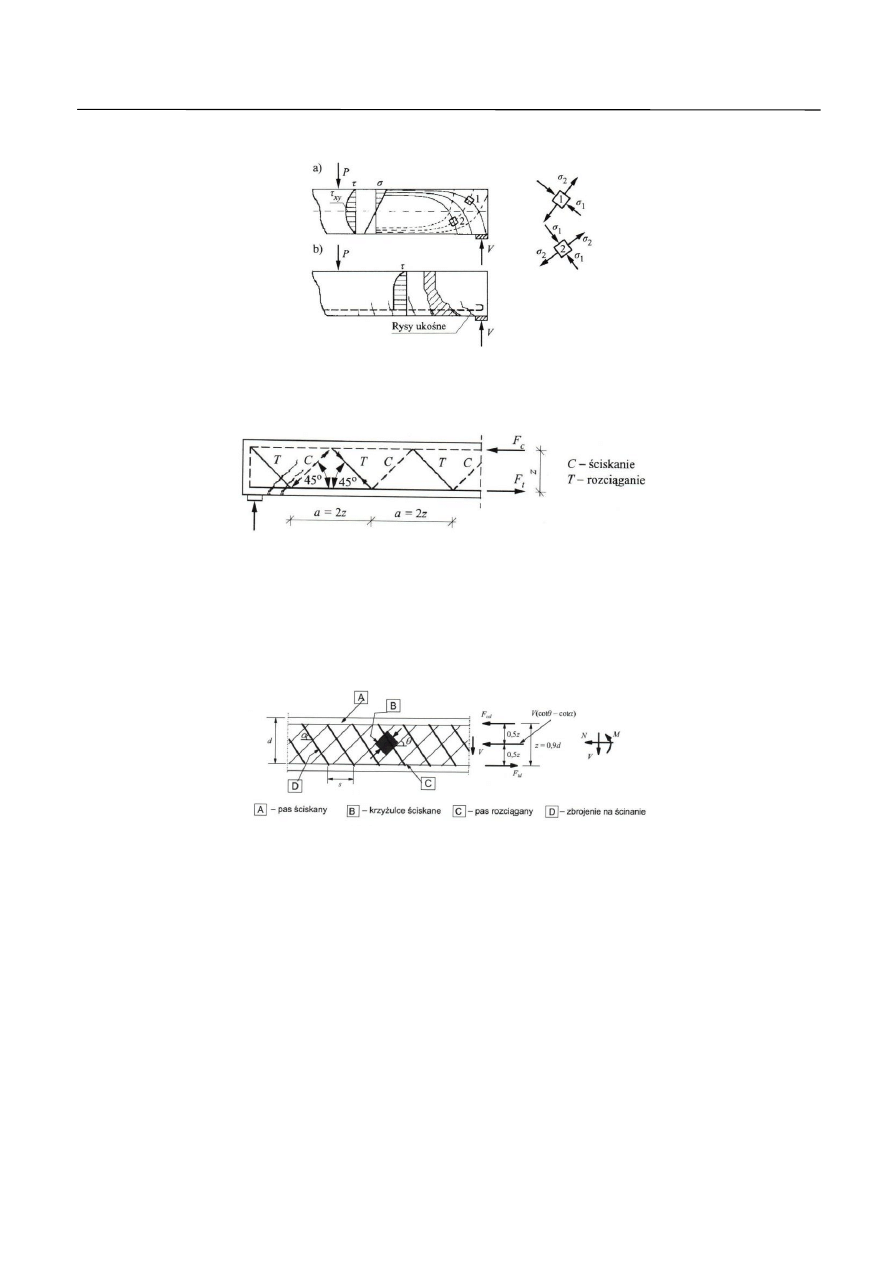
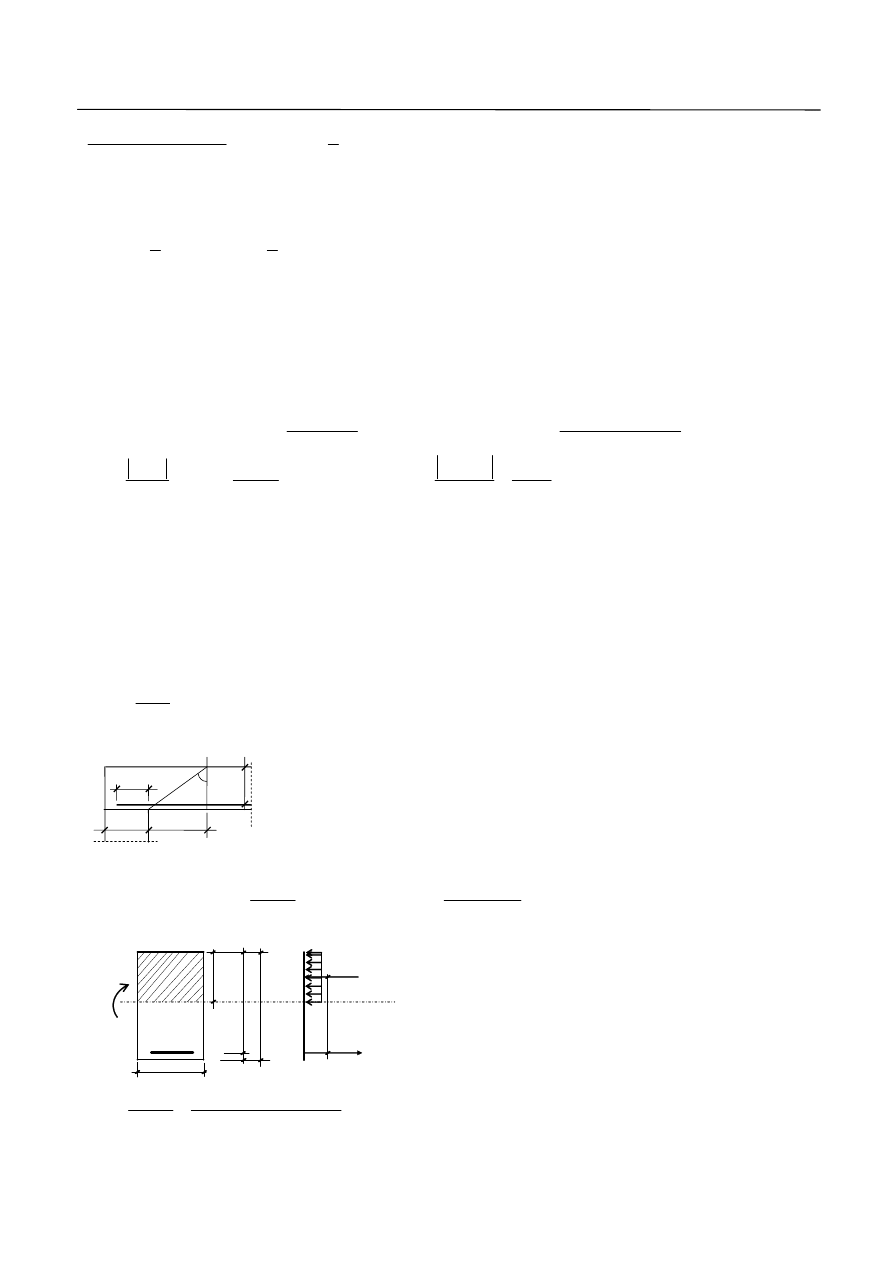
Wymiarowanie na ścinanie według Eurokodu 2 opiera się na modelu kratownicowym. W modelu tym
zakłada się, że na odcinku strefy przypodporowej, na skutek jednoczesnego działania siły poprzecznej
i momentu zginającego powstają rysy pionowe i ukośne. Rysy pionowe powstają w początkowej fazie
i wywołane są działaniem momentu zginającego. Natomiast rysy ukośne są skutkiem działania siły
poprzecznej, która wywołuje ukośne główne naprężenia rozciągające (Rys. 1). Taki typ morfologii rys
nawiązuje do układu sił w strefie przypodporowej zaproponowanego przez Mörscha (Rys. 2). Mörsch przyjął
jako model kratownicę statycznie wyznaczalną składająca się z pasa ściskanego przenoszącego wypadkową
naprężeń ściskających F

c

, pasa rozciąganego przenoszącego wypadkową naprężeń rozciągających F

t

oraz

ściskanych krzyżulców betonowych C, nachylonych do osi elementu pod kątem 45

o

, rozciąganych

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

2

krzyżulców T odpowiadającym prętom zbrojeniowym projektowanym ze względu na ścinanie i nachylonych
do osi elementu pod kątem 45

o

.

Rys. 1. Naprężenia główne w belce strefie przypodporowej: a) kierunki naprężeń głównych, b) rysy ukośne jako efekt

głównych naprężeń rozciągających.

Rys. 2. Model analogii kratownicowej Mörscha.

I. ZŁAŻENIA

1. Zakłada się, że element żelbetowy składa się ze strefy ściskanej, strefy rozciąganej (zbrojenia

podłużnego) i strefy ścinania, położonej pomiędzy wypadkowymi sił

cd

F i

td

F w strefach ściskanej

i rozciąganej (Rys. 3).

Rys. 3. Ścinanie odcinka belki, schemat rozkładu sił.

2. Strefa ścinania składa się ze ściskanych krzyżulców betonowych nachylonych pod kątem



do osi

elementu i z rozciąganego zbrojenia poprzecznego rozmieszczonego w płaszczyznach o rozstawie s ,
nachylonego pod kątem



do osi elementu.

3. Kat nachylenia zbrojenia poprzecznego

o

45





– zbrojenie ukośne lub

o

90





– zbrojenie pionowe.

(Dla strzemion pionowych

0

cot





.)

4. Kat nachylenia krzyżulców betonowych



można dobierać dowolnie z przedziału:

5

,

2

cot

0

,

1







zgodnie z PN-EN 1992-1-1:2008 (EC2),

0

,

2

cot

0

,

1







zgodnie z załącznikiem krajowym NA do PN-EN 1992-1-1:2008 (EC2).

5. Wysokość strefy ścinania jest równa ramieniu sił wywnętrzanych, której wartość przybliżoną można

przyjmować:

d

z

9

,

0



.

(1)

Jeżeli nie korzysta się z uproszczenia, to należy przyjmować najmniejsze ramię sił wewnętrznych na
rozpatrywanym odcinku, obliczane z pominięciem wpływu ukośnego zbrojenia na ścinanie.

6. Naprężenia

c



w krzyżulcach betonowych nie powinny przekraczać wartości

cd

f



.

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

3

7. Naprężenia

sw



w zbrojeniu poprzecznym nie powinny przekraczać obliczeniowej granicy plastyczności

tego zbrojenia

ywd

f

.

8. Stan graniczny nośności jest osiągnięty kiedy

cd

c

f







lub

ywd

sw

f





.

II. OGÓLNE ZASADY SPRAWDZANIA NOŚNOŚCI NA ŚCINANIE

1. Przy sprawdzeniu nośności przekroju żelbetowego na ścinanie wykorzystujemy następujące wartości:

V

Ed

–

obliczeniowa siła poprzeczna od obciążeń zewnętrznych,

V

Rd,c

– obliczeniowa siła poprzeczna przenoszona przez element bez zbrojenia na ścinanie,

V

Rd,s

– obliczeniowa siła poprzeczna przenoszona przez zbrojenia na ścinanie,

V

Rd,max

– obliczeniowa siła poprzeczna wywołująca w zastrzałach betonowych kratownicy stan

graniczny nośności. Siła ta jest ograniczona przez zmiażdżenie ściskanych krzyżulców
betonowych.

2. W strefie ścinania, gdzie obliczeniowe wartości sił ścinających spełniają warunek

c

Rd

Ed

V

V

,



, nie jest

konieczne obliczeniowe zbrojenie na ścinanie.

3. W przypadku, gdy nie jest konieczne obliczeniowe zbrojenie na ścianie należy wówczas zastosować

poprzeczne zbrojenie minimalne. Minimalne zbrojenie poprzeczne może być zaniechane w płytach
pełnych i wielootworowych lub żebrowych oraz w elementach drugorzędnych, które nie wpływają
w istotny sposób na ogólną nośność i stateczność konstrukcji (np.: nadproża o rozpiętości

m

2



).

4. W przypadku zmiennej wysokości strefy przypodporowej (Rys. 4) lub nachylonego cięgna sprężającego,

składowe pionowe wynikające z nachylenia sił rozciągających lub ściskających w pasach powinny być
uwzględnione przy obliczaniu nośności ścinania:

td

ccd

s

Rd

Rd

V

V

V

V







,

,

(2)

w którym:
V

ccd

– obliczeniowa wartość składowej siły ścinającej wywołana nachyleniem pasa ściskanego,

V

td

– obliczeniowa wartość składowej siły ścinającej wywołana nachyleniem pasa rozciąganego.

Rys. 4. Składowe poprzeczne w elementach z nachylonymi pasami.

5. W strefie ścinania, gdzie obliczeniowe wartości sił ścinających spełniają warunek

c

Rd

Ed

V

V

,



,należy

zastosować zbrojenie na ścianie wystarczające do spełnienia warunku

Rd

Ed

V

V



.

6. W żadnym przekroju suma obliczeniowej siły poprzecznej i składowych poprzecznych sił w półkach

td

ccd

Ed

V

V

V





nie powinna przekraczać maksymalnej siły granicznej

max

,

Rd

V

.

7. Rozciągane zbrojenie podłużne powinno być zdolne do przeniesienia dodatkowej siły rozciągającej

wywołanej ścinaniem.

8. Zgodnie z zaleceniami PN-EN 1992-1-1:2008 (EC2) przy wymiarowaniu zbrojenia na ścinanie, dla

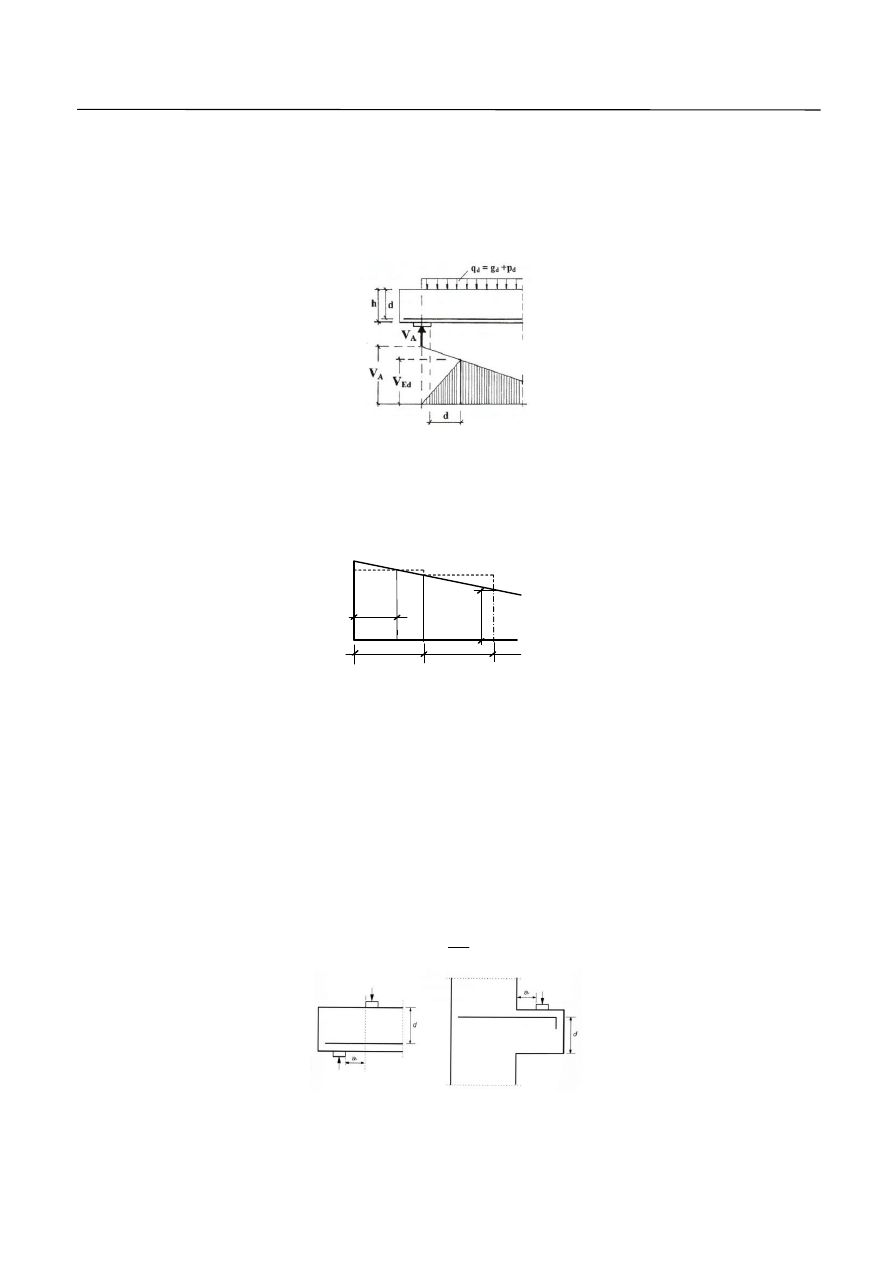
których obciążenie równomiernie rozłożone jest obciążeniem dominującym, to nie wymaga się
sprawdzania obliczeniowej siły poprzecznej w przekrojach, które leżą bliżej niż d od lica podpory
(Rys. 5). Obliczeniową wartość siły ścinającej wyznaczmy dla przekroju położonego w odległości d od
krawędzi podpory. Wynika to stąd, że obciążenie pomiędzy tym przekrojem a podporą jest bezpośrednio
przekazywane poprzez ściskany beton na podporę, bez udziału zbrojenia. Tej redukcji nie uwzględnia
się przy sprawdzaniu maksymalnej nośności krzyżulca betonowego. Należy także sprawdzić, czy siła
poprzeczna na podporze nie przekracza wartości maksymalnej

max

,

Rd

V

. Zbrojenie na ścinanie

rozmieszczamy zarówno na rozpatrywanym odcinku ścinania jak i na odcinku przypodporowym
(odcinek pomiędzy licem podpory a odległością d) bez zmiany intensywności.

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

4

W innych przypadkach za

Ed

V

należy przyjmować największą co do wartości, co do wartości

bezwzględnej, obliczeniową siłę poprzeczną na rozpatrywanym odcinku.

Uwaga: Jeżeli przy sprawdzaniu warunków

c

Rd

Ed

V

V

,



i

Rd

Ed

V

V



na rozpatrywanym odcinku

przypodporowym weźmiemy maksymalną, co do wartości bezwzględnej, siłę wyznaczoną w miejscu
teoretycznego punktu podparcia, lub na krawędzi podpory, nie popełnimy większego błędu bo
będziemy po stronie bezpiecznej.

Rys. 5. Obliczeniowa siła ścinająca w odległości d od podpory.

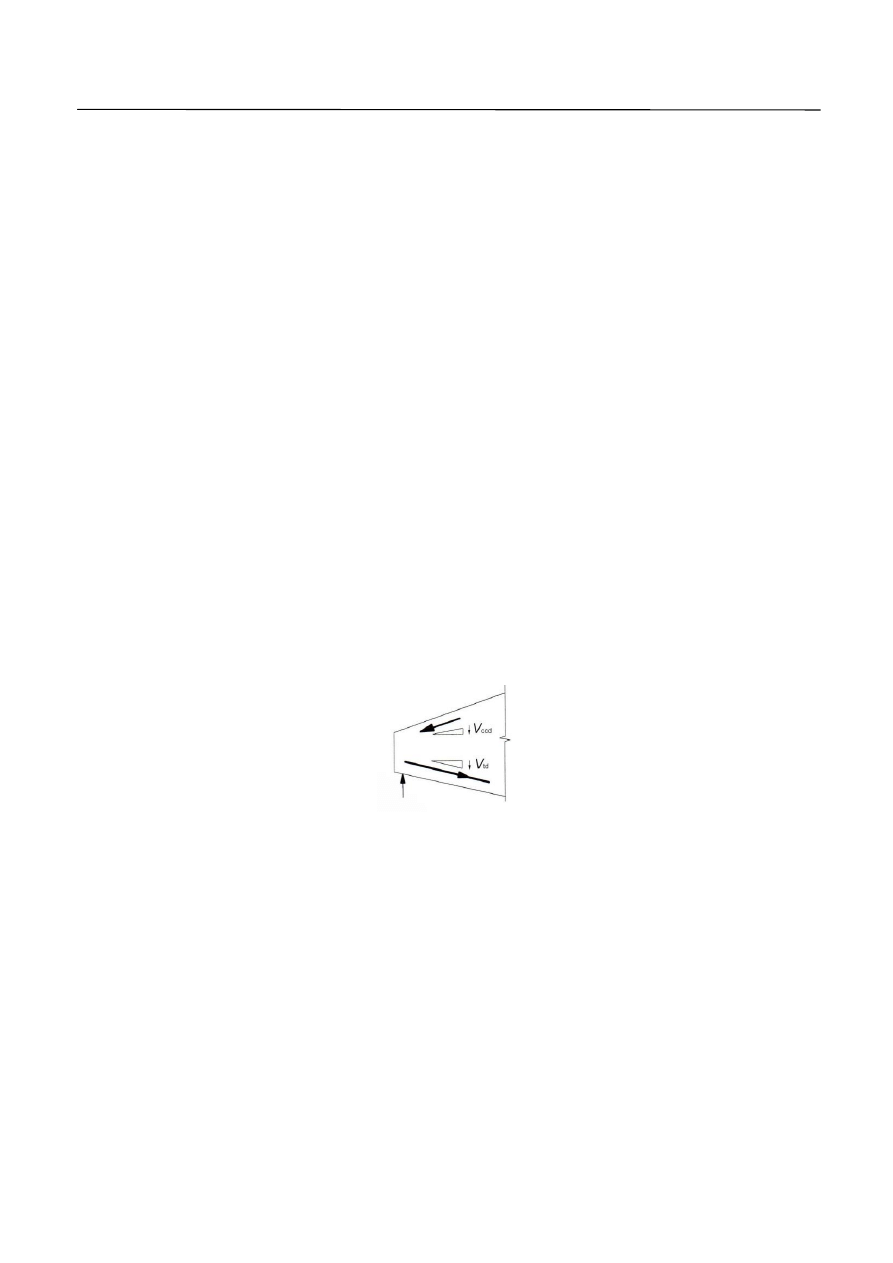
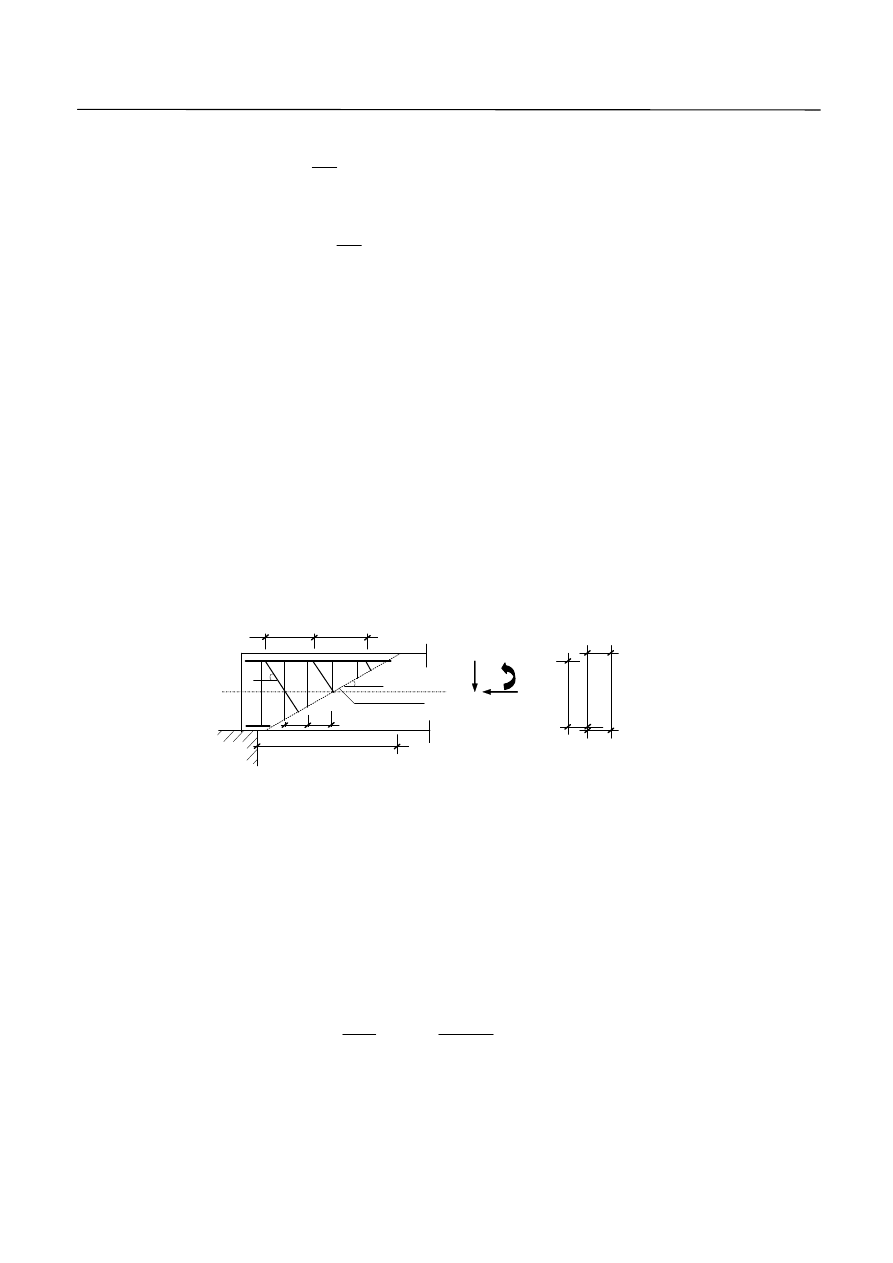
9. W obszarach, w których

Ed

V

zmienia się w sposób ciągły (np.: przy obciążeniu równomiernie

rozłożonym), zbrojenie na ścinanie na każdym przyroście długości



cot

z

l



można obliczać na

podstawie najmniejszej wartości

Ed

V

na tym przyroście (Rys. 6).

Rys. 6. Sposób przyjmowania siły V

Ed

dla kolejnych odcinków zcot



.

10. Minimalna długość odcinka, na którym należy zastosować zbrojenie ze względu na siły poprzeczne

wynosi



cot

z

.

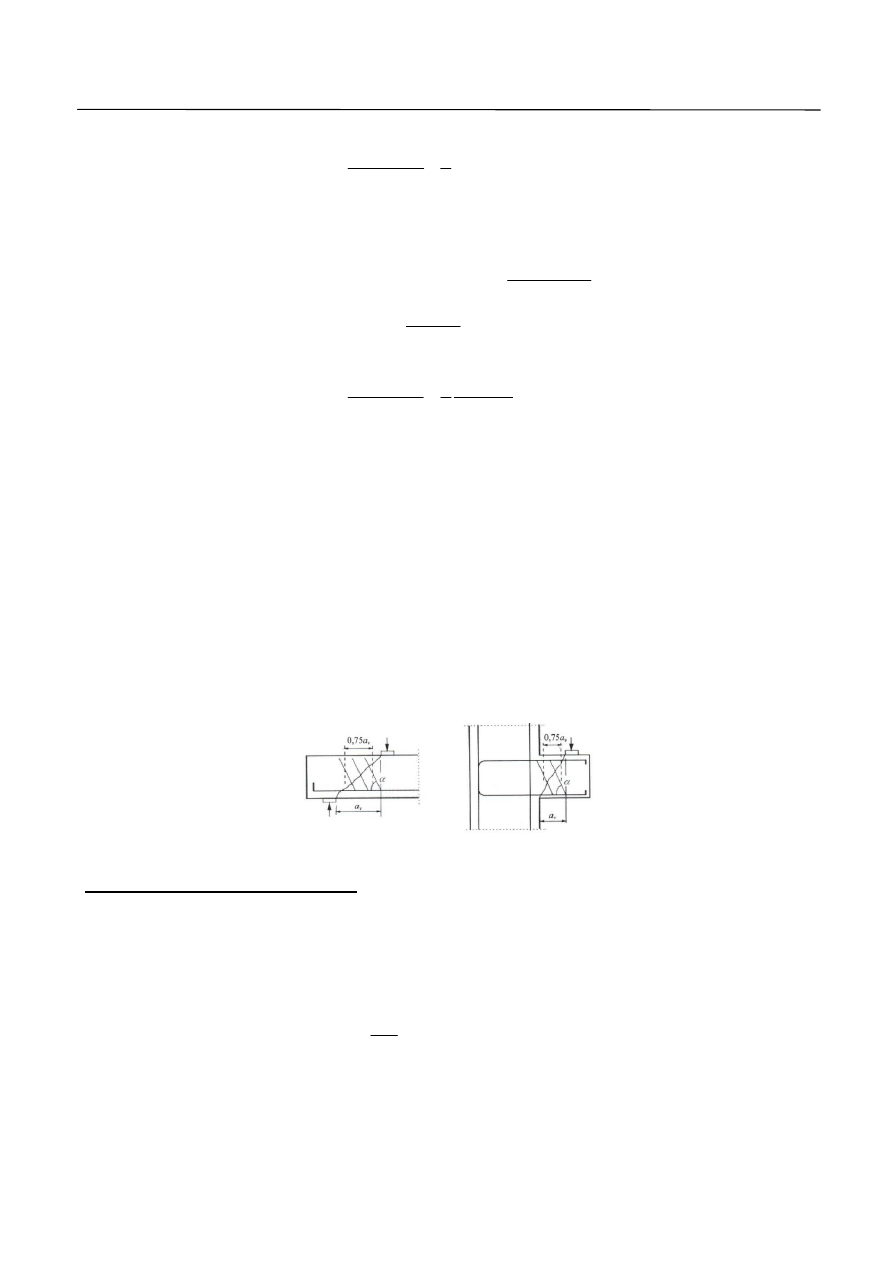
11. Jeżeli obciążenie przyłożone jest blisko dolnej części przekroju, to oprócz zbrojenia na ścinanie należy

zastosować zbrojenie pionowe wystarczające do przeniesienia obciążenia na górną część przekroju.

12. W przypadku gdy obciążenie skupione działa na odcinku

d

a

d

v

2

5

,

0





od krawędzi podpory

(Rys. 7), to część tego obciążenia jest przekazywana na podporę przez ukośny krzyżulec i w tej sytuacji
tylko część obciążenia (

Ed

V



) pochodzącego od siły skupionej przenoszone jest przez zbrojenie

poprzeczne. Zmniejszenie można stosować tylko wtedy, gdy zbrojenie podłużne jest w pełni zakotwione
w podporze. Jeżeli

d

a

v

5

,

0



, to należy przyjąć

d

a

v

5

,

0



. Współczynnik



należy przyjąć według

wzoru:

d

a

v

2





.

(3)

Rys. 7. Obciążenie skupione w pobliżu podpory: a) belka swobodnie podparta, b) wspornik.

13. Projektując zbrojenie podłużne obszaru zarysowanego na skutek zginania należy linię

Ed

M

przesunąć

w kierunku niekorzystnym o odcinek

d

a

l



.

a)

b)

V

Rd,c

z cot



V

Ed

z cot



V

Ed

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

5

III. ZBROJENIE NA ŚCINANIE

1. Elementy nie wymagające zbrojenia na ścinanie

1.1. Stan graniczny nośności przekrojów elementów ścinanych, nie wymagających obliczeniowo zbrojenia

na ścianie, sprawdza się z warunku:

c

Rd

Ed

V

V

,



,

(4)

1.2. Obliczeniową nośność przekroju na ścinanie

c

Rd

V

,

elementu bez zbrojenia na ścinanie wyznacza się ze

wzoru:





d

b

k

f

k

c

V

w

cp

ck

l

c

Rd

c

Rd

100

1

3

1

,

,

















,

(5)

lecz nie mniej niż:





d

b

k

V

w

cp

c

Rd

1

min

,









(6)

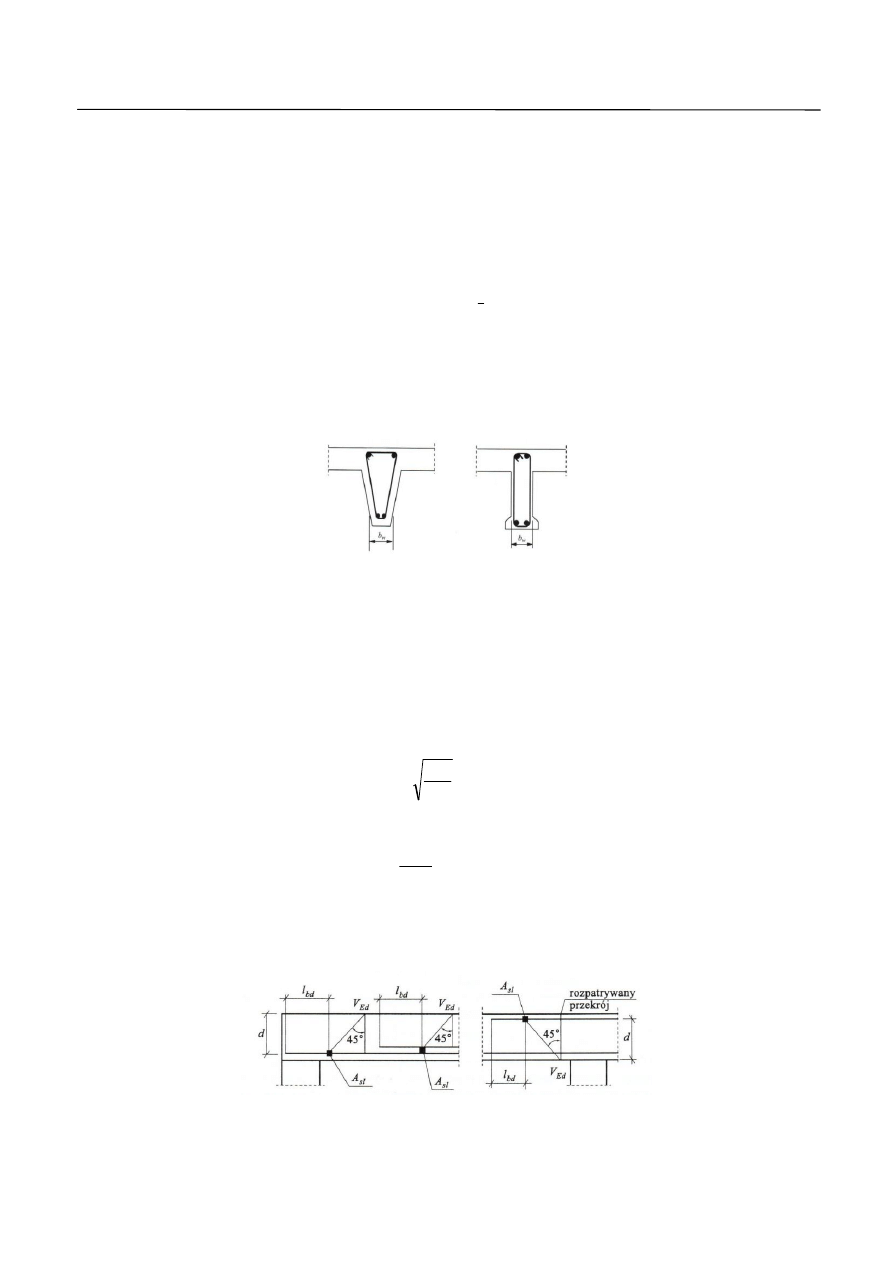
w których: d – wysokość użyteczna przekroju,

b

w

– najmniejsza szerokość strefy ścinania według rysunku 8,

Rys.8. Szerokość strefy ścinania – oznaczenia.

Uwaga: Norma PN-EN 1992-1-1:2008 (EC2) zaleca aby we wzorach (5) i (6) wymiary przekroju
poprzecznego b

w

i d przyjmować w [mm]. Jednak przyjmując te wartości w [m] nie popełnimy błędu

obliczeniowego. Wstawiając do wzoru (5) i (6) wartości w [mm] wartość siły V

Rd,c

otrzymujemy w [N],

natomiast przy przyjęciu b

w

i d w [m] wartość siły V

Rd,c

otrzymujemy w [MN]. Przy sprawdzaniu warunku

nośności przekroju należy pamiętać o zgodności jednostek.

f

ck

– wytrzymałość charakterystyczna betonu na ściskanie w [MPa],

k – współczynnik wyznaczany z zależności (7):

0

,

2

200

1







d

k

,

(7)

we wzorze (7) wartość d przyjmowana jest w [mm],



l

– stopień zbrojenia podłużnego:

0,02

l





d

b

A

w

sl



,

(8)

gdzie: A

sl

– pole przekroju prętów głównego zbrojenia rozciąganego, mającego długość nie

mniejszą niż

bd

l

d



poza rozpatrywanym przekrojem elementu (Rys. 9),

l

bd

– obliczeniowa długość zakotwienia prętów zbrojeniowych podłużnych,

Rys. 9. Zasady definiowania podłużnego zbrojenia rozciąganego A

sl

elementów poddanych ścinaniu.



cp

– naprężenie normalne w przekroju elementu:

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

6

cd

c

Ed

cp

f

A

N

σ

2

,

0





(9)

gdzie: N

Ed

– siła podłużna wywołana obciążeniem obliczeniowym lub sprężeniem (dodatnia przy

ściskaniu). Wpływ obciążeń wymuszonych na

Ed

N

można pominąć,

A

c

– całkowite pole przekroju betonu,

f

cd

– wytrzymałość obliczeniowa betonu na ściskanie w [MPa].

c

Rd,c

– wartością zalecaną współczynnika jest wartość wyznaczona ze wzoru:

c

c

Rd

c



18

,

0

,



(10)



c

– współczynnik bezpieczeństwa dla betonu,

k

1

– wartością zalecaną współczynnika jest

15

,

0

1



k

,



min

–wartością zalecaną współczynnika jest wartość wyznaczona ze wzoru:

2

1

2

3

min

035

,

0

ck

f

k





.

(11)

1.3. Jeżeli obciążenie skupione działa na odcinku

d

a

d

v

2

5

,

0





od krawędzi podpory (Rys. 7), to udział

tego obciążenia w sile poprzecznej

Ed

V

można pomnożyć przez



(3). Zmniejszenie to można

stosować przy sprawdzaniu siły

c

Rd

V

,

opisanej wzorem (5).

1.4. Siła poprzeczna bez zmniejszania za pomocą współczynnika



, powinna spełniać warunek:

d

b

f

V

w

cd

Ed

5

,

0





(12)

w którym:



– współczynnik redukcji wytrzymałości betonu zarysowanego przy ścinaniu.

Wartość zalecana współczynnika efektywności



wynika ze wzoru:











 



250

1

6

,

0

ck

f



,





MPa

w

ck

f

.

(13)

2. Elementy wymagające zbrojenia na ścinanie

2.1. Jeżeli na jakimś odcinku elementu żelbetowego nie jest spełniony warunek (4) stanów granicznych

nośności to należy zastosować na tym odcinku, wymagane obliczeniowo, zbrojenie poprzeczne
(strzemiona, pręty odgięte lub strzemiona ukośne). W belkach strzemiona ukośne lub pręty odgięte
mogą być uwzględnione jako zbrojenie na ścinanie tylko wtedy, gdy strzemiona pionowe przenoszą co
najmniej 50% siły

Ed

V

.

2.2. Stan graniczny nośności przekrojów elementów ścinanych, wymagających obliczeniowo zbrojenia na

ścinanie, sprawdza się z następujących warunków:

s

Rd

Ed

V

V

,



,

(14)

max

,

Rd

Ed

V

V



,

(15)

gdzie: V

Rd,s

–

obliczeniowa siła poprzeczna przenoszona przez zbrojenia na ścinanie,

V

Rd,max

– obliczeniowa siła poprzeczna wywołująca w zastrzałach betonowych kratownicy stan

graniczny nośności. Siła ta jest ograniczona przez zmiażdżenie ściskanych krzyżulców
betonowych.

2.3. Obliczeniowe nośności przekroju na ścinanie z uwagi na zmiażdżenie ściskanych krzyżulców

betonowych

max

,

Rd

V

i z uwagi na zbrojenie poprzeczne

s

Rd

V

,

określa się ze wzorów:

- jeżeli zbrojenie na ścinanie składa się wyłącznie ze strzemion prostopadłych do osi belki (tzn. gdy nie

stosuje się prętów odgiętych lub strzemion ukośnych, lub pomija się wpływ tych prętów):









tan

cot

1

max

,





cd

w

cw

Rd

f

z

b

V

,

(16)



cot

,

z

s

f

A

V

ywd

sw

s

Rd



.

(17)

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

7

Maksymalne efektywne pole przekroju zbrojenia na ścinanie

max

,

sw

A

przy

0

,

1

cot





określa wzór:

cd

cw

w

ywd

sw

f

s

b

f

A

1

max

,

2

1







(18)

- jeżeli zbrojenie na ścinanie składa się ze zbrojenia ukośnego (pręty odgięte lub strzemiona ukośne) to

nośności

max

,

Rd

V

i

s

Rd

V

,

oblicza się ze wzorów:











2

1

max

,

cot

1

cot

cot







cd

w

cw

Rd

f

z

b

V

,

(19)











sin

cot

cot

,





z

s

f

A

V

ywd

sw

s

Rd

,

(20)

Maksymalne efektywne pole przekroju zbrojenia na ścinanie

max

,

sw

A

przy

0

,

1

cot





określa wzór:







sin

2

1

1

max

,

cd

cw

w

ywd

sw

f

s

b

f

A



(21)

Uwaga: W przypadku stosowaniu zbrojenia na ścinanie w postaci strzemion pionowych i zbrojenia
ukośnego (pręty odgięte, strzemiona ukośne) w celu rozróżnienie zbrojenia dla zbrojenia pionowego przyjęto
indeks „1” a dla zbrojenia ukośnego – „2”.

- jeżeli w przedziale

d

a

d

v

0

,

2

5

,

0





obciążenie jest przyłożone do górnej krawędzi elementu (Rys. 7)

to udział tego obciążenia w sile poprzecznej

Ed

V

można zmniejszyć, mnożąc przez współczynnik



(3). Obliczona w ten sposób siła poprzeczna

Ed

V

powinna spełniać warunek:



sin

ywd

sw

Ed

f

A

V



,

(22)

w którym

ywd

sw

f

A

jest nośnością zbrojenia przecinającego rysę od ścinania między obciążonymi

obszarami (Rys. 10). Pod uwagę można brać tylko zbrojenie na ścinanie leżące w granicach
centralnego odcinka o długości

v

a

75

,

0

. Zmniejszenie

Ed

V

za pomocą współczynnika



można

stosować tylko przy obliczaniu zbrojenia na ścinanie.

Rys. 10. Zbrojenie na ścinanie przy bezpośrednim przekazywaniu obciążenia przez ściskany krzyżulec betonowy.

Oznaczenia we wzorach od (14) do (22):

1



– współczynnik redukcji wytrzymałości betonu zarysowanego przy ścinaniu, wartością zalecaną

1



jest

wartość



wyznaczona ze wzoru (13),

Jeżeli naprężenie obliczeniowe w zbrojeniu na ścinanie jest mniejsze niż 80% charakterystycznej granicy
plastyczności

1



to wartość

1



można przyjąć jako równą:

6

,

0

1





MPa

60

dla



ck

f

(23)

5

,

0

200

9

,

0

1







ck

f



MPa

60

dla



ck

f

(24)

Uwaga: Jeżeli do wyznaczenia wartości współczynnika

1



stosujemy wzory (23) lub (24) to we wzorze (17)

wartość

ywd

f

należy zmniejszyć do

ywd

f

8

,

0

.

cw



– współczynnik zależny od stanu naprężenia w pasie ściskanym,

Zalecana wartość współczynnika

cw



wynosi:

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

8

0

,

1



cw



dla konstrukcji niesprężonych,

(25)

cd

cp

cw

f









1

cd

cp

f

25

,

0

0

dla







,

(26)

25

,

1



cw



cd

cp

cd

f

f

,

5

,

0

25

0

dla







,

(27)

















cd

cp

cw

f





1

5

,

1

cd

cp

cd

f

f

,







5

0

dla

,

(28)

w których

cp



oznacza średnie naprężenie ściskające (ze znakiem plus) w betonie wywołane obliczeniowa

siłą podłużną. W przekroju żelbetowym obliczane z uwzględnieniem zbrojenia. Nie uwzględniamy wpływu

cp



w przekrojach leżących bliżej krawędzi podpory niż



cot

5

,

0 d

.

1

sw

A

– pole przekroju poprzecznego prętów tworzących jedno strzemię prostopadłe do osi elementu (np.:

pole czterech prętów 6



a w przypadku strzemion podwójnych pole dwóch prętów 6



),

1

ywd

f

– obliczeniowa granica plastyczności strzemion prostopadłych do osi elementu,

1

s

– rozstaw strzemion prostopadłych do osi elementu,

2

sw

A

– pole przekroju poprzecznego ukośnych strzemion lub prętów odgiętych tworzących jedną

płaszczyznę odgięć,

2

s

– średni rozstaw płaszczyzn odgięć lub strzemion ukośnych mierzony wzdłuż osi belki,

2

ywd

f

– obliczeniowa granica plastyczności zbrojenia

2

sw

A

,



– kąt nachylenia prętów odgiętych lub ukośnych strzemion,



– kąt nachylenia ściskanego krzyżulca betonowego.

Rys. 11. Podstawowe oznaczenia wykorzystane we wzorach od (14) do (22).

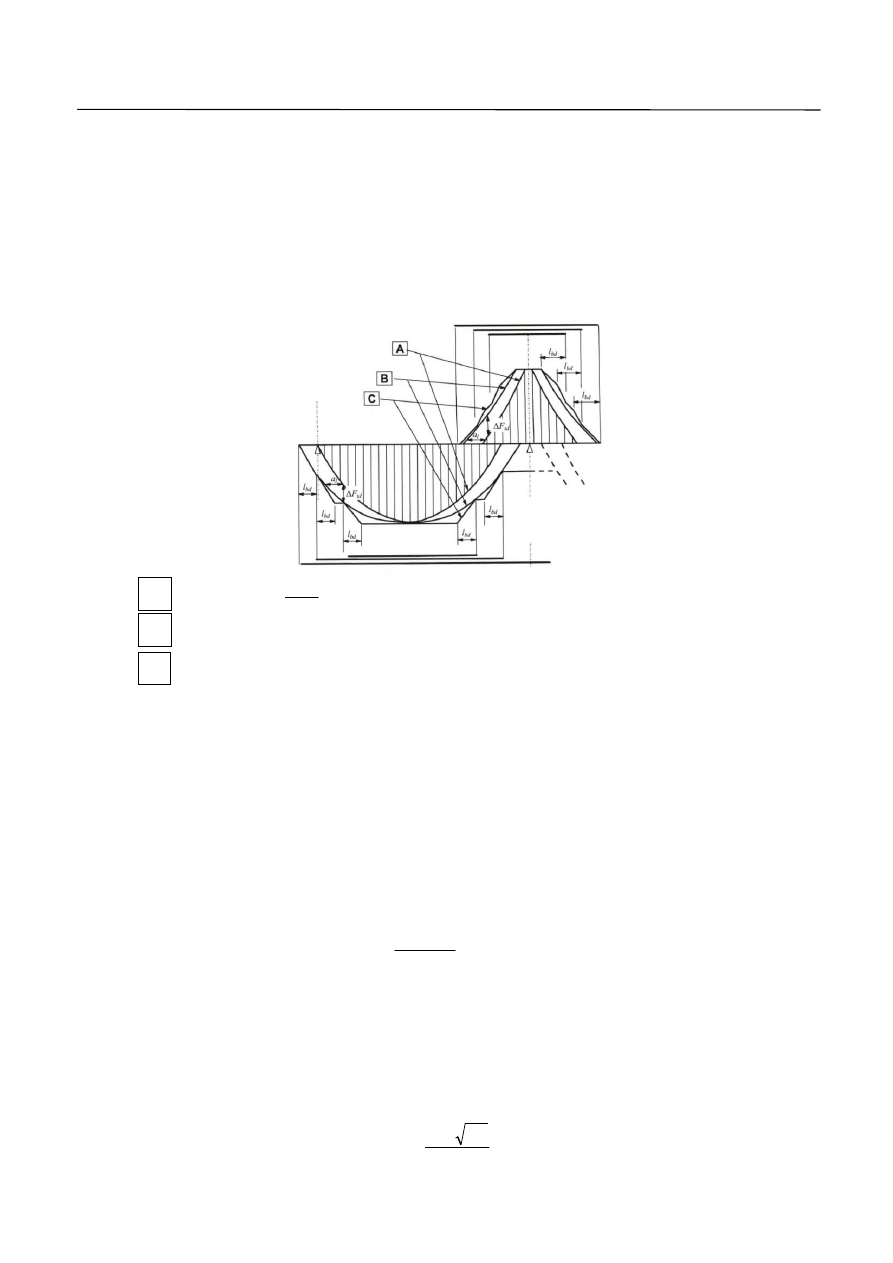
2.4. Zbrojenie podłużne w każdym przekroju poprzecznym elementu powinno być zdolne do przeniesienia

sumarycznej siły rozciągającej

td

F obliczonej z uwzględnieniem siły poprzecznej

td

F



. Wpływ siły

poprzecznej na wzrost siły rozciągającej w zbrojeniu podłużnym określa się według wzoru:





α

θ

V

F

Ed

td

cot

cot

5

,

0







(29)

Na długości elementu, gdzie moment zginający nie zmienia znaku, sumaryczna siła rozciągająca w zbrojeniu
podłużnym

td

F nie może przybierać większej wartości niż wartość bezwzględna maksymalnej siły

rozciągającej wywołanej działaniem momentu zginającego i siły podłużnej.
Siłę

td

F wyznaczamy z zależności:

z

M

F

z

M

F

Ed

td

Ed

td

max

,









,

(30)

gdzie:

Ed

M

– wartość momentu w rozpatrywanym przekroju ścinania,

max

,

Ed

M

– wartość maksymalna momentu na długości belki,

z

– ramię sił wewnętrznych.

s

2

s

1



s

1

s

2

a

1



ściskany
krzyżulec betonowy

z cot



d

z

=

0

,9

d

M

Ed

N

Ed

V

Ed

h

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

9

W elementach ze zbrojeniem na ścinanie wpływ siły poprzecznej oblicza się ze wzoru (29), lub poprzez
poszerzenie wykresu sił o odcinek

l

a przyjmując:





α

θ

z

a

l

cot

cot

5

,

0





(31)

W elementach bez zbrojenia na ścinanie wpływ siły poprzecznej można uwzględniać poszerzając wykres sił
o odcinek

d

a

l



.

Sporządzając obwiednie nośności prętów zbrojenia podłużnego można przyjąć, że siła w nich przyrasta
liniowo na długości zakotwienia

bd

l

.

– obwiednia siły

Ed

Ed

N

z

M



,

– siła rozciągająca w zbrojeniu

s

F

,

– nośność prętów zbrojenia podłużnego na rozciąganie

Rs

F

,

Rys. 12. Kształtowanie zbrojenia podłużnego w elementach zginanych z uwzględnieniem wpływu ścinania i narastania

nośności zbrojenia na długości zakotwienia.

Zakłada się, że na odcinkach, gdzie kotwione są pręty zbrojenia podłużnego, siła w zbrojeniu zmienia się
liniowo (Rys. 12) Pominięcie tych odcinków w nośności zbrojenia przyjmuje się jako bezpieczne
uproszczenie.

Długość zakotwienia prętów odgiętych, które przyczyniają się do wzrostu nośności na ścinanie, powinna być
nie mniejsza niż

bd

l

3

,

1

w strefie rozciąganej i

bd

l

7

,

0

w strefie ściskanej. Długość tę odmierza się od punktu

przecięcia osi pręta odgiętego i zbrojenia podłużnego.

2.5. Stopień zbrojenia na ścinanie

w



oblicza się ze wzoru:





sin

w

sw

w

sb

A



(32)

w którym:

sw

A – pole przekroju zbrojenia na ścinanie przypadającym na odcinek o długości s ,

s – rozstaw zbrojenia na ścianie mierzony wzdłuż osi podłużnej elementu,

w

b – szerokość strefy ścinania elementu,



– kąt nachylenia do poziomu prętów odgiętych lub strzemion ukośnych.

Stopień zbrojenia na ścinanie obliczony z (32) nie może być mniejszy od wartości minimalnej wyznaczanej
z poniższego wzoru:

yk

ck

w,

f

f

ρ

08

,

0

min



(33)

A

B

C

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

10

3. Ścinanie pomiędzy środnikiem a półką

Według PN-EN 1992-1-1:2008 nośność półki na ścianie można obliczać, rozpatrując półkę jako zespół
krzyżulców ściskanych i prętów rozciąganych reprezentowanych przez zbrojenie rozciągane. Stan graniczny
może być osiągnięty przez ściskanie w krzyżulcach betonowych lub poprzez rozciąganie w zbrojeniu
zapewniającym połączenie półki ze środnikiem. Minimalna ilość zbrojenia podłużnego jak i zbrojenia na
styku półki i środnika powinna odpowiadać zaleceniom konstrukcyjnym.

W przekrojach teowych, gdy półka jest ściskana, oś obojętna przechodzi najczęściej niedaleko dolnej
krawędzi tej płyty i naprężenia ścinające mają w półce dość dużą wartość. Ponieważ ścinanie wynika ze
zmiany naprężeń (momentów), podłużne naprężenia styczne w płaszczyźnie styku między jedną stroną półki
i środnikiem jest równe zmianie siły normalnej (podłużnej) na długości rozpatrywanej części półki i oblicza
się ze wzoru:

x

h

F

v

f

d

Ed

Δ

Δ



,

(34)

gdzie:

d

F



– zmiana siły podłużnej w półce po jednej stronie środnika na długości odcina x



,

gdy półka jest ściskana i

f

eff

h

x



to:





w

eff

eff

cd

d

b

b

x

f

F







5

,

0

,

(35)

gdy półka jest ściskana i

f

eff

h

x



to:





w

eff

f

cd

d

b

b

h

f

F







5

,

0

,

(36)

gdy półka jest rozciągana to:

s

yd

d

A

f

F





,

(37)

w którym:

s

A – pole powierzchni zbrojenia znajdującego się w półce po jednej stronie środnika,

x



– długość rozpatrywanego odcinaka.

Długość odcinka x



przyjmuje się nie większą niż:

-

połowa odległości między przekrojami

0



M

oraz

max

M

M



,

-

odległość między siłami skupionymi.

Krzyżulce ściskane

Zakotwienie zbrojenia podłużnego

A-A – rozpatrywany przekrój

Rys. 13. Oznaczenia dotyczące połączenia półki ze środnikiem.

Siła ta jest przenoszona w przyjętym modelu przez ściskane krzyżulce betonowe i rozciągane cięgna stalowe.
W belkach teowych role tych cięgien spełniają zwykle strzemiona znajdujące się w półce, a w stropach
płytowo-belkowych – zbrojenie płyty nad belką.
Nośność krzyżulców betonowych sprawdza się z warunku:

f

f

cd

Ed

f

v







cos

sin



,

(38)

drugi warunek dotyczy rozciągania zbrojenia poprzecznego na jednostkę długości

s

A

f

sf

i ma postać:

f

f

Ed

yd

f

sf

θ

h

f

s

A

cot





,

(39)

A

B

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

11

w których:

sf

A – pole przekroju prętów zbrojenia poprzecznego w półce na grubości

f

h ,

f

s – rozstaw prętów zbrojenia

sf

A ,

f

h – grubość półki,

f



– kąt nachylenia ściskanego krzyżulca betonowego w półce,



– współczynnik należy wyznaczać zgodnie ze wzorem (13).

Wartość kąta

f



przyjmuje się:

-

dla półki ściskanej

0

,

2

cot

0

,

1





f



,

-

dla półki rozciąganej

25

,

1

cot

0

,

1





f



.

Praktycznie wzór (39) służy do wyznaczenia niezbędnego zbrojenia (strzemion) w półce belki. Najczęściej
rozstaw strzemion

f

s i ich powierzchnia

sf

A są takie same jak wyliczone dla środnika ze względu na

ścinanie.

Jeżeli ścinanie między półką i środnikiem występuje jednocześnie z poprzecznym zginaniem to za pole
zbrojenia poprzecznego należy przyjąć pole większe niż:
-

pole obliczone ze wzoru (38),

-

pole wymagane ze względu na zginanie plus płowa pola wyznaczonego ze wzoru (38).

Jeżeli naprężenie

Ed

v

spełnia warunek (40), to zbrojenie dodatkowe, poza zbrojeniem koniecznym ze

względu na zginanie, nie jest konieczne. W przeciwnym przypadku należy wyznaczyć zbrojnie dodatkowe.

ctd

Ed

kf

v



,

(40)

w którym

4

,

0



k

i jest wartością zalecaną.

Podłużne, rozciągane zbrojenie półki powinno być zakotwione poza ściskanym krzyżulcem betonowym,
niezbędnym do przeniesienia siły z powrotem do środnika, w przekroju, w którym zbrojenie to jest
konieczne (Rys. 13., przekrój A-A).

4. Wymagania konstrukcyjne dotyczące zbrojenia na ścinanie

4.1. Zbrojenie na ścinanie
Zbrojenie na ścianie może być kombinacją strzemion obejmujących zbrojenie podłużne w strefie ściskanej
i rozciąganej (Rys. 14), z prętów odgiętych odpowiednio zakotwionych w ściskanej i rozciąganej strefie
elementu, oraz zbrojenia dodatkowego. Zbrojenie dodatkowe może mieć kształt koszy, drabinek, strzemion
otwartych itp. I nie musi obejmować podłużnego zbrojenia rozciąganego, jednak powinno być dobrze
zakotwione zarówno w strefie ściskanej jak i rozciąganej betonu.

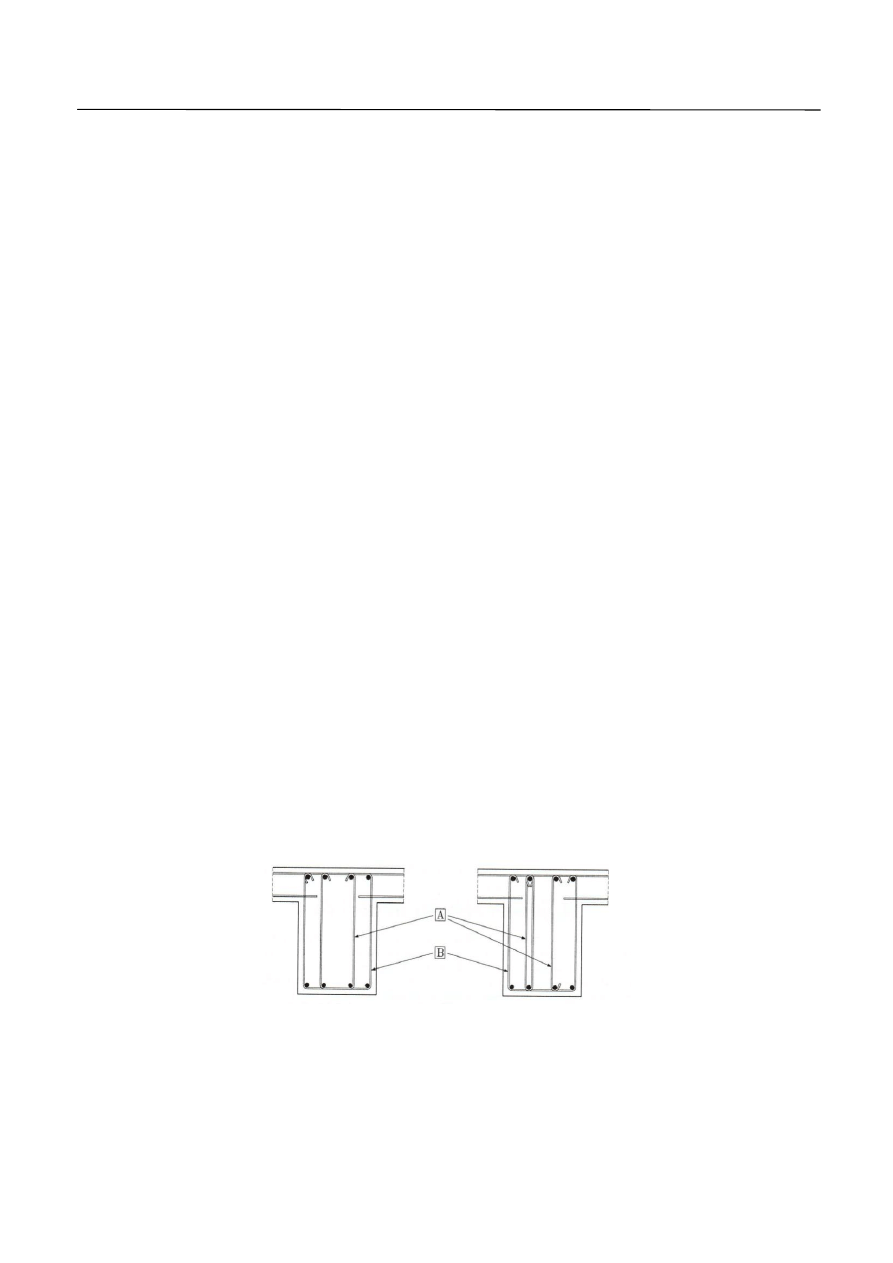
Rys. 14. Przykładowe zbrojenie na ścinanie. A – strzemiona wewnętrzne, B – strzemiona zamykające.

Uwaga. Stosowanie dodatkowego zbrojenia w postaci strzemion otwartych, koszy czy drabinek budzi pewne
obawy ze względu na możliwość wystąpienia zbyt słabego ich zakotwienia. Proponuje się, by
w obliczeniach uwzględniać jedynie 70% powierzchni przekroju poprzecznego tego zbrojenia.

Strzemiona powinny być zakotwione efektywnie. Łączenie strzemion na zakład w pobliżu bocznej
powierzchni jest dopuszczalne pod warunkiem, że strzemiona nie są potrzebne ze względu na skręcanie.

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

12

4.2. Strzemiona
Norma PN-EN 1992-1-1:2008 (EC2) nie definiuje i minimalnej i maksymalnej średnicy prętów
zbrojeniowych za stosowanych na strzemiona. Ze względów wykonawczych (konieczność stosowania
kilkukrotnych odgięć) wydaje się być uzasadniony fakt przyjęcia średnic strzemion od 4,5 do 12 mm.
Strzemiona oprócz przenoszenia głównych naprężeń rozciągających wywołanych ścinaniem powinny także
zapewnić odpowiednią sztywność szkieletu zbrojenia. Przy doborze minimalnej średnicy strzemion można
się więc wspomagać zaleceniami konstrukcyjnymi podanymi we wcześniejszych normach (PN-B-
03264:1999 i PN-B-03264:2002). Dla początkującego projektanta może to być swego rodzaju podpowiedź
przy doborze tych średnic. Według tych zaleceń średnica strzemion powinna być nie mniejsza niż:

















0,2

wanych

prefabryko

belkach

w

-

mm

3,0

budowy

miejscu

na

konywanych

belkach wy

w

-

mm

4,5

w

,

(41)

gdzie



– średnica zbrojenia podłużnego.

Maksymalny rozstaw strzemion w kierunku podłużnym i poprzecznym zestawiono w tablicy 1.

Tablica 1.

Maksymalny rozstaw strzemion

max

s

.

W kierunku podłużnym

(rozstaw strzemion na długości elementu)







cot

1

75

,

0

max

,







d

s

s

l

W kierunku poprzecznym

(rozstaw ramion strzemion)









mm

600

75

,

0

max

,

d

s

t

Jeżeli w belce zastosowano pręty ściskane, potrzebne ze względów obliczeniowych, rozstaw strzemion
zamkniętych powinien być nie większy niż 20 średnic tego zbrojenia.

4.3. Pręty odgięte
Pręty odgięte uwzględniane w obliczeniach powinny być rozmieszczone w strefie przypodporowej tak aby
maksymalny podłużny rozstaw nie przekraczał wartości:







cot

1

6

,

0

max

,





d

s

b

.

(42)

5. Tok wymiarowania ze względu na ścinanie elementów żelbetowych
5.1. Zbrojenie na ścinanie w postaci strzemion pionowych

Dane lub założone:

Ed

V

,

Ed

M

,

Ed

N

,

ck

f

,

c



,

cd

f

,

05

,

0

,

ctk

f

,

ctd

f

,

yk

f

,

yd

f

,

w

b ,

1

d , h ,

1



,

w



.

Szukane:

sw

A , s .

5.1.1. Obliczamy:

1

d

h

d





.

W przypadku gdy

0



Ed

N

, obliczamy również

c

A .

5.1.2. Zakładamy:

d

z

9

,

0



.

5.1.3. Wyznaczamy miarodajną wartość siły

Ed

V

na krawędzi podpory –

k

Ed

V

,

i w odległości d od podpory

–

d

Ed

V

,

.

5.1.4. Z (10) obliczamy wartość

c

Ed

c

,

.

5.1.5. Z (7) obliczamy współczynnik k .
5.1.6. Z (8) obliczamy procent zbrojenia podłużnego

l



.

5.1.7. Z (9) obliczamy naprężenia normalne

cp



i przyjmujemy współczynnik

1

k . Gdy

0



Ed

N

to

0



cp



.

5.1.8. Z (18) obliczamy

min



.

5.1.9. Z (5) określamy nośność obliczeniową na ścianie ze względu na rozciąganie batonu, powstające przy

ścinaniu w elemencie nie mającym zbrojenia poprzecznego na ścianie i sprawdzamy czy jest ona
większa od wartości wyznaczonej z (6). Do dalszych obliczeń przyjmujemy wartość większą.

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

13

5.1.10. Jeżeli

c

Rd

Ed

V

V

,



nie zachodzi konieczność obliczania zbrojenia poprzecznego. Element zbroimy

zgodnie z zaleceniami PN-EN 1992-1-1:2008 (EC2).

5.1.11. Jeżeli

c

Rd

Ed

V

V

,



to wówczas zachodzi konieczność obliczania zbrojenia poprzecznego.

Obliczenie zbrojenia
5.1.12. Wyznaczamy długość odcinka, na którym potrzebne jest obliczeniowo zbrojenie poprzeczne

(długość odcinka ścinania) –

w

a .

W przypadku obciążenia równomiernie rozłożonego (Rys. 15a) długość odcinka ścinania wyznaczamy
z zależności:

d

c

Rd

Ed

w

q

- V

V

a

,



.

(43)

Dla obciążenia w postaci sił skupionych długość odcinka ścinania

w

a jest równa odległości od podpory do

siły skupionej (Rys. 15b).
Minimalna długość odcinka ścinania wynosi:



cot

z

a

w



.

a)

l

eff

q

d

V

Ed,A

V

Ed,B

A

B

V

Ed,c

V

Ed,c

a

w

a

w

b)

l

eff

F

d

V

Ed,A

V

Ed,B

A

B

V

Ed,c

V

Ed,b

a

w

F

d

a

b

V

Ed,a

Rys. 15. Długość odcina ścinania a

w2

dla różnych sposobów obciążenia elementu:

a)

obciążenie równomiernie rozłożone,

b)

obciążenie siłami skupionymi.

Odcinek ścinania

w

a można podzielić na krótsze części (Rys. 6) i wykonać obliczenia każdej części

w zależności od występującej na niej miarodajnej siły

Ed

V

przyjmowanej do obliczeń. Części nie mogą być

jednak krótsze niż



cot

z

.

Można też nie wyznaczać odcinka ścinania, tylko obliczać ścinanie dla odcinków równych



cot

z

aż do

momentu gdy siła

Ed

V

osiągnie wartość

c

Rd

V

,

(

c

Rd

Ed

V

V

,



) licząc od podpory w kierunku przęsła.

Na odcinku bezpośrednio sąsiadującym podporą jako siłę miarodajną do obliczenia niezbędnej ilości
zbrojenia poprzecznego przyjmujemy wartość siły

Ed

V

wyznaczoną w odległości d od podpory. Na

pozostałych odcinkach przyjmujemy siłę maksymalną na rozpatrywanym odcinku.
5.1.13. Kąt nachylenia krzyżulców betonowych



należy przyjmować zgodnie założeniem 4, str. 2.

5.1.14. Przyjmujemy:
-

średnicę strzemion zgodnie z punktem 4.2,

-

gatunek stali, z której zostaną wykonane strzemiona





ywd

yk

f

f

,

-

liczbę ramion strzemion

w

n (strzemiona dwu–, lub czteroramienne).

5.1.15. Obliczamy pole powierzchni jednego strzemienia:

w

sw

n

A

4

2





(44)

5.1.16. Ze wzoru (17) obliczamy rozstaw strzemion zakładając

Ed

s

Rd

V

V



,

:

Ed

ywd

sw

s

Rd

V

z

s

f

A

V







cot

,



cot

z

V

f

A

s

Ed

ywd

sw



.

(45)

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

14

gdzie:

Ed

V

jest miarodajną siłą potrzebną do obliczenia potrzebnej ilości zbrojenia poprzecznego.

Rozstaw strzemion przyjmujemy z zaokrągleniem do 10 mm w dół, pamiętając ponadto o warunkach
konstrukcyjnych kształtowania zbrojenia na ścinanie oraz o stopniu przyjętego zbrojenia na ścinanie tak by:

min

,

w

w







(46)

gdzie:

min

,

w



– minimalny stopień zbrojenia na ścinanie (29).

5.1.17. Sprawdzenie z (18) warunku maksymalnego efektywnego pola przekroju zbrojenia na ścinanie przy

0

,

1

cot





.

5.1.18. Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

max

,

Rd

Ed

V

V



(47)

gdzie:

Ed

V

– siła poprzeczna przyjmowana do obliczeń,

max

,

Rd

V

– wartość siły wyznaczona z (16).

5.1.19. Sprawdzenie nośności zbrojenia podłużnego

td

F .

Do przeniesienia tej siły potrzebne jest zbrojenia rozciągane

yd

td

d

s

f

F

A



1

, zakotwione poza rozpatrywanym

przekrojem zgodnie z rysunkiem 9. Jeżeli pole powierzchni zbrojenia rozciąganego w rozpatrywanym
przekroju jest mniejsze od

d

s

A

1

to należy przekrój dozbroić.

5.1.20. Określamy rozstaw strzemion na całej długości belki zgodnie z wykonanymi obliczeniami

i zaleceniami konstrukcyjnymi. Należy pamiętać, by suma rozstawu strzemion w kierunku
podłużnym nie była większa niż rozpiętość belki w świetle podpór.

5.1.21. Jeżeli rozpatrywaliśmy kilka odcinków ścinania o długości



cot

z

(Rys. 6), to po wykonaniu

obliczeń dla pierwszego odcinka przechodzimy do następnego. Obliczamy kolejny przekrój
elementu ścinanego w odległości



cot

z

. Jeżeli w tym przekroju

c

Rd

Ed

V

V

,



, to obliczenia

powtarzamy od punktu 5.1.14. Natomiast jeżeli

c

Rd

Ed

V

V

,



kończymy obliczenia.

5.2. Zbrojenie na ścinanie w postaci strzemion pionowych i prętów odgiętych lub strzemion

ukośnych.

Dane lub założone:

Ed

V

,

Ed

M

,

Ed

N

,

ck

f

,

c



,

cd

f

,

05

,

0

,

ctk

f

,

ctd

f

,

yk

f

,

yd

f

,

w

b ,

1

d , h ,

1



,

2



1

w



,

2

w



.

Szukane:

1

sw

A

,

2

sw

A

,

1

s ,

2

s .

W przypadku zastosowania zbrojenia na ścianie w postaci strzemion pionowych i prętów odgiętych lub
strzemion ukośnych do sprawdzenia, czy zachodzi konieczność stosowania zbrojenia poprzecznego czy też
nie postępujemy jak w punkcie 5.1. Obliczenia wykonujemy zgodnie z punktami od 5.1.1. do 5.1.13. A
następnie:
5.2.1. Przyjmujemy:

- przyjmujemy średnicę strzemion

1

w



, i liczbę ramion

1

w

n oraz gatunek stali z której będą wykonane,

- przyjmujemy średnicę strzemion ukośnych

2

w



, liczbę ramion

2

w

n

, kąt pochylenia oraz gatunek

stali z której będą wykonane,

- przyjmujemy średnicę pręta odgiętego

2

w



oraz gatunek stali (jeżeli jest to odginany pręt, który był

wcześniej przyjęty przy wymiarowaniu na zginanie to gatunek stali nie ulega zmianie).

5.2.2. Z (19) obliczamy siłę jaka przenoszona jest przez strzemiona ukośne lub pręty odgięte.
5.2.3. Obliczamy wartość siły jaką powinny przenieść strzemiona pionowe

1

,s

Rd

V

.

Przy zastosowaniu ze względu na siły poprzeczne zbrojenia w postaci strzemion pionowych i prętów
odgiętych lub strzemion ukośnych minimum 50% siły

Sd

V

powinny przenieść strzemiona pionowe.

Ed

s

Rd

s

Rd

s

Rd

V

V

V

V







2

,

1

,

,

(48)

Ed

s

Rd

s

Rd

s

Rd

V

V

V

V

5

,

0

2

,

,

1

,







(49)

Rozstaw strzemion liczymy zgodnie z punktem 5.1.16 (wzór 45) przyjmując

Ed

s

Rd

V

V

5

,

0

1

,



.

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

15

5.2.4. Sprawdzenie z (21) warunku maksymalnego efektywnego pola przekroju zbrojenia na ścinanie przy

0

,

1

cot





.

5.2.5. Sprawdzenie zgodnie z (47) nośności krzyżulców betonowych. W tym przypadku siłę

max

,

Rd

V

wyznaczamy z (19).

5.2.6. Sprawdzenie nośności zbrojenia podłużnego

td

F .

5.2.7. Określamy rozstaw zbrojenia ukośnego i strzemion na całej długości belki zgodnie z wykonanymi

obliczeniami i zaleceniami konstrukcyjnymi.

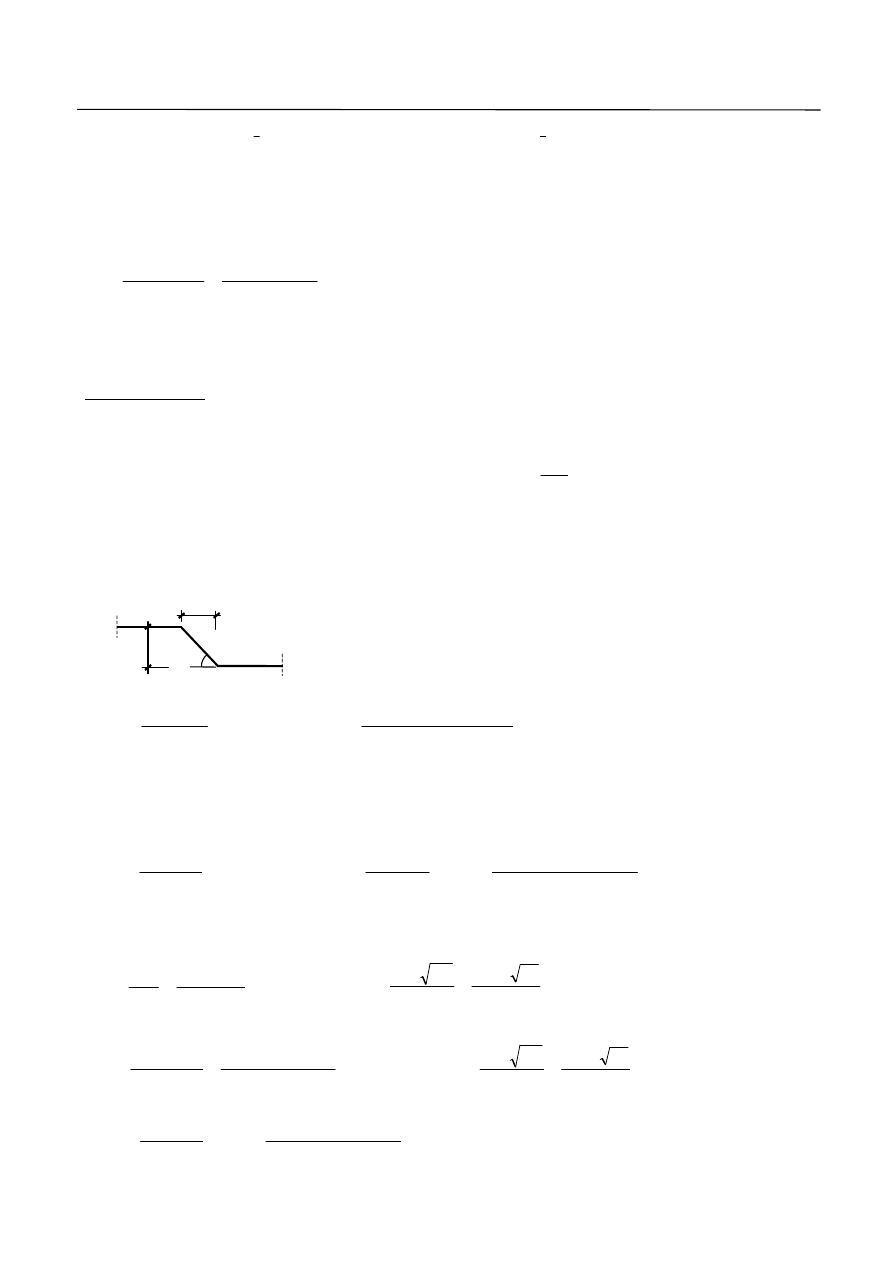
IV. PRZYKŁADY OBLICZENIOWE

PRZYKŁAD 1

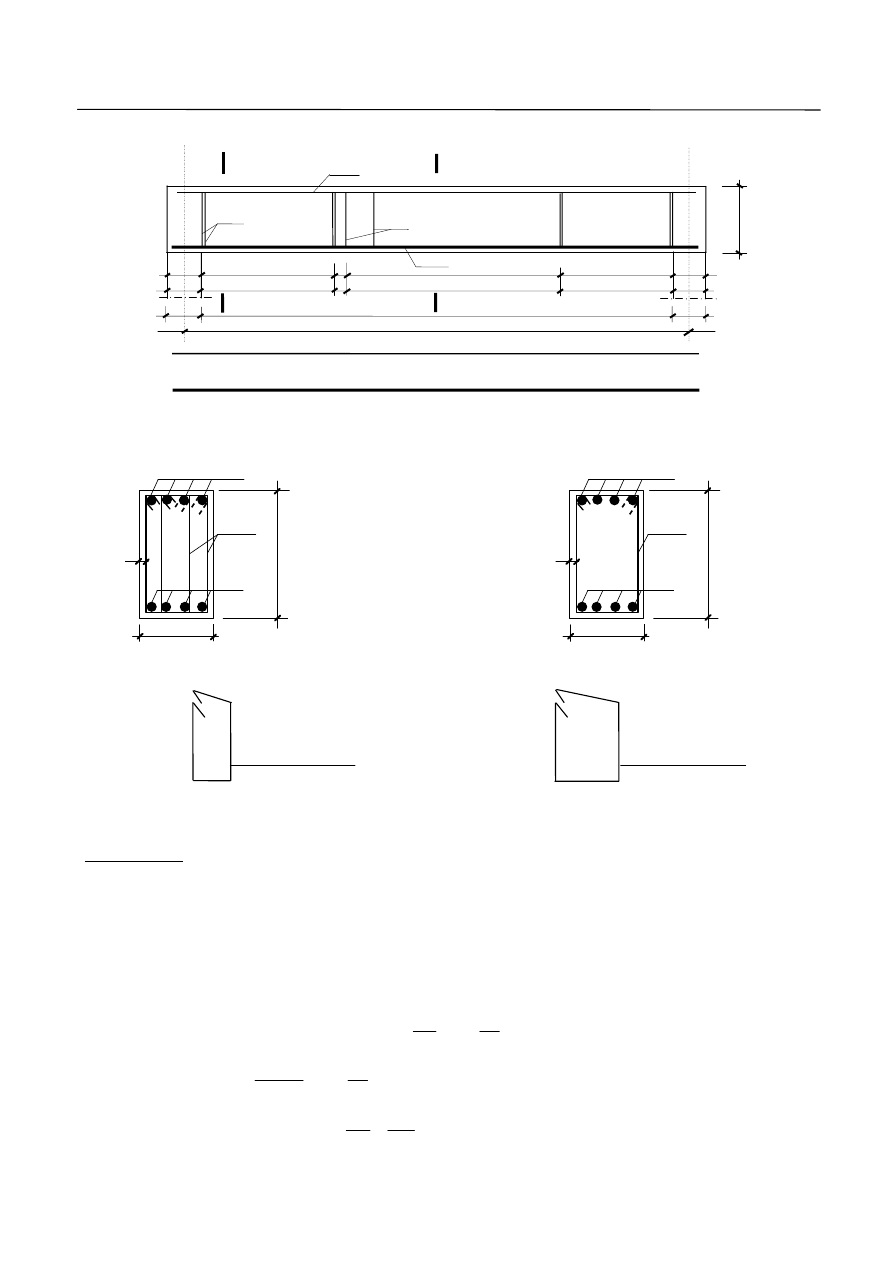
Obliczyć zbrojenie na ścinanie mając dane: beton C20/25, stal o

MPa

355



yk

f

, klasa stali B,

cm

30



b

,

cm

60



h

. Sytuacja obliczeniowa stała i przejściowa. Otulina

cm

5

,

2



nom

c

.

l

eff

=6,0 m

M

Ed,max

= 270 kNm

q

d

= 60 kN/m

V

Ed,A

= 180 kN

V

Ed,B

= 180 kN

V

Ed

= V

Ed,A

= V

Ed,B

A

B

Dane materiałowe
Beton C20/25:

MPa

20



ck

f

4

,

1



c



,

MPa

3

,

14

4

,

1

20

0

,

1









c

ck

cc

cd

f

f





,

MPa

5

,

1

05

,

0

,



ctk

f

,

MPa

07

,

1

4

,

1

5

,

1

0

,

1

05

,

0

,









c

ctk

ct

ctd

f

f





Stal:

MPa

355



yk

f

,

15

,

1



s



,

MPa

7

,

308

15

,

1

355







s

yk

yd

f

f



Zbrojenie podłużne:
zbrojenie rozciągane –

2

1

cm

18

,

10



s

A

zbrojenie ściskane –

2

2

cm

0

,

1



s

A

2



8

4 # 18

250

250

5500

2



8

4 # 18

300

600

Wysokość użyteczna przekroju:

m

06

,

0

60

,

0

1

,

0

1

,

0

1









h

d

m

54

,

0

06

,

0

60

,

0

1











a

h

d

Wyznaczenie miarodajnej siły poprzecznej:

V

Ed

= 180 kN

0,25 m

V

Ed,k

= 172,0 kN

V

Ed,d

= 140,10 kN

d = 0,54 m

Wielkość siły na krawędzi podpory:

kN

5

,

172

60

25

,

0

5

,

0

180

5

,

0

,















d

Ed

k

Ed

tq

V

V

Miarodajna siła w odległości d od krawędzi podpory:

kN

1

,

140

60

54

,

0

50

,

172

,

,













d

k

Ed

d

Ed

dq

V

V

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

16

Nośność przekroju na ścinanie bez zbrojenia na ścianie

13

,

0

4

,

1

18

,

0

18

,

0

,







c

c

Rd

c



0

,

2

61

,

1

540

200

1

200

1













d

k

0,02

006

,

0

54

,

0

0,30

4

-

10

10,18

l













d

b

A

w

sl





cp

= 0 (nie występują podłużne siły ściskające)

MPa

32

,

0

20

61

,

1

035

,

0

035

,

0

2

1

2

3

2

1

2

3

min











ck

f

k















kN

51,84

MN

05184

,

0

54

,

0

30

,

0

32

,

0

kN

63

,

77

MN

07763

,

0

54

,

0

30

,

0

20

006

,

0

100

61

,

1

13

,

0

100

1

min

3

1

1

3

1

,

,















































d

b

k

d

b

k

f

k

c

V

w

cp

w

cp

ck

l

c

Rd

c

Rd









kN

63

,

77

kN

10

,

140

,

,







c

Rd

d

Ed

V

V

, należy zastosować zbrojenie na ścinanie

Długość odcinek belki, na którym należy zastosować zbrojenie na ścinanie:

V

Ed,k

V

Ed,c

a

w

m

58

,

1

60

7763

5

,

172

,

,











d

c

Rd

k

Ed

w

q

V

V

a

Jako zbrojenie na ścinanie zastosowano strzemiona pionowe, czterocięte (czteroramienne) średnicy

mm

6



w



, o

2

cm

13

,

1



sw

A

, ze stali o

MPa

355



yk

f

,

MPa

7

,

308

4

,

1

355







s

yk

ywd

f

f



, przyjęto

0

,

1

cot





.

m

486

,

0

54

,

0

9

,

0

9

,

0









d

z

d

Ed

ywd

sw

s

Rd

V

z

s

f

A

V

,

,

cot







cm

12,1

m

0121

0

,

1

486

,

0

1

,

140

10

7

,

308

10

13

,

1

cot

3

4

,























z

V

f

A

s

d

ed

ywd

sw

Przyjęto rozstaw strzemion:

cm

12



s

.

Procent zbrojenia ze względu na ścinanie:

003

,

0

30

,

0

12

,

0

10

13

,

1

4













w

sw

w

s b

A



>

001

,

0

355

20

08

,

0

08

,

0

min







yk

ck

w,

f

f

ρ

Sprawdzenie warunku maksymalnego efektywnego pola przekroju zbrojenia na ścianie







sin

2

1

1

max

,

cd

cw

w

ywd

sw

f

s

b

f

A



552

,

0

250

20

1

6

,

0

250

1

6

,

0

1













 















 





ck

f





0

,

1



cw



– konstrukcja niesprężona

0

,

1

sin





– strzemiona pionowe

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

17

kN

8

,

3946

10

3

,

14

552

,

0

0

,

1

2

1

kN

98

,

968

12

,

0

3

,

0

10

7

,

308

10

13

,

1

3

3

4

























Sprawdzenie nośności krzyżulców betonowych ze względu na ich zmiażdżenie:
dla

0

,

1

cot





mamy

44

,

375

10

3

,

14

552

,

0

486

,

0

30

,

0

0

,

1

2

1

2

1

3

1

max

,



















cd

w

cw

Rd

f

z

b

V





kN

44

,

375

kN

5

,

172

,

,







s

Rd

k

Ed

V

V

Sprawdzenie siły w zbrojeniu rozciąganym:
Dodatkowa siła rozciągająca w zbrojeniu podłużnym

td

F



wywołana przez siłę poprzeczną

dla

0

,

1

cot





mamy

kN

05

.

50

0

,

1

1

,

140

5

,

0

cot

5

,

0

,















d

Ed

td

V

F

















kNm

43

,

106

2

54

,

0

25

,

0

5

,

0

60

54

,

0

25

,

0

5

,

0

180

2

5

,

0

5

,

0

2

2

max

,

,



























d

t

q

d

t

V

M

d

Ed

d

Ed

.

kN

56

,

555

486

,

0

270

kN

04

,

289

05

,

70

486

,

0

43

,

106

max

,



















z

M

F

z

M

F

Ed

td

Edd

td

Określamy nośność zbrojenia rozciąganego w strefie przypodporowej i porównujemy z siła

td

F .

kN

26

,

314

10

7

,

308

10

18

,

10

kN

04

,

289

3

4

1



















yd

s

s

td

f

A

F

F

Długość zakotwienia prętów zbrojeniowych (kotwienie w strefie rozciąganej)

min

,

,

5

4

3

2

1

b

rqd

b

bd

l

l

l















Podstawowa długość zakotwienia

bd

sd

rqd

b

f

l

4

,





sd



– naprężenie obliczone w miejscu na, od którego odmierza się długość zakotwienia

l

bd

0,25 m

45

o

d = 0,54 m

d

Wartość momentu na krawędzi podpory

 





kNm

03

,

22

2

25

,

0

5

,

0

60

25

,

0

5

,

0

180

2

5

,

0

5

,

0

2

2

max

,

,



















t

q

t

V

M

d

Ed

k

Ed

cm

7,33

m

0733

,

0

10

3

,

14

0

,

1

30

,

0

10

7

,

308

10

18

,

10

3

3

4

1























cd

yd

s

eff

f

b

f

A

x



A

s1

b

x

eff

d

d

1

h

M

Ed,k



f

cd

z

c

=d

-0

,5

x

eff

F

s1

=A

s1

f

yd

F

cc

=bx

eff



f

cd

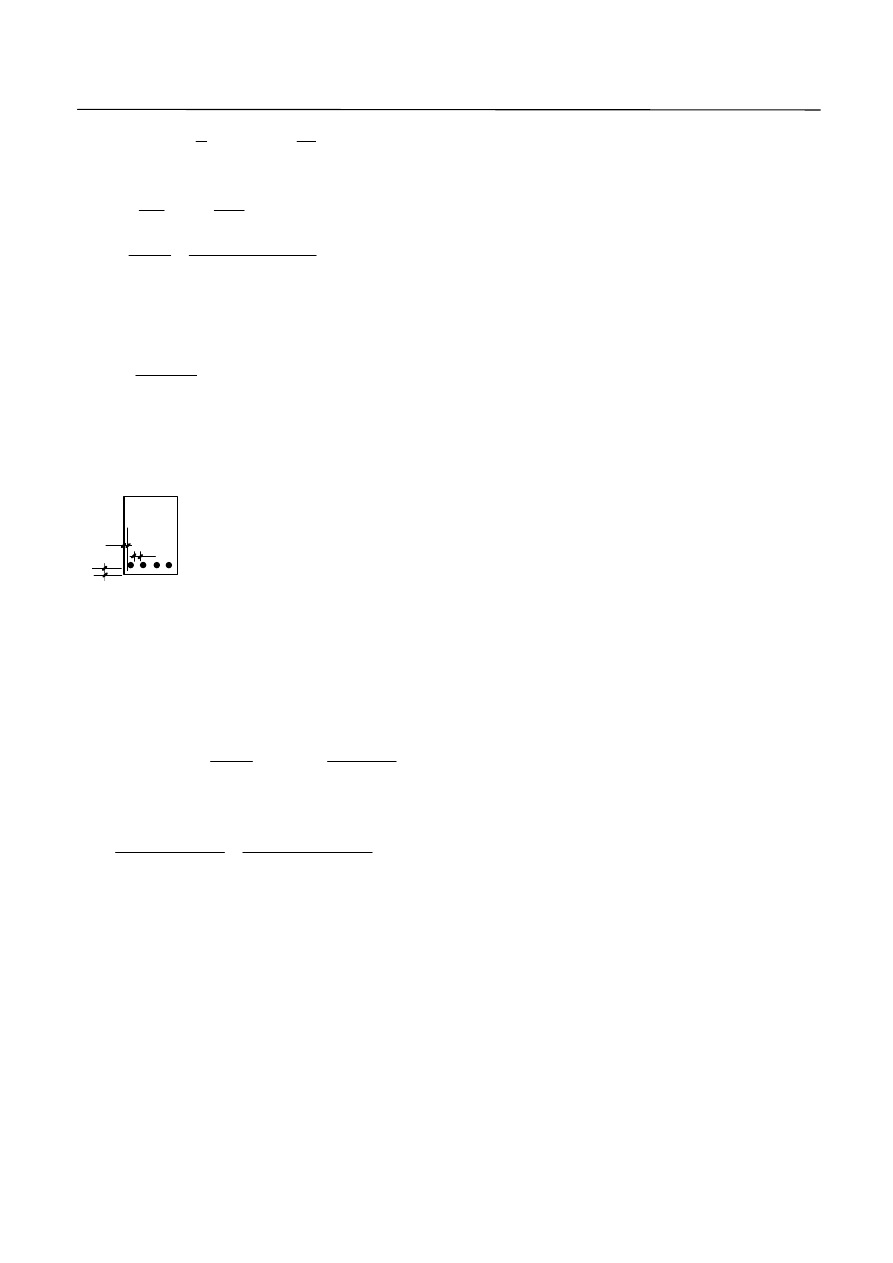
Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

18

cm

4

2

8

,

1

6

,

0

5

,

2

2

1



















w

nom

c

d

cm

56

4

60

1











d

h

d

m

0,5234

cm

34

,

52

2

33

,

7

56

2













eff

x

d

z

MPa

41,35

kPa

95

,

41345

10

18

,

10

5234

,

0

03

,

22

4

1

,















s

k

Ed

sd

zA

M



MPa

1,69

07

,

1

0

,

1

7

,

0

25

,

2

25

,

2

2

1













ctd

bd

f

f





7

,

0

1





0

,

1

2





(

mm

32

mm

18







)

mm

10

,

110

69

,

1

4

35

,

41

18

,









rqd

b

l

0

,

1

1





– pręty proste

Otulenie betonem

c

c

1

a

cm

3,1

mm

31

6

25

1













w

nom

c

c



cm

3,1

mm

31

6

25













w

nom

c

c



cm

5,13

mm

3

,

51





a























mm

31

mm

31

mm

65

,

25

3

,

51

5

,

0

5

,

0

1

c

c

a

c

d

0

,

1

94

,

0

18

18

65

,

25

15

,

0

1

15

,

0

1

7

,

0

2



























d

c

0

,

1

1

7

,

0

3













K

11

,

0

54

,

2

18

,

10

25

,

0

13

,

1

2

min

,





















s

st

st

A

A

A



K , przyjąć wg PN-EN 1992-1-1:2008, str. 125, Rys. 8.4





0

,

1

011

,

1

11

,

0

1

,

0

1

7

,

0

3

















Przyjęto

0

,

1

3





0

,

1

4





– nie występuje spajanie

0

,

1

5





7

,

0

94

,

0

0

,

1

0

,

1

94

,

0

5

3

2





















































mm

100

mm

180

18

10

10

mm

03

,

33

1

,

110

3

,

0

3

,

0

max

mm

50

,

103

10

,

110

0

,

1

94

,

0

0

,

1

,

min

,



rqd

b

b

bd

l

l

l

Przyjęto długość zakotwienia

mm

180



bd

l

Rozstaw strzemion na odcinku belki, gdzie nie jest wymagane zbrojenie naścinanie:





cm

42

m

42

,

0

56

,

0

75

,

0

cot

1

75

,

0

max

,















d

s

l

. Przyjęto

cm.

25



s

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

19

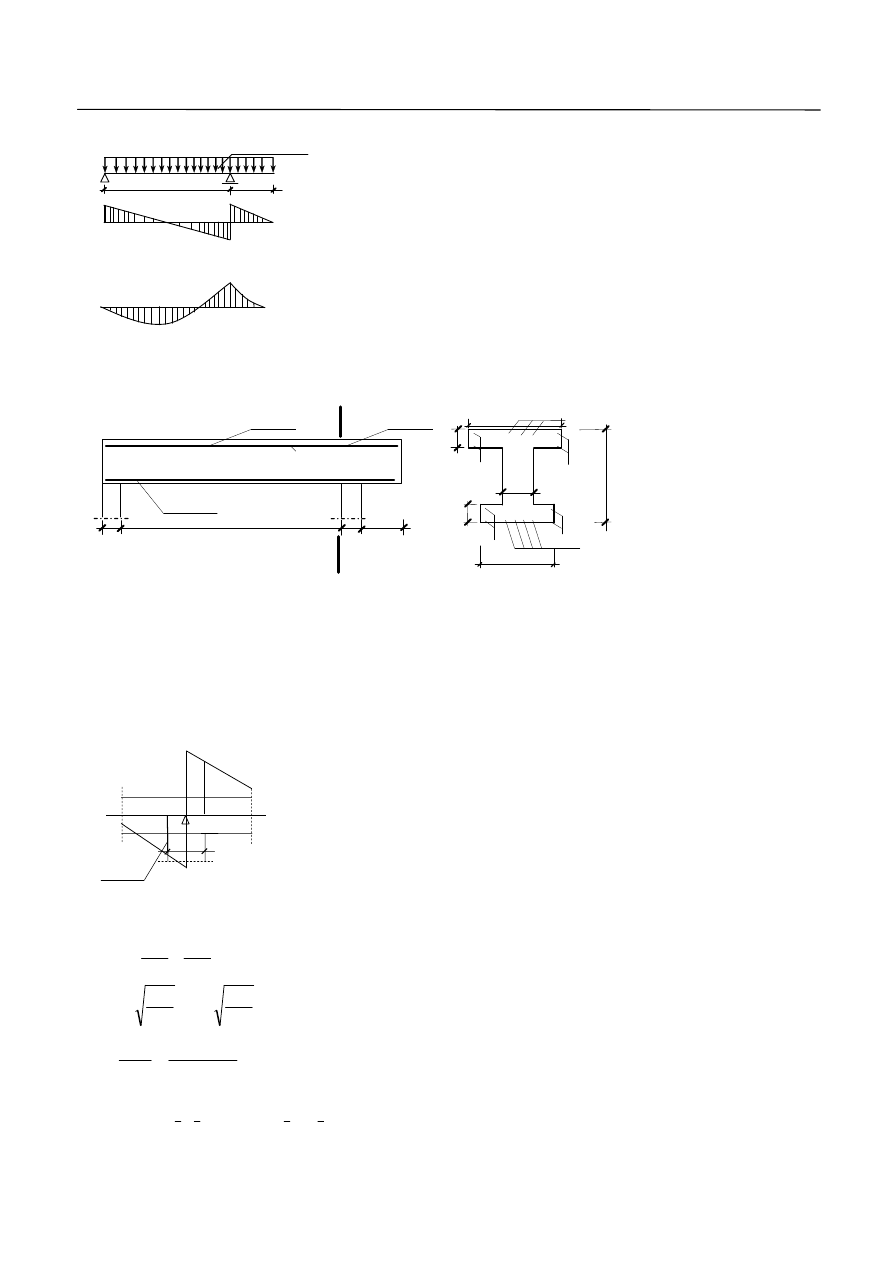
NR 1

NR 2

2 NR 3

NR 4

2 NR 3 co 120 mm

250

4 NR 2 # 8 l = 6150 mm

6150

6

0

0

2 NR 3 co 120 mm

NR 4 co 250 mm

250

250

250

250

250

6000

5750

1680

1680

2250

4 NR 1 # 18 l = 6150 mm

6150

A

A

B

B

140

140

PRZEKRÓJ A - A

PRZEKRÓJ B -B

175

175

550

550

60

60

NR 3



6 co 120 mm,

l = 1570 mm, szt. 60

PRZYKŁAD 2
Obliczyć zbrojenie na ścinanie mając dane: beton C20/25, stal o

MPa

410



yk

f

, klasa stali B,

cm

25



w

b

,

cm

60



h

,

cm

10



f

h

,

cm

60



eff

b

cm

8

'



f

h

,

cm

50

'



eff

b

. Sytuacja obliczeniowa stała i przejściowa.

Otulina

cm

5

,

2



nom

c

. Szerokość podpory

cm

25



t

. Zbrojenie podłużne: zbrojenie rozciągane przęsłowe –

2

1

cm

57

,

12



s

A

, zbrojenie rozciągane podporowe –

2

1

cm

03

,

6



s

A

.

Dane materiałowe:

Beton C20/25:

MPa

20



ck

f

4

,

1



c



,

MPa

3

,

14

4

,

1

20

0

,

1









c

ck

cc

cd

f

f





,

MPa

5

,

1

05

,

0

,



ctk

f

,

MPa

07

,

1

4

,

1

5

,

1

0

,

1

05

,

0

,









c

ctk

ct

ctd

f

f





Stal:

MPa

410



yk

f

,

15

,

1



s



,

MPa

52

,

356

15

,

1

410







s

yk

yd

f

f



.

300

600

NR 1

NR 2

2 NR 3

25

300

600

NR 1

NR 2

NR 4

25

250

250

550

550

60

60

NR 4



6 co 250 mm,

l = 1720 mm, szt. 9

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

20

Ścinanie należy sprawdzić przy podporze A oraz z prawej
i lewej strony podpory B.

W przykładzie obliczono przykładowo zbrojenie przy podporze B z lewej strony.

4 # 20

250

250

5500

3 # 16

500

600

2 # 16

875

A

A































4 # 20

2



8

250

600

80

2



8

2



8

2



8

100

3 # 16

Podpora B z lewej strony:

kN

33

,

123



L

Ed

V

Wysokość użyteczna przekroju:

m

06

,

0

60

,

0

1

,

0

1

,

0

1









h

d

m

54

,

0

06

,

0

60

,

0

1











d

h

d

Wyznaczenie miarodajnej siły poprzecznej:

40,0 kN

123,33 kN

0,25 m

118,33 kN

35,0 kN

B

Wielkość siły na krawędzi podpory

kN

33

,

118

40

25

,

0

5

,

0

33

,

123

5

,

0

max

,

,















d

Ed

k

Ed

tq

V

V

Miarodajna siła w odległości d od krawędzi podpory

kN

73

,

96

40

54

,

0

33

,

118

,

,













d

k

Ed

d

Ed

dq

V

V

Obliczamy silę

c

Rd

V

,

:

13

,

0

4

,

1

18

,

0

18

,

0

,







c

c

Rd

c



0

,

2

61

,

1

540

200

1

200

1













d

k

0,02

004

,

0

54

,

0

0,25

4

-

10

6,03

l













d

b

A

w

sl





cp

= 0 (nie występują podłużne siły ściskające)

MPa

32

,

0

20

61

,

1

035

,

0

035

,

0

2

1

2

3

2

1

2

3

min











ck

f

k



6,0 m

q

d

= 40 kN/m

V

EdA

V

L

EdB

A

B

V

EdA

= 116,67 kN

1,0 m

V

P

EdB

V

L

EdB

= 123,33 kN

V

P

EdB

= 40 kN

M

Ed

= 20 kNm

M

Ed

= 170,14 kNm

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

21













kN

43,2

MN

0432

,

0

54

,

0

25

,

0

32

,

0

kN

56,51

MN

05151

,

0

54

,

0

25

,

0

20

004

,

0

100

61

,

1

13

,

0

100

1

min

3

1

1

3

1

,

,















































d

b

k

d

b

k

f

k

c

V

w

cp

w

cp

ck

l

c

Rd

c

Rd









kN

51

,

56

kN

73

,

96

,

,







c

Rd

d

Ed

V

V

, należy zastosować zbrojenie na ścinanie

Długość odcinka belki, na którym należy zastosować zbrojenie na ścinanie:

m

55

,

1

40

51

,

56

33

,

118

,

,











d

c

Rd

k

Ed

w

q

V

V

a

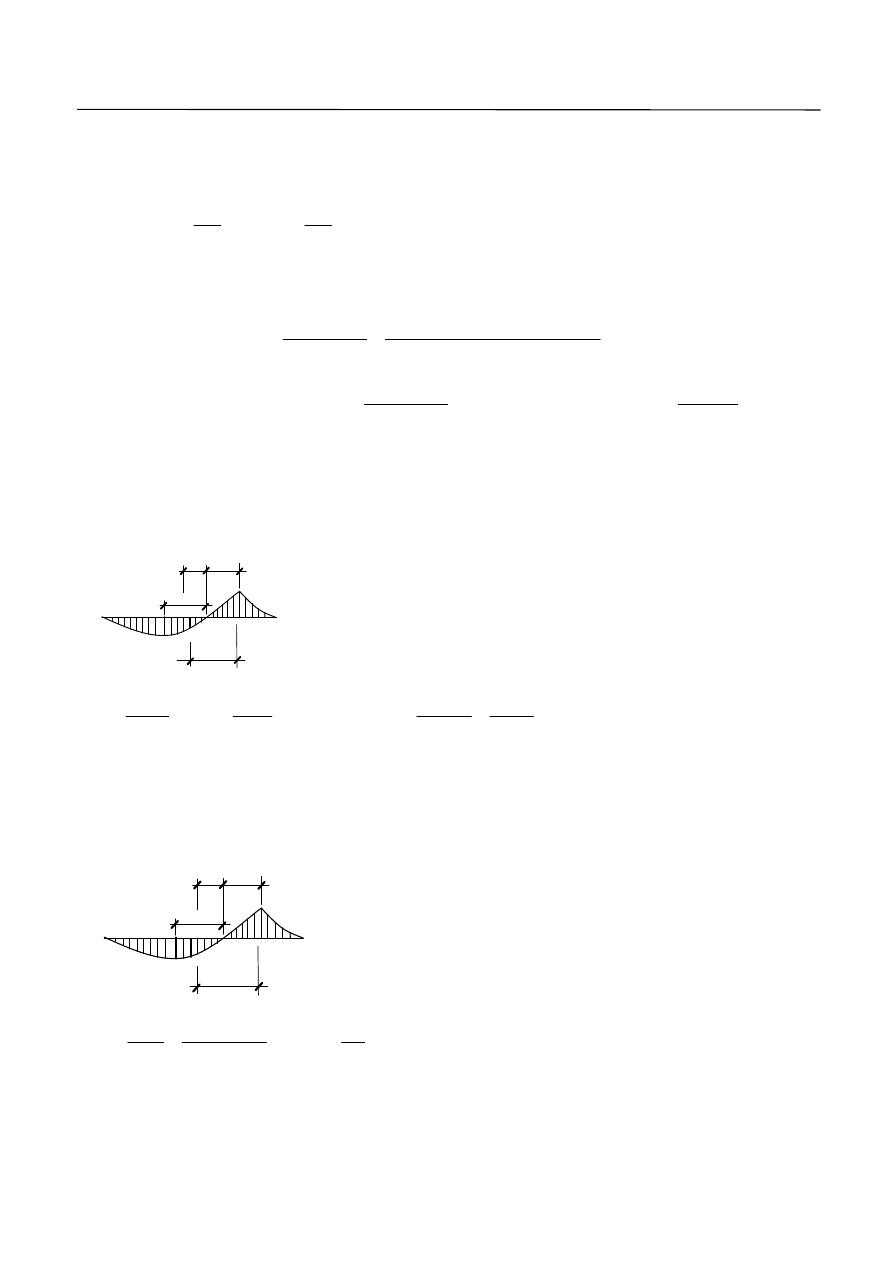
Odcinek ścinania podzielono na dwa krótsze. Na pierwszym z nich zastosowano zbrojenia na ścianie
w postaci prętów odgiętych i strzemion pniowych, natomiast na drugim w postaci samych strzemion
pionowych.

Odcinek pierwszy
Jako zbrojenie na ścinanie zastosowano zbrojenie w postaci 2 prętów odgiętych

mm

20

2



w



o polu

powierzchni

2

2

cm

28

,

6



sw

A

, kącie nachylenia

o

45





i strzemion pionowych, dwuramiennych ze stali

o

MPa

240



yk

f

o średnicy

mm

6

1



w



:

2

1

cm

56

,

0



sw

A

,

MPa

7

,

208

15

,

1

240

1





ywd

f

, przyjęto

5

,

1

cot





.

2

,

1

,

,

s

Rd

s

Rd

s

Rd

V

V

V





m

486

,

0

54

,

0

9

,

0

9

,

0









d

z

Obliczamy udział prętów odgiętych w przenoszeniu siły tnącej.

4

8

c

m

s

2



= 45

O

Maksymalny dopuszczalny rozstaw prętów odgiętych wynosi:





 

m

648

,

0

1

1

54

,

0

6

,

0

cot

1

6

,

0

max

,

















d

s

b

przyjęto:

cm

64

m

64

,

0

2





s









kN

51

,

300

707

,

0

1

5

,

1

486

,

0

64

,

0

10

52

,

356

10

28

,

6

sin

cot

cot

3

4

2

2

2

2

,































z

s

f

A

V

ywd

sw

s

Rd

Siła przenoszona przez strzemiona

d

Ed

s

Rd

s

Rd

s

Rd

V

V

V

V

,

2

,

1

,

,









kN

78

,

203

51

,

300

73

,

96

2

,

,

1

,













s

Rd

d

Ed

s

Rd

V

V

V

Minimum 50% siły tnącej powinny przenieść strzemiona pionowe przyjęto:

d

Ed

s

Rd

V

V

,

1

,

5

,

0



d

Ed

ywd

sw

s

Rd

V

z

s

f

A

V

5

,

0

cot

1

1

1

1

,









m

1762

,

0

5

,

1

486

,

0

73

,

96

5

,

0

10

7

,

208

10

56

,

0

cot

5

,

0

3

4

1

1

1























z

V

f

A

s

Ed

ywd

sw

Przyjęto rozstaw strzemion

m

17

,

0

1



s

.

Procent zbrojenia ze względu na ścinanie:
strzemiona pionowe

001

,

0

25

,

0

17

,

0

10

56

,

0

4

1

1

1













w

sw

w

b

s

A



>

0015

,

0

240

20

08

,

0

08

,

0

min









yk

ck

w,

f

f

ρ

pręty odgięte

006

,

0

707

,

0

25

,

0

64

,

0

10

28

,

6

sin

4

2

2

2



















w

sw

w

b

s

A

>

0009

,

0

410

20

08

,

0

08

,

0

min









yk

ck

w,

f

f

ρ

Siła przenoszona przez strzemiona

kN

17

,

50

5

,

1

486

,

0

17

,

0

10

7

,

208

10

56

,

0

cot

3

4

1

1

1

1

,



















z

s

f

A

V

ywd

sw

s

Rd

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

22

Całkowita siła przenoszona przez strzemiona i pręty odgięte

kN

68

,

350

17

,

50

51

,

300

2

,

1

,

,











s

Rd

s

Rd

s

Rd

V

V

V

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych:

552

,

0

250

20

1

6

,

0

250

1

6

,

0

1













 















 





ck

f





0

,

1



cw



– konstrukcja niesprężona

5

,

1

cot





,

667

,

0

tan





dla strzemion pionowych

kN

58

,

442

667

,

0

5

,

1

10

3

,

14

552

,

0

486

,

0

25

,

0

0

,

1

tan

cot

kN

33

,

118

3

1

max

,

,

































cd

w

cw

Rd

k

Ed

f

z

b

V

V

dla prętów odgiętych

kN

75

,

737

5

,

1

0

,

1

0

,

1

5

,

1

10

3

,

14

552

,

0

486

,

0

25

,

0

0

,

1

cot

1

cot

cot

kN

33

,

118

2

3

2

1

max

,

,









































cd

w

cw

Rd

k

Ed

f

z

b

V

V

Sprawdzenie siły w zbrojeniu rozciąganym
Dodatkowa siła rozciągająca w zbrojeniu podłużnym









kN

18

,

24

0

,

1

5

,

1

73

,

96

5

,

0

cot

cot

5

,

0





















Ed

td

V

F

Wartość momentu zginającego w odległości d od podpory

kNm

18

,

53

,



d

Ed

M

.

kN

08

,

350

486

,

0

14

,

170

kN

6

,

133

18

,

24

486

,

0

18

,

53

max

,

,



















z

M

F

z

M

F

Ed

td

d

Ed

td

Określamy nośność zbrojenia rozciąganego w strefie przypodporowej i porównujemy z siła

td

F .

kN

6

,

133

kN

89

,

223

10

52

,

356

10

28

,

6

3

4

1



















td

yd

s

s

F

f

A

F

Ścinanie między środnikiem a półką:

Zbrojenie po jednej stronie półki: 2 pręty 8



ze stali o

MPa

240



yk

f

,

MPa

7

,

208



yd

f

Sprawdzenie ścinania na odcinku, gdy półka jest rozciągana:

kN

87

,

20

10

0

,

1

10

7

,

208

4

3

1

















s

yd

d

A

f

F

MPa

46

,

2

m

kN

29

,

2455

17

,

0

5

,

0

1

,

0

87

,

20

2

















x

h

F

v

f

d

Ed

0

,

1

cot



f



,

o

45



f



– dla półki rozciąganej

MPa

95

,

3

707

,

0

707

,

0

3

,

14

552

,

0

cos

sin

MPa

46

,

2

















f

f

cd

Ed

f

v







1,38 m

a

w2

= 1,55 m

0,17 m

B

A

2,92 m

1,51 m

0,665 m

0,17 m

B

A

2,92 m

M

Ed,d

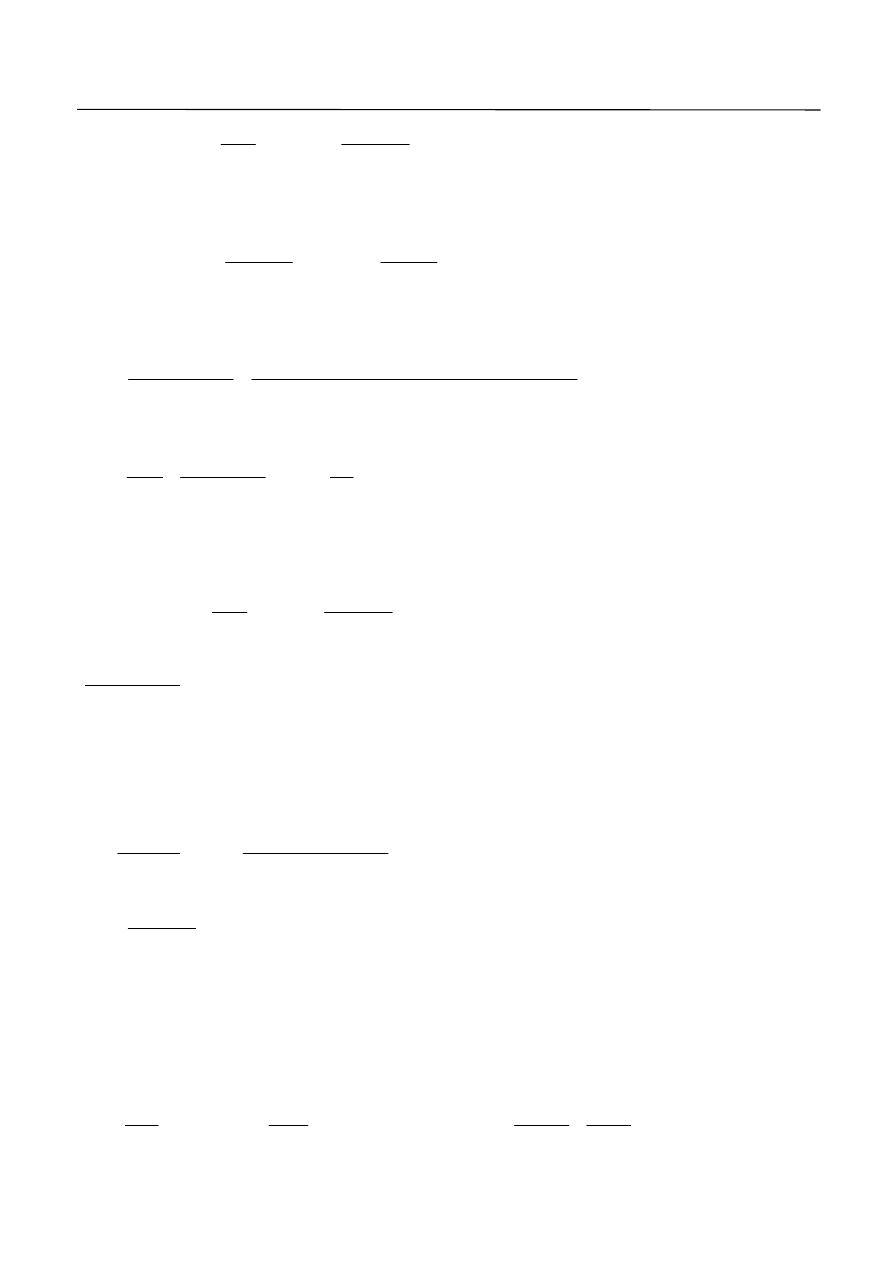
Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

23

MPa

69

,

0

0

,

1

7

,

208

17

,

0

1

,

0

10

56

,

0

cot

MPa

46

,

2

4



















f

yd

f

f

sf

Ed

θ

f

s

h

A

v

Należy dołożyć zbrojenie: przyjęto zbrojenie dodatkowe

sf

A w postaci strzemion

8



ze stali

o

MPa

240



yk

f

,

MPa

7

,

208



yd

f

i rozstawie

m

08

,

0



f

s

i sprawdzamy warunek:

MPa

30

,

3

0

,

1

7

,

208

08

,

0

1

,

0

10

0

,

1

0

,

1

7

,

208

17

,

0

1

,

0

10

56

,

0

MPa

46

,

2

4

4









































v

Ed

Sprawdzenie ścinania w miejscu, gdzie półka jest ściskana:
Z sumy rzutów sił przy założeniu, że przekrój jest przekrojem pozornie teowym obliczamy

eff

x

:

m

027

,

0

10

3

,

14

0

,

1

60

,

0

10

52

,

352

10

03

,

6

10

52

,

356

10

57

,

12

3

3

4

3

4

2

1

































cd

eff

yd

s

yd

s

eff

f

b

f

A

f

A

x











kN

57

,

67

25

,

0

6

,

0

5

,

0

027

,

0

10

3

,

14

0

,

1

5

.

0

3























w

eff

eff

cd

d

b

b

x

f

F



MPa

23

,

0

m

kN

37

,

231

92

,

2

5

,

0

1

,

0

56

,

67

2

















x

h

F

v

f

d

Ed

0

,

1

cot



f



– półka ściskana

MPa

95

,

3

707

,

0

707

,

0

3

,

14

552

,

0

cos

sin

MPa

23

,

0















f

f

cd

Ed

f

v







MPa

69

,

0

0

,

1

7

,

208

17

,

0

1

,

0

10

56

,

0

cot

MPa

23

,

0

4



















θ

f

s

h

A

v

yd

f

f

sf

Ed

Odcinek drugi
Wymiarowanie na ścinanie na odcinku

m

91

,

0

64

,

0

55

,

1

2







w

a

(poza strefą odgięcia pręta).

Maksymalna siła ścinająca na rozpatrywanym odcinku

kN

73

,

92

64

,

0

40

33

,

118









Ed

V

Jako zbrojenie na ścinanie zastosowano strzemiona pionowe, dwuramienne ze stali o średnicy

mm

6

1



w



i o

2

1

cm

56

,

0



sw

A

,

MPa

7

,

208

1



ywd

f

,

MPa

240



yk

f

.

Rozstaw strzemion

m

0918

,

0

5

,

1

486

,

0

73

,

92

10

7

,

208

10

56

,

0

cot

3

4

1

1

1





















z

V

f

A

s

Ed

ywd

sw

Przyjęto rozstaw strzemion

m

09

,

0

1



s

0015

,

0

0024

,

0

25

,

0

09

,

0

10

56

,

0

min

,

4

1















w

w





Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych:

kN

58

,

442

kN

73

,

92

max

,







Rd

Ed

V

V

Sprawdzenie nośności podłużnego zbrojenia rozciąganego w strefie przypodporowej
Wartość momentu

Ed

M

odpowiadająca sile

kN

73

,

92



Ed

V

kNm

07

,

56



Ed

M

kN

08

,

350

486

,

0

14

,

170

kN

92

,

184

5

,

1

73

,

92

5

,

0

486

,

0

07

,

56

cot

5

,

0

max

,





















z

M

V

z

M

F

Ed

Ed

Ed

td



kN

15

,

448

10

52

,

356

10

57

,

12

kN

03

,

187

3

4

















s

td

F

F

Podstawy konstrukcji żelbetowych

Do użytku wewnętrznego (na prawach rękopisu)

Ścinanie według PN-EN 1992-1-1:2008 (EC2) Wersja 2009 dr inż. Maria WŁODARCZYK

24

Ścinanie między środnikiem a półką:
Półka jest ściskana:
Z sumy rzutów sił przy założeniu, że przekrój jest przekrojem pozornie teowym obliczamy x

eff

:

MPa

95

,

3

707

,

0

707

,

0

3

,

14

552

,

0

cos

sin

MPa

23

,

0















f

f

cd

Ed

f

v







MPa

30

,

1

0

,

1

7

,

208

09

,

0

1

,

0

10

56

,

0

cot

MPa

23

,

0

4



















θ

f

s

h

A

v

yd

f

f

sf

Ed

Uwaga: W tym przykładzie zamieszczono jedynie fragment obliczeń, aby pokazać sposób wymiarowania,
jeżeli stosuje się na ścinanie pręty odgięte i strzemiona pionowe.

MATERIAŁY POMOCNICZE:

1.

PN–EN 1992–1–1:2008. Eurokod 2 - Projektowanie konstrukcji z betonu. Część 1–1. Reguły ogólne i reguły dla
budynków.

2.

Załącznik krajowy NA (informacyjny). Postanowienia krajowe w zakresie przedmiotowym EN 1992-1-1, 2008.

3.

PN–EN 1990:2004. Eurokod. Podstawy projektowania konstrukcji.

4.

PN–EN 1991-1-1:2004. Eurokod1: Oddziaływania na konstrukcję. Część 1.1: Oddziaływania ogólne. Ciężar
objętościowy ciężar wlany, obciążenia użytkowe w budynkach.

5.

PN–EN 206-1:2003. Beton. Część 1: Wymagania, właściwości, produkcja i zgodność.

6.

PN–EN 206-1:2003/A1. Zmiany, marzec 2005, do PN–EN 206-1:2003. Beton. Część 1: Wymagania,
właściwości, produkcja i zgodność.

7.

PN–EN 206-1:2003/A2. Zmiany, lipiec 2006, do PN–EN 206-1:2003. Beton. Część 1: Wymagania, właściwości,
produkcja i zgodność.

8.

PN-EN 10080:2007. Stal do zbrojenia betonu. Spawalna stal zbrojeniowa. Postanowienia ogólne.

9.

Eurocode 2. Design of concrete structures. Part 1. General rules and rules for buildings.

10. PN – B – 03264:2002. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i projektowanie.
11. Praca zbiorowa pod redakcją Lecha Czarneckiego.: Beton według normy PN-EN 206-1:2003 – komentarz.

Cement Polski, PKN. Kraków 2007.

12. Starosolski W.: Konstrukcje żelbetowe według PN – B – 03264:2002 i Eurokodu 2. PWN, Warszawa 2006,

Tom I.

13. Praca zbiorowa Sekcji Konstrukcji Betonowych KILiW PAN. Podstawy projektowania konstrukcji żelbetowych i

sprężonych według Eurokodu 2. Dolnośląskie Wydawnictwo Edukacyjne, Wrocław 2006.

14. Eurokod 2. Podręczny skrót dla projektantów konstrukcji żelbetowych. Pod redakcją prof. Andrzeja Ajdukiewicza.

Stowarzyszenie Producentów Cementu. Kraków 2009.

15. Private communication: Goszczyńska B.
16. Łapko A.: Projektowanie konstrukcji żelbetowych. Arkady, Warszawa 2001.
17. Kamiński M., Pędziwiatr J., Styś D.: Projektowanie konstrukcji żelbetowych według PN-B-03264:2002.

Dolnośląskie Wydawnictwo Edukacyjne, Wrocław 2004.

18. Dąbrowski K., Stachurski W., Zieliński J.L.: Konstrukcje betonowe. Arkady, Warszawa 1982.
19. Private communication: Szwed A.
20. Piasta J., Piasta W. G.: Beton zwykły. Arkady, Warszawa 1997.
21. Godycki-Ćwirko T.: Mechanika betonu. Arkady, Warszawa 1982.
22. Łapko A., Jansen B.J.: Podstawy projektowania i algorytmy obliczeń konstrukcji żelbetowych. Arkady, Warszawa

2005.

23. Private communication: Jemioło S.
24. Neville A.M.: Właściwości betonu. Polski Cement, Kraków 2000.
25. Kobiak J., Stachurski W.: Konstrukcje żelbetowe. Arkady, Warszawa 1984, tom I.
26. Private communication: Goszczyński S.
27. Firkowicz S.: Statystyczne badanie wyrobów. WNT, Warszawa 1970.
28. Ajdukiewicz A., Starosolski W., Sulimoswki Z.: Konstrukcje betonowe. Laboratorium. Skrypty uczelniane

Politechniki Śląskiej Nr 929, Gliwice 1980.

29. Instrukcja 194/98. Badania cech mechanicznych betonu na próbkach wykonanych w formach. Instytut techniki

Budowlanej. Warszawa 1998.

30. Żmuda J.: Podstawy projektowania konstrukcji metalowych. Arkady, Warszawa 1997.
31. Praca pod redakcją naukową Zybury A.: Konstrukcje żelbetowe. Atlas rysunków. Wydawnictwo Naukowe PWN.

Warszawa 2009.