1

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Modelowanie i symulacja

dr inż. Piotr Piela

Zakład Metod Matematycznych

kontakt: pokój 28

[e-mail]

2

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – sposoby opisu

Nieliniowe systemy dynamiczne:

opis

zależności

wejście-wyjście

za

pomocą

równań

różniczkowych,

opis za pomocą równań stanu.

Liniowe systemy dynamiczne:

opis zależności „wejście-wyjście” za pomocą równań
różniczkowych,

opis za pomocą równań stanu,

opis zależności „wejście-wyjście” w formie operatorowej

3

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Rachunek operatorowy

Operatory

odwzorowują wielkości wejściowe, będące funkcjami np.

czasu – w inne funkcje czasu – reprezentujące wielkości wyjściowe.
Posługiwanie się operatorami ułatwia obliczenia, gdyż pozwala
operacje na funkcjach zastąpić operacjami na liczbach.

4

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Przekształcenie Laplace'a

Przekształcenie Laplace'a

jest operatorem przekształcającym

funkcję zmiennej rzeczywistej f(t) na pewną funkcję F(s) zmiennej

zespolonej s = c + j

ω

zgodnie ze wzorem:

L

[ f t]=F s=

∫

0

∞

x

t⋅e

−st

dt

Odwrotne przekształcenie Laplace'a

– znając transformatę

funkcji F(s) możemy wyznaczyć samą funkcję f(t) za pomocą
wzoru:

f

t =L

−1

[ F s]=

1

2

 j

∫

c

− j ∞

c

 j ∞

F

s⋅e

st

ds ,

t0 ,

c = Re s

5

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny - model liniowy w przestrzeni stanów

{

˙X t=F

1

 X t

0

 ,U t ,t

0



Y

t=F

2

 X t

0

 ,U t , t

0



Dany jest system opisany równaniami stanu:

Dla liniowego systemu dynamicznego równania te można

przedstawić w formie macierzowej.

6

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny - model liniowy w przestrzeni stanów

C

D



y

1

y

2

⋮

y

p



=



c

11

c

12

⋯ c

1n

c

21

c

22

⋯ c

2n

⋮

⋮ ⋯ ⋮

c

p1

c

p2

⋯ c

pn



⋅



x

1

x

2

⋮

x

n







d

11

d

12

⋯ d

1m

d

21

d

22

⋯ d

2m

⋮

⋮

⋯

⋮

d

p1

d

p2

⋯ d

pm



⋅



u

1

u

2

⋮

u

m



A

B



˙x

1

˙x

2

⋮

˙x

n



=



a

11

a

12

⋯ a

1n

a

21

a

22

⋯ a

2n

⋮

⋮ ⋯ ⋮

a

n1

a

n2

⋯ a

nn



⋅



x

1

x

2

⋮

x

n







b

11

b

12

⋯ b

1m

b

21

b

22

⋯ b

2m

⋮

⋮ ⋯ ⋮

b

n1

b

n2

⋯ b

nm



⋅



u

1

u

2

⋮

u

m



7

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny - model liniowy w przestrzeni stanów

{

˙X t=A⋅X tB⋅U t

Y

t=C⋅X tD⋅U t

Postać równania stanów i równania wyjścia w postaci wektorowo-
macierzowej dla systemu liniowego stacjonarnego jest następująca:

gdzie:
A – macierz stanu, dim A = n x n
B – macierz wejścia, dim B = n x m,
C – macierz wyjścia, dim C = n x p,
D – bezpośrednia macierz transmisji, dim D = m x p
n – ilość stanów,
m – ilość wejść,
p – ilość wyjść,
X(t) – wektor stanu,
U(t) – wektor wejść,
Y(t) – wektor wyjść

8

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

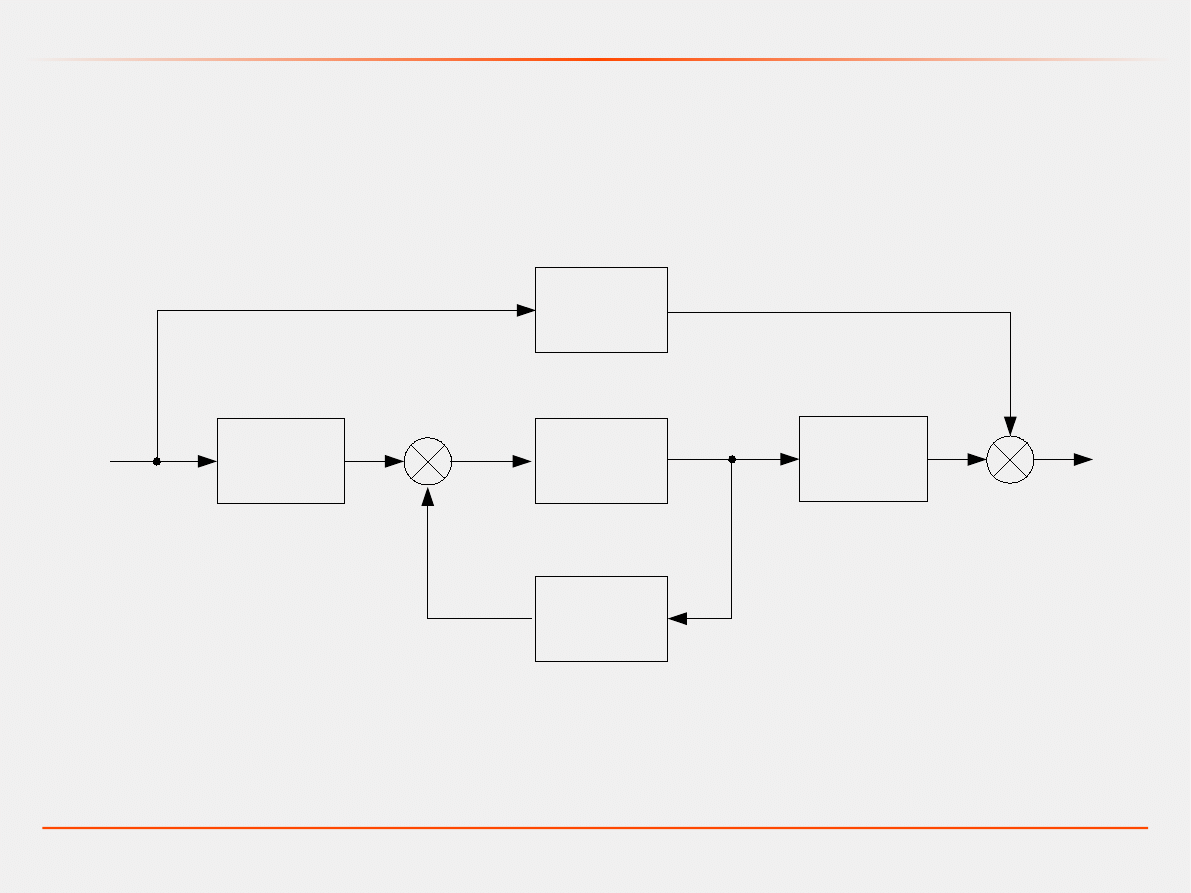
Model dynamiczny - model liniowy w przestrzeni stanów

{

˙X t=A⋅X tB⋅U t

Y

t=C⋅X tD⋅U t

D

+

A

C

B

∫

dt

+

+

+

U

t 

Y

t 

X

t 

˙X t

9

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – równania stanu → transmitancja operatorowa

Zależność pomiędzy równaniami stanu i wyjścia a

transmitancją operatorową dla układu liniowego z jednym

wejściem i jednym wyjściem.

Stosując przekształcenie Laplace'a dla równań stanu i

wyjścia otrzymamy:

{

s X

s=A⋅X sB⋅U s

Y

s=C⋅X sD⋅U s

Przekształcając:

X

s=s⋅I −A

−1

⋅B⋅U s

Y

s=C⋅s⋅I −A

−1

⋅B⋅U sD⋅U s

Ostatecznie:

G

s=

Y

s

X

s

=C⋅s⋅I −A

−1

⋅BD

10

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

C

A

B

Model dynamiczny – równania stanu → transmitancja operatorowa

Przykład. Dany jest model liniowy w postaci równań stanu:



˙x

1

˙x

2



=



0

1

−1 −2



⋅



x

1

x

2







0
1



⋅u

y

t =−1 1⋅



x

1

x

2



G

s=

Y

s

X

s

=C⋅s⋅I −A

−1

⋅B

Poszukujemy transmitancji układu.

11

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – równania stanu → transmitancja operatorowa

Przykład.

G

s=−1 1⋅





s 0

0 s



−



0

1

−1 −2





−1

⋅



0
1



G

s=−1 1⋅



s

−1

1 s

2



−1

⋅



0
1



G

s=

s

1

s

2

2s1

12

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Dana jest transmitancja operatorowa systemu liniowego z

jednym wejściem i jednym wyjściem:

Wprowadzamy oznaczenia:

Otrzymamy:

G

s=

Y

s

U

s

=

b

m

s

m

b

m

−1

s

m

−1

b

0

a

n

s

n

a

n

−1

s

n

−1

a

0

b

m

s

m

b

m

−1

s

m

−1

b

0

=P s

a

n

s

n

a

n

−1

s

n

−1

a

0

=Qs

Q

s⋅Y s=Ps⋅U s

13

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Stosując odwrotne przekształcenie Laplace'a oraz

wprowadzając operator różniczkowania p=d/dt otrzymamy:

gdzie:

P

 p=b

m

p

m

b

m

−1

p

m

−1

b

0

Q

 p=a

n

p

n

a

n

−1

p

n

−1

a

0

Q

 p⋅yt =P  p⋅ut

Do równania wprowadzamy

nową zmienną x(t), tak że spełnione jest równanie:

Q

 p⋅yt =P  p⋅ut

y

t =P  p⋅xt 

14

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Otrzymamy:

Zapiszmy pierwsze równanie w postaci równania

różniczkowego:

{

Q

 p⋅xt =u t 

P

 p⋅xt = yt 

x

n

a

n

−1

x

n−1

a

1

˙xa

0

x

=u

Przekształcając podane równanie do układu równań

różniczkowych pierwszego rzędu otrzymamy:



˙x

1

˙x

2

⋮

˙x

n



=



0

1

⋯

0

0

0

⋯

0

⋮

⋮

⋯

⋮

−a

0

−a

1

⋯ −a

n

−1



⋅



x

1

x

2

⋮

x

n







0
0

⋮

1



⋅ut

15

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Zapiszmy drugie równanie w postaci równania

różniczkowego:

W postaci macierzowej możemy zapisać:

y

t =b

0

b

1

⋯ b

m

0

⋯ 0⋅



x

1

x

2

⋯

x

m

1

⋯

x

n



y

t =b

m

x

m

b

m

−1

x

m−1

b

1

˙xb

0

x

y

t =b

0

x

1

b

1

x

2

b

m

−1

x

m

b

m

x

m

1

16

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

C

B

A

Model dynamiczny – transmitancja operatorowa → równania stanu

Ostatecznie:

y

t =b

0

b

1

⋯ b

m

0

⋯ 0⋅



x

1

x

2

⋯

x

m

1

⋯

x

n





˙x

1

˙x

2

⋮

˙x

n



=



0

1

⋯

0

0

0

⋯

0

⋮

⋮

⋯

⋮

−a

0

−a

1

⋯ −a

n

−1



⋅



x

1

x

2

⋮

x

n







0
0

⋮

1



⋅ut

17

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Przykład. Pewien liniowy system opisany jest następującą

transmitancją operatorową:

G

s=

Y

s

U

s

=

b

1

s

b

0

a

2

s

2

a

1

s

a

0

Poszukujemy opisu tego systemu w przestrzeni stanu.

{

˙X t=A⋅X tB⋅U t

Y

t=C⋅X tD⋅U t

A, B, C, D ?

18

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

G

s=

Y

s

U

s

=

b

1

s

b

0

s

2

a

1

s

a

0

G(s) odpowiada liniowemu równaniu różniczkowemu:

¨ya

1

˙ya

0

y

=b

1

˙ub

0

u

Uwzględniając zależność otrzymamy:

{

Q

 p⋅xt=u t 

P

 p⋅xt= yt

{

¨xa

1

˙xa

0

x

=u

b

1

˙xb

0

x

= y

19

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Wprowadzając oznaczenia:

{

¨xa

1

˙xa

0

x

=u

b

1

˙xb

0

x

= y

x

=x

1,

˙x= ˙x

1

=x

2,

¨x= ˙x

2

dla pierwszego równania otrzymamy układ równań

różniczkowych pierwszego rzędu:

{

˙x

1

=x

2

˙x

2

=−a

0

x

1

−a

1

x

2

u

równanie wyjścia przyjmie postać:

y

=b

0

x

1

b

1

x

2

20

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

C

B

A

Model dynamiczny – transmitancja operatorowa → równania stanu

ostatecznie, w zapisie macierzowym:

{

˙x

1

=x

2

˙x

2

=−a

0

x

1

−a

1

x

2

u



˙x

1

˙x

2



=



0

1

−a

0

−a

1



⋅



x

1

x

2







0
1



⋅u

y

=b

0

b

1

⋅



x

1

x

2



y

=b

0

x

1

b

1

x

2

21

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny – transmitancja operatorowa → równania stanu

Istnieją wzajemne ekwiwalentne przekształcenia pomiędzy

modelami matematycznymi opisanymi za pomocą

transmitancji a modelami opisanymi w przestrzeni stanów.

Ze względu na niejednoznaczność wyboru wektora

zmiennych stanu

jednej transmitancji może odpowiadać

zbiór modeli zapisanych w przestrzeni stanów.

Przekształcenie odwrotne jest jednoznaczne.

22

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

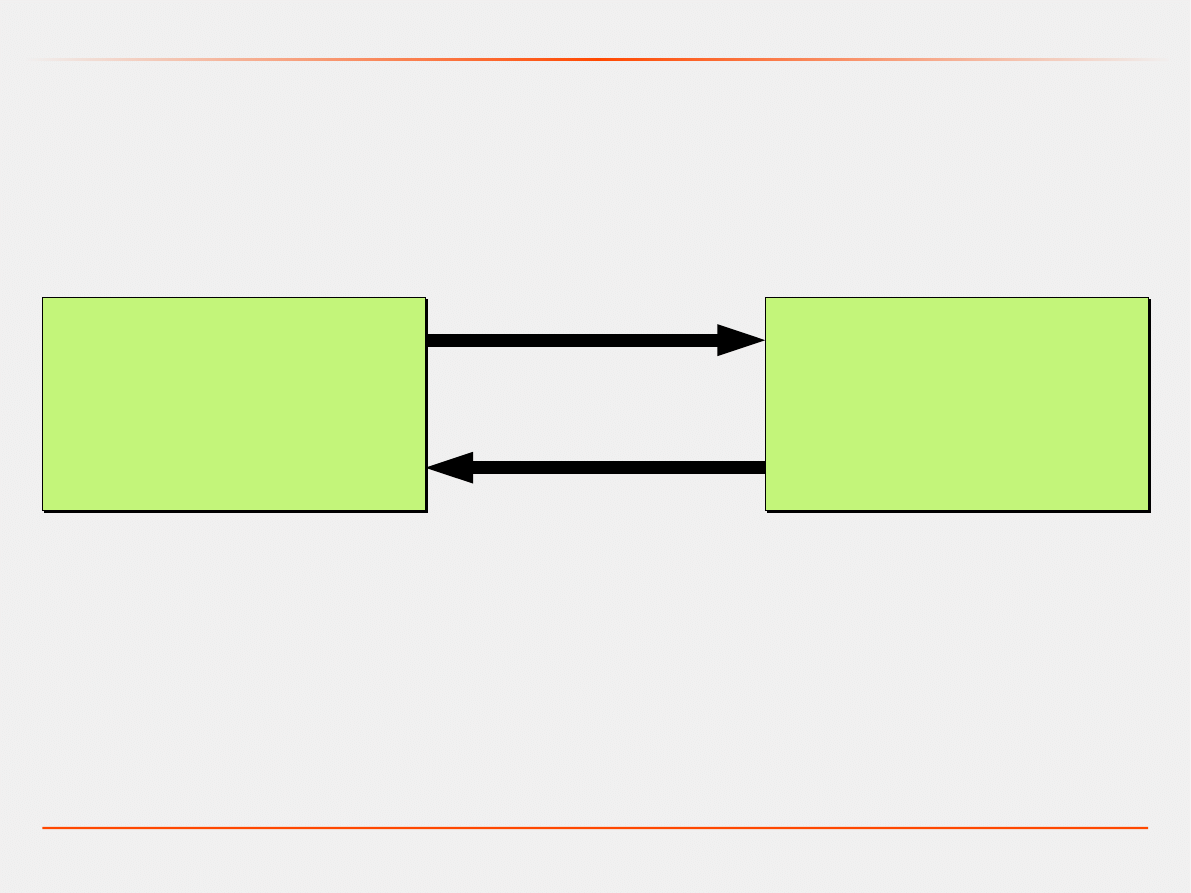
Model dynamiczny – związki pomiędzy różnymi formami opisu

Równania

stanu i wyjścia

Transmitancja

operatorowa

1 : 1

n : 1

23

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

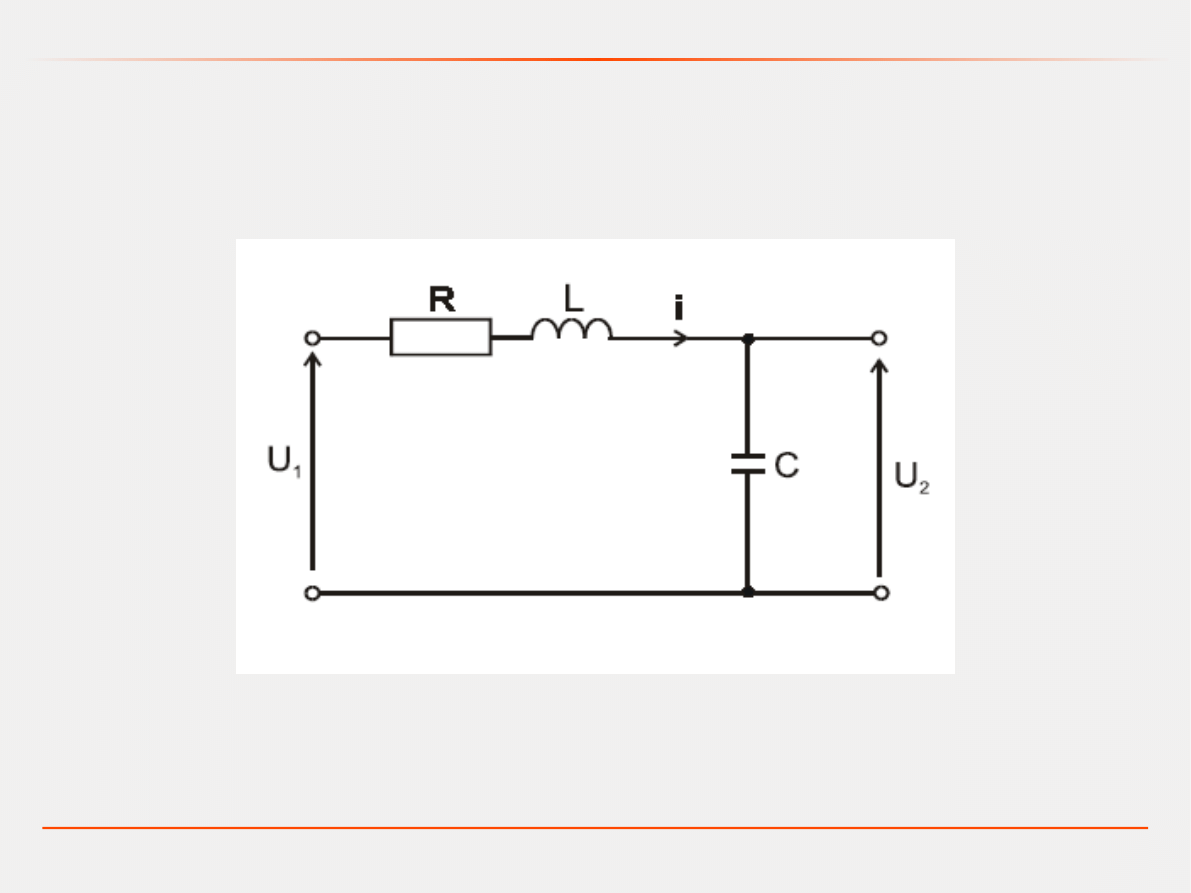
Model dynamiczny

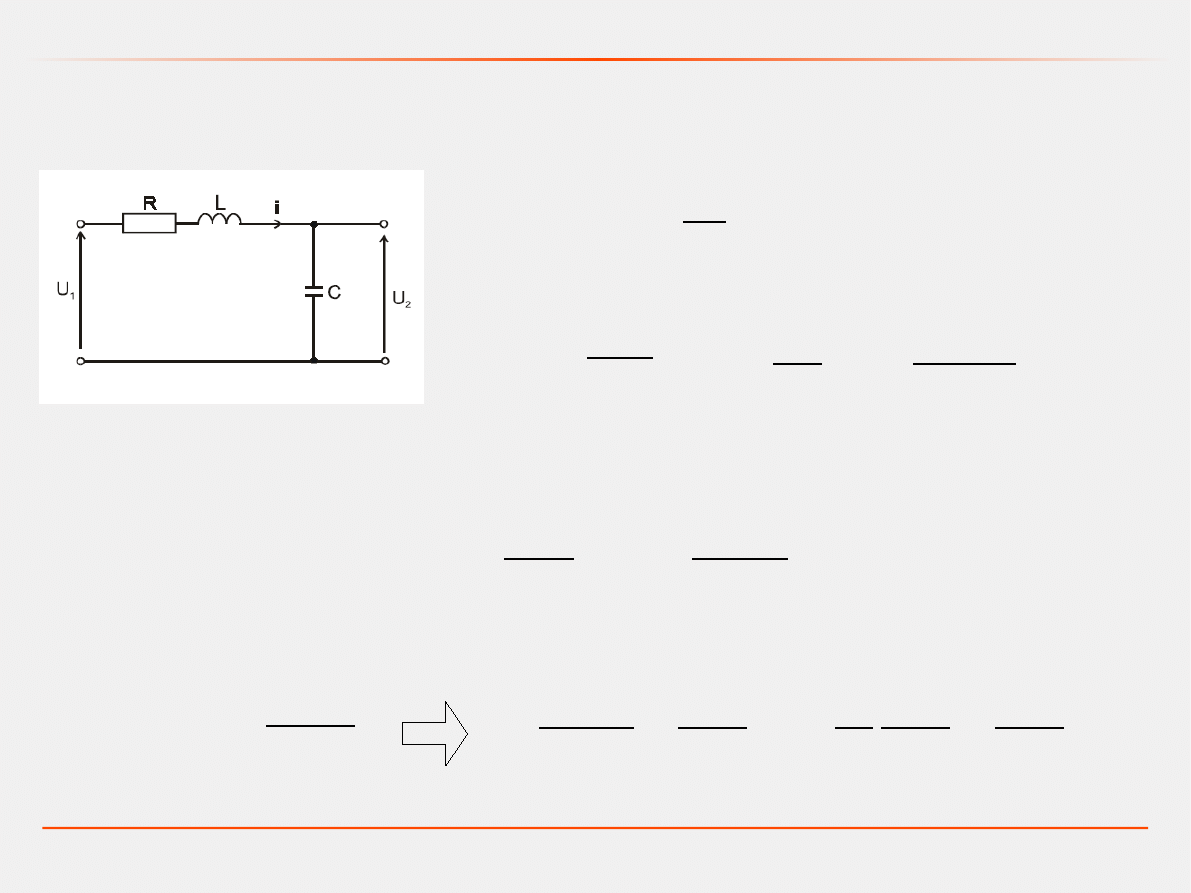
Przykład. Obwód elektryczny RLC

Poszukujemy modelu w przestrzeni stanów i transmitancji.

24

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

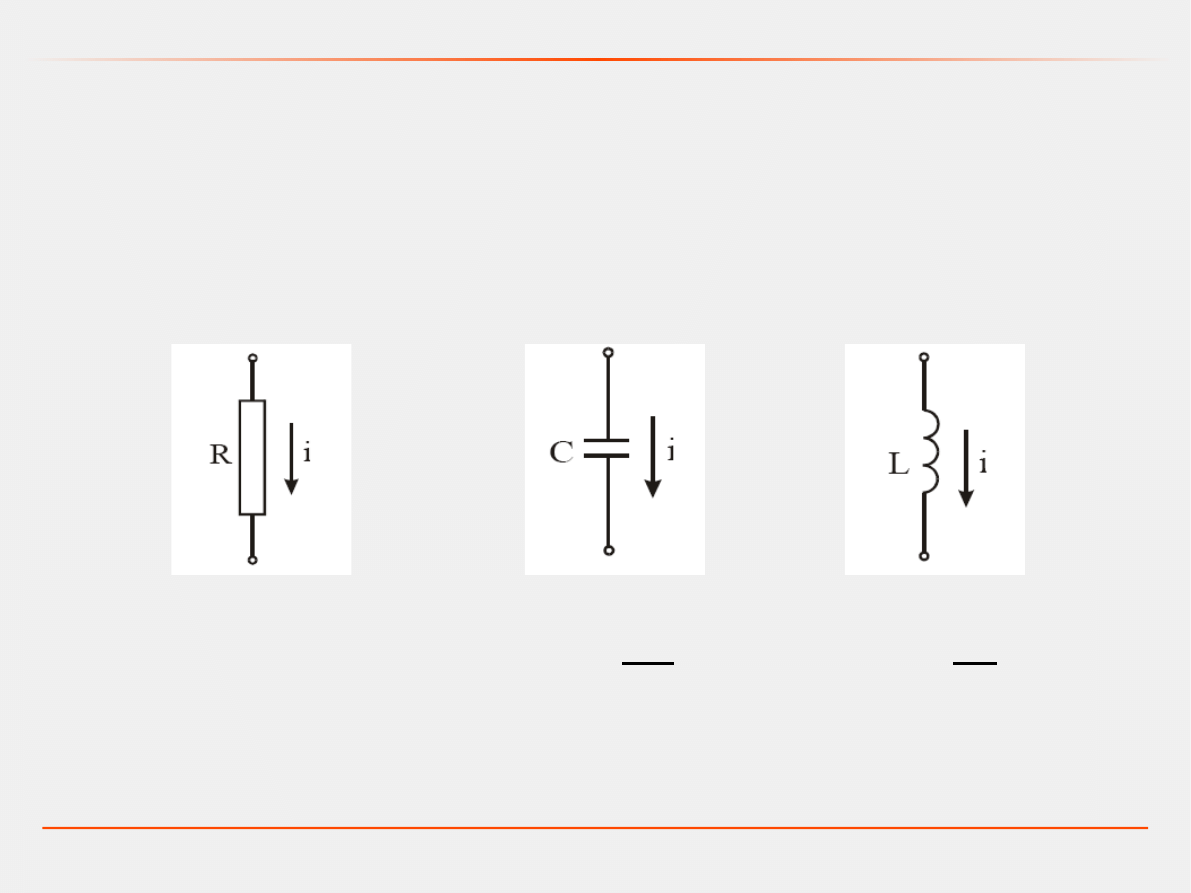
Model dynamiczny

Modele obwodów elektrycznych budujemy w oparciu o

prawo Ohma i prawa Kirchhoffa.

Rezystor

Pojemność

Indukcyjność

u

=R⋅i

i

=C

du

dt

u

=L

di

dt

25

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny

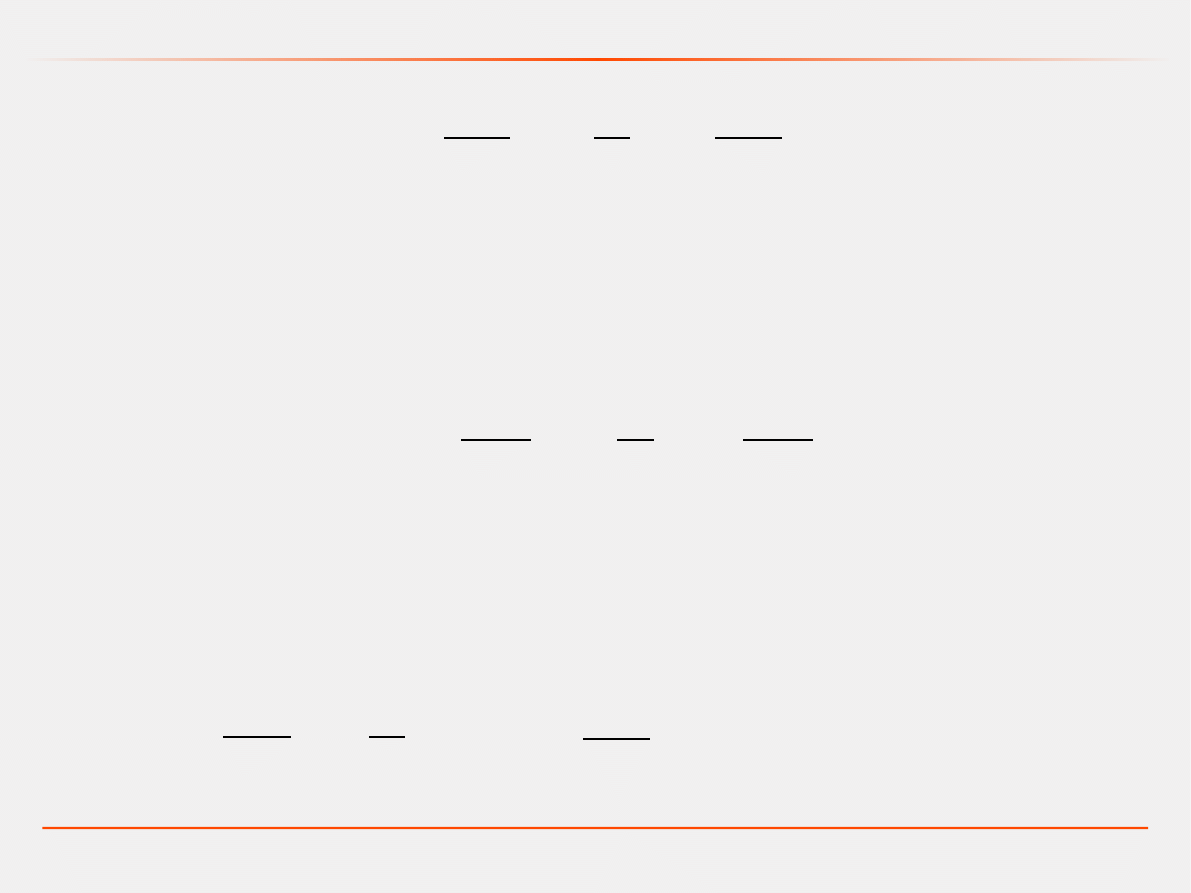
Stosujemy II prawo Kirchhoffa.

u

1

=RiL

di
dt

u

2

i

=C

du

2

dt

di

dt

=C

d

2

u

2

dt

2

u

1

=RC

du

2

dt

L C

d

2

u

2

dt

2

u

2

d

2

u

2

dt

2

=

1

LC

u

1

−

R

L

du

2

dt

−

1

LC

u

2

po podstawieniu otrzymujemy:

Obliczamy

d

2

u

2

dt

2

26

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny

¨u

2

=

1

LC

u

1

−

R

L ˙

u

2

−

1

LC

u

2

{

˙x

1

=x

2

˙x

2

=

1

LC

u

1

−

R
L

x

2

−

1

LC

x

1

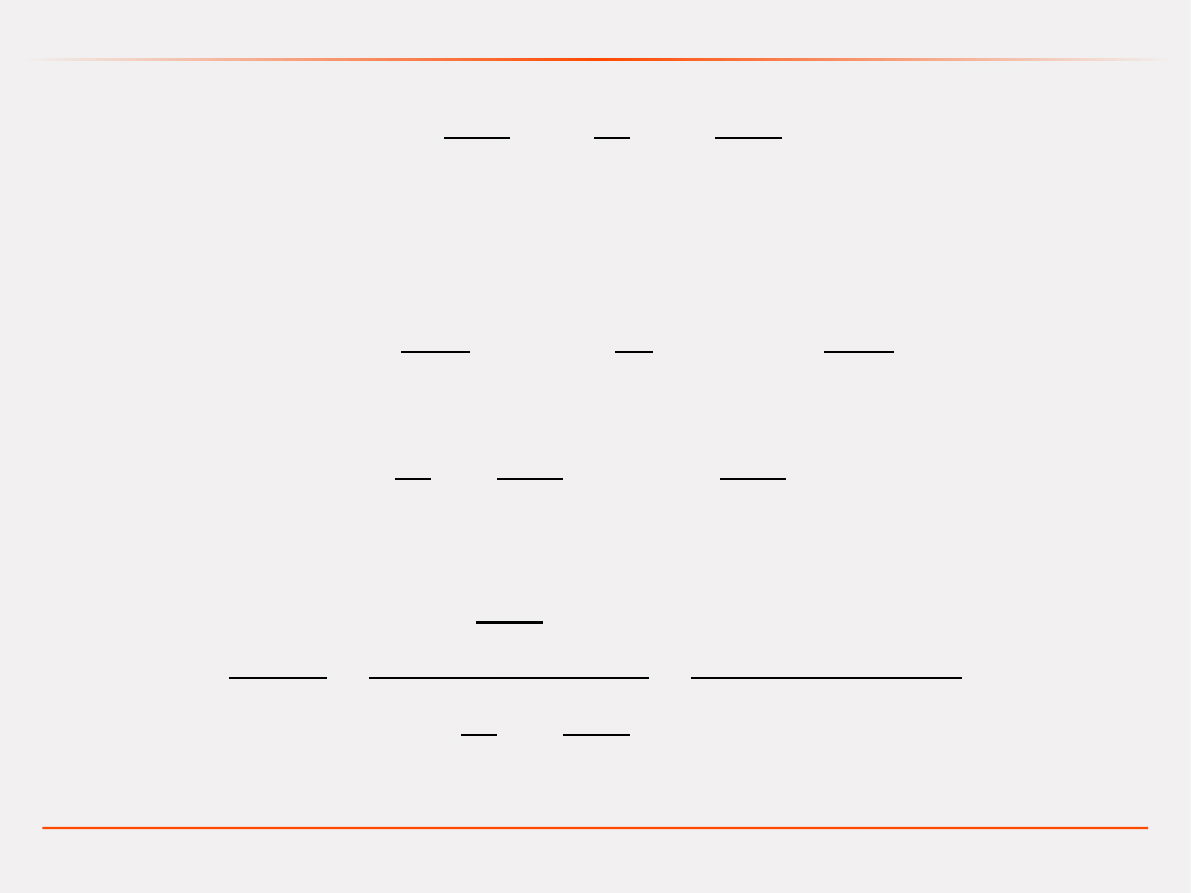
Równanie II rzędu zapisujemy w postaci układu równań

różniczkowych I rzędu:

Równanie stanu i równanie wyjścia:



˙x

1

˙x

2



=



0

1

−

1

LC

−

R

L



⋅



x

1

x

2







0
1

LC



⋅u

1

y

=



1 0



⋅



x

1

x

2



27

MODELOWANIE I SYMULACJA

Szczecin - 2006-06-01

Model dynamiczny

Transmitancja operatorowa:

s

2

u

2

s=

1

LC

u

1

s−

R

L

s u

2

s−

1

LC

u

2

s

s

2



R

L

s



1

LC

u

2

s=

1

LC

u

1

s

u

2

s

u

1

s

=

1

LC

s

2



R

L

s



1

LC



=

1

LCs

2

RCs1

¨u

2

=

1

LC

u

1

−

R

L ˙

u

2

−

1

LC

u

2